A Combinatorial Grassmannian Representation of the Magic Three-Qubit Veldkamp Line

Abstract

It is demonstrated that the magic three-qubit Veldkamp line occurs naturally within the Veldkamp space of a combinatorial Grassmannian of type $G_2\left(7\right)$, $\mathcal{V}\left(G_2\left(7\right)\right)$. The lines of the ambient symplectic polar space are those lines of $\mathcal{V}\left(G_2\left(7\right)\right)$ whose cores feature an odd number of points of $G_2\left(7\right)$. After introducing the basic properties of three different types of points and seven distinct types of lines of $\mathcal{V}\left(G_2\left(7\right)\right)$, we explicitly show the combinatorial Grassmannian composition of the magic Veldkamp line; we first give representatives of points and lines of its core generalized quadrangle GQ$(2,2)$, and then additional points and lines of a specific elliptic quadric ${\mathcal{Q}}^{-}$(5, 2), a hyperbolic quadric ${\mathcal{Q}}^{+}$(5, 2), and a quadratic cone $\widehat{\mathcal{Q}}$(4, 2) that are centered on the GQ$(2,2)$. In particular, each point of ${\mathcal{Q}}^{+}$(5, 2) is represented by a Pasch configuration and its complementary line, the (Schläfli) double-six of points in ${\mathcal{Q}}^{-}$(5, 2) comprise six Cayley–Salmon configurations and six Desargues configurations with their complementary points, and the remaining Cayley–Salmon configuration stands for the vertex of $\widehat{\mathcal{Q}}$(4, 2).

1. Introduction

One of the most startling results of the finite-geometric approach to the field of quantum information and the so-called black-hole/qubit correspondence is undoubtedly the recent discovery [1,2] of the existence of a magic Veldkamp line associated with the five-dimensional binary symplectic polar space $\mathcal{W}(5,2)$ (the finite-geometrical concepts, symbols, and notation are explained in the next section) underlying the geometry of the three-qubit Pauli group. There are as many as five different types of Veldkamp lines in $\mathcal{W}(5,2)$ [3] (see also [4] for a detailed discussion of the Veldkamp space of $\mathcal{W}(3,2)$). The one we are interested in features an elliptic quadric, a hyperbolic quadric, and a quadratic cone over a parabolic quadric $\mathcal{Q}(4,2)$, the three objects having the latter quadric in common and no other pairwise intersection. The three basic constituents of this line (also illustrated graphically in Figure 1) host a number of extensions of generalized quadrangles, with lines of size three isomorphic to affine polar spaces of rank three and order two, each having distinguished physical interpretation and in their totality offering a remarkable unifying framework for form theories of gravity and black hole entropy. The main reason why this particular Veldkamp line is referred to as “magic” is the fact that it features a remarkable 20-point extension of the generalized quadrangle of type GQ$(2,1)$ that hosts 12 particularly interwoven copies of a so-called magic Mermin pentagram; i. e., of a specific set of ten three-qubit observables arranged in quadruples of pairwise commuting ones into five edges of a pentagram that provides one of the simplest (three-qubit) observable proofs of quantum contextuality [5]. Moreover, even a GQ$(2,1)$ itself, when viewed as embedded into $\mathcal{W}(3,2)$ and with a two-qubit labeling of its points inherited from the latter polar space, furnishes an analogous contextuality proof, usually referred to as a magic Mermin square [5]. The purpose of this paper is to show that this magic line also has a remarkable representation in the Veldkamp space of a combinatorial Grassmannian of type $G_2\left(7\right)$.

2. Relevant Finite-Geometrical Background

To this end, we first give an overview of relevant finite geometry. We start with a finite point-line incidence structure $\mathcal{C}=(\mathcal{P},\mathcal{L},I)$ where $\mathcal{P}$ and $\mathcal{L}$ are, respectively, finite sets of points and lines and where incidence $I\subseteq \mathcal{P}\times \mathcal{L}$ is a binary relation indicating which point–line pairs are incident (e. g., [6]). Here, we shall only be concerned with specific point–line incidence structures called configurations [7]. A $(v_r,b_k)$-configuration is a $\mathcal{C}$ where: (1) $v=\left|\mathcal{P}\right|$ and $b=\left|\mathcal{L}\right|$; (2) every line has k points and every point is on r lines; and 3) two distinct lines intersect in at most one point and every two distinct points are joined by at most one line; a configuration where $v=b$ and $r=k$ is called symmetric (or balanced), and usually denoted as a $\left(v_r\right)$-configuration. A $(v_r,b_k)$-configuration with $v=\left(\genfrac{}{}{0pt}{}{r+k-1}{r}\right)$ and $b=\left(\genfrac{}{}{0pt}{}{r+k-1}{k}\right)$ is called a $binomial$ configuration. Next, a geometric hyperplane of $\mathcal{C}=(\mathcal{P},\mathcal{L},I)$ is a proper subset of $\mathcal{P}$ such that a line from $\mathcal{C}$ either lies fully in the subset, or shares only one point with it. If $\mathcal{C}$ possesses geometric hyperplanes, then one can define the Veldkamp space of $\mathcal{C}$, $\mathcal{V}\left(\mathcal{C}\right)$, as follows [8]: (i) a point of $\mathcal{V}\left(\mathcal{C}\right)$ is a geometric hyperplane of $\mathcal{C}$; and (ii) a line of $\mathcal{V}\left(\mathcal{C}\right)$ is the collection $H^{\prime }{H}^{″}$ of all geometric hyperplanes H of $\mathcal{C}$ such that $H^{\prime }\cap H^{″}=H^{\prime }\cap H=H^{″}\cap H$ or $H=H^{\prime },H^{″}$, where $H^{\prime }$ and $H^{″}$ are distinct geometric hyperplanes. The set $H^{\prime }\cap H^{″}$ is sometimes called the core. If each line of $\mathcal{C}$ has three points, a line of $\mathcal{V}\left(\mathcal{C}\right)$ is also of size three and of the form $\{H^{\prime },H^{″},\overline{H^{\prime }\Delta H^{″}}\}$, where the symbol $\Delta$ stands for the symmetric difference of the two geometric hyperplanes and an overbar denotes the complement of the object indicated. Our central concept is that of a combinatorial Grassmannian (e. g., [9,10]) $G_k\left(\right|X\left|\right)$, where k is a positive integer and X is a finite set, which is a point–line incidence structure whose points are k-element subsets of X and whose lines are $(k+1)$-element subsets of X, incidence being inclusion. It is known [9] that if $\left|X\right|=N$ and $k=2$, $G_2\left(N\right)$ is a binomial $\left({\left(\genfrac{}{}{0pt}{}{N}{2}\right)}_{N-2},{\left(\genfrac{}{}{0pt}{}{N}{3}\right)}_3\right)$-configuration; in particular, $G_2\left(3\right)$ is a single line, $G_2\left(4\right)$ is the Pasch $(6_2,4_3)$-configuration, $G_2\left(5\right)$ is the Desargues $\left({10}_3\right)$-configuration, and $G_2\left(6\right)$ is the Cayley–Salmon $({15}_4,{20}_3)$-configuration [11].

A (finite-dimensional) classical polar space (see, for example, [12,13]) describes the geometry of a d-dimensional vector space over the Galois field GF$\left(q\right)$, $V(d,q)$, carrying a non-degenerate reflexive sesquilinear form $\sigma (x,y)$. The polar space is called symplectic, and is usually denoted as $\mathcal{W}(d-1,q)$, if this form is bilinear and alternating; i.e., if $\sigma (x,x)=0$ for all $x\in V(d,q)$. Such a space exists only if $d=2N$, where $N\ge 2$ is called its rank. A subspace of $V(d,q)$ is called totally isotropic if $\sigma$ vanishes identically on it. $\mathcal{W}(2N-1,q)$ can then be regarded as the space of totally isotropic subspaces of the ambient space PG$(2N-1,q)$, the ordinary $(2N-1)$-dimensional projective space over GF$\left(q\right)$, with respect to a symplectic form (also known as a null polarity). A quadric in PG$(d,q)$, $d\ge 1$, is the set of points whose coordinates satisfy an equation of the form ${\sum }_{i,j=1}^{d+1}{a}_{ij}{x}_i{x}_j=0$, where at least one $a_{ij}\ne 0$. Up to transformations of coordinates, there is one or two distinct kinds of non-singular quadrics in PG$(d,q)$ according as d is even or odd, namely [12]: $\mathcal{Q}(2N,q)$, the parabolic quadric formed by all points of PG$(2N,q)$ satisfying the standard equation $x_1{x}_2+\cdots +x_{2N-1}{x}_{2N}+x_{2N+1}^2=0$; ${\mathcal{Q}}^{-}(2N-1,q)$, the elliptic quadric formed by all points of PG$(2N-1,q)$ satisfying the standard equation $f(x_1,x_2)+x_3{x}_4+\cdots +x_{2N-1}{x}_{2N}=0$, where f is irreducible over GF$\left(q\right)$; and ${\mathcal{Q}}^{+}(2N-1,q)$, the hyperbolic quadric formed by all points of PG$(2N-1,q)$ satisfying the standard equation $x_1{x}_2+x_3{x}_4+\cdots +x_{2N-1}{x}_{2N}=0$, where $N\ge 1$. The number of points lying on quadrics is as follows [12]: ${\left|Q(2N,q)\right|}_p=(q^{2N}-1)/(q-1)$, $|Q^{-}{(2N-1,q)|}_p=(q^{N-1}-1)(q^N+1)/(q-1)$, $|Q^{+}{(2N-1,q)|}_p=(q^{N-1}+1)(q^N-1)/(q-1)$. Given the hyperbolic quadric ${\mathcal{Q}}^{+}(2N-1,q)$ of PG$(2N-1,q)$, $N\ge 2$, a set S of points such that each line joining two distinct points of S has no point in common with ${\mathcal{Q}}^{+}(2N-1,q)$ is called an exterior set of the quadric. It is known that $\left|S\right|\le (q^N-1)/(q-1)$; if $\left|S\right|=(q^N-1)/(q-1)$, then S is called a maximal exterior set. Interestingly [14], ${\mathcal{Q}}^{+}(5,2)$ has, up to isomorphism, a unique such set — also known, after its discoverer, as a Conwell hetpad [15].

Finally, one has to introduce a finite generalized quadrangle of order $(s,t)$, usually denoted GQ($s,t$), which is a $\mathcal{C}$ satisfying the following axioms [16]: (i) each point is incident with $1+t$ lines ($t\ge 1$) and two distinct points are incident with at most one line; (ii) each line is incident with $1+s$ points ($s\ge 1$) and two distinct lines are incident with at most one point; and (iii) if x is a point and L is a line not incident with x, then there exists a unique line through x that is incident with L; from these axioms, it readily follows that $\left|\mathcal{P}\right|=(s+1)(st+1)$ and $\left|\mathcal{L}\right|=(t+1)(st+1)$. In what follows, we shall only be concerned with its two particular types: GQ$(2,2)\cong \mathcal{Q}(4,2)\cong \mathcal{W}(3,2)$ and GQ$(2,4)\cong {\mathcal{Q}}^{-}(5,2)$.

3. Veldkamp Space of ${\mathit{G}}_{\mathbf{2}}\mathbf{\left(}\mathbf{7}\mathbf{\right)}$

The Veldkamp space of $G_2\left(7\right)$, $\mathcal{V}\left(G_2\left(7\right)\right)$ is isomorphic to PG$(5,2)$. Its detailed computer-aided analysis was carried out in [11], from which we highlight its basic properties. Let us take $X=\{1,2,3,4,5,6,7\}$ and assume that $a,b,c,d,e,f,$ and g—all different—belong to X. The 63 points of $\mathcal{V}\left(G_2\left(7\right)\right)$ are of three different types, as shown in

Table 1. The three different types of points of $\mathcal{V}\left(G_2\left(7\right)\right)$.

Type	Form	Geometrical Constituents	Number
$\alpha$	$abcd$:$efg$	Pasch configuration and its complementary line	35
$\beta$	$abcde$:$fg$	Desargues configuration and its complementary point	21
$\gamma$	$abcdef$:g	Cayley–Salmon configuration	7

, whereas its 651 lines fall into seven distinct orbits, whose properties are given in

Table 2. The seven different types of lines of $\mathcal{V}\left(G_2\left(7\right)\right)$.

Type	Form	Core Composition	Number
	$abcd$:$efg$
$(\alpha ,\alpha ,\alpha )$	$abef$:$cdg$	three mutually non-collinear points ($ab$, $cd$, and $ef$)	105
	$cdef$:$abg$
	$abcd$:$efg$
$(\alpha ,\alpha ,\beta )$	$abce$:$dfg$	a line ($abc$) and a point ($fg$)	210
	$abcfg$:$de$
	$abc$:$defg$
$(\alpha ,\alpha ,\gamma )$	$def$:$abcg$	two disjoint lines ($abc$ and $def$)	70
	$abcdef$:g
	$abcd$:$efg$
$(\alpha ,\beta ,\beta )$	$ab$:$cdefg$	a line ($efg$) and two non-collinear points ($ab$ and $cd$)	105
	$cd$:$abefg$
	$abcd$:$efg$
$(\alpha ,\beta ,\gamma )$	$abcde$:$fg$	a Pasch configuration ($abcd$) and a point ($fg$)	105
	$abcdfg$:e
	$abcde$:$fg$
$(\beta ,\beta ,\beta )$	$abcdf$:$eg$	a Pasch configuration ($abcd$)	35
	$abcdg$:$ef$
	$abcde$:$fg$
$(\beta ,\gamma ,\gamma )$	$abcdef$:g	a Desargues configuration ($abcde$)	21
	$abcdeg$:f

; here, for example, $abcd$:$efg$ indicates both a particular partition of X into two complementary sets (i. e., $\{a,b,c,d\}$ and $\{e,f,g\}$) and the two combinatorial Grassmannians defined on these sets (i. e., $G_2\left(4\right)$ and $G_2\left(3\right)$). We briefly note that every point of $\mathcal{V}\left(G_2\left(7\right)\right)$ is a pair of complementary Grassmannians, and that there are no lines of type $(\alpha ,\gamma ,\gamma )$, $(\beta ,\beta ,\gamma )$ and $(\gamma ,\gamma ,\gamma )$.

In $\mathcal{V}\left(G_2\left(7\right)\right)$, there exists a distinguished symplectic polar space $\overline{\mathcal{W}}$(5, 2) whose lines comprise three orbits of lines of type $(\alpha ,\alpha ,\alpha )$, $(\alpha ,\beta ,\beta )$, and $(\alpha ,\beta ,\gamma )$—that is, the orbits whose cores feature an odd number of points of $G_2\left(7\right)$. Other prominent geometrical objects of $\mathcal{V}\left(G_2\left(7\right)\right)$ are: a hyperbolic quadric ${\mathcal{Q}}_0^{+}$(5, 2) ∈$\overline{\mathcal{W}}$(5, 2) formed by 35 points of type $\alpha$ and 105 lines of type $(\alpha ,\alpha ,\alpha )$; a combinatorial Grassmannian $G_2\left(7\right)$ formed by 21 points of type $\beta$ and 35 lines of type $(\beta ,\beta ,\beta )$; and a Conwell heptad with respect to the above-defined ${\mathcal{Q}}_0^{+}$(5, 2) represented by seven points of type $\gamma$ (see also [17]).

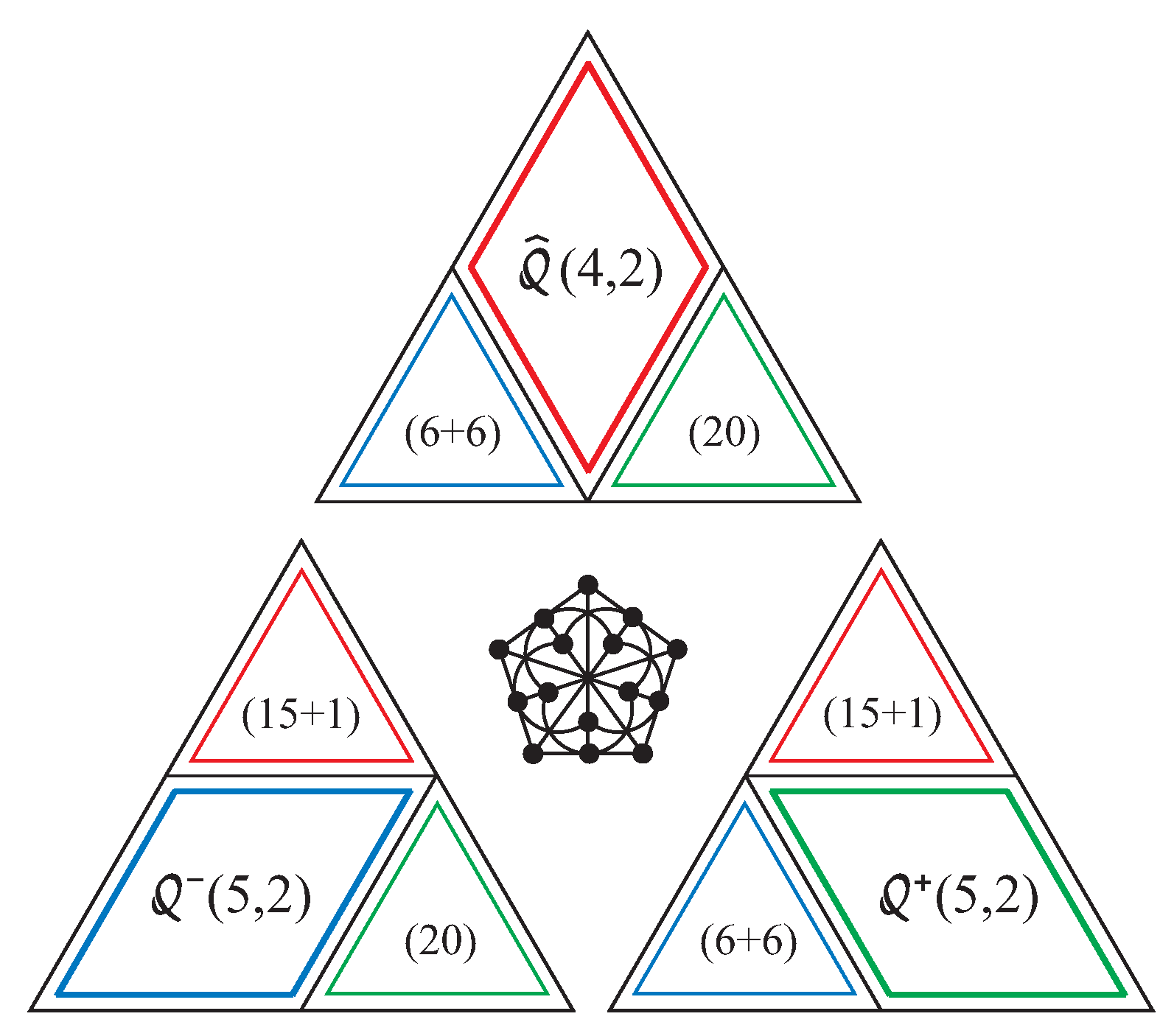
4. Magic Three-Qubit Veldkamp Line in $\mathcal{V}\mathbf{\left(}{\mathit{G}}_{\mathbf{2}}\mathbf{\left(}\mathbf{7}\mathbf{\right)}\mathbf{\right)}$

There are seven distinguished magic Veldkamp lines living in $\overline{\mathcal{W}}$(5, 2), one per each element of X. A representative of them—also depicted in Figure 2—is structured as follows:

• Core GQ(2, 2): Its 15 points are represented by those $\alpha$-points that share one digit in the second set; that is, by points whose representatives are $abcd$:$ef7$ if the common digit is “7”; its 15 lines are those of type $(\alpha ,\alpha ,\alpha )$ of the following particular form

  $$\begin{array}{c}abcd:ef7,\\ abef:cd7,\\ cdef:ab7.\end{array}$$
• ${\mathcal{Q}}^{-}$(5, 2) ≅ GQ(2, 4): The 12 additional points (the double-six) are represented by six $\beta$-points of the form $abcde$:$f7$ and six $\gamma$-points of the form $abcde7$:f; the 30 additional lines lie in the $(\alpha ,\beta ,\gamma )$-orbit, being of the (complementary) form

  $$\begin{array}{c}abcd:ef7,abcd:ef7,\\ abcdf:e7,abcde:f7,\\ abcde7:f,abcdf7:e.\end{array}$$
• ${\mathcal{Q}}^{+}$(5, 2) ≡${\mathcal{Q}}_0^{+}$(5, 2): The 20 additional points are represented by $\alpha$-points of the form $abc7$:$def$; the 90 additional lines, belonging to the $(\alpha ,\alpha ,\alpha )$-orbit, read

  $$\begin{array}{c}abcd:ef7,abcd:ef7,\\ abe7:cdf,abf7:cde,\\ cde7:abf,cdf7:abe.\end{array}$$
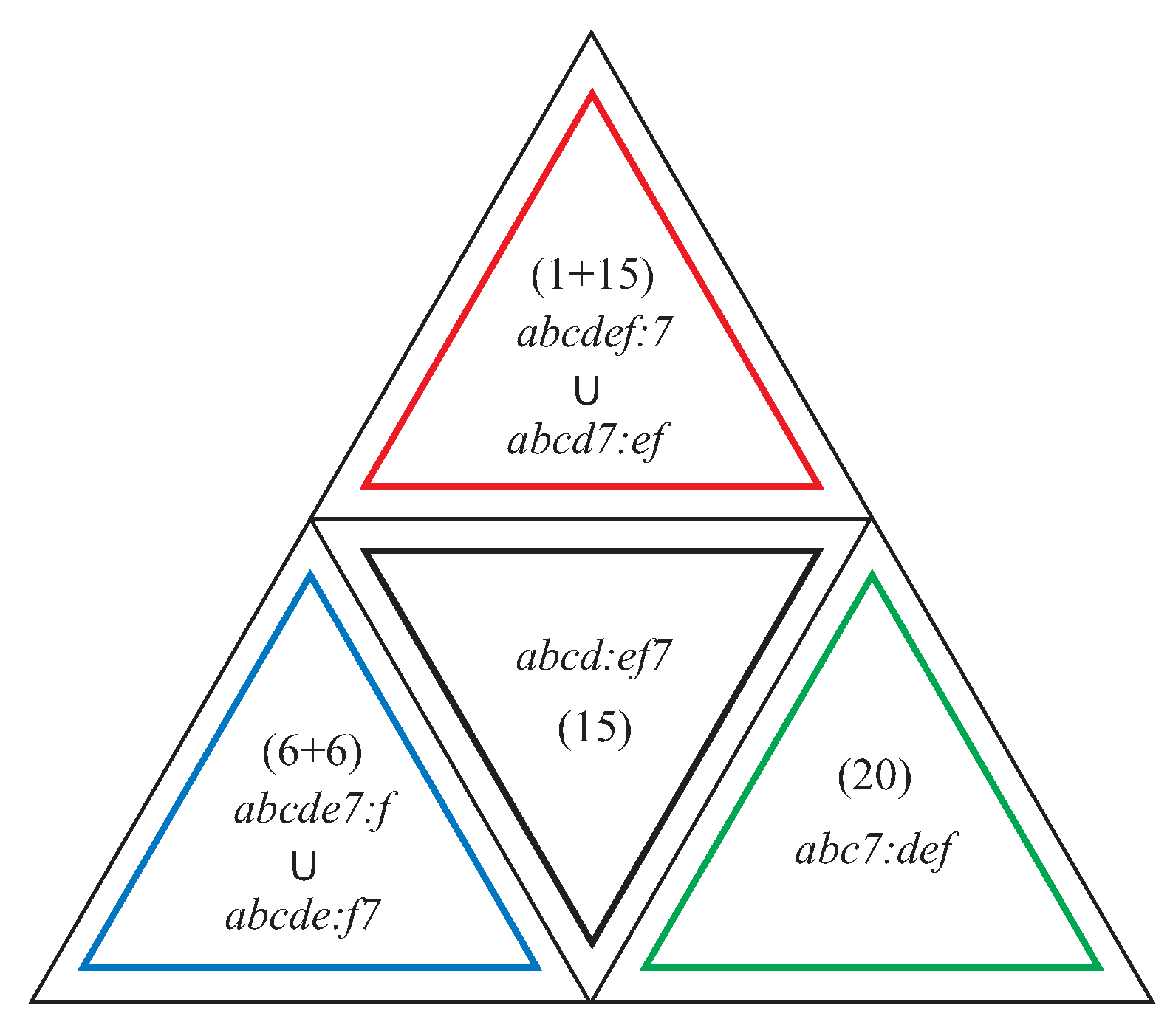
• $\widehat{\mathcal{Q}}$(4, 2): The 16 additional points are represented by 15 $\beta$-points of the form $abcd7$:$ef$ and a single $\gamma$-point $abcdef$:7 (the vertex of the cone); the 15 additional lines are located in the $(\alpha ,\beta ,\gamma )$-orbit, having the form

  $$\begin{array}{c}abcd:ef7,\\ abcd7:ef,\\ abcdef:7.\end{array}$$

5. Conclusions

We have demonstrated that the Veldkamp space $\mathcal{V}\left(G_2\left(7\right)\right)$ provides a rather natural environment for the magic Veldkamp line of three-qubits. Interestingly, $\mathcal{V}\left(G_2\left(7\right)\right)$ was recently found to be also related to finite geometry behind the 64-dimensional real Cayley–Dickson algebra [11]. Hence, our findings seem to indicate that the nature of magic Veldkamp line may well have something to do with this particular algebra. It has to be made clear that at this stage we cannot offer any rigorous analytical proof(s) of our findings; in fact, all the results presented above were found by explicit (both computer-aided and by-hand) computations. The main reason why this is so is the fact that the theory of Veldkamp spaces in its generality is still far from being able to handle all physically attractive/relevant geometries, especially when it comes to point–line incidence geometries featuring geometric hyperplanes contained in other geometric hyperplanes, which may be relevant for addressing questions related to quantum non-locality. However, this “lack of rigor” should not be regarded as a drawback, because the main message of the paper is to address a wider—preferably interdisciplinary—audience with a novel mathematical concept that is not only relevant for foundational issues of quantum information theory, but can also have serious bearing on other scientific disciplines (e. g., quantum physical chemistry and/or condensed matter physics). Finally, a curious reader may well ask why we employ the concept of Veldkamp space when one can just look at the universal embedding from which one can obtain all the above results, even without much use of a computer. The reason is rather simple. When a $\mathcal{W}(5,2)$ is viewed as an abstract geometry per se, all its points and lines have, so to speak, the same footing. However, when this polar space occurs as a subgeometry of the Veldkamp space of a certain point–line incidence structure, this is no longer the case, as it shows a refined structure, strongly depending on properties of the point–line incidence structure employed. In our particular case, when the point–line incidence in question is the combinatorial Grassmannian of type $G_2\left(7\right)$, it features (see Section 3) three different kinds of points and the same number of distinct types of lines; but, more importantly, this intrinsic stratification of points/lines of $\mathcal{W}(5,2)$ has just the right combinatorial structure to account for the composition of our magic Veldkamp line. This can be compared to the case of $\mathcal{W}(3,2)$, where the use of the notion of Veldkamp space [4] enabled us to reveal straightforwardly that all three distinguished kinds of sets of two-qubit quantum observables correspond geometrically to nothing but three different types of geometric hyperplanes (aka Veldkamp points) of $\mathcal{W}(3,2)$; or to the case of GQ$(2,4)$, whose Veldkamp points have their physical counterparts in specific truncations of certain black-hole entropy formulas [18].