Maximum Entropy-Copula Method for Hydrological Risk Analysis under Uncertainty: A Case Study on the Loess Plateau, China
Abstract
:1. Introduction
2. Study Area and Dataset
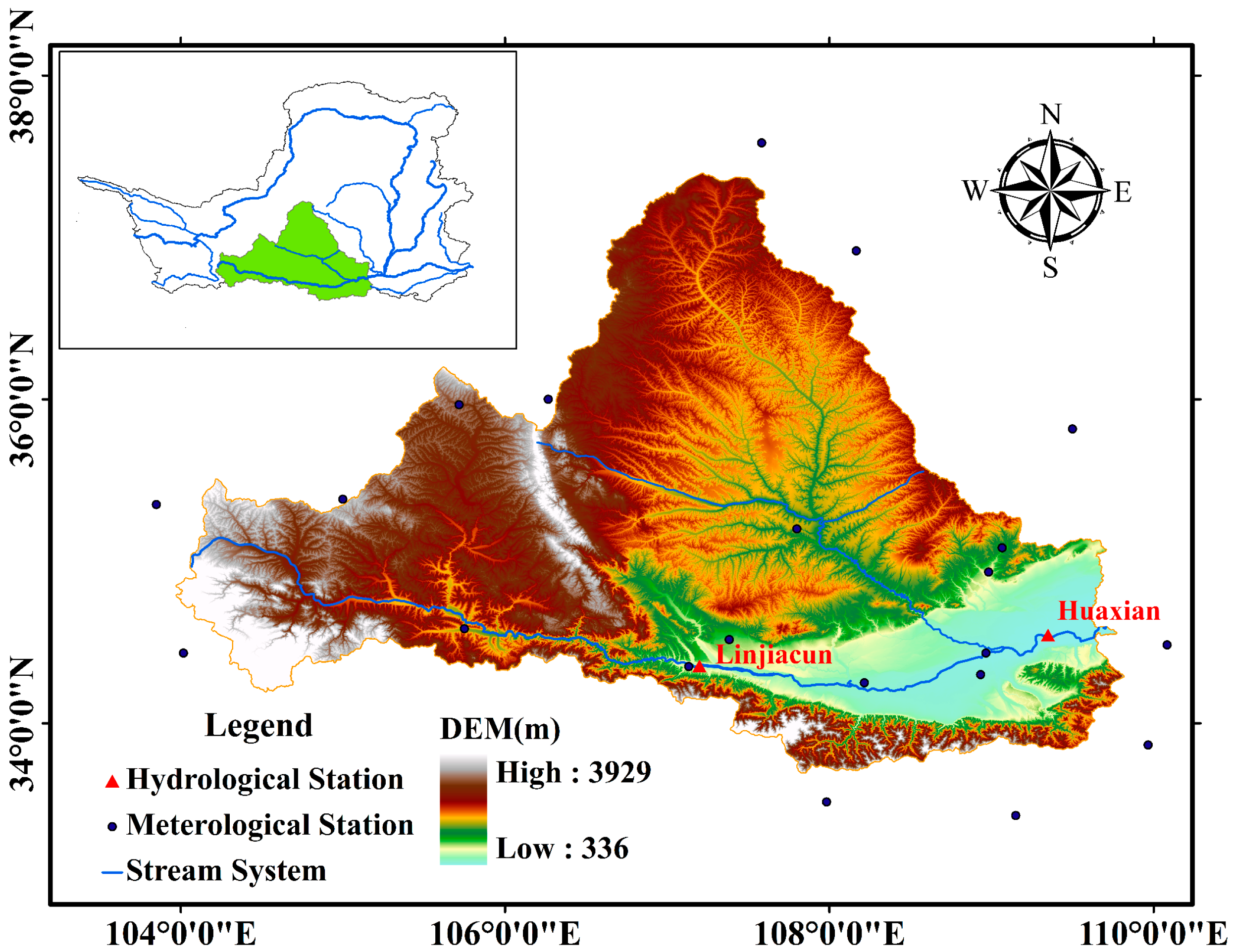
2.1. Study Area
2.2. Dataset
3. Methodologies
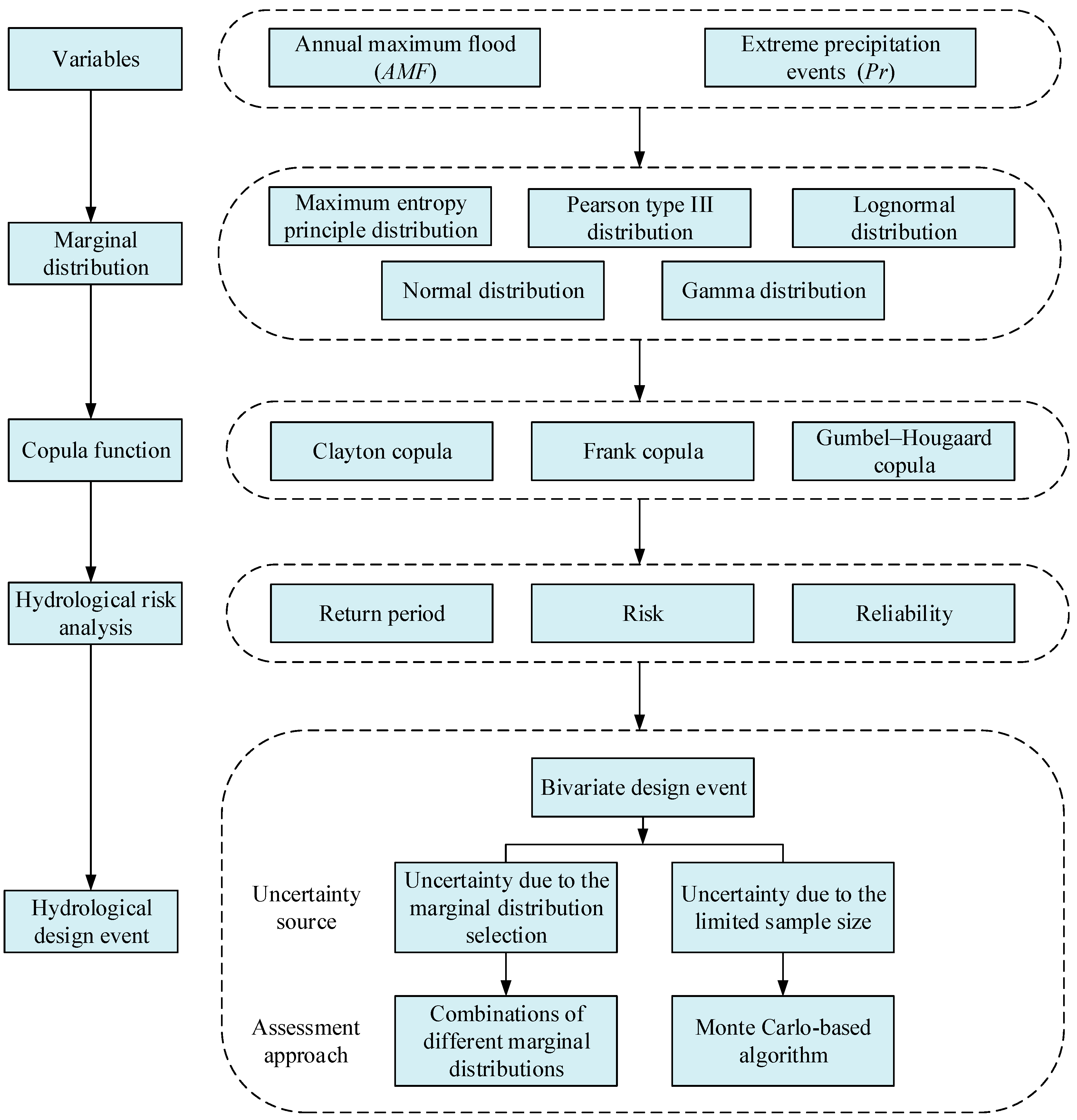
3.1. Methodological Framework
3.2. Maximum Entropy Principle Distribution (MEP)
3.3. Copula Function
3.4. Joint Return Periods, Risk and Reliability
3.5. Bivariate Design Event Derived from Joint Distribution
3.5.1. Uncertainty Due to the Marginal Distribution Selection
3.5.2. Sampling Uncertainty
- Estimate the parameter of the copula for the observations (i.e., X and Y) as well as the parameters and of the marginal distributions for X and Y, respectively;
- Simulate bivariate samples of size on the basis of the copula parameter, and then apply the marginal backward transformations using the estimated parameters and . The simulated bivariate samples are denoted as . n is equal to the length of the observed sample. Here, B is set equal to 10,000;
- Estimate the parameters , and for the simulated sample using the same estimation method used for the observations;
- Identify the most-likely design realization for different pairs.
- Estimate the confidence intervals for at 95% confidence level by the method of highest density regions (denoted as HDR) propose by Hyndman et al. (1996) [63].
4. Results and Discussion
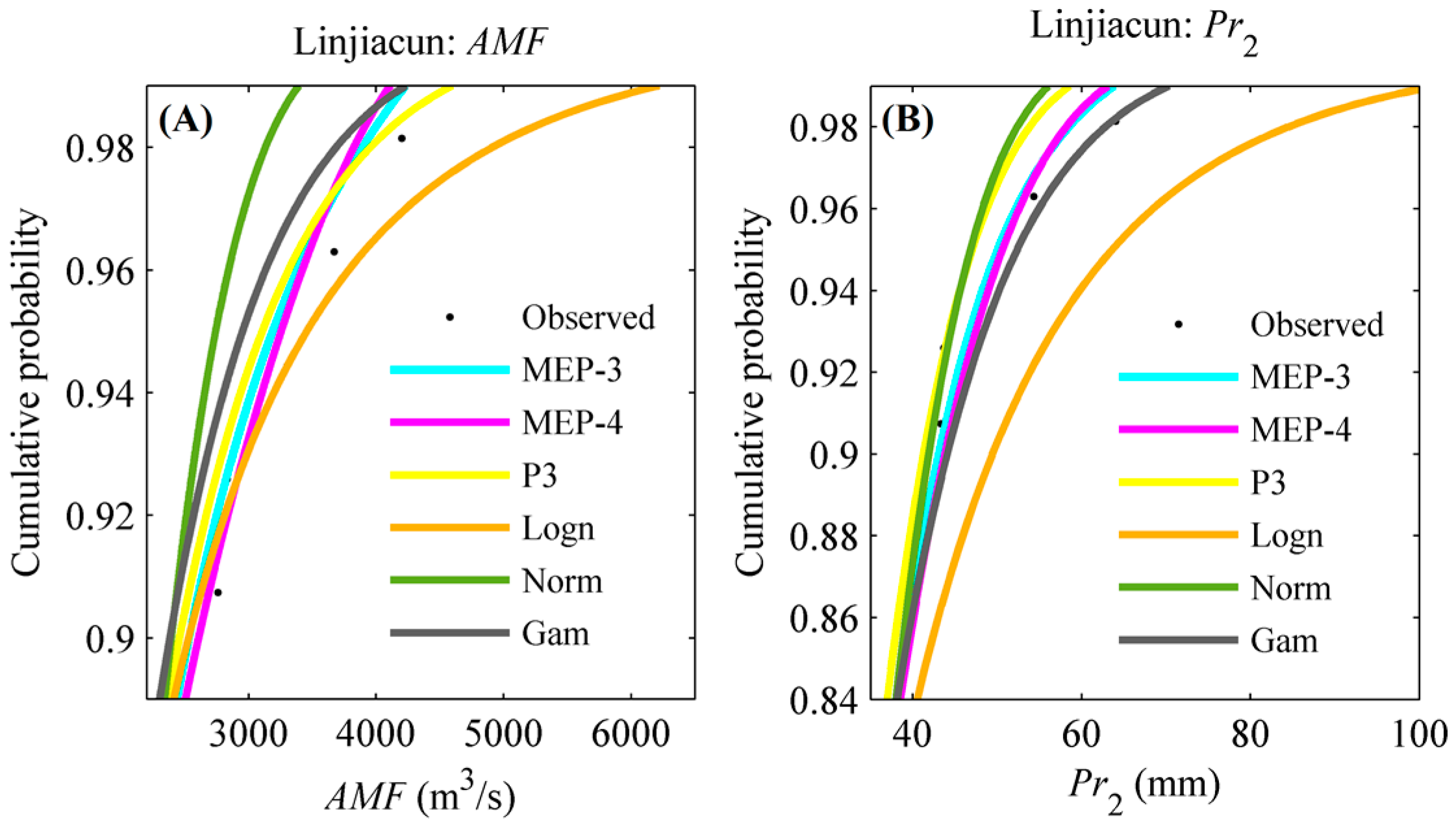
4.1. Marginal Distribution Selection
4.2. Copula Function Construction
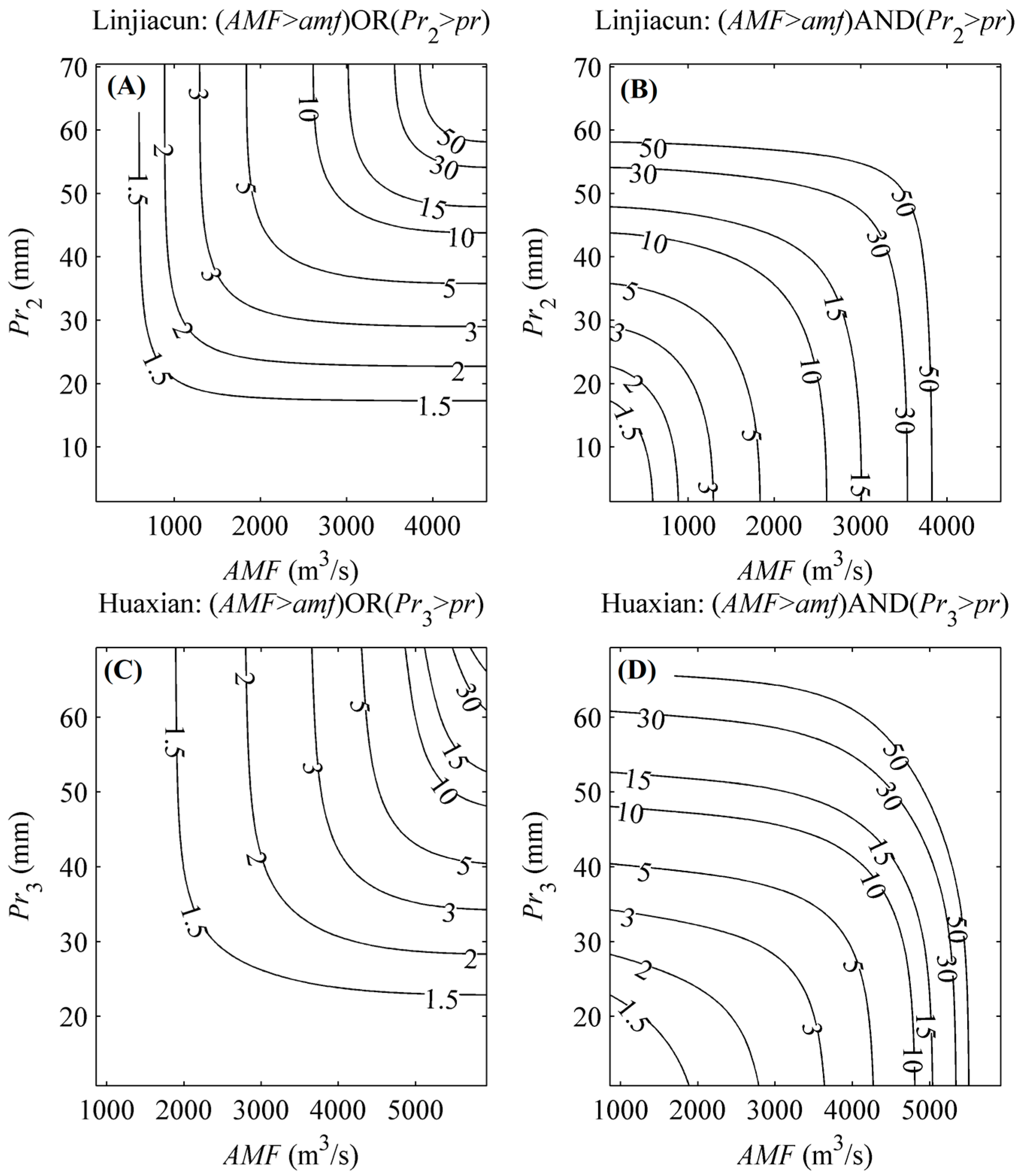
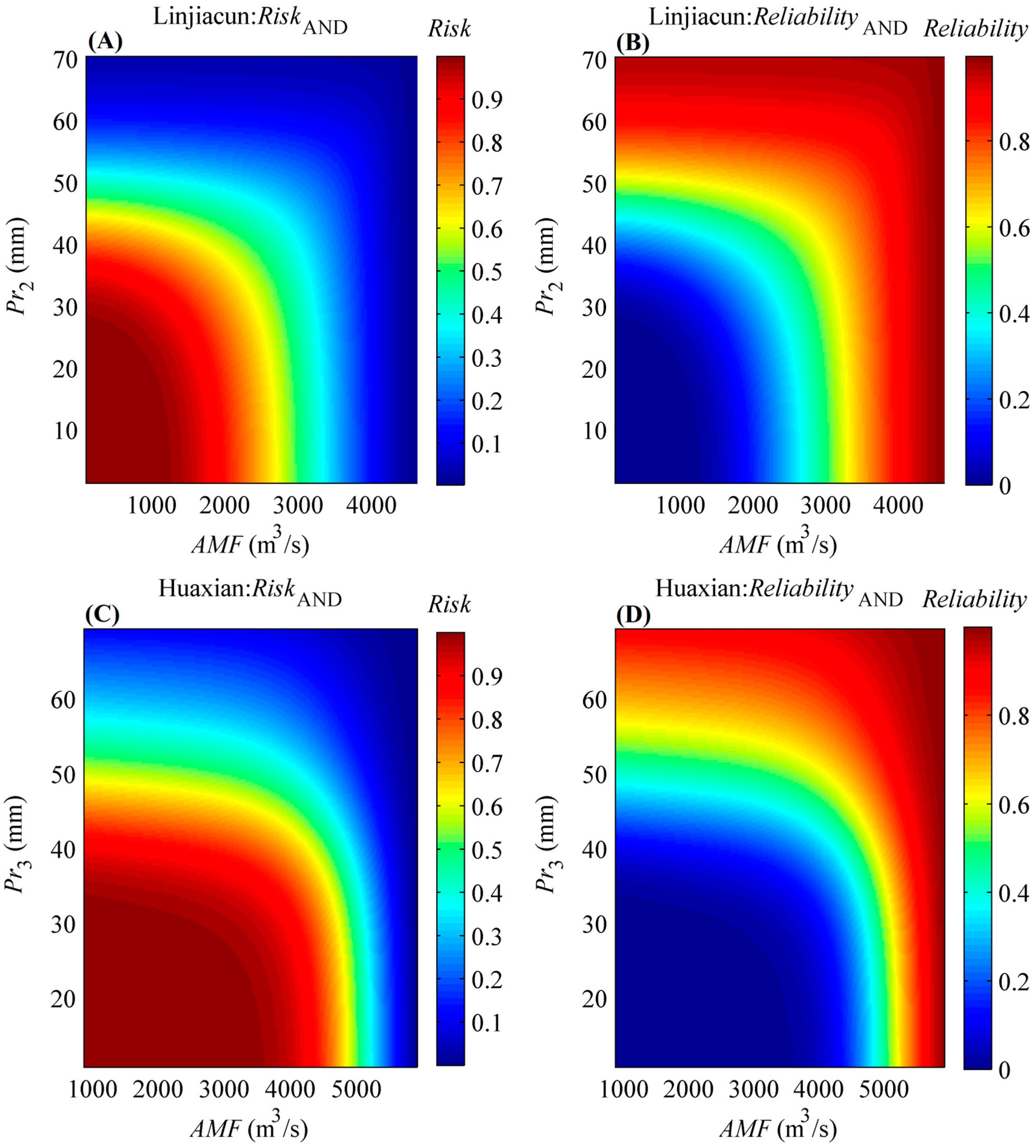
4.3. Bivariate Return Period, Risk and Reliability Analysis Based on the MEP-Copula
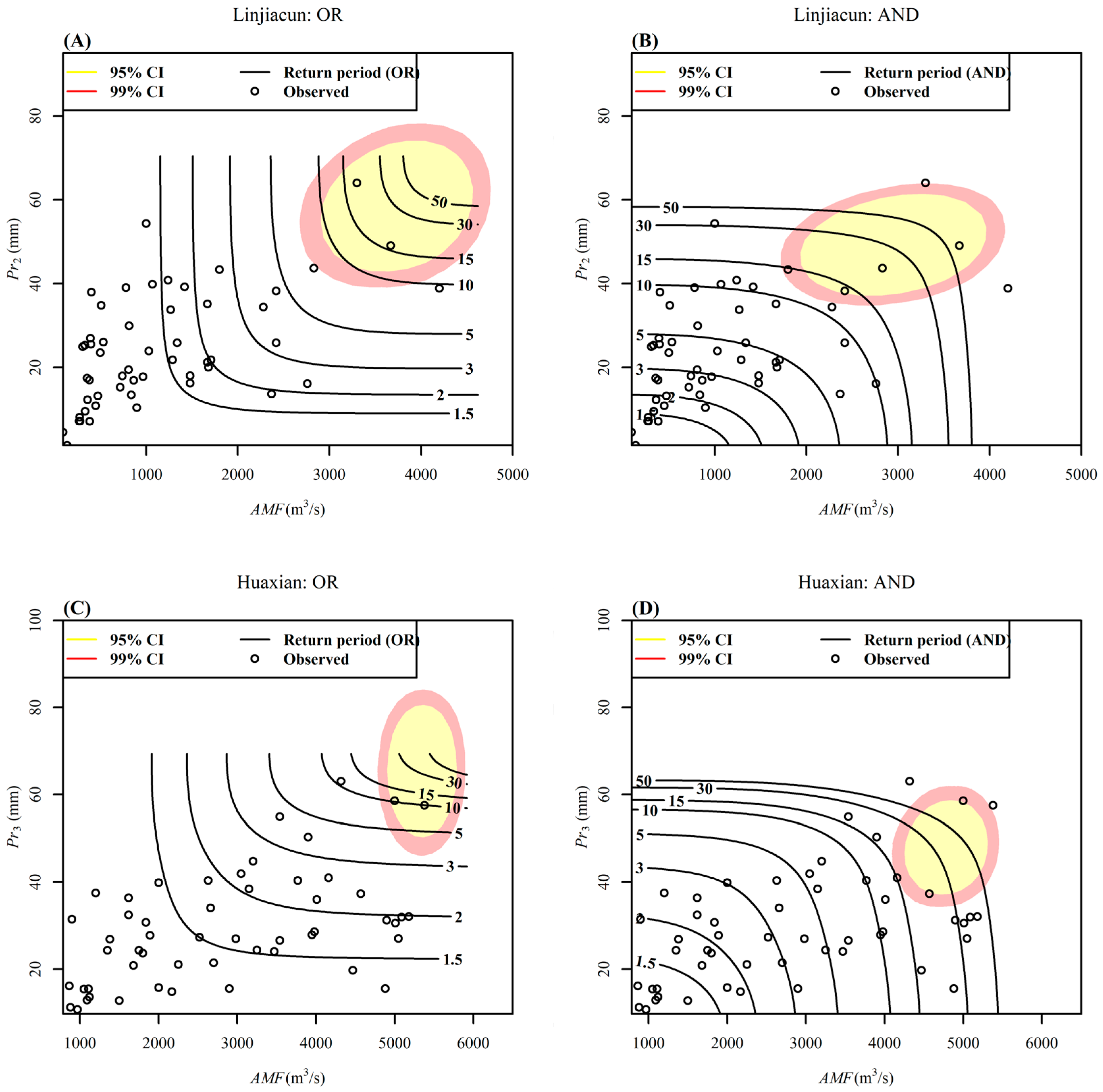
4.4. Bivariate Design Event Identification
4.4.1. Uncertainty Due to Marginal Distribution Selection
4.4.2. Uncertainty Due to the Limited Size of Hydrological Records
5. Summary and Conclusions
- (1)
- The maximum entropy principle (MEP)-based distributions outperform the conventional distributions (i.e., P3, Logn, Norm and Gam at least in this study) in quantifying the probability of flood and extreme precipitation events. Results of this study indicate the better performance of MEP distribution, suggesting that it could be an attractive alternative for quantifying the marginal probability of random variables.
- (2)
- The Gumbel and Frank copulas were suitable dependence models for quantifying the joint probabilities of flood and extreme precipitation events in the upper catchments of Linjiacun and Huaxian stations, respectively.
- (3)
- The bivariate return periods, risk and reliability of flood and extreme precipitation events for the two study regions were calculated based on the coupled maximum entropy-copula models, which were expected to provide practical support for the local flood control and disaster mitigation.
- (4)
- The bivariate design realizations were estimated for the study regions. Comprehensive uncertainty analysis revealed that the fitting performance of univariate distribution is closely related to the bivariate design event identification. If the difference of the fitting performance between two marginal distributions is small, values of the bivariate design events are similar, and vice versa. Therefore, advanced univariate distribution is critical for the bivariate design event selection.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nie, C.; Li, H.; Yang, L.; Wu, S.; Liu, Y.; Liao, Y. Spatial and temporal changes in flooding and the affecting factors in China. Nat. Hazards 2012, 61, 425–439. [Google Scholar] [CrossRef]
- Merz, B.; Nguyen, V.D.; Vorogushyn, S. Temporal clustering of floods in Germany: Do flood-rich and flood-poor periods exist? J. Hydrol. 2016, 541B, 824–883. [Google Scholar] [CrossRef]
- Swierczynski, T.; Ionita, M.; Pino González, D. Using archives of past floods to estimate future flood hazards. EOS Trans. 2017, 98. [Google Scholar] [CrossRef]
- UNISDR. The Human Cost of Weather-Related Disasters 1995–2015. 2015. Available online: http://www.unisdr.org/archive/46793 (accessed on 11 November 2017).
- Svetlana, D.; Radovan, D.; Ján, D. The economic impact of floods and their importance in different regions of the world with emphasis on Europe. Procedia Econ. Financ. 2015, 34, 649–655. [Google Scholar] [CrossRef]
- Fan, Y.R.; Huang, W.W.; Huang, G.H.; Huang, K.; Li, Y.P.; Kong, X.M. Bivariate hydrologic risk analysis based on a coupled entropy-copula method for the Xiangxi river in the three Gorges Reservoir area, China. Theor. Appl. Climatol. 2016, 125, 381–397. [Google Scholar] [CrossRef]
- Li, F.; Zheng, Q. Probabilistic modelling of flood events using the entropy copula. Adv. Water Res. 2016, 97, 233–240. [Google Scholar] [CrossRef]
- Blöschl, G.; Gaál, L.; Hall, J.; Kiss, A.; Komma, J.; Nester, T.; Parajka, J.; Perdigão, R.A.P.; Plavcová, L.; Rogger, M.; et al. Increasing river floods: Fiction or reality? WIREs Water 2015, 2, 329–344. [Google Scholar] [CrossRef] [PubMed]
- Machado, M.J.; Botero, B.A.; López, J.; Francés, F.; Díez-Herrero, A.; Benito, G. Flood frequency analysis of historical flood data under stationary and non-stationary modelling. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 525–568. [Google Scholar] [CrossRef]
- Kiem, A.S.; Verdon-Kidd, D.C. The importance of understanding drivers of hydroclimatic variability for robust flood risk planning in the coastal zone. Australas. J. Water Res. 2013, 17, 126–134. [Google Scholar] [CrossRef]
- Madsen, H.; Lawrence, D.; Lang, M.; Martinkova, M.; Kjeldsen, T.R. Review of trend analysis and climate change projections of extreme precipitation and floods in Europe. J. Hydrol. 2014, 519, 3634–3650. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Wang, L.; Zou, X.; Chen, Y.; Chen, X. Optimal moment determination in POME-copula based hydrometeorological dependence modelling. Adv. Water Res. 2017, 105, 39–50. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate flood frequency analysis using the copula method. J. Hydrol. Eng. 2006, 11, 150–164. [Google Scholar] [CrossRef]
- Karmakar, S.; Simonovic, S.P. Bivariate flood frequency analysis. Part 2: A copula-based approach with mixed marginal distributions. J. Flood Risk Manag. 2009, 2, 32–44. [Google Scholar] [CrossRef]
- Ozga-Zielinski, B.; Ciupak, M.; Adamowski, J.; Khalil, B.; Malard, J. Snow-melt flood frequency analysis by means of copula based 2D probability distributions for the Narew river in Poland. J. Hydrol. Reg. Stud. 2016, 6, 26–51. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S.; Mishra, A.K.; Guo, J. Drought analysis using copulas. J. Hydrol. Eng. 2013, 18, 797–808. [Google Scholar] [CrossRef]
- She, D.; Mishra, A.K.; Xia, J.; Zhang, L.; Zhang, X. Wet and dry spell analysis using copulas. Int. J. Climatol. 2016, 36, 476–491. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Khedun, C.P.; Mishra, A.K.; Singh, V.P.; Giardino, J.R. A copula-based precipitation forecasting model: Investigating the interdecadal modulation of ENSO’s impacts on monthly precipitation. Water Resour. Res. 2014, 50, 580–600. [Google Scholar] [CrossRef]
- Fan, Y.R.; Huang, G.H.; Baetz, B.W.; Li, Y.P.; Huang, K. Development of copula-based particle filter (CopPF) approach for hydrologic data assimilation under consideration of parameter interdependence. Water Resour. Res. 2017, 53, 4850–4875. [Google Scholar] [CrossRef]
- Laux, P.; Vogl, S.; Qiu, W.; Knoche, H.R.; Kunstmann, H. Copula-based statistical refinement of precipitation in RCM simulations over complex terrain. Hydrol. Earth Syst. Sci. 2011, 15, 2401–2419. [Google Scholar] [CrossRef] [Green Version]
- Bobee, B.; Cavidas, G.; Ashkar, F.; Bernier, J.; Rasmussen, P. Towards a systematic approach to comparing distributions used in flood frequency analysis. J. Hydrol. 1993, 142, 121–136. [Google Scholar] [CrossRef]
- Volpi, E.; Fiori, A. Design event selection in bivariate hydrological frequency analysis. Hydrol. Sci. J. 2012, 57, 1506–1515. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate rainfall and runoff analysis using entropy and copula theories. Entropy 2012, 14, 1784–1812. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620. [Google Scholar] [CrossRef]
- AghaKouchak, A. Entropy—Copula in hydrology and climatology. J. Hydrometeorol. 2014, 15, 2176–2189. [Google Scholar] [CrossRef]
- Zhao, N.; Lin, W.T. A copula entropy approach to correlation measurement at the country level. Appl. Math. Comput. 2011, 218, 628–642. [Google Scholar] [CrossRef]
- Dong, S.; Wang, N.; Liu, W.; Soares, C.G. Bivariate maximum entropy distribution of significant wave height and peak period. Ocean Eng. 2013, 59, 86–99. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Xiong, F. An Entropy-based generalized gamma distribution for flood frequency analysis. Entropy 2017, 19, 239. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Integrating entropy and copula theories for hydrologic modeling and analysis. Entropy 2015, 17, 2253–2280. [Google Scholar] [CrossRef]
- Mishra, A.K.; Özger, M.; Singh, V.P. An entropy-based investigation into the variability of precipitation. J. Hydrol. 2009, 370, 139–154. [Google Scholar] [CrossRef]
- Rajsekhar, D.; Mishra, A.K.; Singh, V.P. Regionalization of drought characteristics using an entropy approach. J. Hydrol. Eng. 2013, 18, 870–887. [Google Scholar] [CrossRef]
- Michailidi, E.M.; Bacchi, B. Dealing with uncertainty in the probability of overtopping of a flood mitigation dam. Hydrol. Earth Syst. Sci. 2017, 21, 2497–2507. [Google Scholar] [CrossRef]
- Serinaldi, F. An uncertain journey around the tails of multivariate hydrological distributions. Water Resour. Res. 2013, 49, 6527–6547. [Google Scholar] [CrossRef]
- Dung, N.V.; Merz, B.; Bardossy, A.; Apel, H. Handling uncertainty in bivariate quantile estimation—An application to flood hazard analysis in the Mekong Delta. J. Hydrol. 2015, 527, 704–717. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Stationarity is undead: Uncertainty dominates the distribution of extremes. Adv. Water Resour. 2015, 77, 17–36. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Zhao, J.; Rustomji, P.; Hairsine, P. Responses of streamflow to changes in climate and land use/cover in the Loess Plateau, China. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Shi, H.; Shao, M. Soil and water loss from the Loess Plateau in China. J. Arid Environ. 2000, 45, 9–20. [Google Scholar] [CrossRef]
- Du, T.; Xiong, L.; Xu, C.Y.; Gippel, C.J.; Guo, S.; Liu, P. Return period and risk analysis of nonstationary low-flow series under climate change. J. Hydrol. 2015, 527, 234–250. [Google Scholar] [CrossRef]
- Ma, M.; Song, S.; Ren, L.; Jiang, S.; Song, J. Multivariate drought characteristics using trivariate Gaussian and student copula. Hydrol. Process. 2013, 27, 1175–1190. [Google Scholar] [CrossRef]
- Peng, H.; Jia, Y.W.; Tague, C.; Slaughter, P. An eco-hydrological model-based assessment of the impacts of soil and water conservation management in the Jinghe river basin, China. Water 2015, 7, 6301–6320. [Google Scholar] [CrossRef]
- Guo, A.; Chang, J.; Huang, Q.; Wang, Y.; Liu, D.; Li, Y.; Tian, T. Hybrid method for assessing the multi-scale periodic characteristics of the precipitation—Runoff relationship: A case study in the Weihe river basin, China. J. Water Clim. Chang. 2017, 8, 62–77. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.V. Floods in Changing Climate; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Kamal, V.; Mukherjee, S.; Singh, P.; Sen, R.; Vishwakarma, C.A.; Sajadi, P.; Asthana, H.; Rena, V. Flood frequency analysis of Ganga river at Haridwar and Garhmukteshwar. Appl. Water Sci. 2017, 7, 1979–1986. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communications. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Jaynes, E.T. On the rationale of maximum-entropy methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Maximum entropy spectral analysis for streamflow forecasting. Phys. A Stat. Mech. Appl. 2016, 442, 91–99. [Google Scholar] [CrossRef]
- Li, C.; Singh, V.P.; Mishra, A.K. Entropy theory-based criterion for hydrometric network evaluation and design: Maximum information minimum redundancy. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Mishra, A.K.; Ines, A.V.M.; Singh, V.P.; Hansen, J.W. Extraction of information content from stochastic disaggregation and bias corrected downscaled precipitation variables for crop simulation. Stoch. Environ. Res. Risk Access. 2013, 27, 449–457. [Google Scholar] [CrossRef]
- Singh, V.P. Hydrologic synthesis using entropy theory. J. Hydrol. Eng. 2011, 16, 421–433. [Google Scholar] [CrossRef]
- Singh, V.P.; Rajagopal, A.K. A new method of parameter estimation for hydrologic frequency analysis. Hydrol. Sci. Technol. 1987, 2, 33–40. [Google Scholar]
- Sklar, A. Functions de Repartition à n Dimensions et Luers Marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Salvadori, G.; De Michele, C.; Kottegoda, N.T.; Rosso, R. Extremes in Nature: An Approach Using Copulas; Springer: New York, NY, USA, 2007. [Google Scholar]
- Vandenberghe, S.; Verhoest, N.E.C.; Onof, C.; De Baets, B. A comparative copula-based bivariate frequency analysis of observed and simulated storm events: A case study on Bartlett-Lewis modeled rainfall. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Fan, Y.R.; Huang, W.; Huang, G.H.; Li, Y.P.; Huang, K. Hydrologic risk analysis in the Yangtze river basin through coupling Gaussian mixtures into copulas. Adv. Water Resour. 2016, 88, 170–185. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J. Revisiting the concepts of return period and risk for nonstationary hydrologic extreme events. J. Hydrol. Eng. 2013, 19, 554–568. [Google Scholar] [CrossRef]
- Mood, A.; Graybill, F.; Boes, D.C. Introduction to the Theory of Statistics, 3rd ed.; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Tung, Y.K. Risk/Reliability-Based Hydraulic Engineering Design in Hydraulic Design Handbook; Mays, L., Ed.; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Read, L.K.; Vogel, R.M. Reliability, return periods, and risk under nonstationarity. Water Resour. Res. 2015, 51, 6381–6398. [Google Scholar] [CrossRef]
- Corbella, S.; Stretch, D.D. Predicting coastal erosion trends using non-stationary statistics and process-based models. Coast. Eng. 2012, 70, 40–49. [Google Scholar] [CrossRef]
- Brunner, M.I.; Seibert, J.; Favre, A.C. Bivariate return periods and their importance for flood peak and volume estimation. WIRs Water 2016, 3, 819–833. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C.; Durante, F. On the return period and design in a multivariate framework. Hydrol. Earth Syst. Sci. 2011, 15, 3293–3305. [Google Scholar] [CrossRef] [Green Version]
- Hyndman, R.J.; Bashtannyk, D.M.; Grunwald, G.K. Estimating and visualizing conditional densities. J. Comput. Graph. Stat. 1996, 5, 315–336. [Google Scholar]
- Massey, J.F. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Zhou, J.; Erdem, E.; Li, G.; Shi, J. Comprehensive evaluation of wind speed distribution models: A case study for North Dakota sites. Energy Convers. Manag. 2010, 51, 1449–1458. [Google Scholar] [CrossRef]
- Liu, F.J.; Chang, T.P. Validity analysis of maximum entropy distribution based on different moment constraints for wind energy assessment. Energy 2011, 36, 1820–1826. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel inference: Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Serinaldi, F. Can we tell more than we can know? The limits of bivariate drought analyses in the United States. Stoch. Environ. Res. Risk A 2016, 30, 1691–1704. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, M.; Singh, V.P. Uncertainty evaluation of copula analysis of hydrological droughts in the East River basin, China. Glob. Planet Chang. 2015, 129, 1–9. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. Flood frequency hydrology: 1. Temporal, spatial, and causal expansion of information. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]



| Station | Correlation Coefficient | ||||
|---|---|---|---|---|---|
| (AMF, Pr1) | (AMF, Pr2) | (AMF, Pr3) | (AMF, Pr4) | (AMF, Pr5) | |
| Linjiacun | 0.1420 | 0.4192 ** | 0.3654 ** | 0.3582 ** | 0.3320 ** |
| Huaxian | 0.1586 | 0.2369 * | 0.3756 ** | 0.3175 ** | 0.3320 ** |
| Distribution | Parameter | Linjiacun | Huaxian | |||
|---|---|---|---|---|---|---|
| AMF | Pr2 | AMF | Pr3 | |||
| MEP-3 | f (x|λ1, λ2, λ3) | λ1 | 4.04 × 10−4 | −0.15 | 3.50 × 10−3 | −0.15 |
| λ2 | 2.64 × 10−7 | 4.65 × 10−3 | −1.14 × 10−6 | 4.01 × 10−3 | ||
| λ3 | −4.02 × 10−11 | −2.93 × 10−5 | 1.19 × 10−10 | −2.25 × 10−8 | ||
| MEP-4 | f (x|λ1, λ2, λ3, λ4) | λ1 | 7.63 × 10−4 | −0.23 | −3.20 × 10−4 | 0.07 |
| λ2 | 1.57 × 10−6 | 9.65 × 10−3 | 1.03 × 10−6 | −6.73 × 10−3 | ||
| λ3 | −5.40 × 10−10 | −1.48 × 10−4 | −3.73 × 10−10 | −1.87 × 10−4 | ||
| λ4 | 6.01 × 10−14 | 9.13 × 10−7 | 3.83 × 10−14 | −1.41 × 10−6 | ||
| P3 | f (x|a, b, α) | a | 1.23 | 13.19 | 0.99 | 21.65 |
| b | 88.08 | −22.69 | 866 | −26.25 | ||
| α | 880.82 | 3.56 | 1999.35 | 2.57 | ||
| Logn | f (x|μ, σ) | μ | 6.73 | 3.01 | 7.82 | 3.29 |
| σ | 0.86 | 0.69 | 0.56 | 0.44 | ||
| Norm | f (x|μ, σ) | μ | 1170.32 | 24.52 | 2853.66 | 29.54 |
| σ | 954.42 | 13.55 | 1413.64 | 12.7 | ||
| Gam | f (x|μ, σ) | μ | 1.65 | 2.82 | 3.71 | 5.53 |
| σ | 707.28 | 8.68 | 770.06 | 5.34 | ||
| Station | Series | Functions | K-S Test | RMSE | Series | Functions | K-S Test | RMSE | ||
|---|---|---|---|---|---|---|---|---|---|---|
| S | p | S | p | |||||||
| Linjiacun | AMF | MEP-3 | 0.09 | 0.72 | 0.0303 | Pr2 | MEP-3 | 0.08 | 0.89 | 0.0293 |
| MEP-4 | 0.07 | 0.85 | 0.0296 | MEP-4 | 0.07 | 0.95 | 0.0248 | |||
| P3 | 0.08 | 0.85 | 0.0309 | P3 | 0.09 | 0.80 | 0.0373 | |||
| Logn | 0.09 | 0.80 | 0.0366 | Logn | 0.10 | 0.58 | 0.0450 | |||
| Norm | 0.15 | 0.19 | 0.0823 | Norm | 0.12 | 0.43 | 0.0473 | |||
| Gam | 0.11 | 0.53 | 0.0405 | Gam | 0.08 | 0.87 | 0.0275 | |||
| Huaxian | AMF | MEP-3 | 0.06 | 0.98 | 0.0195 | Pr3 | MEP-3 | 0.09 | 0.73 | 0.0306 |
| MEP-4 | 0.06 | 0.97 | 0.0202 | MEP-4 | 0.08 | 0.78 | 0.0267 | |||
| P3 | 0.14 | 0.25 | 0.0686 | P3 | 0.10 | 0.65 | 0.0299 | |||
| Logn | 0.10 | 0.59 | 0.0553 | Logn | 0.10 | 0.62 | 0.0390 | |||
| Norm | 0.12 | 0.37 | 0.0534 | Norm | 0.09 | 0.76 | 0.0382 | |||
| Gam | 0.09 | 0.74 | 0.0513 | Gam | 0.10 | 0.63 | 0.0300 | |||
| Station | Copula | Parameter | Cramér–von Mises Test | AICc | |
|---|---|---|---|---|---|
| Sn | p-Value | ||||
| Linjiacun | Clayton | 0.31 | 0.03 | 0.23 | −10.83 |
| Frank | 4.09 | 0.04 | 0.10 | −19.54 | |
| Gumbel | 1.59 | 0.03 | 0.15 | −22.38 | |
| Huaxian | Clayton | 0.42 | 0.03 | 0.45 | −11.67 |
| Frank | 3.72 | 0.02 | 0.59 | −17.03 | |
| Gumbel | 1.50 | 0.03 | 0.36 | −16.22 | |
| Distribution | Most-Likely Design Event (AMF, Pr) | ||||
|---|---|---|---|---|---|
| TOR = 30 | TAND = 30 | ||||
| AMF | Pr | Linjiacun | Huaxian | Linjiacun | Huaxian |
| MEP-3 | MEP-3 | (3921.34, 56.26) | (5626.03, 63.42) | (2877.37, 46.53) | (4976.51, 42.52) |
| MEP-4 | (3920.99, 56.72) | (5369.10, 73.46) | (2864.31, 48.00) | (5017.84, 41.64) | |
| P3 | (3937.32, 57.06) | (5653.22, 55.68) | (2921.17, 46.92) | (4924.88, 41.07) | |
| Logn | (3930.55, 78.62) | (5678.83, 64.63) | (3065.06, 56.57) | (5028.83, 39.38) | |
| Norm | (3961.55, 51.29) | (5642.49, 54.98) | (2760.59, 44.54) | (4882.04, 42.83) | |
| Gam | (3925.95, 60.35) | (5660.16, 59.29) | (2960.32, 48.86) | (4966.30, 40.87) | |
| MEP-4 | MEP-3 | (3833.86, 57.87) | (5492.61, 65.46) | (3105.70, 45.48) | (4969.43, 42.53) |
| MEP-4 | (3825.82, 56.95) | (5290.03, 73.46) | (3052.79, 46.76) | (4991.76, 41.49) | |
| P3 | (3849.07, 52.66) | (5521.30, 56.98) | (3034.24, 42.96) | (4928.09, 40.94) | |
| Logn | (3834.21, 79.18) | (5539.27, 67.13) | (3204.83, 54.23) | (5010.76, 39.49) | |
| Norm | (3849.58, 51.53) | (5513.93, 56.04) | (2980.19, 43.39) | (4894.56, 42.64) | |
| Gam | (3830.33, 60.66) | (5526.09, 60.98) | (3126.29, 47.38) | (4960.69, 40.82) | |
| P3 | MEP-3 | (3828.15, 57.44) | (8613.13, 67.16) | (2772.63, 47.11) | (4897.99, 49.50) |
| MEP-4 | (3842.96, 57.74) | (7635.10, 73.46) | (2750.37, 48.44) | (5372.34, 46.50) | |
| P3 | (3860.18, 58.30) | (8866.89, 57.89) | (2802.71, 47.44) | (4591.65, 46.52) | |
| Logn | (3867.76, 81.16) | (8984.54, 68.75) | (2936.73, 57.73) | (5204.69, 46.98) | |
| Norm | (3868.93, 52.20) | (8820.36, 56.80) | (2654.70, 44.82) | (4400.06, 47.56) | |
| Gam | (3853.61, 61.71) | (8897.28, 62.14) | (2839.67, 49.46) | (4809.40, 47.38) | |
| Logn | MEP-3 | (4609.04, 57.71) | (7749.23, 67.64) | (2843.58, 48.19) | (4499.62, 49.81) |
| MEP-4 | (4636.79, 57.96) | (6941.66, 73.46) | (2807.61, 49.49) | (4890.92, 46.87) | |
| P3 | (4665.66, 58.58) | (7989.66, 58.14) | (2898.54, 48.52) | (4289.21, 46.69) | |
| Logn | (4670.78, 81.59) | (8094.99, 69.23) | (3141.70, 60.07) | (4729.38, 47.43) | |
| Norm | (4681.88, 52.44) | (7948.81, 57.00) | (2618.77, 45.66) | (4155.63, 47.64) | |
| Gam | (4653.58, 61.99) | (8017.00, 62.46) | (2969.72, 50.66) | (4437.30, 47.64) | |
| Norm | MEP-3 | (3108.07, 57.79) | (5793.91, 66.33) | (2524.13, 44.13) | (4699.00, 44.79) |
| MEP-4 | (3119.85, 58.02) | (5446.16, 73.46) | (2497.94, 45.68) | (4782.48, 43.07) | |
| P3 | (3130.51, 58.61) | (5861.15, 57.45) | (2534.21, 44.25) | (4606.08, 43.07) | |
| Logn | (3152.78, 82.35) | (5898.04, 67.97) | (2603.77, 47.62) | (4797.38, 41.64) | |
| Norm | (3124.46, 52.27) | (5846.46, 56.43) | (2481.91, 43.14) | (4535.18, 44.65) | |
| Gam | (3132.06, 62.18) | (5870.99, 61.58) | (2542.46, 45.41) | (4676.33, 43.10) | |
| Gam | MEP-3 | (3586.49, 57.56) | (6654.48, 66.89) | (2633.78, 46.68) | (4677.02, 47.24) |
| MEP-4 | (3601.58, 57.84) | (6096.07, 73.46) | (2604.74, 48.09) | (4883.48, 44.83) | |
| P3 | (3617.00, 58.41) | (6785.93, 57.75) | (2660.38, 46.99) | (4515.48, 44.90) | |
| Logn | (3632.96, 81.57) | (6850.96, 68.51) | (2769.53, 56.15) | (4846.30, 44.36) | |
| Norm | (3620.10, 52.24) | (6760.41, 56.68) | (2540.92, 44.61) | (4401.43, 46.19) | |
| Gam | (3613.57, 61.86) | (6803.04, 61.96) | (2687.53, 48.87) | (4631.91, 45.35) | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, A.; Chang, J.; Wang, Y.; Huang, Q.; Guo, Z. Maximum Entropy-Copula Method for Hydrological Risk Analysis under Uncertainty: A Case Study on the Loess Plateau, China. Entropy 2017, 19, 609. https://doi.org/10.3390/e19110609
Guo A, Chang J, Wang Y, Huang Q, Guo Z. Maximum Entropy-Copula Method for Hydrological Risk Analysis under Uncertainty: A Case Study on the Loess Plateau, China. Entropy. 2017; 19(11):609. https://doi.org/10.3390/e19110609
Chicago/Turabian StyleGuo, Aijun, Jianxia Chang, Yimin Wang, Qiang Huang, and Zhihui Guo. 2017. "Maximum Entropy-Copula Method for Hydrological Risk Analysis under Uncertainty: A Case Study on the Loess Plateau, China" Entropy 19, no. 11: 609. https://doi.org/10.3390/e19110609





