Maximum Correntropy Criterion Kalman Filter for α-Jerk Tracking Model with Non-Gaussian Noise
Abstract
:1. Introduction
- The first approach is to develop filters for the systems with non-Gaussian noises directly. Noise distributions such as heavy-tailed distributions and t-distributions are considered in these filters [18,19]. However, it is difficult to handle more than one dimension, which limits its applicability [20].
- Approximating the posteriori probability density is another practical approach to handle the non-Gaussian noises. The unscented Kalman filter (UKF) uses the unscented transformation (UT) technique to capture the mean and the covariance of the state estimation with sigma points [21]. The ensemble Kalman filter (EnKF) is a method to approximate the state estimation with a set of samples to handle non-Gaussian noises [22]. Gaussian sum filter (GSF) is an algorithm to obtain the filtering distribution and the predictive distribution recursively approximated as Gaussian mixtures [23,24,25].
- A new robust Kalman filter is proposed by Chang [31] in recent years. It handles the outliers based on the hypothesis testing theory, which defines a judging index as the square of the Mahalanobis distance from the observation to its prediction. It can effectively resist the heavy-tailed distribution of the observation noises and the outliers in the actual observations.
- Multi-sensor data fusion Kalman filter is a fuzzy logical method proposed by Rodger [32]. It can effectively improve the computational burden and the robustness of Kalman filter. Furthermore, it has been applied on the vehicle health maintenance system.
- Maximum correntropy criterion is the latest optimization criterion that is used for improving Kalman filter. Maximum correntropy Kalman filter (MCKF) is a newly proposed filter to process the non-Gaussian noises [33]. In addition, several improved MCKF algorithms have been proposed and applied on state estimation [34,35,36,37].
2. -Jerk Model
3. Design for Maximum Correntropy Criterion Kalman Filter with Non-Gaussian Noise
3.1. Standard Kalman Filter
3.2. Design of Maximum Correntropy Criterion Kalman Filter
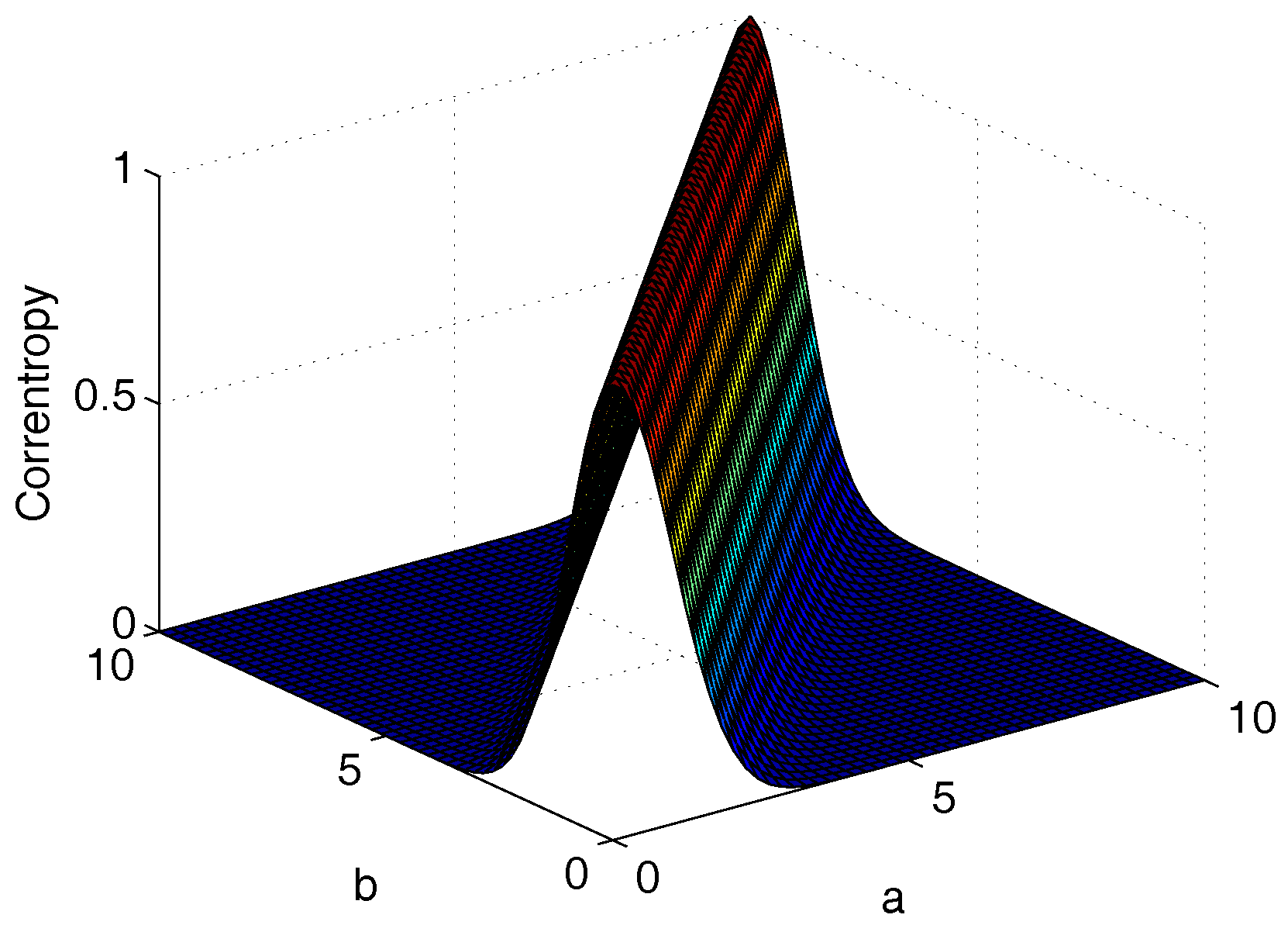
3.2.1. Correntropy
3.2.2. Maximum Correntropy Criterion Kalman Filter Algorithm
- State Prediction
- Covariance Prediction
- Filter Gain
- State Update
- Covariance Update
3.3. Robustness of MCCKF
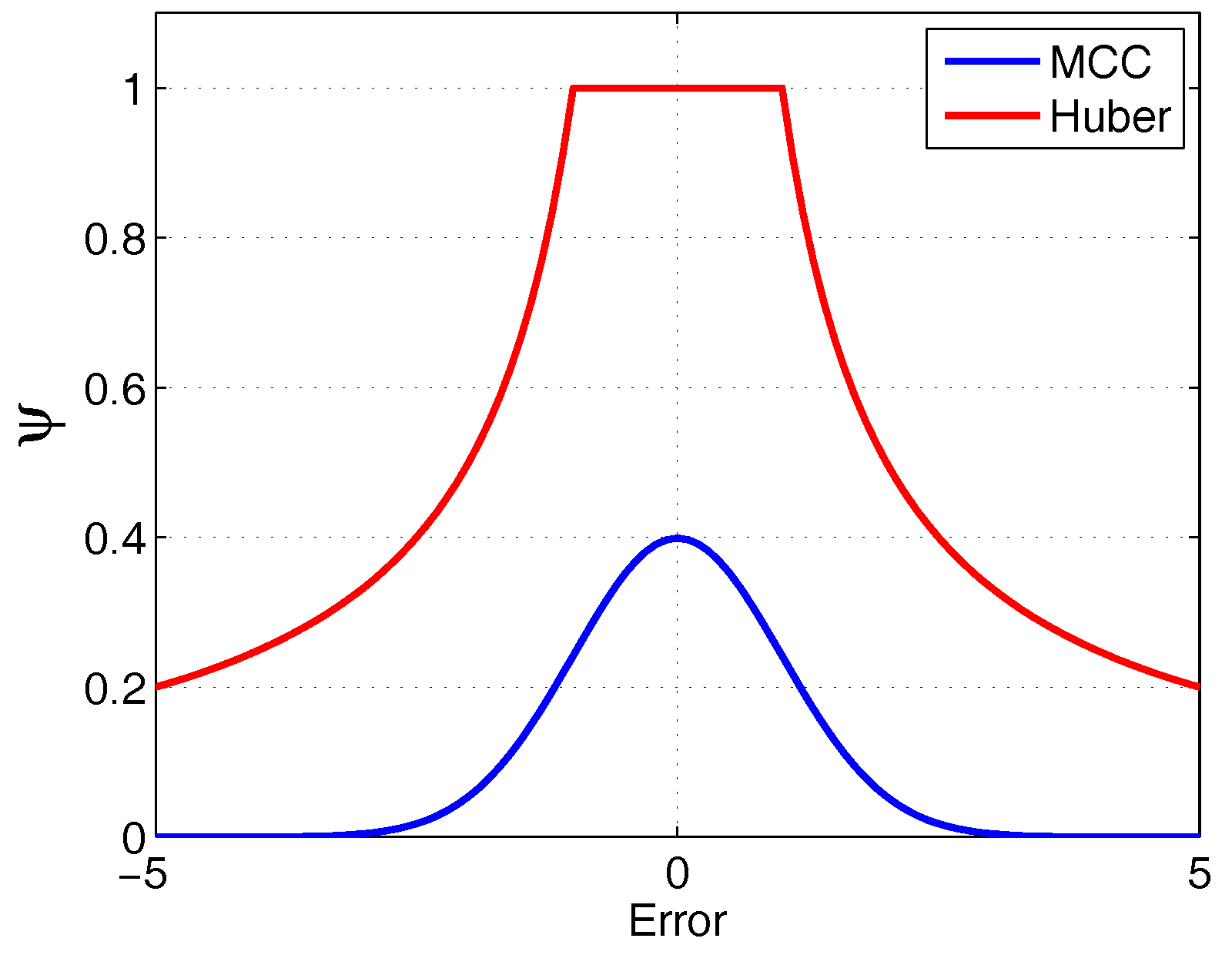
3.3.1. Influence Function of MCCKF
- Fix , and is bounded in the interval .
3.3.2. Comparison with Huber Filter
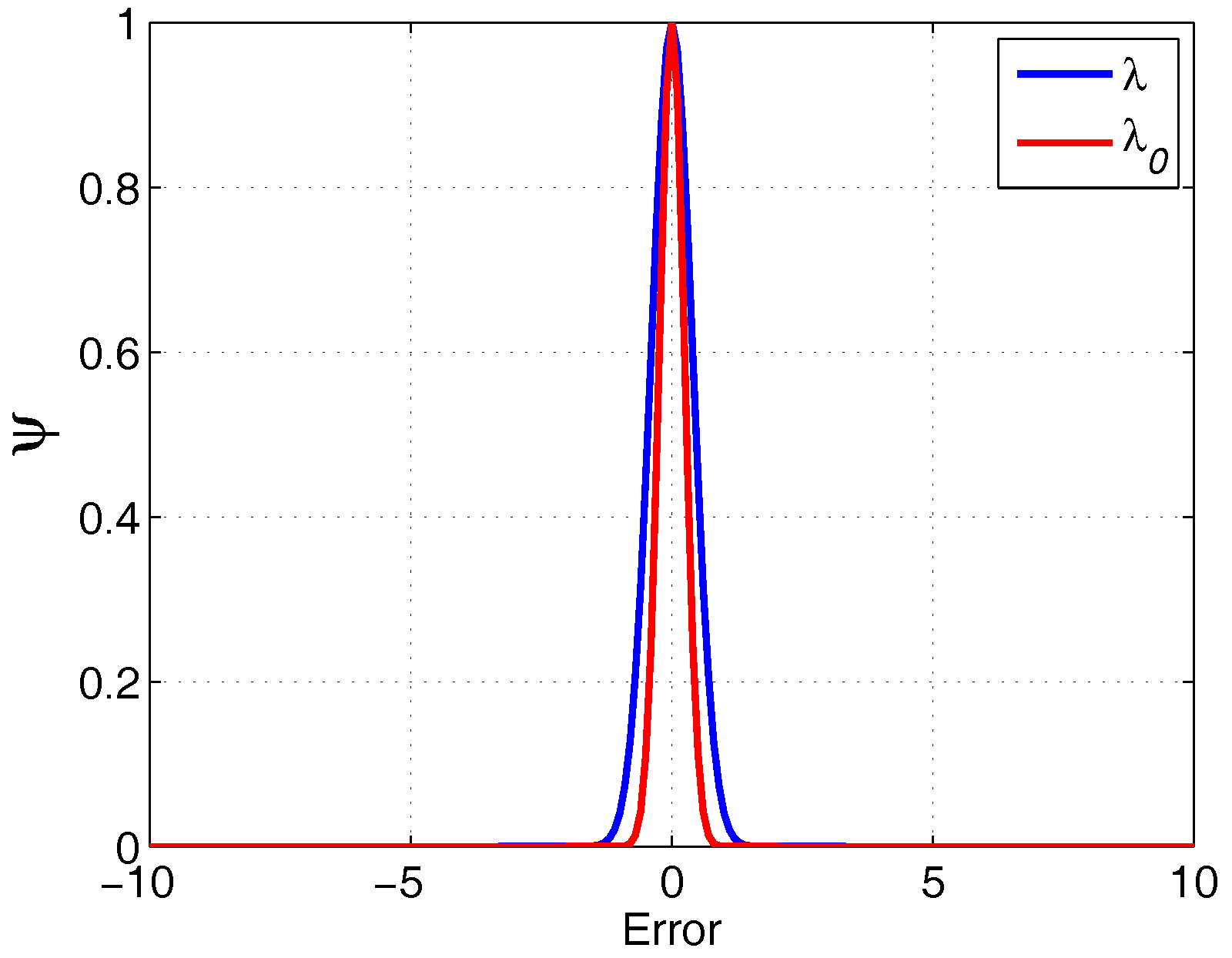
3.4. Kernel Size Selection
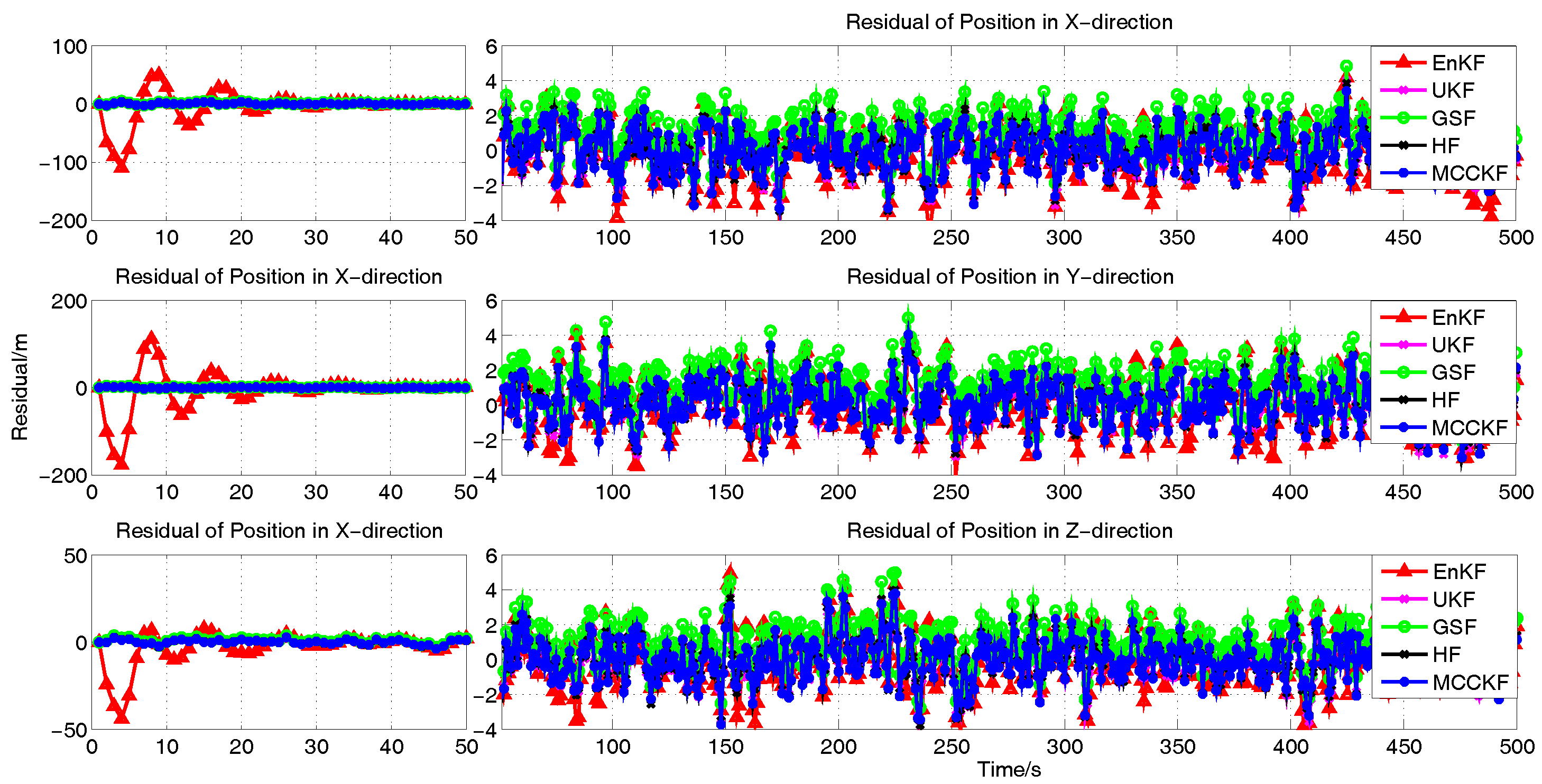
4. Simulation
4.1. Simulation Conditions
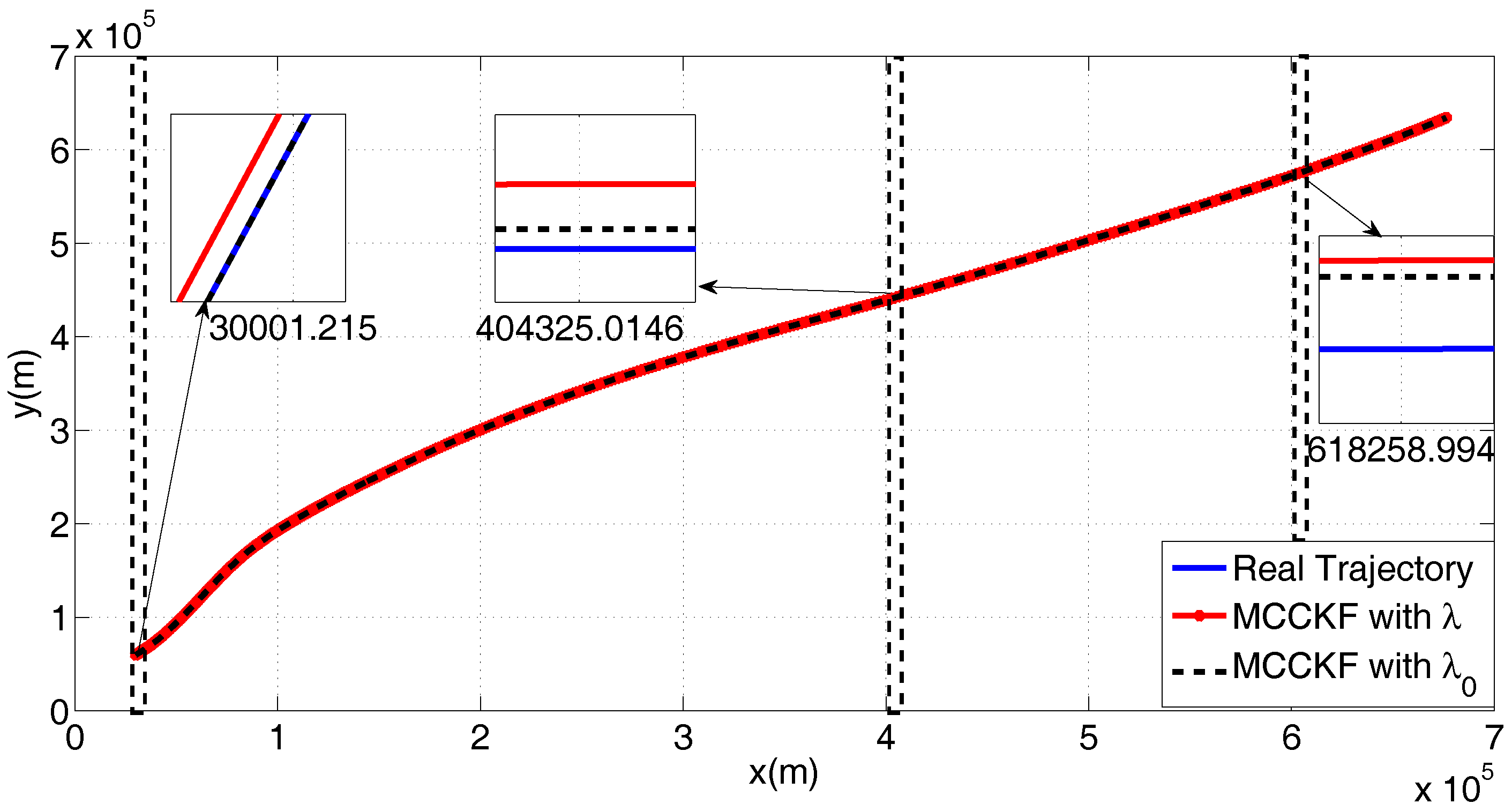
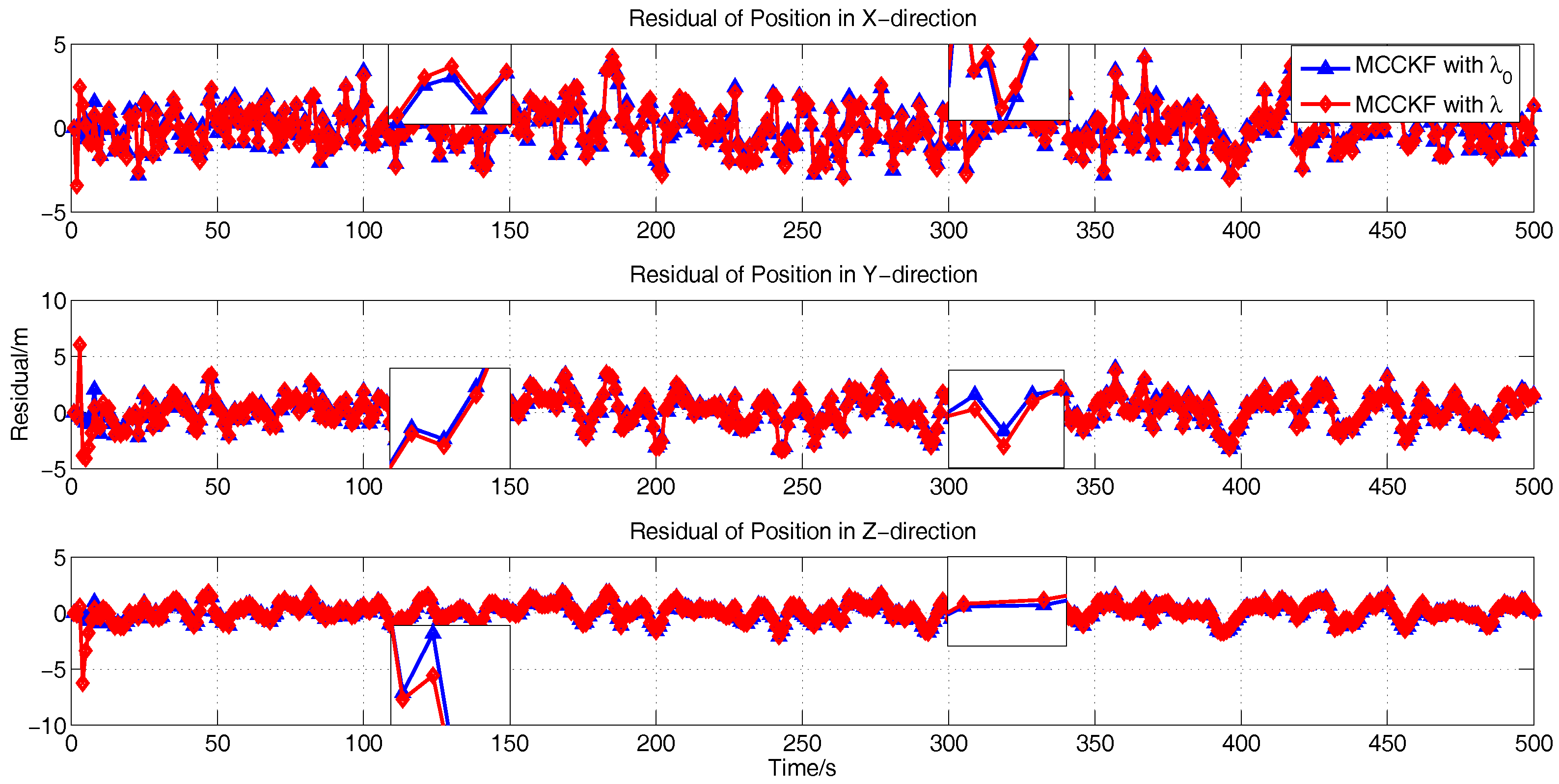
4.2. The Kernel Size Adaptive Method
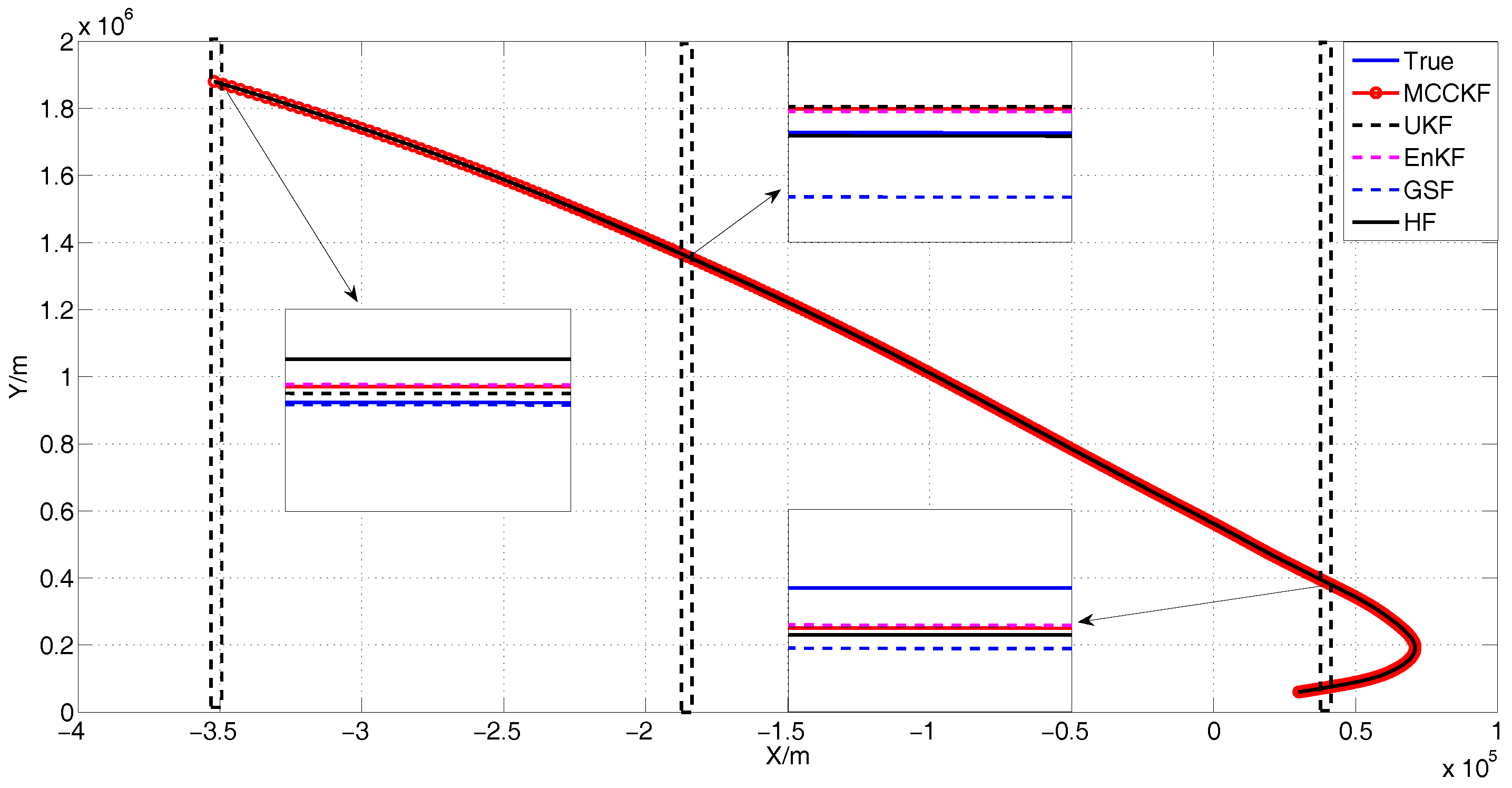
4.3. The Presence of Gaussian Noise
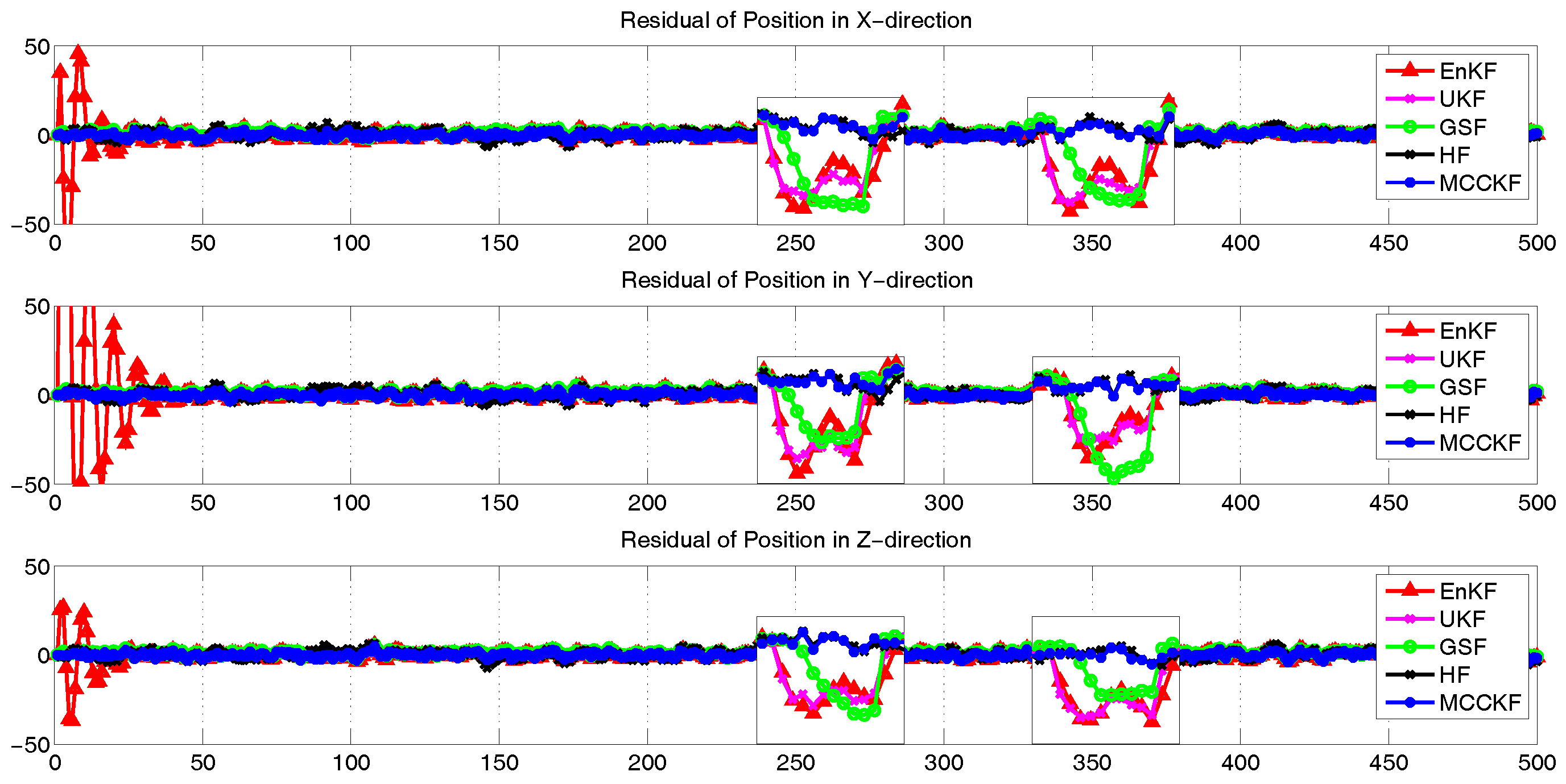
4.4. The Presence of Large Outliers
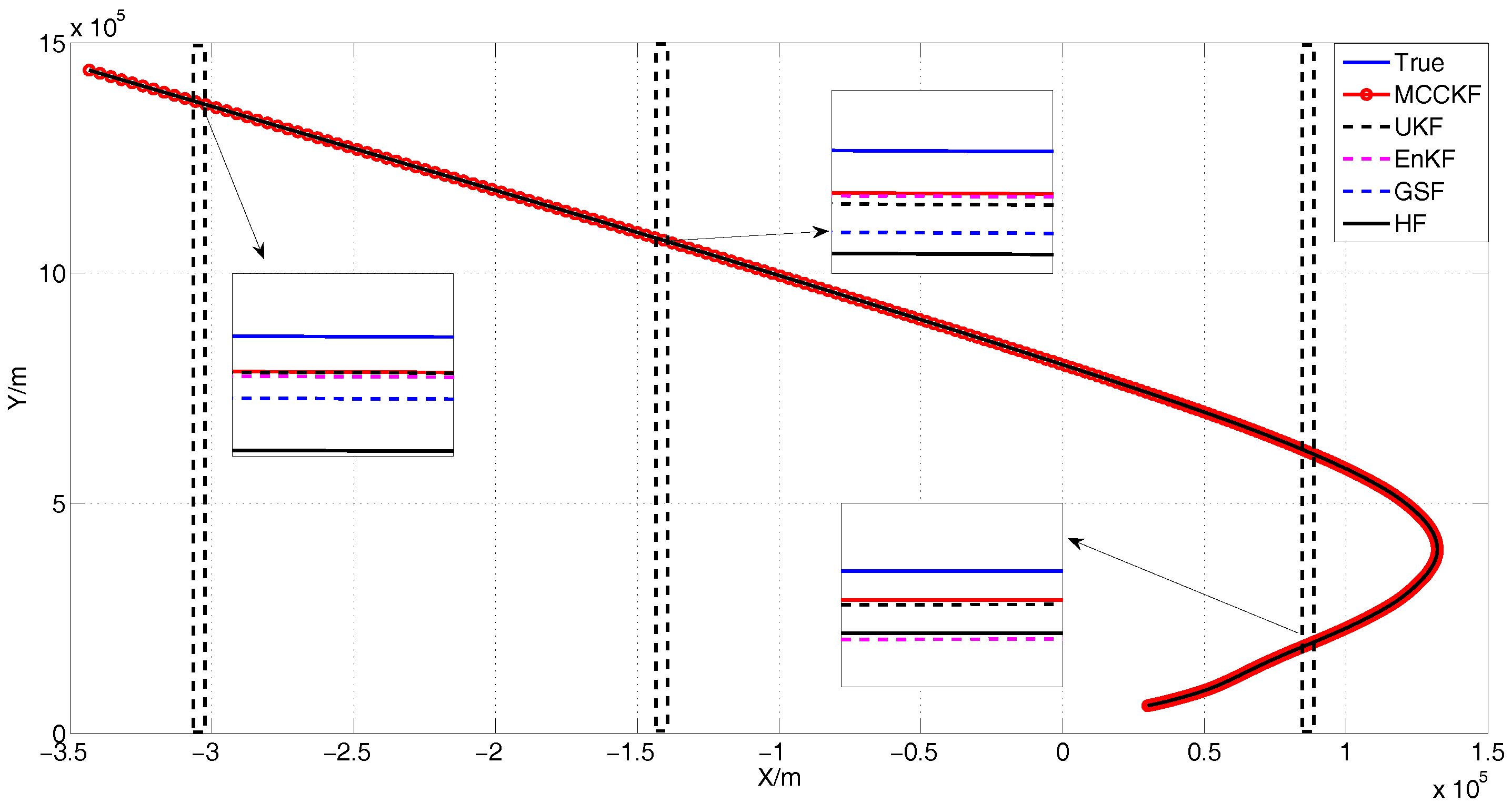
4.5. The Presence of Gaussian Mixture Noises
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part I. Dynamic models. IEEE Trans. Aerosp. Electron. Syst. 2004, 39, 1333–1364. [Google Scholar]
- Yang, X.; Xing, K.; Feng, X. Maneuvering target tracking in dense clutter based on particle filtering. Chin. J. Aeronaut. 2011, 24, 171–180. [Google Scholar] [CrossRef]
- Singer, R.A. Estimating optimal tracking filter performance for manned maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 1970, AES-6, 473–483. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Birmiwal, K. Variable dimension filter for maneuvering target tracking. IEEE Trans. Aerosp. Electron. Syst. 1982, AES-18, 621–629. [Google Scholar] [CrossRef]
- Kumar, K.S.P.; Zhou, H.; Kumar, K.S.P.; Zhou, H. A “current” statistical model and adaptive algorithm for estimating maneuvering targets. J. Guidance Control Dyn. 1984, 7, 596–602. [Google Scholar] [CrossRef]
- Mehrotra, K.; Mahapatra, P.R. A jerk model for tracking highly maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 1094–1105. [Google Scholar] [CrossRef]
- Luo, X.B. A α-jerk model for tracking maneuvering targets. Signal Process. 2007, 4, 481–484. [Google Scholar]
- Li, X.R.; Jilkov, V.P. A survey of maneuvering target tracking: Approximation techniques for nonlinear filtering. Proc. SPIE 2004, 5428. [Google Scholar] [CrossRef]
- Roth, M.; Hendeby, G.; Fritsche, C.; Gustafsson, F. The ensemble kalman filter: A signal processing perspective. Eurasip J. Adv. Signal Process. 2017, 2017, 56. [Google Scholar] [CrossRef]
- Ammann, N.; Andert, F. Visual navigation for autonomous, precise and safe landing on celestial bodies using unscented kalman filtering. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017. [Google Scholar]
- Zhang, C.; Hwang, I. Gaussian sum-based maneuvering target tracking using unmanned aerial vehicle. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017; pp. 1–12. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K.; Durrant-Whyte, H.F. A new approach for filtering nonlinear systems. In Proceedings of the American Control Conference, Seattle, WA, USA, 21–23 June 1995; Volume 3, pp. 1628–1632. [Google Scholar]
- Uhlmann, J.K.; Julier, S.J. A new extension of the kalman filter to nonlinear systems. Proc. SPIE 1997, 3068, 182–193. [Google Scholar]
- Maybeck, P.S. Stochastic Models, Estimation and Control Volume 3; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Stein, D.W.J. Detection of random signals in gaussian mixture noise. In Proceedings of the 1994 28th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 31 October–2 November 1994; Volume 2, pp. 791–795. [Google Scholar]
- Wu, W.R. Target racking with glint noise. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 174–185. [Google Scholar]
- Plataniotis, K.N.; Androutsos, D.; Venetsanopoulos, A.N. Nonlinear filtering of non-gaussian noise. J. Intell. Robot. Syst. 1997, 19, 207–231. [Google Scholar] [CrossRef]
- Sorenson, H.W.; Alspach, D.L. Recursive bayesian estimation using gaussian sums. Automatica 1971, 7, 465–479. [Google Scholar] [CrossRef]
- Harvey, A.; Luati, A. Filtering with heavy tails. J. Am. Stat. Assoc. 2014, 109, 1112–1122. [Google Scholar] [CrossRef]
- Izanloo, R.; Fakoorian, S.A.; Yazdi, H.S.; Dan, S. Kalman filtering based on the maximum correntropy criterion in the presence of non-gaussian noise. In Proceedings of the Information Science and Systems, Princeton, NJ, USA, 16–18 March 2016; pp. 500–505. [Google Scholar]
- Wan, E.A.; van der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium, Lake Louise, AB, Canada, 4 October 2000; pp. 153–158. [Google Scholar]
- Curn, J.; Marinescu, D.; Lacey, G.; Cahill, V. Estimation with non-white gaussian observation noise using a generalised ensemble kalman filter. In Proceedings of the IEEE International Symposium on Robotic and Sensors Environments, Magdeburg, Germany, 16–18 November 2012; pp. 85–90. [Google Scholar]
- Kotecha, J.H.; Djuric, P.M. Gaussian sum particle filtering. IEEE Trans. Signal Process. 2003, 51, 2602–2612. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, K.; Wang, H.; Liu, J.; He, Y.; Pan, L. Adaptive gaussian sum squared-root cubature kalman filter with split-merge scheme for state estimation. Chin. J. Aeronaut. 2014, 27, 1242–1250. [Google Scholar] [CrossRef]
- Yin, J.; Zhang, J.; Zhuang, Z. Gaussian sum phd filtering algorithm for nonlinear non-gaussian models. Chin. J. Aeronaut. 2008, 21, 341–351. [Google Scholar]
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection. J. R. Stat. Soc. 1989, 152, 133–134. [Google Scholar]
- Wang, R.; Xiong, Z.; Liu, J.Y.; Li, R.; Peng, H. SINS/GPS/CNS information fusion system based on improved huber filter with classified adaptive factors for high-speed UAVs. In Proceedings of the 2012 IEEE/ION Position Location and Navigation Symposium (PLANS), Myrtle Beach, SC, USA, 23–26 April 2012; pp. 441–446. [Google Scholar]
- Huang, J.; Yan, B.; Hu, S. Centralized fusion of unscented kalman filter based on huber robust method for nonlinear moving target tracking. Math. Probl. Eng. 2015, 2015, 291913. [Google Scholar] [CrossRef]
- Chang, L.; Li, K.; Hu, B. Huber’s m-estimation-based process uncertainty robust filter for integrated ins/gps. IEEE Sens. J. 2015, 15, 3367–3374. [Google Scholar] [CrossRef]
- Chien-Hao, T.; Lin, S.F.; Dah-Jing, J. Robust huber-based cubature kalman filter for gps navigation processing. J. Navigat. 2016, 70, 527–546. [Google Scholar]
- Chang, G. Robust kalman filtering based on mahalanobis distance as outlier judging criterion. J. Geodesy 2014, 88, 391–401. [Google Scholar] [CrossRef]
- Rodger, J.A. Toward reducing failure risk in an integrated vehicle health maintenance system: A fuzzy multi-sensor data fusion kalman filter approach for ivhms. Expert Syst. Appl. 2012, 39, 9821–9836. [Google Scholar] [CrossRef]
- Chen, B.; Liu, X.; Zhao, H.; Principe, J.C. Maximum correntropy kalman filter. Automatica 2017, 76, 70–77. [Google Scholar] [CrossRef]
- Liu, X.; Qu, H.; Zhao, J.; Yue, P.; Wang, M. Maximum correntropy unscented kalman filter for spacecraft relative state estimation. Sensors 2016, 16, 1530. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Chen, B.; Xu, B.; Wu, Z.; Honeine, P. Maximum correntropy unscented filter. Int. J. Syst. Sci. 2017, 48, 1607–1615. [Google Scholar] [CrossRef]
- Xi, L.; Hua, Q.; Zhao, J.; Chen, B. Extended Kalman filter under maximum correntropy criterion. In Proceedings of the International Joint Conference on Neural Networks, Vancouver, BC, Canada, 24–29 July 2016; pp. 1733–1737. [Google Scholar]
- Wang, J.J.-Y.; Wang, Y.; Jing, B.-Y.; Gao, X. Regularized maximum correntropy machine. Neurocomputing 2015, 160, 85–92. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part V. multiple-model methods. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1255–1321. [Google Scholar]
- Lewis, F.L. Applied optimal control. IEEE Trans. Autom. Control 2003, 17, 186–188. [Google Scholar]
- Jiang, C.; Zhang, S.B.; Zhang, Q.Z. A new adaptive h-infinity filtering algorithm for the GPS/INS integrated navigation. Sensors 2016, 16, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Príncipe, J.C. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives; Springer Publishing Company, Incorporated: Berlin, Germany, 2010. [Google Scholar]
- Chen, B.; Xing, L.; Liang, J.; Zheng, N.; Príncipe, J.C. Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion. IEEE Signal Process. Lett. 2014, 21, 880–884. [Google Scholar]
- Chen, B.; Wang, J.; Zhao, H.; Zheng, N.; Príncipe, J.C. Convergence of a fixed-point algorithm under maximum correntropy criterion. IEEE Signal Process. Lett. 2015, 22, 1723–1727. [Google Scholar] [CrossRef]
- Chen, B.; Príncipe, J.C. Maximum correntropy estimation is a smoothed map estimation. IEEE Signal Process. Lett. 2012, 19, 491–494. [Google Scholar] [CrossRef]
- Liu, W.; Pokharel, P.P.; Príncipe, J.C. Correntropy: Properties and applications in non-gaussian signal processing. IEEE Trans. Signal Process. 2007, 55, 5286–5298. [Google Scholar] [CrossRef]
- He, R.; Hu, B.; Yuan, X.; Wang, L. Robust Recognition via Information Theoretic Learning; Springer International Publishing: Berlin, Germany, 2014. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Chang, G.; Liu, M. M-estimator-based robust kalman filter for systems with process modeling errors and rank deficient measurement models. Nonlinear Dyn. 2015, 80, 1431–1449. [Google Scholar] [CrossRef]
- Chang, G.; Xu, T.; Wang, Q. M-estimator for the 3d symmetric helmert coordinate transformation. J. Geodesy 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- He, Y.; Wang, F.; Yang, J.; Rong, H.; Chen, B. Kernel adaptive filtering under generalized maximum correntropy criterion. In Proceedings of the International Joint Conference on Neural Networks, Vancouver, BC, Canada, 24–29 July 2016; pp. 1738–1745. [Google Scholar]
- Wang, Y.; Zheng, W.; Sun, S.; Li, L. Robust information filter based on maximum correntropy criterion. J. Guidance Control Dyn. 2016, 39, 1–6. [Google Scholar] [CrossRef]
- Huber, P.J. The 1972 wald lecture robust statistics: A review. Ann. Math. Stat. 1972, 43, 1041–1067. [Google Scholar] [CrossRef]
- Taylor, A.E. L’hospital’s rule. Am. Math. Mon. 1952, 59, 20–24. [Google Scholar] [CrossRef]
- He, R.; Zheng, W.S.; Hu, B.G. Maximum correntropy criterion for robust face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1561–1576. [Google Scholar] [PubMed]
- Liu, W.; Príncipe, J.C.; Haykin, S.S. Kernel Adaptive Filtering: A Comprehensive Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Cinar, G.T.; Príncipe, J.C. Hidden state estimation using the correntropy filter with fixed point update and adaptive kernel size. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012. [Google Scholar]


| Position (m) | Velocity (m/s) | Accelaration (m/s) | Jerk () | ||
|---|---|---|---|---|---|
| 1.2331 | 1.3251 | 0.7766 | 0.3512 | 0.2637 | |
| 1.2821 | 1.3590 | 0.7961 | 0.3531 | 0.2764 |
| Position (m) | Velocity (m/s) | Accelaration () | Jerk () | ||
|---|---|---|---|---|---|
| 1.2325 | 1.2203 | 0.6863 | 0.3248 | 0.3232 | |
| 1.2538 | 1.2451 | 0.6905 | 0.32 | 0.3232 |
| Position (m) | Velocity (m/s) | Accelaration () | Jerk () | ||
|---|---|---|---|---|---|
| 1.3477 | 1.3768 | 0.8037 | 0.3581 | 0.7747 | |
| 1.3747 | 1.3968 | 0.8256 | 0.3682 | 0.7936 |
| Position (m) | Velocity (m/s) | Accelaration () | Jerk () | ||
|---|---|---|---|---|---|
| EnKF | 7.0350 | 4.7926 | 2.3029 | 0.5543 | 1.7291 |
| UKF | 1.2892 | 1.3825 | 0.8940 | 0.4424 | 1.6125 |
| GSF | 1.5990 | 1.2220 | 0.8072 | 0.4202 | 1.6125 |
| HF | 1.2843 | 1.2220 | 0.8072 | 0.4202 | 1.6125 |
| MCCKF | 1.2901 | 1.2252 | 0.8076 | 0.4201 | 1.6125 |
| Position (m) | Velocity (m/s) | Accelaration () | Jerk () | ||
|---|---|---|---|---|---|
| EnKF | 3.2812 | 3.9866 | 2.1125 | 0.5019 | 3.2963 |
| UKF | 1.2856 | 1.5343 | 0.9418 | 0.4299 | 1.1582 |
| GSF | 1.5749 | 1.3181 | 0.8666 | 0.4245 | 1.1582 |
| HF | 1.2695 | 1.3181 | 0.8666 | 0.4245 | 1.1582 |
| MCCKF | 1.2695 | 1.3195 | 0.8685 | 0.4245 | 1.1582 |
| Position (m) | Velocity (m/s) | Accelaration () | Jerk () | ||
|---|---|---|---|---|---|
| EnKF | 4.5702 | 3.5353 | 1.9189 | 0.5649 | 1.9978 |
| UKF | 1.2178 | 1.4724 | 0.9319 | 0.4700 | 1.1227 |
| GSF | 1.5931 | 1.2563 | 0.8887 | 0.4738 | 1.1227 |
| HF | 1.2071 | 1.2562 | 0.8887 | 0.4738 | 1.1227 |
| MCCKF | 1.2125 | 1.2617 | 0.8907 | 0.4741 | 1.1227 |
| Position (m) | Velocity (m/s) | Accelaration () | Jerk () | ||
|---|---|---|---|---|---|
| EnKF | 6.9390 | 6.4846 | 3.7753 | 0.6530 | 1.3750 |
| UKF | 3.3104 | 1.7170 | 0.9083 | 0.4238 | 0.9707 |
| GSF | 3.0822 | 1.5156 | 0.8306 | 0.4258 | 0.9707 |
| HF | 2.3903 | 1.4708 | 1.7734 | 1.3180 | 1.0783 |
| MCCKF | 1.4252 | 1.3336 | 0.8153 | 0.4245 | 0.9707 |
| Position (m) | Velocity (m/s) | Accelaration () | Jerk () | ||
|---|---|---|---|---|---|
| EnKF | 3.7977 | 2.8730 | 1.7031 | 0.5630 | 5.5318 |
| UKF | 3.3085 | 1.6968 | 0.9586 | 0.4464 | 0.3219 |
| GSF | 3.5637 | 1.6479 | 0.8553 | 0.4259 | 0.3219 |
| HF | 2.2420 | 3.2366 | 1.6525 | 1.3194 | 0.8478 |
| MCCKF | 1.3119 | 1.2571 | 0.8020 | 0.4244 | 0.3219 |
| Position (m) | Velocity (m/s) | Accelaration () | Jerk () | ||
|---|---|---|---|---|---|
| EnKF | 11.6641 | 9.4672 | 4.7836 | 0.8071 | 2.8136 |
| UKF | 3.1840 | 1.6303 | 0.9613 | 0.4324 | 0.6726 |
| GSF | 2.8279 | 1.3632 | 0.8259 | 0.4192 | 0.6726 |
| HF | 2.2469 | 3.2751 | 1.6901 | 1.3161 | 0.9380 |
| MCCKF | 1.3696 | 1.2799 | 0.8209 | 0.4188 | 0.6726 |
| Position (m) | Velocity (m/s) | Accelaration () | Jerk () | ||
|---|---|---|---|---|---|
| EnKF | 6.4009 | 6.4574 | 3.3219 | 0.5756 | 2.0893 |
| UKF | 1.3171 | 1.5839 | 1.0426 | 0.4578 | 0.9669 |
| GSF | 1.6669 | 1.4316 | 0.9840 | 0.4498 | 0.9669 |
| HF | 1.5411 | 1.4907 | 0.9834 | 0.4703 | 0.9669 |
| MCCKF | 1.3080 | 1.4194 | 0.9714 | 0.4497 | 0.9669 |
| Position (m) | Velocity (m/s) | Accelaration () | Jerk () | ||
|---|---|---|---|---|---|
| EnKF | 5.6661 | 6.9973 | 3.8323 | 0.6798 | 1.6025 |
| UKF | 1.2481 | 1.4203 | 0.9216 | 0.4233 | 1. 5972 |
| GSF | 1.6537 | 1.2715 | 0.8655 | 0.412 | 1. 5972 |
| HF | 1.2348 | 1.2715 | 0.8655 | 0.4122 | 1. 5972 |
| MCCKF | 1.0214 | 1.2607 | 0.8226 | 0.4117 | 1.5972 |
| Position (m) | Velocity (m/s) | Accelaration () | Jerk () | ||
|---|---|---|---|---|---|
| EnKF | 2.4590 | 2.6990 | 1.5505 | 0.5314 | 3.0559 |
| UKF | 1.2806 | 1.5766 | 1.0119 | 0.4717 | 0.4726 |
| GSF | 1.5664 | 1.3625 | 0.9533 | 0.4678 | 0.4726 |
| HF | 1.2877 | 1.3625 | 0.9529 | 0.4678 | 0.4726 |
| MCCKF | 1.2548 | 1.3602 | 0.9134 | 0.4678 | 0.4726 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, B.; He, Z.; Zhou, X.; Zhou, H.; Li, D.; Wang, J. Maximum Correntropy Criterion Kalman Filter for α-Jerk Tracking Model with Non-Gaussian Noise. Entropy 2017, 19, 648. https://doi.org/10.3390/e19120648
Hou B, He Z, Zhou X, Zhou H, Li D, Wang J. Maximum Correntropy Criterion Kalman Filter for α-Jerk Tracking Model with Non-Gaussian Noise. Entropy. 2017; 19(12):648. https://doi.org/10.3390/e19120648
Chicago/Turabian StyleHou, Bowen, Zhangming He, Xuanying Zhou, Haiyin Zhou, Dong Li, and Jiongqi Wang. 2017. "Maximum Correntropy Criterion Kalman Filter for α-Jerk Tracking Model with Non-Gaussian Noise" Entropy 19, no. 12: 648. https://doi.org/10.3390/e19120648
APA StyleHou, B., He, Z., Zhou, X., Zhou, H., Li, D., & Wang, J. (2017). Maximum Correntropy Criterion Kalman Filter for α-Jerk Tracking Model with Non-Gaussian Noise. Entropy, 19(12), 648. https://doi.org/10.3390/e19120648




