Classification of Normal and Pre-Ictal EEG Signals Using Permutation Entropies and a Generalized Linear Model as a Classifier
Abstract
:1. Introduction
2. Brief Review on Permutation Entropy, Renyi Permutation Entropy, Min-Permutation Entropy, Weighted Permutation Entropy, and Tsallis Entropy
3. EEG Data
4. Classification Models
4.1. Logistic Regression
4.2. ROC Curve: Classifier Performance
4.3. The Validation Set Approach: 10-Fold Cross-Validation
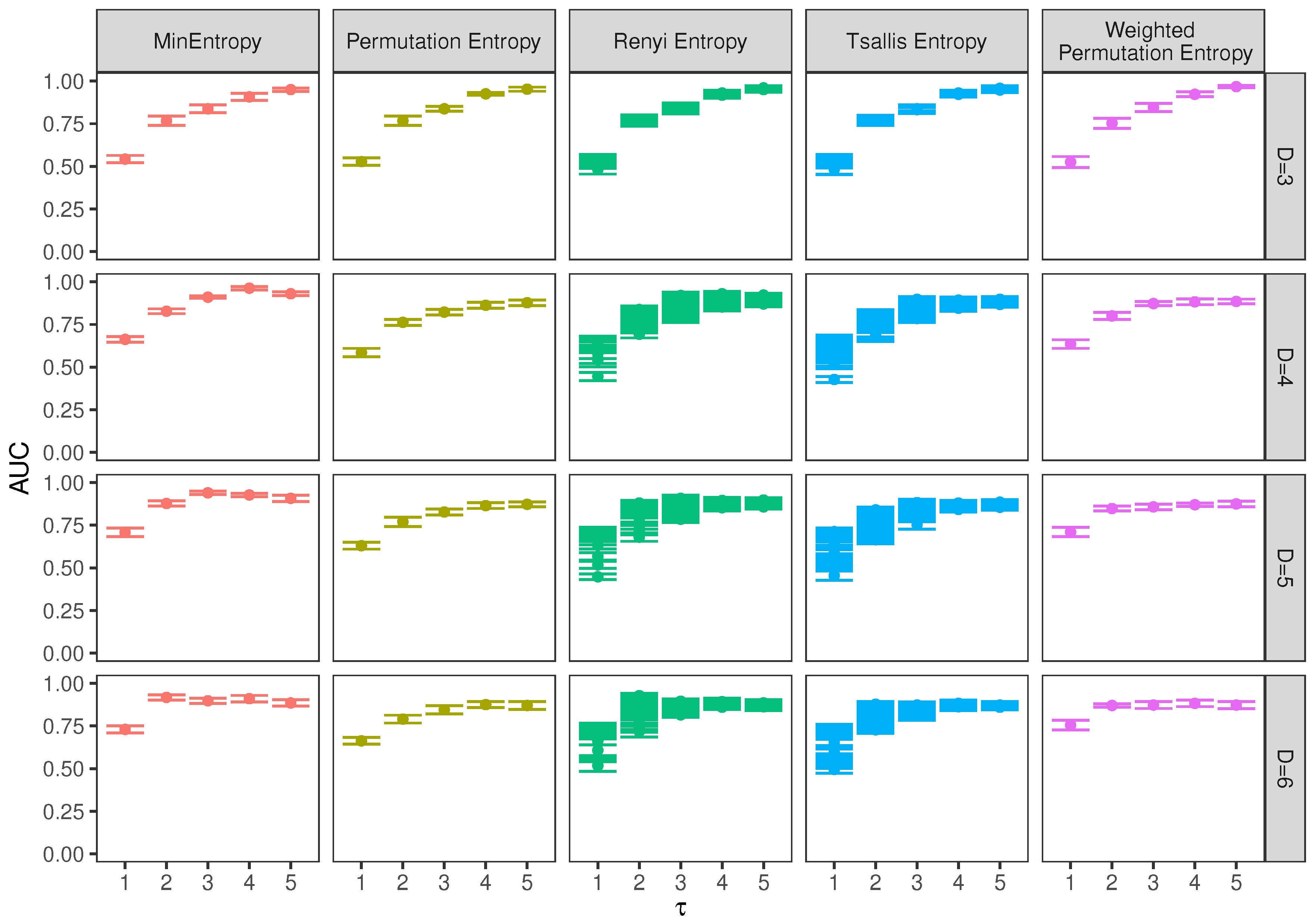
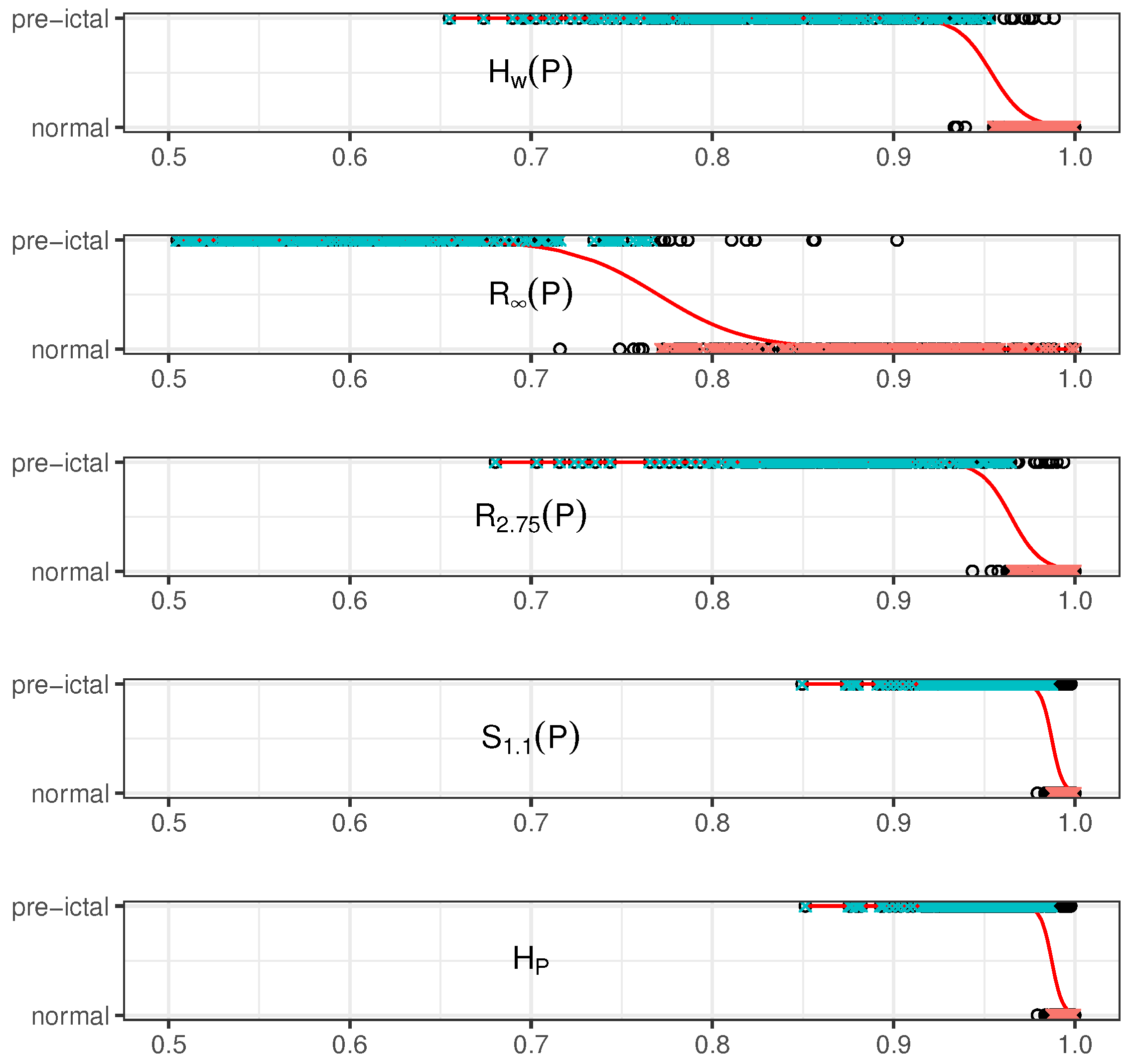
5. Results and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fisher, R.S.; Boas, W.E.; Blume, W.; Elger, C.; Genton, P.; Lee, P.; Engel, J. Epileptic seizures and epilepsy: Definitions proposed by the International League Against Epilepsy (ILAE) and the International Bureau for Epilepsy (IBE). Epilepsia 2005, 46, 470–472. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.S.; Acevedo, C.; Arzimanoglou, A.; Bogacz, A.; Cross, J.H.; Elger, C.E.; Engel, J.; Forsgren, L.; French, J.A.; Glynn, M.; et al. ILAE official report: A practical clinical definition of epilepsy. Epilepsia 2014, 55, 475–482. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Tung, W.; Gao, J.; Protopopescu, V.A.; Hively, L.M. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E 2004, 70, 046217. [Google Scholar] [CrossRef] [PubMed]
- Keller, K.; Wittfeld, K. Distances of time series components by means of symbolic dynamics. Int. J. Bifurc. Chaos 2004, 14, 693–703. [Google Scholar] [CrossRef]
- Veisi, I.; Pariz, N.; Karimpour, A. Fast and robust detection of epilepsy in noisy EEG signals using permutation entropy. In Proceedings of the 2007 IEEE 7th International Symposium on BioInformatics and BioEngineering, Boston, MA, USA, 14–17 October 2007; pp. 200–203.
- Li, X.; Ouyang, G.; Richards, D.A. Predictability analysis of absence seizures with permutation entropy. Epilepsy Res. 2007, 77, 70–74. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, G.; Li, X.; Dang, C.; Richards, D.A. Deterministic dynamics of neural activity during absence seizures in rats. Phys. Rev. E 2009, 79, 041146. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, G.; Dang, C.; Richards, D.A.; Li, X. Ordinal pattern based similarity analysis for EEG recordings. Clin. Neurophysiol. 2010, 121, 694–703. [Google Scholar] [CrossRef] [PubMed]
- Bruzzo, A.A.; Gesierich, B.; Santi, M.; Tassinari, C.A.; Birbaumer, N.; Rubboli, G. Permutation entropy to detect vigilance changes and preictal states from scalp EEG in epileptic patients. A preliminary study. Neurol. Sci. 2008, 29, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Schindler, K.; Gast, H.; Stieglitz, L.; Stibal, A.; Hauf, M.; Wiest, R.; Mariani, L.; Rummel, C. periictal intracranial EEG indicate deterministic dynamics in human epileptic seizures. Epilepsia 2011, 53, 225. [Google Scholar]
- Nicolaou, N.; Georgiou, J. Detection of epileptic electroencephalogram based on permutation entropy and support vector machines. Expert Syst. Appl. 2012, 39, 202–209. [Google Scholar] [CrossRef]
- Li, H.; Heusdens, R.; Muskulus, M.; Wolters, L. Analysis and synthesis of pseudo-periodic job arrivals in grids: A matching pursuit approach. In Proceedings of the Seventh IEEE International Symposium on Cluster Computing and the Grid (CCGrid’07), Rio de Janeiro, Brazil, 14–17 May 2007; pp. 183–196.
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Kannathal, N.; Choo, M.L.; Acharya, U.R.; Sadasivan, P. Entropies for detection of epilepsy in EEG. Comput. Methods Programs Biomed. 2005, 80, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Zunino, L.; Olivares, F.; Rosso, O.A. Permutation min-entropy: An improved quantifier for unveiling subtle temporal correlations. EPL (Europhys. Lett.) 2015, 109, 10005. [Google Scholar] [CrossRef]
- Capurro, A.; Diambra, L.; Lorenzo, D.; Macadar, O.; Martín, M.; Mostaccio, C.; Plastino, A.; Perez, J.; Rofman, E.; Torres, M.; et al. Human brain dynamics: the analysis of EEG signals with Tsallis information measure. Physica A 1999, 265, 235–254. [Google Scholar] [CrossRef]
- Fadlallah, B.; Chen, B.; Keil, A.; Principe, J. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E 2013, 87, 022911. [Google Scholar] [CrossRef] [PubMed]
- Vuong, P.L.; Malik, A.S.; Bornot, J. Weighted-permutation entropy as complexity measure for electroencephalographic time series of different physiological states. In Proceedings of the 2014 IEEE Conference on Biomedical Engineering and Sciences (IECBES), Kuala Lumpur, Malaysia, 8–10 December 2014; pp. 979–984.
- Srinivasan, V.; Eswaran, C.; Sriraam, N. Artificial neural network based epileptic detection using time-domain and frequency-domain features. J. Med. Syst. 2005, 29, 647–660. [Google Scholar] [CrossRef] [PubMed]
- Polat, K.; Güneş, S. Classification of epileptiform EEG using a hybrid system based on decision tree classifier and fast Fourier transform. Appl. Math. Comput. 2007, 187, 1017–1026. [Google Scholar] [CrossRef]
- Subasi, A. EEG signal classification using wavelet feature extraction and a mixture of expert model. Expert Syst. Appl. 2007, 32, 1084–1093. [Google Scholar] [CrossRef]
- Ocak, H. Automatic detection of epileptic seizures in EEG using discrete wavelet transform and approximate entropy. Expert Syst. Appl. 2009, 36, 2027–2036. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.; Martin, M.; Plastino, A.; Fuentes, M. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, 154102. [Google Scholar] [CrossRef] [PubMed]
- Zunino, L.; Soriano, M.C.; Rosso, O.A. Distinguishing chaotic and stochastic dynamics from time series by using a multiscale symbolic approach. Phys. Rev. E 2012, 86, 046210. [Google Scholar] [CrossRef] [PubMed]
- Mammone, N.; Duun-Henriksen, J.; Kjaer, T.W.; Morabito, F.C. Differentiating Interictal and Ictal States in Childhood Absence Epilepsy through Permutation Rényi Entropy. Entropy 2015, 17, 4627–4643. [Google Scholar] [CrossRef]
- Parent, A.; Morin, M.; Lavigne, P. Propagation of super-Gaussian field distributions. Opt. Quantum Electron. 1992, 24, S1071–S1079. [Google Scholar] [CrossRef]
- Benveniste, A.; Goursat, M.; Ruget, G. Robust identification of a nonminimum phase system: Blind adjustment of a linear equalizer in data communications. IEEE Trans. Autom. Control 1980, 25, 385–399. [Google Scholar] [CrossRef]
- Pavón, D. Thermodynamics of superstrings. Gen. Relativ. Gravit. 1987, 19, 375–381. [Google Scholar] [CrossRef]
- Cáceres, M.O. Non-Markovian processes with long-range correlations: Fractal dimension analysis. Braz. J. Phys. 1999, 29, 125–135. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 061907. [Google Scholar] [CrossRef] [PubMed]
- Available online: http://www.meb.unibonn.de/epileptologie/science/physik/eegdata.html (accessed on 16 February 2017).
- Andrzejak, R.; Widman, G.; Lehnertz, K.; Rieke, C.; David, P.; Elger, C. The epileptic process as nonlinear deterministic dynamics in a stochastic environment: An evaluation on mesial temporal lobe epilepsy. Epilepsy Res. 2001, 44, 129–140. [Google Scholar] [CrossRef]
- Acharya, U.R.; Molinari, F.; Sree, S.V.; Chattopadhyay, S.; Ng, K.H.; Suri, J.S. Automated diagnosis of epileptic EEG using entropies. Biomed. Signal Process. Control 2012, 7, 401–408. [Google Scholar] [CrossRef]
- Ghosh-Dastidar, S.; Adeli, H. A new supervised learning algorithm for multiple spiking neural networks with application in epilepsy and seizure detection. Neural Netw. 2009, 22, 1419–1431. [Google Scholar] [CrossRef] [PubMed]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef] [Green Version]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: New York, NY, USA, 2013; Volume 398. [Google Scholar]
- Plastino, A.; Rosso, O.A. Entropy and statistical complexity in brain activity. Europhys. News 2005, 36, 224–228. [Google Scholar] [CrossRef]
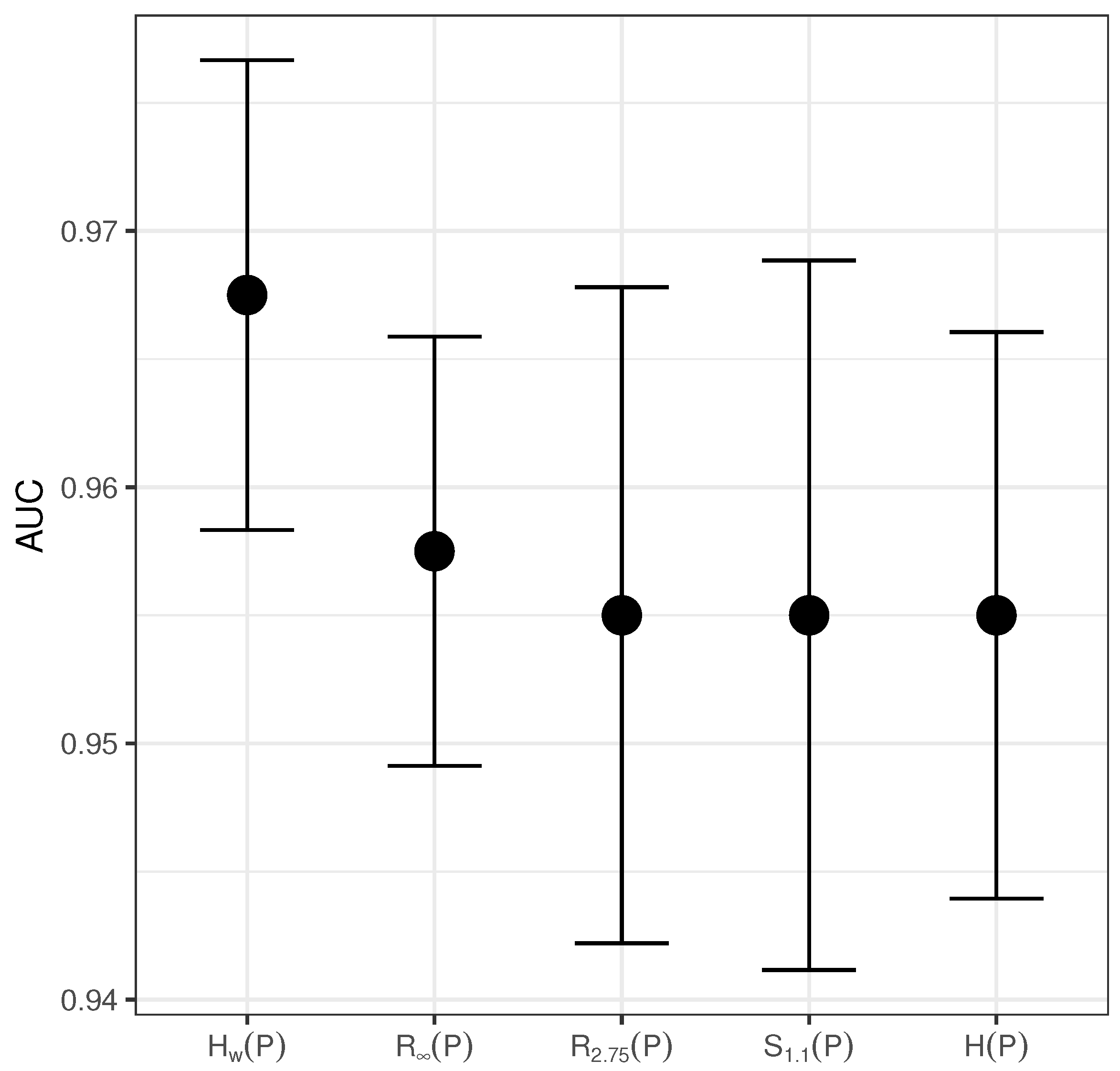
| Entropy | AUC | Accuracy | Sensitivity | Specificity | Regression Coeficient | p-Value |
|---|---|---|---|---|---|---|
| 0.9675 | 0.97 | 0.985 | 0.95 | |||
| 0.9575 | 0.965 | 0.975 | 0.94 | |||
| 0.955 | 0.950 | 0.975 | 0.935 | |||
| 0.955 | 0.950 | 0.97 | 0.94 | |||
| 0.955 | 0.945 | 0.97 | 0.94 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Redelico, F.O.; Traversaro, F.; García, M.D.C.; Silva, W.; Rosso, O.A.; Risk, M. Classification of Normal and Pre-Ictal EEG Signals Using Permutation Entropies and a Generalized Linear Model as a Classifier. Entropy 2017, 19, 72. https://doi.org/10.3390/e19020072
Redelico FO, Traversaro F, García MDC, Silva W, Rosso OA, Risk M. Classification of Normal and Pre-Ictal EEG Signals Using Permutation Entropies and a Generalized Linear Model as a Classifier. Entropy. 2017; 19(2):72. https://doi.org/10.3390/e19020072
Chicago/Turabian StyleRedelico, Francisco O., Francisco Traversaro, María Del Carmen García, Walter Silva, Osvaldo A. Rosso, and Marcelo Risk. 2017. "Classification of Normal and Pre-Ictal EEG Signals Using Permutation Entropies and a Generalized Linear Model as a Classifier" Entropy 19, no. 2: 72. https://doi.org/10.3390/e19020072







