An Entropy-Assisted Shielding Function in DDES Formulation for the SST Turbulence Model
Abstract
:1. Introduction
2. Numerical Methods
2.1. SST-DDES-F2
2.2. SST-DDES-fd_cor
2.3. SST-SDES
3. Results and Discussion
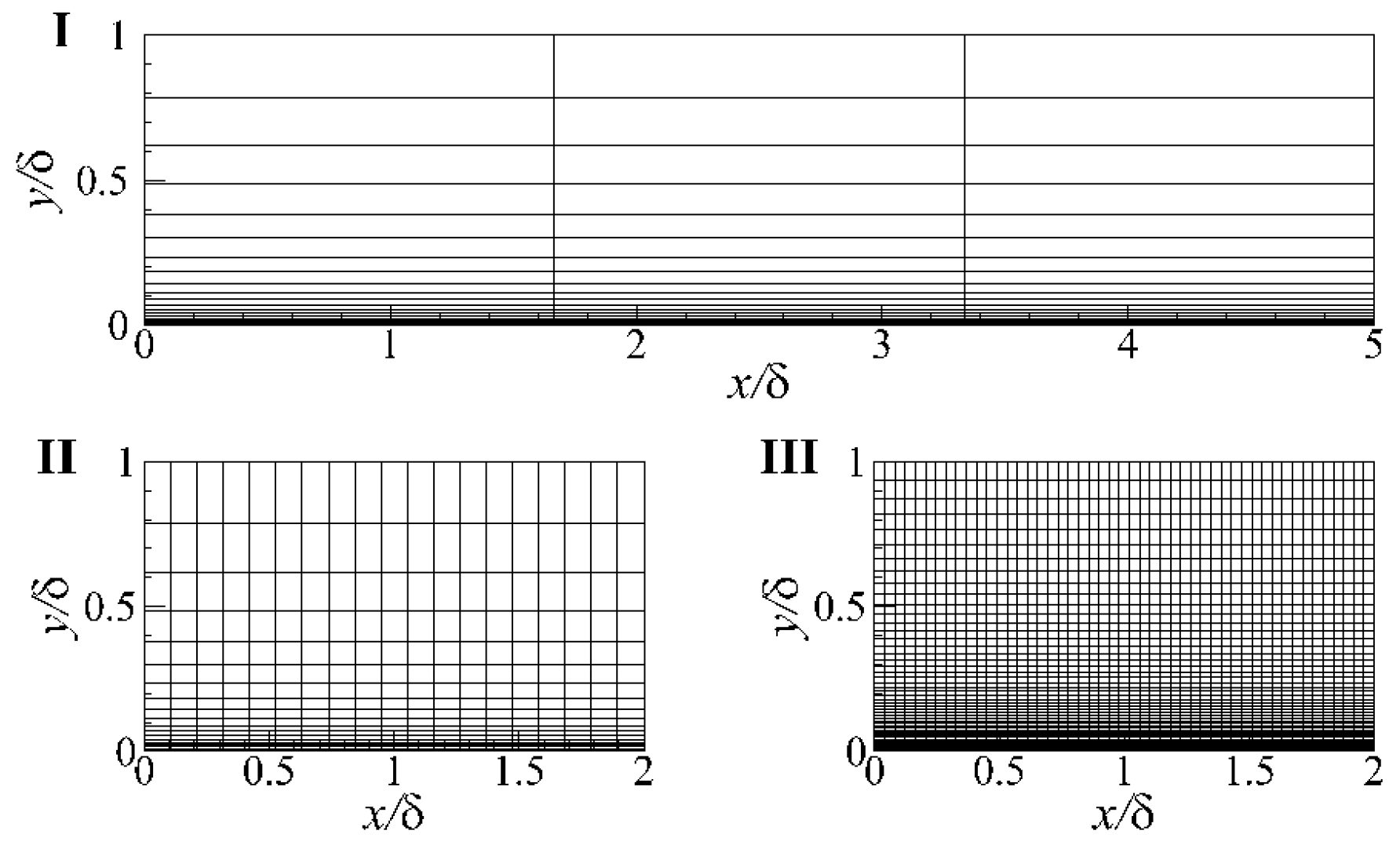
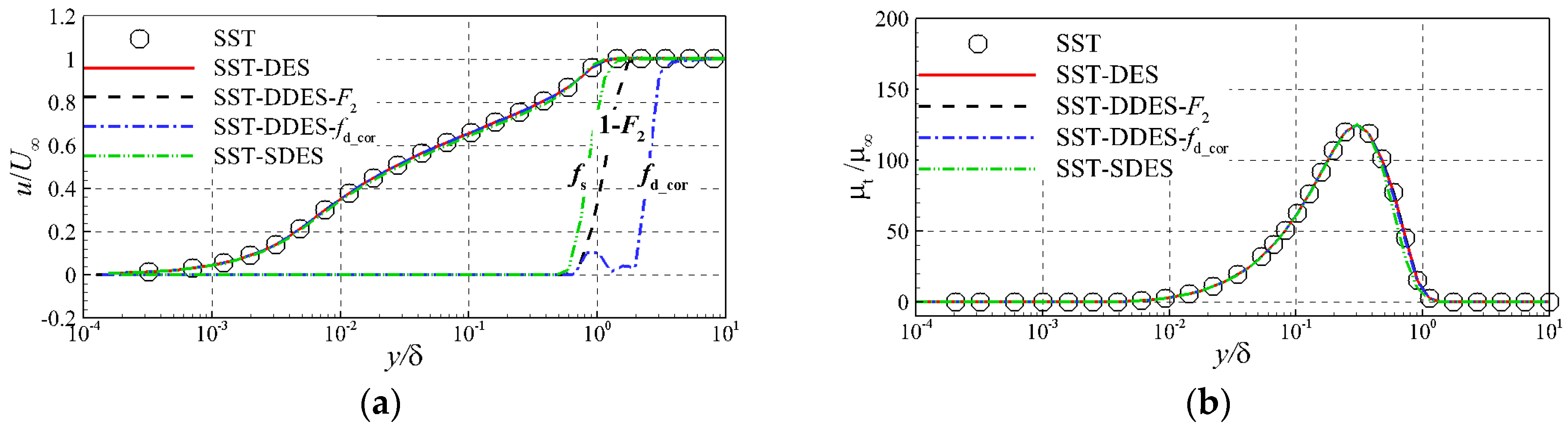
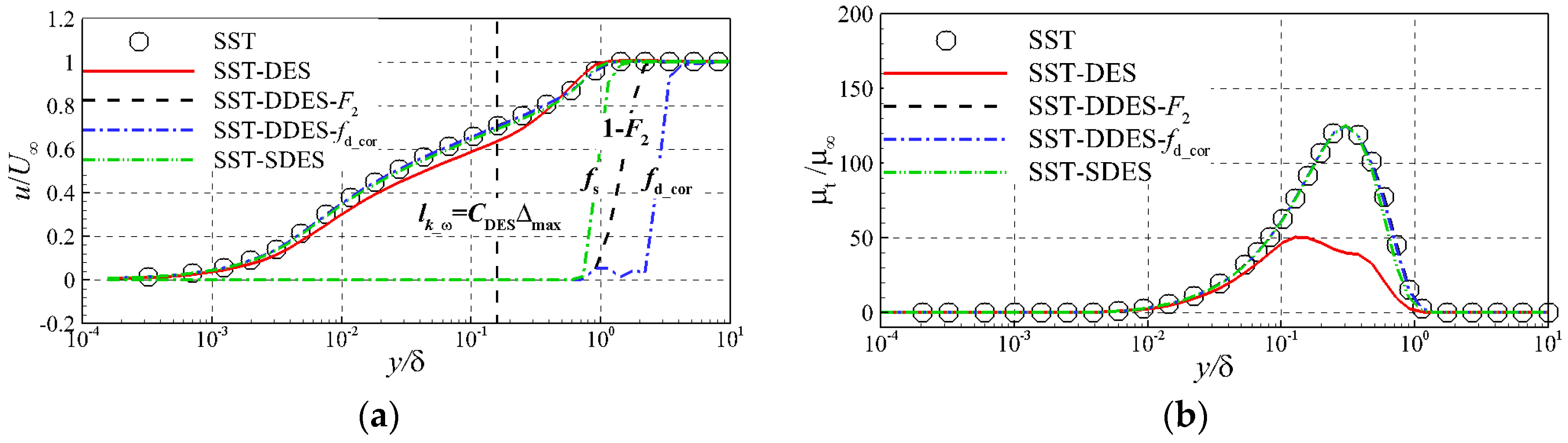
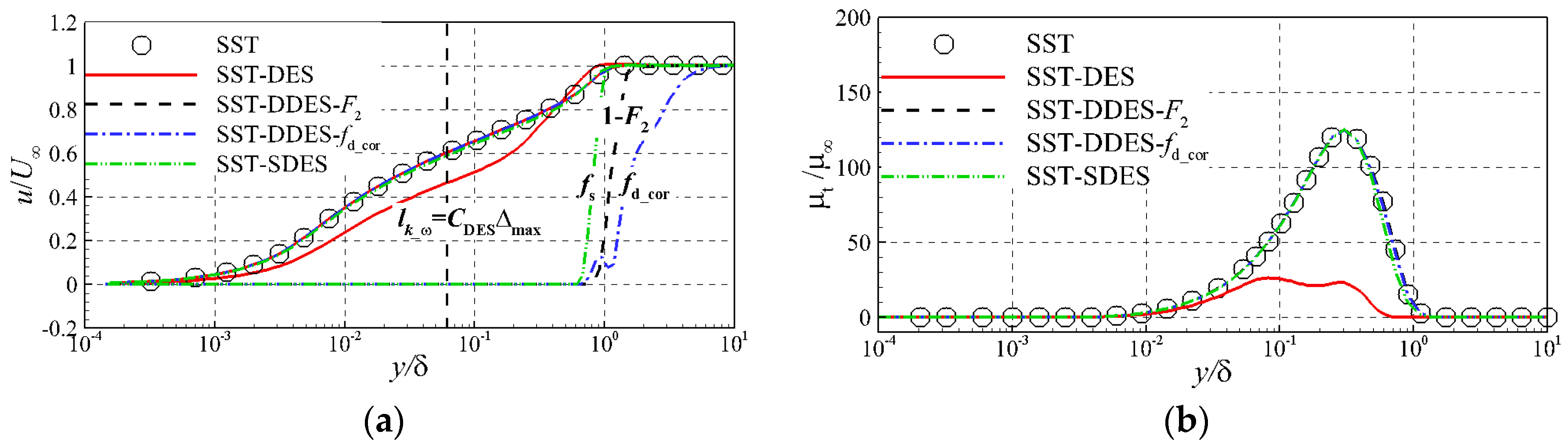
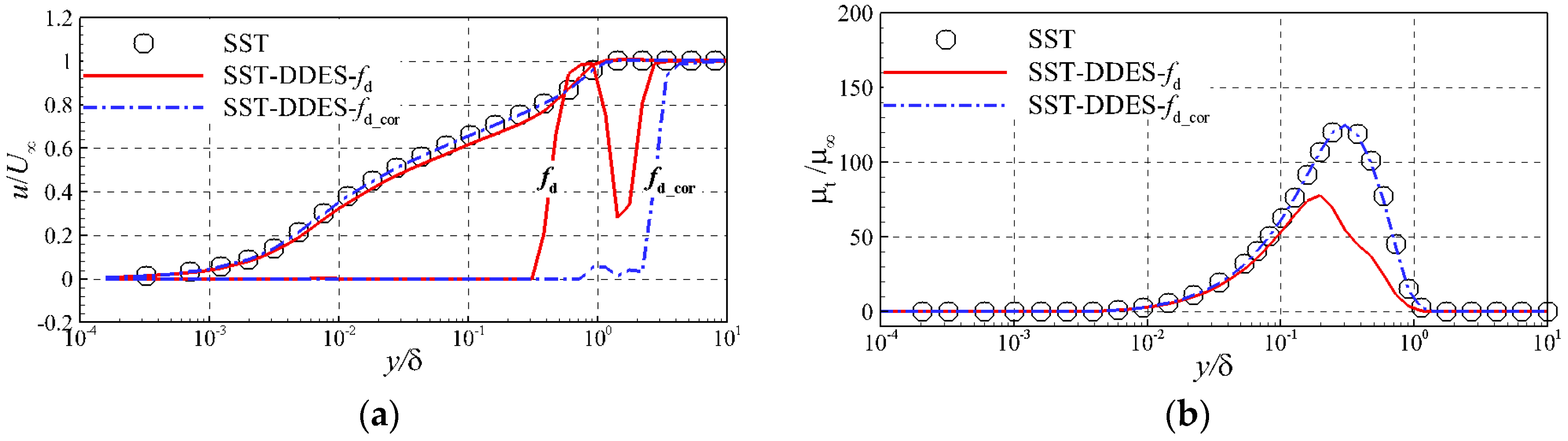
3.1. Flat Plate Flow
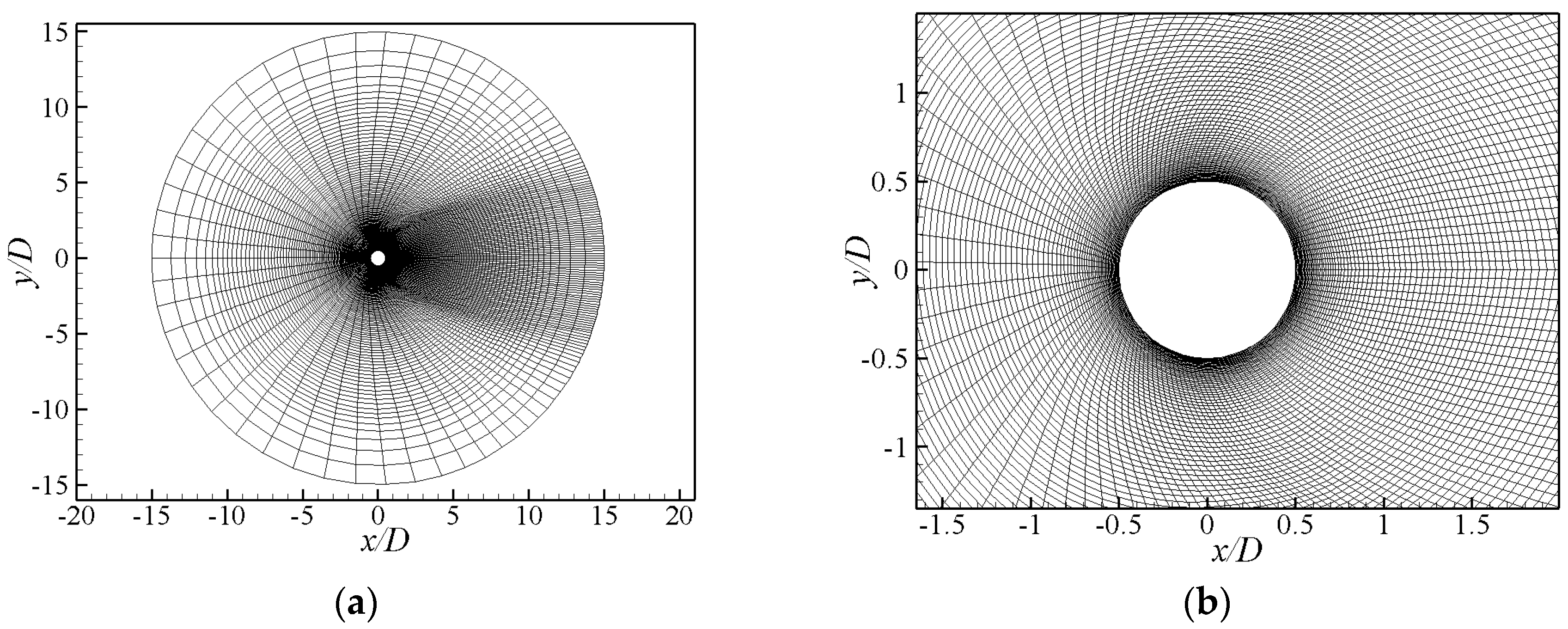
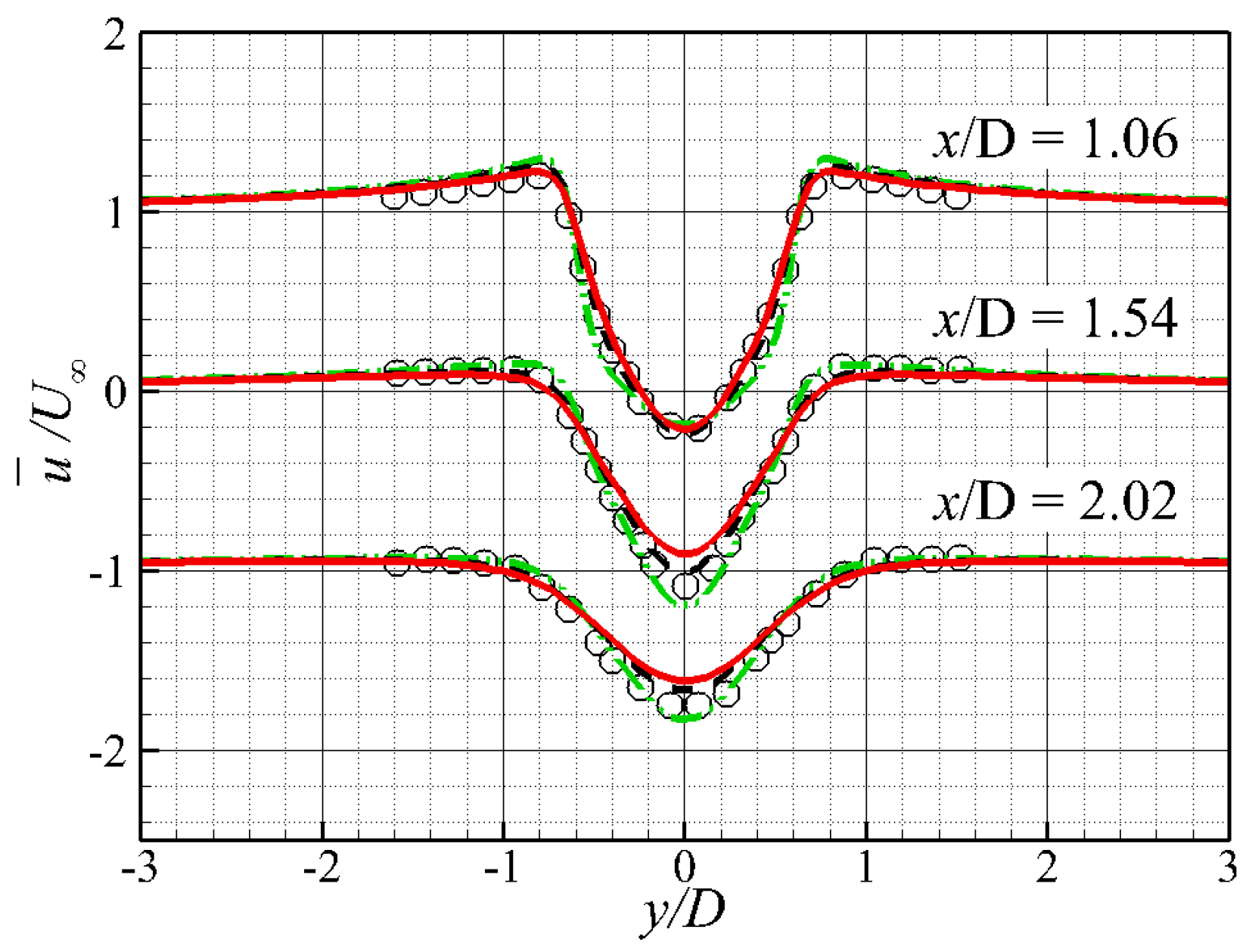
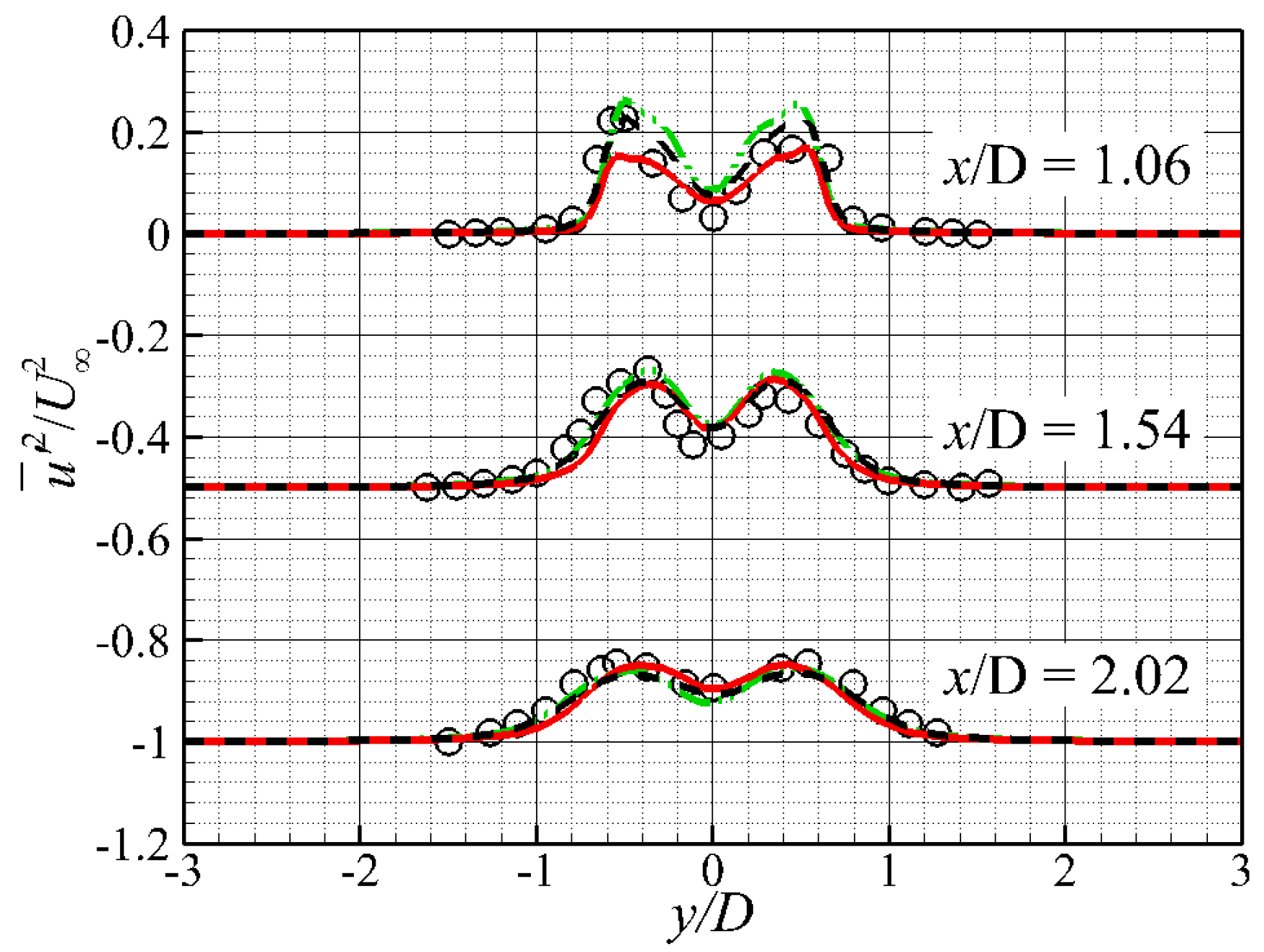
3.2. Circular Cylinder Flow
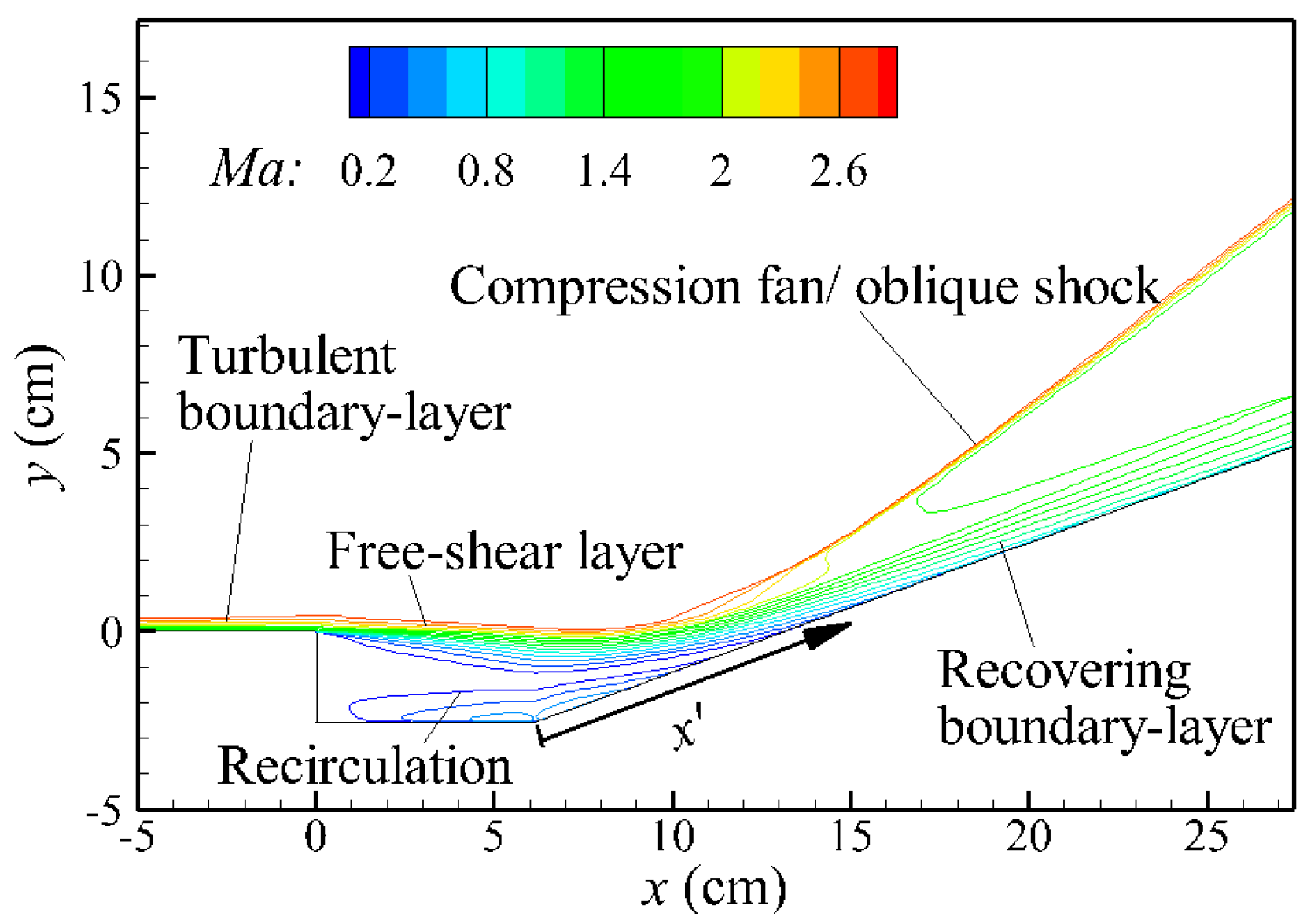
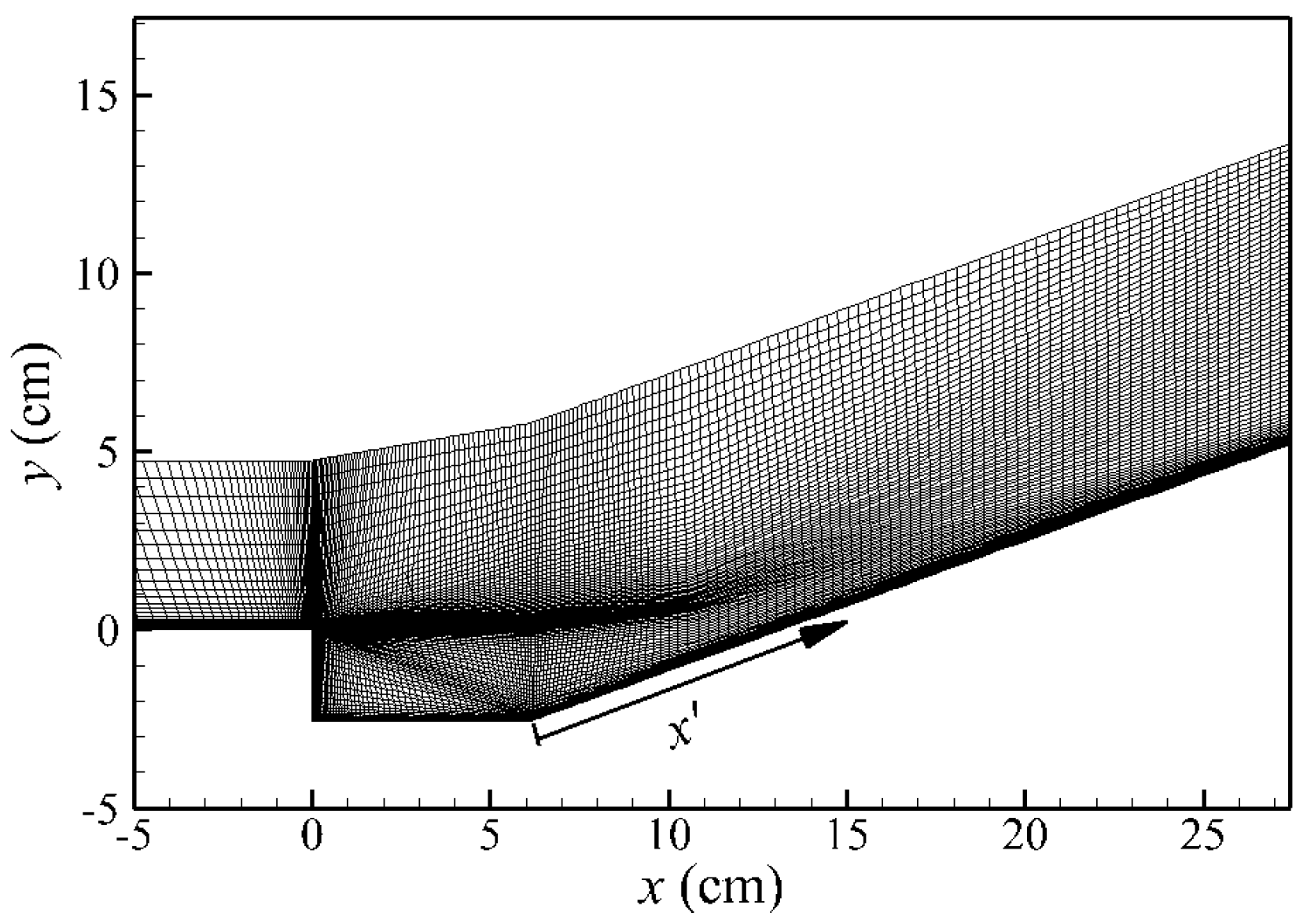
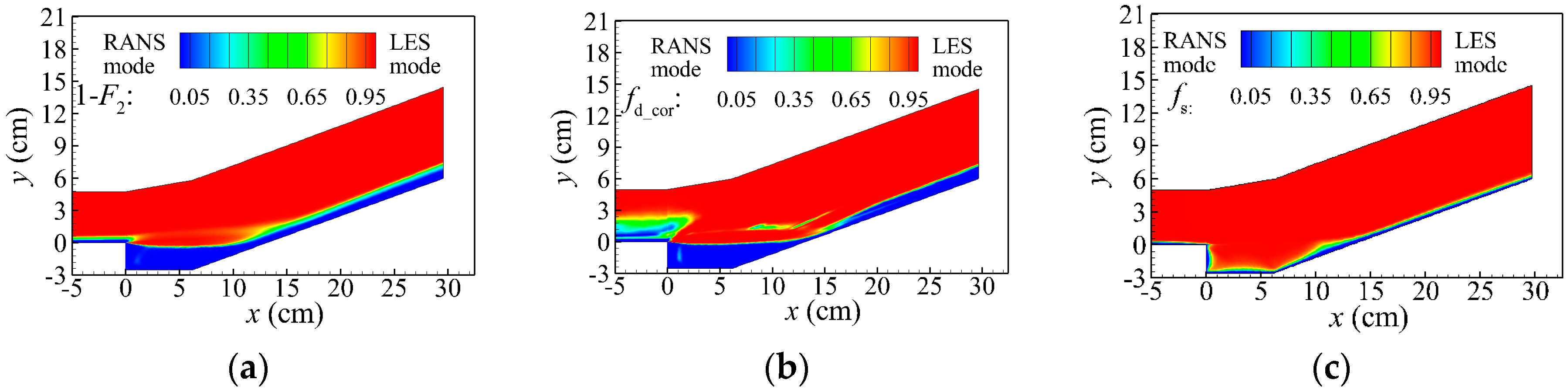
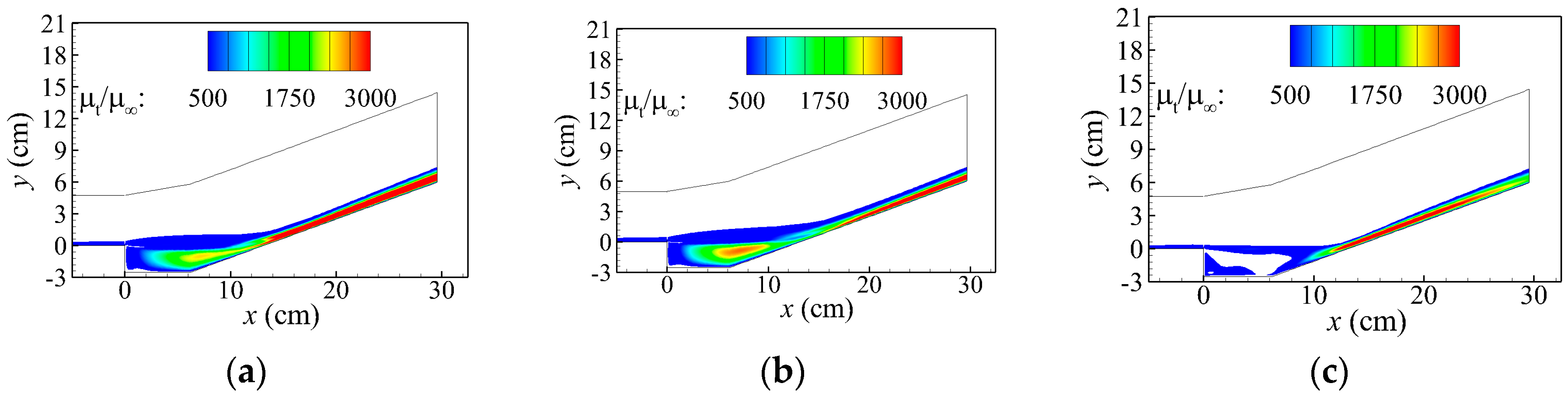
3.3. Cavity-Ramp Flow
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stefan, S.; Frank, T. Comparison of numerical methods applied to the flow over wall-mounted cubes. Int. J. Heat Fluid Flow 2002, 23, 330–339. [Google Scholar]
- Ashton, N.; West, A.; Lardeau, S.; Revell, A. Assessment of RANS and DES methods for realistic automotive models. Comput. Fluids 2016, 128, 1–15. [Google Scholar] [CrossRef]
- Liu, J.L.; Niu, J.L. CFD simulation of the wind environment around an isolated high-rise building: An evaluation of SRANS, LES and DES model. Build. Environ. 2016, 95, 91–106. [Google Scholar] [CrossRef]
- Riéra, W.; Marty, J.; Castillon, L.; Deck, S. Zonal detached-eddy simulation applied to the tip-clearance flow in an axial compressor. AIAA J. 2016, 54, 2377–2391. [Google Scholar] [CrossRef]
- Alam, M.F.; Thompson, D.S.; Walters, D.K. Hybrid Reynolds-Averaged Navier–Stokes/Large-Eddy simulation models for flow around an iced wing. J. Aircr. 2015, 52, 244–256. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M. Lecture Notes in Applied and Computational Mechanics; Springer: Berlin Heidelberg, Germany, 2004; Volume 19, pp. 339–352. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Spalart, P.R.; Allmaras, S.R. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 6–9 January 1992.
- Gritskevich, M.S.; Garbaruk, A.V.; Jochen, S.; Menter, F.R. Development of DDES and IDDES formulations for the k-ω shear stress transport model. Flow Turbul. Combust. 2012, 88, 431–449. [Google Scholar] [CrossRef]
- Gritskevich, M.S.; Garbaruk, A.V.; Menter, F.R. Fine-tuning of DDES and IDDES formulations to the k-ω shear stress transport model. Prog. Flight Phys. 2013, 5, 23–42. [Google Scholar]
- Zhao, R.; Rong, J.L.; Li, X.L. Entropy and its application in turbulence modeling. Chin. Sci. Bull. 2014, 59, 4137–4141. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, C.; Li, X.L.; Kong, W.X. Towards an entropy-based detached eddy simulation. Sci. China Phys. Mech. Astron. 2013, 56, 1970–1980. [Google Scholar] [CrossRef]
- Nichols, R.H.; Tramel, R.W.; Bunning, P.G. Evaluation of two high-order weighted essentially nonoscillatory schemes. AIAA J. 2008, 46, 3090–3102. [Google Scholar] [CrossRef]
- Shen, Y.Q.; Zha, G.C.; Chen, X.Y. High order conservative differencing for viscous terms and the application to vortex-induced vibration flows. J. Comput. Phys. 2009, 228, 8283–8300. [Google Scholar] [CrossRef]
- Xiao, Z.X.; Liu, J.; Huang, J.B.; Fu, S. Numerical dissipation effects on massive separation around tandem cylinders. AIAA J. 2012, 50, 1119–1136. [Google Scholar] [CrossRef]
- Strelets, M.K. Detached eddy simulation of massively separated flows. In Proceedings of the 39th Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 8–11 January 2001.
- Walsh, J.; Davies, R.D.M.; McEligot, M.D. On the use of entropy to predict boundary layer stability. Entropy 2004, 6, 375–387. [Google Scholar] [CrossRef]
- Adeyinka, O.B.; Naterer, G.F. Modeling of entropy production in turbulent flows. J. Fluids Eng. 2004, 126, 893–899. [Google Scholar] [CrossRef]
- Scotti, A.; Meneveau, C.; Lilly, D.K. Generalized smagorinsky model for anisotropic grids. Phys. Fluids A 1993, 5, 2306–2308. [Google Scholar] [CrossRef]
- Travin, A.; Shur, M.; Spalart, P.R.; Strelets, M. Detached eddy simulation past a circular cylinder. Flow Turbul. Combust. 2000, 63, 293–313. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, C. Detailed investigation of detached-eddy simulation for the flow past a circular cylinder at Re = 3900. Appl. Mech. Mater. J. 2012, 401–412. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. Flow around Circular Cylinders; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Bearman, P.W. Investigation of the flow behind a two-dimensional model with a blunt trailing edge and flitted with splitter plates. J. Fluid Mech. 1965, 21, 241–255. [Google Scholar] [CrossRef]
- Philippe, P.; Johan, C.; Dominique, H.; Eric, L. Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys. Fluids 2008, 20, 085101. [Google Scholar]
- Norberg, C. Effects of Reynolds Number, Low-Intensity Free-Stream Turbulence on the Flow around a Circular Cylinder; Chalmer University of Technology: Gothenberg, Sweden, 1987. [Google Scholar]
- Kravchenko, A.G.; Moin, P. Numerical studies of flow over a circular cylinder at ReD = 3900. Phys. Fluids 2000, 12, 403–416. [Google Scholar] [CrossRef]
- Settles, G.S.; Williams, D.R.; Baca, B.K.; Bogdonoff, S.M. Reattachment of a compressible turbulent free shear layer. AIAA J. 1982, 20, 60–67. [Google Scholar]
- Fan, T.C.; Tian, M.; Edwards, J.R.; Hassan, H.A. Validation of a hybrid Reynolds-Averaged/Large-Eddy simulation method for simulating cavity flameholder configurations. In Proceedings of the 31st AIAA Fluid Dynamics Conference & Exhibit, Anaheim, CA, USA, 11–14 June 2001.
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries: La Canada, CA, USA, 2006. [Google Scholar]





| Strategies | Turbulent Length Scale | ||
|---|---|---|---|
| RANS Mode | Transition Mode | LES Mode | |
| SST-DDES-F2 | lk-ω | - | CDESΔmax/(1 − F2) |
| SST-DDES-fd_cor | lk-ω | lk-ω − fd_cor max(0, lk-ω − CDESΔmax) | CDESΔmax |
| SST-SDES | lk-ω | lk-ω − fs max(0, lk-ω − CDESΔmax) | CDESΔmax |
| Strategies | Global Flow Quantities | |||
|---|---|---|---|---|
| St | ||||
| SST-DDES-F2 | 0.92 | 1.18 | 0.2031 | 1.144 |
| SST-DDES-fd_cor | 1.05 | 1.14 | 0.2042 | 1.079 |
| SST-SDES | 1.32 | 1.12 | 0.2048 | 0.957 |
| Experiment [27] | 1.33 ± 0.05 | 0.99 ± 0.05 | 0.215 ± 0.005 | 0.88 ± 0.05 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Zhao, R.; Shi, X.-P. An Entropy-Assisted Shielding Function in DDES Formulation for the SST Turbulence Model. Entropy 2017, 19, 93. https://doi.org/10.3390/e19030093
Zhou L, Zhao R, Shi X-P. An Entropy-Assisted Shielding Function in DDES Formulation for the SST Turbulence Model. Entropy. 2017; 19(3):93. https://doi.org/10.3390/e19030093
Chicago/Turabian StyleZhou, Ling, Rui Zhao, and Xiao-Pan Shi. 2017. "An Entropy-Assisted Shielding Function in DDES Formulation for the SST Turbulence Model" Entropy 19, no. 3: 93. https://doi.org/10.3390/e19030093
APA StyleZhou, L., Zhao, R., & Shi, X.-P. (2017). An Entropy-Assisted Shielding Function in DDES Formulation for the SST Turbulence Model. Entropy, 19(3), 93. https://doi.org/10.3390/e19030093





