Numerical Study of the Magnetic Field Effects on the Heat Transfer and Entropy Generation Aspects of a Power Law Fluid over an Axisymmetric Stretching Plate Structure
Abstract
:1. Introduction
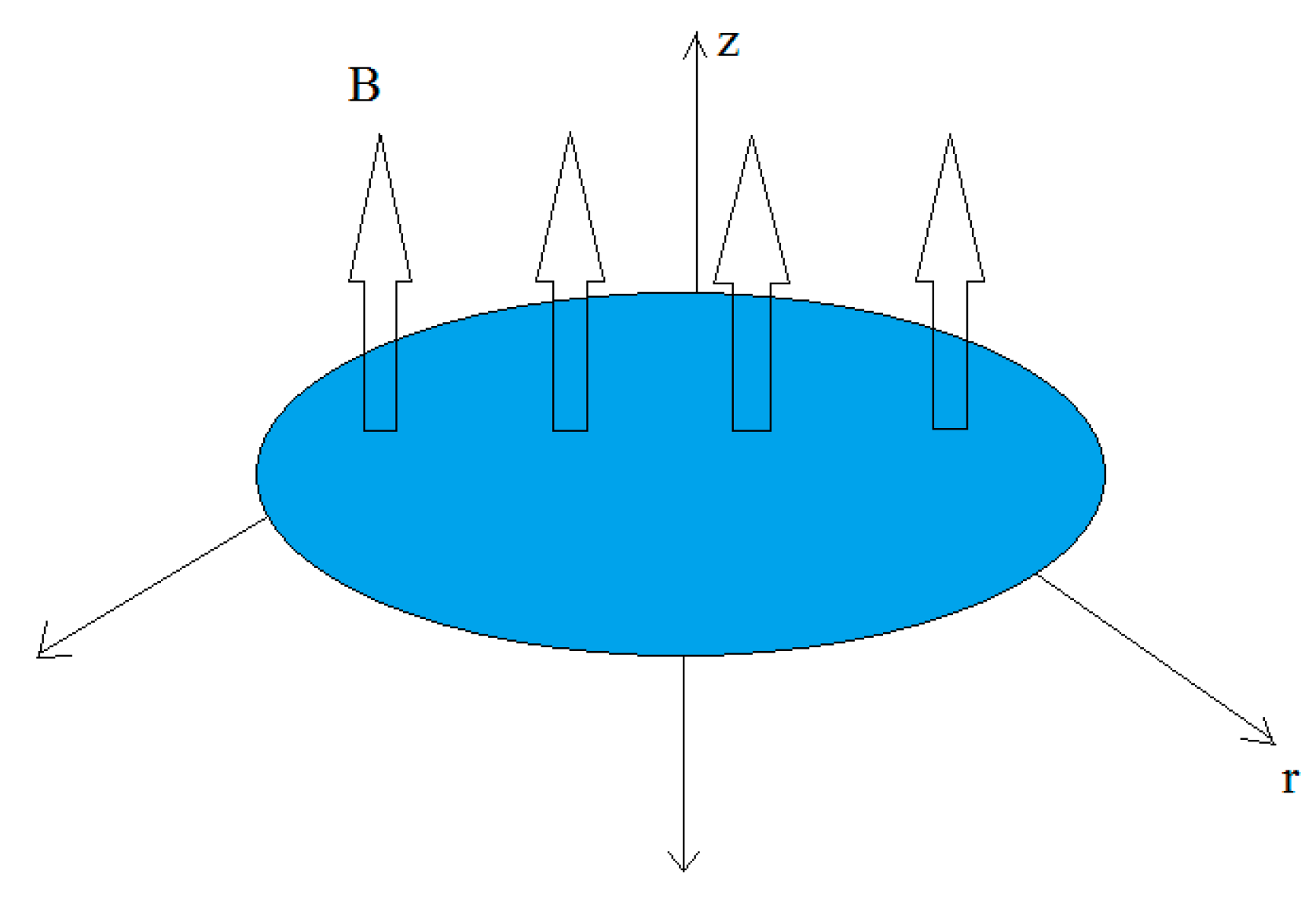
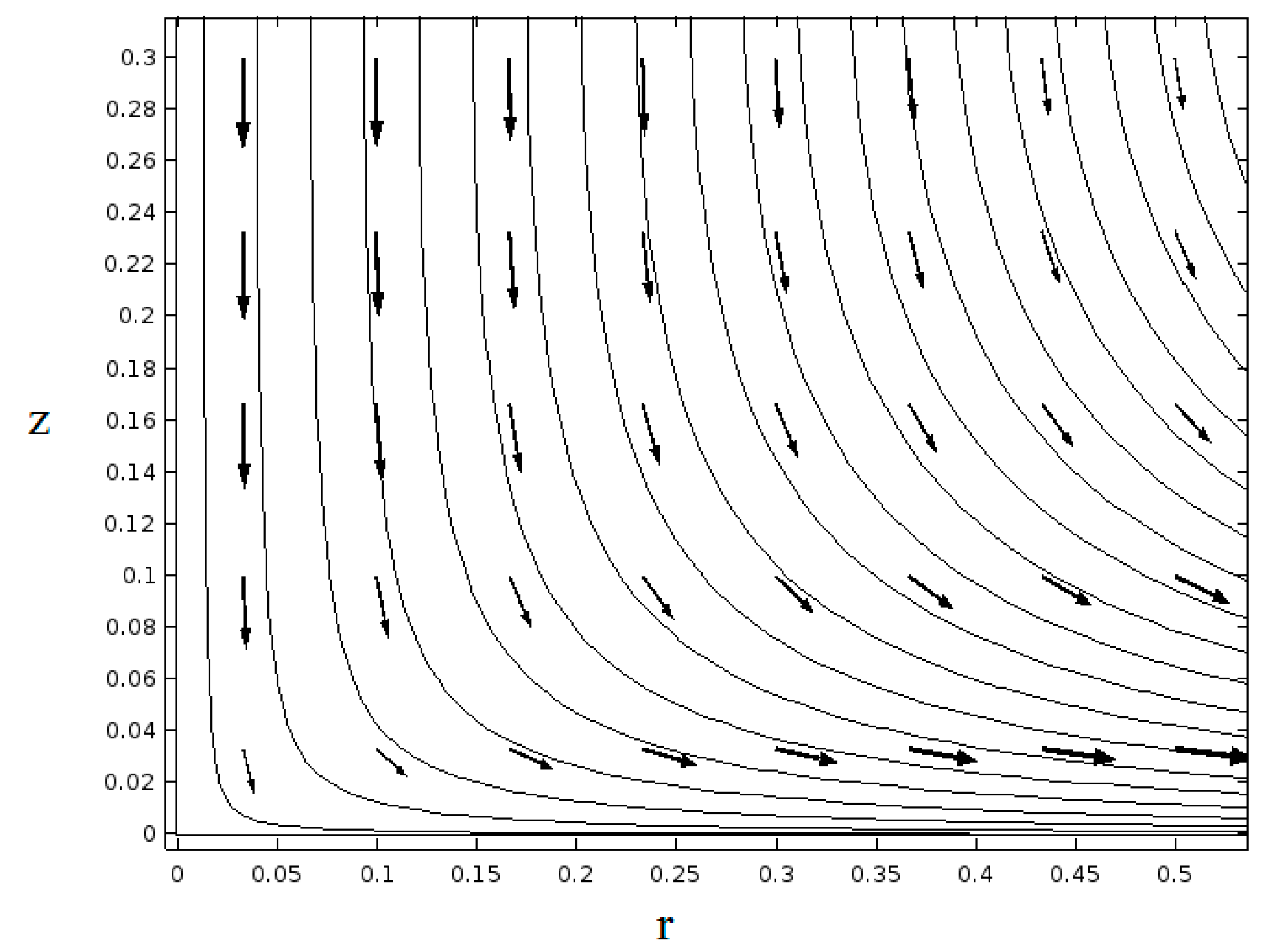
2. Governing Equations
3. Results and Discussion
4. Conclusions
- (1)
- The coupled model is able to simulate the flow of a shear thinning fluid. By increasing n, the boundary layer of heat transfer is decreased and the heat transfer on the stretching sheet is increased. The justification and the reason behind the trends depicted have been explained in detail.
- (2)
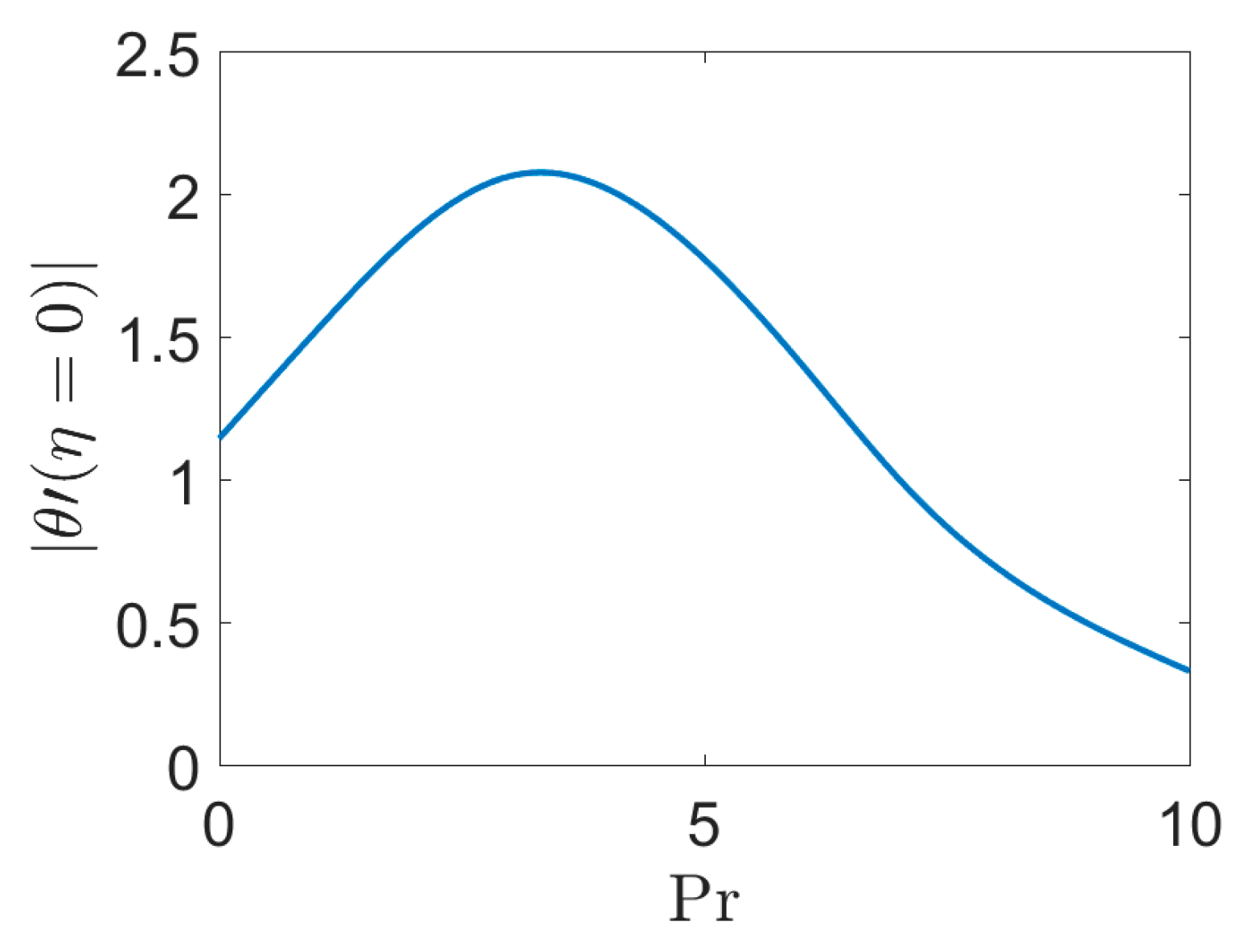
- By increasing Pr, the boundary layer of heat transfer is decreased and the heat transfer rate on the stretching sheet is increased. Such a development of the heat flux over the heat source prevents the cooling of the fluid on the bottom wall. An increment in Prandtl number shows a marked reduction in the temperature profile.
- (3)
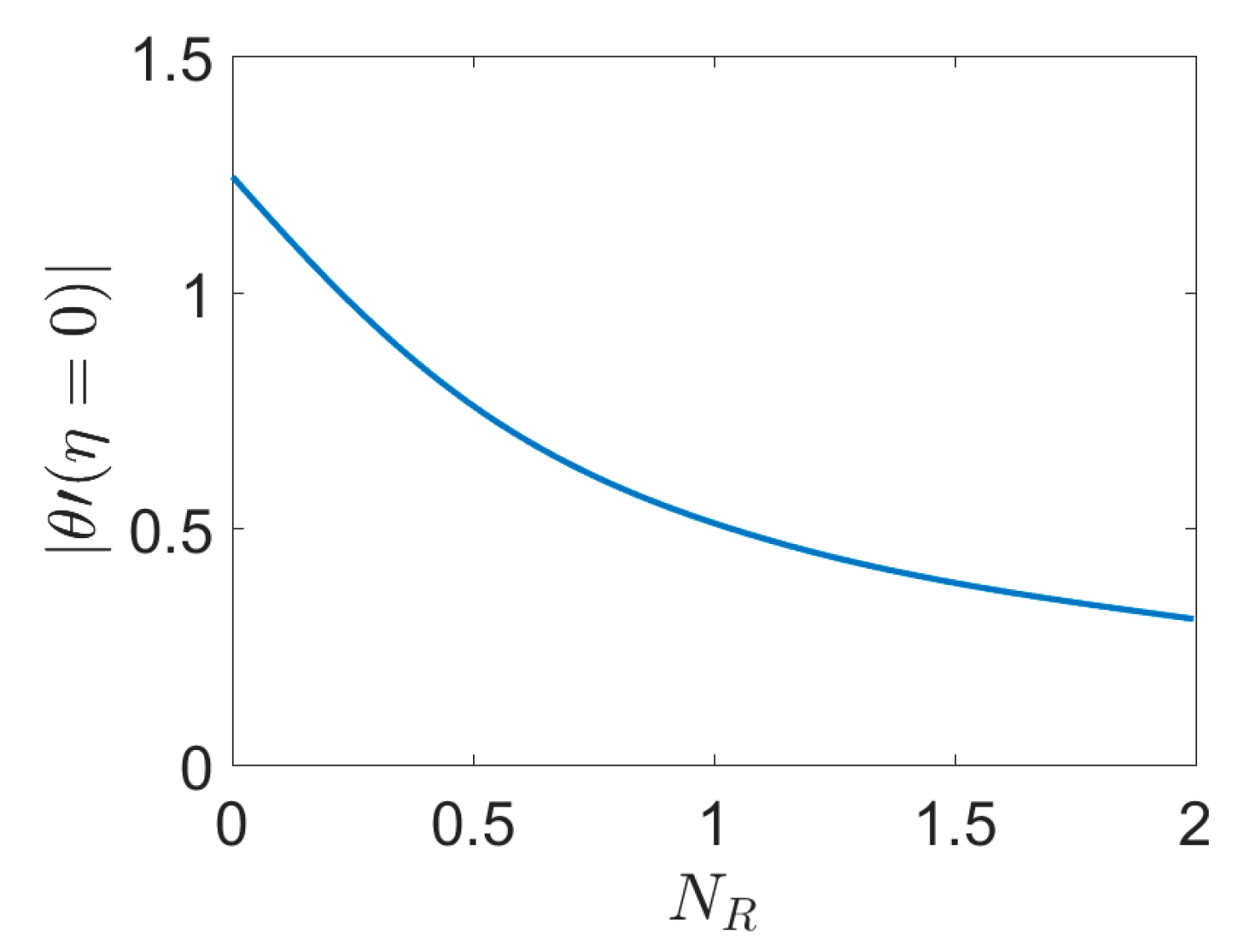
- By increasing NR, the boundary layer of heat transfer is increased and the convective heat transfer rate on the stretching sheet is decreased. A reduction of Nu can be explained by an attenuation of the convective flow and also by narrowing of the boundary layer.
- (4)
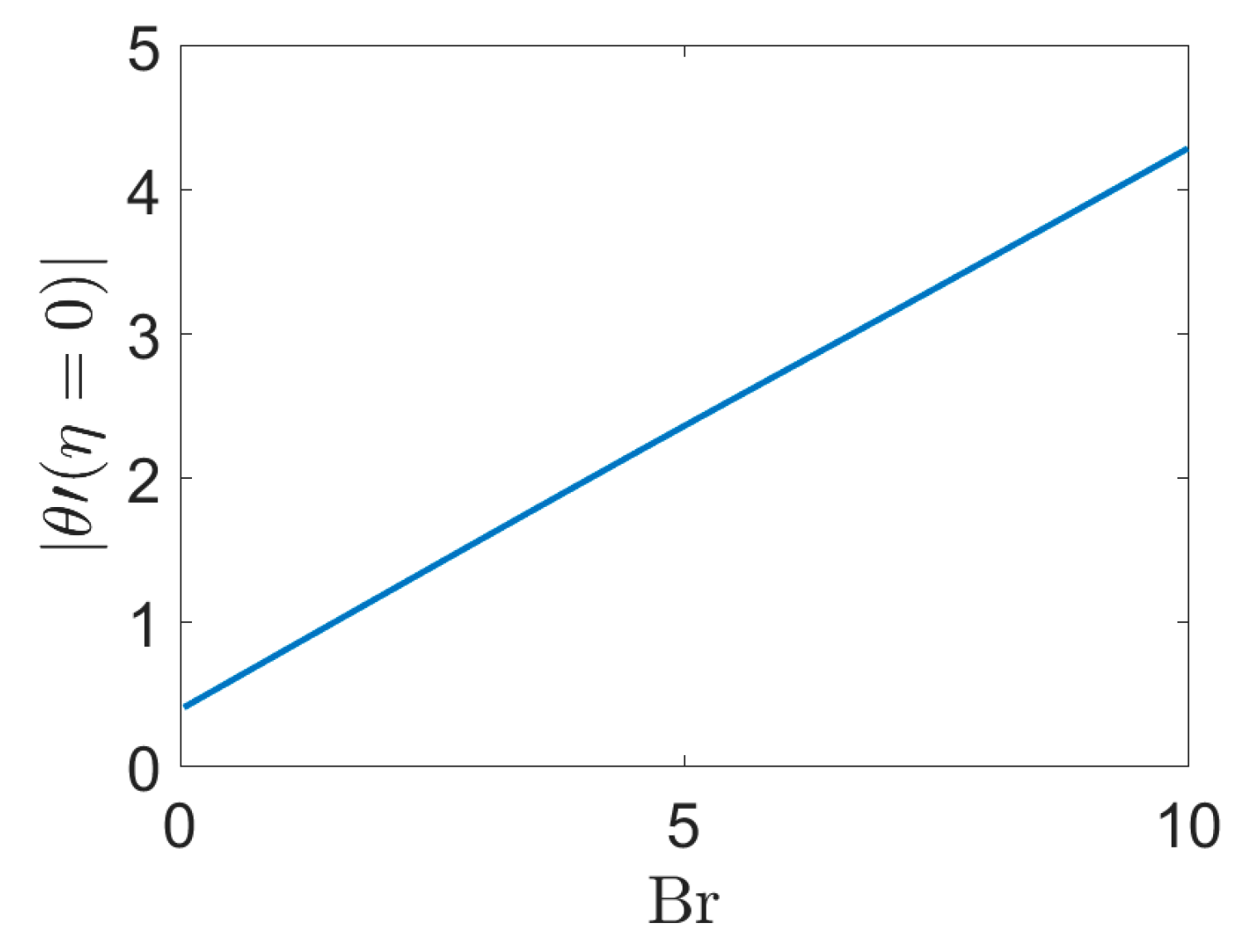
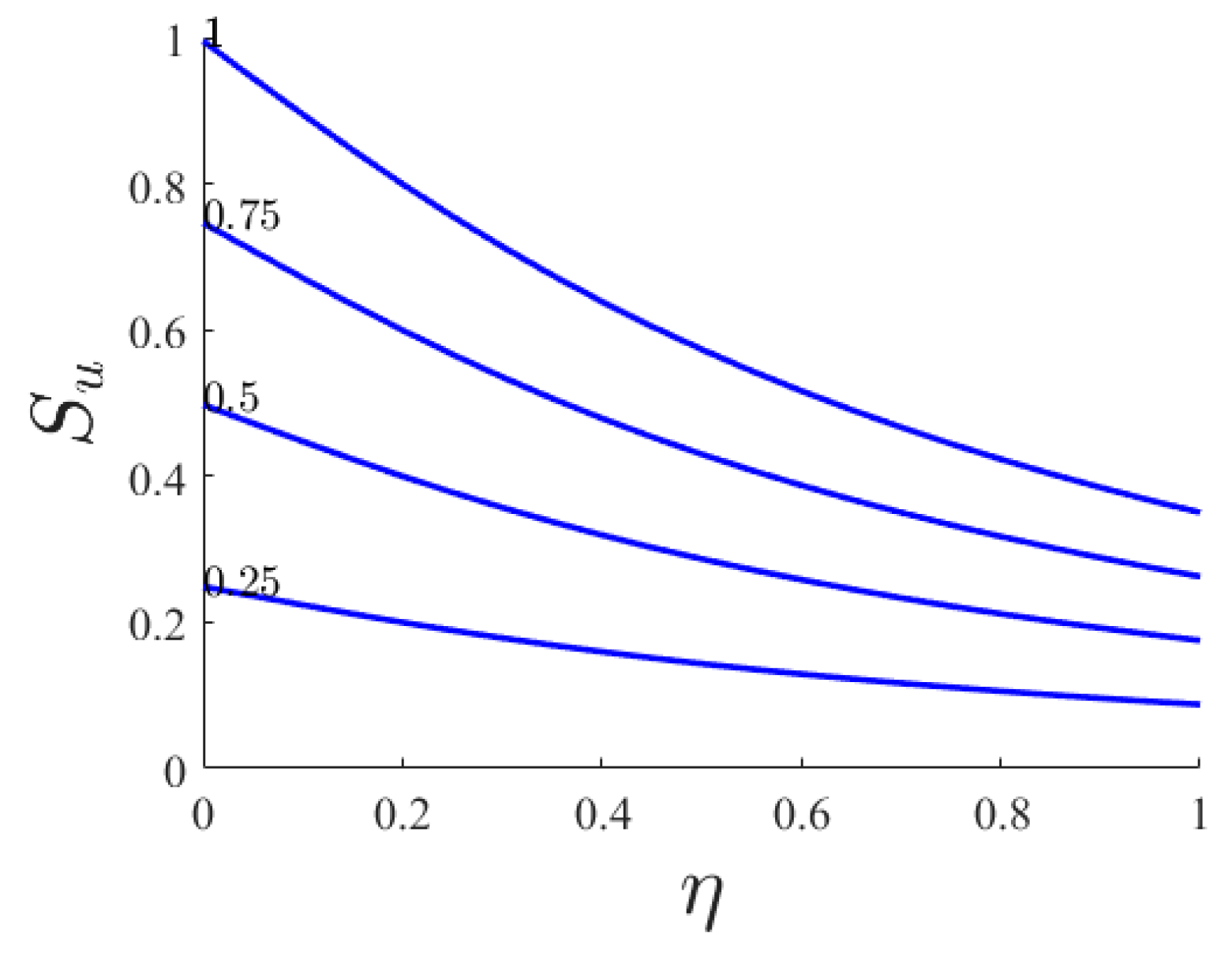
- In two-dimensional (2D) non-Newtonian flow, by increasing Br, the boundary layer of heat transfer and the convective heat transfer rate on the stretching sheet are increased.
- (5)
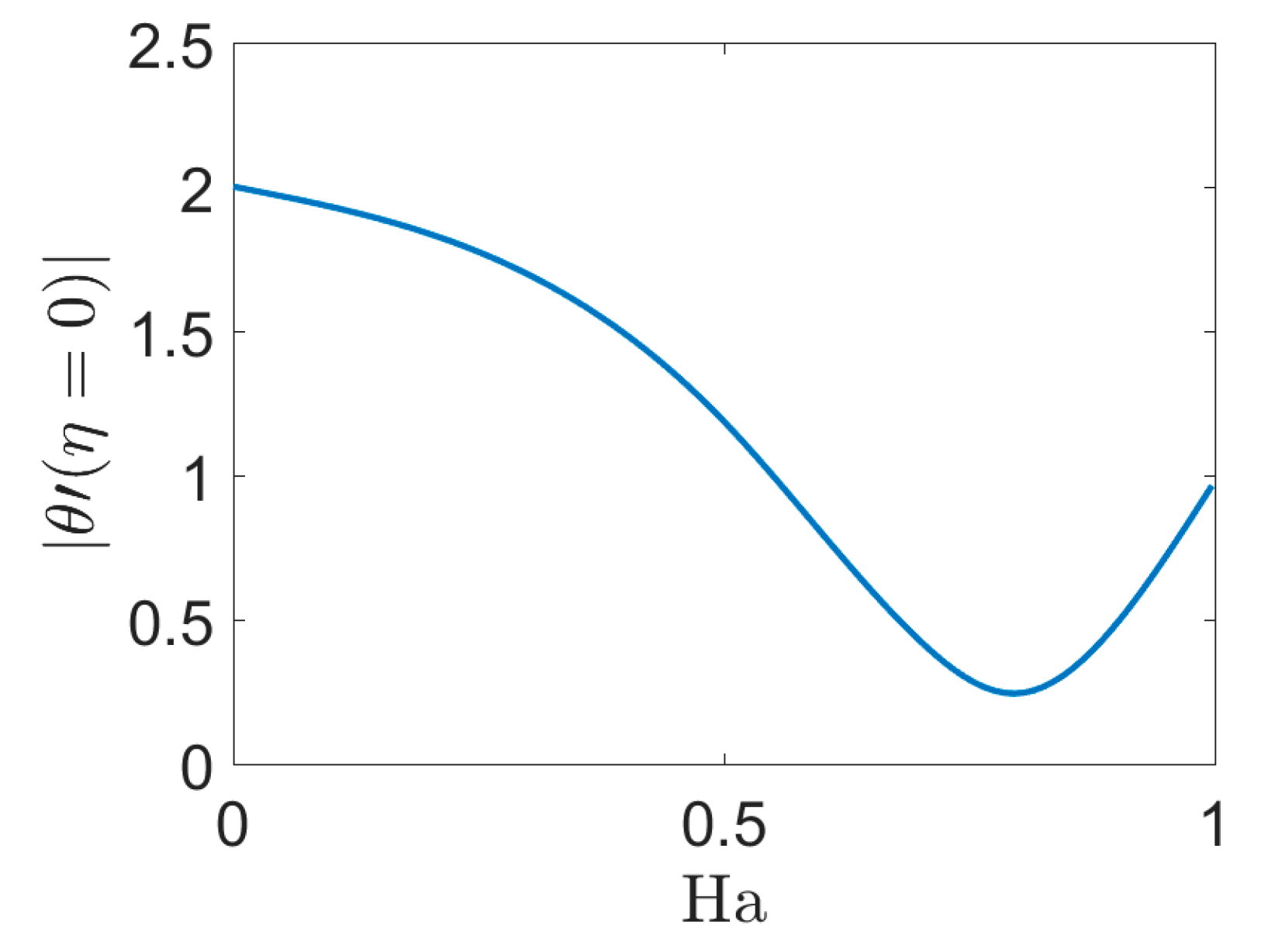
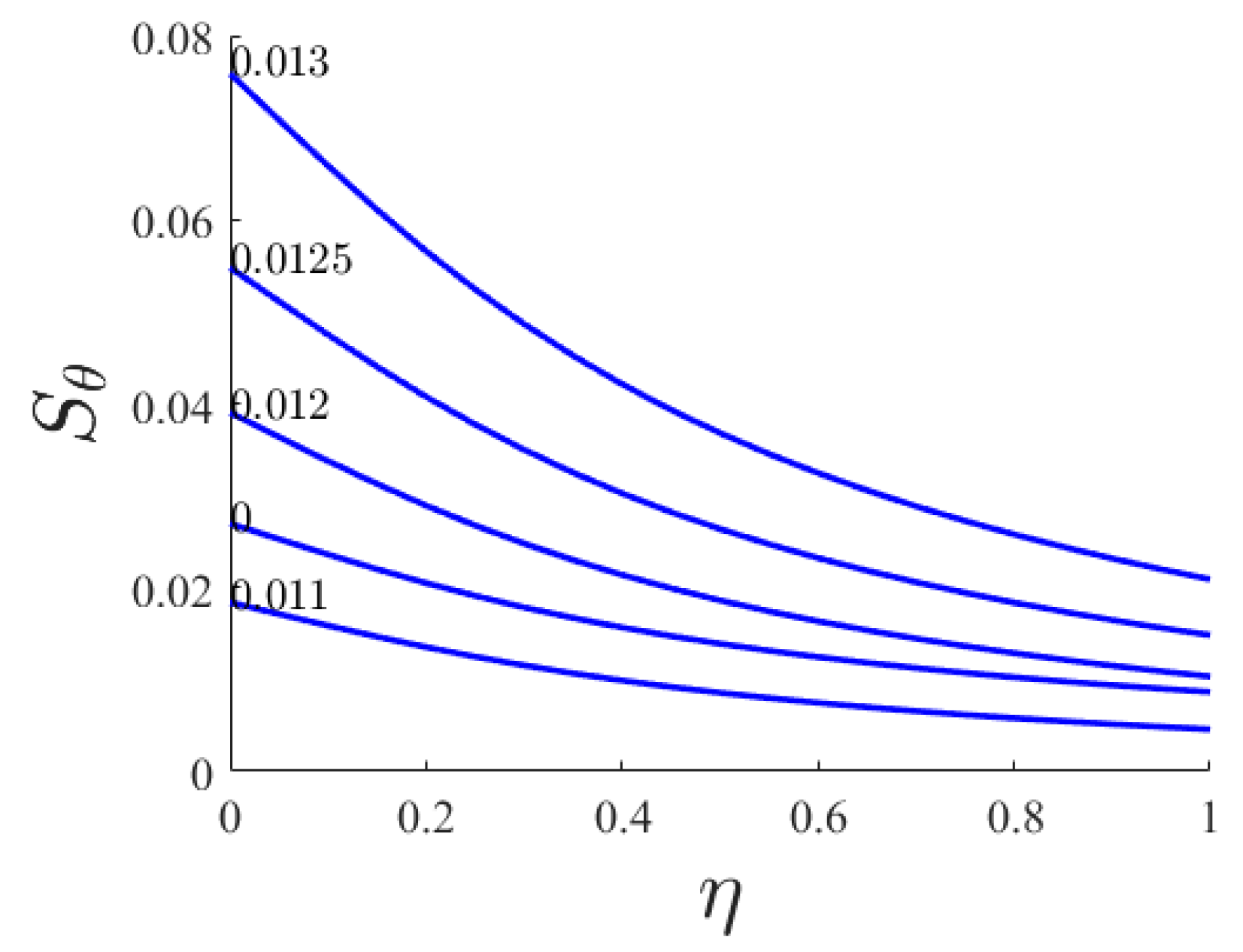
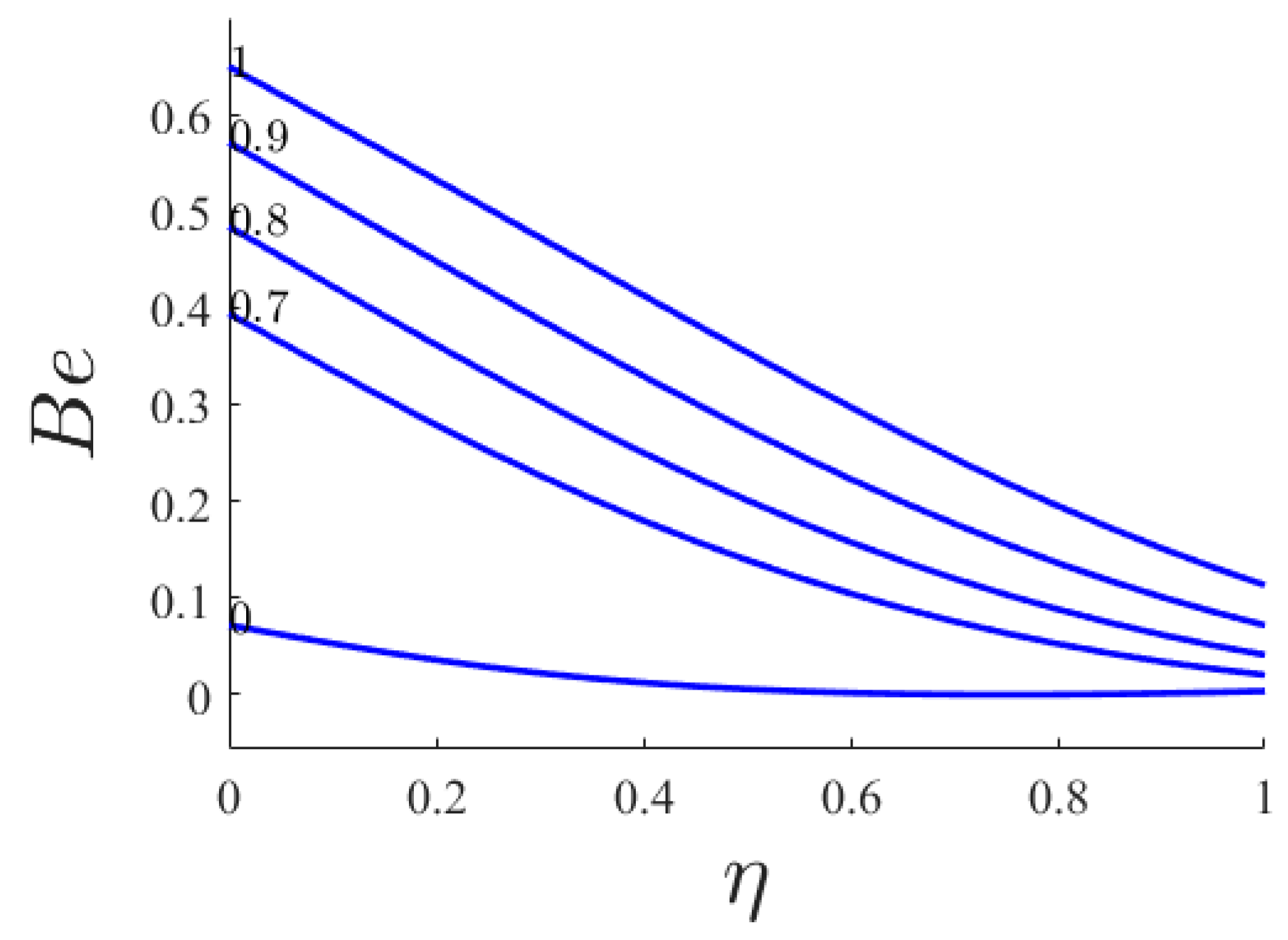
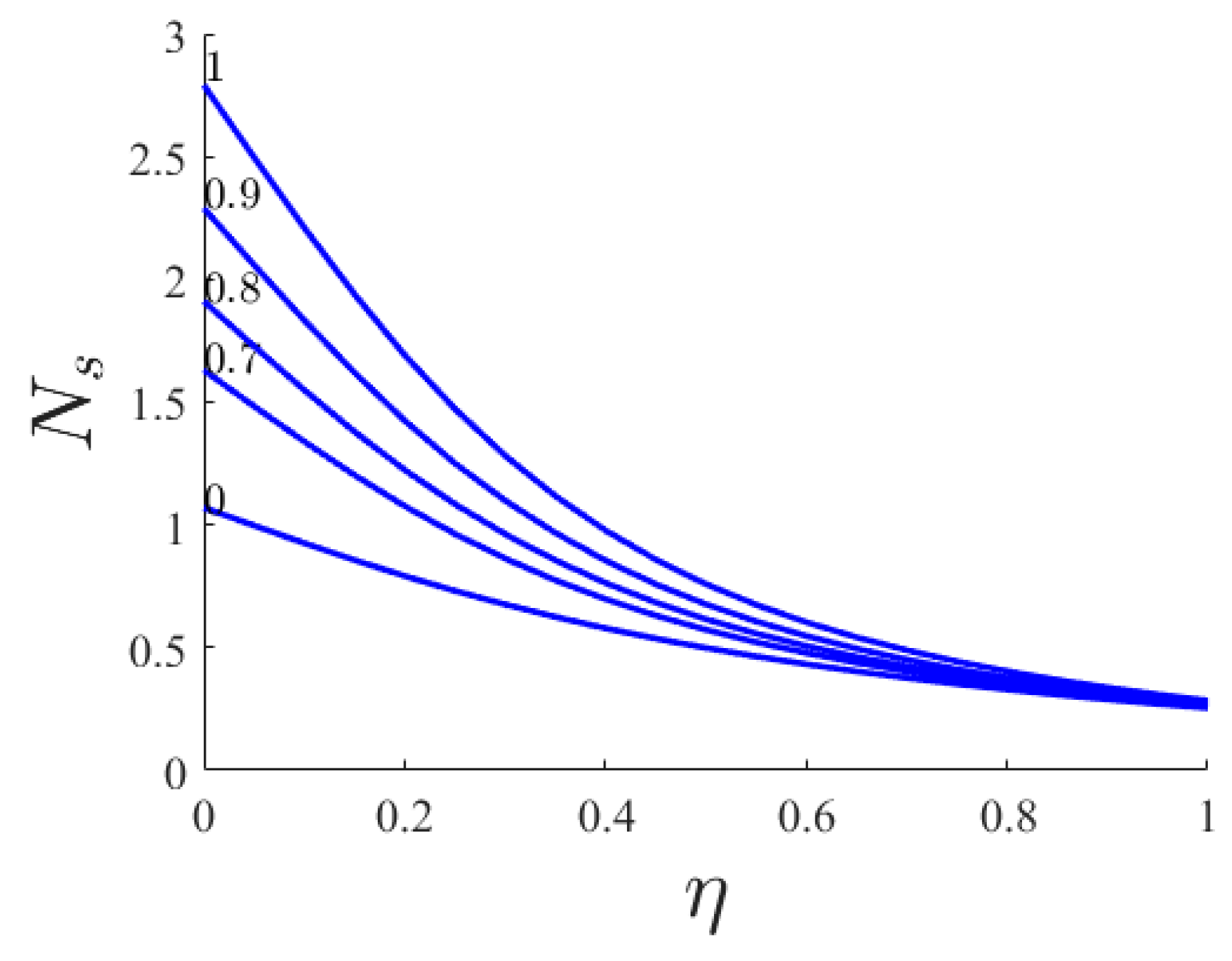
- By increasing Ha, the boundary layer of heat transfer and the convective heat transfer rate on the stretching sheet have a minimum at Ha = 0.8. An increase in the Ha leads to an attenuation of convective flow and less intensive cooling of the bottom part of the cavity. Average Nusselt and Bejan numbers and average total entropy generation are increasing functions of Ha.
- (6)
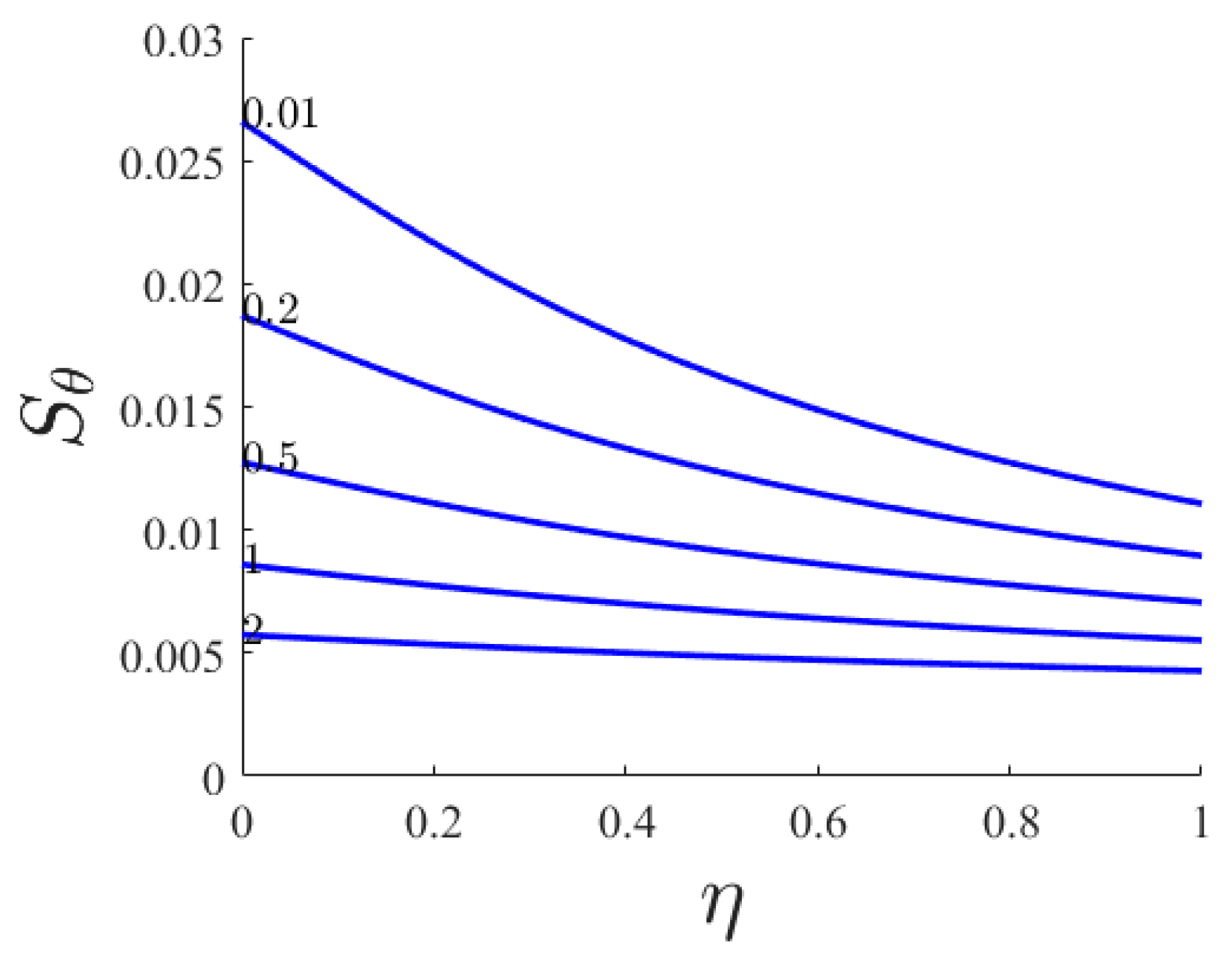
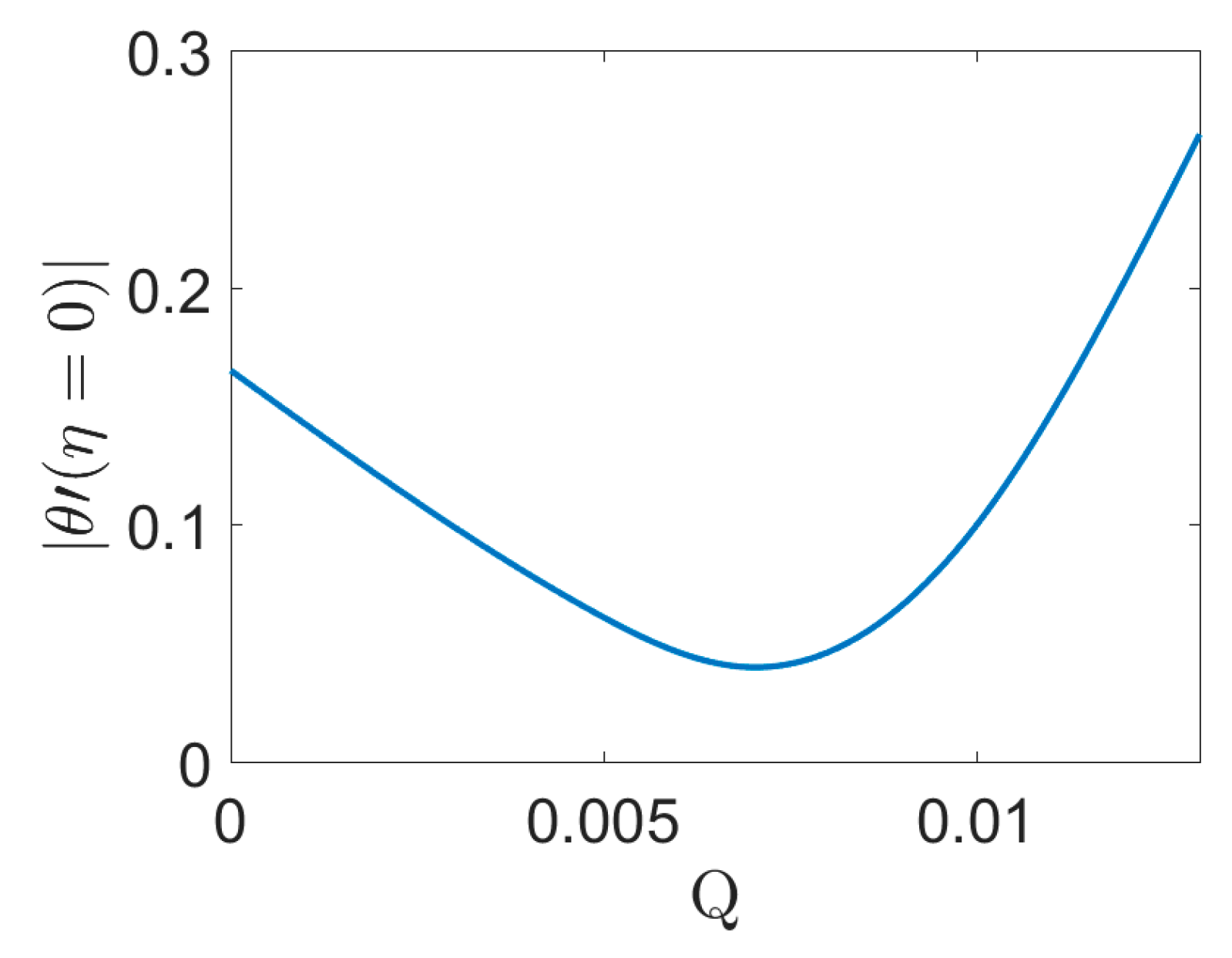
- By increasing Q, the boundary layer of heat transfer and the convective heat transfer rate on the stretching sheet has minimum on Q = 0.006.
- (7)
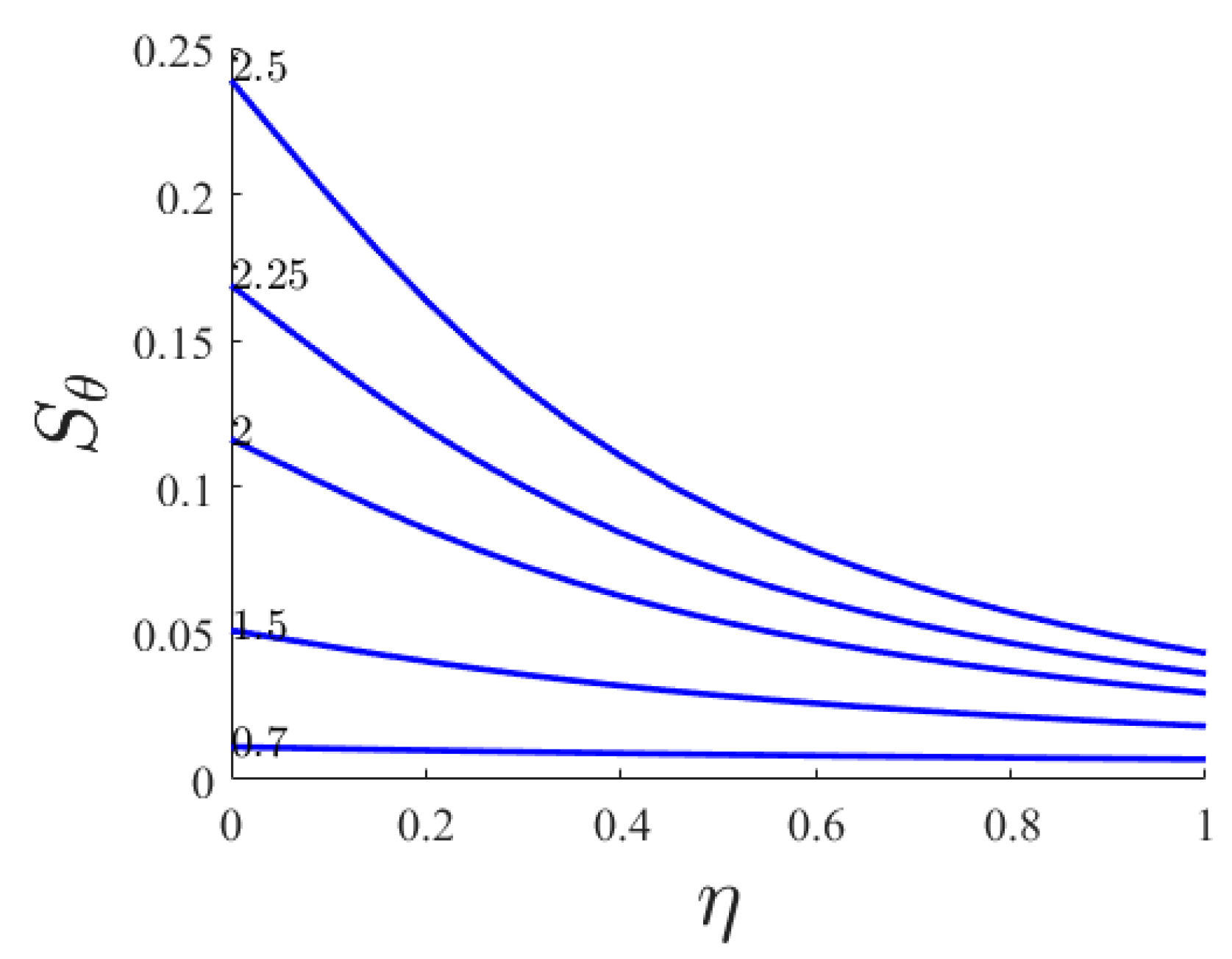
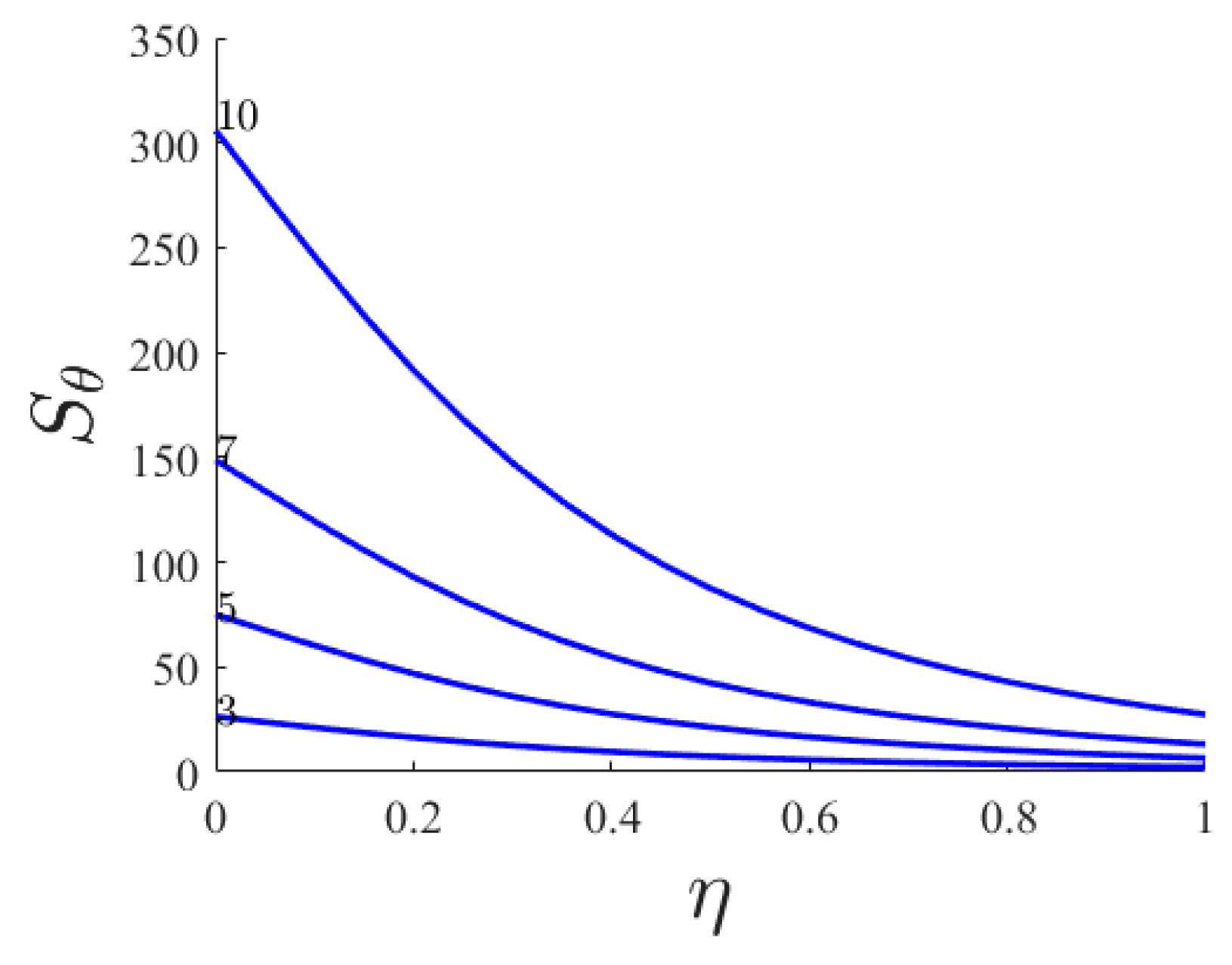
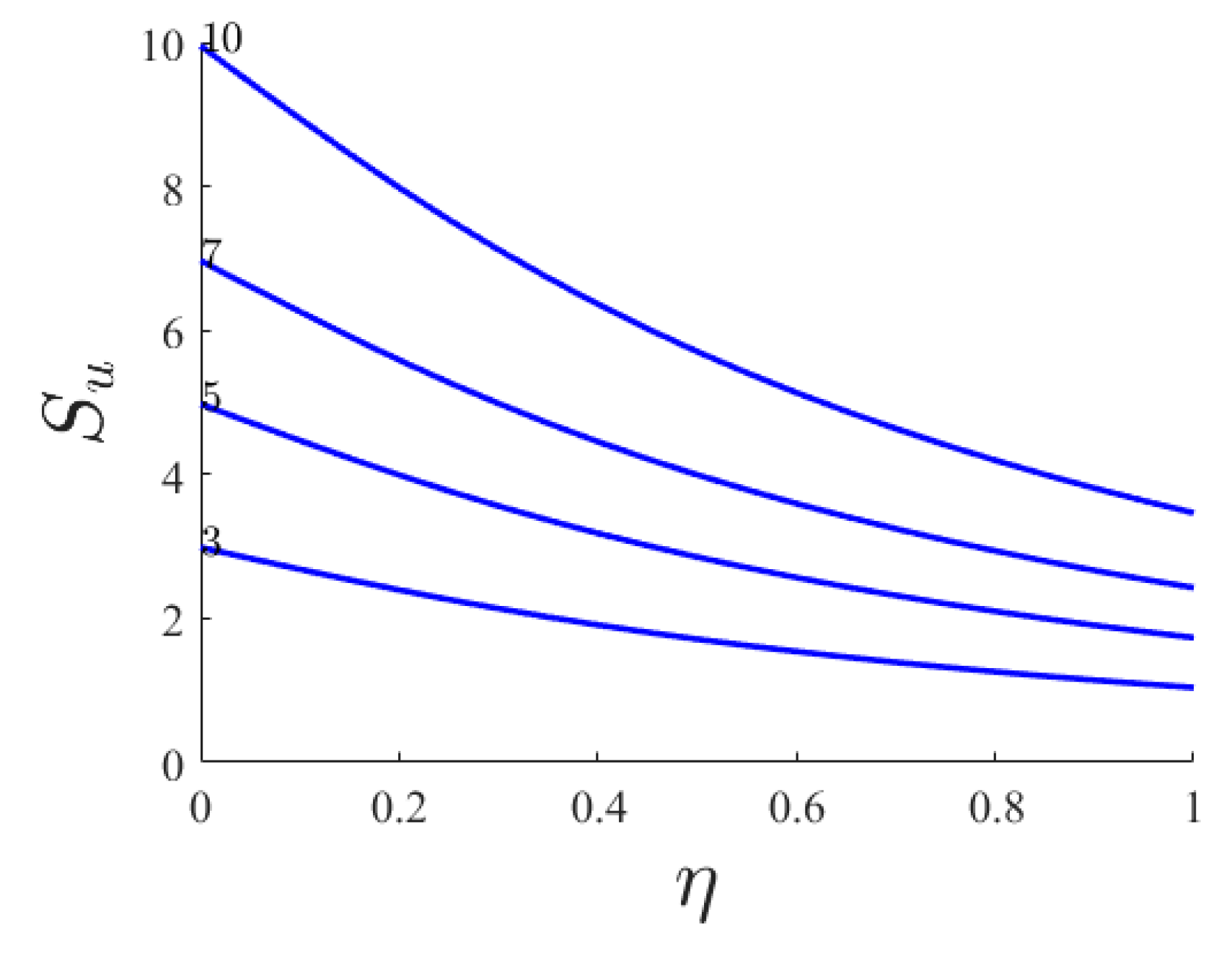
- By increasing n, Pr the heat transfer part of the entropy increases dramatically while the viscous part of the entropy is not changed.
Author Contributions
Conflicts of Interest
Nomenclature
| Be | local Bejan number | |
| Br | Brinkmann number | |
| Cp | specific heat at constant pressure | J/kg·K |
| Ha | Harttmann number | |
| k | thermal conductivity of the fluid | W/mK |
| K | flow consistency index | |
| n | power law index | |
| n* | refractive index | |
| NR | Radiative number | |
| Q | Heat source coefficient | |
| r | Coordinate component | m |
| Pr | Prantdl number | |
| S‴ | dimensionless average entropy generation | J/Ksm3 |
| Su | dimensionless local entropy generation due to fluid friction | J/Ksm3 |
| St | dimensionless local entropy generation due to the heat transfer | J/Ksm3 |
| T | medium temperature | K |
| u | velocity component in the zrdirection | m/s |
| v | velocity component in the r direction | m/s |
| z | Coordinate component | m |
Greek Symbol
| α | thermal diffusivity | m2/s |
| θ | dimensionless temperature | |
| σ | fluid electric conductivity | S/m |
| ρ | fluid density | kg/m3 |
| σ* | Stephan-Boltzman constant | kg·s−3·K−4 |
| χ | Rosseland-mean absorption coefficient | |
| μ | viscosity of the fluid | Pa·s |
| ρCp | heat capacitance | J/m3·K |
References
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Grubka, J.; Bobba, K.M. Heat transfer characteristics of a continuous stretching surface with variable temperature. J. Heat Transf. 1985, 107, 248–250. [Google Scholar] [CrossRef]
- Ali, M.E. On thermal boundary layer on a power law stretched surface with suction or injection. Int. J. Heat Fluid Flow 1995, 16, 280–290. [Google Scholar] [CrossRef]
- Chen, C.H. Laminar mixed convection adjacent to vertical, continuously stretching sheets. Heat Mass Transf. 1998, 33, 471–476. [Google Scholar] [CrossRef]
- Datta, B.K.; Roy, P.; Gupta, A.S. Temperature field in a flow over a stretching that within uniform heat flux. Int. Commun. Heat Transf. 1985, 12, 89–94. [Google Scholar] [CrossRef]
- Chen, C.K.; Char, M.I. Heat transfer on a continuous stretching surface with suction or blowing. J. Math. Anal. Appl. 1988, 135, 568–580. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A. Heat transfer over a stretching surface with variable heat flux. J. Phys. D Appl. Phys. 1998, 31. [Google Scholar] [CrossRef]
- Makhmalbaf, M.H.M. Experimental study on convective heat transfer coefficient around a vertical hexagonal rod bundle. Heat Mass Transf. 2012, 48, 1023–1029. [Google Scholar] [CrossRef]
- Makhmalbaf, H.; Liu, T.; Merati, P. Experimental Simulation of Buoyancy-Driven Vortical Flow in Jupiter Great Red Spot. In Proceedings of the 68th Annual Meeting of the APS Division of Fluid Dynamics, Boston, MA, USA, 22–24 November 2015.
- Cortell, R. Flow and heat transfer of a fluid through a porous medium over a stretching surface with internal heat generation/absorption and suction/blowing. Fluid Dyn. Res. 2005, 37, 231–245. [Google Scholar] [CrossRef]
- Liao, S.J. An analytic solution of unsteady boundary-layer flows caused by an impulsively stretching plate. Commun. Nonlinear Sci. Numer. Simul. 2006, 11, 326–339. [Google Scholar] [CrossRef]
- Mehmood, A.; Ali, A. Analytic homotopy solution of generalized three dimensional channel flow due to uniform stretching of the plate. Acta Mech. Sin. 2007, 23, 502–510. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Hydromagnetic flow and heat transfer adjacent to a stretching vertical sheet. Heat Mass Transf. 2008, 44, 921–927. [Google Scholar] [CrossRef]
- Crane, L.J. Boundary layer flow due to stretching cylinder. Z. Angew. Math. Phys. 1975, 25, 619–622. [Google Scholar] [CrossRef]
- Wang, C.Y. Fluid flow due to stretching cylinder. Phys. Fluids 1988, 31, 466–468. [Google Scholar] [CrossRef]
- Burde, H.I. On the motion of fluid near a stretching circular cylinder. J. Appl. Math. Mech. 1988, 53, 271–273. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R. Laminar boundary layer flow along a stretching cylinder. Eur. J. Sci. Res. 2009, 36, 22–29. [Google Scholar]
- Ishak, A.; Nazar, R.; Pop, I. Magnetohydrodynamic (MHD) flow and heat transfer due to a stretching cylinder. Energy Convers. Manag. 2008, 49, 3265–3269. [Google Scholar] [CrossRef]
- Mastroberardino, A.; Paullet, J.E. Existence and priori bounds for steady stagnation flow toward a stretching cylinder. J. Math. Anal. Appl. 2010, 365, 701–710. [Google Scholar] [CrossRef]
- Weidman, P.D.; Ali, M.E. Aligned and nonaligned radial stagnation flow on a stretching cylinder. Eur. J. Mech. B Fluids 2011, 30, 120–128. [Google Scholar] [CrossRef]
- Wang, C.Y.; Ng, C.O. Slip flow due to a stretching cylinder. Int. J. Nonlinear Mech. 2011, 45, 1191–1194. [Google Scholar] [CrossRef] [Green Version]
- Munawar, S.; Mehmood, A.; Ali, A. Unsteady flow of viscous fluid over the vacillate stretching cylinder. Int. J. Numer. Methods Fluids 2011, 70, 671–681. [Google Scholar] [CrossRef]
- Vajravelu, K.; Prasad, K.V.; Santhi, S.R. Axisymmetric magneto-hydrodynamic (MHD) flow and heat transfer at a non-isothermal stretching cylinder. Appl. Math. Comput. 2012, 219, 3993–4005. [Google Scholar] [CrossRef]
- Joodaki, H.; Forman, J.; Forghani, A.; Overby, B.; Kent, R.; Crandall, J.; Beahlen, B.; Beebe, M.; Bostrom, O. Comparison of kinematic behaviour of a first generation obese dummy and obese PMHS in frontal sled tests. In Proceedings of the 2015 IRCOBI Conference, Lyon, France, 9–11 September 2015; pp. 9–11.
- Forman, J.L.; Joodaki, H.; Forghani, A.; Riley, P.O.; Bollapragada, V.; Lessley, D.J.; Overby, B.; Heltzel, S.; Kerrigan, J.R.; Crandall, J.R.; Yarboro, S. Whole-body Response for Pedestrian Impact with a Generic Sedan Buck. Stapp Car Crash J. 2015, 59, 401–444. [Google Scholar]
- Forman, J.L.; Joodaki, H.; Forghani, A.; Riley, P.; Bollapragada, V.; Lessley, D.; Overby, B.; Heltzel, S.; Crandall, J. Biofidelity Corridors for Whole-Body Pedestrian Impact with a Generic Buck. In Proceedings of the 2015 IRCOBI Conference, Lyon, France, 9–11 September 2015.
- Chen, X.; Pavlish, K.; Benoit, J.N. Myosin phosphorylation triggers actin polymerization in vascular smooth muscle. Am. J. Physiol. Heart Circ. Physiol. 2008, 295, H2172–H2177. [Google Scholar] [CrossRef] [PubMed]
- Jones, E.A.V. The initiation of blood flow and flow induced events in early vascular development. Semin. Cell Dev. Biol. 2011, 22, 1028–1035. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Paul, A.; Taylor, M.D.; Banerjee, R.K. Pulsatile arterial wall-blood flow interaction with wall pre-stress computed using an inverse algorithm. Biomed. Eng. Online 2015, 14, S1–S18. [Google Scholar] [CrossRef] [PubMed]
- Blachon, A.; Marque, S.R.A.; Roubaud, V.; Siri, D. Diasteromeric Effect on the Homolysis of the C–ON Bond in Alkoxyamines: A DFT Investigation of 1,3-Diphenylbutyl-TEMPO. Polymers 2010, 2, 353–363. [Google Scholar] [CrossRef]
- Yu, J.; Liu, F.; Tang, P.; Qiu, F.; Zhang, H.; Yang, Y. Effect of Geometrical Asymmetry on the Phase Behavior of Rod-Coil Diblock Copolymers. Polymers 2016, 8, 184. [Google Scholar] [CrossRef]
- Kogej, K. Thermodynamic Analysis of the Conformational Transition in Aqueous Solutions of Isotactic and Atactic Poly(Methacrylic Acid) and the Hydrophobic Effect. Polymers 2016, 8, 168. [Google Scholar] [CrossRef]
- Munawar, S.; Mehmood, A.; Ali, A. Time-dependent flow and heat transfer over a stretching cylinder. Chin. J. Phys. 2012, 50, 828–848. [Google Scholar]
- Mukhopadhyay, S.; Ishak, A. Mixed convection flow along a stretching cylinder in a thermally stratified medium. J. Appl. Math. 2012, 8. [Google Scholar] [CrossRef]
- Shateyi, S.; Marewo, G.T. A new numerical approach for the laminar boundary layer flow and heat transfer along a stretching cylinder embedded in a porous medium with variable thermal conductivity. J. Appl. Math. 2013, 7. [Google Scholar] [CrossRef]
- Si, X.; Li, L.; Zheng, L.; Zhang, X.; Liu, B. The exterior unsteady viscous flow and heat transfer due to a porous expanding stretching cylinder. Comput. Fluids 2014, 105, 280–284. [Google Scholar] [CrossRef]
- Vajravelu, K.; Prasad, K.V.; Santhi, S.R.; Umesh, V. Fluid flow and heat transfer over a permeable stretching cylinder. J. Appl. Fluids Mech. 2014, 7, 111–120. [Google Scholar]
- Odat, M.Q.A.; Damseh, R.A.; Nimr, M.A.A. Effect of magnetic field on entropy generation due to laminar forced convection past a horizontal flat plate. Entropy 2004, 4, 293–303. [Google Scholar] [CrossRef]
- Makinde, O.D.; Osalusi, E. Entropy generation in a liquid film falling along an inclined porous heated plate. Mech. Res. Commun. 2006, 33, 692–698. [Google Scholar] [CrossRef]
- Makinde, O.D. Irreversibility analysis for a gravity driven non-Newtonian liquid film along an inclined isothermal plate. Phys. Scr. 2006, 74, 642–645. [Google Scholar] [CrossRef]
- Munawar, S.; Ali, A.; Mehmood, A. Thermal analysis of the flow over an oscillatory stretching cylinder. Phys. Scr. 2012, 86. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Entropy analysis of magnetohydrodynamic flow and heat transfer due to a stretching cylinder. J. Taiwan Inst. Chem. Eng. 2014, 45, 780–786. [Google Scholar] [CrossRef]
- Osswald, T.; Baur, E.; Brinkmann, S.; Oberbach, K.; Schmachtenberg, E. International Plastics Handbook 4E: The Resource for Plastics Engineers, 4th ed.; Hanser Publications: Munich, Germany, 2006. [Google Scholar]
- Brostow, W. Mechanical and Thermophysical Properties of Polymer Liquid Crystals; Chapman & Hall: New York, NY, USA, 1998; Volume 3. [Google Scholar]
- Rosseland, S. Theoretical Astrophysics: Atomic Theory and the Analysis of Stellar Atmospheres and Envelopes; Clarendon Press: Oxford, UK, 1936. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Makinde, O.D.; Mabood, F.; Khanc, W.A.; Tshehla, M.S. MHD flow of a variable viscosity nanofluid over a radially stretching convective surface with radiative heat. J. Mol. Liq. 2016, 219, 624–630. [Google Scholar] [CrossRef]
- Motsa, S.S.; Sibanda, P. On the solution of MHD flow over a nonlinear stretching sheet by an efficient semi-analytical technique. Int. J. Numer. Methods Fluids 2012, 68, 1524–1537. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.Y. Entropy generation in boundary layer flow of a micro polar fluid over a stretching sheet embedded in a highly absorbing medium. Front. Heat Mass Transf. 2015, 6, 1–13. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.Y.; Hooshmand, P.; Bagheri, N.; KhakRah, H.; Dousti, M. Numerical Simulation of Williamson Combined Natural and Forced Convective Fluid Flow between Parallel Vertical Walls with Slip Effects and Radiative Heat Transfer in a Porous Medium. Entropy 2016, 18, 147. [Google Scholar] [CrossRef]
- Khan, M.; Munir, A.; Shahzad, A. Convective Heat Transfer to Sisko Fluid over a Nonlinear Radially Stretching Sheet. In Heat Transfer Studies and Applications; Kazi, S.N., Ed.; Intech: Rijeka, Croatia, 2015; pp. 341–361. [Google Scholar]
- Drikakis, D.; Asproulis, N. Multiscale Computational Modelling of Flow and Heat Transfer. Int. J. Numer. Method Heat Fluid Flow 2010, 20, 517–528. [Google Scholar] [CrossRef]
- Asproulis, N.; Kalweit, M.; Drikakis, D. A hybrid molecular continuum method using point wise coupling. Adv. Eng. Softw. 2012, 46, 85–92. [Google Scholar] [CrossRef]
- Kalweit, M.; Drikakis, D. Coupling strategies for hybrid molecular—Continuum simulation methods. Proc. IMechE Part C 2008, 222, 797–806. [Google Scholar] [CrossRef]
- Di Federico, V.; Archetti, R.; Longo, S. Spreading of axisymmetric non-Newtonian power-law gravity currents in porous media. J. Non-Newton. Fluid Mech. 2012, 189–190, 31–39. [Google Scholar] [CrossRef]
- De Haro, M.L.; Cuevas, S.; Beltrán, A. Heat transfer and entropy generation in the parallel plate flow of a power-law fluid with asymmetric convective cooling. Energy 2014, 66, 750–756. [Google Scholar] [CrossRef]
- Anand, V. Slip law effects on heat transfer and entropy generation of pressure driven flow of a power law fluid in a microchannel under uniform heat flux boundary condition. Energy 2014, 76, 716–732. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Oztop, H.F.; Pop, I.; Abu-Hamdeh, N. Analysis of entropy generation in natural convection of nanofluid inside a square cavity having hot solid block: Tiwari and Das’ model. Entropy 2016, 18, 9. [Google Scholar] [CrossRef]
- Pascal, J.P.; Pascal, H. Similarity solutions to gravity flows of non-Newtonian fluids through porous media. Int. J. Non-Linear Mech. 1993, 28, 157–167. [Google Scholar] [CrossRef]
- Chowdhury, M.R.; Testik, F.Y. Viscous propagation of two-dimensional non-Newtonian gravity currents. Fluid Dyn. Res. 2012, 44, 4. [Google Scholar] [CrossRef]
- Tosco, T.; Sethi, R. Transport of Non-Newtonian Suspensions of Highly Concentrated Micro- and Nanoscale Iron Particles in Porous Media: A Modeling Approach. Environ. Sci. Technol. 2010, 44, 9062–9068. [Google Scholar] [CrossRef] [PubMed]
- Ciriello, V.; Longo, S.; Di Federico, V. On shear thinning fluid flow induced by continuous mass injection in porous media with variable conductivity. Mech. Res. Commun. 2013, 52, 101–107. [Google Scholar] [CrossRef]
- Longo, S.; Di Federico, V.; Chiapponi, L.; Archetti, R. Experimental verification of power-law non-Newtonian axisymmetric porous gravity currents. J. Fluid Mech. 2013, 731. [Google Scholar] [CrossRef]
- Longo, S.; di Federico, V.; Archetti, R.; Chiapponi, L.; Ciriello, V.; Ungarish, M. On the axisymmetric spreading of non-Newtonian power-law gravity currents of time-dependent volume: An experimental and theoretical investigation focused on the inference of rheological parameters. J. Non-Newton. Fluid Mech. 2013, 201, 69–79. [Google Scholar] [CrossRef]
- Di Federico, V.; Longo, S.; Chiapponi, L.; Archetti, R.; Ciriello, V. Radial gravity currents in vertically graded porous media: Theory and experiments for Newtonian and power-law fluids. Adv. Water Resour. 2014, 70, 65–76. [Google Scholar] [CrossRef]
- Longo, S.; Di Federic, V.; Chiapponi, L. Non-Newtonian power-law gravity currents propagating in confining boundaries. Environ. Fluid Mech. 2015, 15, 515–535. [Google Scholar] [CrossRef]
- Longo, S.; Ciriello, V.; Chiapponi, L.; Di Federico, V. Combined effect of rheology and confining boundaries on spreading of gravity currents in porous media. Adv. Water Resour. 2015, 79, 140–152. [Google Scholar] [CrossRef]
- Longo, S.; Di Federico, V.; Chiapponi, L. Propagation of viscous gravity currents inside confining boundaries: The effects of fluid rheology and channel geometry. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015. [Google Scholar] [CrossRef]
- Longo, S.; Di Federico, V. Stability Analysis of Gravity Currents of a Power-Law Fluid in a Porous Medium. Math. Probl. Eng. 2015, 2015, 286487. [Google Scholar] [CrossRef]
- Longo, S.; Di Federico, V.; Chiapponi, L. A dipole solution for power-law gravity currents in porous formations. J. Fluid Mech. 2015, 778, 534–551. [Google Scholar] [CrossRef]
- Longo, S.; Di Federico, V. Unsteady Flow of Shear-Thinning Fluids in Porous Media with Pressure-Dependent Properties. Transp. Porous Med. 2015, 110, 429–447. [Google Scholar] [CrossRef]
- Ciriello, V.; Longo, S.; Chiapponi, L.; Di Federico, V. Porous gravity currents: A survey to determine the joint influence of fluid rheology and variations of medium properties. Adv. Water Resour. 2016, 92, 105–115. [Google Scholar] [CrossRef]
- Longo, S.; Chiapponi, L.; di Federico, V. On the propagation of viscous gravity currents of non-Newtonian fluids in channels with varying cross section and inclination. J. Non-Newton. Fluid Mech. 2016, 235, 95–108. [Google Scholar] [CrossRef]
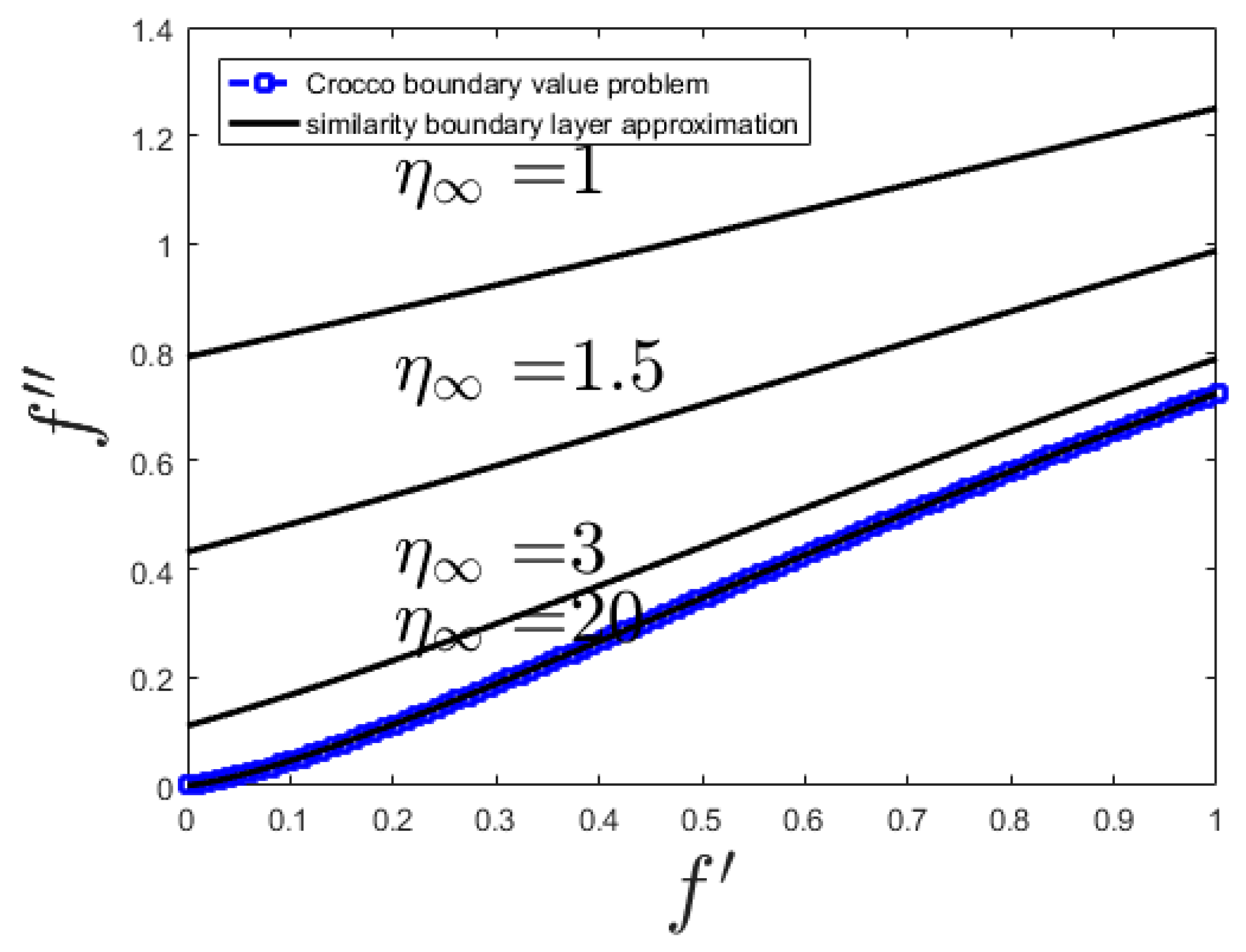
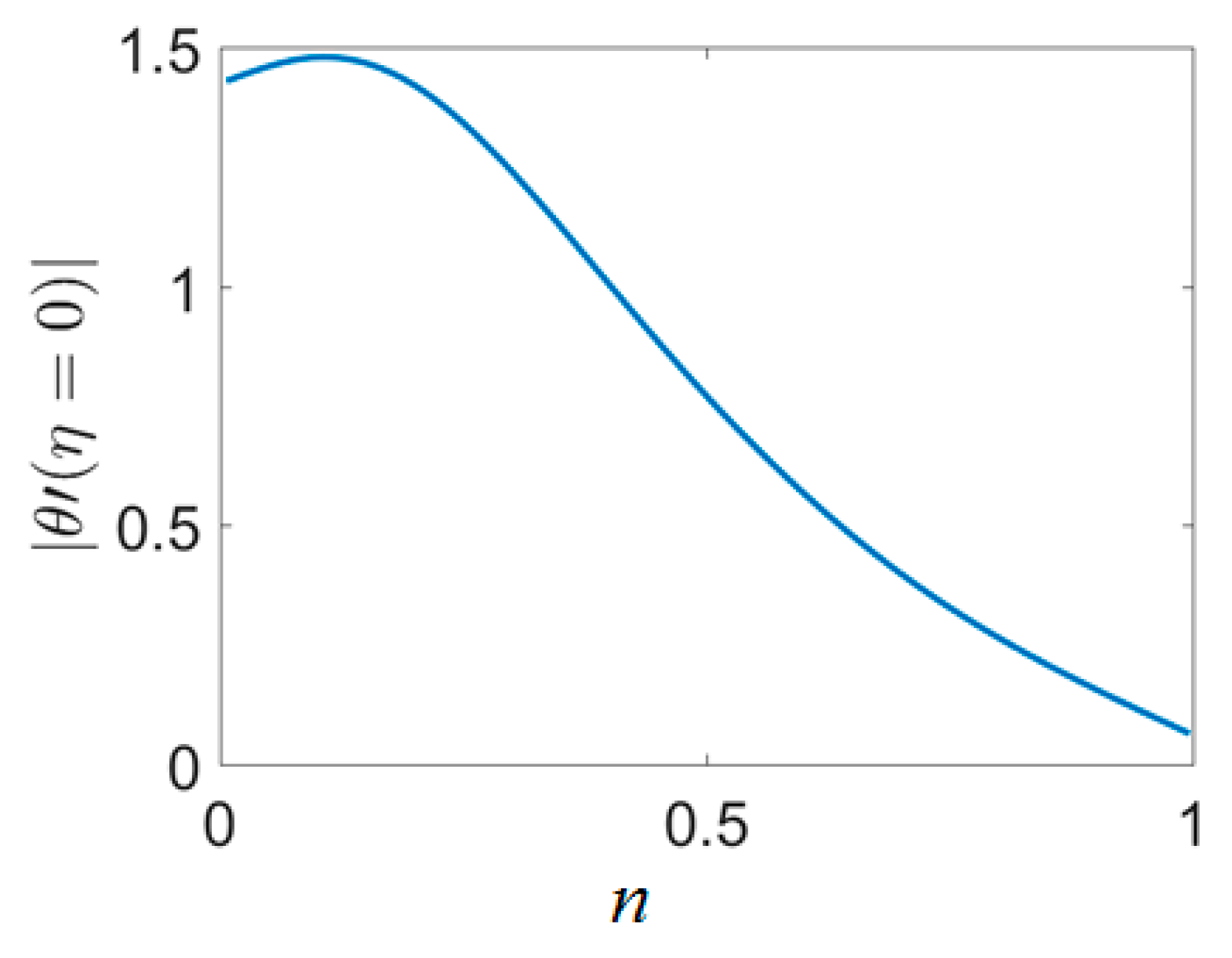
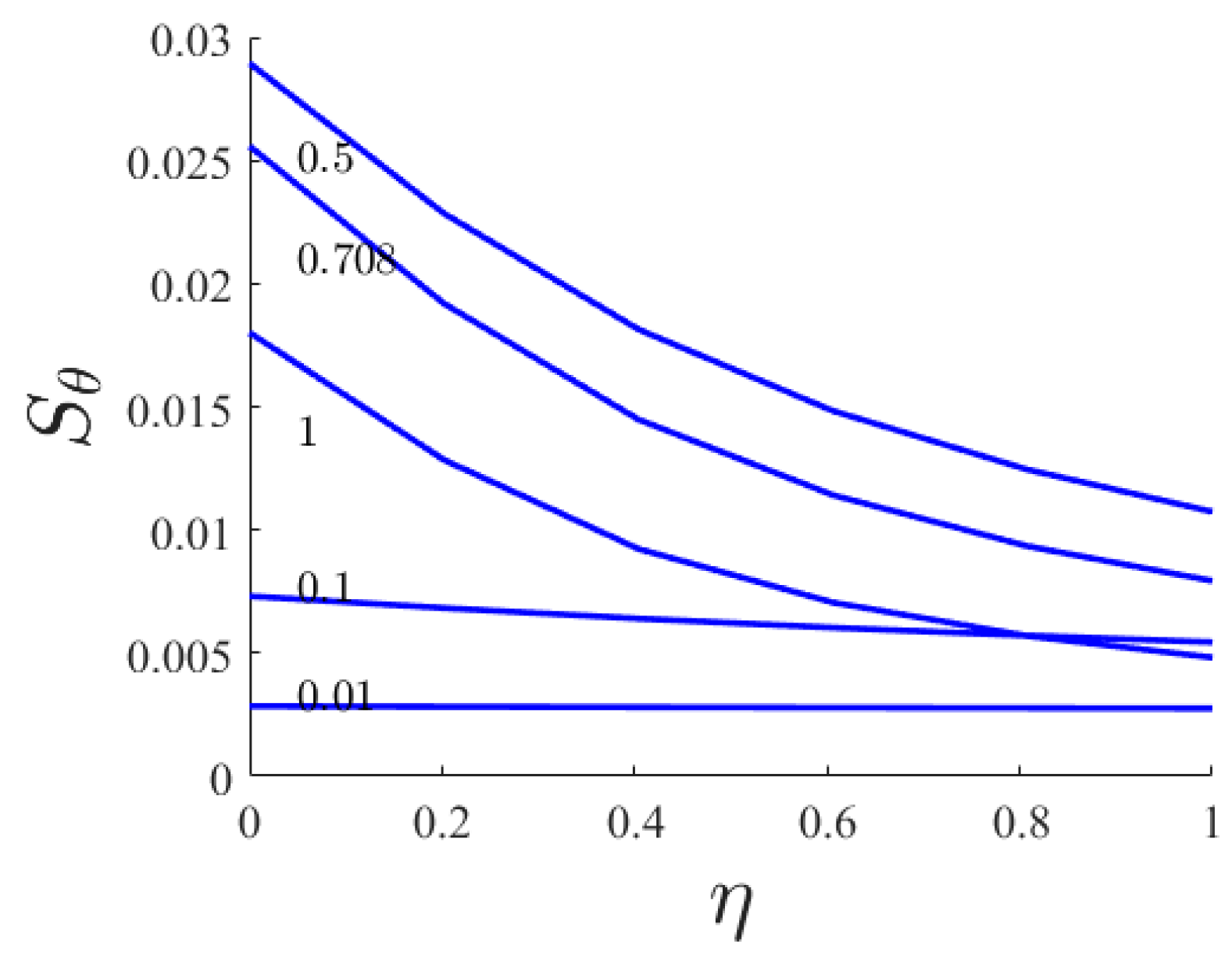

| f″(0) | |
|---|---|
| Present work | Khan et al. [52] |
| 1.17 | 1.173721 |
| δ | Nu | Su | ST | |
|---|---|---|---|---|
| n (0 to 1) | decrease | increase | independent | decrease |
| Pr (0.001 to 10) | decrease | increase | independent | increase |
| NR (0 to 2) | increase | decrease | independent | decrease |
| Br (0 to 10) | increase | increase | increase | increase |
| Ha (0 to 1) | downward parabola | downward parabola | increase | increase |
| Qr (0 to 0.01) | downward parabola | downward parabola | independent | downward parabola |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hooshmand, P.; Gatabi, H.R.; Bagheri, N.; Pirzadeh, I.; Hesabi, A.; Abdollahzadeh Jamalabadi, M.Y.; Oveisi, M. Numerical Study of the Magnetic Field Effects on the Heat Transfer and Entropy Generation Aspects of a Power Law Fluid over an Axisymmetric Stretching Plate Structure. Entropy 2017, 19, 94. https://doi.org/10.3390/e19030094
Hooshmand P, Gatabi HR, Bagheri N, Pirzadeh I, Hesabi A, Abdollahzadeh Jamalabadi MY, Oveisi M. Numerical Study of the Magnetic Field Effects on the Heat Transfer and Entropy Generation Aspects of a Power Law Fluid over an Axisymmetric Stretching Plate Structure. Entropy. 2017; 19(3):94. https://doi.org/10.3390/e19030094
Chicago/Turabian StyleHooshmand, Payam, Hamed Rajabzadeh Gatabi, Navid Bagheri, Isma’il Pirzadeh, Ashkan Hesabi, Mohammad Yaghoub Abdollahzadeh Jamalabadi, and Majid Oveisi. 2017. "Numerical Study of the Magnetic Field Effects on the Heat Transfer and Entropy Generation Aspects of a Power Law Fluid over an Axisymmetric Stretching Plate Structure" Entropy 19, no. 3: 94. https://doi.org/10.3390/e19030094






