Securing Relay Networks with Artificial Noise: An Error Performance-Based Approach †
Abstract
:1. Introduction
- By assuming that instantaneous CSI is available at the untrusted relay and the destination, upon receiving both of the QAM symbols from the source and the AN from the destination, an exact expression for the SER at the relay when decoding the QAM symbols is first derived. Under an average power constraint, this expression is then utilized to obtain the phase and power distribution of the AN symbols to maximize the SER performance at the relay.
- For the case where only statistical CSI is available, we first derive an exact expression for the ASER performance at the relay. Next, the optimal power distribution of the AN symbols that maximizes the ASER performance at the relay is determined. Numerical and simulation results demonstrate that the proposed optimal AN designs guarantee significant error rate performance enhancement compared with conventional AN designs, such as Gaussian distribution.
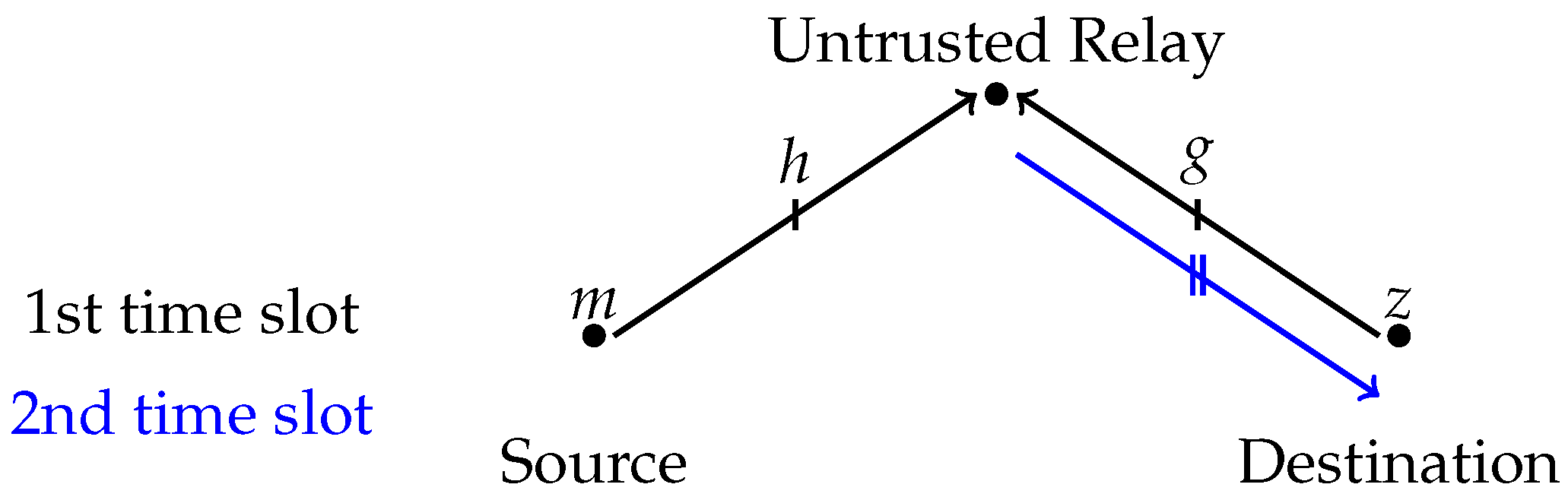
2. System Model and Problem Formulation
3. AN Maximizing Relay’s SER Performance
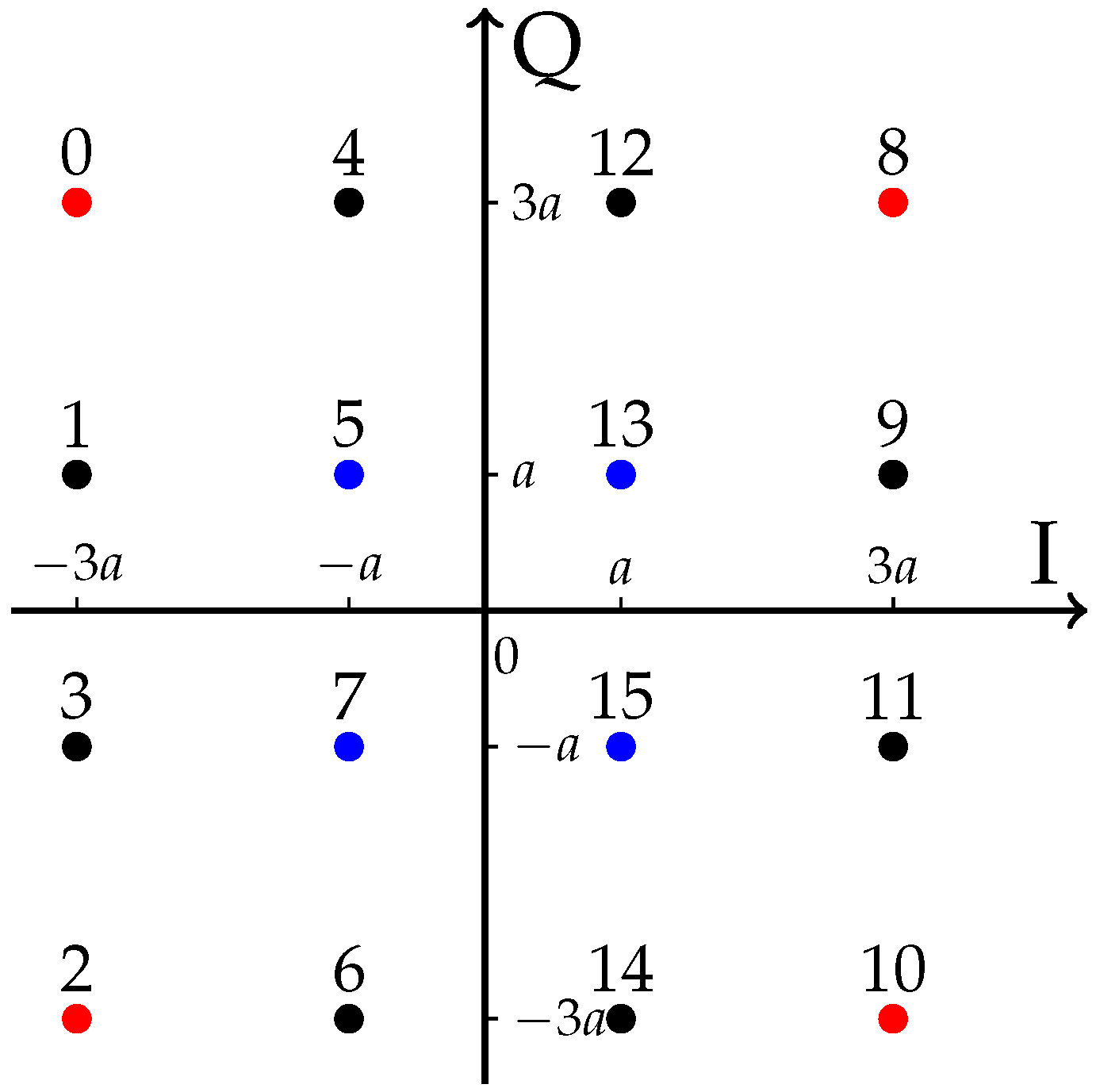
3.1. SER Expression for a Given z
3.2. Selecting for a Fixed
3.3. Assigning for a Given
- (1)
- compute the amplitudes of the AN symbols by numerically maximizing Equation (24),
- (2)
- determine the corresponding phase value for each amplitude using Equation (19),
- (3)
- generate the AN symbols by the obtained amplitudes and phases.
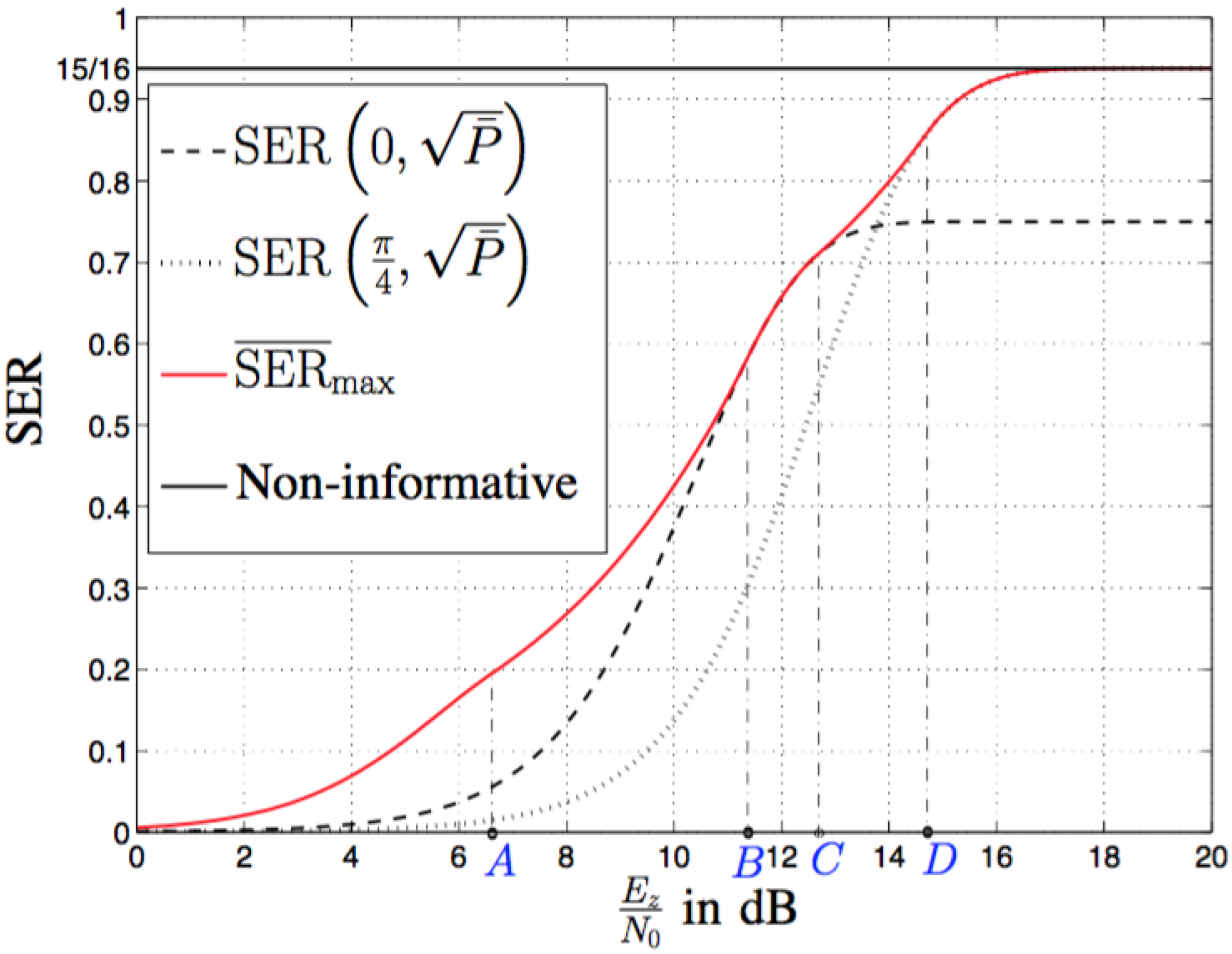
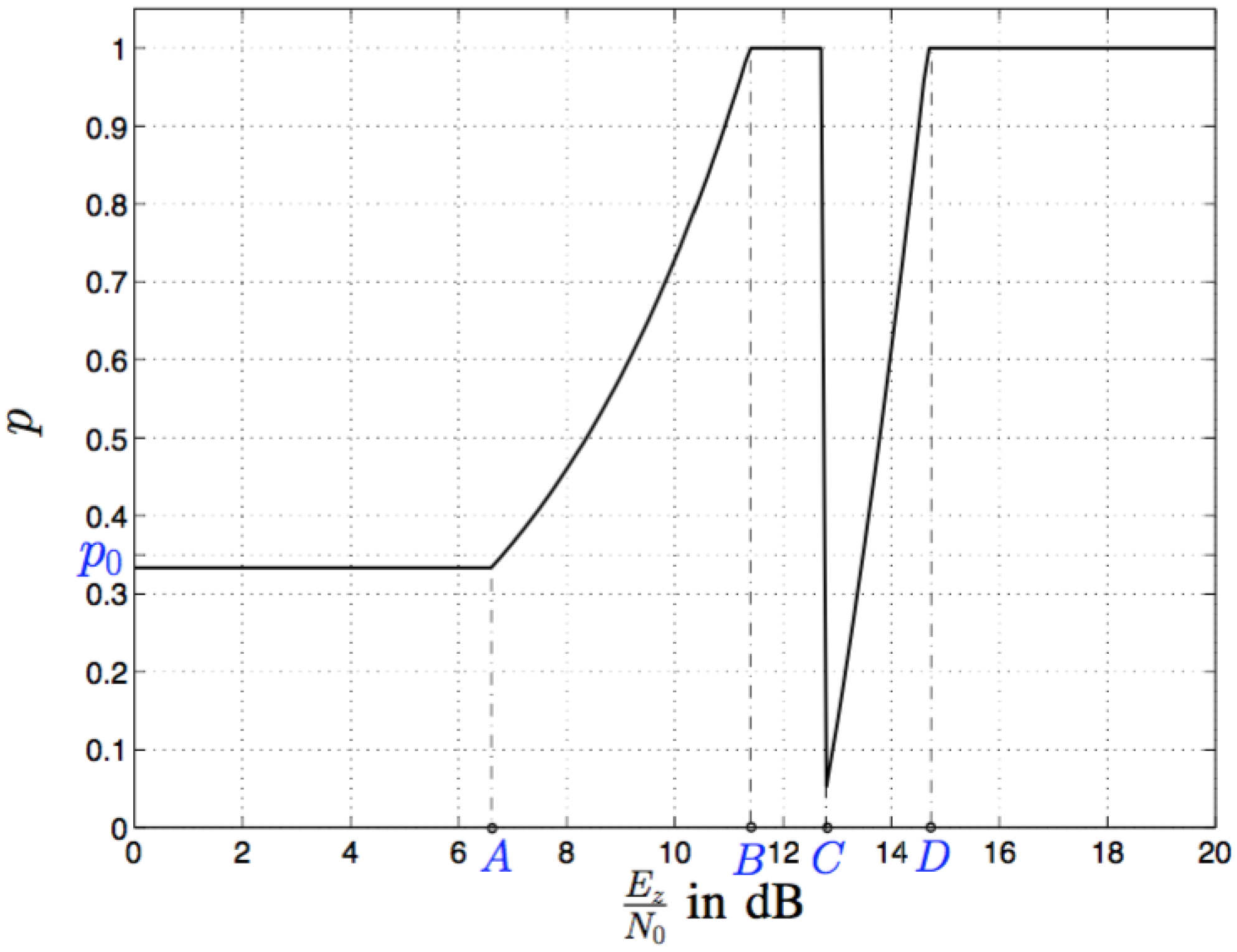
3.4. Relation between Phase Selection and Power Allocation
4. AN Maximizing Relay’s ASER Performance
4.1. ASER Expression for a Given z
4.2. Assigning for a Given
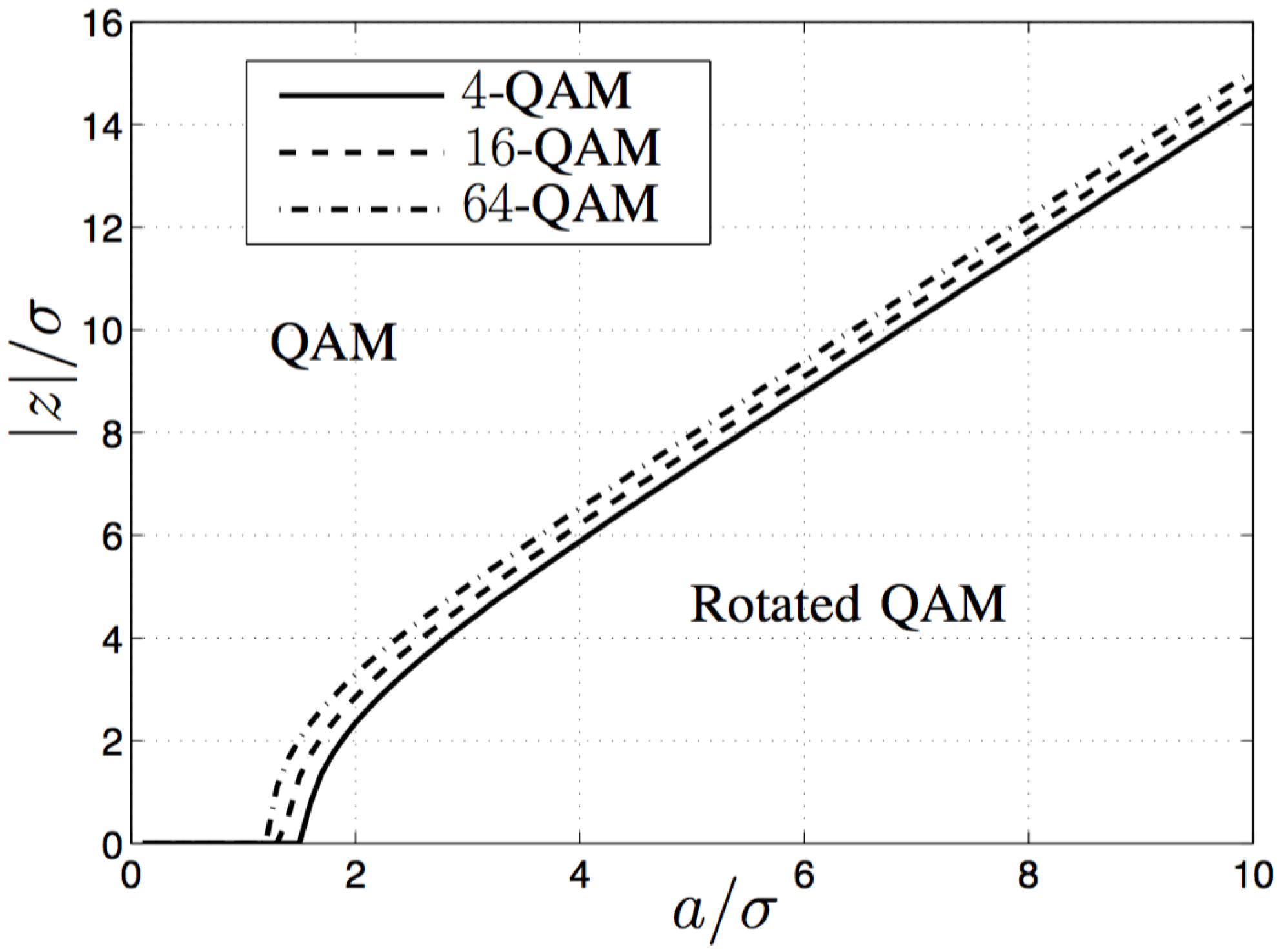
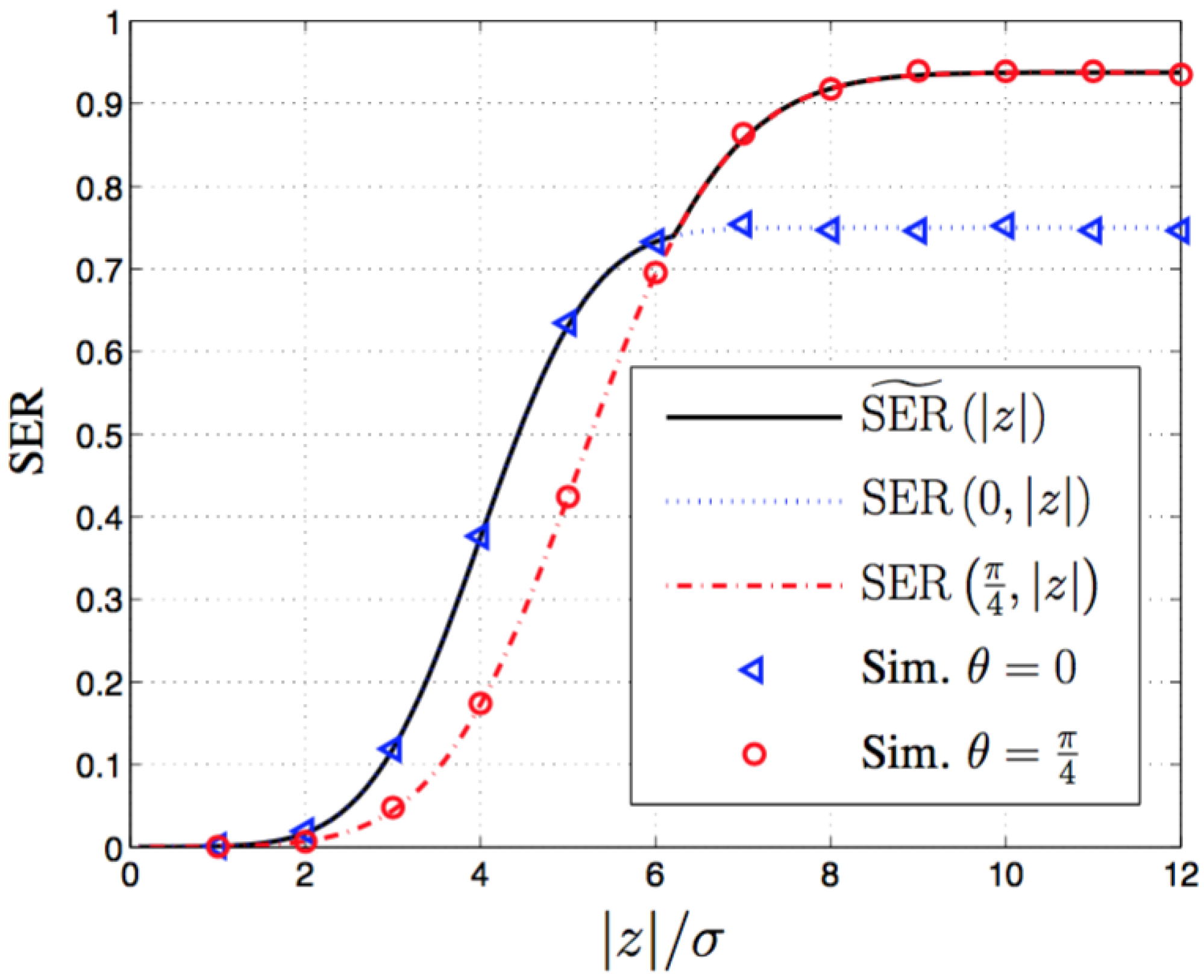
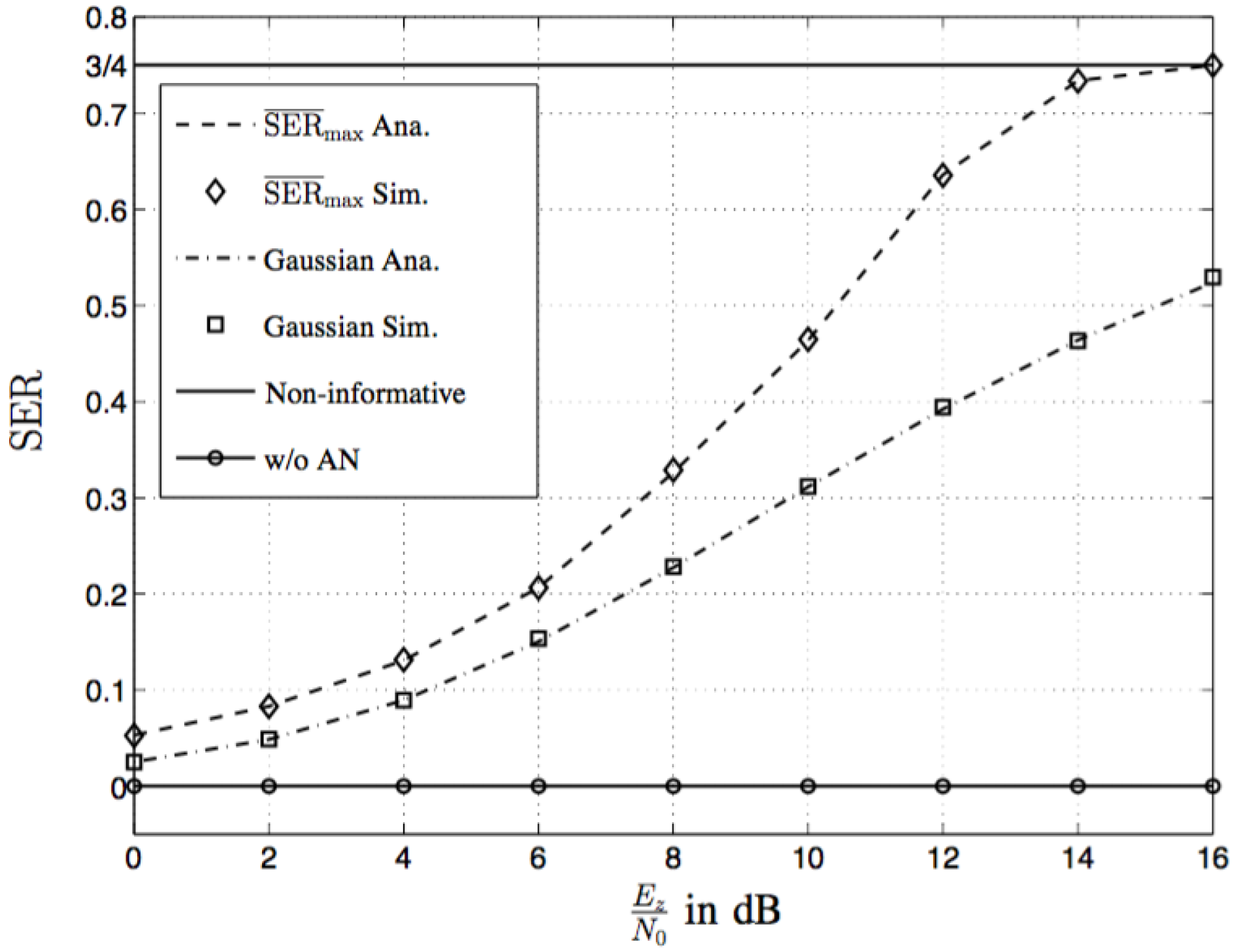
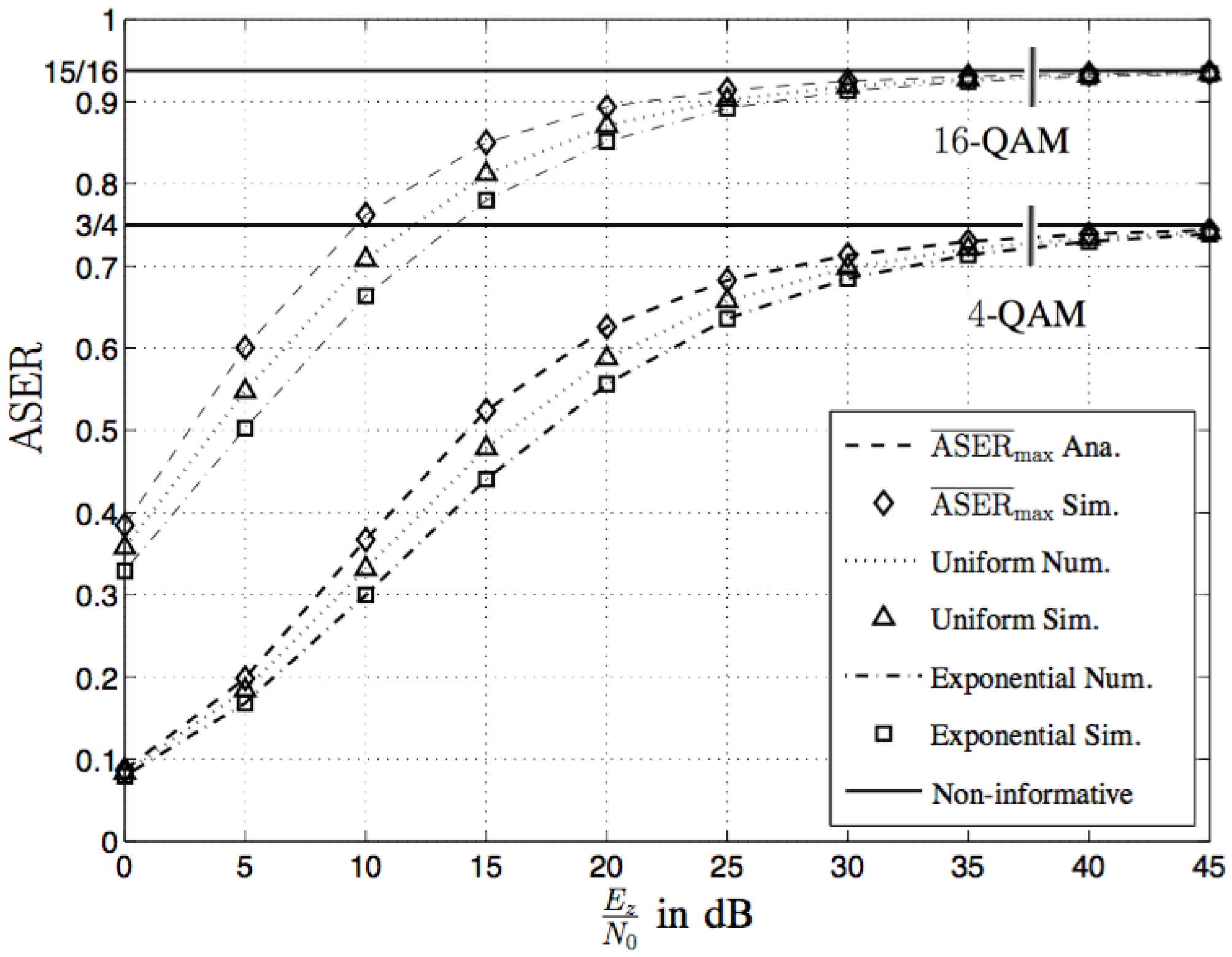
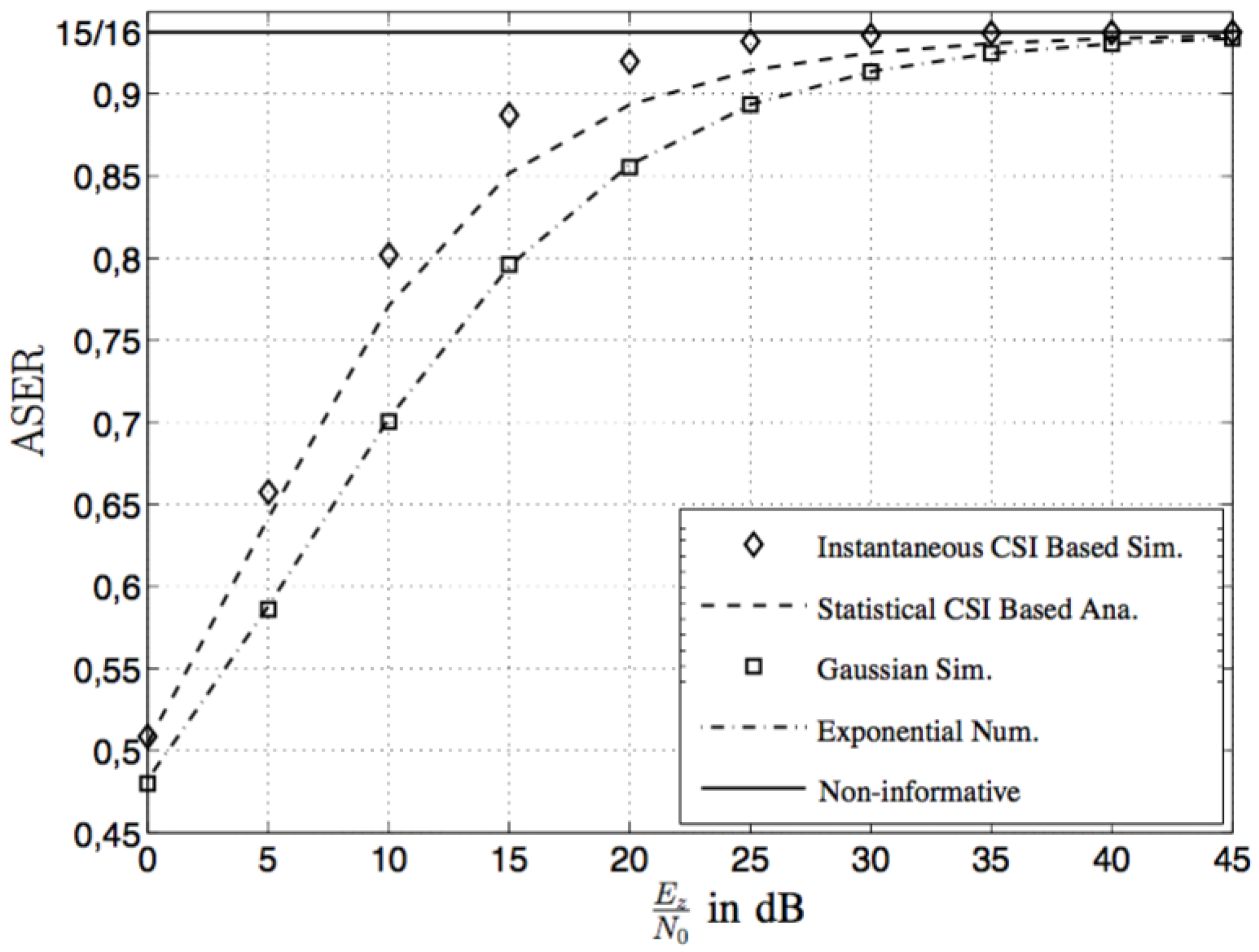
5. Numerical and Simulation Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Theorem 1
References
- Diffie, W.; Hellman, M.E. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comp. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Yang, N.; Wang, L.; Geraci, G.; Elkashlan, M.; Yuan, J.; Di Renzo, M. Safeguarding 5G wireless communication networks using physical layer security. IEEE Commun. Mag. 2015, 53, 20–27. [Google Scholar] [CrossRef]
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Broadcast channels with confidential messages. IEEE Trans. Inf. Theory 1978, 24, 339–348. [Google Scholar] [CrossRef]
- Liang, Y.; Poor, H.V.; Shamai, S. Information theoretic security. Found. Trends Commun. Inf. Theory 2008, 5, 355–580. [Google Scholar] [CrossRef]
- Zhou, X.; McKay, M.R. Secure transmission with artificial noise over fading channels: Achievable rate and optimal power allocation. IEEE Trans. Veh. Technol. 2010, 59, 3831–3842. [Google Scholar] [CrossRef]
- Khisti, A.; Wornell, G.W. Secure transmission with multiple antennas I: The MISOME wiretap channel. IEEE Trans. Inf. Theory 2010, 56, 3088–3104. [Google Scholar] [CrossRef]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Secure resource allocation and scheduling for OFDMA decode-and-forward relay networks. IEEE Trans. Wirel. Commun. 2011, 10, 3528–3540. [Google Scholar] [CrossRef]
- Oggier, F.; Hassibi, B. The secrecy capacity of the MIMO wiretap channel. IEEE Trans. Inf. Theory 2011, 57, 4961–4972. [Google Scholar] [CrossRef]
- Liu, R.; Liu, T.; Poor, H.V.; Shamai, S. New results on multiple-input multiple-output broadcast channels with confidential messages. IEEE Trans. Inf. Theory 2013, 59, 1346–1359. [Google Scholar] [CrossRef]
- Mukherjee, A.; Swindlehurst, A.L. Utility of beamforming strategies for secrecy in multiuser MIMO wiretap channels. In Proceedings of the 47th Annual Allerton Conference on Communication, Control and Computing, Monticello, IL, USA, 30 September–2 October 2009. [Google Scholar]
- Geraci, G.; Egan, M.; Yuan, J.; Razi, A.; Collings, I.B. Secrecy sum-rates for multi-user MIMO regularized channel inversion precoding. IEEE Trans. Commun. 2012, 60, 3472–3482. [Google Scholar] [CrossRef]
- Tekin, E.; Yener, A. The general Gaussian multiple-access and two-way wiretap channels: Achievable rates and cooperative jamming. IEEE Trans. Inf. Theory 2008, 54, 2735–2751. [Google Scholar] [CrossRef]
- Dong, L.; Han, Z.; Petropulu, A.P.; Poor, H.V. Improving wireless physical layer security via cooperating relays. IEEE Trans. Signal Process. 2010, 58, 1875–1888. [Google Scholar] [CrossRef]
- Mukherjee, A.; Swindlehurst, A.L. Securing multi-antenna two-way relay channels with analog network coding against eavesdroppers. In Proceedings of the IEEE Eleventh International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Marrakech, Morocco, 20–23 June 2010. [Google Scholar]
- Fakoorian, S.A.A.; Swindlehurst, A.L. Solutions for the MIMO Gaussian wiretap channel with a cooperative jammer. IEEE Trans. Signal Process. 2011, 59, 5013–5022. [Google Scholar] [CrossRef]
- Mukherjee, A.; Swindlehurst, A.L. Jamming games in the MIMO wiretap channel with an active eavesdropper. IEEE Trans. Signal Process. 2013, 61, 82–91. [Google Scholar] [CrossRef]
- Oohama, Y. Coding for relay channels with confidential messages. In Proceedings of the IEEE Information Theory Workshop (ITW), Cairns, Australia, 2–7 September 2001. [Google Scholar]
- Oohama, Y. Capacity theorems for relay channels with confidential messages. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Nice, France, 24–29 June 2007. [Google Scholar]
- He, X.; Yener, A. Cooperation with an untrusted relay: A secrecy perspective. IEEE Trans. Inf. Theory 2010, 56, 3807–3827. [Google Scholar] [CrossRef]
- Huang, J.; Mukherjee, A.; Swindlehurst, A.L. Secure communication via an untrusted non-regenerative relay in fading channels. IEEE Trans. Signal Process. 2013, 61, 2536–2550. [Google Scholar] [CrossRef]
- Wang, L.; Elkashlan, M.; Huang, J.; Tran, N.H.; Duong, T.Q. Secure transmission with optimal power allocation in untrusted relay networks. IEEE Wirel. Commun. Lett. 2014, 3, 289–292. [Google Scholar] [CrossRef]
- Wang, Y.; Attebury, G.; Ramamurthy, B. A survey of security issues in wireless sensor networks. IEEE Commun. Surv. Tutor. 2006, 8, 2–23. [Google Scholar] [CrossRef]
- Panja, B.; Madria, S.K.; Bhargava, B. A role-based access in a hierarchical sensor network architecture to provide multilevel security. Comput. Commun. 2008, 31, 793–806. [Google Scholar] [CrossRef]
- Lee, J.; Son, S.H.; Singhal, M. Design of an architecture for multiple security levels in wireless sensor networks. In Proceedings of the Seventh International Conference on Networked Sensing Systems (INSS), Kassel, Germany, 15–18 June 2010. [Google Scholar]
- Rohokale, V.M.; Prasad, N.R.; Prasad, R. Cooperative wireless communications and physical layer security: State-of-the-art. J. Cyber Secur. Mobil. 2012, 1, 227–249. [Google Scholar]
- Jeong, C.; Kim, I.M.; Kim, D.I. Joint secure beamforming design at the source and the relay for an amplify-and-forward MIMO untrusted relay system. IEEE Trans. Signal Process. 2012, 60, 310–325. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, T.; Li, Y.; Niu, H. Performance study of two-hop amplify-and-forward systems with untrustworthy relay nodes. IEEE Trans. Veh. Technol. 2012, 61, 3801–3807. [Google Scholar] [CrossRef]
- Mo, J.; Tao, M.; Liu, Y.; Xia, B.; Ma, X. Secure beamforming for MIMO two-way transmission with an untrusted relay. In Proceedings of the Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013. [Google Scholar]
- Vishwakarma, S.; Chockalingam, A. Amplify-and-forward relay beamforming for secrecy with cooperative jamming and imperfect CSI. In Proceedings of the IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013. [Google Scholar]
- Pei, M.; Swindlehurst, A.; Ma, D.; Wei, J. Adaptive limited feedback for MISO wiretap channels with cooperative jamming. IEEE Trans. Signal Process. 2014, 62, 993–1004. [Google Scholar] [CrossRef]
- Klinc, D.; Ha, J.; McLaughlin, S.W.; Barros, J.; Kwak, B.J. LDPC codes for the Gaussian wiretap channel. IEEE Trans. Inf. Forensics Secur. 2011, 6, 532–540. [Google Scholar] [CrossRef]
- Mukherjee, A. Imbalanced beamforming by a multi-antenna source for secure utilization of an untrusted relay. IEEE Commun. Lett. 2013, 17, 1309–1312. [Google Scholar] [CrossRef]
- Sesia, S.; Toufik, I.; Baker, M. LTE—The UMTS Long Term Evolution from Theory to Practice, 2nd ed.; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Dahlman, E.; Parkvall, S.; Sköld, J. 4G: LTE/LTE-Advanced for Mobile Broadband; Elsevier Academic Press: Oxford, UK, 2011. [Google Scholar]
- Cover, T.; El Gamal, A. Capacity theorems for the relay channel. IEEE Trans. Inf. Theory 1979, 25, 572–584. [Google Scholar] [CrossRef]
- Sanguinetti, L.; D’Amico, A.A.; Rong, Y. A tutorial on the optimization of amplify-and-forward MIMO relay systems. IEEE J. Sel. Areas Commun. 2012, 30, 1331–1346. [Google Scholar] [CrossRef]
- Morgenshtern, V.I.; B.ölcskei, H. Crystallization in large wireless networks. IEEE Trans. Inf. Theory 2007, 53, 3319–3349. [Google Scholar] [CrossRef]
- Cui, T.; Gao, F.; Nallanathan, A. Optimal training design for channel estimation in amplify and forward relay networks. In Proceedings of the IEEE Global Telecommunications Conference, Washington, DC, USA, 26–30 November 2007. [Google Scholar]
- He, X.; Yener, A. Two-hop secure communication using an untrusted relay: A case for cooperative jamming. In Proceedings of the IEEE Global Telecommunications Conference, New Orleans, LO, USA, 30 November–4 December 2008. [Google Scholar]
- Guillaud, M.; Slock, D.T.M.; Knopp, R. A practical method for wireless channel reciprocity exploitation through relative calibration. In Proceedings of the International Symposium on Signal Processing and Its Applications, Sydney, Australia, 29 August–1 September 2005. [Google Scholar]
- Liew, S.C.; Zhang, S.; Lu, L. Physical-layer network coding: Tutorial, survey, and beyond. Phys. Commun. 2013, 6, 4–42. [Google Scholar] [CrossRef]
- Laneman, N.; Tse, D.N.C.; Wornell, G. Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans. Inf. Theory 2004, 50, 3062–3080. [Google Scholar] [CrossRef]
- Proakis, J.G. Digital Communications, 4th ed.; McGraw Hill: New York, NY, USA, 2001. [Google Scholar]
- Simon, M.K.; Alouini, M.S. Digital Communication over Fading Channels; John Wiley & Sons: New York, NY, USA, 2005. [Google Scholar]
- Meade, L.; Dillon, C.R. Signals and Systems: Models and Behaviour, 2nd ed.; Chapman & Hall: London, UK, 1991. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Goel, S.; Negi, R. Guaranteeing secrecy using artificial noise. IEEE Trans. Wirel. Commun. 2008, 7, 2180–2189. [Google Scholar] [CrossRef]
- Zhang, X.; McKay, M.; Zhou, X.; Heath, R.W., Jr. Artificial-noise-aided secure multi-antenna transmission with limited feedback. IEEE Trans. Wirel. Commun. 2015, 14, 2742–2754. [Google Scholar] [CrossRef]
- Li, L.; Pesavento, M.; Gershman, A.B. Downlink opportunistic scheduling with low-rate channel state feedback: Error rate analysis and optimization of the feedback parameters. IEEE Trans. Commun. 2010, 58, 2871–2880. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization, 1st ed.; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series and Products, 7th ed.; Academic Press: Orlando, FL, USA, 2007. [Google Scholar]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, L.; Alexandropoulos, G.C.; Pesavento, M. Securing Relay Networks with Artificial Noise: An Error Performance-Based Approach. Entropy 2017, 19, 384. https://doi.org/10.3390/e19080384
Liu Y, Li L, Alexandropoulos GC, Pesavento M. Securing Relay Networks with Artificial Noise: An Error Performance-Based Approach. Entropy. 2017; 19(8):384. https://doi.org/10.3390/e19080384
Chicago/Turabian StyleLiu, Ying, Liang Li, George C. Alexandropoulos, and Marius Pesavento. 2017. "Securing Relay Networks with Artificial Noise: An Error Performance-Based Approach" Entropy 19, no. 8: 384. https://doi.org/10.3390/e19080384




