1. Introduction
In the theoretical analysis of wireless communication systems, the transmitted symbols are typically assumed to be proper complex Gaussian random variables, i.e., the transmitted symbols are complex Gaussian and uncorrelated with their complex conjugate. This is motivated by the fact that such an input distribution achieves the capacity of the point-to-point, broadcast and multiple-access channels [
1]. In more complex interference-limited scenarios, such as the interference channel, transmitting proper Gaussian signals is in general suboptimal, so assuming this input distribution in such cases is not theoretically justified. As a matter of fact, recent works have shown that, when treating interference as noise, a higher transmitted rate may be achieved in interference-limited networks by transmitting improper Gaussian signals, which are correlated with their complex conjugate [
2,
3,
4,
5,
6,
7,
8].
Improper signals are common in communications since many important digital modulation schemes yield improper signals. Examples are binary phase shift keying (BPSK) or Gaussian minimum shift keying (GMSK) [
9]. Additionally, power imbalance between the in-phase and in-quadrature components also yields an improper signal. A substantial body of work has focused on the design of widely linear receivers to exploit the impropriety of a received improper signal (we refer the interested reader to [
10,
11,
12,
13] and the references therein). While these works devise techniques to deal with signals whose impropriety was not intentionally introduced, recent works consider the deliberate transmission of improper signals as a novel way to handle interference in a multiuser channel.
Cadambe et al. showed the benefits of improper signaling for the first time in their pioneering work [
2]. They considered a single-antenna three-user interference channel with constant channel extensions and showed that the number of degrees of freedom (DoF), which is the number of interference-free signals that can be transmitted, was larger when users transmit improper signals as opposed to proper ones. Similar DoF results were derived for the four-user interference channel in [
14]. After that, a number of new works has emerged, and the payoffs of improper signaling have been revealed for different multiuser scenarios such as the interference channel [
3,
4,
5,
15], Z-interference channel [
6,
16,
17,
18], broadcast channels with linear precoding [
19,
20], underlay and overlay cognitive radio networks [
7,
8,
21] and relay channels [
22,
23]. More recently, in [
24], the authors showed the advantages of improper signaling in a multiuser scenario where a point-to-point link coexists with a multiple access channel. Even though these works present new and intriguing results that pave the way for more efficient interference management schemes, the vast majority of them assume Gaussian codebooks (the only exception is [
15], where the symbol error rate is minimized for arbitrary digital modulation schemes) and, hence, can never be realized in practice since practical codes use non-Gaussian finite signaling constellations.
It is well known that the penalty in signal-to-noise ratio (
) paid by constraining the complex symbols to a uniform
M-ary quadrature amplitude modulation (QAM) constellation is given by the shaping loss, which for large
M is 1.53 dB in the proper case [
25]. When dealing with proper signals, this shaping loss is due to enclosing the uniformly-transmitted codewords inside a hypercube rather than a hypersphere, which would be the optimal region that minimizes the transmitted power.
When using non-Gaussian improper signals, different questions arise: What is the optimal way to generate an improper constellation with a given circularity coefficient (i.e., degree of impropriety)? In coded communication systems, what is the reduction in rate compared to the improper Gaussian capacity when the coded channel symbols are constrained to be in a given discrete improper constellation? Is this rate reduction due only to a shaping loss? Should the channel encoder be modified for discrete improper constellations? In this paper, we address these questions and consider the design of improper discrete constellations for the additive white Gaussian noise channel (AWGN). We focus on coded communication systems, and therefore, our aim is the design of discrete improper constellations for the coded bits to approach the improper Gaussian capacity (i.e., maximize the throughput). Consequently, mutual information is the figure of merit to be optimized. The design of practical capacity-achieving encoders-decoders will be considered in a future work. Therefore, the main contribution of this paper is to propose a class of improper constellations and to show that, in terms of mutual information, this family of constellations behaves very similarly to the standard family of M-QAM proper constellations.
Starting with a proper
M-QAM constellation, we analyze the design of a widely linear transformation that generates a family of improper
M-QAM constellations with a prescribed circularity coefficient
. The only free parameter of these improper
M-ary constellations is a phase
. For uncoded communication systems, this phase should be optimized to maximize the minimum Euclidean distance between points of the improper constellation, so that the bit error rate (BER) is minimized. Note that for a given
M (i.e., for a given spectral efficiency), maximizing
is equivalent, at high
, to maximizing the mutual information (MI) between the transmit and the received signals [
26]. On the other hand, for coded improper communication systems with a circularity coefficient
, one should find the
that maximizes, for each snr and
M, the envelope of the resulting family of mutual information values of these
M-ary improper constellations. In this way, the rate gap compared to the improper Shannon capacity is minimized.
One of the main contributions of this paper is to show that except for a shaping loss of 1.53 dB encountered at high , there is no rate loss with respect to the improper Gaussian Shannon capacity when using this family of constellations. We conclude that the proposed family of improper constellations behaves much the same as the standard family of proper M-QAM constellations. Finally, note that as in the case of proper QAM constellations, the shaping loss can be reduced by designing codes that result in a Gaussian-like rather than uniform distribution of the coded symbols.
The rest of the paper is organized as follows.
Section 2 provides preliminaries about improper random variables and introduces the considered model. The design of improper constellations is formulated in
Section 3, and its information-theoretic analysis is done in
Section 4.
Section 5 provides some numerical examples. Finally, concluding remarks are presented in
Section 6.
2. Background and System Model
2.1. Notation
Scalar random variables are denoted by uppercase letters X. Vectors and matrices are denoted by lowercase boldface letters, , and uppercase boldface letters, , respectively. The determinant and trace of a matrix will be denoted as and . is the identity matrix. Probability density functions are denoted by . The superscript denotes complex conjugate, and denotes transpose. denotes mathematical expectation, and denotes the differential entropy of a continuous random variable. indicates that is a complex circular Gaussian random vector of zero mean and covariance , while indicates that is a complex non-circular Gaussian random vector of zero mean, covariance and complementary covariance .
2.2. Improper Random Variables
This section introduces some preliminaries about improper random variables that will be used throughout the paper. The interested reader is referred to [
9] for a comprehensive treatment of the topic.
Definition 1 ([
9])
. A complex-valued random variable X is said to be circular (or circularly symmetric) if has the same probability distribution as X for all real θ. Definition 2 ([
27])
. A complex-valued random variable X is said to be proper if X is uncorrelated with its complex conjugate, i.e., . A circular X is proper, but the converse is not necessarily true. However, for complex Gaussian random variables, propriety implies circularity, so both terms can be used interchangeably. The next definitions characterize an improper random variable.
Definition 3 ([
9])
. The complementary variance of a zero-mean complex random variable X is defined as . Furthermore, and are a valid pair of variance and complementary variance if and only if and .
Definition 4 ([
9])
. The circularity coefficient of a complex random variable X, which measures the degree of impropriety, is defined as: The circularity coefficient satisfies . If , then X is proper, otherwise improper. If , we call X maximally improper.
There are two models that are typically used to express an improper complex random variable
: the augmented complex model and the real composite model. The former defines the augmented random variable
. This way, its covariance matrix (called the augmented covariance matrix) contains all the second-order information of
X, i.e.,
Alternatively, the real composite model defines the real random vector , and its covariance matrix also contains the complete second-order information of X. We now present some well-known results about the differential entropy of a complex Gaussian random variable.
Theorem 1 ([
9])
. The differential entropy of an improper complex Gaussian random variable X is: Taking
in the above expression yields the entropy of a proper Gaussian random variable [
27]. Indeed, it is well known that the entropy of a complex random variable is maximized if it follows a proper complex Gaussian distribution [
27].
2.3. A Motivating Example
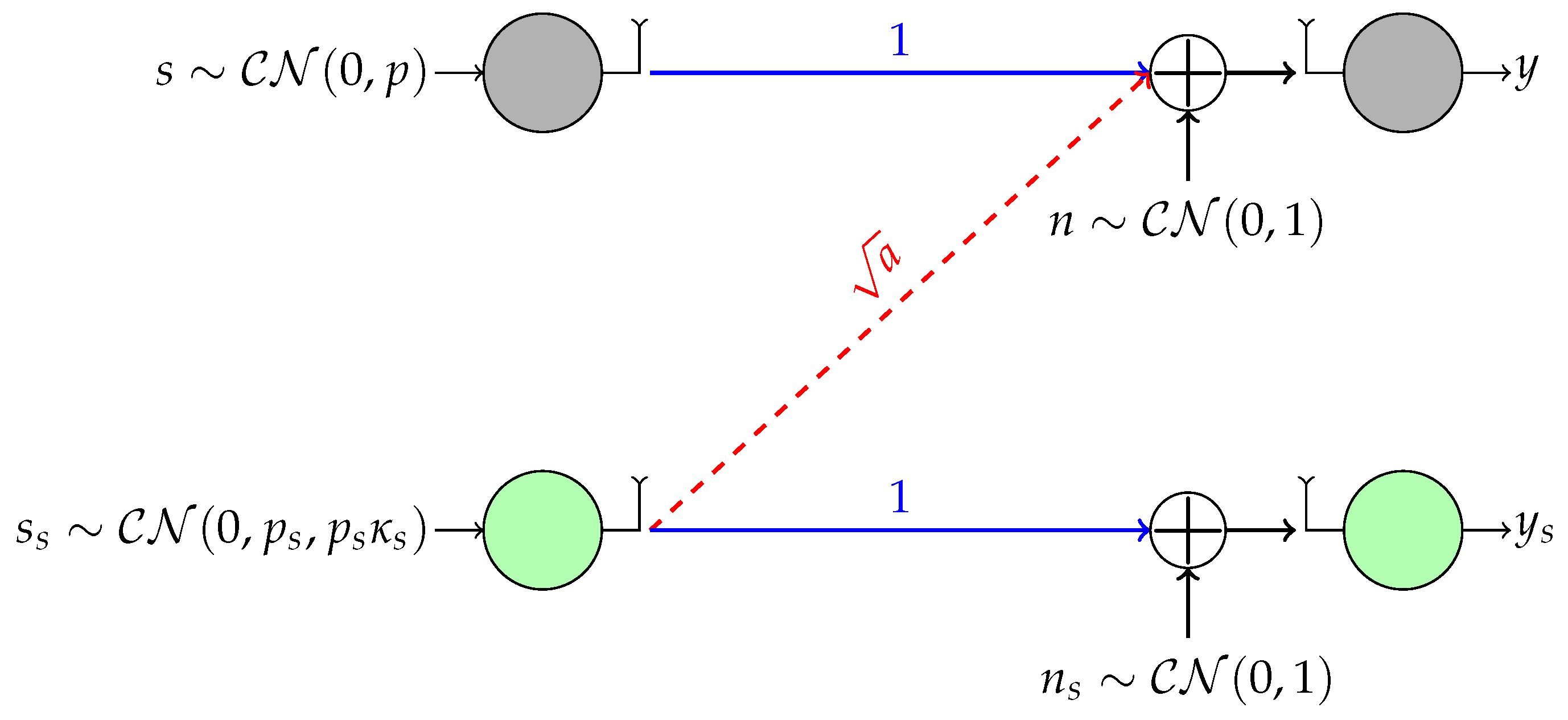
In this subsection, we present a motivating example for the study conducted in this paper. Let us consider an underlay cognitive radio (UCR) system transmitting Gaussian codewords in which one single-antenna secondary user (SU) wishes to access the channel in the presence of a single-antenna primary user (PU) as shown in
Figure 1, where the top and bottom links represent the PU and the SU, respectively. Without loss of generality, we consider the standard or canonical form of this scenario for which the direct channels are normalized to one, and the noise at both receivers is Gaussian and proper with zero mean and unit variance. This scenario is known in the information theory literature as the Z (or one-sided) interference channel [
28].
In the UCR paradigm, the unlicensed SU is allowed to coexist with the PU as long as they ensure a minimum transmission rate
for the PU, where
is the loading factor. That is, the transmit power and signaling scheme of the SU must be selected to control the interference level at the primary receiver such that the PU’s rate requirement is guaranteed. Since the PU is typically unaware of the SU, it is also assumed that the PU always transmits proper Gaussian signals, whereas the SU may transmit either proper or improper Gaussian signals depending on which signaling scheme performs better. This problem has been analyzed in [
7], where it has been proven that the SU improves its rate by transmitting Gaussian improper signals if and only if (cf. Theorem 1 in [
7]):
where
p is the power transmitted by the PU. Furthermore, Theorem 1 in [
7] also gives us the optimal circularity coefficient
that must be used by the SU depending on its power budget.
For example, let us suppose that the cross-link channel is ; the power budgets for the PU and SU are 100 and 20, respectively; and the loading factor is . With these parameters and, since , improper signaling with (close to maximally improper) improves the rate of the SU. Specifically, the rate achieved by the SU using improper Gaussian codewords is b/s/Hz, whereas using proper Gaussian codewords, the rate would be only b/s/Hz.
As we have already argued, practical constraints dictate the use of discrete constellations instead of Gaussian signals. Nevertheless, the previous analysis with Gaussian signals is still valuable as an upper bound in the sense that any finite constellation with the same circularity coefficient will have lower differential entropy than a Gaussian and, consequently, will be less harmful for the PU. Therefore, in our example, for any improper discrete constellation, we might transmit with , and the rate requirement of the PU would still be satisfied.
When the PU transmits Gaussian proper signals and the interference at the SU is treated as noise, the SU link is an AWGN channel over which we have to send improper digital signals with a given . In a more realistic scenario, the PU would also transmit a discrete non-Gaussian constellation. In this case, the interference power tolerated by the PU could potentially vary with respect to Gaussian signaling, and the SU would receive non-Gaussian interference, as well. While all Gaussian signals with a given circularity coefficient are identical in terms of performance, this is not the case with our family of discrete constellations. As we will see shortly, with discrete improper constellations, we have one degree of freedom to optimize the SU performance. In this work, we study a family of improper constellations and design its parameters to maximize the mutual information over the SU link modeled as an AWGN channel. Obviously, if we maximize the mutual information, the SU will cause more harm to the PU, but still, this harm is upper bounded by the harm caused by a Gaussian signal with the same , so the PU will sustain its rate.
2.4. Capacity Results for Gaussian Improper Signals
We consider a complex AWGN channel:
where
is circular,
V is the transmitted signal and the channel is a deterministic and known constant, which we take as
without loss of generality.
The capacity (in bits per channel use) of this channel is [
1]:
where the supremum is taken over all possible input distributions of
V with
, and the logarithms have base two. It is well known that the supremum is achieved when
[
27].
In this paper, we consider the case where the input signal is unit-power improper with circularity coefficient
; then, the channel output is also improper Gaussian with variance
and circularity coefficient
. By Theorem 1, the differential entropy of
Y is:
and the capacity is:
Observe that for
, the second term in (
8) is always negative, and therefore, there is a capacity loss with respect to proper Gaussian signaling. In
Appendix A, we present a heuristic derivation of this formula based on a packing argument similar to [
29].
Remark 1. As , the term:in (8) accounts for the loss in capacity due to enclosing the codewords in a multidimensional ellipsoid rather than in a hypersphere (as proper Gaussian signaling does) [30]. 3. A Family of Improper Constellations Generated by a Widely Linear Transformation
In this section, we propose a family of improper discrete constellations that are generated by a widely linear transformation of a standard
M-QAM constellation, where
with
s a positive integer. To this end, let
be a symbol in a proper
M-QAM constellation of unit power (
). Then, we propose to generate the corresponding improper symbol as:
where
and
are complex scalars such that
(to maintain unit transmit power). Alternatively, the widely linear precoding operation (
9) can be expressed in terms of real variables as:
Under the constraint
, the circularity coefficient of the generated symbol is:
The question that now arises is: given
, what is the simplest parametrization of this family of improper constellations in terms of the complex variables
and
? All values of
and
producing a unit variance improper
V with a given
must satisfy:
The nonlinear system of equations in (
12) has a unique solution for the squared modulus
and
, which can be written in terms of the variable
as:
Since for the AWGN channel considered in (
5), the noise is Gaussian and proper (circular), it is clear that the mutual information does not change when the constellation is rotated by an arbitrary angle. This means that we can always rotate the constellation
V such that
is a real and positive parameter, whereas
is a complex value. With this restriction,
and
can be expressed as:
Furthermore, the original proper
M-QAM constellation
X has a rotational symmetry of
for any integer
n, which means that
in (15) can be restricted to the interval
. Finally, the proposed family of improper constellations with circularity coefficient
can be parameterized as:
where
,
and
. In what follows, to stress the dependency of the improper constellation on
,
and
M, we will denote this family of constellations as
.
In terms of real variables, the transformation in (
16) can be written as:
where
denotes the
transformation matrix.
Observe that by setting
in (
16), one obtains a rather naive rectangular QAM improper constellation, where its real and imaginary components are independent and have a power imbalance determined by the required circularity coefficient
. For any other
the constellation points are enclosed in a non-rectangular parallelogram.
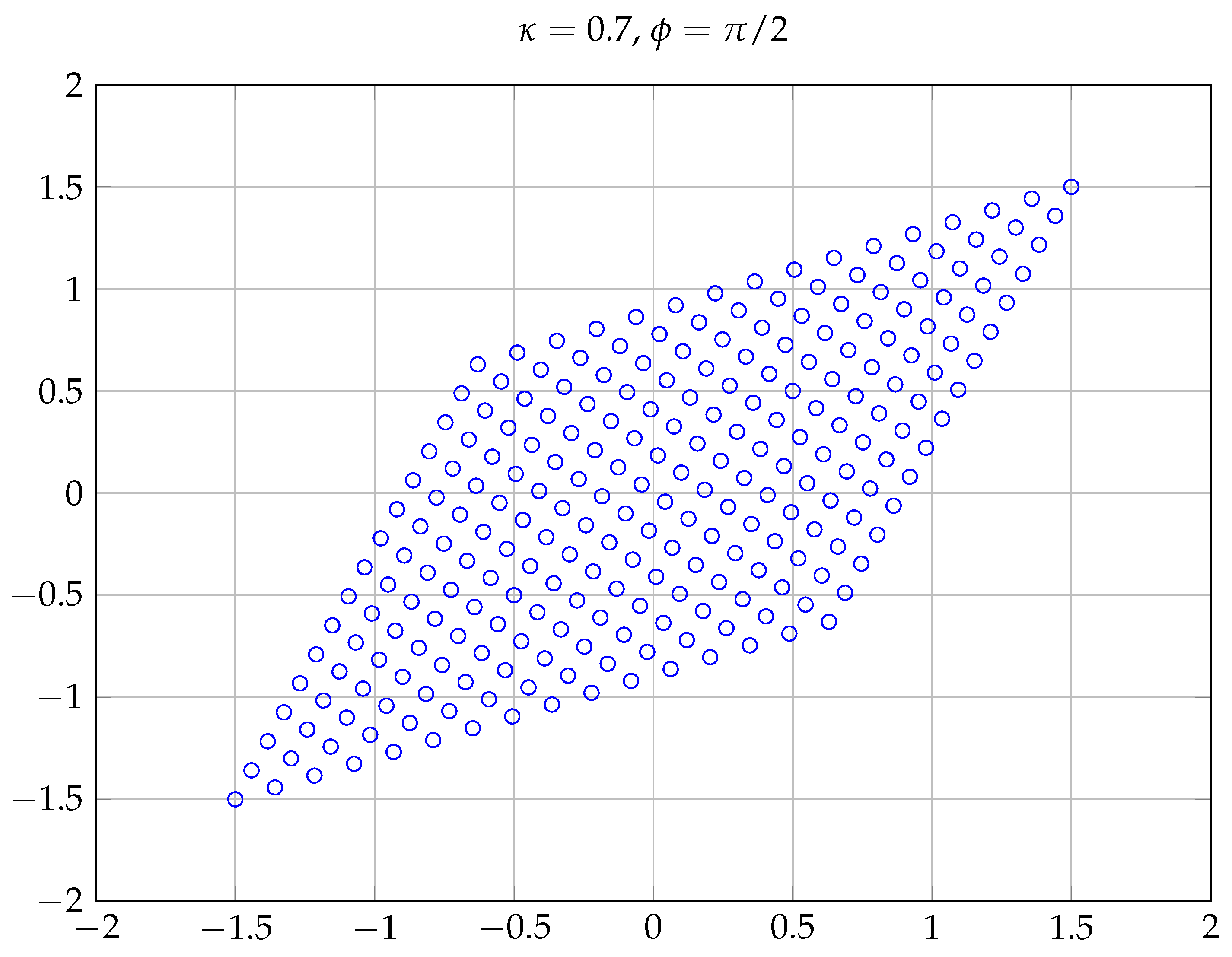
Figure 2 shows four improper constellations generated according to (
16) for different values of
and
when
X is proper QPSK (
). For
(maximally improper signal), in the right bottom panel, the points of the constellation lie on a line. Similarly,
Figure 3 shows the constellation
, where the shape of the constellation, a parallelogram, can be more clearly observed.
We now provide an alternative geometric interpretation of the proposed improper constellations . Consider the 2D integer lattice , consisting of all two-dimensional vectors with a and b integers. Then, the M-QAM constellation can be obtained as the intersection of the translated lattice and the square region .
If we apply the linear transformation
to the lattice
, we obtain the new translated lattice
, where:
Reasoning as before, the unnormalized family of improper constellations
can be obtained as the intersection of the translated lattice
and the parallelogram region
that results from the
-transformation of a centered square with side length
, that is,
Note that by doing this, only
M points of the lattice
are enclosed, and their average energy is
. Since translation of a lattice does not affect its minimum distance between signal points,
, we conclude that the minimum distance of the unnormalized family of constellations
(
19) is given by the minimum distance of the lattice
. For a given
, the optimal
that maximizes
can be obtained as:
This problem will be solved in
Section 4. Taking into account that
does not depend on the scaling of the lattice
, we arrive at the following proposition:
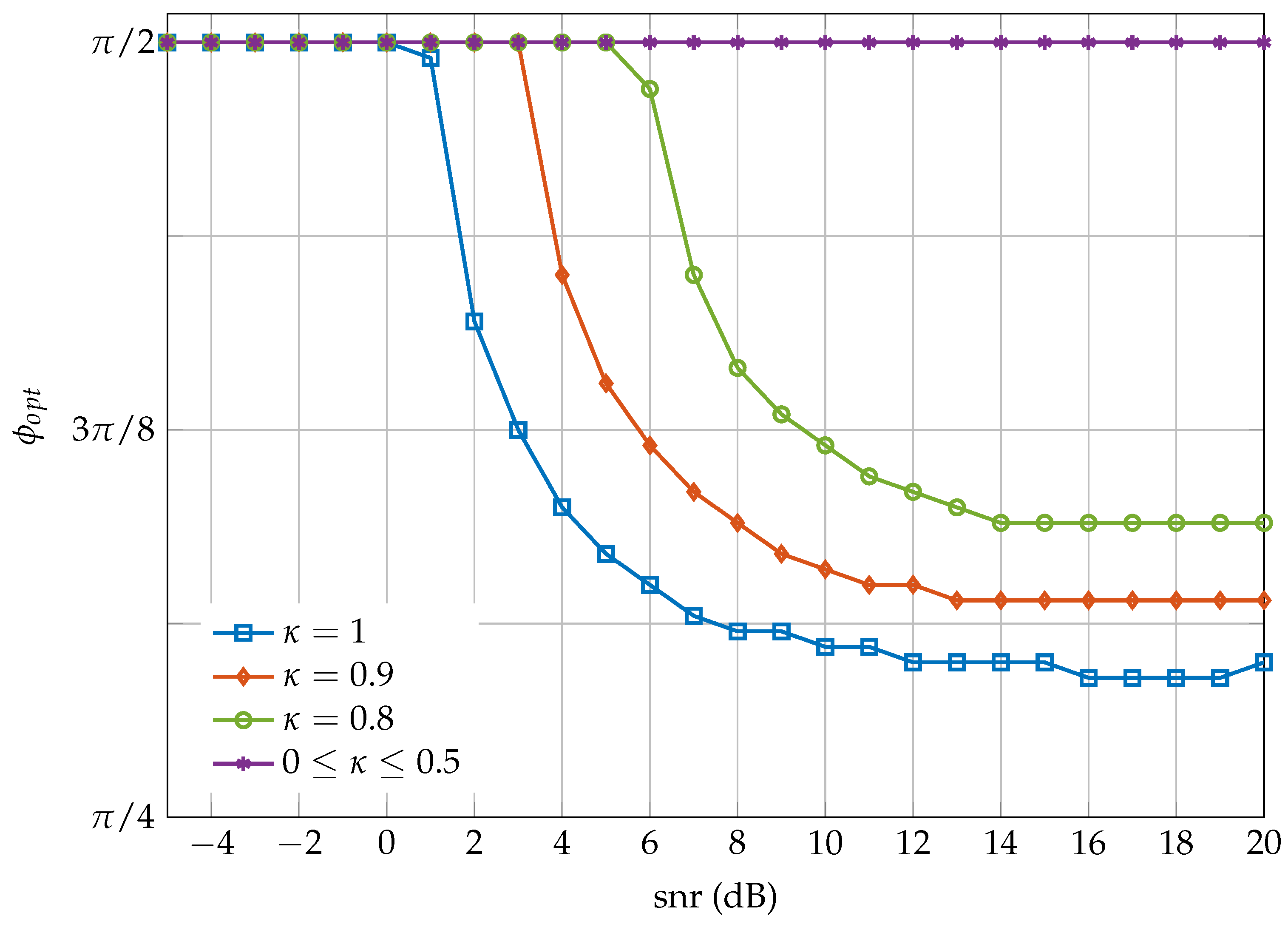
Proposition 1. The angle that maximizes the minimum distance of the family constellations , where μ is an arbitrary normalization factor, only depends on the circularity coefficient κ and is given by (20), where in (18) is the lattice that results from the -transformation of the integer lattice . 6. Conclusions
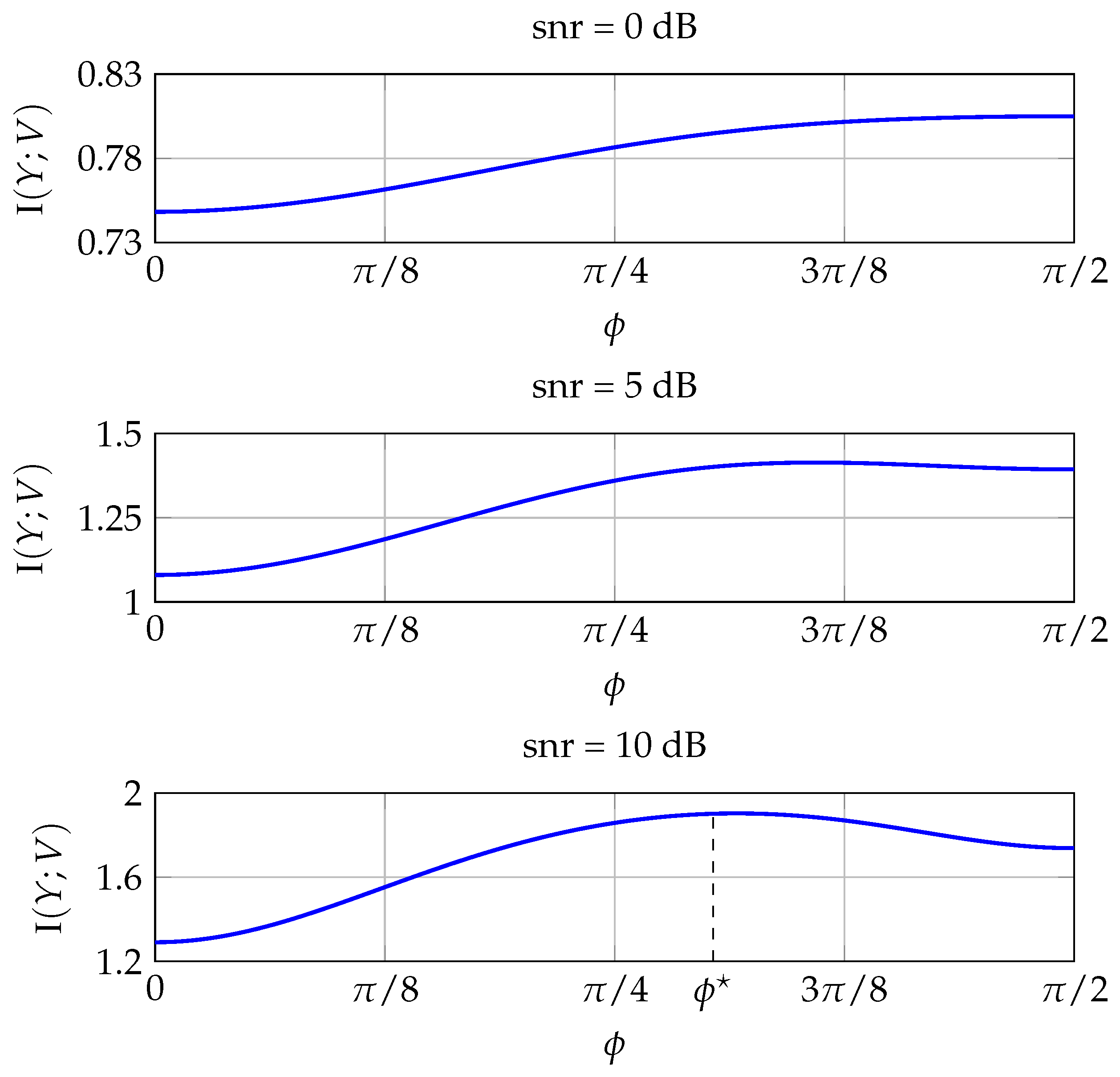
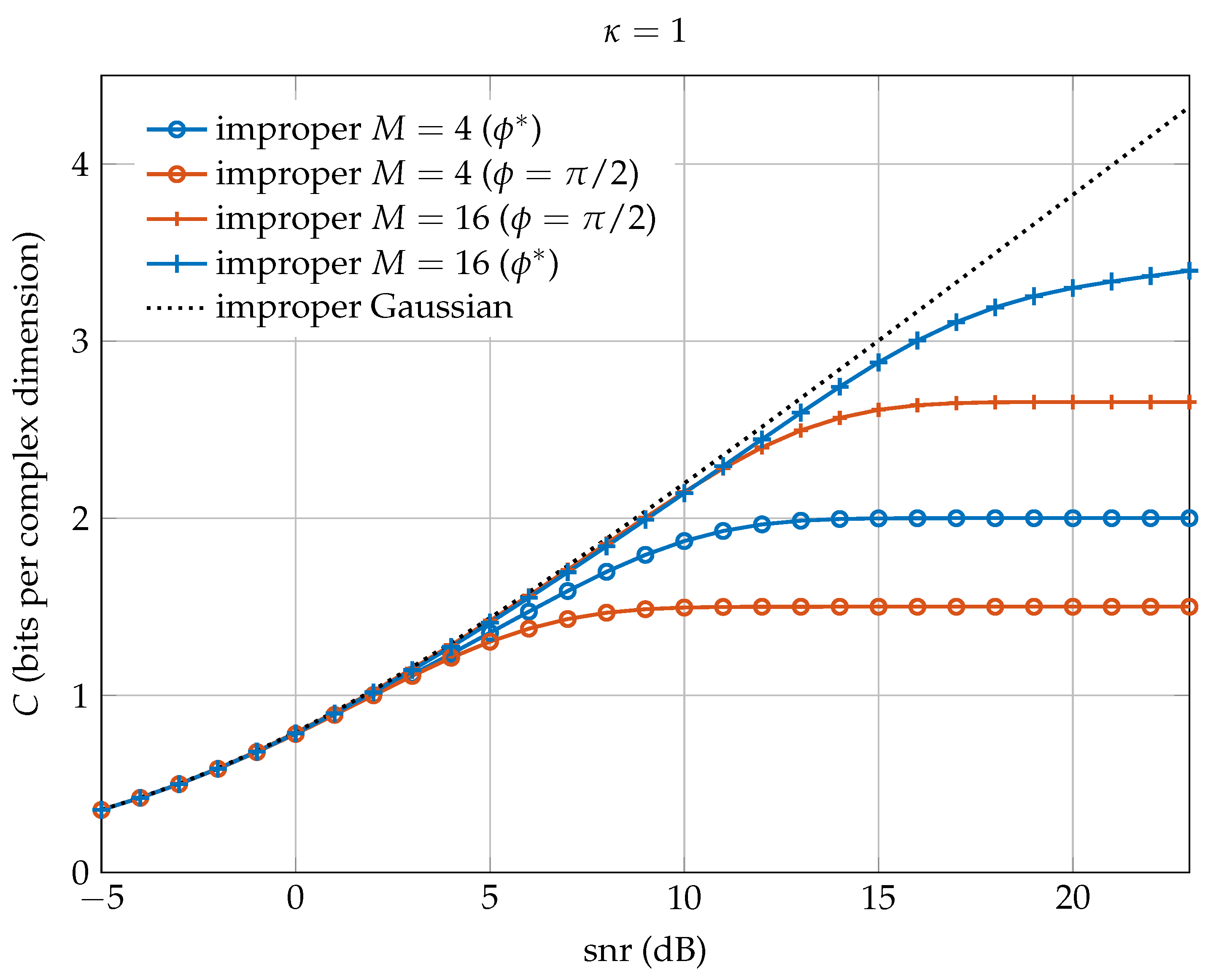
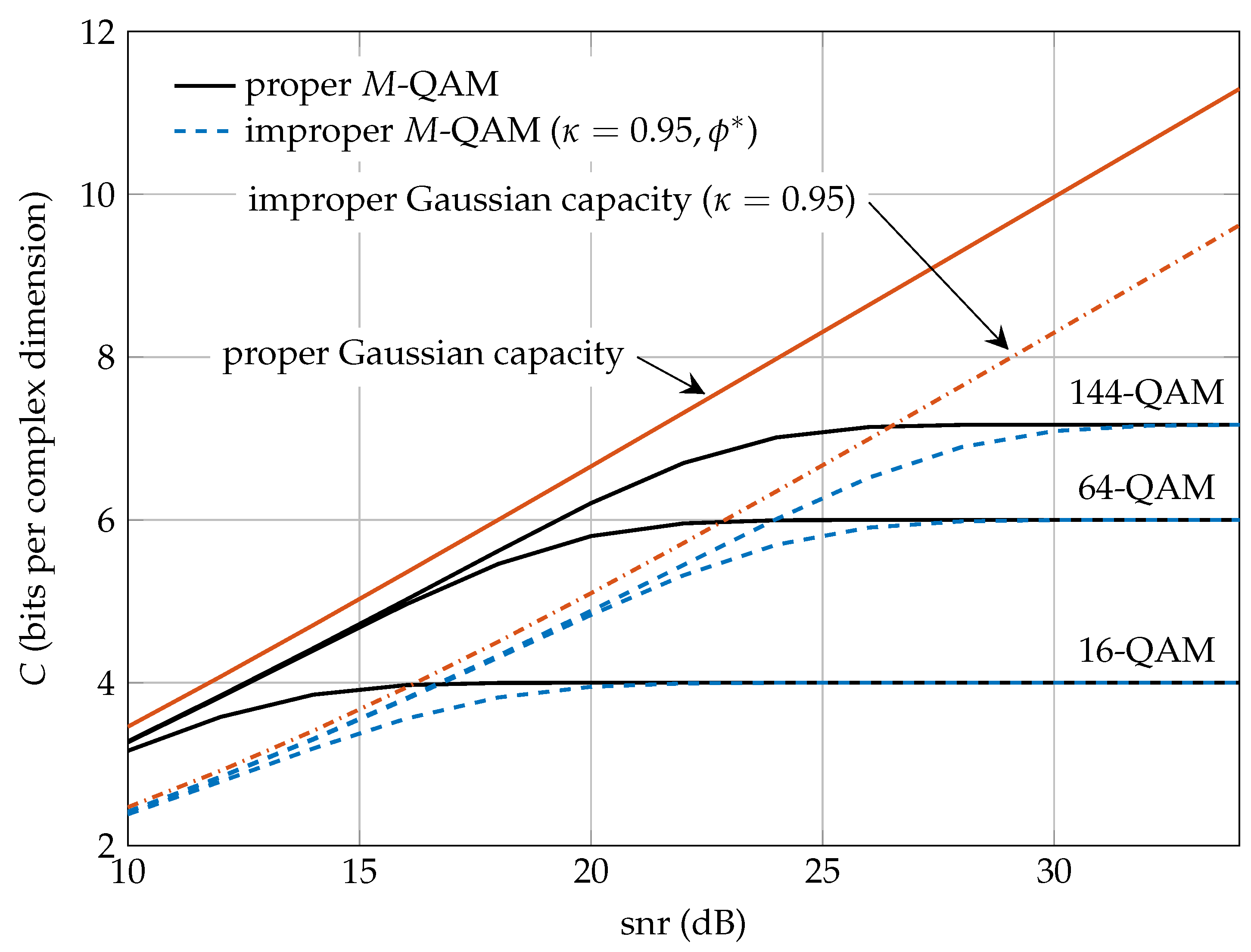
In this paper, we have proposed a family of improper constellations constructed by widely linear processing of proper M-QAM signals. We have shown that, when the coded channel symbols are uniformly drawn from these constellations, the achievable transmission rates are close to the ones dictated by the improper Gaussian capacity. In particular, except for a shaping loss of 1.53 dB encountered at high , there is no rate loss of the proposed improper discrete constellations with respect to the improper Shannon capacity. In practice, we can select the optimal phase at high , , obtained by minimizing the BER of the uncoded system without significant loss in performance at lower . Observe that this fact facilitates the practical implementation of these constellations since does not depend on the and M.
These results are obtained by analyzing at the high- and low- regimes the family of mutual information, , and by obtaining the shaping loss computed as the ratio of the normalized second moments of a multidimensional parallelogram and a multidimensional ellipsoid.
We conclude that the proposed family of improper constellations is a good candidate to be used in communication systems when improper signaling is required over the AWGN channel. In fact, it behaves like the standard family of proper M-QAM constellations and can be viewed as its improper counterpart. In perspective, these results extend the analysis of improper signaling in interference-limited scenarios to non-Gaussian discrete constellations with equiprobable symbols.