Study on Bifurcation and Dual Solutions in Natural Convection in a Horizontal Annulus with Rotating Inner Cylinder Using Thermal Immersed Boundary-Lattice Boltzmann Method
Abstract
:1. Introduction
2. Numerical Model and Method
2.1. Numerical Model
2.2. Thermal IB-LBM
3. Verification
4. Results and Discussion
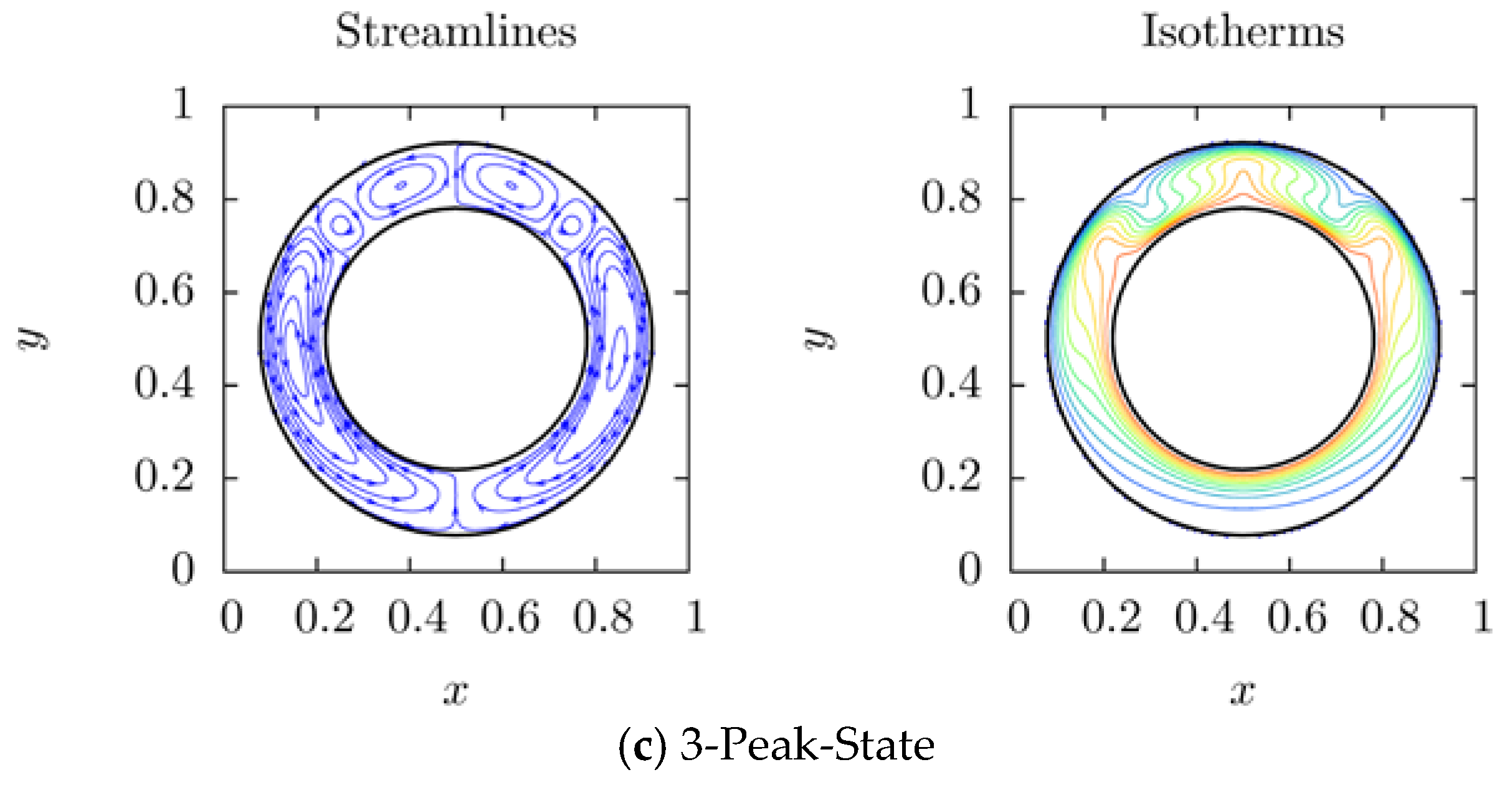
4.1. Bifurcation Solutions in Stationary Concentric Cylinders
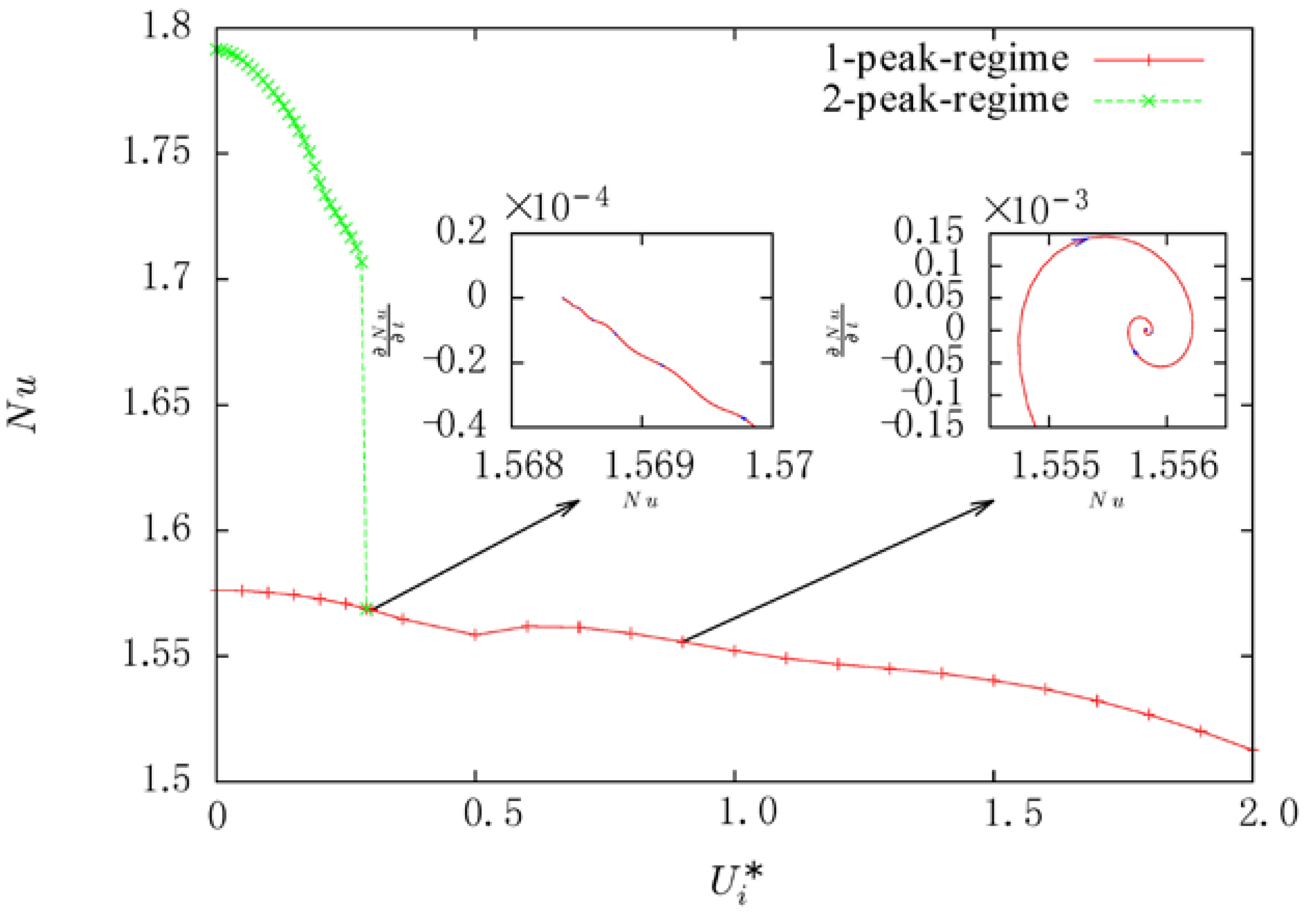
4.2. Rotation Effect on Natural Convection
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Grigull, U.; Hauf, W. Natural convection in horizontal cylindrical annuli. In Proceedings of the 3rd International Heat Transfer Conference, Chicago, IL, USA, 7–12 August 1966; pp. 182–195. [Google Scholar]
- Powe, R.E.; Carley, C.T.; Bishop, E.H. Free convective flow patterns in cylindrical annuli. J. Heat Transf. 1969, 91, 310. [Google Scholar] [CrossRef]
- Kuehn, T.H.; Goldstein, R.J. An experimental and theoretical study of natural convection in the annulus between horizontal concentric cylinders. J. Fluid Mech. 1976, 74, 695–719. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Vasseur, P.; Robillard, L. Natural convection between horizontal concentric cylinders with density inversion of water for low Rayleigh numbers. Int. J. Heat Mass Transf. 1982, 25, 1559–1568. [Google Scholar] [CrossRef]
- Dyko, M.P.; Vafai, K.; Mojtabi, A.K. A numerical and experimental investigation of stability of natural convective flows within a horizontal annulus. J. Fluid Mech. 1999, 381, 27–61. [Google Scholar] [CrossRef]
- Yoo, J.S. Natural convection in a narrow horizontal cylindrical annulus: Pr = 0.3. Int. J. Heat Mass Transf. 1998, 41, 3055–3073. [Google Scholar] [CrossRef]
- Yoo, J.S. Prandtl number effect on bifurcation and dual solutions in natural convection in a horizontal annulus. Int. J. Heat Mass Transf. 1999, 42, 3279–3290. [Google Scholar] [CrossRef]
- Yoo, J.S. Transition and multiplicity of flows in natural convection in a narrow horizontal cylindrical annulus: Pr = 0.4. Int. J. Heat Mass Transf. 1999, 42, 709–722. [Google Scholar] [CrossRef]
- Petrone, G.; Chénier, E.; Lauriat, G. Stability of free convection in air-filled horizontal annuli: Influence of the radius ratio. Int. J. Heat Mass Transf. 2004, 47, 3889–3907. [Google Scholar] [CrossRef]
- Petrone, G.; Chénier, E.; Lauriat, G. Stability analysis of natural convective flows in horizontal annuli: Effects of the axial and radial aspect ratios. Phys. Fluids 2006, 18, 104107. [Google Scholar] [CrossRef] [Green Version]
- Luo, K.; Yi, H.L.; Tan, H.P. Eccentricity effect on bifurcation and dual solutions in transient natural convection in a horizontal annulus. Int. J. Therm. Sci. 2014, 89, 283–293. [Google Scholar] [CrossRef]
- Hu, Y.; Li, D.; Shu, S.; Niu, X.D. Study of multiple steady solutions for the 2D natural convection in a concentric horizontal annulus with a constant heat flux wall using immersed boundary-lattice Boltzmann method. Int. J. Heat Mass Transf. 2015, 81, 591–601. [Google Scholar] [CrossRef]
- Zhang, W.; Wei, Y.K.; Chen, X.P.; Dou, H.-S.; Zhu, Z.C. Partitioning effect on natural convection in a circular enclosure with an asymmetrically placed inclined plate. Int. Commun. Heat Mass Transf. 2018, 90, 11–22. [Google Scholar] [CrossRef]
- Wei, Y.K.; Dou, H.S.; Wang, Z.D.; Qian, Y.H. A novel two-dimensional coupled lattice Boltzmann model for incompressible flow in application of turbulence Rayleigh-Taylor instability. Comput. Fluids 2017, 156, 97–102. [Google Scholar] [CrossRef]
- Wei, Y.K.; Dou, H.S.; Wang, Z.D.; Qian, Y.H.; Yan, W.W. Simulations of natural convection heat transfer in an enclosure at different Rayleigh number using lattice Boltzmann method. Comput. Fluids 2016, 124, 30–38. [Google Scholar] [CrossRef]
- Lopez, J.M.; Marques, F.; Mercader, I.; Batiste, O. Onset of convection in a moderate aspect-ratio rotating cylinder: Eckhaus-Benjamin-Feir instability. J. Fluid Mech. 2007, 590, 187–208. [Google Scholar] [CrossRef]
- Zhang, W.; Wei, Y.K.; Dou, H.-S.; Zhu, Z.C. Transient behaviors of mixed convection in a square enclosure with an inner impulsively rotating circular cylinder. Int. Commun. Heat Mass Transf. 2018, in press. [Google Scholar]
- Qian, Y.H.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Liang, H.; Shi, B.C.; Chai, Z.H. Lattice Boltzmann simulation of three-dimensional Rayleigh-Taylor instability. Phys. Rev. E 2016, 93, 033113–033119. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Xu, J.; Chen, J.; Wang, H.; Chai, Z.H.; Shi, B.C. Phase-field-based lattice Boltzmann modeling of large-density-ratio two-phase flows. Phys. Rev. E 2018, 97, 033309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, Z.G.; Michaelides, E.E. The immersed boundary-lattice Boltzmann method for solving fluid-particles interaction problems. J. Comput. Phys. 2004, 195, 602–628. [Google Scholar] [CrossRef]
- Succi, S. The Lattice-Boltzmann Equation for Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Guo, Z.L.; Shi, B.C.; Zheng, C.G. A coupled lattice BGK model for the Boussinesq equations. Int. J. Numer. Meth. Fluids 2002, 39, 325–342. [Google Scholar] [CrossRef]
- Niu, X.D.; Shu, C.; Chew, Y.T.; Peng, Y. A momentum exchange-based immersed boundary-lattice boltzmann method for simulating incompressible viscous flows. Phys. Lett. A 2006, 354, 173–182. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C. Implicit velocity correction-based immersed boundary-lattice Boltzmann method and its applications. J. Comput. Phys. 2009, 228, 1963–1979. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C.; Zhang, Y.H. Simulation of incompressible viscous flows around moving objects by a variant of immersed boundary-lattice Boltzmann method. Int. J. Numer. Meth. Fluids 2010, 62, 327–354. [Google Scholar] [CrossRef] [Green Version]
- Buick, J.M.; Greated, C.A. Gravity in lattice Boltzmann model. Phys. Rev. E 2000, 61, 5307–5320. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.H.; Lin, K.H.; Mai, H.C.; Lin, C.A. Thermal boundary conditions for thermal lattice Boltzmann simulations. Compt. Math. Appl. 2010, 59, 2178–2193. [Google Scholar] [CrossRef]
- Le, G.; Zhang, J. Boundary slip from the immersed boundary lattice Boltzmann models. Phys. Rev. E 2009, 79, 026701. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Cheng, Y.; Miller, L.A. An iterative source correction based immersed boundary-latticeBoltzmann method for thermal flow simulations. Int. J. Heat Mass Transf. 2017, 115, 450–460. [Google Scholar] [CrossRef]
- Luo, K.; Yi, H.L.; Tan, H.P. Radiation effects on bifurcation and dual solutions in transient natural convection in a horizontal annulus. Int. J. Therm. Sci. 2015, 89, 283–293. [Google Scholar] [CrossRef]
- Amiri, D.A.; Nazari, M.; Kayhani, M.H.; Succi, S. Non-Newtonian unconfined flow and heat transfer over a heated cylinder using the direct-forcing immersed boundary-thermal lattice Boltzmann method. Phys. Rev. E 2014, 89, 053312. [Google Scholar] [CrossRef] [PubMed]









| Grid Size | Experiment [3] | ||||
|---|---|---|---|---|---|
| Extrapolation | |||||
| 1.034 | 1.016 | 1.008 | 1.002 | 1.000~1.002 | |
| 1.101 | 1.092 | 1.087 | 1.081 | 1.081~1.084 | |
| 1.955 | 1.977 | 1.989 | 2.003 | 2.005~2.010 | |
| 2.346 | 2.364 | 2.375 | 2.392 | 2.394~2.405 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Wang, Z.; Qian, Y.; Guo, W. Study on Bifurcation and Dual Solutions in Natural Convection in a Horizontal Annulus with Rotating Inner Cylinder Using Thermal Immersed Boundary-Lattice Boltzmann Method. Entropy 2018, 20, 733. https://doi.org/10.3390/e20100733
Wei Y, Wang Z, Qian Y, Guo W. Study on Bifurcation and Dual Solutions in Natural Convection in a Horizontal Annulus with Rotating Inner Cylinder Using Thermal Immersed Boundary-Lattice Boltzmann Method. Entropy. 2018; 20(10):733. https://doi.org/10.3390/e20100733
Chicago/Turabian StyleWei, Yikun, Zhengdao Wang, Yuehong Qian, and Wenjing Guo. 2018. "Study on Bifurcation and Dual Solutions in Natural Convection in a Horizontal Annulus with Rotating Inner Cylinder Using Thermal Immersed Boundary-Lattice Boltzmann Method" Entropy 20, no. 10: 733. https://doi.org/10.3390/e20100733




