Detection of Parameter Change in Random Coefficient Integer-Valued Autoregressive Models
Abstract
:1. Introduction
2. CLSE for RCINAR Models
3. Parameter Change Test for RCINAR Models
3.1. EF-Based Test
3.2. Residual-Based CUSUM Test
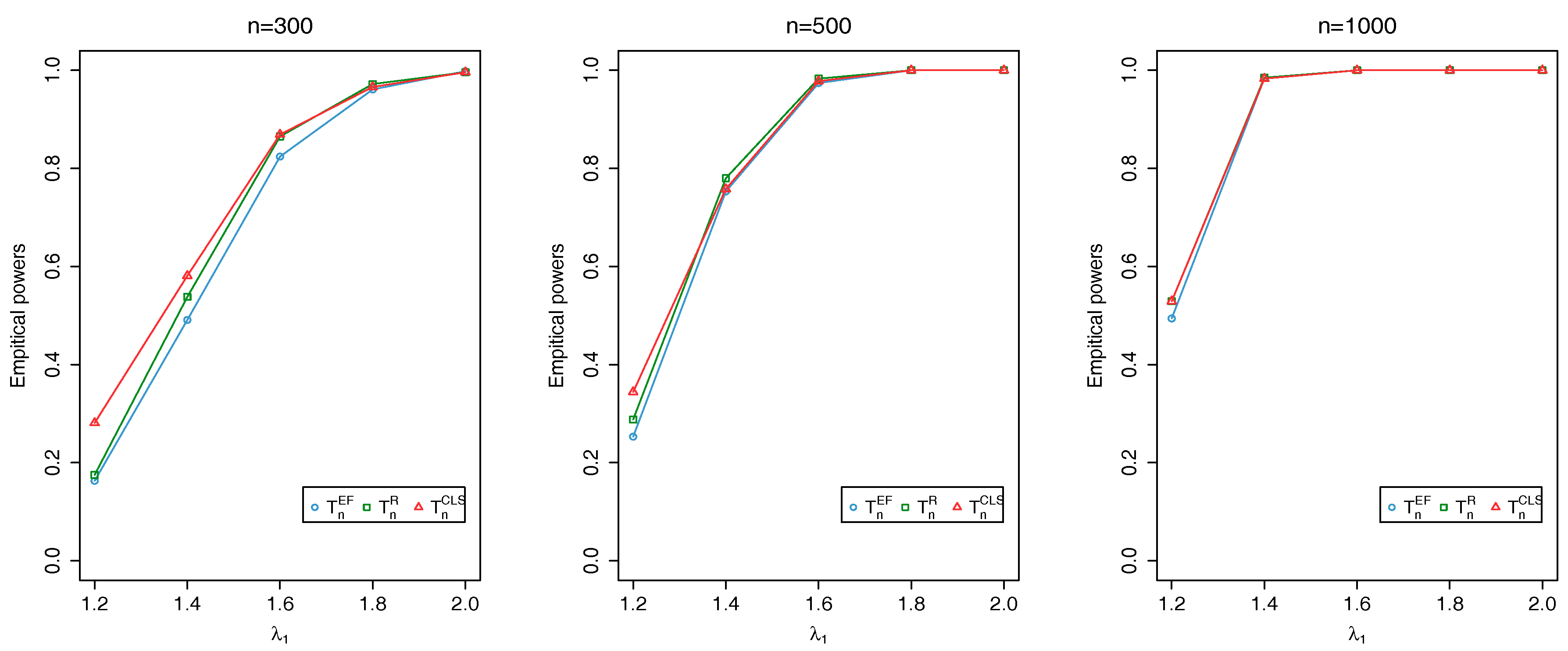
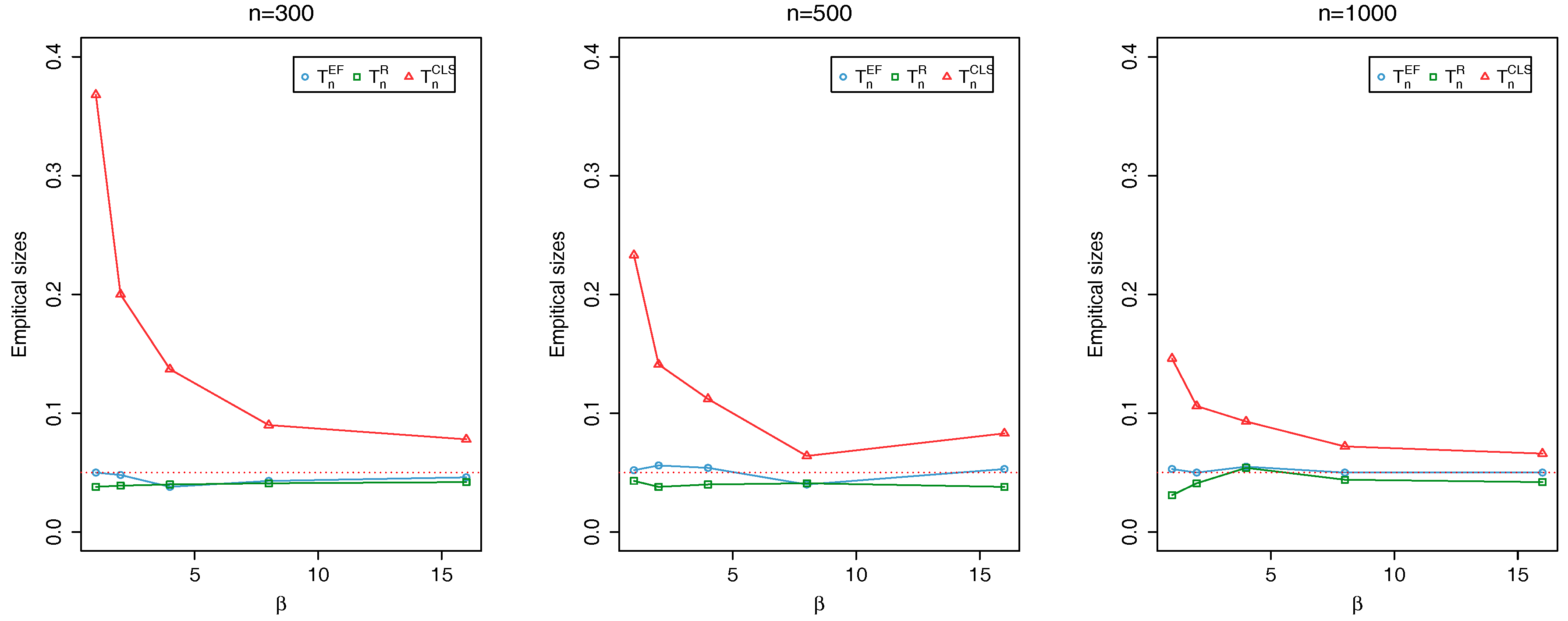
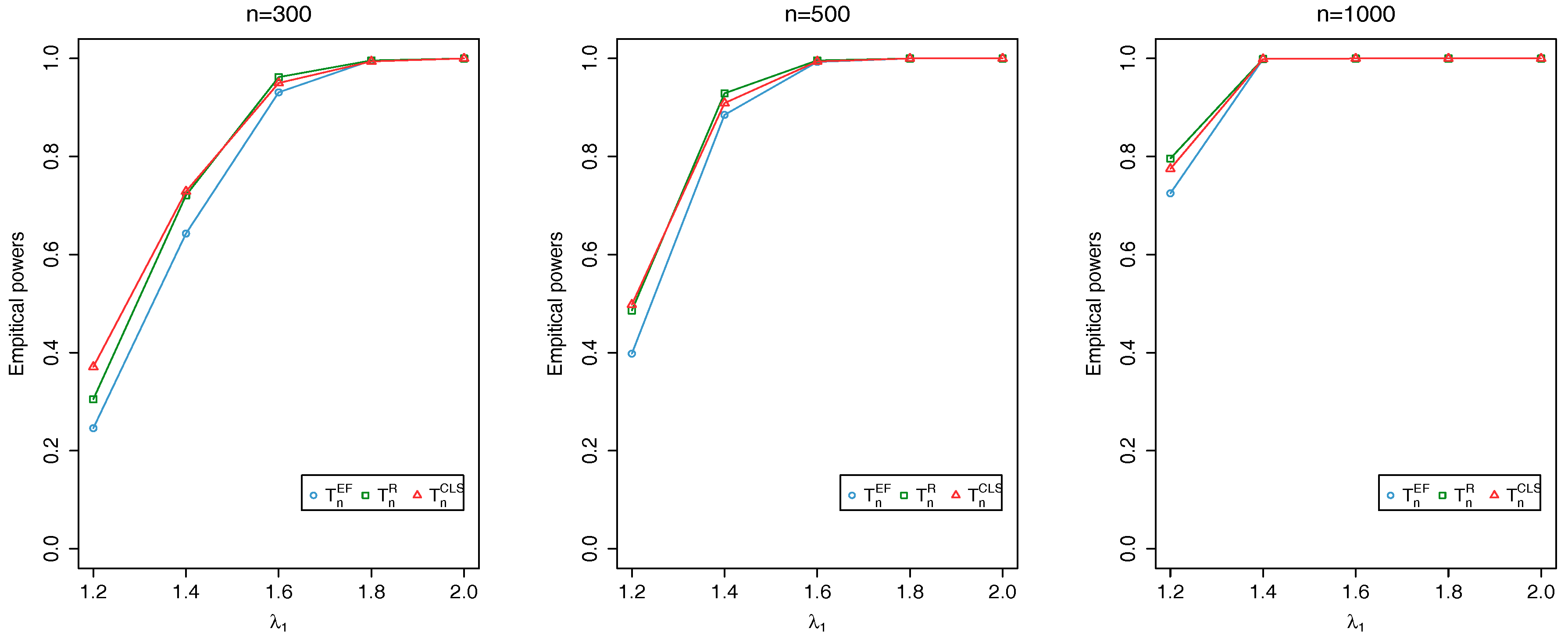
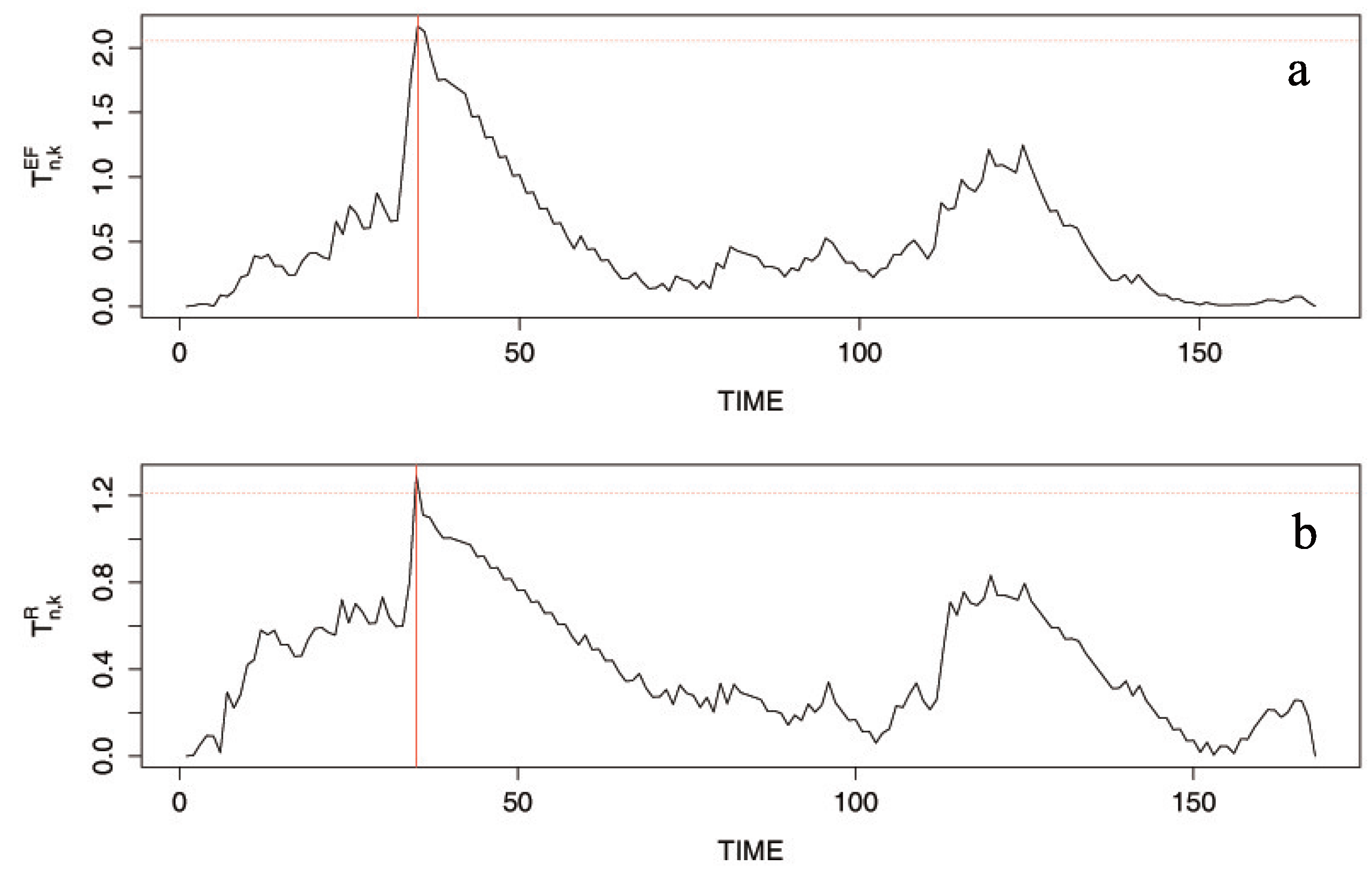
4. Simulation Results
- (i)
- = 1 changes to = 1.2, 1.4, 1.6, 1.8, 2.0 and b = 4 dose not change.
- (ii)
- = 8 changes to = 7, 6 and changes in the same way as in (i).
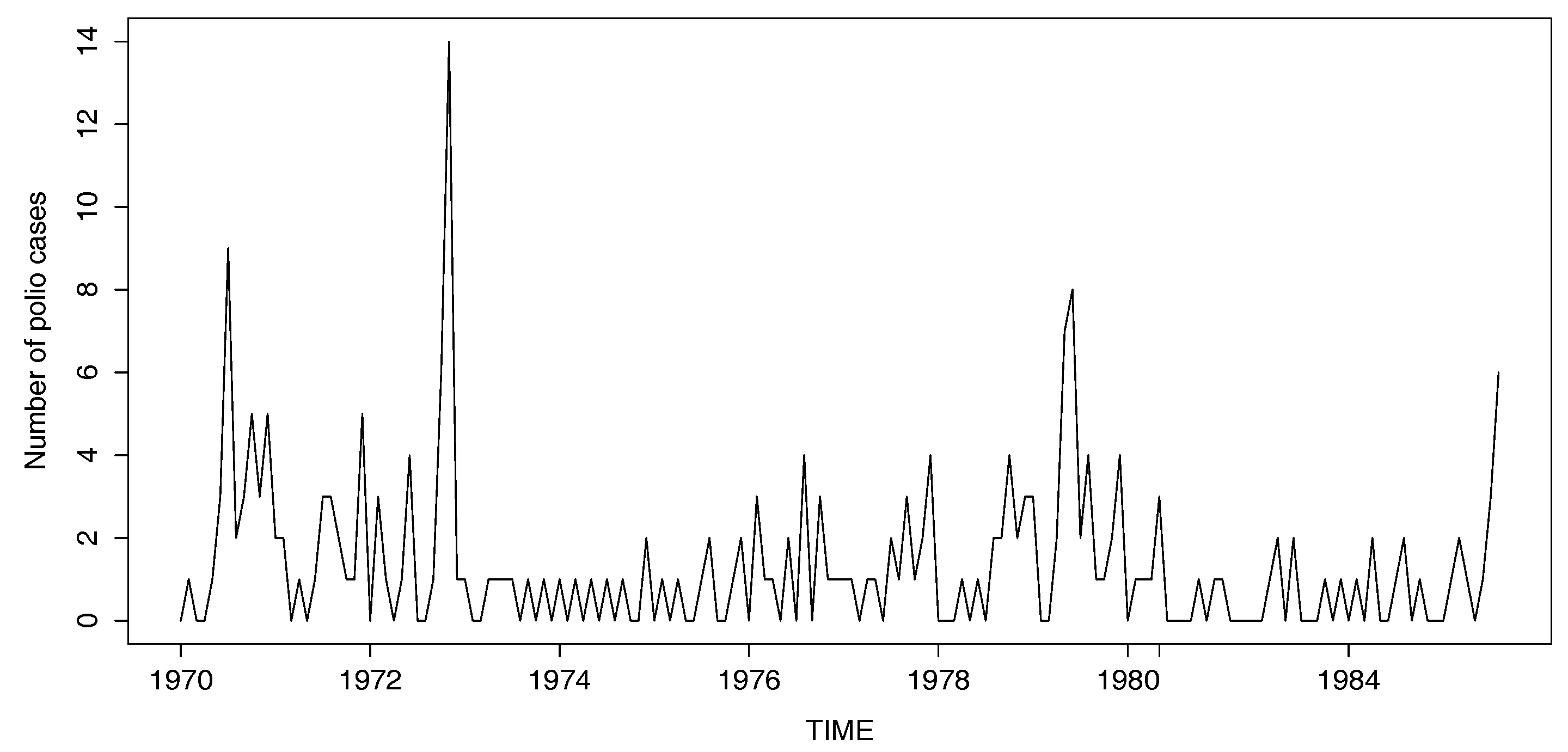
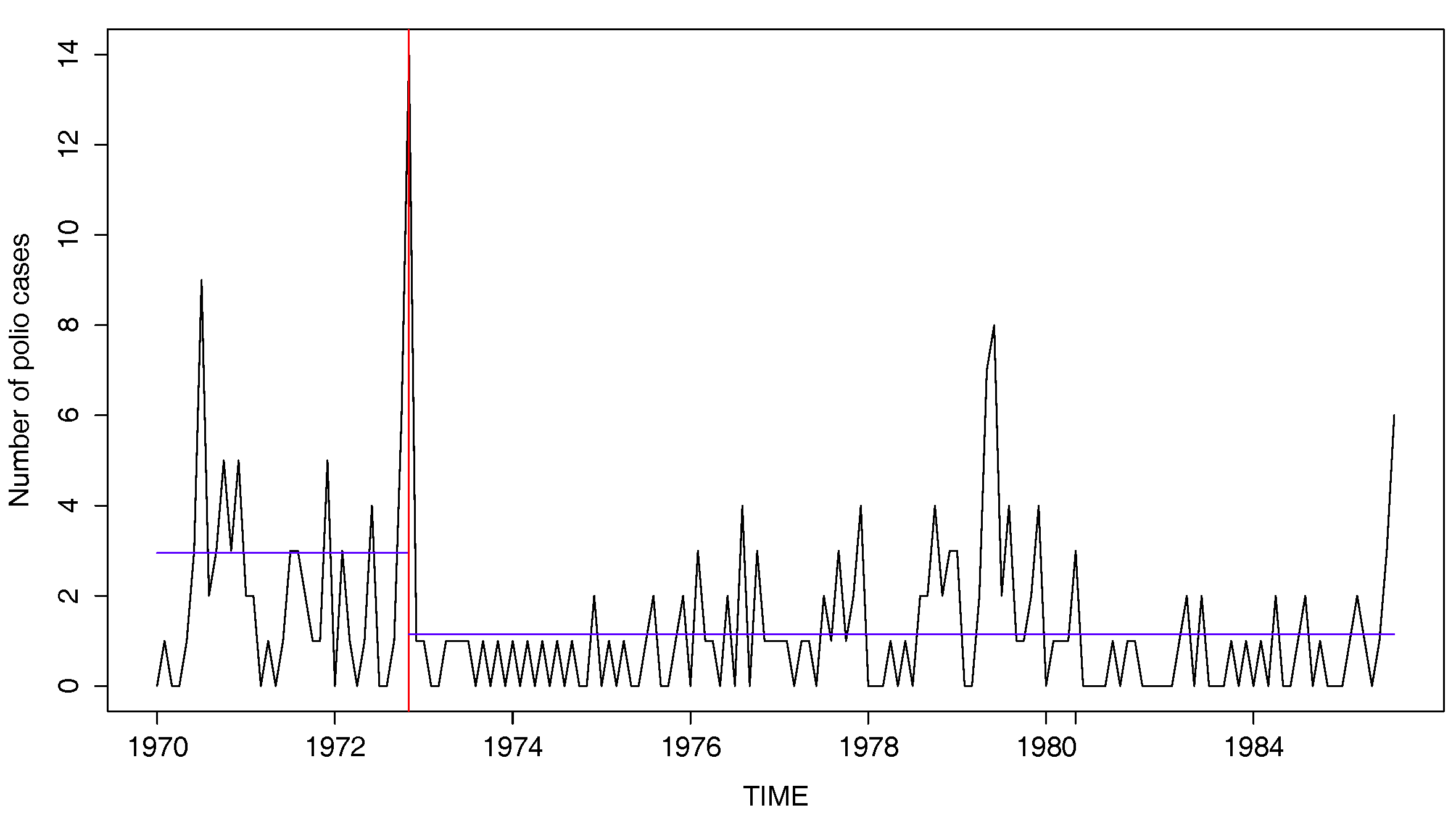
5. Real Data Analysis
6. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Fokianos, K. Some recent progress in count time series. Statistics 2011, 45, 49–58. [Google Scholar] [CrossRef]
- McKenzie, E. Discrete variate time series. Stochastic processes: Modelling and simulation. In Handbook of Statistics; Shanbhag, D.N., Rao, C.R., Eds.; Elsevier Science: Amsterdam, The Netherlands, 2003; Volume 21, pp. 573–606. ISBN 9780444500137. [Google Scholar]
- Weiß, C.H. Thinning operations for modeling time series of counts a survey. AStA Adv. Stat. Anal. 2008, 92, 319–341. [Google Scholar] [CrossRef]
- Scotto, M.G.; Weiß, C.H.; Gouveia, S. Thinning-based models in the analysis of integer-valued time series: A review. Stat. Model. 2015, 15, 590–618. [Google Scholar] [CrossRef]
- Kang, J.; Lee, S. Parameter change test for Poisson autoregressive models. Scand. J. Stat. 2014, 41, 1136–1152. [Google Scholar] [CrossRef]
- Fokianos, K.; Fried, R. Interventions in INGARCH processes. J. Time Ser. Anal. 2010, 31, 210–225. [Google Scholar] [CrossRef]
- Fokianos, K.; Fried, R. Interventions in log-linear Poisson Autoregression. Stat. Model. 2012, 12, 299–322. [Google Scholar] [CrossRef]
- Szabó, T.T. Test statistics for parameter changes in INAR(p) models and a simulation study. Aust. J. Stat. 2011, 40, 265–280. [Google Scholar] [CrossRef]
- Kang, J.; Lee, S. Parameter change test for random coefficient integer-valued autoregressive processes with application to polio data analysis. J. Time Ser. Anal. 2009, 30, 239–258. [Google Scholar] [CrossRef]
- Pap, G.; Szabó, T.T. Change detection in INAR(p) processes against various alternative hypotheses. Commun. Stat. Theory Methods 2013, 42, 1386–1405. [Google Scholar] [CrossRef]
- Doukhan, P.; Kengne, W. Inference and testing for structural change in general Poisson autoregressive models. Electron. J. Stat. 2015, 9, 1267–1314. [Google Scholar] [CrossRef]
- Hudecová, Š.; Hušková, M.; Meintanis, S.G. Detection of changes in INAR models. In Stochastic Models, Statistics and Their Applications; Steland, A., Rafajlowicz, E., Szajowski, K., Eds.; Springer: New York, NY, USA, 2015; pp. 11–18. [Google Scholar]
- Hudecová, Š.; Hušková, M.; Meintanis, S.G. Tests for time series of counts based on the probability generating function. Statistics 2015, 49, 316–337. [Google Scholar] [CrossRef]
- Hudecová, Š.; Hušková, M.; Meintanis, S.G. Change detection in INARCH time series of counts. In Nonparametric Statistics; Cao, R., Gonzalez Manteiga, W., Romo, J., Eds.; Springer: New York, NY, USA, 2016; pp. 47–58. [Google Scholar]
- Hudecová, Š.; Hušková, M.; Meintanis, S.G. Tests for structural changes in time series of counts. Scand. J. Stat. 2017, 44, 843–865. [Google Scholar] [CrossRef]
- Kang, J.; Song, J. Score test for parameter change in Poisson autoregressive models. Econ. Lett. 2017, 160, 33–37. [Google Scholar]
- Zheng, H.T.; Basawa, I.V.; Datta, S. The first order random coefficient integer-valued autoregressive processes. J. Stat. Plan. Inference 2007, 173, 212–229. [Google Scholar] [CrossRef]
- Leonenko, N.N.; Savani, V.; Zhigljavsky, A.A. Autoregressive negative binomial processes. Ann. ISUP 2007, 51, 25–47. [Google Scholar]
- Gomes, D.; e Castro, L.C. Generalized integer-valued random coefficient for a first order structure autoregressive (RCINAR) process. J. Stat. Plan. Inference 2009, 139, 4088–4097. [Google Scholar] [CrossRef]
- Negri, I.; Nishiyama, Y. Z-process method for change point problems with applications to discretely observed diffusion processes. Stat. Methods Appl. 2017, 26, 231–250. [Google Scholar] [CrossRef]
- Horváth, L.; Parzen, E. Limit theorems for Fisher-score change processes. Lect. Notes Monogr. Ser. 1994, 23, 157–169. [Google Scholar]
- Berkes, I.; Horváth, L.; Kokoszka, P. Testing for parameter constancy in GARCH(p,q) models. Stat. Probab. Lett. 2004, 4, 263–273. [Google Scholar] [CrossRef]
- Song, J.; Kang, J. Parameter change tests for ARMA-GARCH models. Comput. Stat. Data Anal. 2018, 121, 41–56. [Google Scholar] [CrossRef]
- Lee, S.; Tokutsu, Y.; Maekawa, K. The cusum test for parameter change in regression models with ARCH errors. J. Jpn. Stat. Soc. 2004, 34, 173–188. [Google Scholar] [CrossRef]
- Kulperger, R.; Yu, H. High moment partial sum processes of residuals in GARCH models and their applications. Ann. Stat. 2005, 33, 2395–2422. [Google Scholar] [CrossRef]
- Steutal, F.; Van Harn, K. Discrete analogues of self decomposability and stability. Ann. Probab. 1979, 7, 893–899. [Google Scholar]
- Klimko, L.A.; Nelson, P.I. On conditional least squares estimation for stochastic processes. Ann. Stat. 1978, 6, 629–642. [Google Scholar] [CrossRef]
- Freeland, R.K.; McCabe, B.P. Analysis of low count time series data by Poisson autoregression. J. Time Ser. Anal. 2004, 25, 701–722. [Google Scholar] [CrossRef]
- Zeger, S.L. A regression model for time series of counts. Biometrika 1988, 75, 621–629. [Google Scholar] [CrossRef]
- Davis, R.A.; Dunsmuir, W.; Wang, Y. On autocorrelation in a Poisson regression model. Biometrika 2000, 87, 491–505. [Google Scholar] [CrossRef]
- Jung, R.C.; Tremayne, A.R. Useful models for time series of counts or simply wrong ones? AStA Adv. Stat. Anal. 2011, 95, 59–91. [Google Scholar] [CrossRef]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J. Detection of Parameter Change in Random Coefficient Integer-Valued Autoregressive Models. Entropy 2018, 20, 107. https://doi.org/10.3390/e20020107
Kang J. Detection of Parameter Change in Random Coefficient Integer-Valued Autoregressive Models. Entropy. 2018; 20(2):107. https://doi.org/10.3390/e20020107
Chicago/Turabian StyleKang, Jiwon. 2018. "Detection of Parameter Change in Random Coefficient Integer-Valued Autoregressive Models" Entropy 20, no. 2: 107. https://doi.org/10.3390/e20020107
APA StyleKang, J. (2018). Detection of Parameter Change in Random Coefficient Integer-Valued Autoregressive Models. Entropy, 20(2), 107. https://doi.org/10.3390/e20020107



