1. Introduction
The statistical problem of estimating binary response variables is very important in many areas including social science, biology and economics [
1]. The vast bibliography of categorical data presents the big evolution of the methods that handle appropriately binary and polychotomous data. More details can be found in Agresti [
2]. Generalized linear model (GLM) has a wide range of tools in regression for count data [
3]. Two important and commonly used symmetric link functions in GLM are the logit and probit links [
4]. Many studies have investigated the limitations of these symmetric link functions. It is well accepted that when the probability of the binary response approaches 0 at a different rate from the rate (as a function of covariate) it approaches 1, symmetric link functions cannot be appropriate [
5]. Many parameteric classes of link functions are in the literature, including the power transform of logit link by Aranda-Ordaz [
6] and the a general link class of Chen et al. [
5]. Other works with one-parameter class include Guerrero and Johnson [
7], Morgan [
8], Whittmore [
9] and a host of others. Existing models for two-parameter families include Stukel [
10], Prentice [
11], Pregibon [
12], Czado [
13] and Czado [
14].
Stukel’s model with transformation of both tails of logit link is very general and can approximate many important links including probit, logit and complementary log–log. However, the Bayesian analysis of Stukel’s model is not straightforward to implement, particularly in presence of multiple covariates and noninformative improper priors. The model proposed by Chen et al. [
5], which includes the skew-probit model, uses a latent variable approach [
15] that is convenient for sampling from the posterior distribution. Using the Albert and Chib [
15] technique, Kim et al. [
16] proposed the generalized t-link models, Naranjo et al. [
17] proposed the asymmetric exponential power (AEP) model, and Rubio and Liseo [
18] discuss the Jeffreys prior for skew-symmetric models. However the frequentist analysis for these models are not trivial. For the skew-probit model, The existence of the maximum likelihood estimator (MLE) of the linear regression parameters (
) can be proved only under the restrictive condition that the skewness parameter of the link function is known [
19].
The majority of the works in literature are devoted to the models for binary response data. For the case of multinomial data, the multinomial extension of the logit link [
20] (Chapter 8) and associated inference tools are simple to perform, and the marginal distribution of each component preserves the logit link. As mentioned before, the symmetric link may not be always appropriate. This is even clearer in multinomial data, where the sense of symmetric link is not simple to state. Generally, some categories has few observations when compared to the other ones, suggesting the idea of asymmetric distribution. We are also not aware of any model with asymmetric link function for multinomial data.
Caron and Polpo [
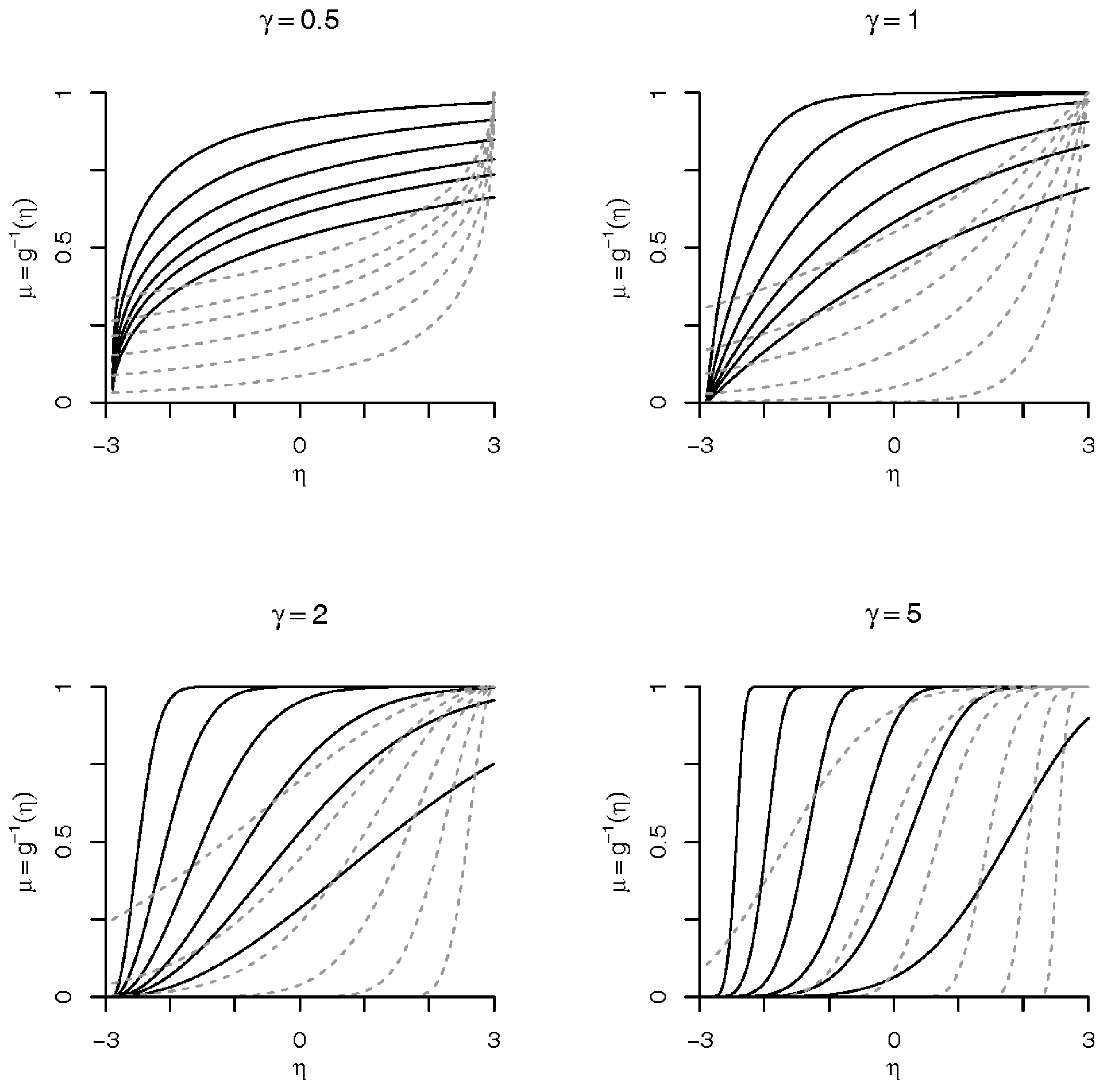
21] briefly suggested an asymmetrical link function, called Weibull link, exclusively for binary response data. The use of Weibull distribution in survival/reliability analysis is well known. One important fact is the simplicity of the distribution, which has an analytic expression for the distribution function. Our proposed link model, based in the Weibull distribution, preserves this simplicity and it is a good option for the analysis of binary data.
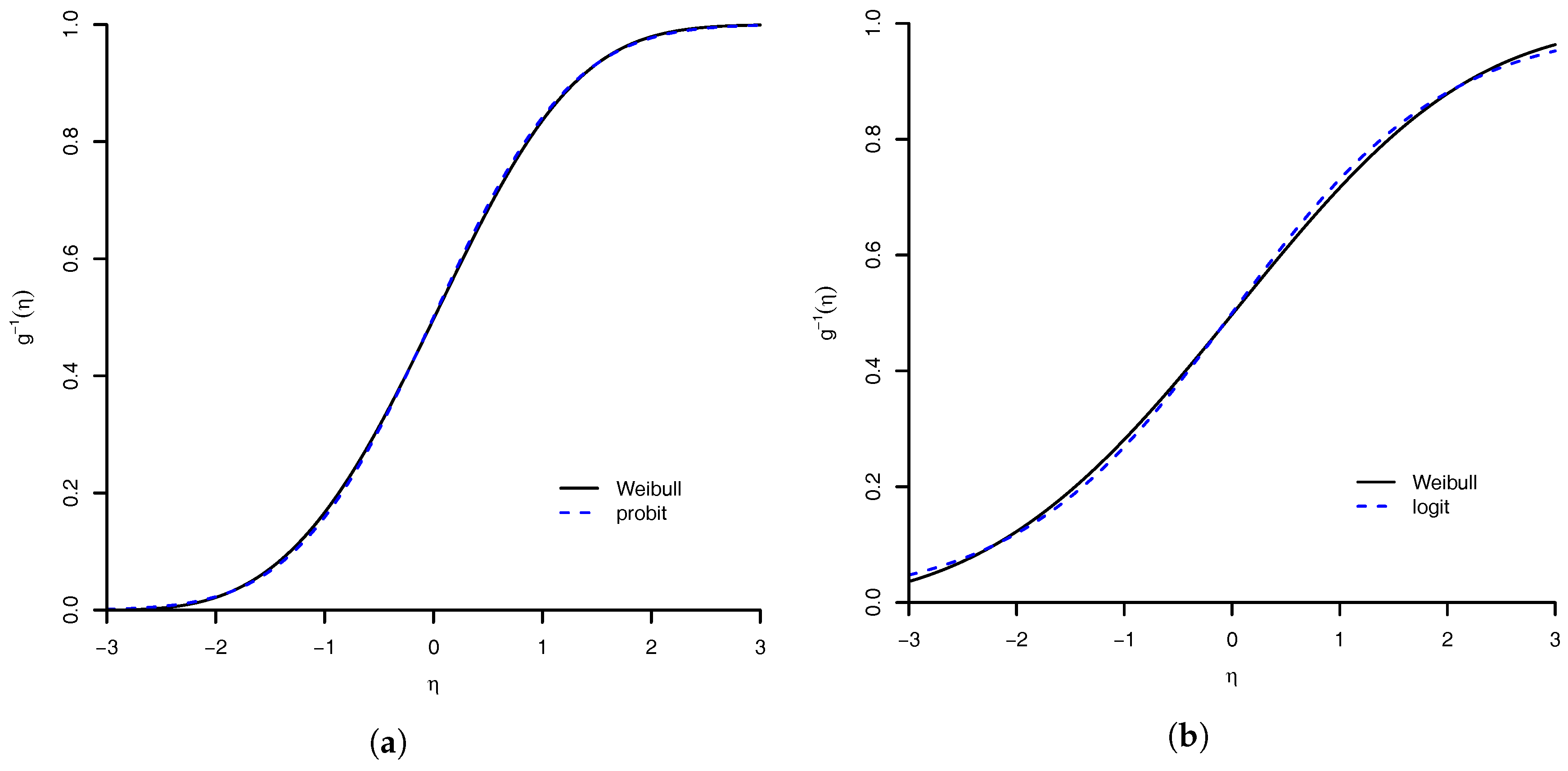
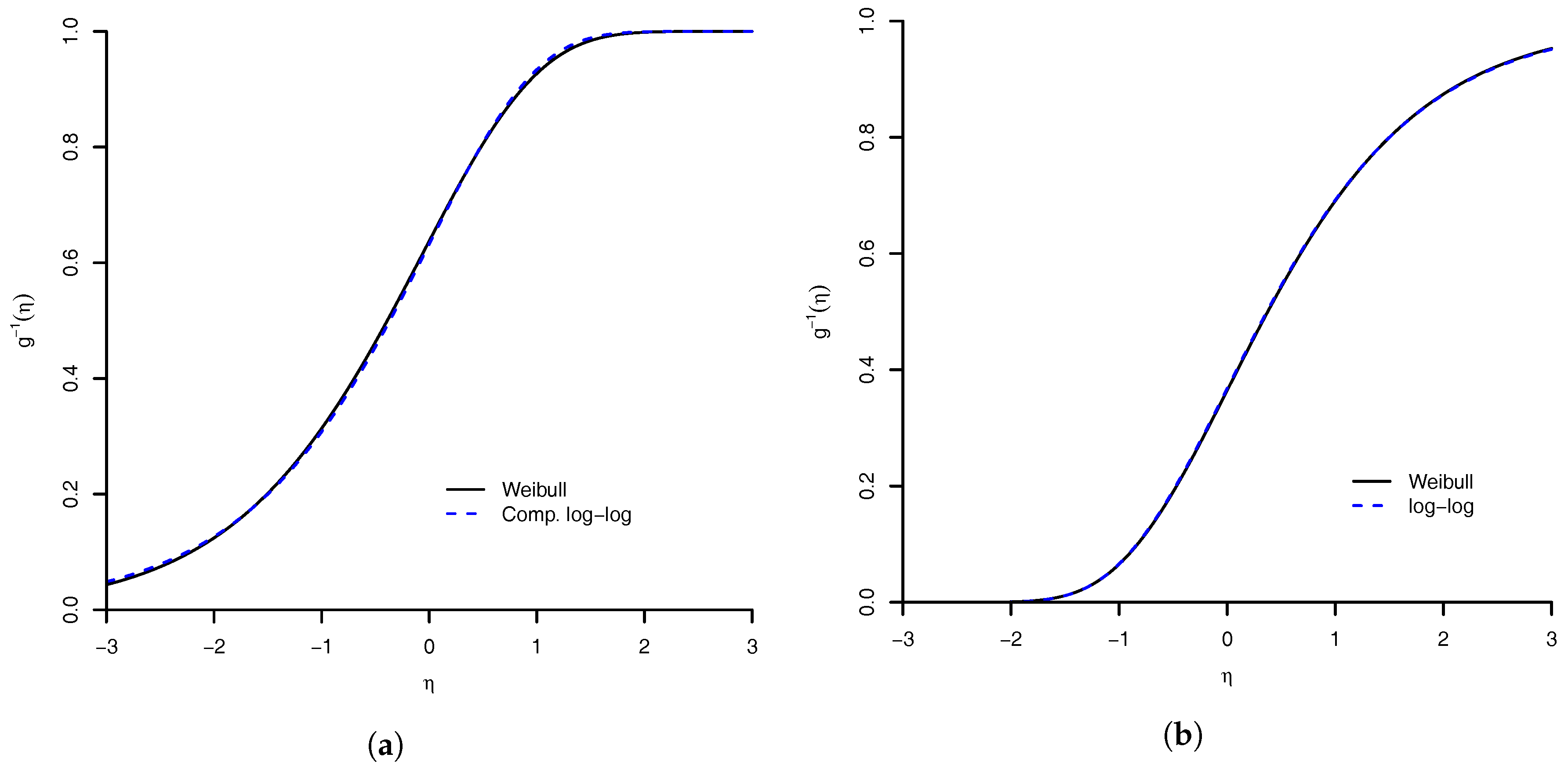
In this paper, we take the Bayesian route and extend their work to multinomial data. Further we present for the first time the associated Bayesian inference tools and explore the properties of the proposed link function. We show that the benefits of this model are as follows: (1) flexibility of the Weibull distribution; (2) logit, probit and complementary log–log links as limiting cases; (3) case of implementation of both frequentist and Bayesian inferences; and (4) a general extension to handle multinomial response. The implementation of the associated Markov chain Monte Carlo (MCMC) algorithm to sample from posterior distribution is not complicated. In addition, we develop an Empirical Bayes tool [
22,
23] to obtain the prior when there is no relevant prior information available to the statistician.
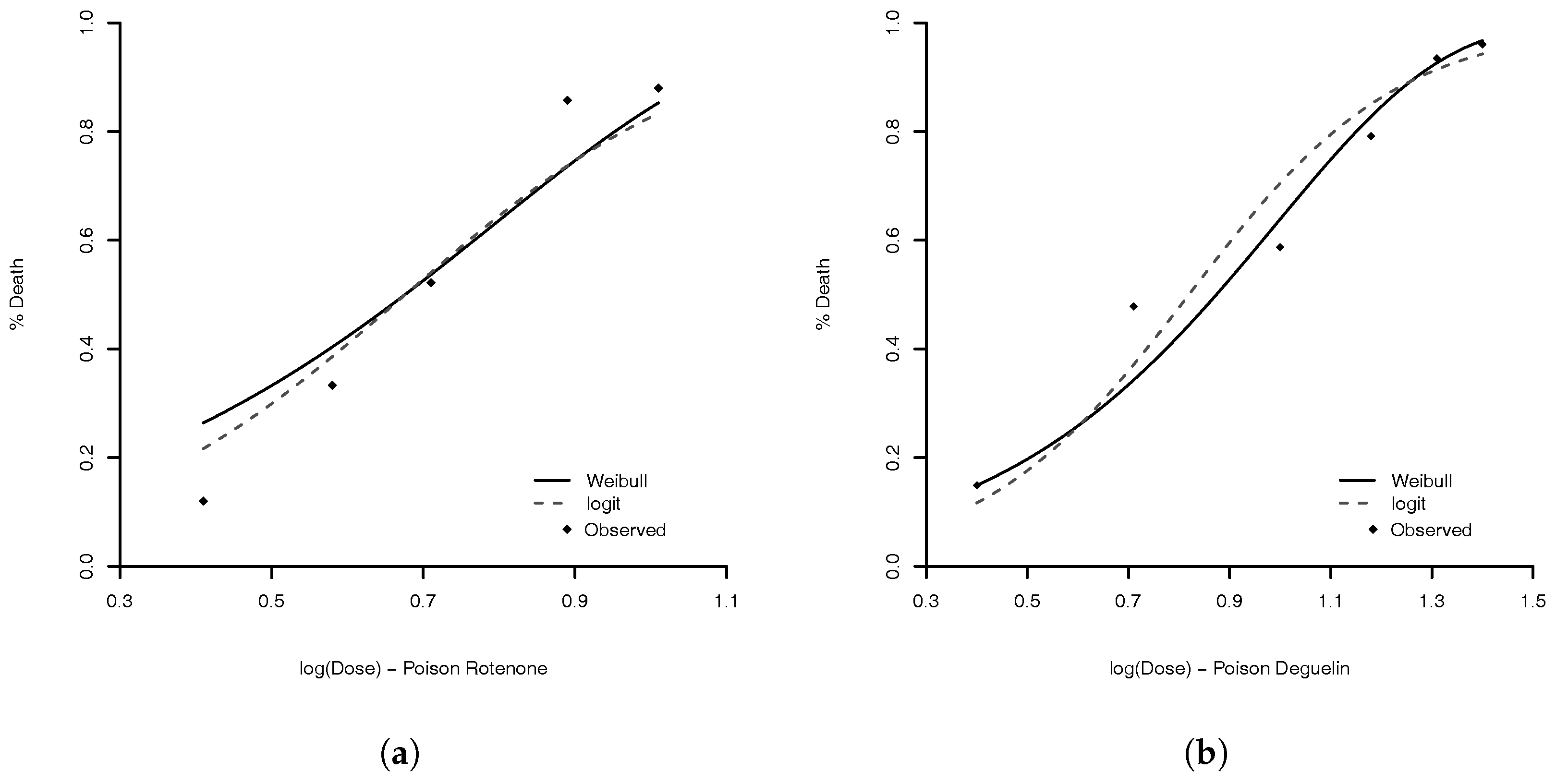
We illustrate the use of Weibull link via analysis of two following data examples. (1) For the experiment to study the potencies of three poisons [
24], the main binary response is whether the insect is alive after being treated with assigned dose level. For this example, we compare our Weibull link model with other asymmetric and symmetric link models. (2) The main response of the study by Grazeffe et al. [
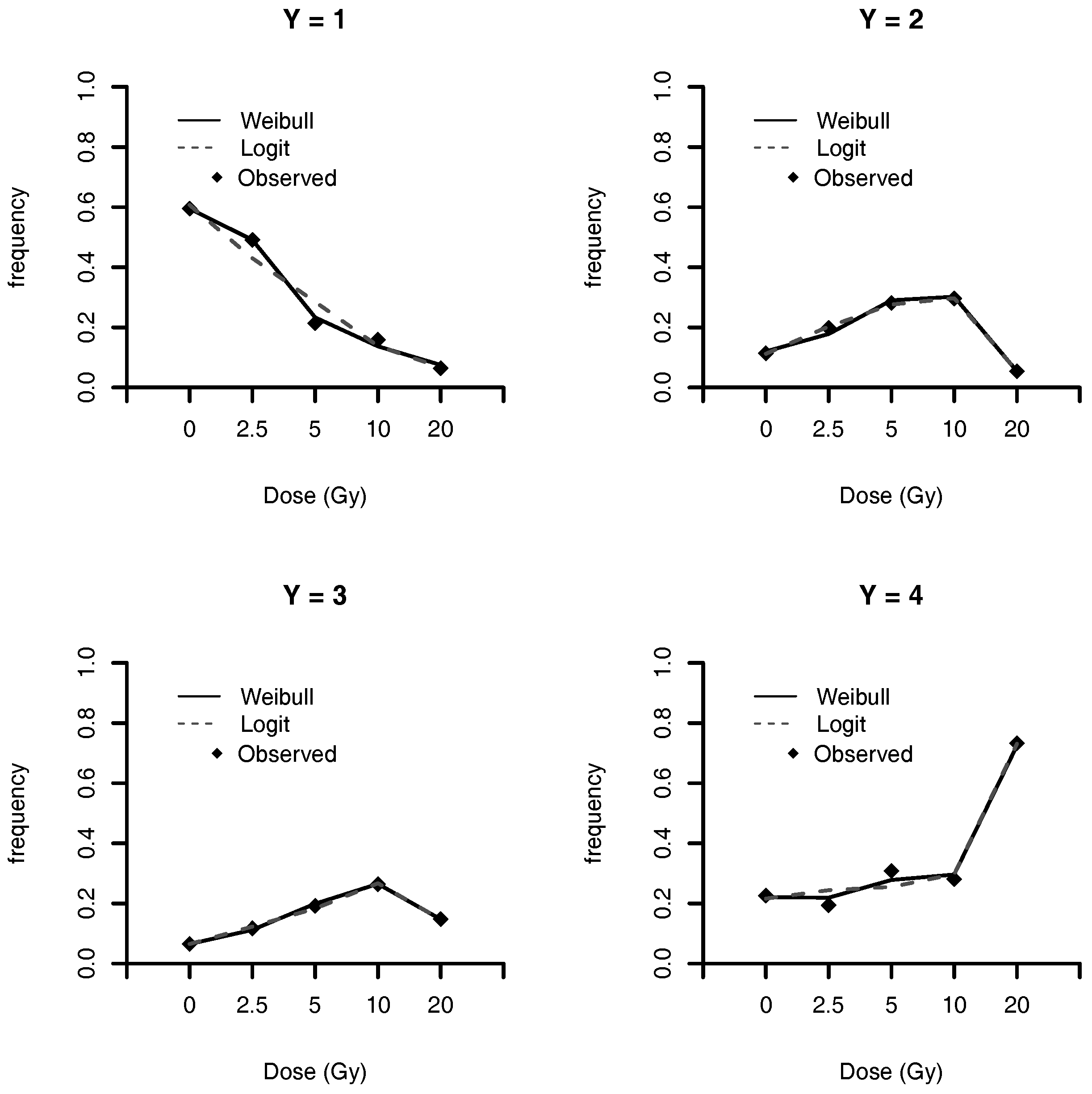
25] is the multiple levels of DNA damage in circulating hemocytes of each adult snail irradiated with an assigned dose. This study is used to illustrate the analysis of multinomial response data under Weibull link model, and comparing the results with those obtained by Grazeffe et al. [
25] using logistic regression.
The article is organized as follows. In
Section 2, we present the Weibull model, its novel properties and some approximations of the link function. In
Section 3, we present the estimation procedures using MLE as well as the Bayesian estimation. In
Section 3, we also present the estimation procedure for multinomial response.
Section 4 is devoted to illustrating the Weibull link for analyzing two real datasets, and comparison with other existing models. Finally,
Section 5 presents some future considerations and final comments.
5. Final Comments
In this paper, we have presented a Weibull model to estimate the problem of binary and multinomial regression analysis. The model is very flexible and capable to handle with many different types of data. The comparison with other skew-link model, in binomial data example (
Section 4.1), shows that the performance of the Weibull link was good when compared to the others models. The model with worst measures was the Prentice model. All others had an equivalent result. We are convinced that our proposed model is a good option. A good feature of the model is that the logit, probit, complementary log–log, and log–log link functions are approximations of Weibull link. Then, the proposed model can accommodate even symmetric link function. For the flexibility of the Weibull link model, we are comfortable to suggest its use in practice.
Other aspect of the proposed Weibull model is that the associated numerical procedure of MLE is very simple to implement, particularly in comparison to other competing. For Bayesian estimates, we also suggest an Empirical Bayes approach to determine the prior. Under full Bayesian estimation, we compare the model with the skew-probit model [
5] and AEP model [
17], in
Section 4.1. Again, all models had similar results, however the KS of Weibull model were the measures with the greatest differences among all models. The performance of our model was good, even under full Bayesian framework, in binomial data example (
Section 4.1).
We also develop a partition scheme for the multinomial regression model simplifying the problem to
binomial regression analysis. This is a general scheme that can be used for other link functions, which opens a vast options to estimate multinomial data. In
Section 4.2, we analyze a multinomial data problem, where the Weibull model had the best measure values when compared with all other models. Our perspective is that the Weibull model is a good option for binary/multinomial regression, mainly due to its simplicity. We have analytic form for the link function, as well as for the gradient and Hessian matrix.