The Gibbs Paradox: Early History and Solutions
Abstract
1. Introduction
2. Diffusion and Dissipation before Gibbs
2.1. Some Background: Clausius’s Axiom, the Second Law, Entropy, Disgregation
- (1)
- The energy of the world is constant.
- (2)
- The entropy of the world tends to a maximum.
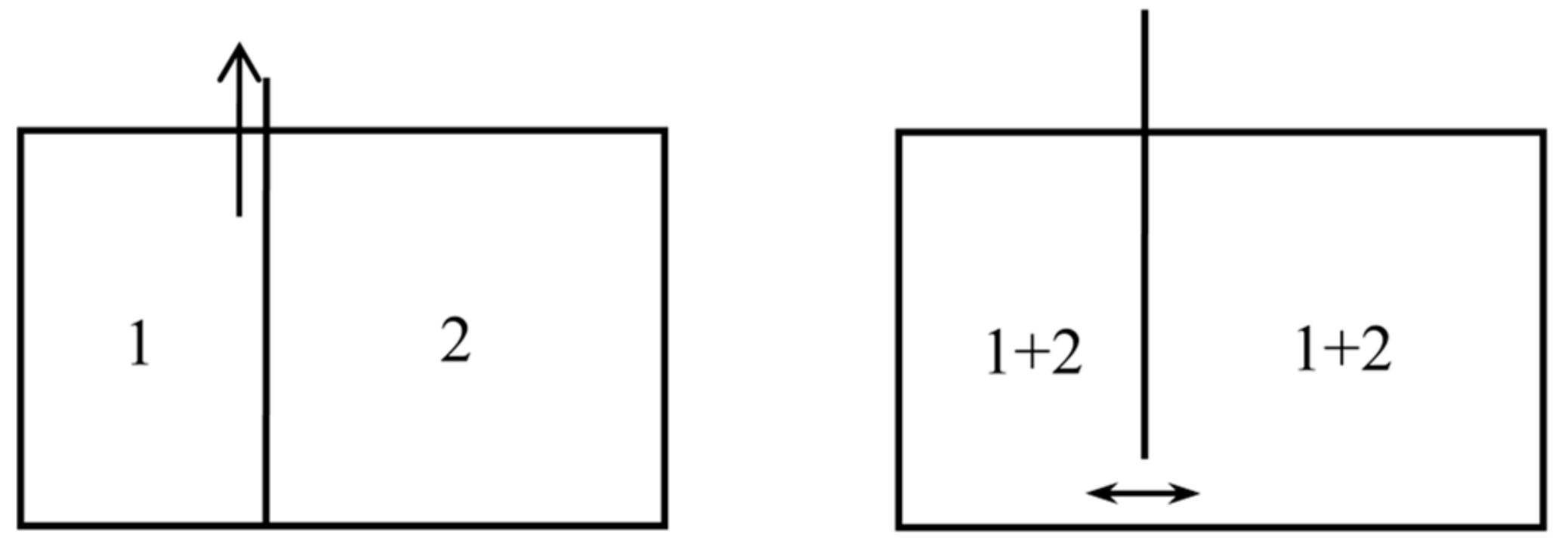
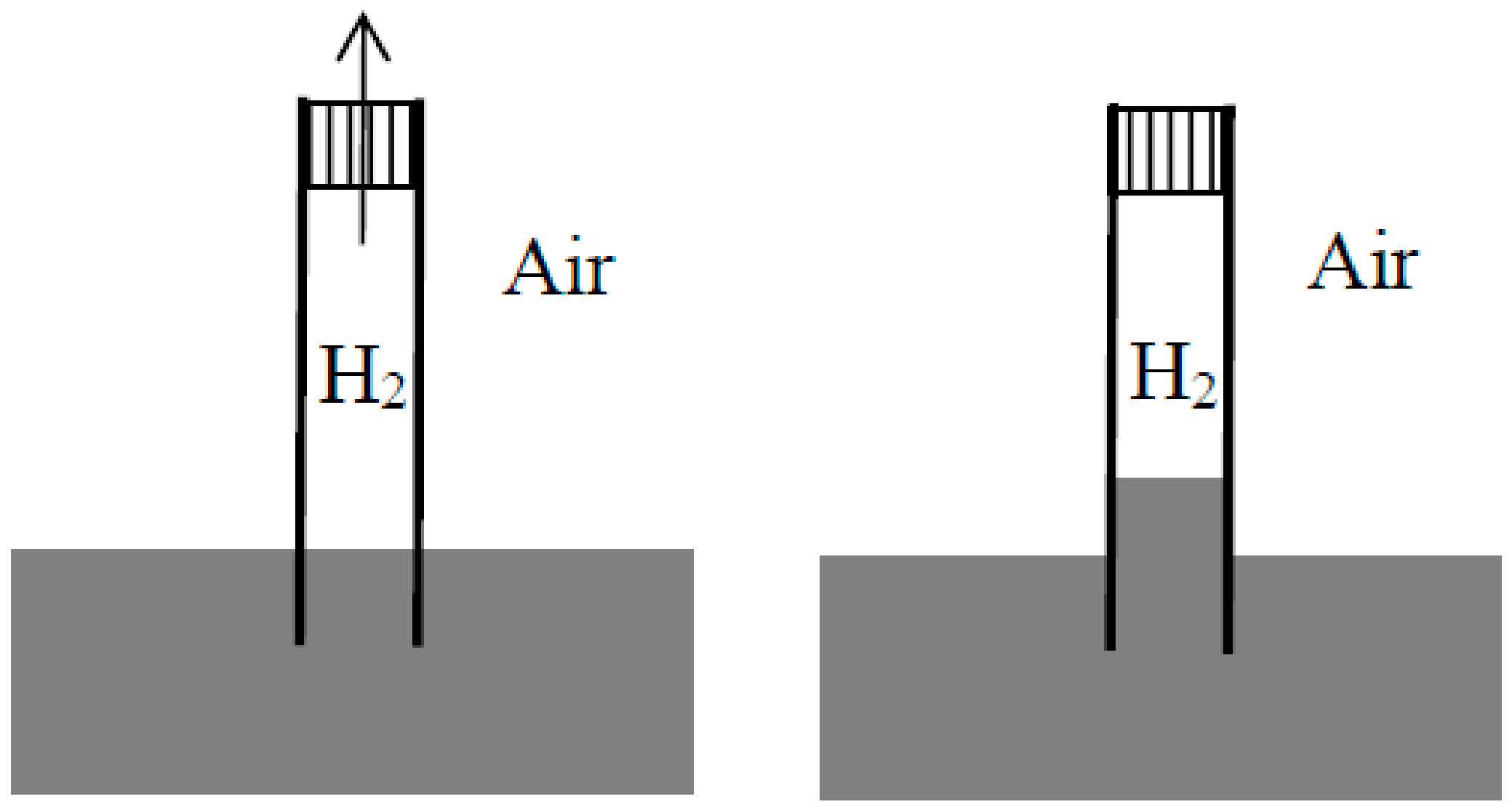
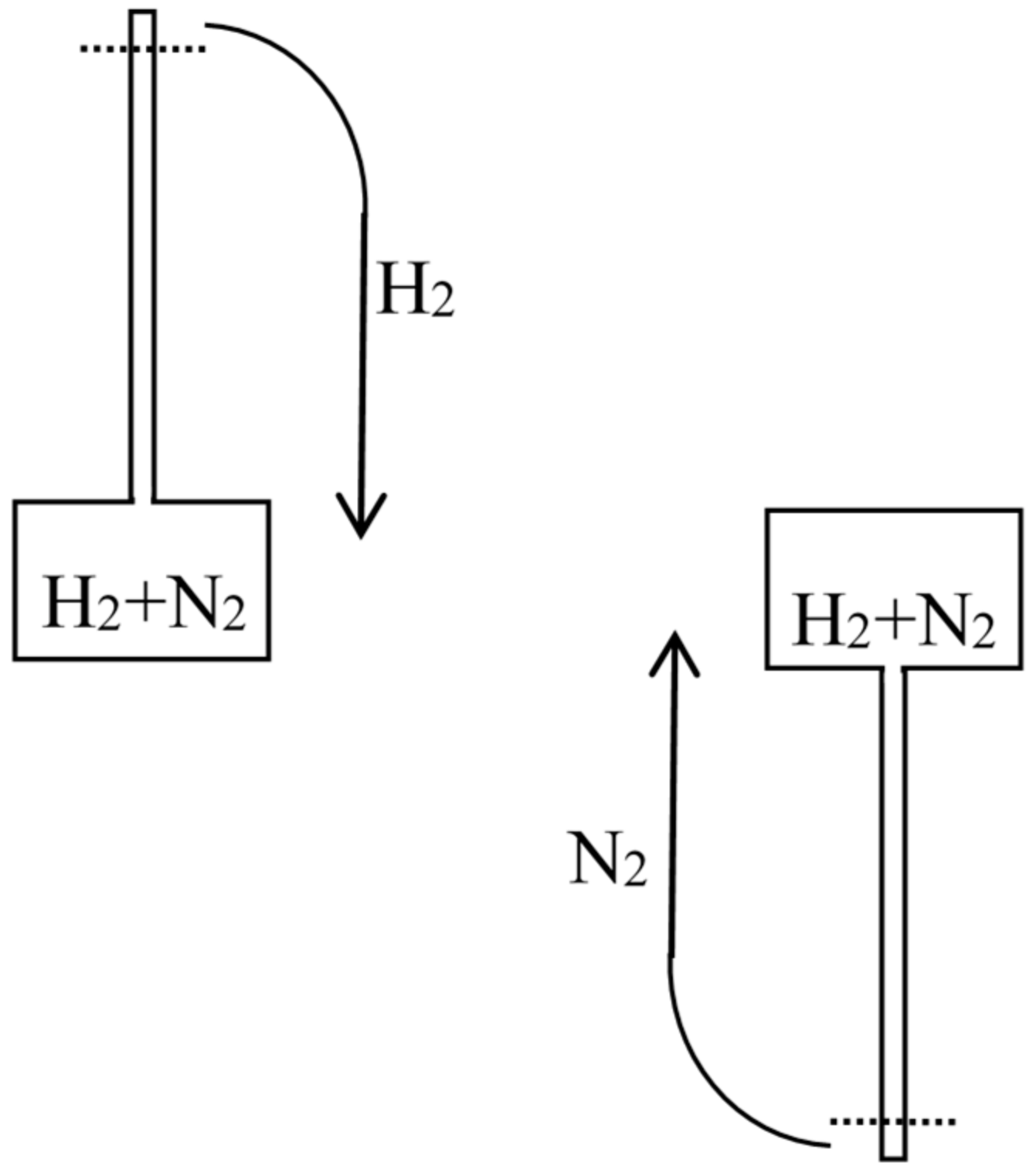
2.2. Loschmidt’s Columns of Salted Water (1869)
2.3. Horstmann’s Dissociation Theory (1873)
2.4. Rayleigh on Dissipation and Diffusion (1875)
The chemical bearings of the theory of dissipation are very important, but have not hitherto received much attention. A chemical transformation is impossible, if its occurrence would involve the opposite of dissipation.
Whenever then two gases are allowed to mix without the performance of work, there is dissipation of energy, and an opportunity of doing work at the expense of low temperature heat has been for ever lost. The present paper is an attempt to calculate this amount of work.
3. Gibbs on the Equilibrium of Heterogeneous Substances
3.1. The Rules of Equilibrium (1873–1876)
We know, . . . a priori, that if the quantity of any homogeneous mass containing s independently variable components varies and not its nature or state, the quantities [U, S, V, ] will all vary in the same proportion.
If several liquid or solid substances which yield different gases or vapors are simultaneously in equilibrium with a mixture of these gases (cases of chemical actions between the gases being excluded), the pressure in the gas mixture is equal to the sum of the pressures of the gases yielded at the same temperature by the various liquid or solid substances taken separately.
The quantities [P, S, U, F, G, H] relating to the gas-mixture may therefore be regarded as consisting of parts which may be attributed to the several components in such a manner that between the parts of these quantities which are assigned to any component, the quantity of that component, the potential for that component, the temperature, and the volume, the same relations shall subsist as if that component existed separately. It is in this sense that we should understand the law of Dalton, that every gas is as a vacuum to every other gas.
3.2. The Gibbs Paradox (April 1876)
It is noticeable that the value of this expression does not depend upon the kinds of gas which are concerned, if the quantities are such as has been supposed, except that the gases which are mixed must be of different kinds. If we should bring into contact two masses of the same kind of gas, they would also mix, but there would be no increase of entropy.
But in regard to the relation which this case bears to the preceding, we must bear in mind the following considerations. When we say that when two different gases mix by diffusion, as we have supposed, the energy of the whole remains constant, and the entropy receives a certain increase, we mean that the gases could be separated and brought to the same volume and temperature which they had at first by means of certain changes in external bodies, for example, by the passage of a certain amount of heat from a warmer to a colder body. But when we say that when two gas-masses of the same kind are mixed under similar circumstances there is no change of energy or entropy, we do not mean that the gases which have been mixed can be separated without change to external bodies. On the contrary, the separation of the gases is entirely impossible. We call the energy and entropy of the gas-masses when mixed the same as when they were unmixed, because we do not recognize any difference in the substance of the two masses.
So when gases of different kinds are mixed, if we ask what changes in external bodies are necessary to bring the system to its original state, we do not mean a state in which each particle shall occupy more or less exactly the same position as at some previous epoch, but only a state which shall be undistinguishable from the previous one in its sensible properties. It is to states of systems thus incompletely defined that the problems of thermodynamics relate.
But if such considerations explain why the mixture of gas-masses of the same kind stands on a different footing from the mixture of gas-masses of different kinds, the fact is not less significant that the increase of entropy due to the mixture of gases of different kinds, in such a case as we have supposed, is independent of the nature of the gases.Now we may without violence to the general laws of gases which are embodied in our equations suppose other gases to exist than such as actually do exist, and there does not appear to be any limit to the resemblance which there might be between two such kinds of gas. But the increase of entropy due to the mixing of given volumes of the gases at a given temperature and pressure would be independent of the degree of similarity or dissimilarity between them. We might also imagine the case of two gases which should be absolutely identical in all the properties (sensible and molecular) which come into play while they exist as gases either pure or mixed with each other, but which should differ in respect to the attractions between their atoms and the atoms of some other substances, and therefore in their tendency to combine with such substances. In the mixture of such gases by diffusion an increase of entropy would take place, although the process of mixture, dynamically considered, might be absolutely identical in its minutest details (even with respect to the precise path of each atom) with processes which might take place without any increase of entropy. In such respects, entropy stands strongly contrasted with energy.
Again, when such gases [differing only through their interaction with a third substance] have been mixed, there is no more impossibility of the separation of the two kinds of molecules in virtue of their ordinary motions in the gaseous mass without any especial external influence, than there is of the separation of a homogeneous gas into the same two parts into which it has once been divided, after these have once been mixed. In other words, the impossibility of an uncompensated decrease of entropy seems to be reduced to improbability.
4. Diffusion and the Second Law
4.1. Maxwell on Diffusion (1877)
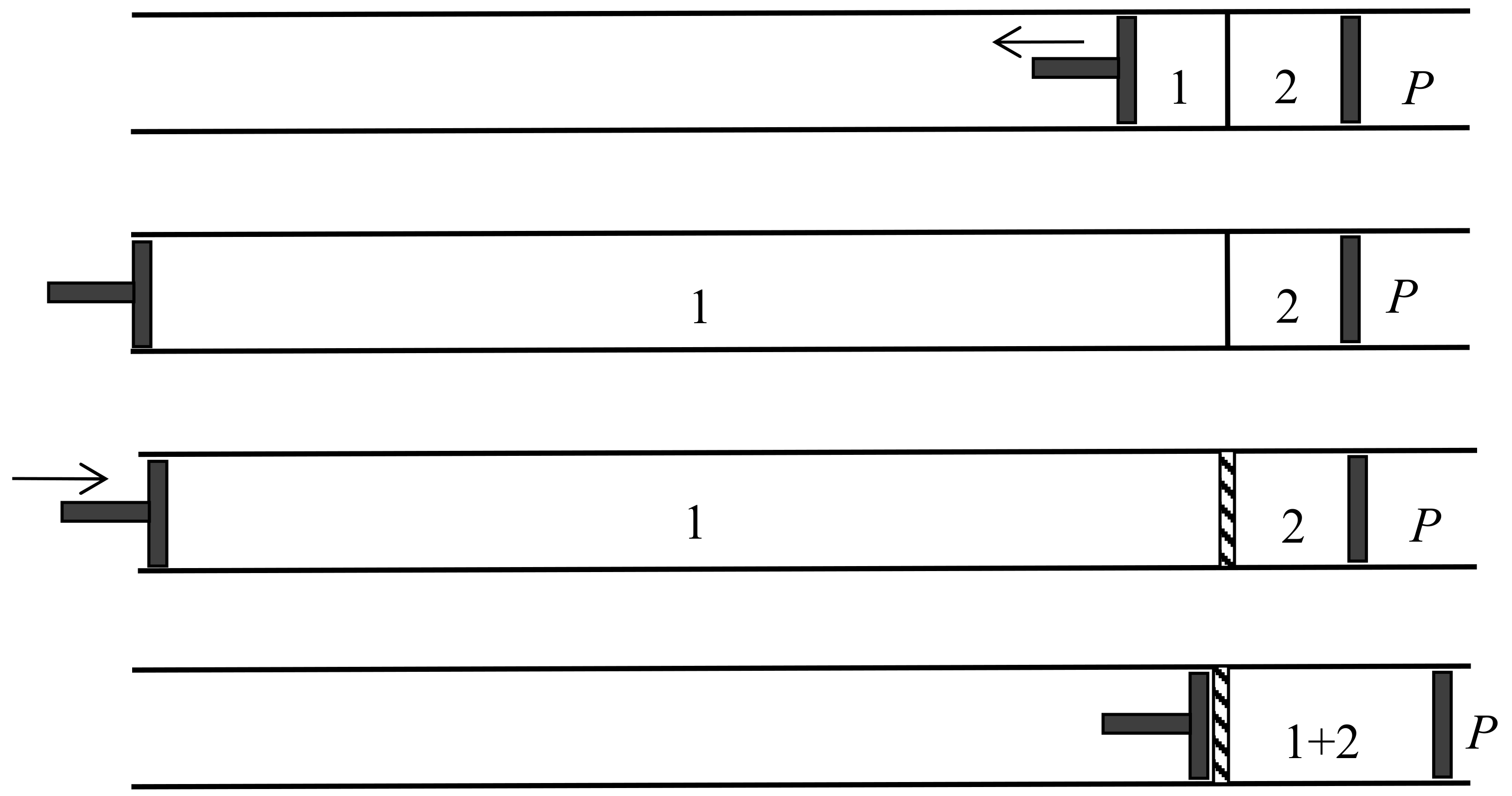
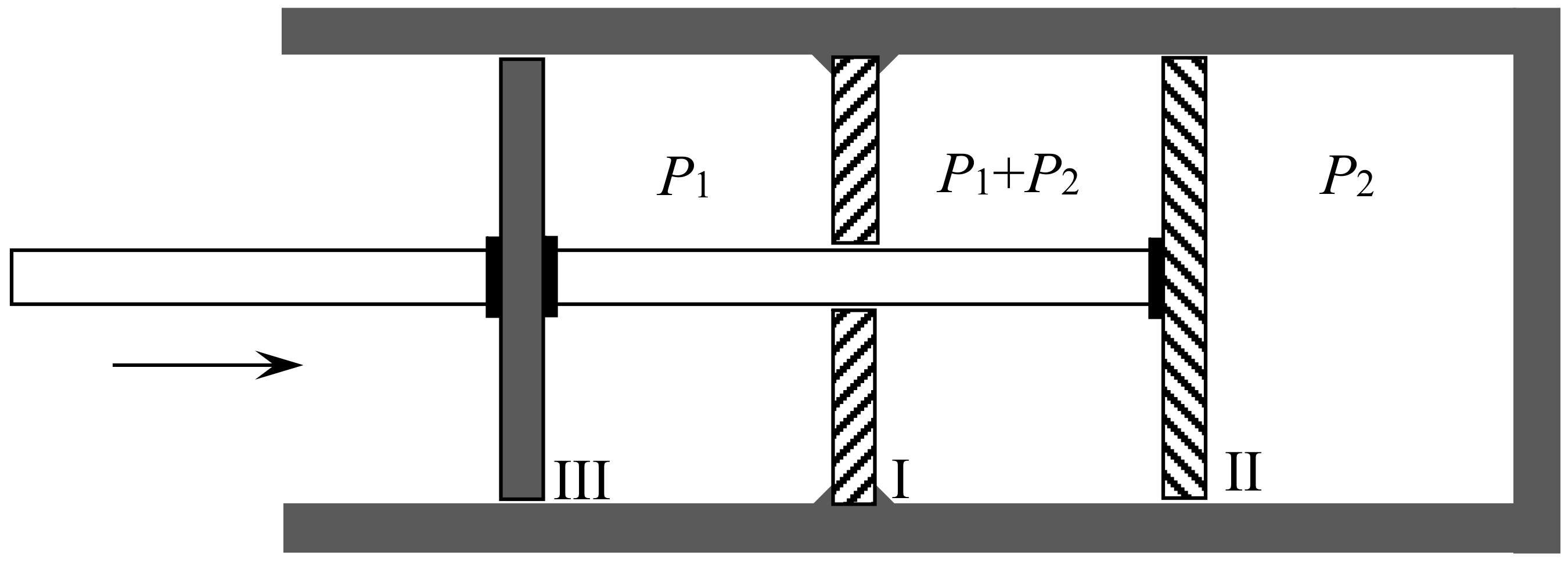
Let us now suppose that we have in a vessel two separate portions of gas of equal volume, and at the same pressure and temperature, with a movable partition between them. If we remove the partition the agitation of the molecules will carry them from one side of the partition to the other in an irregular manner, till ultimately the two portions of gas will be thoroughly and uniformly mixed together. This motion of the molecules will take place whether the two gases are the same or different, that is to say, whether we can distinguish between the properties of the two gases or not.If the two gases are such that we can separate them by a reversible process, then, as we have just shewn, we might gain a definite amount of work by allowing them to mix under certain conditions; and if we allow them to mix by ordinary diffusion, this amount of work is no longer available, but is dissipated forever. If, on the other hand, the two portions of gas are the same, then no work can be gained by mixing them, and no work is dissipated by allowing them to diffuse into each other.It appears, therefore, that the process of diffusion does not involve dissipation of energy if the two gases are the same, but that it does if they can be separated from each other by a reversible process.
Now, when we say that two gases are the same, we mean that we cannot distinguish the one from the other by any known reaction. It is not probable, but it is possible, that two gases derived from different sources, but hitherto supposed to be the same, may hereafter be found to be different, and that a method may be discovered of separating them by a reversible process. If this should happen, the process of interdiffusion which we had formerly supposed not to be an instance of dissipation of energy would now be recognized as such an instance.
It follows from this that the idea of dissipation of energy depends on the extent of our knowledge. Available energy is energy which we can direct into any desired channel. Dissipated energy is energy which we cannot lay hold of and direct at pleasure, such as the energy of the confused agitation of molecules which we call heat. Now, confusion, like the correlative term order, is not a property of material things in themselves, but only in relation to the mind which perceives them. A memorandum-book does not, provided it is neatly written, appear confused to an illiterate person, or to the owner who understands it thoroughly, but to any other person able to read it appears to be inextricably confused. Similarly the notion of dissipated energy could not occur to a being who could not turn any of the energies of nature to his own account, or to one who could trace the motion of every molecule and seize it at the right moment. It is only to a being in the intermediate stage, who can lay hold of some forms of energy while others elude his grasp that energy appears to be passing inevitably from the available to the dissipated state.
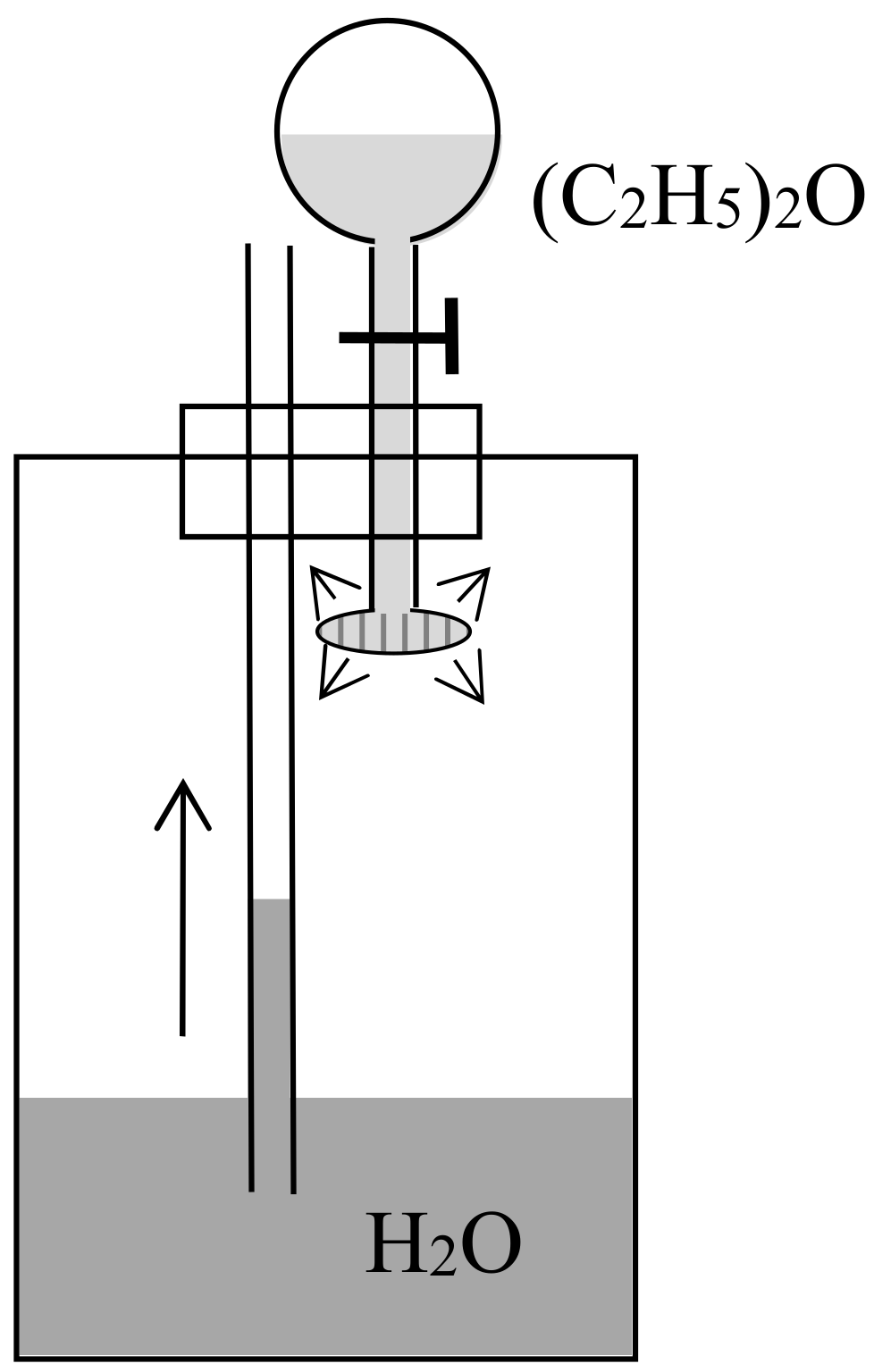
4.2. Preston’s Violation of the Second Law (1877)
4.3. Boltzmann on the Mixing Entropy (1878)
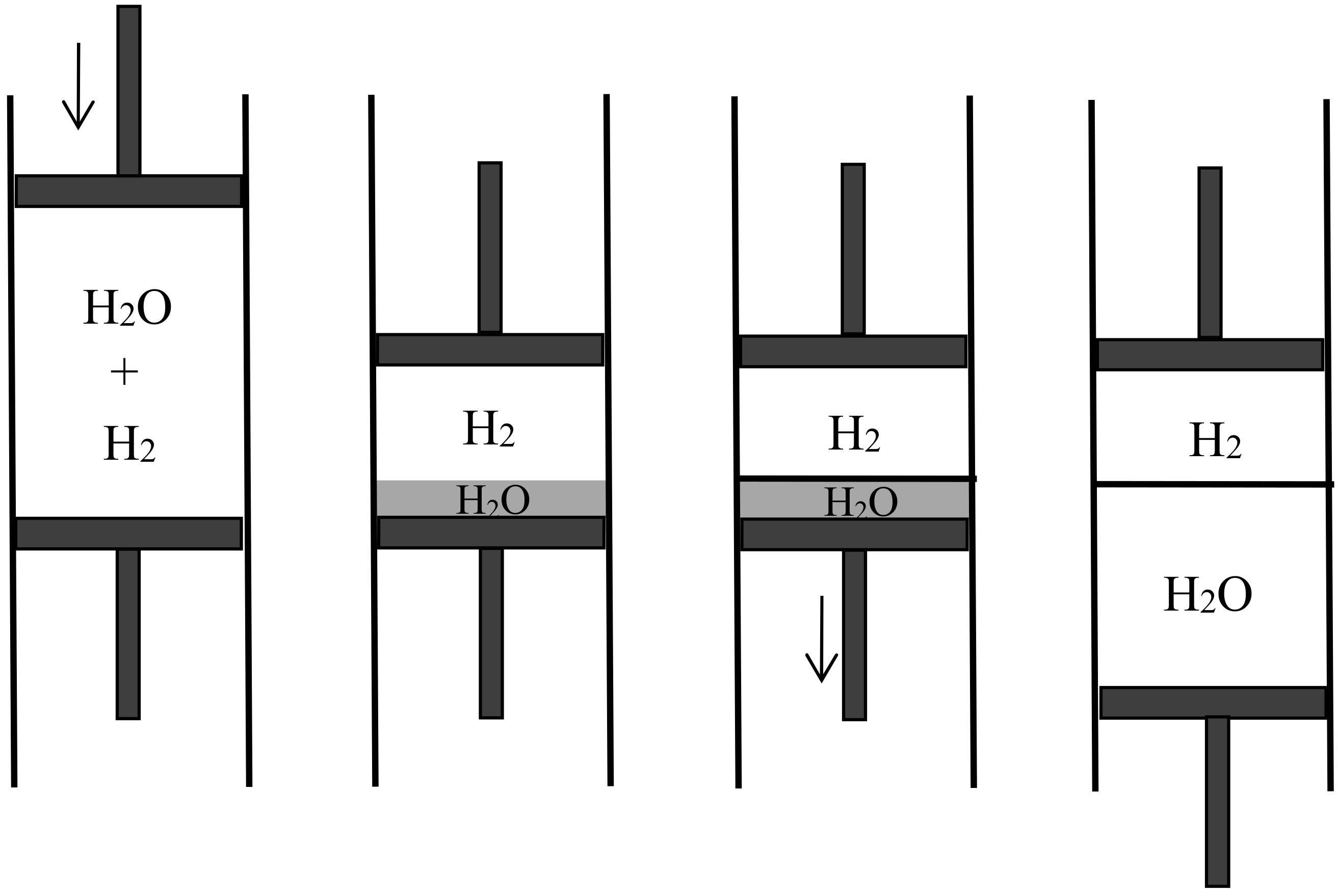
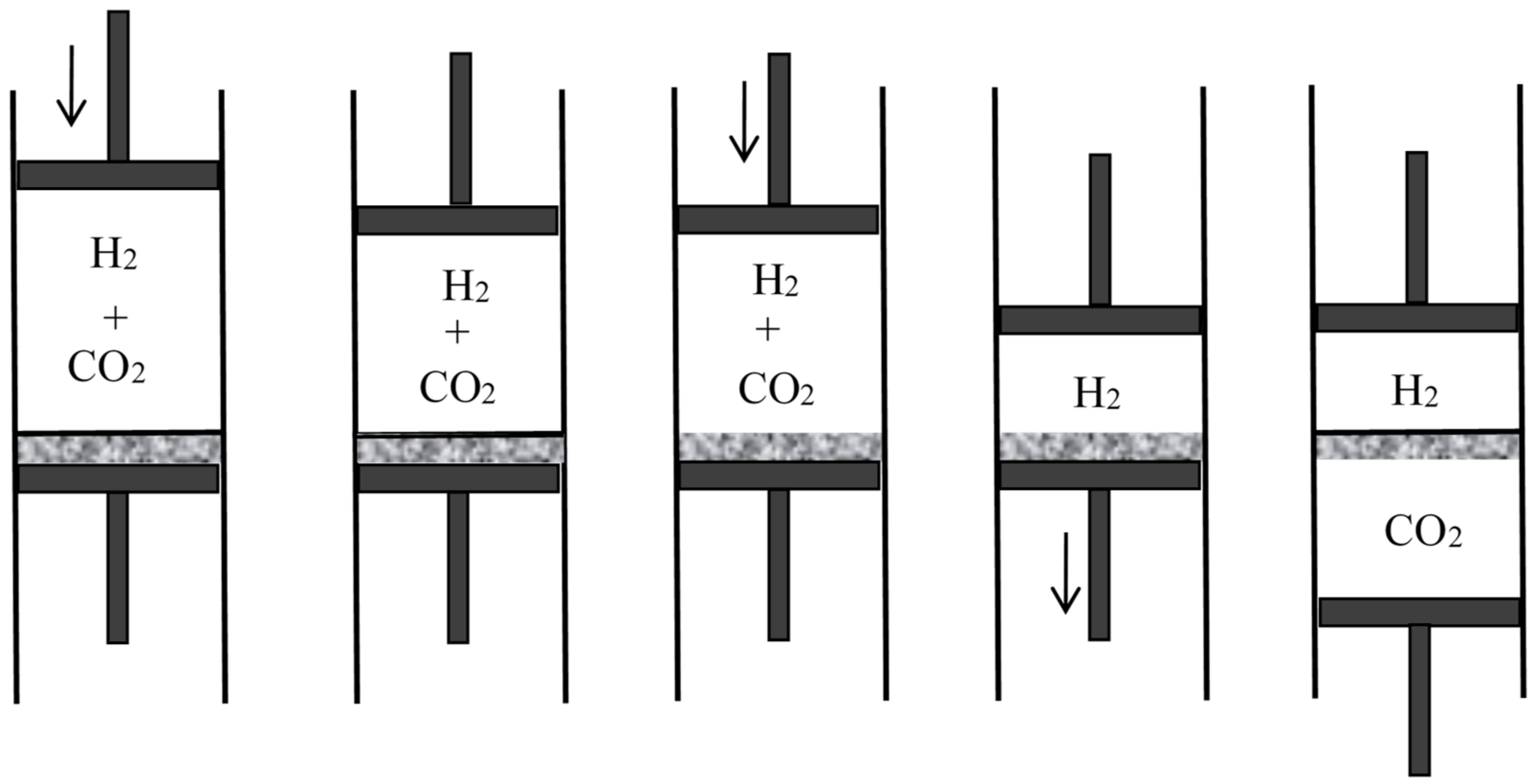
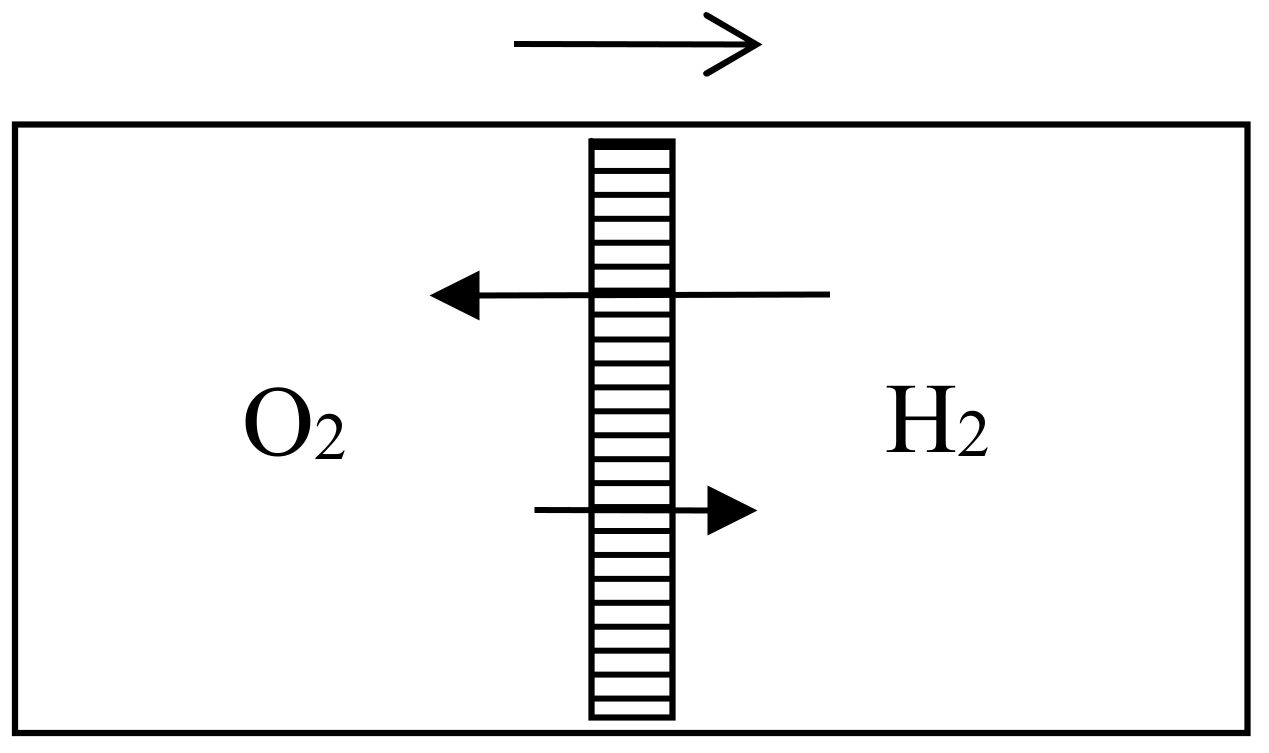
4.4. Semipermeable Walls
5. New Discussions of the Gibbs Paradox
5.1. Duhem and Neumann on Gas Mixtures (1886–1892)
In a recent and very important writing, a good part of it is devoted to the definition [of a gaseous mixture according to Gibbs], Mr. Carl Neumann points to a paradoxical consequence of this definition. This paradox, which must have stricken the mind of anyone interested in these questions and which, in particular, was examined by Mr. J. W. Gibbs, is the following:If we apply the formulas relative to the mixture of two gases to the case when the two gases are identical, we may be driven to absurd consequences.
- -
- Major premise: The notion of mixture of two gases includes the mixture of two masses of the same gas.
- -
- Minor premise: Gibbs’s definition of a mixture leads to absurd results when applied to the mixture of two masses of the same gas.
- -
- Conclusion: Gibbs’s definition is inacceptable.
5.2. Wiedeburg’s “On Gibbs’ Paradox” (1894)
[The mixing entropy] as computed from these assumptions turns out to have a non-zero value independent of the nature of the gases. It would therefore have the same value when gas masses of the same chemical nature diffuse into each other. Yet one surely expects the value zero for the entropy variation, since there is no perceptible change in what is regarded as the ‘state of the system’ in thermodynamics and since entropy depends on this state only.
To this we may object that according to the kinetic intuition the inducement to mixing is equally given in both cases by the constant (though slow) migration of the smallest particles.
However, if we admit the mental or even practical possibility to reversibly mix or unmix similar [gas] masses in such a way that every individually determined smallest particle is found in the same ‘state,’ in particular in the same position, after a complete cycle, it cannot be denied that in such a mixing process work can be won even though it does not involve any outward change. Simply, in this case the concept of ‘state of a system’ must be determined and handled in a much more extensive and precise manner than is usually done.
It should be clear that one need not conclude, as Gibbs himself does, that ‘the impossibility of an uncompensated decrease of the entropy seems to be reduced to an improbability,’ in other words: that the second law of thermodynamics seems not to be absolutely true.
The paradoxical consequences [of the mixing-entropy formula] start to occur only when we follow Gibbs in imagining gases that are infinitely little different from each other in every respect and thus conceive the case of identical gases as the continuous limit of the general case of different gases. On the contrary, we may well conclude that finite differences of the properties belong to the essence of what we call matter.
With regard to the entropy increase by diffusion, it does not make any difference whether the gases are chemically more or less ‘similar’ [ähnlich]. Now, if we take two identical gases, the entropy increase is obviously zero, since there is no change of state at all. Whence follows that the chemical difference between two gases or two substances in general, cannot be represented through a continuously variable quantity, and that we instead have to do with discrete distinctions [sprungweisen Beziehungen]: either equality [Gleichheit] or inequality [Ungleichheit]. This circumstance creates a principal opposition between chemical and physical properties, since the latter must always be regarded as continuously variable.
6. The N! Division
6.1. Boltzmann on Chemical Equilibrium (1883)
6.2. Absolute Entropies (1911–1920)
The law of dependence on N can only be satisfactorily settled by utilizing a process in which N changes reversibly and then comparing the ratios of the probability with the corresponding differences of entropy.
Our method removes, we hope, any remaining obscurities as regards the occurrence of This could only be accomplished, as it appeared to us, by not stopping at the numbers of the molecules in the combinatory computations, but by going down to the atoms.
In the majority of calculations of the chemical constants a special obscurity remains as to the way in which the ‘thermodynamic probability’ of a gas depends on the number of molecules. We shall try to explain in a few words how this obscurity is connected with the use of [Planck’s equation instead of Boltzmann’s ]: it is generally assumed as self-evident, that the entropy of a gas is to be taken twice as large, if the number of molecules and the volume are both doubled. Now it is certainly true, that the increase of the entropy in a given process in a gas of twice the number of molecules is twice as large as the corresponding increase in the original gas. But what is the meaning of taking the entropy itself twice as large and thereby settling the entropy-difference between the doubled and the original gas? By what reversible process is the double quantity of gas to be generated from the original quantity? Without that the entropy difference cannot be clearly defined. In order to remove this obscurity, it is necessary to return to Boltzmann’s equation [] and to apply it to a reversible process in which the numbers of the molecules change.
6.3. Gibbsian Approaches (1902–1916)
First of all, we must define precisely what is meant by statistical equilibrium of such an ensemble of systems. The essence of statistical equilibrium is the permanence of the number of systems which fall within any given limits with respect to phase. We have therefore to define how the term phase is to be understood in such cases. If two phases differ only in that certain entirely similar particles have changed places with one another, are they to be regarded as identical or different phases? If the particles are regarded as indistinguishable, it seems in accordance with the spirit of the statistical method to regard the phases as identical.
To fix our ideas, let us suppose that we have two identical fluid masses in contiguous chambers. The entropy of the whole is equal to the sum of the entropies of the parts, and double that of one part. Suppose a valve is now opened, making a communication between the chambers. We do not regard this as making any change in the entropy, although the masses of gas or liquid diffuse into one another, and although the same process of diffusion would increase the entropy, if the masses of fluid were different. It is evident, therefore, that it is equilibrium with respect to generic phases, and not with respect to specific, with which we have to do in the evaluation of entropy, and therefore, that we must use the average of [] or of [] and not that of [], as the equivalent of entropy, except in the thermodynamics of bodies in which the number of molecules of the various kinds is constant.
It does not help to wrack one’s brain on the meaning of a quantity for a process that does not exist in nature, but one may be satisfied with the following criterion: this quantity will be relevant if its calculated theoretical value for every process which can really be observed agrees with the measured value.
Planck will not be talked out of his metaphysical probability concept. For whoever tries to understand minds of his kind, there is always a left-over irrationality, which escapes assimilation (which keeps reminding me of Fichte, Hegel, etc.).
6.4. Foundations
6.5. The Bose-Einstein Gas (1924–1925)
To conclude, I would like to bring the reader’s attention to a paradox which I have not been able to solve. There is no difficulty, with the method here given, to also treat the case of a mixture of two different gases. In this case, each kind of molecules has its own [quantum] ‘cells.’ Hence follows the additivity of the entropies of the components of the mixture. Thus, each component behaves as if it were alone [in the container] regarding molecular energy, pressure, and statistical distribution. A mixture with the molecule numbers and , wherein the molecules of the first and second kinds differ as little as one wishes (in particular with respect to the molecular masses , ) therefore gives, at given temperature, a pressure and a state-distribution different from those of a homogeneous gas with the molecule number and with practically the same molecular mass and the same volume. This seems virtually impossible [so gut wie unmöglich].
6.6. Von Neumann’s Solution
7. Various Gibbs Paradoxes and Possible Solutions
7.1. In Macroscopic Thermodynamics
7.2. In Classical Statistical Mechanics
7.3. In Quantum Statistical Mechanics
It was a famous paradox pointed out for the first time by W. Gibbs, that the same increase of entropy [for the mixing of two different gases] must not be taken into account, when the two molecules are of the same gas, although (according to naïve gas-theoretical views) diffusion takes place then too, but unnoticeably to us, because all the particles are alike. The modern view solves this paradox by declaring that in the second case there is no real diffusion, because exchange between like particles is not a real event—if it were, we should have to take account of it statistically. It has always been believed that Gibbs’s paradox embodied profound thought. That it was intimately linked up with something so important and entirely new could hardly be foreseen.
8. The Relation between Theory and Experiments in the Light of the Gibbs Paradox
Acknowledgments
Conflicts of Interest
References and Notes
- Van Kampen, N.G. The Gibbs paradox. In Essays in Theoretical Physics: In Honour of Dirk Ter Haar; Parry, W.E., Ed.; Pergamon Press: Oxford, UK, 1984; pp. 303–311. [Google Scholar]
- Cardwell, J. From Watt to Clausius: The Rise of Thermodynamics in the Early Industrial Age; Cornell University Press: Ithaca, NY, USA, 1971. [Google Scholar]
- Clausius, R. Über die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen. Ann. Phys. 1850, 79, 368–397, 500–524. [Google Scholar] [CrossRef]
- Thomson, W. (Lord Kelvin). On the dynamical theory of heat […]. Parts I–VI. Royal Society of Edinburgh, Transactions 1851–1854. Also in Mathematical and Physical Papers; 6 Volumes; 1882–1911; Cambridge University Press: Cambridge, UK, 1882; Volume 1, pp. 174–281. [Google Scholar]
- Clausius, R. Über eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie. Ann. Phys. 1854, 93, 481–506. [Google Scholar] [CrossRef]
- Clausius, R. Über die Anwendung des Satzes von der Äquivalenz der Verwandlungen auf die innere Arbeit. Ann. Phys. 1862, 116, 73–112. [Google Scholar] [CrossRef]
- Daub, E. Clausius, Rudolf-Dictionary of Scientific Biography; 16 Volumes; 1970–1980; Gillispie, C.C., Ed.; Scribner & Sons: New York, NY, USA, 1971; Volume 3, pp. 303–311. [Google Scholar]
- Klein, M.J. Gibbs on Clausius. Hist. Stud. Phys. Sci. 1969, 1, 127–149. [Google Scholar] [CrossRef]
- Clausius, R. Über verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie. Ann. Phys. 1865, 125, 353–400. [Google Scholar] [CrossRef]
- Daub, E. Probability and thermodynamics: The reduction of the second law. Isis 1969, 60, 318–330. [Google Scholar] [CrossRef]
- Daub, E. Entropy and dissipation. Hist. Stud. Phys. Sci. 1970, 2, 321–354. [Google Scholar] [CrossRef]
- Garber, E.; Brush, S.; Everitt, C.W.F. Maxwell on Molecules and Gases; The MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Garber, E.; Brush, S.; Everitt, C.W.F. Maxwell on Heat and Statistical Mechanics; Lehigh University Press: Bethlehem, PA, USA, 1995. [Google Scholar]
- Uffink, J. Compendium to the foundations of classical statistical mechanics. In Handbook for the Philosophy of Physics; Butterfield, J., Earman, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 924–1074. [Google Scholar]
- Darrigol, O. Atoms, Mechanics, and Probability: Boltzmann’s Statistico-Mechanical Writings—An Exegesis; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Loschmidt, J. Zur Grösse der Luftmoleküle. Wien. Ber. 1865, 52, 395–413. [Google Scholar]
- Loschmidt, J. Der zweite Satz der mechanischen Wärmetheorie. Wiener Ber. 1869, 59, 395–418. [Google Scholar]
- Maxwell, J.C. Theory of Heat; Longmans: London, UK, 1871. [Google Scholar]
- Daub, E. Maxwell’s demon. Stud. Hist. Philos. Sci. 1970, 1, 213–227. [Google Scholar] [CrossRef]
- Boltzmann, L. Zur Erinnerung an Josef Loschmidt [1895]. In Populäre Schriften; Barth: Leipzig, Germany, 1905; pp. 229–240. [Google Scholar]
- Horstmann, A. Theorie der Dissociation. Ann. Chem. Pharm. 1873, 170, 192–210. [Google Scholar] [CrossRef]
- Kragh, H.; Weininger, S. Sooner silence than confusion: The tortuous entry of entropy into chemistry. Hist. Stud. Phys. Sci. 1996, 27, 91–130. [Google Scholar] [CrossRef]
- Jensen, W. August Horstmann and the origins of chemical thermodynamics. Bull. Hist. Chem. 2009, 34, 83–91. [Google Scholar]
- Lord Rayleigh. On the dissipation of energy. Royal Institution of Great Britain. Proceedings 1875, 7, 386–389. [Google Scholar]
- Thomson, W. Kinetic theory of the dissipation of energy. Nature 1874, 9, 441–444. [Google Scholar] [CrossRef]
- Lord Rayleigh. On the work that may be gained during the mixing of gases. Philos. Mag. 1875, 49, 311–319. [Google Scholar]
- Schrödinger, E. Isotopie und Gibbsches Paradoxon. Z. Phys. 1921, 5, 163–166. [Google Scholar] [CrossRef]
- Gibbs, J.W. A method of geometrical representation of the thermodynamic properties of substances by means of surfaces. Connecticut Academy of Arts and Sciences. Transactions 1873, 2, 382–404, Also in Scientific Papers of J. Willard Gibbs; Gibbs, J.W., Ed.; Green & Co.: London, UK, 1906; pp. 33–54. [Google Scholar]
- Gibbs, J.W. Graphical methods in the thermodynamics of fluids. Connecticut Academy of Arts and Sciences. Transactions 1873, 2, 309–342, Also in Scientific Papers of J. Willard Gibbs; Green & Co.: London, UK, 1906; pp. 1–32. [Google Scholar]
- Gibbs, J.W. On the equilibrium of heterogeneous substances. Connecticut Academy of Arts and Sciences. Transactions 1875–1878, 3, 108–248, 343–524. [Google Scholar]
- Maxwell, J.C. Diffusion. In The Encyclopaedia Britannica, 9th ed.; Adam and Charles Black: Edinburgh, UK; 1877; Volume 7, pp. 214–221. Also in The Scientific Papers of James Clerk Maxwell; 2 Volumes; Cambridge University Press: Cambridge, UK, 1890; Volume 2, pp. 625–646. [Google Scholar]
- Maxwell, J.C. Tait’s Thermodynamics. Nature 1878, 17, 278–280, Also in The Scientific papers of James Clerk Maxwell; 2 Volumes; Maxwell, J.C., Ed.; Cambridge University Press: Cambridge, UK, 1890; Volume 2, pp. 660–671. [Google Scholar] [CrossRef]
- Brush, S. The Kind of Motion We Call Heat: A History of the Kinetic Theory of Gases in the 19th Century; 2 Volumes; North Holland: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Preston, S.T. On the diffusion of matter in relation to the second law of thermodynamics. Nature 1877, 16, 31–32. [Google Scholar] [CrossRef]
- Preston, S.T. On a means for converting the heat-motion possessed by matter at normal temperature into work. Nature 1878, 17, 202–204. [Google Scholar] [CrossRef]
- Aitken, J. On a means for converting the heat motion possessed by matter at normal temperature into work. Nature 1878, 17, 260. [Google Scholar] [CrossRef]
- Herschel, A.S. On the use of the virial in thermodynamics. Nature 1878, 17, 39–40. [Google Scholar]
- Clausius, R. Über die Beziehung der durch Diffusion geleisteten Arbeit zum zweiten Hauptsatze der mechanischen Wärmetheorie. Ann. Phys. 1878, 4, 341–343. [Google Scholar] [CrossRef]
- Preston, S.T. On the availability of normal-temperature heat-energy. Nature 1878, 17, 92–93. [Google Scholar] [CrossRef]
- Boltzmann, L. On some problems of the mechanical theory of heat. Philos. Mag. 1878, 6, 236–237. [Google Scholar] [CrossRef]
- Boltzmann, L. Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht. Wien. Ber. 1877, 76, 373–435, Also in Abh. Volume 2, pp. 164–223. [Google Scholar]
- Boltzmann, L. Über die Beziehung der Diffusionsphänomene zum zweiten Hauptsatze der mechanischen Wärmetheorie. Wien. Ber. 1878, 78, 733–763, Also in Abh. Volume 2, pp. 289–317. [Google Scholar]
- Helmholtz, H. Zur Thermodynamik chemischer Vorgänge. Dritter Beitrag. Berl. Ber. 1883, 647–665. [Google Scholar]
- Planck, M. Über das thermodynamische Gleichgewicht von Gasgemengen. Ann. Phys. 1883, 19, 358–378. [Google Scholar] [CrossRef]
- Neumann, C. Bemerkungen zur mechanischen Theorie der Wärme. Königliche Sächsische Gesellschaft der Wissenschaften zu Leipzig, Mathematische-physikalische Klasse. Verhandlungen 1891, 75–156. [Google Scholar]
- Planck, M. Grundriss der allgemeinen Thermochemie; Trewende: Breslau, Poland, 1893. [Google Scholar]
- Planck, M. Vorlesungen über Thermodynamik; Veit: Berlin, Germany, 1897. [Google Scholar]
- Duhem, P. Le Potentiel Thermodynamique et ses Applications à la Mécanique Chimique et à L'étude des Phénomènes Électriques; Hermann: Paris, France, 1886. [Google Scholar]
- Duhem, P. Sur la Dissociation Dans les Systèmes qui Renferment un Mélange de gaz Parfaits; Tome 2, Mémoire 8; Travaux et mémoires des facultés de Lille: Lille, France, 1892; 215p. [Google Scholar]
- Poincaré, H. Thermodynamique. Leçons Professées Pendant le Premier Semestre 1888–1889; Carré: Paris, France, 1892. [Google Scholar]
- Wiedeburg, O. Das Gibbs’sche Paradoxon. Ann. Phys. 1894, 53, 684–697. [Google Scholar] [CrossRef]
- Nernst, W. [Review of] J. Willard Gibbs: Thermodynamische Studien (Leipzig: Engelmann, 1992). Naturwissenschaftliche Rundsch. 1994, 8, 93–95. [Google Scholar]
- Boltzmann, L. Über das Arbeitsquantum, welches bei chemischen Verbindungen gewonnen werden kann. Wien. Ber. 1883, 88, 861–896, Also in Abh. vol. 3, pp. 66–100. [Google Scholar]
- Darrigol, O. Statistics and combinatorics in early quantum theory, II: Early symptoms of indistinguishability and holism. Hist. Stud. Phys. Sci. 1991, 21, 237–298. [Google Scholar] [CrossRef]
- Sackur, O. Die Anwendung der kinetischen Theorie der Gase auf chemische Probleme. Ann. Phys. 1911, 36, 958–980. [Google Scholar] [CrossRef]
- Tetrode, H. Die chemische Konstante der Gase und das elementare Wirkungsquantum. Ann. Phys. 1912, 38, 434–442. [Google Scholar] [CrossRef]
- Ehrenfest, P.; Trkal, V. Deduction of the dissociation equilibrium from the theory of quanta and calculation of the chemical constant based on this. Koninklijke Akademie van Wetenschappen te Amsterdam. Proceedings 1820, 23, 162–183. [Google Scholar]
- Klein, M.J. Ehrenfest’s contributions to the development of quantum statistics. Koninklijke Nederlandse Akademie van Wetenschappen. Proceedings 1959, 62, 41–62. [Google Scholar]
- Ehrenfest, P.; Trkal, V. Ableitung des Dissociationsgleichgewichts aus der Quantentheorie und darauf beruhende Berechnung chemischer Konstanten. Ann. Phys. 1921, 65, 609–628. [Google Scholar] [CrossRef]
- Einstein, A. Beiträge zur Quantentheorie. Deutsche physikalische Gesellschaft. Verhandlungen 1914, 16, 820–828. [Google Scholar]
- Einstein, A. Zur Tetrode-Sackur’schen Theorie der Entropie Konstante. Unpub. MS [1916]. In The Collected Papers of Albert Einstein; Princeton University Press: Princeton, NJ, USA, 1996; Volume 6, pp. 250–262. [Google Scholar]
- Gibbs, W.G. Elementary Principles in Statistical Mechanics Developed with Especial Reference to the Rational Foundation of Thermodynamics; Scribner’s Sons: New York, NY, USA, 1902. [Google Scholar]
- Klein, M.J.; Gibbs, J.W. Dictionary of Scientific Biography; 16 Volumes; 1970–1980; Gillispie, C.C., Ed.; Scribner & Sons: New York, NY, USA, 1972; Volume 5, pp. 386–393. [Google Scholar]
- Klein, M.J. The physics of J. Willard Gibbs in his time. Phys. Today 1990, 43, 40–48. [Google Scholar] [CrossRef]
- Planck, M. Über die absolute Entropie einatomiger Körper. Berl. Ber. 1916, 653–667. [Google Scholar]
- Planck, M. Absolute Entropie und Chemische Konstante. Ann. Phys. 1921, 66, 365–372. [Google Scholar] [CrossRef]
- Einstein to Ehrenfest, 14 September 1918. Archive for the History of Quantum Physics.
- Boltzmann, L. Über einige das Wärmegleichgewicht betreffende Sätze. Wien. Ber. 1881, 84, 136–145, Also in Abh. Volume 2, pp. 572–581. [Google Scholar]
- Boltzmann, L. [Review of an article by J. C. Maxwell “On Boltzmann’s theorem on the average distribution of energy in a system of material points”]. Beibl. Ann. Phys. 1881, 5, 403–417, English transl. in Philos. Mag. 1882, 14, 299–313. Also in Abh. Volume 2, pp. 582–595. [Google Scholar]
- Boltzmann, L. Analytischer Beweis des zweiten Hauptsatzes der mechanischen Wärmetheorie aus den Sätzen über das Gleichgewicht der lebendigen Kraft. Wien. Ber. 1871, 63, 712–732, Also in Abh. Volume 1, pp. 288–308. [Google Scholar]
- Einstein, A. Quantentheorie des einatomigen idealen Gases. Berl. Ber. 1924, 261–267. [Google Scholar]
- Einstein, A. Quantentheorie des einatomigen idealen Gases, 2. Abh. Berl. Ber. 1925, 3–14. [Google Scholar]
- Ehrenfest, P.; Uhlenbeck, G. Zum Einsteinschen “Mischungsparadoxon”. Z. Phys. 1925, 41, 576–582. [Google Scholar] [CrossRef]
- Von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin, Germany, 1932. [Google Scholar]
- Dieks, D.; van Dijk, V. Another look at the quantum mechanical entropy of mixing. Am. J. Phys. 1998, 56, 430–434. [Google Scholar] [CrossRef]
- Saunders, S. Indistinguishability. In Oxford Handbook in Philosophy of Physics; Batterman, R., Ed.; Oxford University Press: Oxford, UK, 2013; pp. 340–380. [Google Scholar]
- Jaynes, E.T. The Gibbs paradox. In Maximum Entropy and Bayesian Methods; Smith, C.R., Erickson, G.J., Neudorfer, P.O., Eds.; Kluwer: Dordrecht, The Netherlands, 1992; pp. 1–22. [Google Scholar]
- Larmor, J. A dynamical theory of the electric and luminiferous medium. Part III. Royal Society of London. Philos. Trans. 1997, 190, 205–300. [Google Scholar] [CrossRef]
- Boyer, T. Sharpening Bridgman’s resolution of the Gibbs paradox. Am. J. Phys. 1970, 38, 771–773. [Google Scholar] [CrossRef]
- Denbigh, K.; Redhead, M. Gibbs’ paradox and non-uniform convergence. Synthese 1989, 81, 283–312. [Google Scholar] [CrossRef]
- Bridgman, P.W. The Nature of Thermodynamics; Harvard University Press: Cambridge, MA, USA, 1941. [Google Scholar]
- Bais, F.A.; Farmer, J.D. The physics of information. arXiv, 2007; arXiv:0708.2837. [Google Scholar]
- Dieks, D. The Gibbs paradox revisited. In Explanation, Prediction, and Confirmation; Dieks, D., Hartmann, S., Gonzalez, W.J., Uebel, Th., Weber, M., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 367–377. [Google Scholar]
- Grad, H. The many faces of entropy. Commun. Pure Appl. Math. 1961, 14, 323–354. [Google Scholar] [CrossRef]
- Nagle, J. In defense of Gibbs and the traditional definition of the entropy of distinguishable Particles. Entropy 2010, 12, 1936–1945. [Google Scholar] [CrossRef]
- Casper, B.; Freier, S. ‘Gibbs Paradox’ paradox. Am. J. Phys. 1972, 41, 509–511. [Google Scholar] [CrossRef]
- Landé, A. Continuity, a key to quantum mechanics. Philos. Sci. 1953, 20, 101–109. [Google Scholar] [CrossRef]
- Landé, A. Solution of the Gibbs entropy paradox. Philos. Sci. 1965, 32, 192–193. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Nieuwenhuizen, T.M. Explanation of the Gibbs paradox within the framework of quantum thermodynamics. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006, 73, 066119. [Google Scholar] [CrossRef] [PubMed]
- Schrödinger, E. Statistical Thermodynamics; Cambridge University Press: Cambridge, UK, 1946. [Google Scholar]
- Saunders, S. On the explanation for quantum statistics. Stud. Hist. Philos. Mod. Phys. 2006, 37, 192–211. [Google Scholar] [CrossRef]
- Dieks, D.; Lubberdink, A. How classical particles emerge from the quantum world. Found. Phys. 2011, 41, 1051–1064. [Google Scholar] [CrossRef]
- Darrigol, O. The modular structure of physical theories. Synthese 2008, 162, 195–223. [Google Scholar] [CrossRef]
- Darrigol, O. Physics and Necessity: Rationalist Pursuits from the Cartesian Past to the Quantum Present; Oxford University Press: Oxford, UK, 2014. [Google Scholar]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darrigol, O. The Gibbs Paradox: Early History and Solutions. Entropy 2018, 20, 443. https://doi.org/10.3390/e20060443
Darrigol O. The Gibbs Paradox: Early History and Solutions. Entropy. 2018; 20(6):443. https://doi.org/10.3390/e20060443
Chicago/Turabian StyleDarrigol, Olivier. 2018. "The Gibbs Paradox: Early History and Solutions" Entropy 20, no. 6: 443. https://doi.org/10.3390/e20060443
APA StyleDarrigol, O. (2018). The Gibbs Paradox: Early History and Solutions. Entropy, 20(6), 443. https://doi.org/10.3390/e20060443



