Quantification and Analysis of the Irreversible Flow Loss in a Linear Compressor Cascade
Abstract
:1. Introduction
2. Local and Integral Loss Models Based on a Hybrid RANS/LES Model
2.1. Entropy Generation Rate
2.2. Local Loss Model
2.3. Integral Loss Model
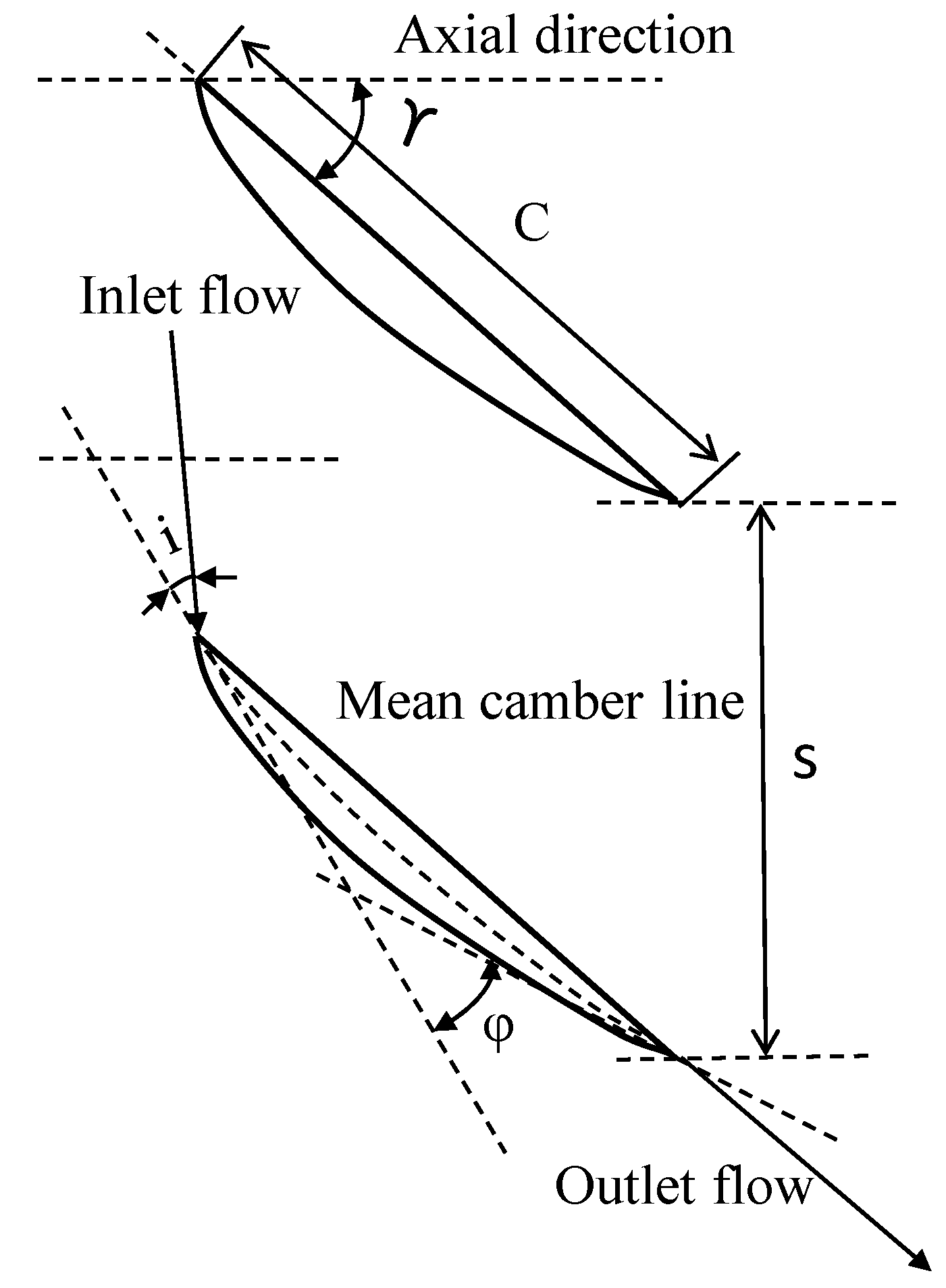
3. The Studied Cascade and Numerical Configuration
3.1. The Studied Cascade
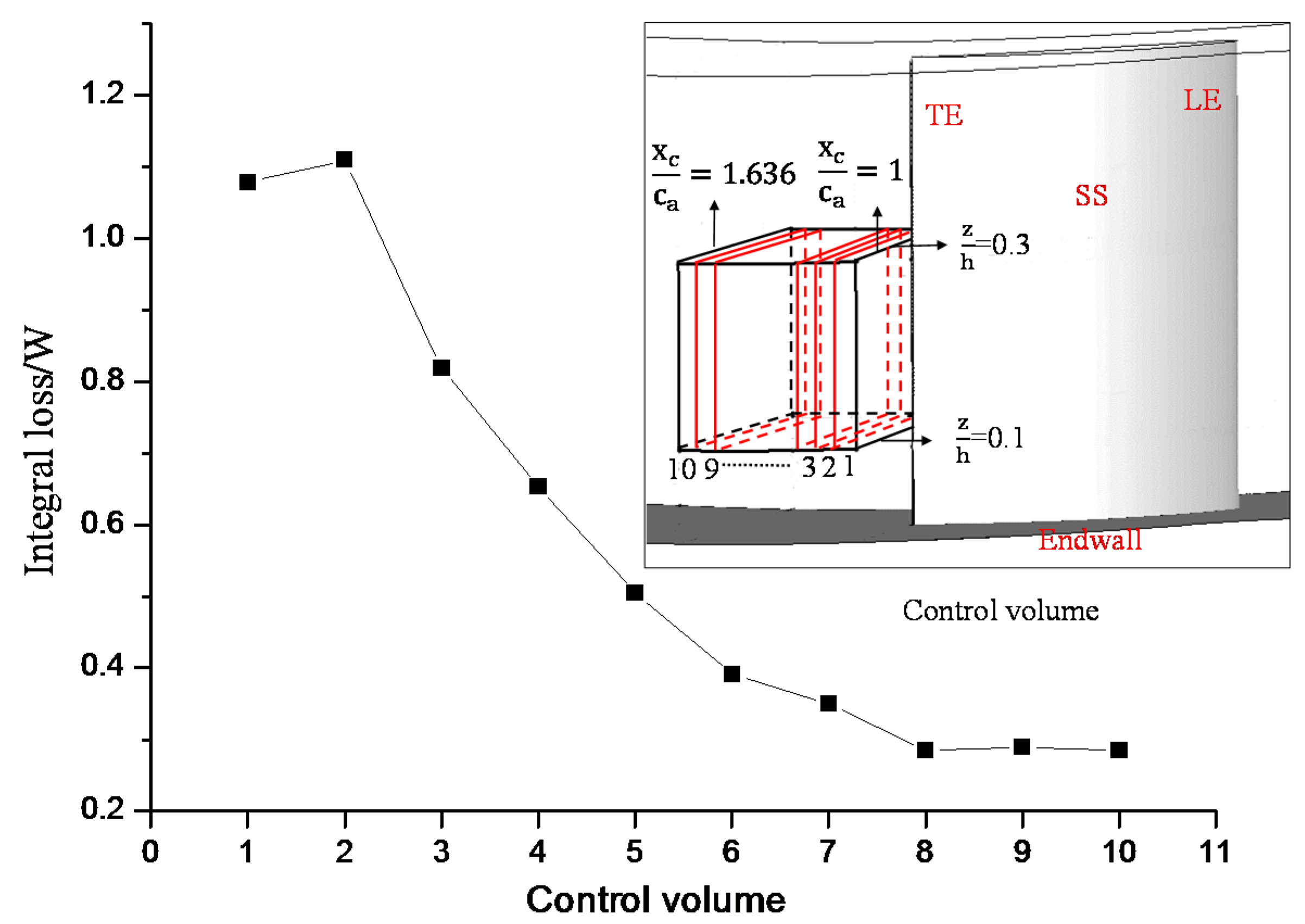
3.2. Numerical Method
4. Validation of the Simulation Results
4.1. Time-Averaged Static Pressure Coefficient on the Blade
4.2. Local Loss Coefficient and Integral Loss
5. Loss Mechanism Variation with Incidence Angle
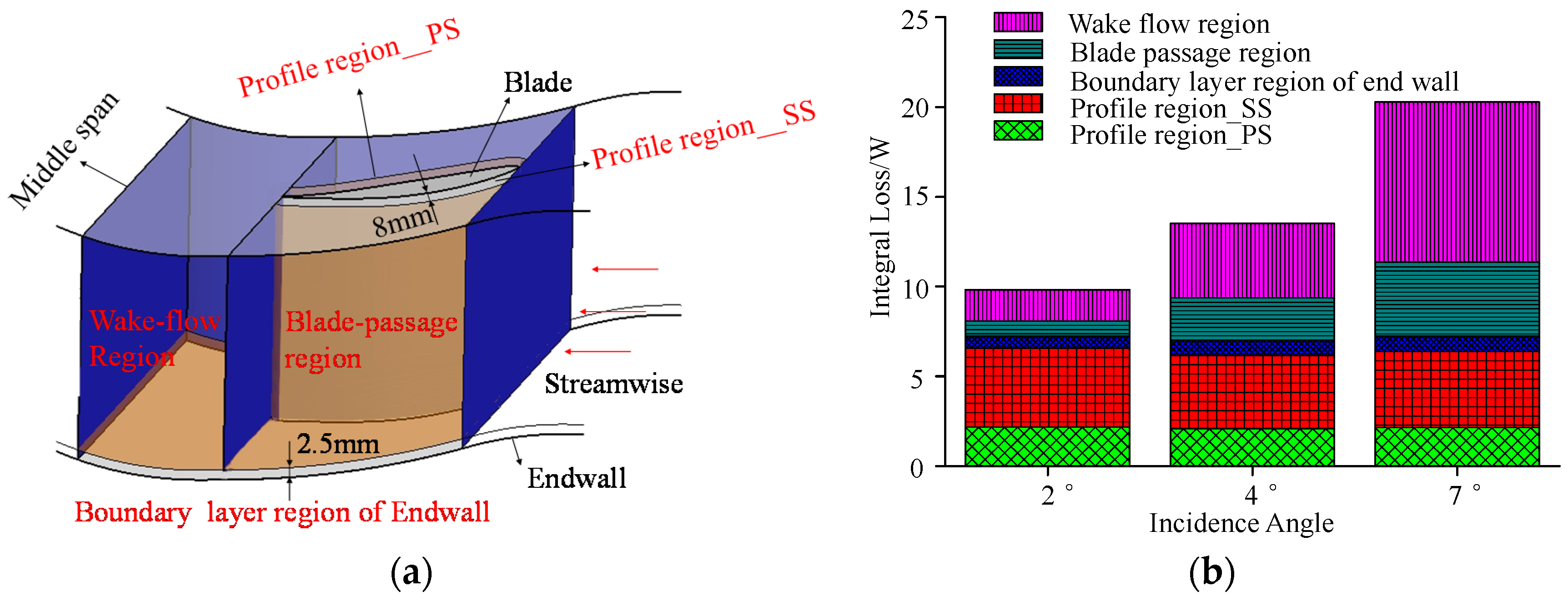
5.1. Quantitative Analysis of Loss Sources
5.2. Loss Generated in the Wake-Flow Region, and the Blade Passage
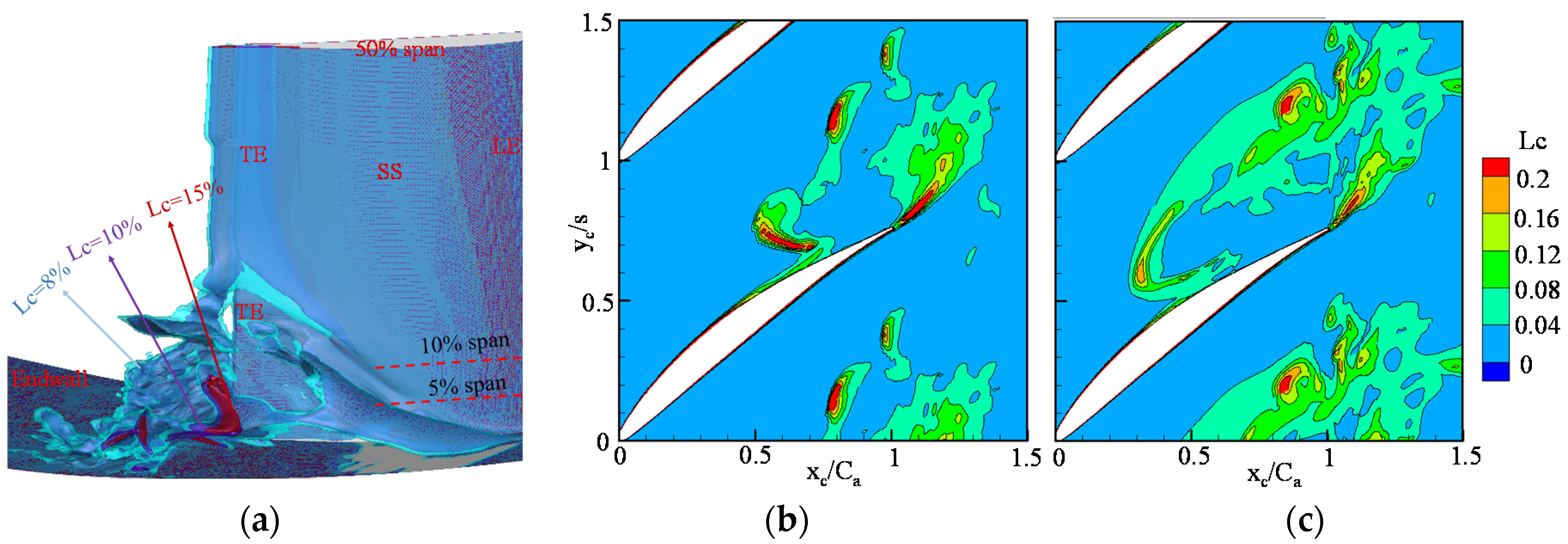
5.3. Analysis of 3D Loss Distribution
6. Discussion
- (1)
- The local and integral loss models, derived on a rigorous theoretical basis, can be used to quantify the local loss and analyze the loss mechanism once the simulation results calculated by the SSTDES model are independent of the computational mesh. The local loss-intensity distribution described by the local loss model can be explained well by the 3D flow structures. The trend of the total flow loss calculated by the integral loss model is the same as that exhibited by the total pressure loss coefficient with the incidence angle.
- (2)
- The boundary layer shear loss is almost uninfluenced by the incidence angle. The secondary flow loss in the wake flow and blade-passage regions changes dramatically with the flow condition due to the occurrence of corner stall. For this cascade, the secondary flow loss accounts for 26.1%, 48.3% and 64.3% of the total loss for the flow at incidence angles of 2°, 4° and 7°, respectively.
- (3)
- Insight can be derived using the iso-surface contours of Lc to identify the 3D loss distribution. With increasing incidence angle, three types of secondary flow loss change dramatically. They are the passage shear loss, which is located at the interface region between the main flow and the outside of the corner separation flow; the corner wake-flow shear loss, which is located in the mixing region between the boundary layer flow of the pressure side and the corner separation flow; and the tornado-vortex trailing loss, which represents the loss generated at the top of corner separation flow where the main flow structure is the tail of the corner tornado vortex.
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| C, ca | blade chord, axial blade chord |
| Cp | static pressure coefficient |
| Cf | skin friction coefficient |
| h | blade span |
| i | incidence angle |
| k | turbulence kinetic energy |
| L | loss intensity |
| Lc | local loss coefficient |
| p | pressure |
| Re | Reynolds number |
| s | pitch spacing |
| sij | fluctuating strain-rate tensor |
| Sij | shear strain rate |
| entropy generation of viscosity dissipation | |
| entropy generation of heat transfer | |
| U | velocity |
| xc, yc | axial, longitudinal direction of cascade frame |
| zc | spanwise direction of cascade frame |
| ρ | density |
| ϒ | stagger angle |
| ϕ | Camber line |
| υ | kinematic viscosity |
| μ | dynamic viscosity |
| ω | specific dissipation rate |
| τw | wall shear stress |
| LE, TE | leading edge, trailing edge |
| PS, SS | pressure surface, suction surface |
References
- Lu, H.; Li, Q. Cantilevered Stator Hub Leakage Flow Control and Loss Reduction Using Non-uniform Clearances. Aerosp. Sci. Technol. 2016, 51, 1–10. [Google Scholar] [CrossRef]
- Chu, W.; Li, X.; Wu, Y.; Zhang, H. Reduction of End Wall Loss in Axial Compressor by Using Non-axisymmetric Profiled End Wall: A New Design Approach Based on End Wall Velocity Modification. Aerosp. Sci. Technol. 2016, 55, 76–91. [Google Scholar] [CrossRef]
- Denton, J.D. Loss Mechanisms in Turbomachines. ASME J. Turbomach. 1993, 115, 621–656. [Google Scholar] [CrossRef]
- Moore, J.; Moore, J.G. Entropy Production Rates from Viscous Flow Calculations: Part 1-A Turbulent Boundary Layer Flow; ASME Paper No. 83-GT-70; ASME: Phoenix, AZ, USA, 1983. [Google Scholar]
- Zlatinov, M.; Tan, C.S.; Montgomery, M.; Islam, T.; Seco-Soley, M. Turbine Hub and Shroud Sealing Flow Loss Mechanisms; ASME Paper No. GT2011-46718; ASME: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Plamer, T.R.; Tan, C.S.; Zuniga, H.; Little, D.; Montgomery, M.; Malandra, A. Quantifying Loss Mechanisms in Turbine Tip Shroud Cavity Flows. ASME J. Turbomach. 2016, 138, 091006. [Google Scholar] [CrossRef]
- Kramer-Bevan, J.S. A Tool for Analysing Fluid Flow Losses. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 1992. [Google Scholar]
- Kock, F.; Herwig, H. Entropy Production Calculation for Turbulent Shear Flows and Their Implementation in CFD Codes. Int. J. Heat Fluid Flow 2005, 26, 672–680. [Google Scholar] [CrossRef]
- Takakura, T. Entropy Generation in the Tip Region of a High-Pressure Turbine. Ph.D. Thesis, University of Notre Dame, Notre Dame, IN, USA, 2016. Available online: https://curate.nd.edu/show/xs55m903b0m (accessed on 1 September 2016).
- Spalart, P.R. Strategies for Turbulence Modelling and Simulations. Int. J. Heat Fluid Flow 2000, 21, 252–263. [Google Scholar] [CrossRef]
- Greitzer, E.M.; Tan, C.S.; Graf, M.B. Internal Flow Concepts and Applications; Cambridge University Press: Cambridge, UK, 2004; pp. 26–27. ISBN 9780521036726. [Google Scholar]
- Menter, F.R.; Kuntz, M. Adaptation of Eddy-Viscosity Turbulence Models to Unsteady Separated Flow behind Vehicles. In The Aerodynamics of Heavy Vehicles: Trucks, Buses, and Trains; Springer: Berlin/Heidelberg, Germany, 2004; pp. 339–352. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; Chapter 7; ISBN 9780521598866. [Google Scholar]
- Petukhov, B.S. Advances in Heat Transfer; Academic Press: New York, NY, USA, 2000; Volume 6, pp. 503–504. ISBN 9780080575605. [Google Scholar]
- Ma, W.; Ottavy, X.; Lu, L.; Leboeuf, F. Intermittent Corner Separation in a Linear Compressor Cascade. Exp. Fluids 2013, 54, 1546. [Google Scholar]
- Zambonini, G.; Ottavy, X. Unsteady Pressure Investigations of Corner Separation Flow in a Linear Compressor Cascade; ASME Paper No. GT2015-42073; ASME: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Zambonini, G.; Ottavy, X.; Kriegseis, J. Corner Separation Dynamics in a Linear Compressor Cascade. J. Fluids Eng. 2017, 139, 061101. [Google Scholar] [CrossRef]
- Robertson, E.; Choudhury, V.; Bhushan, S.; Walters, D.K. Validation of OpenFOAM numerical methods and turbulence models for incompressible bluff body flows. Comput. Fluids 2015, 123, 122–145. [Google Scholar] [CrossRef]
- Van Der Velden, W.C.P.; Van Zuijlen, A.H.; De Jong, A.T.; Bijl, H. Estimation of spanwise pressure coherence under a turbulent boundary layer. AIAA J. 2015, 53, 3134–3138. [Google Scholar] [CrossRef]
- Li, Z.Y.; Du, J.; Jemcov, A.; Ottavy, X.; Lin, F. A Study of Loss Mechanism in a Linear Compressor Cascade at the Corner Stall Condition; ASME Paper No. GT2017-65192; ASME: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Ma, W.; Ottavy, X.; Lu, L.U.; Leboeuf, F.; Feng, G.A.O. Experimental Study of Comer Stall in a Linear Compressor Cascade. Chin. J. Aeronaut. 2011, 24, 235–242. [Google Scholar] [CrossRef]
- Lei, V.; Spakovszky, Z.; Greitzer, E. A Criterion for Axial Compressor Hub Corner Stall. ASME J. Turbomach. 2008, 130, 031006. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the Identification of a Vortex. J. Fluid Mech. 1995, 289, 69–94. [Google Scholar] [CrossRef]
- Gao, F.; Ma, W.; Zambonini, G.; Boudet, J.; Ottavy, X.; Lu, L.; Shao, L. Large-eddy simulation of 3-D corner separation in a linear compressor cascade. Phys. Fluids 2015, 27, 85–105. [Google Scholar] [CrossRef]








| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Chord (mm) | 150 | Blade span (mm) | 370 |
| Camber angle (°) | 23.22 | Aspect ratio | 2.47 |
| Stagger angle (°) | 42.7 | Design upstream flow angle (°) | 54.31 |
| Pitch spacing (mm) | 134 | Design downstream flow angle (°) | 31.09 |
| Solidity | 1.12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Du, J.; Ottavy, X.; Zhang, H. Quantification and Analysis of the Irreversible Flow Loss in a Linear Compressor Cascade. Entropy 2018, 20, 486. https://doi.org/10.3390/e20070486
Li Z, Du J, Ottavy X, Zhang H. Quantification and Analysis of the Irreversible Flow Loss in a Linear Compressor Cascade. Entropy. 2018; 20(7):486. https://doi.org/10.3390/e20070486
Chicago/Turabian StyleLi, Zhiyuan, Juan Du, Xavier Ottavy, and Hongwu Zhang. 2018. "Quantification and Analysis of the Irreversible Flow Loss in a Linear Compressor Cascade" Entropy 20, no. 7: 486. https://doi.org/10.3390/e20070486





