On the Importance of Electron Diffusion in a Bulk-Matter Test of the Pauli Exclusion Principle
Abstract
1. Introduction
2. Mathematical Model
2.1. Quick Refresher of Some Basic Concepts of Electron Conduction in Metals
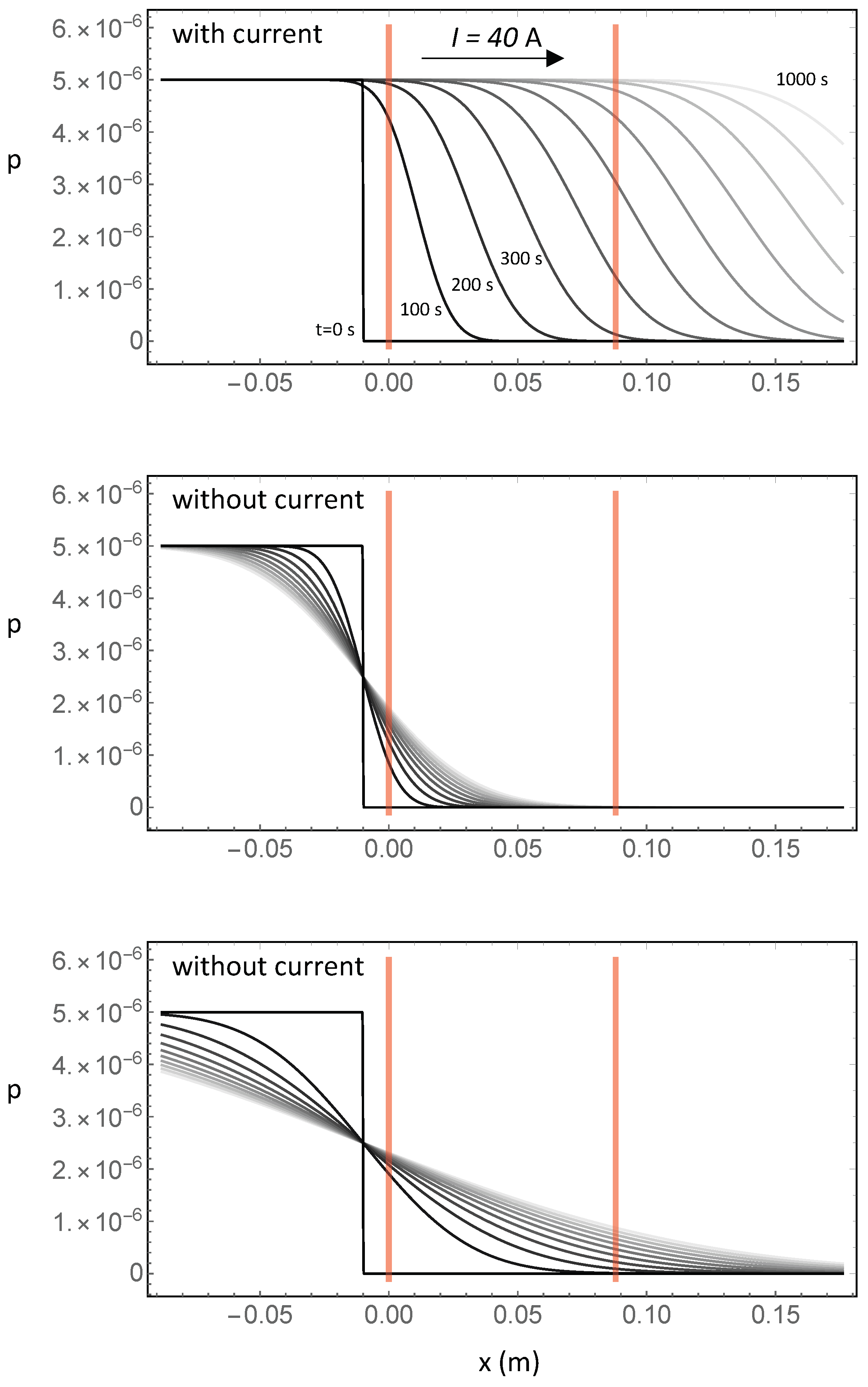
2.2. A Simple 1D Diffusion-Transport Model
3. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ramberg, E.; Snow, G.A. Experimental limit on a small violation of the Pauli principle. Phys. Lett. B 1990, 238, 438–441. [Google Scholar] [CrossRef]
- Pauli, W. Exclusion principle and quantum mechanics. In Writings on Physics and Philosophy; Springer: New York, NY, USA, 1994; pp. 165–181. [Google Scholar]
- Bartalucci, S.; Bertolucci, S.; Bragadireanu, M.; Cargnelli, M.; Catitti, M.; Curceanu, C.; Di Matteo, S.; Egger, J.P.; Guaraldo, C.; Iliescu, M.; et al. New experimental limit on the Pauli exclusion principle violation by electrons. Phys. Lett. B 2006, 641, 18–22. [Google Scholar] [CrossRef]
- Curceanu, C.; Shi, H.; Bartalucci, S.; Bertolucci, S.; Bazzi, M.; Berucci, C.; Bragadireanu, M.; Cargnelli, M.; Clozza, A.; De Paolis, L.; et al. Test of the Pauli Exclusion Principle in the VIP-2 Underground Experiment. Entropy 2017, 19, 300. [Google Scholar] [CrossRef]
- Shi, H.; Milotti, E.; Bartalucci, S.; Bazzi, M.; Bertolucci, S.; Bragadireanu, A.; Cargnelli, M.; Clozza, A.; De Paolis, L.; Di Matteo, S.; et al. Experimental search for the violation of Pauli exclusion principle. Eur. Phys. J. C 2018, 78, 319. [Google Scholar] [CrossRef] [PubMed]
- Kittel, C. Elementary Statistical Mechanics; Dover: Mineola, NY, USA, 1958. [Google Scholar]
- Mendenhall, M.H.; Henins, A.; Hudson, L.T.; Szabo, C.I.; Windover, D.; Cline, J.P. High-precision measurement of the x-ray Cu Kα spectrum. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 115004. [Google Scholar] [CrossRef] [PubMed]
- Ignatiev, A.Y.; Kuzmin, V. Search for slight violation of the Pauli principle. JETP Lett. 1987, 47, 6–8. [Google Scholar]
- Okun, L.B. Possible violation of the Pauli principle in atoms. JETP Lett. 1987, 46, 529–532. [Google Scholar]
- Okun, L.B. Comments on Testing Charge Conservation and Pauli Exclusion Principle. Comments Nucl. Part. Phys. 1988, 19, 99–116. [Google Scholar]
- Okun, L.B. Tests of electric charge conservation and the Pauli principle. Sov. Phys. Uspekhi 1989, 32, 543. [Google Scholar] [CrossRef]
- Rahal, V.; Campa, A. Thermodynamical implications of a violation of the Pauli principle. Phys. Rev. A 1988, 38, 3728–3731. [Google Scholar] [CrossRef]
- Greenberg, O. Particles with small violations of Fermi or Bose statistics. Phys. Rev. D 1991, 43, 4111. [Google Scholar] [CrossRef]
- Greenberg, O.; Mohapatra, R.N. Difficulties with a local quantum field theory of possible violation of the Pauli principle. Phys. Rev. Lett. 1989, 62, 712. [Google Scholar] [CrossRef] [PubMed]
- Greenberg, O. On the surprising rigidity of the Pauli exclusion principle. Nucl. Phys. B Proc. Suppl. 1989, 6, 83–89. [Google Scholar] [CrossRef]
- Govorkov, A. Can the Pauli principle be deduced with local quantum field theory? Phys. Lett. A 1989, 137, 7–10. [Google Scholar] [CrossRef]
- Govorkov, A. Does the existence of antiparticles forbid violations of statistics? Mod. Phys. Lett. A 1992, 7, 2383–2388. [Google Scholar] [CrossRef]
- Pauli, W. The connection between spin and statistics. Phys. Rev. 1940, 58, 716. [Google Scholar] [CrossRef]
- Carvalho, J.C. Derivation of the Mass of the Observable Universe. Int. J. Theor. Phys. 1995, 34, 2507–2509. [Google Scholar] [CrossRef]
- Scofield, J.H. Frequency-domain description of a lock-in amplifier. Am. J. Phys. 1994, 62, 129–133. [Google Scholar] [CrossRef]


| VIP | VIP-2 | |
|---|---|---|
| Target material | Cu | Cu |
| Copper target shape | Cylinder (45-mm radius) | Strip |
| Copper target length (L) | 88 mm | 71 mm |
| Copper target thickness (z) | 50 m | 50 m |
| Copper target width (w) | 282.74 mm | 20 mm |
| Target cross-section () | m | m |
| Target volume () | m | m |
| Detectors (multiplicity) | Pairs of rectangular Charge Coupled Devices (CCD) in octagonal arrangement about the target (8 pairs) | 1 cm× 3 (on one side of the Cu strip) × 2 (two sides) |
| Geometric factor | 0.01 | 0.018 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milotti, E.; Bartalucci, S.; Bertolucci, S.; Bazzi, M.; Bragadireanu, M.; Cargnelli, M.; Clozza, A.; Curceanu, C.; De Paolis, L.; Egger, J.-P.; et al. On the Importance of Electron Diffusion in a Bulk-Matter Test of the Pauli Exclusion Principle. Entropy 2018, 20, 515. https://doi.org/10.3390/e20070515
Milotti E, Bartalucci S, Bertolucci S, Bazzi M, Bragadireanu M, Cargnelli M, Clozza A, Curceanu C, De Paolis L, Egger J-P, et al. On the Importance of Electron Diffusion in a Bulk-Matter Test of the Pauli Exclusion Principle. Entropy. 2018; 20(7):515. https://doi.org/10.3390/e20070515
Chicago/Turabian StyleMilotti, Edoardo, Sergio Bartalucci, Sergio Bertolucci, Massimiliano Bazzi, Mario Bragadireanu, Michael Cargnelli, Alberto Clozza, Catalina Curceanu, Luca De Paolis, Jean-Pierre Egger, and et al. 2018. "On the Importance of Electron Diffusion in a Bulk-Matter Test of the Pauli Exclusion Principle" Entropy 20, no. 7: 515. https://doi.org/10.3390/e20070515
APA StyleMilotti, E., Bartalucci, S., Bertolucci, S., Bazzi, M., Bragadireanu, M., Cargnelli, M., Clozza, A., Curceanu, C., De Paolis, L., Egger, J.-P., Guaraldo, C., Iliescu, M., Laubenstein, M., Marton, J., Miliucci, M., Pichler, A., Pietreanu, D., Piscicchia, K., Scordo, A., ... Zmeskal, J. (2018). On the Importance of Electron Diffusion in a Bulk-Matter Test of the Pauli Exclusion Principle. Entropy, 20(7), 515. https://doi.org/10.3390/e20070515







