Analysis and Comparison of Spatial–Temporal Entropy Variability of Tehran City Microclimate Based on Climate Change Scenarios
Abstract
1. Introduction
2. Materials and Method
2.1. Effective Temperature
2.2. Introducing the Method of Projecting and Downscaling of Climate Variables
2.3. Introducing Statistical Methods to Calibrate and Validate the Climate Model
2.4. Shannon Entropy Indicator
3. Research Findings
3.1. Validating Climate Modeling Results
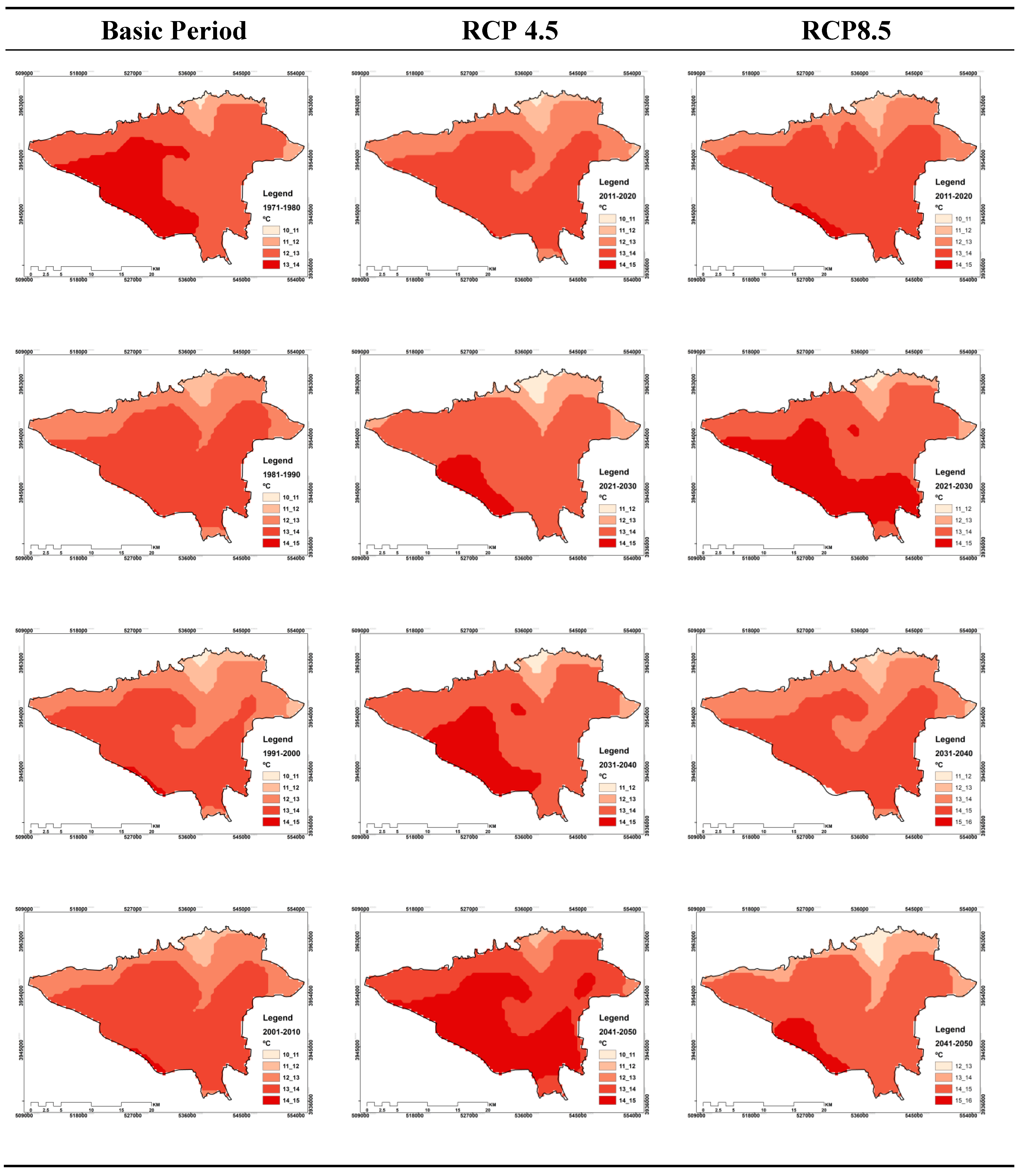
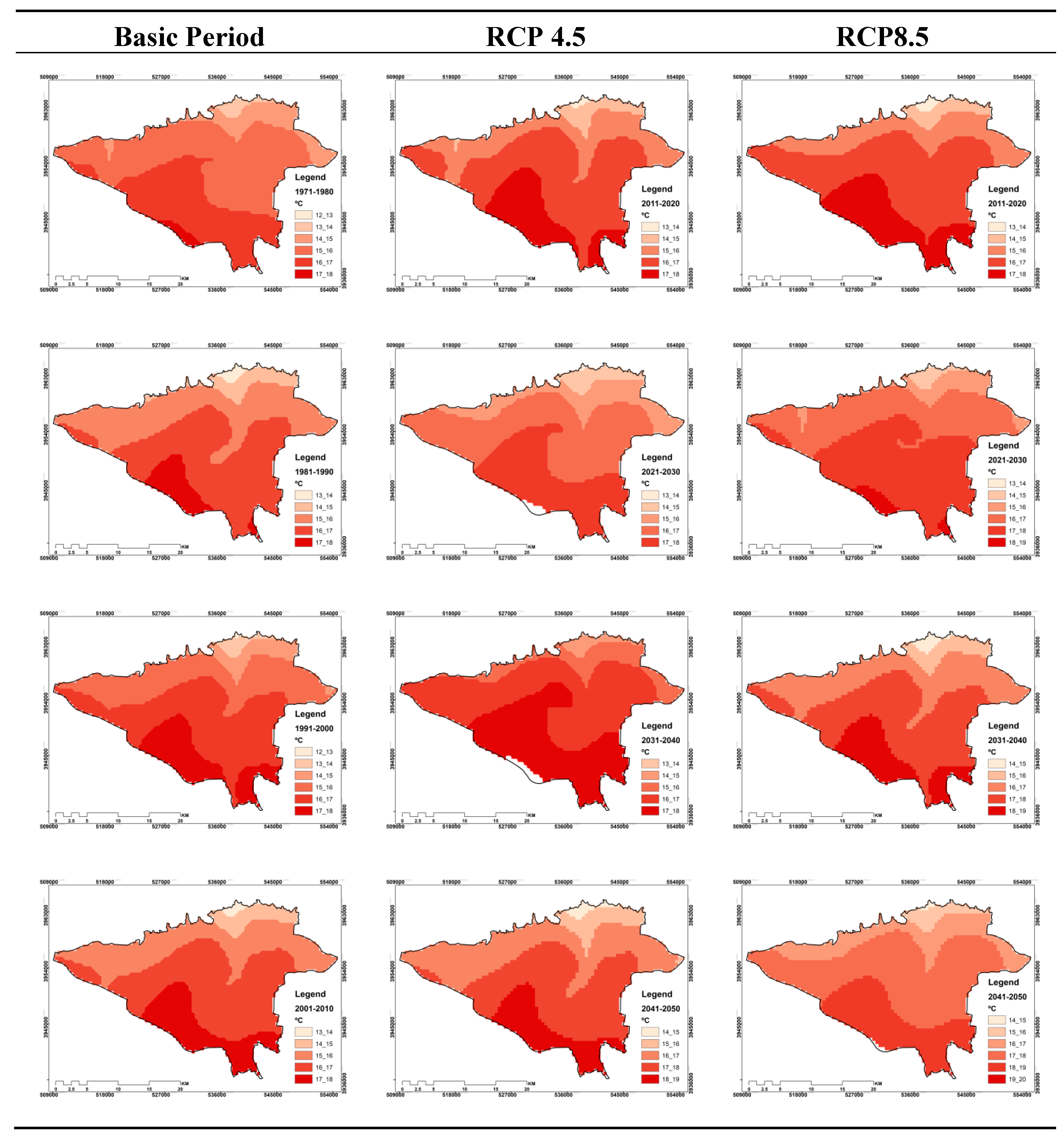
3.2. Zoning of Effective Temperature Index for Different Study Periods
3.3. Spatial–Temporal Analysis of Shannon’s Entropy Values from the Effective Temperature Index
3.3.1. Shannon Entropy Effective Temperature Indicator for 3:00 GMT
3.3.2. Shannon Entropy of Effective Temperature Indicator for 15:00 GMT
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roshan, G.; Ghanghermeh, A.; Kong, Q. Spatial and temporal analysis of outdoor human thermal comfort during heat and cold waves in Iran. Weather Clim.Extrem. 2018, 19, 58–67. [Google Scholar] [CrossRef]
- Bagheri, B.; NedaeTousi, S. An explanation of urban sprawl phenomenon in Shiraz Metropolitan Area (SMA). Cities 2018, 73, 71–90. [Google Scholar] [CrossRef]
- Emadodin, I.; Taravat, A.; Rajaei, M. Effects of urban sprawl on local climate: A case study, north central Iran. Urban Clim. 2016, 17, 230–247. [Google Scholar] [CrossRef]
- Sarvestania, S.; Ibrahima, L.; Kanaroglou, P. Three decades of urban growth in the city of Shiraz, Iran: A remote sensing and geographic information systems application. Cities 2011, 28, 320–329. [Google Scholar] [CrossRef]
- Sikder, S.K.; Nagarajan, M.; Kar, S.; Koetter, T. A geospatial approach of downscaling urban energy consumption density in mega-city Dhaka, Bangladesh. Urban Clim. 2018, 26, 10–30. [Google Scholar] [CrossRef]
- Zare, S.; Hasheminezhad, N.; Sarebanzadeh, K.; Zolala, F.; Hemmatjo, R.; Hassanvand, D. Assessing thermal comfort in tourist attractions through objective and subjective procedures based on ISO 7730 standard: A field study. Urban Clim. 2018, 26, 1–9. [Google Scholar] [CrossRef]
- Estela, L.B. Biometeorological forecasts for health surveillance and prevention of meteor-tropic effects. Int. J. Biometeorol. 2018, 62, 741–771. [Google Scholar] [CrossRef] [PubMed]
- Roshan, G.; Yousefi, R.; Błażejczyk, K. Assessment of the climatic potential for tourism in Iran through biometeorology clustering. Int. J. Biometeorol. 2018, 62, 525–542. [Google Scholar] [CrossRef] [PubMed]
- Åström, D.O.; Forsberg, B.; Ebi, K.L.; Rocklöv, J. Attributing mortality from extreme temperatures to climate change in Stockholm, Sweden. Nat. Clim. Chang. 2013, 3, 1050–1054. [Google Scholar] [CrossRef]
- Fouillet, A.; Rey, G.; Laurent, F.; Pavillon, G.; Bellec, S.; Guihenneuc-Jouyaux, C.; Hémon, D. Excess mortality related to the August 2003 heat wave in France. Int. Arch. Occup. Environ. Health 2006, 80, 16–24. [Google Scholar] [CrossRef]
- Hajat, S.; Kovats, R.S.; Lachowycz, K. Heat-related and cold-related deaths in England and Wales: Who is at risk? Occup. Environ. Med. 2007, 64, 93–100. [Google Scholar] [CrossRef] [PubMed]
- Shen, T.; Chow, D.; Darkwa, J. Simulating the influence of microclimatic design on mitigating the Urban Heat Island effect in the Hangzhou Metropolitan Area of China. Int. J. Low-Carbon Technol. 2013, 11, 130–139. [Google Scholar] [CrossRef]
- Akbari, H.; Pomerantz, M.; Taha, H. Cool surfaces and shade trees to reduce energy use andimprove air quality in urban areas. Sol. Energy 2001, 70, 295–310. [Google Scholar] [CrossRef]
- McKibben, B. Climate Change 2007: The Physical Science Basis: Summary for Policymakers. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. N. Y. Rev. Books 2007, 54, 1–44. [Google Scholar]
- Jacob, D.J.; Winner, D.A. Effect of climate change on air quality. Atmos. Environ. 2009, 43, 51–63. [Google Scholar] [CrossRef]
- Weaver, C.; Cooter, E.; Gilliam, R.; Gilliland, A.; Grambsch, A.; Grano, D.; Winner, D.A. preliminary synthesis of modeled climate change impacts on US regional ozone concentrations. Bull. Am. Meteorol. Soc. 2009, 90, 1843–1863. [Google Scholar] [CrossRef]
- UN, World Urbanization Prospects: The 2016 Revision; United National Population Division, Department of Economic and Social Affairs, United Nations Secretariat: New York, NY, USA, 2016.
- UN-Habitat, Asia-Pacific Issue Brief Series on Urbanization and Climate Change No. 1, Addressing Urban Poverty, Inequality, and Vulnerability in a Warming World; UNDP: Bangkok, Thailand, 2013; pp. 1–12.
- Ghrakhlou, M.; ZanganeShahraki, S. The pattern of urban spatial-physical growth using quantitative models (Case study: Tehran city). Geogr. Reg. Dev. 2009, 23, 17–29. [Google Scholar]
- Taravat, A.; Rajaei, M.; Emadodin, I. Urbanization dynamics of Tehran city (1975–2015) using artificial neural networks. J. Maps 2017, 13, 24–30. [Google Scholar] [CrossRef]
- Mohammmadzad, R. Investigating the environmental impacts of accelerated physical development in cities with emphasis on Tehran and Tabriz cities. Geogr. Reg. Dev. 2007, 9, 35–43. [Google Scholar]
- Roshan, G.; Rousta, I.; Ramesh, M. Studying the effects of urban sprawl of metropolis on tourism-climate index oscillation: A case study of Tehran city. J. Geogr. Reg. Plan. 2009, 12, 310–321. [Google Scholar]
- Roshan, G.R.; Shahraki, S.Z.; Sauri, D.; Borna, R. Urban sprawl and climatic changes in Tehran. Iran. J. Environ. Health Sci. Eng. 2010, 7, 43–52. [Google Scholar]
- Saboohi, R.; Soltani, S.; Khodagholi, M. Trend analysis of temperature parameters in Iran. Theor. Appl. Climatol 2012, 109, 529–547. [Google Scholar] [CrossRef]
- Ghanghermeh, A.; Roshan, G.; Orosa, J.A.; Calvo-Rolle, J.L.; Costa, Á.M. New Climatic Indicators for Improving Urban Sprawl: A Case Study of Tehran City. Entropy 2013, 15, 999–1013. [Google Scholar] [CrossRef]
- Roy, S.S.; Keikhosravi Kiany, M.S.; Balling, R.C. A Significant Population Signal in Iranian Temperature Records. Int. J. Atmos. Sci. 2016, 2016, 1603693. [Google Scholar] [CrossRef]
- Dwivedi, D.; Mohanty, B.P. Hot Spots and Persistence of Nitrate in Aquifers across Scales. Entropy 2016, 18, 25. [Google Scholar] [CrossRef]
- Fortak, H.G. Entropy and Climate. Dev. Atmos. Sci. 1979, 10, 1–14. [Google Scholar]
- Tapiador, J. Hurricane Footprints in Global Climate Models Francisco. Entropy 2008, 10, 613–620. [Google Scholar] [CrossRef]
- Lucarini1, V.; Fraedrich, K.; Lunkeit, F. Thermodynamics of climate change: Generalized sensitivities. Atmos. Chem. Phys. 2010, 10, 9729–9737. [Google Scholar] [CrossRef]
- Pascale, S.; Gregory, J.M.; Ambaum, M.; Tailleux, R. Climate entropy budget of the HadCM3 atmosphere–ocean general circulation model and of FAMOUS, its low-resolution version. Clim. Dyn. 2011, 36, 1189–1206. [Google Scholar] [CrossRef]
- Paillard, D.; Herbert, C. Maximum Entropy Production and Time Varying Problems: The Seasonal Cycle in a Conceptual Climate Model. Entropy 2013, 15, 2846–2860. [Google Scholar] [CrossRef]
- Zhang, G.; Su, X.; Singh, V.P.; Ayantobo, O.O. Modeling NDVI Using Joint Entropy Method Considering Hydro-Meteorological Driving Factors in the Middle Reaches of Hei River Basin. Entropy 2017, 19, 502. [Google Scholar] [CrossRef]
- Vu, T.M.; Mishra, A.K.; Konapala, G. Information Entropy Suggests Stronger Nonlinear Associations between Hydro-Meteorological Variables and ENSO. Entropy 2018, 20, 38. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration Goddard Institute for Space Studies (NASA). Available online: https://www.giss.nasa.gov/projects/gcm/ (accessed on 30 November 2018).
- Cubasch, U.; Wuebbles, D.; Chen, D.; Facchini, M.C.; Frame, D.; Mahowald, N.; Winther, J.G. Introduction. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- IPCC (Intergovernmental Panel on Climate Change). Towards New Scenarios for Analysis of Emissions, Climate Change, Impacts, and Response Strategies. IPCC Expert Meeting Report 19–21. September, 2007 Noordwijkerhout, The Netherlands. Technical Summary; IPCC: Geneva, Switzerland, 2007; p. 25. [Google Scholar]
- Van Vuuren, D.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.; Kram, T.; Krey, V.; Lamarque, J.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; Van Vuuren, D.P.; Carter, T.R.; Emori, S.; Kainuma, M.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Ayoade, J. Spatial and seasonal patterns of physiologic comfort in Nigeria. Theor. Appl. Climatol. 1978, 26, 319–337. [Google Scholar] [CrossRef]
- SpohrNedel, A.; Teixeira Gonçalves, F.L.; Macedo Junior, C.; Alves Cardoso, M.R. Climatology of the human thermal comfort on Sao Paulo metropolitan area, Brazil: Indoors and outdoors. Rev. Bras. Geofísica 2015, 33, 185–204. [Google Scholar]
- Al Abadla, Z.; Robaa, S.M.; Abdel Wahab, M.M. Application of outdoor human thermal indices in nablus, Palestine. Glob. J. Adv. Res. 2018, 5, 190–196. [Google Scholar]
- Wu, J.; Gao, X.; Giorgi, F.; Chen, D. Changes of effective temperature and cold/hot days in late decades over China based on a high resolution gridded observation dataset. Int. J. Climatol. 2017. [Google Scholar] [CrossRef]
- Gregorczuk, M.; Cena, K. Distribution of effective temperature over the surface of the earth. Int. J. Biometeorol. 1967, 11, 145–149. [Google Scholar] [CrossRef]
- Eludoyin, O.M.; Adelekan, I.O. The physiologic climate of Nigeria. Int. J. Biometeorol. 2013, 57, 241–264. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Dwivedi, D.; Mohanty, B.P.; Lesikar, B.J. Estimating Escherichia coli loads in streams based on various physical, chemical, and biological factors. Water Resour. Res. 2013, 49, 2896–2906. [Google Scholar] [CrossRef] [PubMed]
- Ghanghermeh, A.; Roshan, G.R.; Al-Yahyai, S. The influence of Atlantic-Eurasian teleconnection patterns on temperature regimes in South Caspian Sea coastal areas: A study of Golestan Province, North Iran. Pollution 2015, 1, 67–83. [Google Scholar]
- Arora, B.; Wainwright, H.M.; Dwivedi, D.; Vaughn, L.J.S.; Curtis, J.B.; Torn, M.S.; Dafflon, B.; Hubbard, S.S. Evaluating Temporal Controls on Greenhouse Gas (GHG) Fluxes in an Arctic Tundra Environment: An Entropy-Based Approach. Sci. Total Environ. 2019. [Google Scholar] [CrossRef] [PubMed]
- Arora, B.; Dwivedi, D.; Hubbard, S.S.; Steefel, C.I.; Williams, K.H. Identifying geochemical hot moments and their controls on a contaminated river-floodplain system using wavelet and entropy approaches. Environ. Model. Softw. 2016. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Batty, M. Urban density and entropy functions. J. Cybern. 1974, 4, 41–55. [Google Scholar] [CrossRef]
- Batty, M.; Morphet, R.; Masucci, P.; Stanilov, K. Entropy, complexity, and spatial information. J. Geogr. Syst. 2014, 16, 363–385. [Google Scholar] [CrossRef] [PubMed]
- Tucek, P.; Paszto, V.; Vozenilek, V. Regular use of entropy for studying dissimilar geographical phenomena. Geografie 2009, 114, 117–129. [Google Scholar]
- Roshan, G.; Negahban, S. Modeling of the effects of climate change on rainy and gully erosion potential of Kor-chamriz watershed in Fars province. Model. Earth Syst. Environ. 2015, 1, 26. [Google Scholar] [CrossRef]
- Ghanghermeh, A.A.; Roshan, G.; Shahkooeei, E. Evaluation of the effect of Siberia’s high pressure extension on daily minimum temperature changes in Iran. Model. Earth Syst. Environ. 2015, 1, 20. [Google Scholar] [CrossRef]
- Tisseuil, C.; Roshan, G.; Nasrabadi, T.; Asadpour, G.A. Statistical modeling of future lake level under climatic conditions, case study of Urmia Lake (Iran). Int. J. Environ. Res. 2012, 7, 69–80. [Google Scholar]
- Nik, V.; Kalagasidis, A.S. Impact study of the climate change on the energy performance of the building stock in Stockholm considering four climate uncertainties. Build. Environ. 2013, 60, 291–304. [Google Scholar] [CrossRef]
- Barbosa, R.; Vicente, R.; Santos, R. Climate change and thermal comfort in Southern Europe housing: A case study from Lisbon. Build. Environ. 2015, 92, 440–451. [Google Scholar] [CrossRef]
- Jylhä, K.; Jokisalo, J.; Ruosteenoja, K.; Pilli-Sihvola, K.; Kalamees, T.; Seitola, T.; Drebs, A. Energy demand for the heating and cooling of residential houses in Finland in a changing climate. Energy Build. 2015, 99, 104–116. [Google Scholar] [CrossRef]
- Orosa, J.A.; Costa, A.M.; Roshan, G.R.; García-Bustelo, E.J. Wind turbines design corrections for next Galicia climatic conditions. Sci. Iran. 2017, 24, 926–932. [Google Scholar] [CrossRef]
- Wang, X.; Chen, D.; Ren, Z. Assessment of climate change impact on residential building heating and cooling energy requirement in Australia. Build. Environ. 2010, 45, 1663–1682. [Google Scholar] [CrossRef]






| Number of Row | Circulate Components | Number of Row | Circulate Components |
|---|---|---|---|
| 1 | zg = Geopotential Height | 42 | ra = Carbon Mass Flux into Atmosphere due to Autotrophic (Plant) Respiration on Land |
| 2 | wap = omega (=dp/dt) | 43 | psl = Sea Level Pressure |
| 3 | vo = Sea Water Y Velocity | 44 | ps = Surface Air Pressure |
| 4 | vas = Northward Near-Surface Wind | 45 | prw = Water Vapor Path |
| 5 | va = Northward Wind | 46 | prveg = Precipitation onto Canopy |
| 6 | uo = Sea Water X Velocity | 47 | prsn = Snowfall Flux |
| 7 | uas = Eastward Near-Surface Wind | 48 | prc = Convective Precipitation |
| 8 | ua = Eastward Wind | 49 | pr = Precipitation |
| 9 | tsl = Temperature of Soil | 50 | npp = Carbon Mass Flux out of Atmosphere due to Net Primary Production on Land |
| 10 | ts = Surface Temperature | 51 | nep = Net Carbon Mass Flux out of Atmosphere due to Net Ecosystem Productivity on Land. |
| 11 | transiy = Y-Component of Sea Ice Mass Transport | 52 | mrsos = Moisture in Upper Portion of Soil Column |
| 12 | transix = X-Component of Sea Ice Mass Transport | 53 | mrso = Total Soil Moisture Content |
| 13 | tran = Transpiration | 54 | mrros = Surface Runoff |
| 14 | tos = Sea Surface Temperature | 55 | mrso = Total Soil Moisture Content |
| 15 | thetao = Sea Water Potential Temperature | 56 | mrro = Total Runoff |
| 16 | tauv = Surface Downward Northward Wind Stress | 57 | mrlsl = Water Content of Soil Layer |
| 17 | tauu = Surface Downward Eastward Wind Stress | 58 | mrfso = Soil Frozen Water Content |
| 18 | tasmin = Daily Minimum Near-Surface Air Temperature | 59 | mc = Convective Mass Flux |
| 19 | tasmax = Daily Maximum Near-Surface Air Temperature | 60 | huss = Near-Surface Specific Humidity |
| 20 | tas = Near-Surface Air Temperature | 61 | hus = Specific Humidity |
| 21 | ta = Air Temperature | 62 | hurs = Near-Surface Relative Humidity |
| 22 | sos = Sea Surface Salinity | 63 | hur = Relative Humidity |
| 23 | so = Sea Water Salinity | 64 | hfss = Surface Upward Sensible Heat Flux |
| 24 | snw = Surface Snow Amount | 65 | hfls = Surface Upward Latent Heat Flux |
| 25 | snm = Surface Snow Melt | 66 | gpp = Carbon Mass Flux out of Atmosphere due to Gross Primary Production on Land |
| 26 | snd = Snow Depth | 67 | evspsblveg = Evaporation from Canopy |
| 27 | snc = Snow Area Fraction | 68 | evspsblsoi = Water Evaporation from Soil |
| 28 | sit = Sea Ice Thickness | 69 | evspsbl = Evaporation |
| 29 | sic = Sea Ice Area Fraction | 70 | evap = Water Evaporation Flux from Sea Ice |
| 30 | sfcWind = Near-Surface Wind Speed | 71 | clwvi = Condensed Water Path |
| 31 | sci = Fraction of Time Shallow Convection Occurs | 72 | clw = Mass Fraction of Cloud Liquid Water |
| 32 | sbl = Surface Snow and Ice Sublimation Flux | 73 | clt = Total Cloud Fraction |
| 33 | rtmt = Net Downward Flux at Top of Model | 74 | clivi = Ice Water Path |
| 34 | rsutcs = TOA Outgoing Clear-Sky Shortwave Radiation | 75 | cli = Mass Fraction of Cloud Ice |
| 35 | rsut = TOA Outgoing Shortwave Radiation | 76 | cl = Cloud Area Fraction |
| 36 | rsuscs = Surface Upwelling Clear-Sky Shortwave Radiation | 77 | ci = Fraction of Time Convection Occurs |
| 37 | rsus = Surface Upwelling Shortwave Radiation | 78 | cct = Air Pressure at Convective Cloud Top |
| 38 | rlus = Surface Upwelling Longwave Radiation | 79 | ccb = Air Pressure at Convective Cloud Base |
| 39 | rldscs = Surface Downwelling Clear-Sky Longwave Radiation | 80 | cSoil = Carbon Mass in Soil Pool |
| 40 | rlds = Surface Downwelling Longwave Radiation | 81 | baresoilFrac = Bare Soil Fraction |
| 41 | rh = Carbon Mass Flux into Atmosphere due to Heterotrophic Respiration on Land | - | - |
| Dry Temp at 3:00 GMT | Verification | Period | Mean | Max | Min |
|---|---|---|---|---|---|
| RMSE | Training | 1971–2000 | 2.049 | 2.899 | 1.680 |
| Testing | 2001–2010 | 2.026 | 2.597 | 1.557 | |
| Testing rcp4.5 | 2011–2014 | 2.067 | 2.689 | 1.646 | |
| Testing rcp8.5 | 2011–2014 | 2.094 | 2.982 | 1.787 | |
| R2 | Training | 1971–2000 | 0.941 | 0.963 | 0.872 |
| Testing | 2001–2010 | 0.943 | 0.958 | 0.914 | |
| Testing rcp4.5 | 2011–2014 | 0.948 | 0.962 | 0.917 | |
| Testing rcp8.5 | 2011–2014 | 0.941 | 0.949 | 0.905 | |
| BIAS | Training | 1971–2000 | 0.454 | 7.896 | −23.570 |
| Testing | 2001–2010 | 0.384 | 2.571 | −12.103 | |
| Testing rcp4.5 | 2011–2014 | 0.560 | 4.003 | −6.217 | |
| Testing rcp8.5 | 2011–2014 | 0.584 | 4.237 | −4.572 | |
| NS | Training | 1971–2000 | 0.941 | 0.963 | 0.872 |
| Testing | 2001–2010 | 0.939 | 0.957 | 0.908 | |
| Testing rcp4.5 | 2011–2014 | 0.938 | 0.959 | 0.886 | |
| Testing rcp8.5 | 2011–2014 | 0.937 | 0.948 | 0.895 |
| Dry Temp at 15:00 GMT | Verification | Period | Mean | Max | Min |
|---|---|---|---|---|---|
| RMSE | Training | 1971–2000 | 2.326 | 2.785 | 1.840 |
| Testing | 2001–2010 | 2.308 | 3.148 | 1.770 | |
| Testing rcp4.5 | 2011–2014 | 2.233 | 2.909 | 1.884 | |
| Testing rcp8.5 | 2011-–2014 | 2.248 | 2.990 | 1.934 | |
| R2 | Training | 1971–2000 | 0.946 | 0.962 | 0.903 |
| Testing | 2001–2010 | 0.949 | 0.961 | 0.910 | |
| Testing rcp4.5 | 2011–2014 | 0.956 | 0.968 | 0.901 | |
| Testing rcp8.5 | 2011–2014 | 0.956 | 0.964 | 0.903 | |
| BIAS | Training | 1971–2000 | 0.436 | 3.962 | 0.213 |
| Testing | 2001–2010 | 0.399 | 3.204 | 0.212 | |
| Testing rcp4.5 | 2011–2014 | 0.376 | 3.214 | 0.199 | |
| Testing rcp8.5 | 2011–2014 | 0.368 | 2.428 | 0.203 | |
| NS | Training | 1971–2000 | 0.946 | 0.962 | 0.903 |
| Testing | 2001–2010 | 0.944 | 0.961 | 0.896 | |
| Testing rcp4.5 | 2011–2014 | 0.953 | 0.965 | 0.896 | |
| Testing rcp8.5 | 2011–2014 | 0.953 | 0.963 | 0.896 |
| Wet Temp at 03:00 GMT | Verification | Period | Mean | Max | Min |
|---|---|---|---|---|---|
| RMSE | Training | 1971–2000 | 1.726 | 2.411 | 1.476 |
| Testing | 2001–2010 | 1.652 | 2.592 | 1.252 | |
| Testing rcp4.5 | 2011–2014 | 1.697 | 2.922 | 1.482 | |
| Testing rcp8.5 | 2011–2014 | 1.796 | 2.898 | 1.615 | |
| R2 | Training | 1971–2000 | 0.935 | 0.951 | 0.892 |
| Testing | 2001–2010 | 0.940 | 0.962 | 0.876 | |
| Testing rcp4.5 | 2011–2014 | 0.947 | 0.955 | 0.896 | |
| Testing rcp8.5 | 2011–2014 | 0.934 | 0.945 | 0.893 | |
| BIAS | Training | 1971–2000 | −0.690 | 12.134 | −73.193 |
| Testing | 2001–2010 | 0.595 | 9.786 | −4.044 | |
| Testing rcp4.5 | 2011–2014 | 0.558 | 6.502 | −9.196 | |
| Testing rcp8.5 | 2011–2014 | 0.619 | 7.649 | −10.444 | |
| NS | Training | 1971–2000 | 0.935 | 0.951 | 0.892 |
| Testing | 2001–2010 | 0.933 | 0.959 | 0.842 | |
| Testing rcp4.5 | 2011–2014 | 0.933 | 0.952 | 0.762 | |
| Testing rcp8.5 | 2011–2014 | 0.926 | 0.943 | 0.766 |
| Wet Temp at 15:00 GMT | Verification | Period | Mean | Max | Min |
|---|---|---|---|---|---|
| RMSE | Training | 1971–2000 | 1.848 | 2.515 | 1.522 |
| Testing | 2001–2010 | 1.808 | 3.199 | 1.525 | |
| Testing rcp4.5 | 2011–2014 | 2.028 | 4.813 | 1.672 | |
| Testing rcp8.5 | 2011–2014 | 1.942 | 4.875 | 1.579 | |
| R2 | Training | 1971–2000 | 0.928 | 0.947 | 0.888 |
| Testing | 2001–2010 | 0.938 | 0.954 | 0.862 | |
| Testing rcp4.5 | 2011–2014 | 0.946 | 0.960 | 0.906 | |
| Testing rcp8.5 | 2011–2014 | 0.939 | 0.952 | 0.907 | |
| BIAS | Training | 1971–2000 | 0.480 | 3.335 | 0.212 |
| Testing | 2001–2010 | 0.411 | 1.965 | 0.176 | |
| Testing rcp4.5 | 2011–2014 | 0.582 | 3.407 | 0.253 | |
| Testing rcp8.5 | 2011–2014 | 0.532 | 3.024 | 0.198 | |
| NS | Training | 1971–2000 | 0.928 | 0.947 | 0.888 |
| Testing | 2001–2010 | 0.924 | 0.944 | 0.759 | |
| Testing rcp4.5 | 2011–2014 | 0.905 | 0.945 | 0.337 | |
| Testing rcp8.5 | 2011–2014 | 0.914 | 0.943 | 0.320 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghanghermeh, A.; Roshan, G.; Orosa, J.A.; Costa, Á.M. Analysis and Comparison of Spatial–Temporal Entropy Variability of Tehran City Microclimate Based on Climate Change Scenarios. Entropy 2019, 21, 13. https://doi.org/10.3390/e21010013
Ghanghermeh A, Roshan G, Orosa JA, Costa ÁM. Analysis and Comparison of Spatial–Temporal Entropy Variability of Tehran City Microclimate Based on Climate Change Scenarios. Entropy. 2019; 21(1):13. https://doi.org/10.3390/e21010013
Chicago/Turabian StyleGhanghermeh, Abdolazim, Gholamreza Roshan, José A. Orosa, and Ángel M. Costa. 2019. "Analysis and Comparison of Spatial–Temporal Entropy Variability of Tehran City Microclimate Based on Climate Change Scenarios" Entropy 21, no. 1: 13. https://doi.org/10.3390/e21010013
APA StyleGhanghermeh, A., Roshan, G., Orosa, J. A., & Costa, Á. M. (2019). Analysis and Comparison of Spatial–Temporal Entropy Variability of Tehran City Microclimate Based on Climate Change Scenarios. Entropy, 21(1), 13. https://doi.org/10.3390/e21010013






