Non-Equilibrium Quantum Brain Dynamics: Super-Radiance and Equilibration in 2 + 1 Dimensions
Abstract
1. Introduction
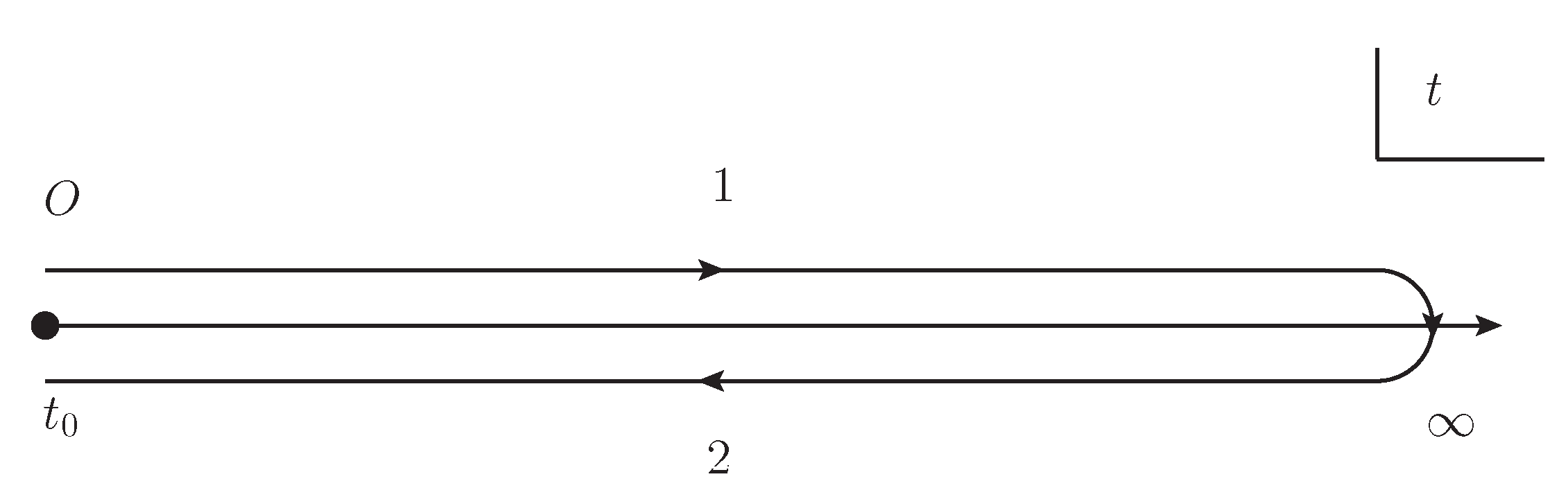
2. The Two-Particle-Irreducible Effective Action and Time Evolution Equations
3. Kinetic Entropy Current in the Kadanoff–Baym Equations and the H-Theorem
4. Time Evolution Equations in Spatially Homogeneous Systems and Conserved Energy
5. Dynamics of Coherent Fields
5.1. Super-Radiance
5.2. Higgs Mechanism and Tachyonic Instability
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Quantum Fluctuations in the Klein–Gordon Equations
References
- Day, J.J.; Sweatt, J.D. DNA methylation and memory formation. Nat. Neurosci. 2010, 13, 1319. [Google Scholar] [CrossRef] [PubMed]
- Adolphs, R. The unsolved problems of neuroscience. Trends Cogn. Sci. 2015, 19, 173–175. [Google Scholar] [CrossRef] [PubMed]
- Kukushkin, N.V.; Carew, T.J. Memory takes time. Neuron 2017, 95, 259–279. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jibu, M.; Yasue, K. Quantum Brain Dynamics and Consciousness; John Benjamins: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Vitiello, G. My Double Unveiled: The Dissipative Quantum Model of Brain; John Benjamins: Amsterdam, The Netherlands, 2001; Volume 32. [Google Scholar]
- Sabbadini, S.A.; Vitiello, G. Entanglement and Phase-Mediated Correlations in Quantum Field Theory. Application to Brain-Mind States. Appl. Sci. 2019, 9, 3203. [Google Scholar] [CrossRef]
- Lashley, K.S. Brain Mechanisms and Intelligence: A Quantitative Study of Injuries to the Brain; PsycBOOKS: Chicago, IL, USA, 1929. [Google Scholar]
- Pribram, K.H. Languages of the brain: Experimental paradoxes and principles in neuropsychology. Nerv. Ment. Dis. 1973, 157, 69–70. [Google Scholar]
- Pribram, K. Brain and Perception: Holonomy and Structure in Figural Processing; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1991. [Google Scholar]
- Umezawa, H. Advanced Field Theory: Micro, Macro, and Thermal Physics; AIP: College Park, MD, USA, 1995. [Google Scholar]
- Nambu, Y.; Lasinio, G.J. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 112, 345. [Google Scholar] [CrossRef]
- Goldstone, J. Field theories with «Superconductor» solutions. Il Nuovo Cim. (1955–1965) 1961, 19, 154–164. [Google Scholar] [CrossRef]
- Goldstone, J.; Salam, A.; Weinberg, S. Broken symmetries. Phys. Rev. 1962, 127, 965. [Google Scholar] [CrossRef]
- Ricciardi, L.M.; Umezawa, H. Brain and physics of many-body problems. Kybernetik 1967, 4, 44–48. [Google Scholar] [CrossRef]
- Stuart, C.; Takahashi, Y.; Umezawa, H. On the stability and non-local properties of memory. J. Theor. Biol. 1978, 71, 605–618. [Google Scholar] [CrossRef]
- Stuart, C.; Takahashi, Y.; Umezawa, H. Mixed-system brain dynamics: Neural memory as a macroscopic ordered state. Found. Phys. 1979, 9, 301–327. [Google Scholar] [CrossRef]
- Fröhlich, H. Bose condensation of strongly excited longitudinal electric modes. Phys. Lett. A 1968, 26, 402–403. [Google Scholar] [CrossRef]
- Fröhlich, H. Long-range coherence and energy storage in biological systems. Int. J. Quantum Chem. 1968, 2, 641–649. [Google Scholar] [CrossRef]
- Fröhlich, H. Long range coherence and the action of enzymes. Nature 1970, 228, 1093. [Google Scholar] [CrossRef]
- Fröhlich, H. Selective long range dispersion forces between large systems. Phys. Lett. A 1972, 39, 153–154. [Google Scholar] [CrossRef]
- Fröhlich, H. Evidence for Bose condensation-like excitation of coherent modes in biological systems. Phys. Lett. A 1975, 51, 21–22. [Google Scholar] [CrossRef]
- Fröhlich, H. Long-range coherence in biological systems. La Riv. Del Nuovo Cim. (1971–1977) 1977, 7, 399–418. [Google Scholar] [CrossRef]
- Davydov, A.; Kislukha, N. Solitons in One-Dimensional Molecular Chains. Phys. Status Solidi (B) 1976, 75, 735–742. [Google Scholar] [CrossRef]
- Tuszyński, J.; Paul, R.; Chatterjee, R.; Sreenivasan, S. Relationship between Fröhlich and Davydov models of biological order. Phys. Rev. A 1984, 30, 2666. [Google Scholar] [CrossRef]
- Del Giudice, E.; Doglia, S.; Milani, M.; Vitiello, G. Spontaneous symmetry breakdown and boson condensation in biology. Phys. Lett. A 1983, 95, 508–510. [Google Scholar] [CrossRef]
- Del Giudice, E.; Doglia, S.; Milani, M.; Vitiello, G. A quantum field theoretical approach to the collective behaviour of biological systems. Nucl. Phys. B 1985, 251, 375–400. [Google Scholar] [CrossRef]
- Del Giudice, E.; Preparata, G.; Vitiello, G. Water as a free electric dipole laser. Phys. Rev. Lett. 1988, 61, 1085. [Google Scholar] [CrossRef] [PubMed]
- Del Giudice, E.; Smith, C.; Vitiello, G. Magnetic Flux Quantization and Josephson Systems. Phys. Scr. 1989, 40, 786–791. [Google Scholar] [CrossRef]
- Jibu, M.; Yasue, K. A physical picture of Umezawa’s quantum brain dynamics. Cybern. Syst. Res. 1992, 92, 797–804. [Google Scholar]
- Jibu, M.; Yasue, K. Intracellular quantum signal transfer in Umezawa’s quantum brain dynamics. Cybern. Syst. 1993, 24, 1–7. [Google Scholar] [CrossRef]
- Jibu, M.; Hagan, S.; Hameroff, S.R.; Pribram, K.H.; Yasue, K. Quantum optical coherence in cytoskeletal microtubules: Implications for brain function. Biosystems 1994, 32, 195–209. [Google Scholar] [CrossRef]
- Jibu, M.; Yasue, K. What is mind?- Quantum field theory of evanescent photons in brain as quantum theory of consciousness. INF 1997, 21, 471–490. [Google Scholar]
- Dicke, R.H. Coherence in spontaneous radiation processes. Phys. Rev. 1954, 93, 99. [Google Scholar] [CrossRef]
- Gross, M.; Haroche, S. Superradiance: An essay on the theory of collective spontaneous emission. Phys. Rep. 1982, 93, 301–396. [Google Scholar] [CrossRef]
- Preparata, G. Quantum field theory of superradiance. Probl. Fundam. Mod. Phys. 1990, 303. [Google Scholar] [CrossRef]
- Preparata, G. QED Coherence in Matter; World Scientific: Singapore, 1995. [Google Scholar]
- Enz, C.P. On Preparata’s theory of a superradiant phase transition. Helv. Phys. Acta 1997, 70, 141–153. [Google Scholar]
- Vitiello, G. Dissipation and memory capacity in the quantum brain model. Int. J. Mod. Phys. 1995, 9, 973–989. [Google Scholar] [CrossRef]
- Vitiello, G. Classical chaotic trajectories in quantum field theory. Int. J. Mod. Phys. B 2004, 18, 785–792. [Google Scholar] [CrossRef]
- Zheng, J.M.; Pollack, G.H. Long-range forces extending from polymer-gel surfaces. Phys. Rev. E 2003, 68, 031408. [Google Scholar] [CrossRef] [PubMed]
- Del Giudice, E.; Voeikov, V.; Tedeschi, A.; Vitiello, G. The origin and the special role of coherent water in living systems. F. Cell 2014, 95–111. [Google Scholar] [CrossRef]
- Tegmark, M. Importance of quantum decoherence in brain processes. Phys. Rev. E 2000, 61, 4194. [Google Scholar] [CrossRef]
- Craddock, T.J.; Tuszynski, J.A.; Hameroff, S. Cytoskeletal signaling: Is memory encoded in microtubule lattices by CaMKII phosphorylation? PLoS Comput. Biol. 2012, 8, e1002421. [Google Scholar] [CrossRef]
- Baym, G.; Kadanoff, L.P. Conservation laws and correlation functions. Phys. Rev. 1961, 124, 287. [Google Scholar] [CrossRef]
- Kadanoff, L.P.; Baym, G. Quantum Statistical Mechanics: Green’s Function Methods in Equilibrium Problems; WA Benjamin: Los Angeles, CA, USA, 1962. [Google Scholar]
- Baym, G.; Kadanoff, L.P. Self-Consistent Approximations in Many-Body Systems. Phys. Rev. 1962, 127, 1391. [Google Scholar] [CrossRef]
- Cornwall, J.M.; Jackiw, R.; Tomboulis, E. Effective action for composite operators. Phys. Rev. D 1974, 10, 2428. [Google Scholar] [CrossRef]
- Niemi, A.J.; Semenoff, G.W. Finite-temperature quantum field theory in Minkowski space. Ann. Phys. 1984, 152, 105–129. [Google Scholar] [CrossRef]
- Calzetta, E.; Hu, B.L. Nonequilibrium quantum fields: Closed-time-path effective action, Wigner function, and Boltzmann equation. Phys. Rev. D 1988, 37, 2878. [Google Scholar] [CrossRef] [PubMed]
- Schwinger, J. Brownian motion of a quantum oscillator. J. Math. Phys. 1961, 2, 407–432. [Google Scholar] [CrossRef]
- Keldysh, L.V. Diagram technique for nonequilibrium processes. Sov. Phys. Jetp. 1965, 20, 1018–1026. [Google Scholar]
- Kluberg-Stern, H.; Zuber, J. Renormalization of non-Abelian gauge theories in a background-field gauge. I. Green’s functions. Phys. Rev. D 1975, 12, 482. [Google Scholar] [CrossRef]
- Abbott, L.F. The background field method beyond one loop. Nucl. Phys. B. 1981, 185, 189–203. [Google Scholar] [CrossRef]
- Abbott, L.F. Introduction to the background field method. Acta Phys. Pol. B. 1981, 13, 33–50. [Google Scholar]
- Wang, Q.; Redlich, K.; Stöcker, H.; Greiner, W. From the Dyson–Schwinger to the transport equation in the background field gauge of QCD. Nucl. Phys. A 2003, 714, 293–334. [Google Scholar] [CrossRef]
- Ivanov, Y.B.; Knoll, J.; Voskresensky, D. Resonance transport and kinetic entropy. Nucl. Phys. A 2000, 672, 313–356. [Google Scholar] [CrossRef]
- Kita, T. Entropy in nonequilibrium statistical mechanics. J. Phys. Soc. Jpn. 2006, 75, 114005. [Google Scholar] [CrossRef]
- Nishiyama, A. Entropy production in 2D λϕ4 theory in the Kadanoff–Baym approach. Nucl. Phys. A 2010, 832, 289–313. [Google Scholar] [CrossRef][Green Version]
- Nishiyama, A.; Tuszynski, J.A. Non-Equilibrium ϕ4 in open systems as a toy model of quantum field theory of the brain. Ann. Phys. 2018, 398, 214. [Google Scholar] [CrossRef]
- Myöhänen, P.; Stan, A.; Stefanucci, G.; van Leeuwen, R. A many-body approach to quantum transport dynamics: Initial correlations and memory effects. EPL (Europhys. Lett.) 2008, 84, 67001. [Google Scholar] [CrossRef]
- Myöhänen, P.; Stan, A.; Stefanucci, G.; Van Leeuwen, R. Kadanoff-Baym approach to quantum transport through interacting nanoscale systems: From the transient to the steady-state regime. Phys. Rev. B 2009, 80, 115107. [Google Scholar] [CrossRef]
- Wang, J.S.; Agarwalla, B.K.; Li, H.; Thingna, J. Nonequilibrium Green’s function method for quantum thermal transport. Front. Phys. 2014, 9, 673–697. [Google Scholar] [CrossRef]
- Dražić, M.S.; Cerovski, V.; Zikic, R. Theory of time-dependent nonequilibrium transport through a single molecule in a nonorthogonal basis set. Int. J. Quantum Chem. 2017, 117, 57–73. [Google Scholar] [CrossRef]
- Stratonovich, R.L. Gauge Invariant Generalization of Wigner Distribution. Dok. Akad. Nauk SSSR 1956, 109, 72–75. [Google Scholar]
- Fujita, S. Introduction to Non-Equilibrium Quantum Statistical Mechanics; Krieger Pub Co: Malabar, FL, USA, 1966. [Google Scholar]
- Groenewold, H.J. On the Principles of Elementary Quantum Mechanics; Springer: The Netherlands, 1946; Volume 12, pp. 1–56. [Google Scholar]
- Moyal, J.E. Quantum mechanics as a statistical theory. Math. Proc. Camb. Philos. Soc. 1949, 45, 99–124. [Google Scholar] [CrossRef]
- Knoll, J.; Ivanov, Y.B.; Voskresensky, D.N. Exact conservation laws of the gradient expanded Kadanoff–Baym equations. Ann. Phys. 2001, 293, 126–146. [Google Scholar] [CrossRef]
- Ivanov, Y.B.; Knoll, J.; Voskresensky, D. Self-consistent approach to off-shell transport. Phys. At. Nucl. 2003, 66, 1902–1920. [Google Scholar] [CrossRef][Green Version]
- Bonifacio, R.; Preparata, G. Coherent spontaneous emission. Phys. Rev. A 1970, 2, 336. [Google Scholar] [CrossRef]
- Benedict, M.G. Super-Radiance: Multiatomic Coherent Emission; Routledge: London, UK, 2018. [Google Scholar]
- Nishiyama, A.; Tuszynski, J.A. Nonequilibrium quantum electrodynamics: Entropy production during equilibration. Int. J. Mod. Phys. B 2018, 32, 1850265. [Google Scholar] [CrossRef]
- Nishiyama, A.; Tuszynski, J.A. Non-Equilibrium ϕ4 theory for networks: Towards memory formations with quantum brain dynamics. J. Phys. Commun. 2019, 3, 055020. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nishiyama, A.; Tanaka, S.; Tuszynski, J.A. Non-Equilibrium Quantum Brain Dynamics: Super-Radiance and Equilibration in 2 + 1 Dimensions. Entropy 2019, 21, 1066. https://doi.org/10.3390/e21111066
Nishiyama A, Tanaka S, Tuszynski JA. Non-Equilibrium Quantum Brain Dynamics: Super-Radiance and Equilibration in 2 + 1 Dimensions. Entropy. 2019; 21(11):1066. https://doi.org/10.3390/e21111066
Chicago/Turabian StyleNishiyama, Akihiro, Shigenori Tanaka, and Jack A. Tuszynski. 2019. "Non-Equilibrium Quantum Brain Dynamics: Super-Radiance and Equilibration in 2 + 1 Dimensions" Entropy 21, no. 11: 1066. https://doi.org/10.3390/e21111066
APA StyleNishiyama, A., Tanaka, S., & Tuszynski, J. A. (2019). Non-Equilibrium Quantum Brain Dynamics: Super-Radiance and Equilibration in 2 + 1 Dimensions. Entropy, 21(11), 1066. https://doi.org/10.3390/e21111066





