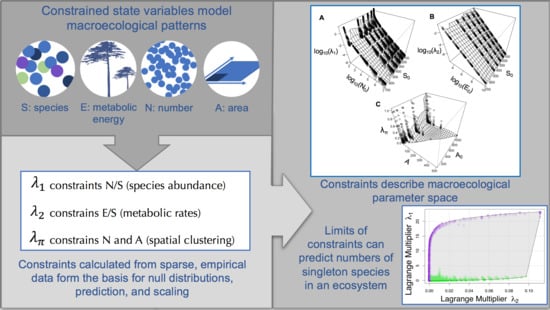
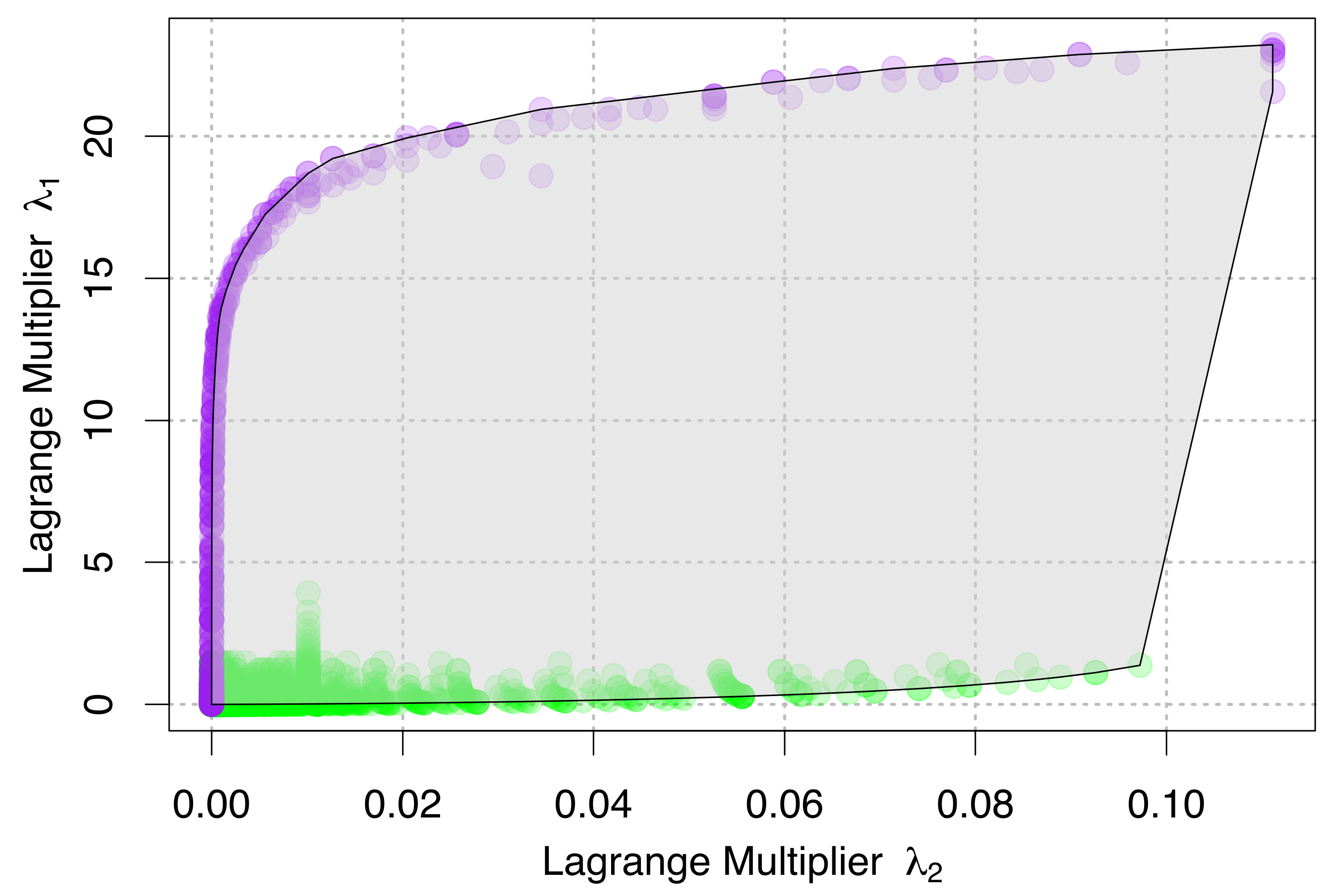
Derivations of the Core Functions of the Maximum Entropy Theory of Ecology
Abstract
1. The Maximum Entropy Theory of Ecology
2. Information Entropy Maximization: A Primer
2.1. Writing Down the Constraints
2.2. The Method of Lagrange Multipliers and Optimization
3. The Structure of METE
3.1. A State Variable Theory
3.2. The Spatial Structure Function
3.3. The Ecosystem Structure Function
4. Relationships between State Variables and Lagrange Multipliers
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Examples of Applying MaxEnt to Known Distributions
Appendix A.1. A Fair Three-Sided Die Constrained by the Mean
Appendix A.2. A Fair Three-Sided die Constrained by the Standard Deviation
Appendix A.3. The Gaussian/Normal Distribution, or Using n and n2 as “Constraint Functions”
Appendix A.4. The Log-Normal Distribution, Constraining log(n) and log2(n)
Appendix B. Approximations in the Original Version of METE
Appendix B.1. Approximation 1: ∑e−nβ ≈ 1/β
Appendix B.2. Approximation 2: ∑e−nβ/n ≈ log(1/β)
References
- Brown, J.H. Macroecology; University of Chicago Press: Chicago, IL, USA, 1995. [Google Scholar]
- McGill, B.J.; Etienne, R.S.; Gray, J.S.; Alonso, D.; Anderson, M.J.; Benecha, H.K.; Dornelas, M.; Enquist, B.J.; Green, J.L.; He, F.; et al. Species abundance distributions: Moving beyond single prediction theories to integration within an ecological framework. Ecol. Lett. 2007, 10, 995–1015. [Google Scholar] [CrossRef] [PubMed]
- Yoda, K. Self-thinning in overcrowded pure stands under cultivated and natural conditions (Intraspecific competition among higher plants. XI). J. Inst. Polytech. Osaka 1963, 14, 107–129. [Google Scholar]
- Damuth, J. Population density and body size in mammals. Nature 1981, 290, 699. [Google Scholar] [CrossRef]
- Enquist, B.J.; Niklas, K.J. Invariant scaling relations across tree-dominated communities. Nature 2001, 410, 655. [Google Scholar] [CrossRef] [PubMed]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Gillooly, J.F.; Brown, J.H.; West, G.B.; Savage, V.M.; Charnov, E.L. Effects of size and temperature on metabolic rate. Science 2001, 293, 2248–2251. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.H.; Gillooly, J.F.; Allen, A.P.; Savage, V.M.; West, G.B. Toward a metabolic theory of ecology. Ecology 2004, 85, 1771–1789. [Google Scholar] [CrossRef]
- Harte, J.; Zillio, T.; Conlisk, E.; Smith, A.B. Maximum entropy and the state-variable approach to macroecology. Ecology 2008, 89, 2700–2711. [Google Scholar] [CrossRef]
- Harte, J. Maximum Entropy and Ecology: A Theory of Abundance, Distribution, and Energetics; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Harte, J.; Newman, E.A. Maximum information entropy: A foundation for ecological theory. Trends Ecol. Evol. 2014, 29, 384–389. [Google Scholar] [CrossRef]
- Harte, J.; Smith, A.B.; Storch, D. Biodiversity scales from plots to biomes with a universal species–area curve. Ecol. Lett. 2009, 12, 789–797. [Google Scholar] [CrossRef]
- White, E.P.; Thibault, K.M.; Xiao, X. Characterizing species abundance distributions across taxa and ecosystems using a simple maximum entropy model. Ecology 2012, 93, 1772–1778. [Google Scholar] [CrossRef] [PubMed]
- Newman, E.A.; Harte, M.E.; Lowell, N.; Wilber, M.; Harte, J. Empirical tests of within-and across-species energetics in a diverse plant community. Ecology 2014, 95, 2815–2825. [Google Scholar] [CrossRef]
- Harte, J.; Kitzes, J. Inferring regional-scale species diversity from small-plot censuses. PloS ONE 2015, 10, e0117527. [Google Scholar] [CrossRef] [PubMed]
- McGlinn, D.; Xiao, X.; Kitzes, J.; White, E.P. Exploring the spatially explicit predictions of the Maximum Entropy Theory of Ecology. Glob. Ecol. Biogeogr. 2015, 24, 675–684. [Google Scholar] [CrossRef]
- Wilber, M.Q.; Kitzes, J.; Harte, J. Scale collapse and the emergence of the power law species–area relationship. Glob. Ecol. Biogeogr. 2015, 24, 883–895. [Google Scholar] [CrossRef]
- Xiao, X.; McGlinn, D.J.; White, E.P. A strong test of the maximum entropy theory of ecology. Am. Nat. 2015, 185, E70–E80. [Google Scholar] [CrossRef] [PubMed]
- Harte, J.; Newman, E.A.; Rominger, A.J. Metabolic partitioning across individuals in ecological communities. Glob. Ecol. Biogeogr. 2017, 26, 993–997. [Google Scholar] [CrossRef]
- Shoemaker, W.R.; Locey, K.J.; Lennon, J.T. A macroecological theory of microbial biodiversity. Nat. Ecol. Evol. 2017, 1, 0107. [Google Scholar] [CrossRef]
- Favretti, M. Remarks on the maximum entropy principle with application to the maximum entropy theory of ecology. Entropy 2017, 20, 11. [Google Scholar] [CrossRef]
- Harte, J. Maximum Entropy and Theory Construction: A Reply to Favretti. Entropy 2018, 20, 285. [Google Scholar] [CrossRef]
- Favretti, M. Maximum Entropy Theory of Ecology: A Reply to Harte. Entropy 2018, 20, 308. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620. [Google Scholar] [CrossRef]
- Haegeman, B.; Etienne, R.S. Entropy maximization and the spatial distribution of species. Am. Nat. 2010, 175, E74–E90. [Google Scholar] [CrossRef] [PubMed]
- McGill, B.J. The what, how and why of doing macroecology. Glob. Ecol. Biogeogr. 2019, 28, 6–17. [Google Scholar] [CrossRef]
- Hubbell, S.P. The Unified Neutral Theory of Biodiversity and Biogeography (MPB-32); Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Harte, J.; Rominger, A.; Zhang, W. Integrating macroecological metrics and community taxonomic structure. Ecol. Lett. 2015, 18, 1068–1077. [Google Scholar] [CrossRef]
- Shipley, B. Limitations of entropy maximization in ecology: A reply to Haegeman and Loreau. Oikos 2009, 118, 152–159. [Google Scholar] [CrossRef]
- Mayr, E. The biological species concept. In Species Concepts and Phylogenetic Theory: A Debate; Columbia University Press: New York, NY, USA, 2000; pp. 17–29. [Google Scholar]
- Harte, J.; Kitzes, J.; Newman, E.A.; Rominger, A.J. Taxon Categories and the Universal Species-Area Relationship: (A Comment on Šizling et al.,“Between Geometry and Biology: The Problem of Universality of the Species-Area Relationship”). Am. Nat. 2013, 181, 282–287. [Google Scholar] [CrossRef]
- Shipley, B.; Vile, D.; Garnier, É. From plant traits to plant communities: A statistical mechanistic approach to biodiversity. Science 2006, 314, 812–814. [Google Scholar] [CrossRef]
- Haegeman, B.; Loreau, M. Limitations of entropy maximization in ecology. Oikos 2008, 117, 1700–1710. [Google Scholar] [CrossRef]
- Haegeman, B.; Loreau, M. Trivial and non-trivial applications of entropy maximization in ecology: A reply to Shipley. Oikos 2009, 118, 1270–1278. [Google Scholar] [CrossRef]
- Pueyo, S.; He, F.; Zillio, T. The maximum entropy formalism and the idiosyncratic theory of biodiversity. Ecol. Lett. 2007, 10, 1017–1028. [Google Scholar] [CrossRef] [PubMed]
- Banavar, J.; Maritan, A. The maximum relative entropy principle. arXiv 2007, arXiv:0703622. [Google Scholar]
- Dewar, R.C.; Porté, A. Statistical mechanics unifies different ecological patterns. J. Theor. Biol. 2008, 251, 389–403. [Google Scholar] [CrossRef] [PubMed]
- Dewar, R. Maximum entropy production as an inference algorithm that translates physical assumptions into macroscopic predictions: Don’t shoot the messenger. Entropy 2009, 11, 931–944. [Google Scholar] [CrossRef]
- Shipley, B. From Plant Traits to Vegetation Structure: Chance and Selection in the Assembly of Ecological Communities; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- He, F. Maximum entropy, logistic regression, and species abundance. Oikos 2010, 119, 578–582. [Google Scholar] [CrossRef]
- McGill, B.J. Towards a unification of unified theories of biodiversity. Ecol. Lett. 2010, 13, 627–642. [Google Scholar] [CrossRef]
- Frank, S.A. Measurement scale in maximum entropy models of species abundance. J. Evol. Biol. 2011, 24, 485–496. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Harte, J. Population dynamics and competitive outcome derive from resource allocation statistics: The governing influence of the distinguishability of individuals. Theor. Popul. Biol. 2015, 105, 53–63. [Google Scholar] [CrossRef]
- Bertram, J.; Newman, E.A.; Dewar, R. Maximum entropy models elucidate the contribution of metabolic traits to patterns of community assembly. bioRxiv 2019. [Google Scholar] [CrossRef]
- Newman, E.A.; Wilber, M.Q.; Kopper, K.E.; Moritz, M.A.; Falk, D.A.; McKenzie, D.; Harte, J. Disturbance macroecology: Integrating disturbance ecology and macroecology in different-age post-fire stands of a closed-cone pine forest as a case study. bioRxiv 2018. [Google Scholar] [CrossRef]
- Rominger, A.J.; Merow, C. meteR: An r package for testing the maximum entropy theory of ecology. Methods Ecol. Evol. 2017, 8, 241–247. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Bertram, J. Entropy-Related Principles for Non-Equilibrium Systems: Theoretical Foundations and Applications to Ecology and Fluid Dynamics. Ph.D. Thesis, Australian National University, Canberra, Australia, 2015. [Google Scholar]
- Kapur, J.N. Maximum-Entropy Models in Science and Engineering; John Wiley & Sons: Hoboken, NY, USA, 1989. [Google Scholar]
- Enquist, B.J.; Norberg, J.; Bonser, S.P.; Violle, C.; Webb, C.T.; Henderson, A.; Sloat, L.L.; Savage, V.M. Scaling from traits to ecosystems: Developing a general trait driver theory via integrating trait-based and metabolic scaling theories. In Advances in Ecological Research; Elsevier: Amsterdam, The Netherlands, 2015; Volume 52, pp. 249–318. [Google Scholar]
- Wieczynski, D.J.; Boyle, B.; Buzzard, V.; Duran, S.M.; Henderson, A.N.; Hulshof, C.M.; Kerkhoff, A.J.; McCarthy, M.C.; Michaletz, S.T.; Swenson, N.G.; et al. Climate shapes and shifts functional biodiversity in forests worldwide. Proc. Natl. Acad. Sci. USA 2019, 116, 587–592. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brummer, A.B.; Newman, E.A. Derivations of the Core Functions of the Maximum Entropy Theory of Ecology. Entropy 2019, 21, 712. https://doi.org/10.3390/e21070712
Brummer AB, Newman EA. Derivations of the Core Functions of the Maximum Entropy Theory of Ecology. Entropy. 2019; 21(7):712. https://doi.org/10.3390/e21070712
Chicago/Turabian StyleBrummer, Alexander B., and Erica A. Newman. 2019. "Derivations of the Core Functions of the Maximum Entropy Theory of Ecology" Entropy 21, no. 7: 712. https://doi.org/10.3390/e21070712
APA StyleBrummer, A. B., & Newman, E. A. (2019). Derivations of the Core Functions of the Maximum Entropy Theory of Ecology. Entropy, 21(7), 712. https://doi.org/10.3390/e21070712