Sending-or-Not-Sending Twin-Field Quantum Key Distribution with Light Source Monitoring
Abstract
:1. Introduction
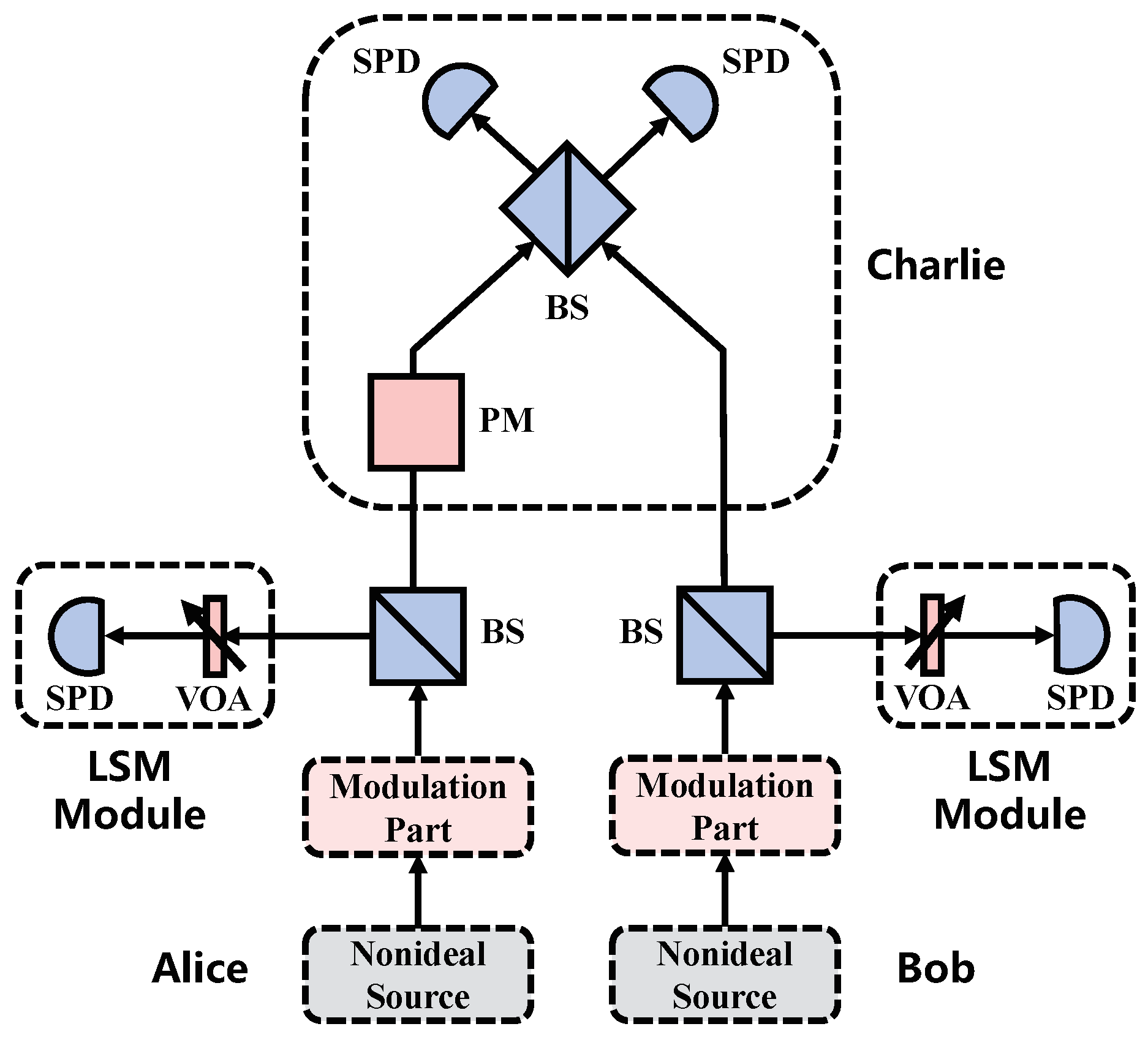
2. SNS Protocol with LSM
2.1. Security Analysis under UPC
Secret Key Rate
2.2. Parameters Estimation with LSM
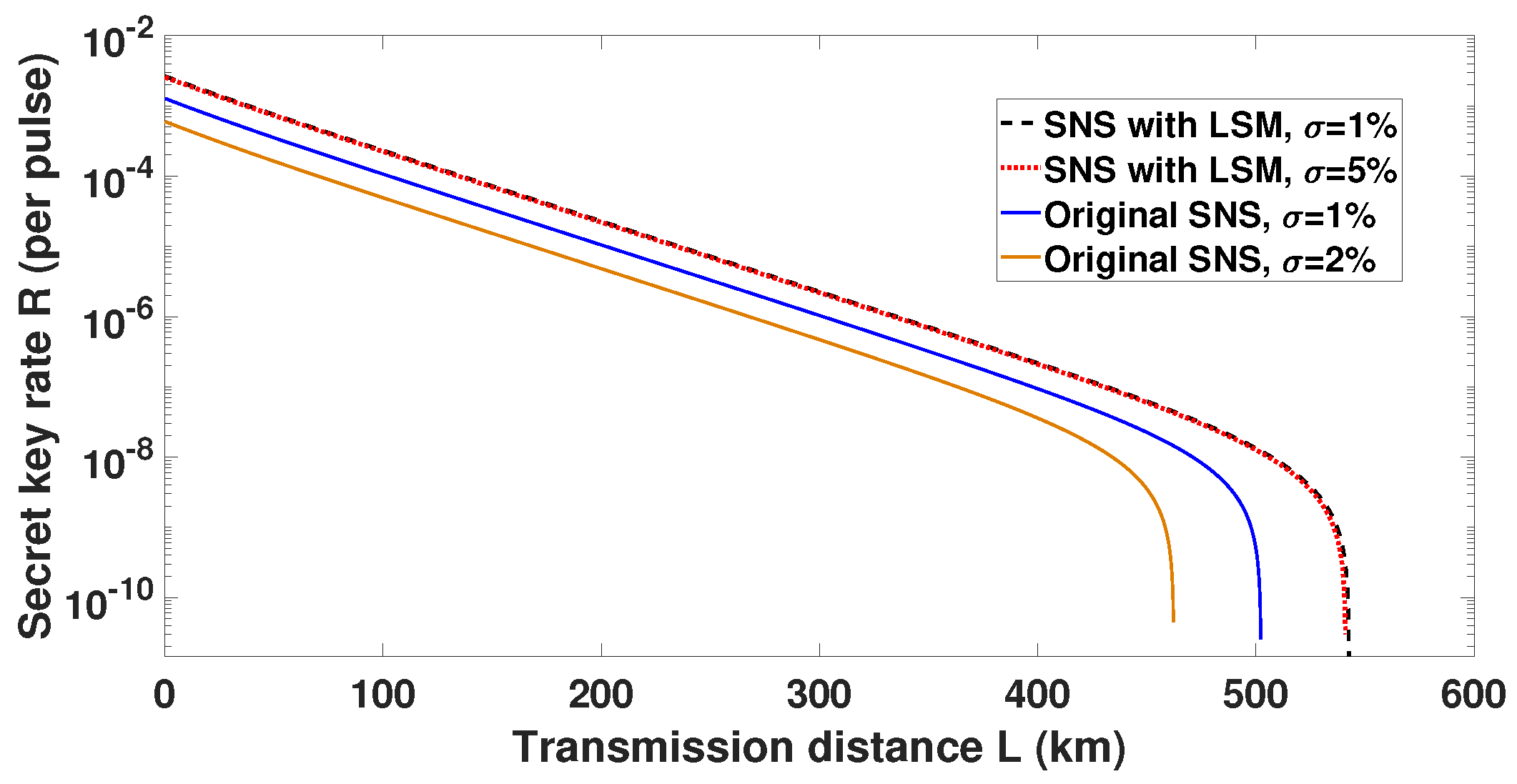
3. Performance with Numerical Simulation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Convex Form of under UPC
References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef] [Green Version]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.-K.; Curty, M.; Tamaki, K. Secure quantum key distribution. Nat. Photonics 2014, 8, 595–604. [Google Scholar] [CrossRef] [Green Version]
- Pirandola, S.; Vitali, D.; Tombesi, P.; Lloyd, S. Macroscopic entanglement by entanglement swapping. Phys. Rev. Lett. 2006, 97, 150403. [Google Scholar] [CrossRef] [Green Version]
- Braunstein, S.L.; Pirandola, S. Side-channel-free quantum key distribution. Phys. Rev. Lett. 2012, 108, 130502. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.-K.; Curty, M.; Qi, B. Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Curty, M.; Qi, B.; Lo, H.-K. Practical aspects of measurement-device-independent quantum key distribution. New J. Phys. 2013, 15, 113007. [Google Scholar] [CrossRef]
- Zhou, Y.-H.; Yu, Z.-W.; Wang, X.-B. Tightened estimation can improve the key rate of measurement-device-independent quantum key distribution by more than 100%. Phys. Rev. A 2014, 89, 052325. [Google Scholar] [CrossRef]
- Zhou, Y.-H.; Yu, Z.-W.; Wang, X.-B. Making the decoy-state measurement-device-independent quantum key distribution practically useful. Phys. Rev. A 2016, 93, 042324. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Razavi, M. Alternative schemes for measurement-device-independent quantum key distribution. Phys. Rev. A 2012, 86, 062319. [Google Scholar] [CrossRef] [Green Version]
- Rubenok, A.; Slater, J.A.; Chan, P.; Lucio-Martinez, I.; Tittel, W. Real-World Two-Photon Interference and Proof-of-Principle Quantum Key Distribution Immune to Detector Attacks. Phys. Rev. Lett. 2013, 111, 130501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, Y.; Yin, H.-L.; Chen, T.-Y.; Chen, Z.-B. Long-Distance Measurement-Device-Independent Multiparty Quantum Communication. Phys. Rev. Lett. 2015, 114, 090501. [Google Scholar] [CrossRef] [Green Version]
- Yin, H.-L.; Chen, T.-Y.; Yu, Z.-W.; Liu, H.; You, L.-X.; Zhou, Y.-H.; Chen, S.J.; Mao, Y.Q.; Huang, M.Q.; Zhang, W.J.; et al. Measurement-Device-Independent Quantum Key Distribution Over a 404 km Optical Fiber. Phys. Rev. Lett. 2016, 117, 190501. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.-C.; Xu, F.; Peng, X.; Guo, H. Continuous-variable measurement-device-independent quantum key distribution. Phys. Rev. A 2014, 89, 052301. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.-C.; Li, Z.; Yu, S.; Gu, W.; Peng, X.; Guo, H. Continuous-variable measurement-device-independent quantum key distribution using squeezed states. Phys. Rev. A 2014, 90, 052325. [Google Scholar] [CrossRef] [Green Version]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.L.; Lloyd, S.; Gehring, T.; Jacobsen, C.S.; Andersen, U.L. High-rate measurement-device-independent quantum cryptography. Nat. Photonics 2015, 9, 397. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Li, Z.; Yang, J.; Wei, S.; Su, Q.; Huang, W.; Zhang, Y.; Guo, H. High speed continuous variable source-independent quantum random number generation. Quantum Sci. Technol. 2019, 4, 025013. [Google Scholar] [CrossRef] [Green Version]
- Hwang, W.-Y. Quantum key distribution with high loss: Toward global secure communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar] [CrossRef] [Green Version]
- Lucamarini, M.; Yuan, Z.L.; Dynes, J.F.; Shields, A.J. Overcoming the rate-distance limit of quantum key distribution without quantum repeaters. Nature 2018, 557, 400–403. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.-B.; Yu, Z.-W.; Hu, X.-L. Twin-field quantum key distribution with large misalignment error. Phys. Rev. A 2018, 98, 062323. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Zeng, P.; Zhou, H. Phase-Matching Quantum Key Distribution. Phys. Rev. X 2018, 8, 031043. [Google Scholar] [CrossRef] [Green Version]
- Tamaki, K.; Lo, H.-K.; Wang, W.Y.; Lucamarini, M. Information theoretic security of quantum key distribution overcoming the repeaterless secret key capacity bound. arXiv 2018, arXiv:1805.05511. [Google Scholar]
- Curty, M.; Azuma, K.; Lo, H.-K. Simple security proof of twin-field type quantum key distribution protocol. NPJ Quantum Inform. 2019, 5, 64. [Google Scholar] [CrossRef]
- Grasselli, F.; Curty, M. Practical decoy-state method for twin-field quantum key distribution. New J. Phys. 2019, 21, 073001. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.-W.; Hu, X.-L.; Jiang, C.; Hu, H.; Wang, X.-B. Sending-or-not-sending twin-field quantum key distribution in practice. Sci. Rep. 2019, 9, 3080. [Google Scholar] [CrossRef] [Green Version]
- Minder, M.; Pittaluga, M.; Roberts, G.L.; Lucamarini, M.; Dynes, J.F.; Yuan, Z.L.; Shields, A.J. Experimental quantum key distribution beyond the repeaterless secret key capacity. Nat. Photonics 2019, 13, 334. [Google Scholar] [CrossRef]
- Wang, S.; He, D.-Y.; Yin, Z.-Q.; Lu, F.-Y.; Cui, C.-H.; Chen, W.; Zhou, Z.; Guo, G.-C.; Han, Z.-F. Beating the Fundamental Rate-Distance Limit in a Proof-of-Principle Quantum Key Distribution System. Phys. Rev. X 2019, 9, 021046. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.-B.; Hu, X.-L.; Yu, Z.-W. Effective Eavesdropping to Twin-Field Quantum Key Distribution. arXiv 2018, arXiv:1805.02272. [Google Scholar]
- Wang, X.-B. Decoy-state quantum key distribution with large random errors of light intensity. Phys. Rev. A 2007, 75, 052301. [Google Scholar] [CrossRef] [Green Version]
- Gisin, N.; Fasel, S.; Kraus, B.; Zbinden, H.; Ribordy, G. Trojan-horse attacks on quantum-key-distribution systems. Phys. Rev. A 2006, 73, 022320. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Qi, B.; Lo, H.-K. Quantum key distribution with an unknown and untrusted source. Phys. Rev. A 2008, 77, 052327. [Google Scholar] [CrossRef] [Green Version]
- Peng, X.; Jiang, H.; Xu, B.; Ma, X.; Guo, H. Experimental quantum-key distribution with an untrusted source. Opt. Lett. 2008, 33, 2077–2079. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, X.; Xu, B.; Guo, H. Passive-scheme analysis for solving the untrusted source problem in quantum key distribution. Phys. Rev. A 2010, 81, 042320. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Peng, X.; Guo, H. Passive scheme with a photon-number-resolving detector for monitoring the untrusted source in a plug-and-play quantum-key-distribution system. Phys. Rev. A 2010, 82, 042301. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Li, Z.; Qiao, Y.; Chen, Z.; Peng, X.; Guo, H. Light Source Monitoring in Quantum Key Distribution With Single-Photon Detector at Room Temperature. IEEE J. Quantum Electron. 2018, 54, 9300110. [Google Scholar] [CrossRef] [Green Version]
- Qiao, Y.; Wang, G.; Li, Z.; Xu, B.; Guo, H. Monitoring an untrusted light source with single-photon detectors in measurement-device-independent quantum key distribution. Phys. Rev. A 2019, 99, 052302. [Google Scholar] [CrossRef]
- Wang, X.-B.; Peng, C.-Z.; Zhang, J.; Yang, L.; Pan, J.-W. General theory of decoy-state quantum cryptography with source errors. Phys. Rev. A 2008, 77, 042311. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Qi, B.; Lo, H.-K.; Qian, L. Security analysis of an untrusted source for quantum key distribution: passive approach. New J. Phys. 2010, 12, 023024. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, Y.; Zhou, Z.; Chen, W.; Han, Z.; Guo, G. Experimental demonstration of counteracting imperfect sources in a practical one-way quantum-key-distribution system. Phys. Rev. A 2009, 80, 062309. [Google Scholar] [CrossRef]

| f | ||||
|---|---|---|---|---|
| f | ||||
|---|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, Y.; Chen, Z.; Zhang, Y.; Xu, B.; Guo, H. Sending-or-Not-Sending Twin-Field Quantum Key Distribution with Light Source Monitoring. Entropy 2020, 22, 36. https://doi.org/10.3390/e22010036
Qiao Y, Chen Z, Zhang Y, Xu B, Guo H. Sending-or-Not-Sending Twin-Field Quantum Key Distribution with Light Source Monitoring. Entropy. 2020; 22(1):36. https://doi.org/10.3390/e22010036
Chicago/Turabian StyleQiao, Yucheng, Ziyang Chen, Yichen Zhang, Bingjie Xu, and Hong Guo. 2020. "Sending-or-Not-Sending Twin-Field Quantum Key Distribution with Light Source Monitoring" Entropy 22, no. 1: 36. https://doi.org/10.3390/e22010036





