Complexity Changes in the US and China’s Stock Markets: Differences, Causes, and Wider Social Implications
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
2.2.1. Lempel–Ziv (LZ) Complexity
2.2.2. Permutation Entropy (PE)
2.2.3. Adaptive Fractal Analysis (AFA)
3. Results
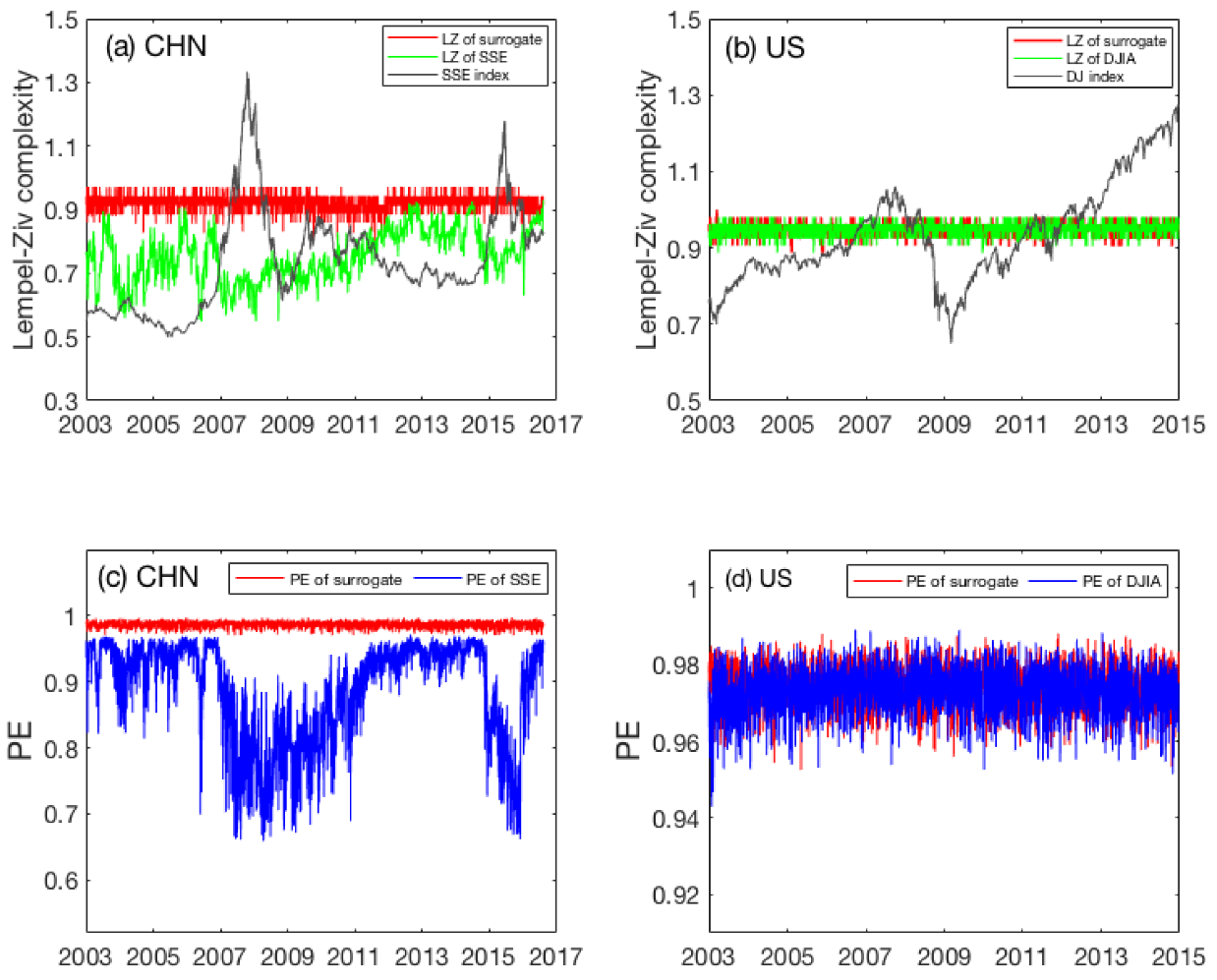
3.1. Detecting Complexity Changes by LZ and PE Using Low-Frequency Data
3.2. Detecting Complexity Changes by LZ and PE Using High-Frequency Data
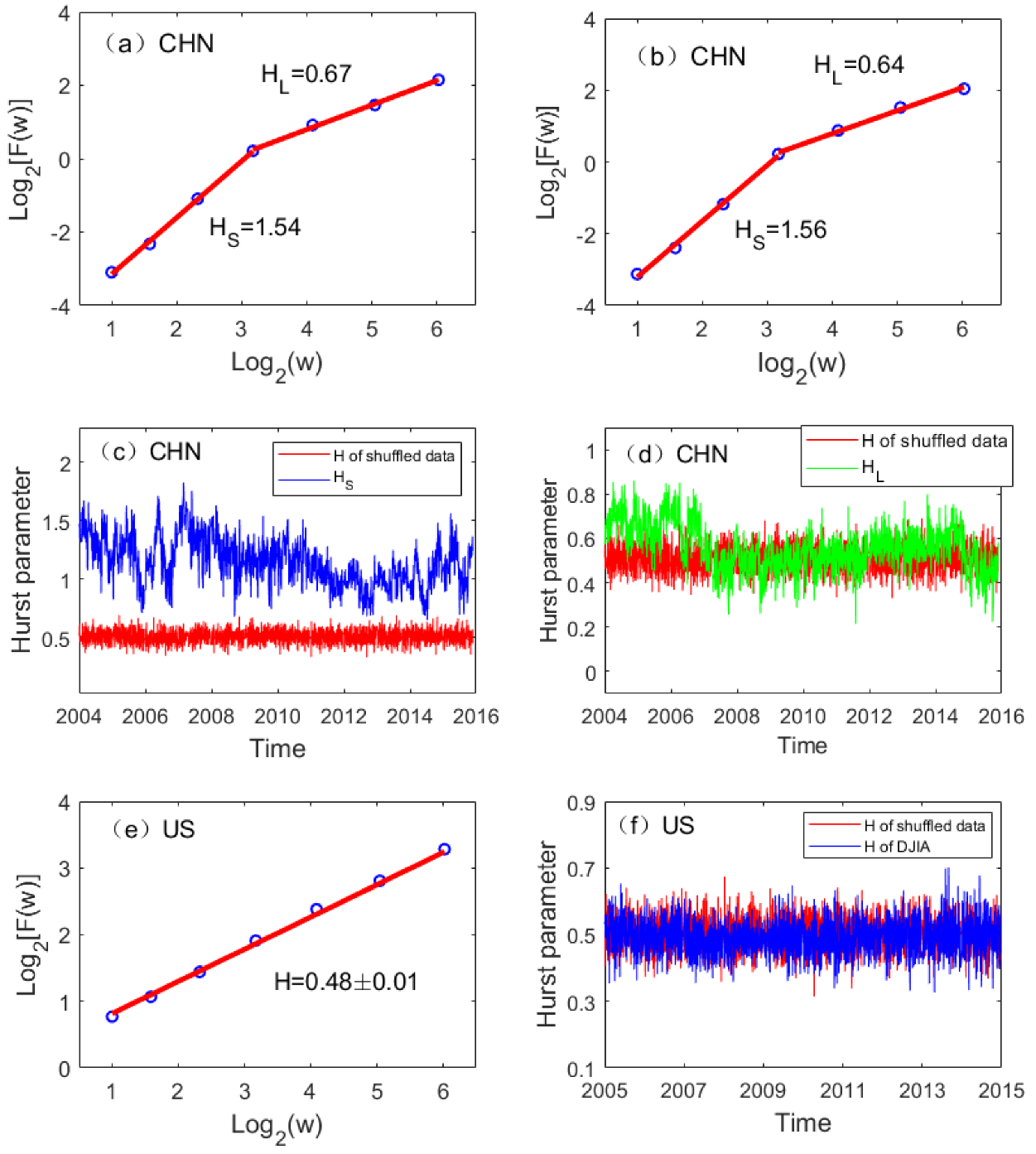
3.3. Cause of Complexity Changes: Long-Range Correlation
3.4. Correlation between LZ, PE, and H for SSE and DJIA
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Samuelson, P.A. Proof that properly anticipated prices fluctuate randomly. Ind. Manag. Rev. 1965, 6, 41. [Google Scholar]
- Fama, E.F. The behavior of stock-market prices. J. Bus. 1965, 38, 34–105. [Google Scholar] [CrossRef]
- Roberts, H.V. Statistical Versus Clinical Prediction in the Stock Market; Center for Research in Security Prices, University of Chicago: Chicago, IL, USA, Unpublished manuscript; 1967. [Google Scholar]
- Fama, E.F. Effcient capital markets: A review of theory and empirical work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Solnik, B.H. Note on the validity of the random walk for European stock prices. J. Financ. 1973, 28, 1151–1159. [Google Scholar] [CrossRef]
- Chiang, T.C. Market efficiency and news dynamics: Evidence from International equity markets. Economies 2019, 7, 7. [Google Scholar] [CrossRef] [Green Version]
- Pharasi, H.K.; Sharma, K.; Chatterjee, R.; Chakraborti, A.; Leyvraz, F.; Seligman, T.H. Identifying long-term precursors of financial market crashes using correlation patterns. New J. Phys. 2018, 20, 103041. [Google Scholar] [CrossRef] [Green Version]
- Lo, A.W.; MacKinlay, A.C. Stock market prices do not follow random walks: Evidence from a simple specification test. Rev. Financ. Stud. 1988, 1, 41–66. [Google Scholar] [CrossRef]
- Hamid, K.; Suleman, M.T.; Ali Shah, S.Z.; Akash, I.; Shahid, R. Testing the weak form of efficient market hypothesis: Empirical evidence from Asia-Pacific markets. Int. Res. J. Financ. Econ. 2010, 58. [Google Scholar] [CrossRef] [Green Version]
- John, M.G.; Patrick, J.K.; Federico, N. Do market efficiency measures yield correct inferences? a comparison of developed and emerging markets. Rev. Financ. Stud. 2010, 23, 3225–3277. [Google Scholar]
- Zhu, Z.; Bai, Z.; Vieito, J.P.; Wong, W.K. The impact of the global financial crisis on the efficiency and performance of Latin American stock markets. Estud. Econ. 2019, 46, 5–30. [Google Scholar] [CrossRef] [Green Version]
- Rehman, S.; Chhapra, I.U.; Kashif, M.; Rehan, R. Are stock prices a random walk? An empirical evidence of Asian stock markets. ETIKONOMI 2018, 17, 237–252. [Google Scholar] [CrossRef]
- Zhang, X.S.; Zhu, Y.S.; Thakor, N.V.; Wang, Z.Z. Detecting ventricular tachycardia and fibrillation by complexity measure. IEEE Trans. Biomed. Eng. 1999, 46, 548–555. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.S.; Roy, R.J.; Jensen, E.W. EEG complexity as a measure of depth of anesthesia for patients. IEEE Trans. Biomed. Eng. 2001, 48, 1424–1433. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, R. Quantifying physiological data with Lempel–Ziv complexity – certain issues. IEEE Trans. Biomed. Eng. 2002, 49, 1371–1373. [Google Scholar] [CrossRef]
- Giglio, R.; Matsushita, R.; Figueiredo, A.; Gleria, I.; Da Silva, S. Algorithmic complexity theory and the relative efficiency of financial markets. Europhys. Lett. 2008, 84, 48005. [Google Scholar] [CrossRef] [Green Version]
- Giglio, R.; Da Silva, S. Ranking the stocks listed on Bovespa according to their relative efficiency. Appl. Math. Sci. 2009, 43, 2133–2142. [Google Scholar]
- Fiedor, P. Frequency effects on predictability of stock returns. In Proceedings of the 2014 IEEE Conference on Computational Intelligence for Financial Engineering & Economics (CIFEr), London, UK, 27–28 March 2014; pp. 247–254. [Google Scholar]
- Li, R.; Wang, J.; Wang, G. Complex similarity and fluctuation dynamics of financial markets on voter interacting dynamic system. Int. J. Bifurc. Chaos 2018, 28, 1850156. [Google Scholar] [CrossRef]
- Aghamohammadi, C.; Ebrahimian, M.; Tahmooresi, H. Permutation approach, high frequency trading and variety of micro patterns in financial time series. Phys. A Stat. Mech. Appl. 2014, 413, 25–30. [Google Scholar] [CrossRef] [Green Version]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 0031–9007. [Google Scholar] [CrossRef]
- Cao, Y.H.; Tung, W.W.; Gao, J.B.; Protopopescu, V.A.; Hively, L.M. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E. 2004, 70, 1539–3755. [Google Scholar] [CrossRef] [Green Version]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Zunino, L.; Soriano, M.C.; Fischer, I.; Rosso, O.A.; Mirasso, C.R. Permutation-information-theory approach to unveil delay dynamics from time-series analysis. Phys. Rev. E 2010, 82, 046212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zunino, L.; Zanin, M.; Tabak, B.M.; Pérez, D.G.; Rosso, O.A. Forbidden patterns, permutation entropy and stock market inefficiency. Phys. A Stat. Mech. Appl. 2009, 388, 2854–2864. [Google Scholar] [CrossRef]
- Zunino, L.; Zanin, M.; Tabak, B.M.; Pérez, D.G.; Rosso, O.A. Complexity-entropy causality plane: A useful approach to quantify the stock market inefficiency. Phys. A Stat. Mech. Appl. 2010, 389, 1891–1901. [Google Scholar] [CrossRef] [Green Version]
- Zunino, L.; Bariviera, A.F.; Guercio, M.B.; Martinez, L.B.; Rosso, O.A. On the efficiency of sovereign bond markets. Phys. A Stat. Mech. Appl. 2012, 391, 4342–4349. [Google Scholar] [CrossRef] [Green Version]
- Hou, Y.F.; Liu, F.Y.; Gao, J.B.; Cheng, C.X.; Song, C.Q. Characterizing complexity changes in Chinese stock market by permutation entropy. Entropy 2017, 19, 514. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Shang, P.; Zhang, X. Financial time series analysis based on fractional and multiscale permutation entropy. Commun. Nonlinear Sci. Numer. Simul. 2019, 78, 104880. [Google Scholar] [CrossRef]
- Zhang, N.; Sun, Y.; Zhang, Y.; Yang, P.; Lin, A.; Shang, P. Distinguishing stock indices and detecting economic crises based on weighted symbolic permutation entropy. Fluct. Noise Lett. 2019, 18, 1950026. [Google Scholar] [CrossRef]
- Cuesta-Frau, D.; Murillo-Escobar, J.P.; Orrego, D.A.; Delgado-Trejos, E. Embedded dimension and time series length. Practical influence on permutation entropy and its applications. Entropy 2019, 21, 385. [Google Scholar] [CrossRef] [Green Version]
- Sigaki, H.Y.; Perc, M.; Ribeiro, H.V. Clustering patterns in efficiency and the coming-of-age of the cryptocurrency market. Sci. Rep. 2019, 9, 1440. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Cox, D.R. Longe Range Dependence: A Review; Statistics: An Appraisal; David, H.A., Davis, H.T., Eds.; The Iowa State University Press: Ames, IA, USA, 1984; pp. 55–74. [Google Scholar]
- Gao, J.B.; Cao, Y.H.; Tung, W.W.; Hu, J. Multiscale Analysis of Complex Time Series: Integration of Chaos and Random Fractal Theory, and Beyond; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Gao, J.B.; Hu, J.; Tung, W.W.; Cao, Y.H.; Sarshar, N.; Roychowdhury, V.P. Assessment of long range correlation in time series: How to avoid pitfalls. Phys. Rev. E. 2006, 73, 016117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, J.B.; Hu, J.; Tung, W.W. Facilitating joint chaos and fractal analysis of biosignals through nonlinear adaptive filtering. PLoS ONE 2011, 6, e24331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, J.B.; Hu, J.; Mao, X.; Perc, M. Culturomics meets random fractal theory: Insights into long-range correlations of social and natural phenomena over the past two centuries. J. R. Soc. Interface 2012, 9, 1956–1964. [Google Scholar] [CrossRef] [Green Version]
- Cajueiro, D.O.; Tabak, B.M. Evidence of long range dependence in Asian equity markets: The role of liquidity and market restriction. Phys. A 2004, 342, 654–664. [Google Scholar]
- Cajueiro, D.O.; Tabak, B.M. The Hurst exponent over time: Testing the assertion that emerging markets are becoming more efficient. Phys. A 2004, 336, 521–537. [Google Scholar] [CrossRef]
- Grech, D.; Mazur, Z. Can one make any crash prediction in finance using the local Hurst exponent idea? Phys. A 2004, 336, 133–145. [Google Scholar] [CrossRef] [Green Version]
- Di Matteo, T.; Aste, T.; Dacorogna, M.M. Long-term memories of developed and emerging markets: Using the scaling analysis to. characterize their stage of development. J. Bank. Financ. 2005, 29, 827–851. [Google Scholar] [CrossRef] [Green Version]
- Eom, C.; Choi, S.; Oh, G.; Jung, W.S. Hurst exponent and prediction based on weak-form efficient market hypothesis of stock market. Phys. A 2008, 387, 4630–4636. [Google Scholar] [CrossRef] [Green Version]
- Eom, C.; Choi, S.; Oh, G.; Jung, W.S. Relationship between efficiency and predictability in stock change. Phys. A 2008, 387, 5511–5517. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.D.; Liu, L.; Gu, R.B. Analysis of efeficiency for Shenzhen stock market based on multifractal detrended fluctuation analysis. Int. Rev. Financ. Anal. 2009, 18, 271–276. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Gu, R.; Cao, J.; Wang, H. Analysis of market efficiency for the Shanghai Stock Market over time. Phys. A 2010, 389, 1635–1642. [Google Scholar] [CrossRef]
- Zhou, W.J.; Dang, Y.G.; Gu, R.B. Efficiency and multifractality analysis of CSI 300 based on multifractal detrending moving average algorithm. Phys. A 2013, 392, 1429–1438. [Google Scholar] [CrossRef]
- Dittrich, L.O.; Srbek, P. Long-range dependence in daily return stock market series. In. Adv. Econ. Res. 2018, 24, 285–286. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, C.; Yang, X.; Yan, L.; Lai, Y. Analysis of the efficiency of Hong Kong REITs market based on Hurst exponent. Phys. A Stat. Mech. Appl. 2019, 534, 122035. [Google Scholar] [CrossRef]
- Ali, S.; Shahzad, S.J.H.; Raza, N.; Al-Yahyaee, K.H. Stock market efficiency: A comparative analysis of Islamic and conventional stock markets. Phys. A Stat. Mech. Appl. 2018, 503, 139–153. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Aye, G.C.; Gupta, R. Stock market efficiency analysis using long spans of data: A multifractal detrended fluctuation approach. Financ. Res. Lett. 2019, 28, 398–411. [Google Scholar] [CrossRef] [Green Version]
- Helbing, D.; Brockmann, D.; Chadefaux, T.; Donnay, K.; Blanke, U.; Woolley-Meza, O.; Moussaid, M.; Johansson, A.; Krause, J.; Schutte, S.; et al. Saving human lives: What complexity science and information systems can contribute. J. Stat. Phys. 2015, 158, 735–781. [Google Scholar] [CrossRef]
- Gao, J.; Fang, P.; Liu, F. Empirical scaling law connecting persistence and severity of global terrorism. Phys. A 2017, 482, 74–86. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Probl. Inf. Transm. 1965, 1, 1–7. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Combinatorial foundations of information theory and the calculus of probabilities. Russ. Math. Surv. 1983, 38, 29. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Rapp, P.E.; Cellucci, C.J.; Korslund, K.E.; Wantanabe, T.A.A.; Jimenez-Montano, M.A. Effective normalization of complexity measurements for epoch length and sampling frequency. Phys. Rev. E. 2001, 64, 016209. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Gao, J.B.; Principe, J.C. Analysis of biomedical signals by the Lempel–Ziv complexity: The effect of finite data size. IEEE Trans. Biomed. Eng. 2006, 53, 2606–2609. [Google Scholar] [PubMed]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 1976. [Google Scholar]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of dna nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef] [Green Version]
- Hu, K.; Ivanov, P.C.; Chen, Z.; Carpena, P.; Stanley, H.E. Effect of trends on detrended fluctuation analysis. Phys. Rev. E. 2001, 64, 011114. [Google Scholar] [CrossRef] [Green Version]
- Stanley, H.E.; Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A 2002, 316, 87–114. [Google Scholar]
- Chen, Z.; Hu, K.; Carpena, P.; Bernaola-Galvan, P.; Stanley, H.E.; Ivanov, P.C. Effect of nonlinear filters on detrended fluctuation analysis. Phys. Rev. E 2005, 71, 011104. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Gao, J.B.; Wang, X.S. Multifractal analysis of sunspot time series: The effects of the 11-year cycle and fourier truncation. J. Stat. Mech. 2009, 2, 02066. [Google Scholar] [CrossRef]
- Lillo, F.; Moro, E.; Vaglica, G.; Mantegna, R.N. Specialization and herding behavior of trading firms in a financial market. New J. Phys. 2008, 10, 043019. [Google Scholar] [CrossRef]
- Shapira, Y.; Berman, Y.; Ben-Jacob, E. Modelling the short term herding behaviour of stock markets. New J. Phys. 2014, 16, 053040. [Google Scholar] [CrossRef]
- Hou, Y.F.; Gao, J.B.; Fan, F.L.; Liu, F.Y.; Song, C.Q. Identifying herding effect in Chinese stock market by high-frequency data. In Proceedings of the 2017 International Conference on Behavioral, Economic, Socio-cultural Computing (BESC), Krakow, Poland, 16–18 October 2017; pp. 16–18. [Google Scholar]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Hou, Y.; Fan, F.; Liu, F. Complexity Changes in the US and China’s Stock Markets: Differences, Causes, and Wider Social Implications. Entropy 2020, 22, 75. https://doi.org/10.3390/e22010075
Gao J, Hou Y, Fan F, Liu F. Complexity Changes in the US and China’s Stock Markets: Differences, Causes, and Wider Social Implications. Entropy. 2020; 22(1):75. https://doi.org/10.3390/e22010075
Chicago/Turabian StyleGao, Jianbo, Yunfei Hou, Fangli Fan, and Feiyan Liu. 2020. "Complexity Changes in the US and China’s Stock Markets: Differences, Causes, and Wider Social Implications" Entropy 22, no. 1: 75. https://doi.org/10.3390/e22010075




