Generalizations of Fano’s Inequality for Conditional Information Measures via Majorization Theory †
Abstract
:1. Introduction
1.1. Main Contributions
- (i)
- the alphabet of a discrete r.v. X to be estimated is countably infinite,
- (ii)
- the marginal distribution of X is fixed,
- (iii)
- the inequality is established on a general class of conditional information measures, and
- (iv)
- the decoding rule is a list decoding scheme in contrast to a unique decoding scheme.
- First, we show that a generalized conditional information measure can be bounded from above by with a certain pair in which the conditional distribution of U given V can be thought of as a so-called uniformly dispersive channel [11,12] (see also Section II-A of [13]). We prove this fact via Jensen’s inequality (cf. Proposition A-2 of [14]) and the symmetry of the considered information measures . Moreover, we establish a novel characterization of uniformly dispersive channels via a certain majorization relation; we show that the output distribution of a uniformly dispersive channel is majorized by its transition probability distribution for any fixed input symbol. This majorization relation is used to obtain a sharp upper bound via the Schur-concavity property of the considered information measures .
- Second, we ensure the existence of a joint distribution of which satisfies all constraints in our maximization problems stated in (7) and the conditional distribution is uniformly dispersive. Here, a main technical difficulty is to maintain a marginal distribution of X over a countably infinite alphabet ; see (ii) above. Using a majorization relation for a uniformly dispersive channel, we express a desired marginal distribution by the multiplication of a doubly stochastic matrix and a uniformly dispersive . This characterization of the majorization relation via a doubly stochastic matrix was proven by Hardy–Littleweed–Pólya [15] in the finite-dimensional case, and by Markus [16] in the infinite-dimensional case. From this doubly stochastic matrix, we construct a marginal distribution of Y so that the joint distribution has the desired marginal distribution . The construction of is based on the infinite-dimensional version of Birkhoff’s theorem, which was posed by Birkhoff [17] and was proven by Révész [18] via Kolmogorov’s extension theorem. Although the finite-dimensional version of Birkhoff’s theorem [19] (also known as the Birkhoff–von Neumann decomposition) is well-known, the application of the infinite-dimensional version of Birkhoff’s theorem in information theory appears to be novel; its application aids in dealing with communication systems over countably infinite alphabets.
- Third, we introduce an extremal distribution on a countably infinite alphabet . Showing that is the infimum of a certain class of discrete probability distributions with respect to the majorization relation, our maximization problems can be bounded from above by the considered information measure . Namely, our Fano-type inequality is expressed by a certain information measure of the extremal distribution. When the cardinality of the alphabet of Y is large enough, by constructing a joint distribution achieving equality in our generalized Fano-type inequality, we say that the inequality is sharp.
1.2. Related Works
1.2.1. Information Theoretic Tools on Countably Infinite Alphabets
1.2.2. Fano’s Inequality with List Decoding
1.2.3. Fano’s Inequality for Rényi’s Information Measures
1.2.4. Lower Bounds on Mutual Information
1.3. Paper Organization
2. Preliminaries
2.1. A General Class of Conditional Information Measures
2.2. Minimum Average Probability of List Decoding Error
3. Main Results: Fano-Type Inequalities
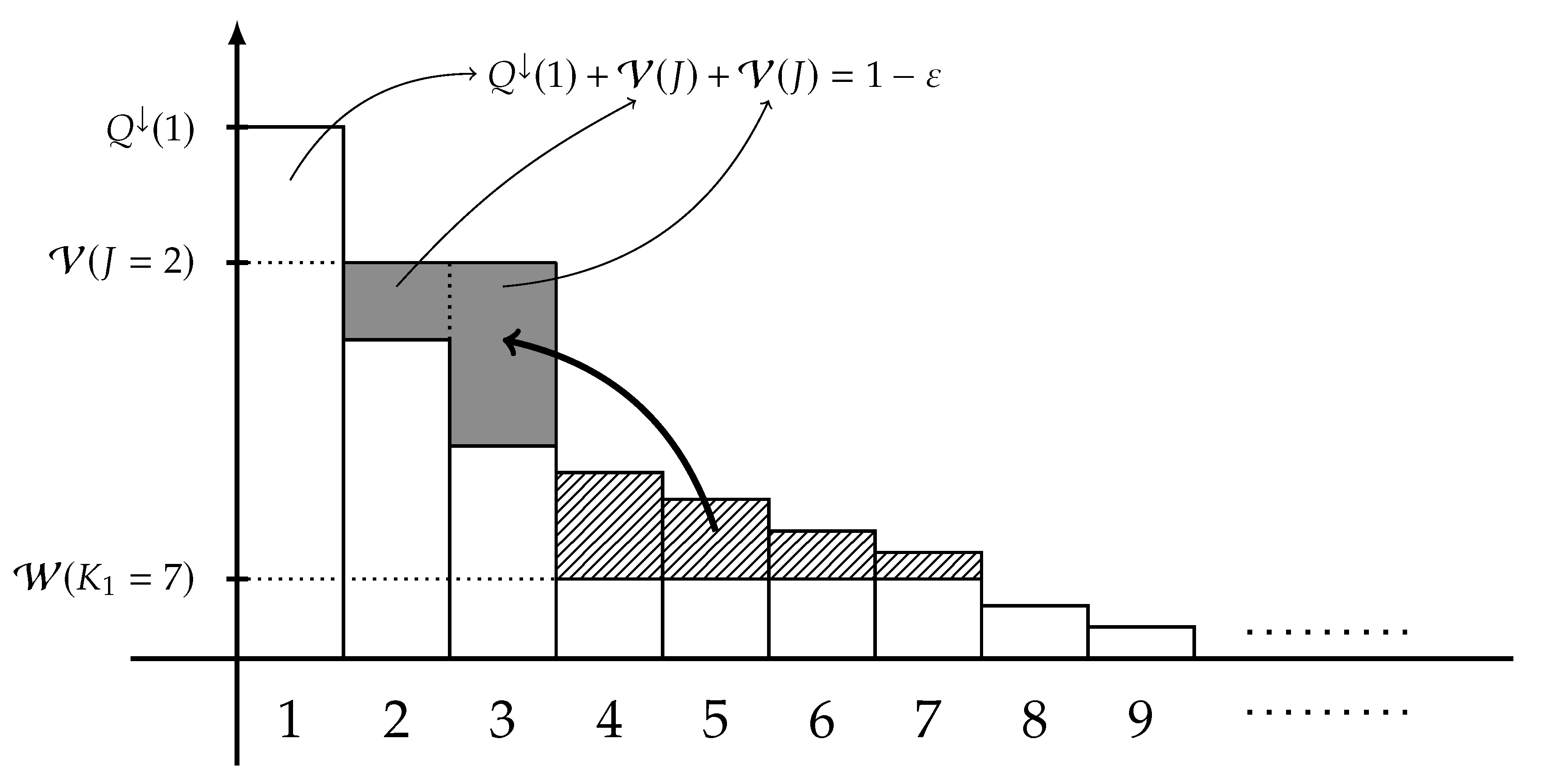
- the probability masses are nonincreasing in , i.e.,
- the sum of first L probability masses of is equal to , i.e.,consequently, it holds that
- the first probability masses are equal to that of , i.e.,
- the probability masses for are equal to , i.e.,
- the probability masses for are equal to , i.e.,
- the probability masses for are equal to that of , i.e.,and
- it holds that majorizes Q.
4. Special Cases: Fano-Type Inequalities on Shannon’s and Rényi’s Information Measures
4.1. On Shannon’s Information Measures
4.2. On Rényi’s Information Measures
4.3. Generalization of Erokhin’s Function to α-Mutual Information
5. Asymptotic Behaviors on Equivocations
5.1. Fano’s Inequality Meets the AEP
5.2. Vanishing Unnormalized Rényi’s Equivocations
- (a)
- the order α is strictly larger than 1, i.e., ,
- (b)
- the sequence satisfies the AEP and as ,
- (c)
- there exists an such that majorizes for every ,
- (d)
- the sequence converges in distribution to X and as .
5.3. Under the Symbol-Wise Error Criterion
6. Proofs of Fano-Type Inequalities
6.1. Proof of Theorem 1
- (a) and (c) follow from Proposition 2, and
- and (b) follows from (136).
- (a) follows from (137),
- (b) follows by the identity ,
- (c) follows from the fact that is connected uniform-dispersively,
- (d) follows from (136),
- (e) follows by the definition of ,
- (f) follows by the Fubini–Tonelli theorem, and
- (f) follows from the fact that the inverse of a permutation matrix is its transpose.
- (a) follows by the definition of stated in (129),
- (b) follows by the inclusion ,
- (c) follows from Lemma 2 and the fact that has balanced conditional distributions,
- (d) follows by the symmetry of both and ,
- (e) follows from Lemma 1, and
- (f) follows from Proposition 1 and Lemma 5.
6.2. Proof of Theorem 2
6.3. Proof of Theorem 3
- (a) follows by the independence and , and
- (b) follows by (177) and defining so thatfor each and .
- (a) follows by the symmetry of and (177),
- (b) follows by ,
- (c) follows by Jensen’s inequality, and
- (d) follows by the independence .
6.4. Proof of Theorem 4
7. Proofs of Asymptotic Behaviors on Equivocations
7.1. Proof of Theorem 5
- (a) follows by the definitionfor each ,
- (b) follows by the continuity of the map and the fact that as , i.e., there exists a sequence of positive reals satisfying as andfor each ,
- (c) follows by constructing the subset so thatfor each ,
- (d) follows by defining the typical set so thatwith some for each , and
- (e) follows by the definition of .
7.2. Proof of Theorem 6
7.3. Proof of Theorem 7
- (a) follows by Corollary 4 and ,
- (b) follows by Condition (b) of Theorem 6 and the same manner as ([21], Lemma 1), and
- (c) follows by Lemma 12 together with the following definition
8. Concluding Remarks
8.1. Impossibility of Establishing Fano-Type Inequality
8.2. Postulational Characterization of Conditional Information Measures
- If , then coincides with the (unnormalized) Bhattacharyya parameter (cf. Definition 17 of [80] and Section 4.2.1 of [81]) defined byNote that the Bhattacharyya parameter is often defined so that to normalize as , provided that X is -valued. When X takes values in a finite alphabet with a certain algebraic structure, the Bhattacharyya parameter is useful in analyzing the speed of polarization for non-binary polar codes (cf. [80,81]). Note that is a monotone function of Arimoto’s conditional Rényi entropy (64) of order .
- If X is -valued, then one can define the following (variational distance-like) conditional quantity:Note that . This quantity was introduced by Shuval–Tal [84] to analyze the speed of polarization of non-binary polar codes for sources with memory. When we define the function byit holds that . Clearly, the function is symmetric, convex, and continuous.
- As is concave, lower bounded, and lower semicontinuous, it follows from Jensen’s inequality for an extended real-valued function on a closed, convex, and bounded subset of a Banach space ([14], Proposition A-2) thatThis bound is analogous to the property that conditioning reduces entropy (cf. [2], Theorem 2.6.5).
- It is easy to check that for any (deterministic) mapping with , the conditional distribution majorizes a.s. Thus, it follows from Proposition 1 that for any mapping ,which is a counterpart of the data processing inequality (cf. Equations (26)–(28) of [72]).
- As shown in Section 3, the quantity also satisfies appropriate generalizations of Fano’s inequality.
8.3. When Does Vanishing Error Probabilities Imply Vanishing Equivocations?
8.4. Future Works
- Important technical tools used in our analysis include the finite- and infinite-dimensional versions of Birkhoff’s theorem; they were employed to satisfy the constraint that . As a similar constraint is imposed in many information-theoretic problems, e.g., coupling problems (cf. [7,88,89]), finding further applications of the infinite-dimensional version of Birkhoff’s theorems would refine technical tools, and potentially results, when we are dealing with communication systems on countably infinite alphabets.
- We have described a novel connection between the AEP and Fano’s inequality in Theorem 5; its role in the classifications of sources and channels and its applications to other coding problems are of interest.
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Proposition 2
Appendix B. Proof of Proposition 3
- (a) follows from Proposition 2,
- (b) follows from by the construction of , and
- (c) follows from the facts that and .
Appendix C. Proof of Proposition 4
Appendix D. Proof of Proposition 9
- (a) follows by the definition of stated in (129),
- (b) follows by the inclusions
- (c) follows from the fact that implies thatfor and , and
- (d) follows from the facts that
Appendix E. Proof of Lemma 6
References
- Fano, R.M. Class Notes for Transmission of Information; MIT press: Cambridge, MA, USA, 1952. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: New York, NY, USA, 2006. [Google Scholar]
- El Gamal, A.; Kim, Y.H. Network Information Theory; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Yeung, R.W. Information Theory and Network Coding; Springer: New York, NY, USA, 2008. [Google Scholar]
- Zhang, Z. Estimating mutual information via Kolmogorov distance. IEEE Trans. Inf. Theory 2007, 53, 3280–3283. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Sason, I. Entropy bounds for discrete random variables via maximal coupling. IEEE Trans. Inf. Theory 2013, 59, 7118–7131. [Google Scholar] [CrossRef] [Green Version]
- Arimoto, S. Information measures and capacity of order α for discrete memoryless channels. Topics Inf. Theory 1977, 16, 41–52. [Google Scholar]
- Hayashi, M. Exponential decreasing rate of leaked information in universal random privacy amplification. IEEE Trans. Inf. Theory 2011, 57, 3989–4001. [Google Scholar] [CrossRef] [Green Version]
- Marshall, A.W.; Olkin, I.; Arnold, B.C. Inequalities: Theory of Majorization and Its Applications, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Fano, R.M. Transmission of Information: A Statistical Theory of Communication; MIT Press: New York, NY, USA, 1961. [Google Scholar]
- Massey, J.L. Applied digital information theory I, Signal and Information Processing Laboratory, ETH Zürich. Lecture note. Available online: http://www.isiweb.ee.ethz.ch/archive/massey_scr/ (accessed on 20 January 2020).
- Sakai, Y.; Iwata, K. Extremality between symmetric capacity and Gallager’s reliability function E0 for ternary-input discrete memoryless channels. IEEE Trans. Inf. Theory 2018, 64, 163–191. [Google Scholar] [CrossRef]
- Shirokov, M.E. On properties of the space of quantum states and their application to the construction of entanglement monotones. Izv. Math. 2010, 74, 849–882. [Google Scholar] [CrossRef] [Green Version]
- Hardy, G.H.; Littlewood, J.E.; Pólya, G. Some simple inequalities satisfied by convex functions. Messenger Math. 1929, 58, 145–152. [Google Scholar]
- Markus, A.S. The eigen- and singular values of the sum and product of linear operators. Russian Math. Surv. 1964, 19, 91–120. [Google Scholar] [CrossRef]
- Birkhoff, G. Lattice Theory, revised ed.; American Mathematical Society: Providence, RI, USA, 1948. [Google Scholar]
- Révész, P. A probabilistic solution of problem 111 of G. Birkhoff. Acta Math. Hungar. 1962, 3, 188–198. [Google Scholar] [CrossRef]
- Birkhoff, G. Tres observaciones sobre el algebra lineal. Univ. Nac. Tucumán Rev. Ser. A 1946, 5, 147–151. [Google Scholar]
- Erokhin, V. ε-entropy of a discrete random variable. Theory Probab. Appl. 1958, 3, 97–100. [Google Scholar] [CrossRef]
- Ho, S.-W.; Verdú, S. On the interplay between conditional entropy and error probability. IEEE Trans. Inf. Theory 2010, 56, 5930–5942. [Google Scholar] [CrossRef]
- Sakai, Y.; Iwata, K. Sharp bounds on Arimoto’s conditional Rényi entropies between two distinct orders. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 2975–2979. [Google Scholar]
- Sason, I.; Verdú, S. Arimoto–Rényi conditional entropy and Bayesian M-ary hypothesis testing. IEEE Trans. Inf. Theory 2018, 64, 4–25. [Google Scholar] [CrossRef]
- Sibson, R. Information radius. Z. Wahrsch. Verw. Geb. 1969, 14, 149–161. [Google Scholar] [CrossRef]
- Verdú, S.; Han, T.S. The role of the asymptotic equipartition property in noiseless coding theorem. IEEE Trans. Inf. Theory 1997, 43, 847–857. [Google Scholar] [CrossRef]
- Nummelin, E. Uniform and ratio limit theorems for Markov renewal and semi-regenerative processes on a general state space. Ann. Inst. Henri Poincaré Probab. Statist. 1978, 14, 119–143. [Google Scholar]
- Athreya, K.B.; Ney, P. A new approach to the limit theory of recurrent Markov chains. Trans. Amer. Math. Soc. 1978, 245, 493–501. [Google Scholar] [CrossRef]
- Kumar, G.R.; Li, C.T.; El Gamal, A. Exact common information. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 161–165. [Google Scholar]
- Vellambi, B.N.; Kliewer, J. Sufficient conditions for the equality of exact and Wyner common information. In Proceedings of the 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 27–30 September 2016; pp. 370–377. [Google Scholar]
- Vellambi, B.N.; Kliewer, J. New results on the equality of exact and Wyner common information rates. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 151–155. [Google Scholar]
- Yu, L.; Tan, V.Y.F. On exact and ∞-Rényi common informations. IEEE Trans. Inf. Theory 2020. [Google Scholar] [CrossRef]
- Yu, L.; Tan, V.Y.F. Exact channel synthesis. IEEE Trans. Inf. Theory 2020. [Google Scholar] [CrossRef]
- Han, T.S. Information-Spectrum Methods in Information Theory; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Ho, S.-W.; Yeung, R.W. On the discontinuity of the Shannon information measures. IEEE Trans. Inf. Theory 2009, 55, 5362–5374. [Google Scholar]
- Kovačević, M.; Stanojević, I.; Šenk, V. Some properties of Rényi entropy over countably infinite alphabets. Probl. Inf. Transm. 2013, 49, 99–110. [Google Scholar] [CrossRef] [Green Version]
- Ho, S.-W.; Yeung, R.W. On information divergence measures and a unified typicality. IEEE Trans. Inf. Theory 2010, 56, 5893–5905. [Google Scholar] [CrossRef] [Green Version]
- Madiman, M.; Wang, L.; Woo, J.O. Majorization and Rényi entropy inequalities via Sperner theory. Discrete Math. 2019, 342, 2911–2923. [Google Scholar] [CrossRef] [Green Version]
- Sperner, E. Ein staz über untermengen einer endlichen menge. Math. Z. 1928, 27, 544–548. [Google Scholar] [CrossRef]
- Berger, T. Rate Distortion Theory: A Mathematical Basis for Data Compression; Prentice-Hall: Englewood Cliffs, NJ, USA, 1971. [Google Scholar]
- Ahlswede, R. Extremal properties of rate-distortion functions. IEEE Trans. Inf. Theory 1990, 36, 166–171. [Google Scholar] [CrossRef]
- Kostina, V.; Polyanskiy, Y.; Verdú, S. Variable-length compression allowing errors. IEEE Trans. Inf. Theory 2015, 61, 4316–4330. [Google Scholar] [CrossRef] [Green Version]
- Ahlswede, R.; Gács, P.; Körner, J. Bounds on conditional probabilities with applications in multi-user communication. Z. Wahrsch. Verw. Geb. 1976, 34, 157–177. [Google Scholar] [CrossRef] [Green Version]
- Raginsky, M.; Sason, I. Concentration of measure inequalities in information theory, communications, and coding. Found. Trends Commun. Inf. Theory 2014, 10, 1–259. [Google Scholar] [CrossRef]
- Wolfowitz, J. Coding Theorems of Information Theory, 3rd ed.; Springer: New York, NY, USA, 1978. [Google Scholar]
- Dueck, G. The strong converse to the coding theorem for the multiple-access channel. J. Combinat. Inf. Syst. Sci. 1981, 6, 187–196. [Google Scholar]
- Fong, S.L.; Tan, V.Y.F. A proof of the strong converse theorem for Gaussian multiple access channels. IEEE Trans. Inf. Theory 2016, 62, 4376–4394. [Google Scholar] [CrossRef] [Green Version]
- Fong, S.L.; Tan, V.Y.F. A proof of the strong converse theorem for Gaussian broadcast channels via the Gaussian Poincaré inequality. IEEE Trans. Inf. Theory 2017, 63, 7737–7746. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Sutivong, A.; Cover, T.M. State amplification. IEEE Trans. Inf. Theory 2008, 54, 1850–1859. [Google Scholar] [CrossRef] [Green Version]
- Kovalevsky, V.A. The problem of character recognition from the point of view of mathematical statistics. Character Readers and Pattern Recognition; Spartan Books: Wasington, DC, USA, 1968; pp. 3–30, (Russian edition in 1965). [Google Scholar]
- Chu, J.; Chueh, J. Inequalities between information measures and error probability. J. Franklin Inst. 1966, 282, 121–125. [Google Scholar] [CrossRef]
- Tebbe, D.L.; Dwyer, S.J., III. Uncertainty and probability of error. IEEE Trans. Inf. Theory 1968, 14, 516–518. [Google Scholar] [CrossRef]
- Feder, M.; Merhav, N. Relations between entropy and error probability. IEEE Trans. Inf. Theory 1994, 40, 259–266. [Google Scholar] [CrossRef] [Green Version]
- Prasad, S. Bayesian error-based sequences of statistical information bounds. IEEE Trans. Inf. Theory 2015, 61, 5052–5062. [Google Scholar] [CrossRef]
- Ben-Bassat, M.; Raviv, J. Rényi entropy and probability of error. IEEE Trans. Inf. Theory 1978, 24, 324–331. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Han, T.S.; Verdú, S. Generalizing the Fano inequality. IEEE Trans. Inf. Theory 1994, 40, 1247–1251. [Google Scholar]
- Polyanskiy, Y.; Verdú, S. Arimoto channel coding converse and Rényi divergence. In Proceedings of the 2010 48th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Allerton, IL, USA, 29 September–1 October 2010; pp. 1327–1333. [Google Scholar]
- Sason, I. On data-processing and majorization inequalities for f-divergences with applications. Entropy 2019, 21, 1022. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Verdú, S. Beyond the blowing-up lemma: sharp converses via reverse hypercontractivity. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 943–947. [Google Scholar]
- Topsøe, F. Basic concepts, identities and inequalities—the toolkit of information theory. Entropy 2001, 3, 162–190. [Google Scholar] [CrossRef]
- Van Erven, T.; Harremoës, P. Rényi divergence and Kullback–Leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef] [Green Version]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423 and 623–656. [Google Scholar] [CrossRef] [Green Version]
- Dudley, R.M. Real Analysis and Probability, 2nd ed.; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Sakai, Y.; Tan, V.Y.F. Variable-length source dispersions differ under maximum and average error criteria. arXiv 2019, arXiv:1910.05724. [Google Scholar]
- Fehr, S.; Berens, S. On the conditional Rényi entropy. IEEE Trans. Inf. Theory 2014, 60, 6801–6810. [Google Scholar] [CrossRef]
- Iwamoto, M.; Shikata, J. Information theoretic security for encryption based on conditional Rényi entropies. In Information Theoretic Security; Springer: New York, NY, USA, 2014; pp. 103–121. [Google Scholar]
- Teixeira, A.; Matos, A.; Antunes, L. Conditional Rényi entropies. IEEE Trans. Inf. Theory 2012, 58, 4273–4277. [Google Scholar] [CrossRef]
- Verdú, S. α-mutual information. In Proceedings of the 2015 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 1–6 February 2015; pp. 1–6. [Google Scholar]
- Csiszar, I. Generalized cutoff rates and Rényi’s information measures. IEEE Trans. Inf. Theory 1995, 41, 26–34. [Google Scholar] [CrossRef]
- Ho, S.W.; Verdú, S. Convexity/concavity of Rényi entropy and α-mutual information. In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 745–749. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Hayashi, M.; Tan, V.Y.F. Equivocations, exponents, and second-order coding rates under various Rényi information measures. IEEE Trans. Inf. Theory 2017, 63, 975–1005. [Google Scholar] [CrossRef] [Green Version]
- Tan, V.Y.F.; Hayashi, M. Analysis of remaining uncertainties and exponents under various conditional Rényi entropies. IEEE Trans. Inf. Theory 2018, 64, 3734–3755. [Google Scholar] [CrossRef] [Green Version]
- Chung, K.L. A Course in Probability Theory, 3rd ed.; Academic Press: New York, NY, USA, 2000. [Google Scholar]
- Marcus, M.; Ree, R. Diagonals of doubly stochastic matrices. Q. J. Math. 1959, 10, 296–302. [Google Scholar] [CrossRef]
- Farahat, H.K.; Mirsky, L. Permutation endomorphisms and refinement of a theorem of Birkhoff. Math. Proc. Camb. Philos. Soc. 1960, 56, 322–328. [Google Scholar] [CrossRef]
- Ho, S.-W.; Yeung, R.W. The interplay between entropy and variational distance. IEEE Trans. Inf. Theory 2010, 56, 5906–5929. [Google Scholar] [CrossRef]
- Aczél, J.; Daróczy, Z. On Measures of Information and Their Characterizations; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Roberts, G.O.; Rosenthal, J.S. General state space Markov chains and MCMC algorithms. Probab. Surv. 2004, 1, 20–71. [Google Scholar] [CrossRef] [Green Version]
- Mori, R.; Tanaka, T. Source and channel polarization over finite fields and Reed–Solomon matrices. IEEE Trans. Inf. Theory 2014, 60, 2720–2736. [Google Scholar] [CrossRef]
- Şaşoğlu, E. Polarization and polar codes. Found. Trends Commun. Inf. Theory 2012, 8, 259–381. [Google Scholar] [CrossRef] [Green Version]
- Cover, T.M.; Hart, P.E. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Muramatsu, J.; Miyake, S. On the error probability of stochastic decision and stochastic decoding. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 1643–1647. [Google Scholar]
- Shuval, B.; Tal, I. Fast polarization for processes with memory. IEEE Trans. Inf. Theory 2019, 65, 2004–2020. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.S.; Silvey, D. A general class of coefficients of divergence of one distribution from another. J. Roy. Statist. Soc. series B 1966, 28, 131–142. [Google Scholar] [CrossRef]
- Csiszár, I. Eine Informationstheoretische Ungleichung und ihre Anwendung auf den Bewis der Ergodizität von Markhoffschen Ketten. Publ. Math. Inst. Hungar. Acad. Sci. 1963, 8, 85–108. [Google Scholar]
- Elias, P. List Decoding for Noisy Channels. Available online: https://dspace.mit.edu/bitstream/handle/1721.1/4484/RLE-TR-335-04734756.pdf?sequence=1 (accessed on 28 January 2020).
- Yu, L.; Tan, V.Y.F. Asymptotic coupling and its applications in information theory. IEEE Trans. Inf. Theory 2018, 64, 1321–1344. [Google Scholar] [CrossRef] [Green Version]
- Thorisson, H. Coupling, Stationarity, and Regeneration; Springer: New York, NY, USA, 2000; Volume 14. [Google Scholar]
- Merhav, N. List decoding—Random coding exponents and expurgated exponents. IEEE Trans. Inf. Theory 2014, 60, 6749–6759. [Google Scholar] [CrossRef]


© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakai, Y. Generalizations of Fano’s Inequality for Conditional Information Measures via Majorization Theory. Entropy 2020, 22, 288. https://doi.org/10.3390/e22030288
Sakai Y. Generalizations of Fano’s Inequality for Conditional Information Measures via Majorization Theory. Entropy. 2020; 22(3):288. https://doi.org/10.3390/e22030288
Chicago/Turabian StyleSakai, Yuta. 2020. "Generalizations of Fano’s Inequality for Conditional Information Measures via Majorization Theory" Entropy 22, no. 3: 288. https://doi.org/10.3390/e22030288




