Thermodynamics of the Coarse-Graining Master Equation
Abstract
1. Introduction
2. Fixed-Time Coarse-Graining
- For the conventional fixed-time coarse-graining master equation [22,23] is reproduced. Notationally, we will denote this limit as . Previous studies (for [22]) have shown that is always of LGKS form, and we can also confirm this for finite , see Appendix C. Thus, Spohn’s inequality [12]holds with any nonequilibrium steady state obeying (which may in general depend on as well).
- It has been debated whether local or global LGKS approaches are more suitable to discuss quantum thermodynamics [34,38,39,40]. To see how the dissipator (4) locates in this discussion, let us assume that our system is composed of multiple subsystems that are coupled by some constant interaction. Then, system coupling operators that in the Schrödinger picture act locally on a subsystem component will in general transfer to non-local interaction-picture operators . Thereby, the Lindblad operators from the LGKS generator (4) will in general globally act on the whole system. An obvious exception arises in the case when the time-dependence of the system operators itself is negligible , which happens, e.g., in the singular coupling limit [8] or for very short coarse-graining times. Another exception arises when the couplings between the subsystem components are comparably weak, such that the operators in the interaction picture remain approximately local over the course of the coarse-graining timescale .
- By going to the energy eigenbasis of the system, it is possible to cast the dissipator (4) into a single-integral form. Furthermore, for , the Born-Markov-secular (BMS) master equation [8] is reproduced [10]such that the secular approximation can be performed by , which we detail also for finite in Appendix D. We also find that in the secular limit, the energy current entering the system and the energy current leaving the reservoir are identical, which demonstrates that a secular approximation imposes energy conservation between system and reservoir.
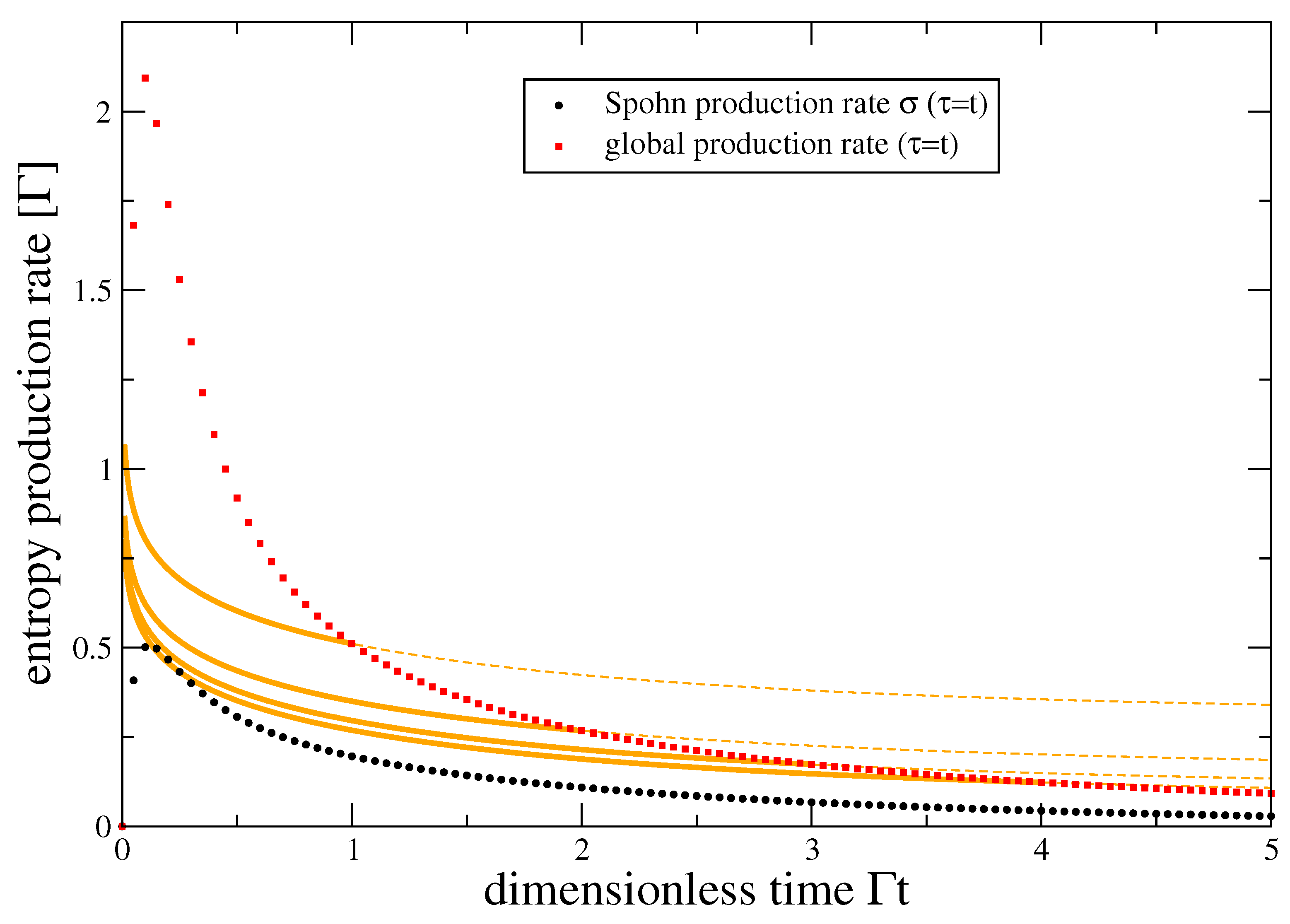
- When the dissipator does not depend on the initial time —this happens, e.g., when only certain combinations of coupling operators contribute and such that the integrand in Equation (4) depends only on — the system will under repeated system-reservoir couplings relax to the nonequilibrium steady state . When this nonequilibrium steady state is reached, Spohn’s inequality (7) would predict a vanishing entropy production rate.
3. Thermodynamics
3.1. Energetic Balance
3.2. Entropic Balance
4. Example: Pure-Dephasing Spin-Boson Model
4.1. Model and Exact Results
4.2. Coarse-Graining Dynamics
4.3. Energetic Balance
4.4. Entropic Balance
5. Example: Single Resonant Level
5.1. Model
5.2. Coarse-Graining Dynamics
5.3. Energetic Balance
5.4. Entropic Balance
6. Example: Single Electron Transistor
7. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Coarse-Graining Dissipator
Appendix B. Inclusion of Full Counting Statistics
Appendix C. Demonstration of LGKS Form
Appendix D. Single Integral Representation and Secular Limit
Appendix E. Conservation of Energy
Appendix F. Entropy Production Rate
Appendix G. Exact Solution of the Pure Dephasing Model
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Kraus, K. General state changes in quantum theory. Ann. Phys. 1971, 64, 311–335. [Google Scholar] [CrossRef]
- Lindblad, G. Completely Positive Maps and Entropy Inequalities. Commun. Math. Phys. 1975, 40, 147. [Google Scholar] [CrossRef]
- Lindblad, G. On the Generators of Quantum Dynamical Semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821. [Google Scholar] [CrossRef]
- Wolf, M.M.; Eisert, J.; Cubitt, T.S.; Cirac, J.I. Assessing Non-Markovian Quantum Dynamics. Phys. Rev. Lett. 2008, 101, 150402. [Google Scholar] [CrossRef]
- Weiss, U. Quantum Dissipative Systems; Series of Modern Condensed Matter Physics; World Scientific: Singapore, 1993; Volume 2. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Rivas, A.; Huelga, S.F. Open Quantum Systems—An Introduction; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Schaller, G. Open Quantum Systems Far from Equilibrium; Lecture Notes in Physics; Springer: Cham, Switzerland, 2014; Volume 881. [Google Scholar]
- Spohn, H.; Lebowitz, J.L. Irreversible thermodynamics for quantum systems weakly coupled to thermal reservoirs. Adv. Chem. Phys. 1978, 38, 109. [Google Scholar] [CrossRef]
- Spohn, H. Entropy production for quantum dynamical semigroups. J. Math. Phys. 1978, 19, 1227. [Google Scholar] [CrossRef]
- Dümcke, R.; Spohn, H. The Proper Form of the Generator in the Weak Coupling Limit. Zeitschrift für Physik B 1979, 34, 419–422. [Google Scholar] [CrossRef]
- Alicki, R. The quantum open system as a model of the heat engine. J. Phys. Math. Gen. 1979, 12, L103. [Google Scholar] [CrossRef]
- Binder, F.; Correa, L.A.; Gogolin, C.; Anders, J.; Adesso, G. (Eds.) Thermodynamics in the Quantum Regime—Fundamental Aspects and New Directions; Fundamental Theories of Physics; Springer: Berlin/Heidelberg, Germany, 2019; Volume 195. [Google Scholar] [CrossRef]
- Mäkelä, H.; Möttönen, M. Effects of the rotating-wave and secular approximations on non-Markovianity. Phys. Rev. A 2013, 88, 052111. [Google Scholar] [CrossRef]
- Schaller, G.; Kießlich, G.; Brandes, T. Transport statistics of interacting double dot systems: Coherent and non-Markovian effects. Phys. Rev. 2009, 80, 245107. [Google Scholar] [CrossRef]
- Hartmann, R.; Strunz, W.T. Accuracy assessment of perturbative master equations: Embracing nonpositivity. Phys. Rev. A 2020, 101, 012103. [Google Scholar] [CrossRef]
- Whitney, R.S. Staying positive: Going beyond Lindblad with perturbative master equations. J. Phys. Math. Gen. 2008, 41, 175304. [Google Scholar] [CrossRef]
- Kiršanskas, G.; Franckié, M.; Wacker, A. Phenomenological position and energy resolving Lindblad approach to quantum kinetics. Phys. Rev. B 2018, 97, 035432. [Google Scholar] [CrossRef]
- Ptaszyński, K.; Esposito, M. Thermodynamics of Quantum Information Flows. Phys. Rev. Lett. 2019, 122, 150603. [Google Scholar] [CrossRef]
- Lidar, D.A.; Bihary, Z.; Whaley, K.B. From completely positive maps to the quantum Markovian semigroup master equation. Chem. Phys. 2001, 268, 35–53. [Google Scholar] [CrossRef]
- Schaller, G.; Brandes, T. Preservation of Positivity by Dynamical Coarse-Graining. Phys. Rev. 2008, 78, 022106. [Google Scholar] [CrossRef]
- Schaller, G.; Zedler, P.; Brandes, T. Systematic perturbation theory for dynamical coarse-graining. Phys. Rev. 2009, 79, 032110. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R.; Marzolino, U. Environment-induced entanglement in a refined weak-coupling limit. EPL 2009, 88. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R.; Marzolino, U. Entangling two unequal atoms through a common bath. Phys. Rev. A 2010, 81, 012105. [Google Scholar] [CrossRef]
- Majenz, C.; Albash, T.; Breuer, H.P.; Lidar, D.A. Coarse graining can beat the rotating-wave approximation in quantum Markovian master equations. Phys. Rev. 2013, 88, 012103. [Google Scholar] [CrossRef]
- Rivas, A. Refined weak-coupling limit: Coherence, entanglement, and non-Markovianity. Phys. Rev. 2017, 95, 042104. [Google Scholar] [CrossRef]
- Cresser, J.D.; Facer, C. Coarse-graining in the derivation of Markovian master equations and its significance in quantum thermodynamics. arXiv 2017, arXiv:1710.09939. [Google Scholar]
- Ángel Rivas. Quantum Thermodynamics in the Refined Weak Coupling Limit. Entropy 2019, 8, 725. [Google Scholar] [CrossRef]
- Farina, D.; Giovannetti, V. Open-quantum-system dynamics: Recovering positivity of the Redfield equation via the partial secular approximation. Phys. Rev. A 2019, 100, 012107. [Google Scholar] [CrossRef]
- Cattaneo, M.; Giorgi, G.L.; Maniscalco, S.; Zambrini, R. Symmetry and block structure of the Liouvillian superoperator in partial secular approximation. Phys. Rev. A 2020, 101, 042108. [Google Scholar] [CrossRef]
- Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. Quantum and Information Thermodynamics: A Unifying Framework Based on Repeated Interactions. Phys. Rev. 2017, 7, 021003. [Google Scholar] [CrossRef]
- Chiara, G.D.; Landi, G.; Hewgill, A.; Reid, B.; Ferraro, A.; Roncaglia, A.J.; Antezza, M. Reconciliation of quantum local master equations with thermodynamics. New J. Phys. 2018, 20, 113024. [Google Scholar] [CrossRef]
- Rodrigues, F.L.S.; De Chiara, G.; Paternostro, M.; Landi, G.T. Thermodynamics of Weakly Coherent Collisional Models. Phys. Rev. Lett. 2019, 123, 140601. [Google Scholar] [CrossRef]
- Seah, S.; Nimmrichter, S.; Scarani, V. Nonequilibrium dynamics with finite-time repeated interactions. Phys. Rev. E 2019, 99, 042103. [Google Scholar] [CrossRef]
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 2009, 81, 1665–1702. [Google Scholar] [CrossRef]
- Hofer, P.P.; Perarnau-Llobet, M.; David, L.; Miranda, M.; Haack, G.; Silva, R.; Brask, J.B.; Brunner, N. Markovian master equations for quantum thermal machines: Local versus global approach. New J. Phys. 2017, 19, 123037. [Google Scholar] [CrossRef]
- Cattaneo, M.; Giorgi, G.L.; Maniscalco, S.; Zambrini, R. Local versus global master equation with common and separate baths: Superiority of the global approach in partial secular approximation. New J. Phys. 2019, 21, 113045. [Google Scholar] [CrossRef]
- Farina, D.; Filippis, G.D.; Cataudella, V.; Polini, M.; Giovannetti, V. Going beyond Local and Global approaches for localized thermal dissipation. arXiv 2020, arXiv:2003.11845. [Google Scholar]
- Esposito, M.; Mukamel, S. Fluctuation theorems for quantum master equations. Phys. Rev. 2006, 73, 046129. [Google Scholar] [CrossRef]
- Unruh, W.G. Maintaining coherence in quantum computers. Phys. Rev. 1995, 51, 992–997. [Google Scholar] [CrossRef]
- Polkovnikov, A. Microscopic diagonal entropy and its connection to basic thermodynamic relations. Ann. Phys. 2011, 326, 486. [Google Scholar] [CrossRef]
- Morozov, V.; Röpke, G. Entropy production in open quantum systems: Exactly solvable qubit models. Condens. Matter Phys. 2012, 15, 43004. [Google Scholar] [CrossRef][Green Version]
- Esposito, M.; Lindenberg, K.; den Broeck, C.V. Entropy production as correlation between system and reservoir. New J. Phys. 2010, 12, 013013. [Google Scholar] [CrossRef]
- Haug, H.; Jauho, A.P. Quantum Kinetics in Transport and Optics of Semiconductors; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Topp, G.E.; Brandes, T.; Schaller, G. Steady-state thermodynamics of non-interacting transport beyond weak coupling. Europhys. Lett. 2015, 110, 67003. [Google Scholar] [CrossRef]
- Engelhardt, G.; Schaller, G. Maxwell’s demon in the quantum-Zeno regime and beyond. New J. Phys. 2018, 20, 023011. [Google Scholar] [CrossRef]
- Esposito, M.; Lindenberg, K.; den Broeck, C.V. Thermoelectric efficiency at maximum power in a quantum dot. Europhys. Lett. 2009, 85, 60010. [Google Scholar] [CrossRef]
- Barato, A.C.; Seifert, U. Thermodynamic Uncertainty Relation for Biomolecular Processes. Phys. Rev. Lett. 2015, 114, 158101. [Google Scholar] [CrossRef] [PubMed]
- Kosloff, R.; Levy, A. Quantum Heat Engines and Refrigerators: Continuous Devices. Annu. Rev. Phys. Chem. 2014, 65, 365. [Google Scholar] [CrossRef]
- Alecce, A.; Galve, F.; Gullo, N.L.; Dell’Anna, L.; Plastina, F.; Zambrini, R. Quantum Otto cycle with inner friction: Finite-time and disorder effects. New J. Phys. 2015, 17, 075007. [Google Scholar] [CrossRef]
- Kosloff, R.; Rezek, Y. The Quantum Harmonic Otto Cycle. Entropy 2017, 19, 136. [Google Scholar] [CrossRef]
- Newman, D.; Mintert, F.; Nazir, A. Performance of a quantum heat engine at strong reservoir coupling. Phys. Rev. E 2017, 95, 032139. [Google Scholar] [CrossRef]
- Scopa, S.; Landi, G.T.; Karevski, D. Lindblad-Floquet description of finite-time quantum heat engines. Phys. Rev. A 2018, 97, 062121. [Google Scholar] [CrossRef]
- Kloc, M.; Cejnar, P.; Schaller, G. Collective performance of a finite-time quantum Otto cycle. Phys. Rev. E 2019, 100, 042126. [Google Scholar] [CrossRef]
- Abiuso, P.; Perarnau-Llobet, M. Optimal Cycles for Low-Dissipation Heat Engines. Phys. Rev. Lett. 2020, 124, 110606. [Google Scholar] [CrossRef]
- Lee, S.; Ha, M.; Park, J.M.; Jeong, H. Finite-time quantum Otto engine: Surpassing the quasistatic efficiency due to friction. Phys. Rev. E 2020, 101, 022127. [Google Scholar] [CrossRef] [PubMed]
- Cuetara, G.B.; Esposito, M.; Schaller, G. Quantum Thermodynamics with Degenerate Eigenstate Coherences. Entropy 2016, 18, 447. [Google Scholar] [CrossRef]
- Edwards, R.E. Fourier Series—A Modern Introduction; Graduate Texts in Mathematics; Springer: New York, NY, USA, 1979; Volume 64. [Google Scholar]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schaller, G.; Ablaßmayer, J. Thermodynamics of the Coarse-Graining Master Equation. Entropy 2020, 22, 525. https://doi.org/10.3390/e22050525
Schaller G, Ablaßmayer J. Thermodynamics of the Coarse-Graining Master Equation. Entropy. 2020; 22(5):525. https://doi.org/10.3390/e22050525
Chicago/Turabian StyleSchaller, Gernot, and Julian Ablaßmayer. 2020. "Thermodynamics of the Coarse-Graining Master Equation" Entropy 22, no. 5: 525. https://doi.org/10.3390/e22050525
APA StyleSchaller, G., & Ablaßmayer, J. (2020). Thermodynamics of the Coarse-Graining Master Equation. Entropy, 22(5), 525. https://doi.org/10.3390/e22050525




