Observable and Unobservable Mechanical Motion
Abstract
1. Introduction
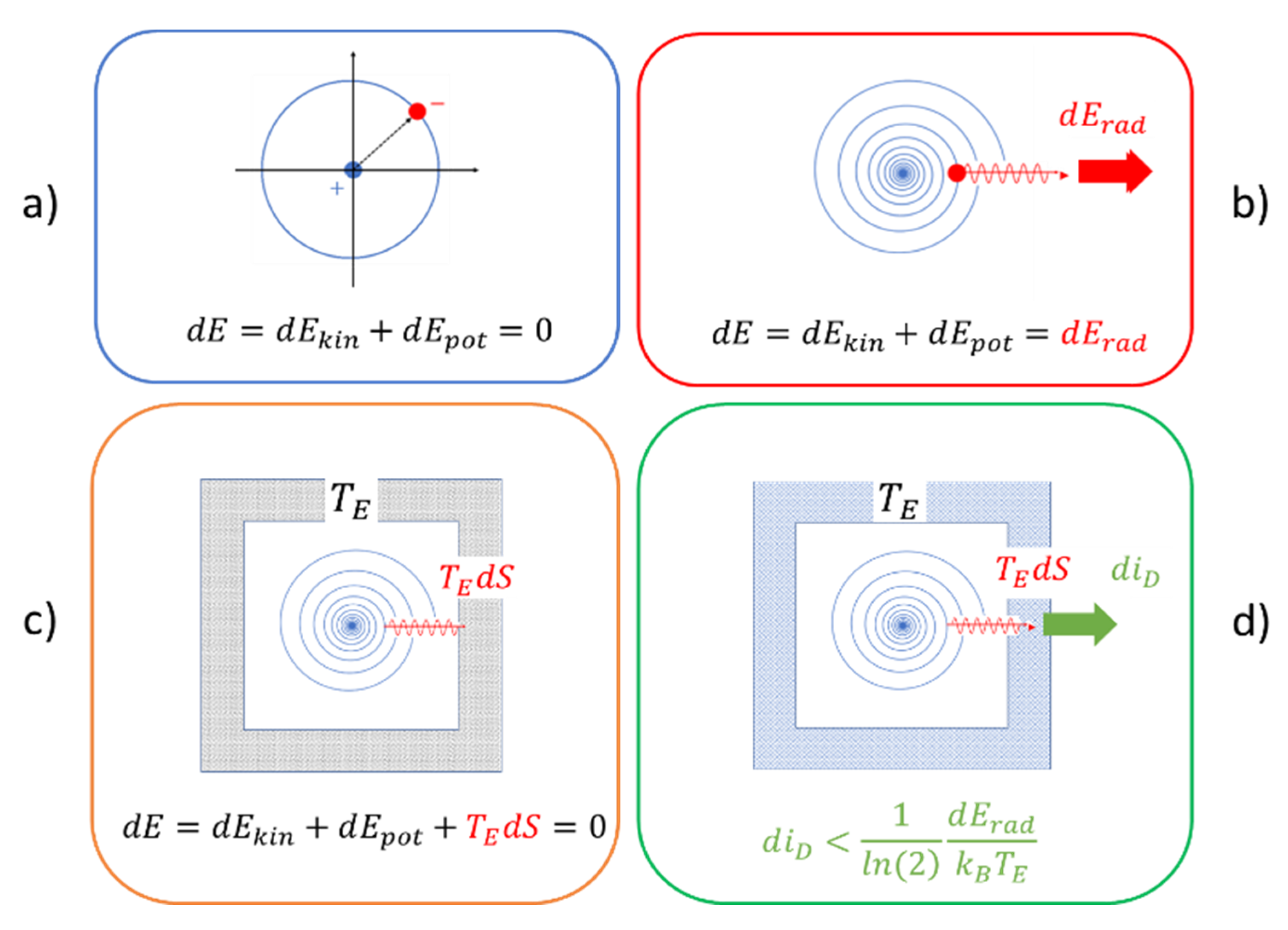
2. Thermodynamic Approach to Classical Mechanical Motion
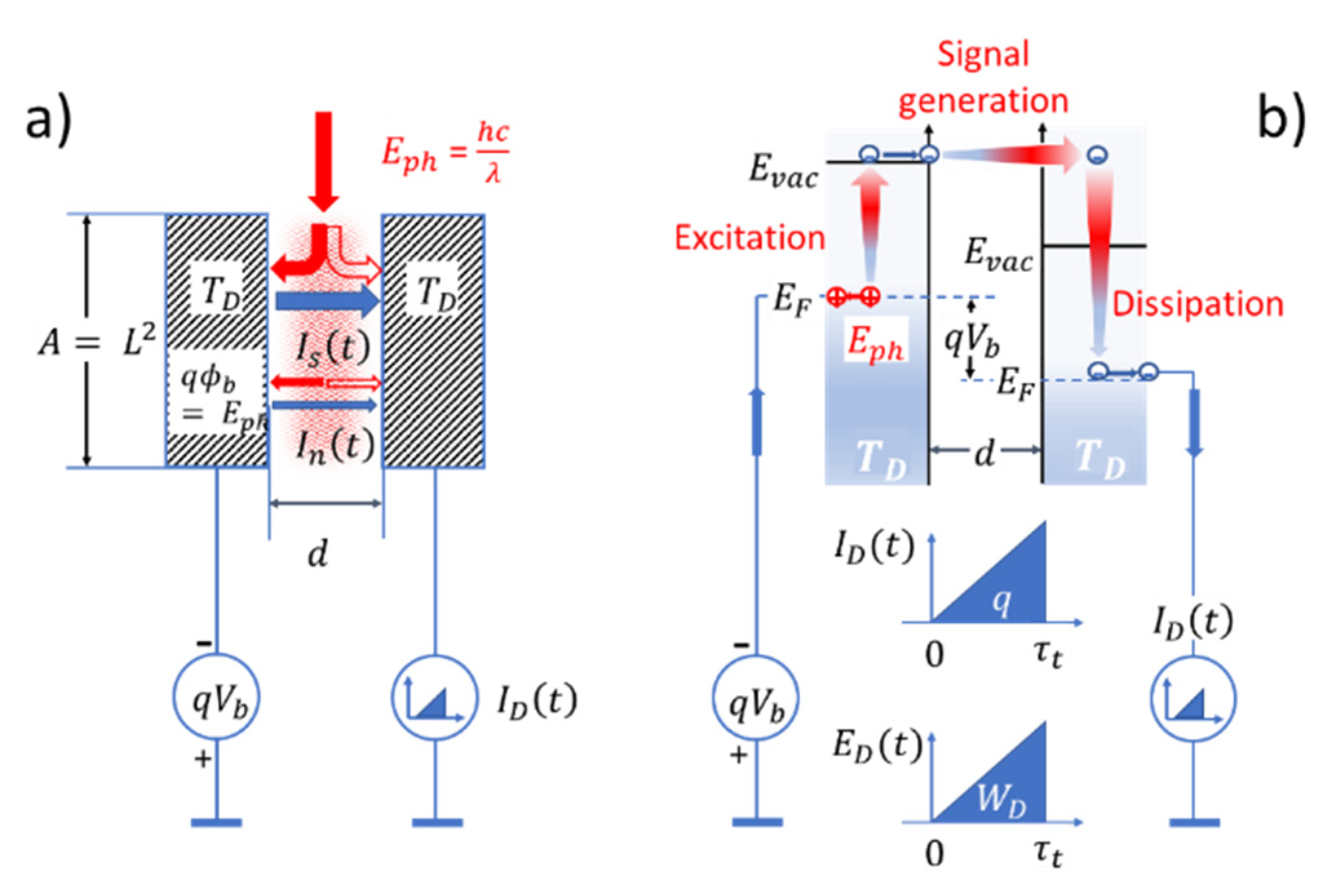
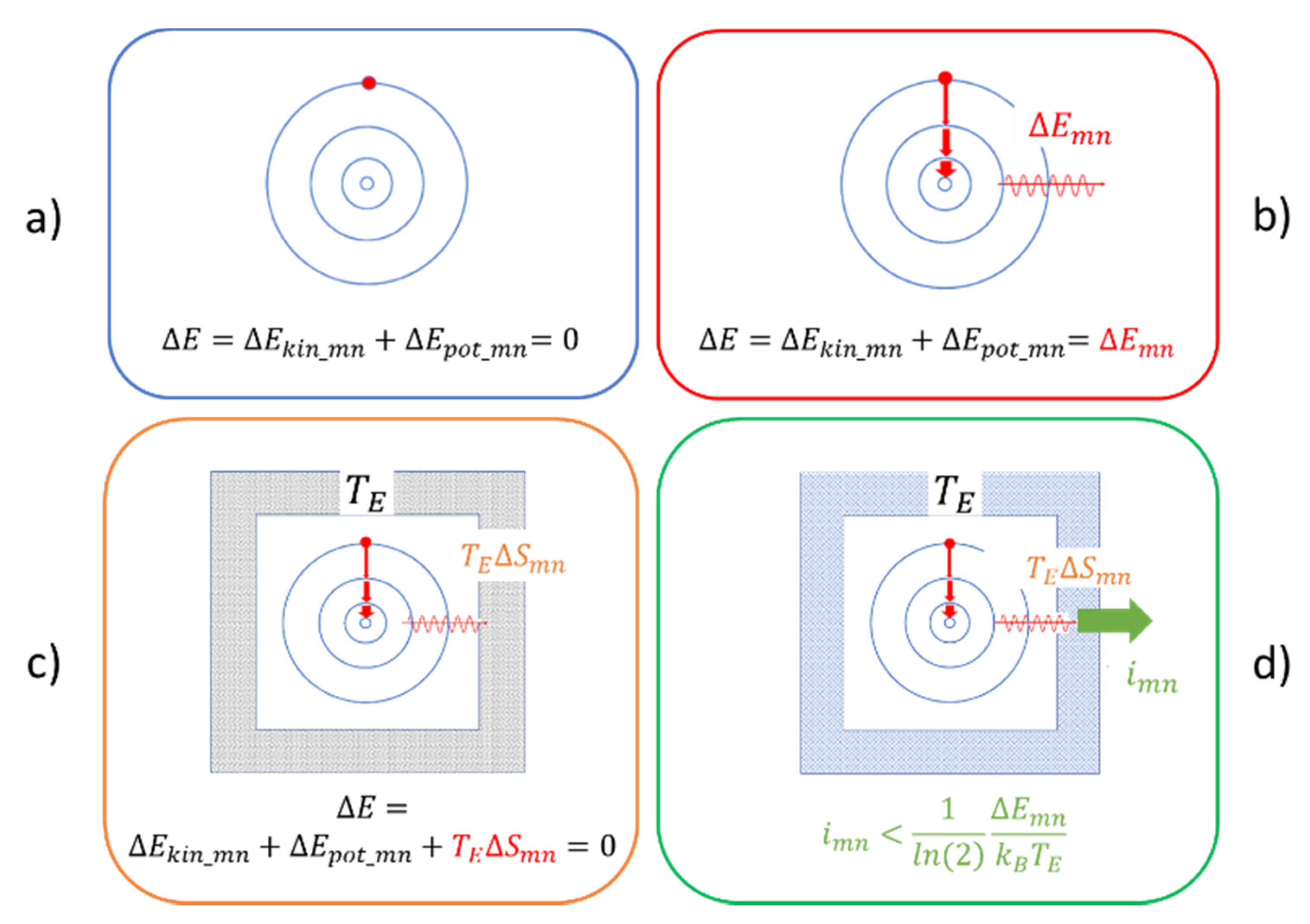
3. Mechanical Motion in the Quantum Domain
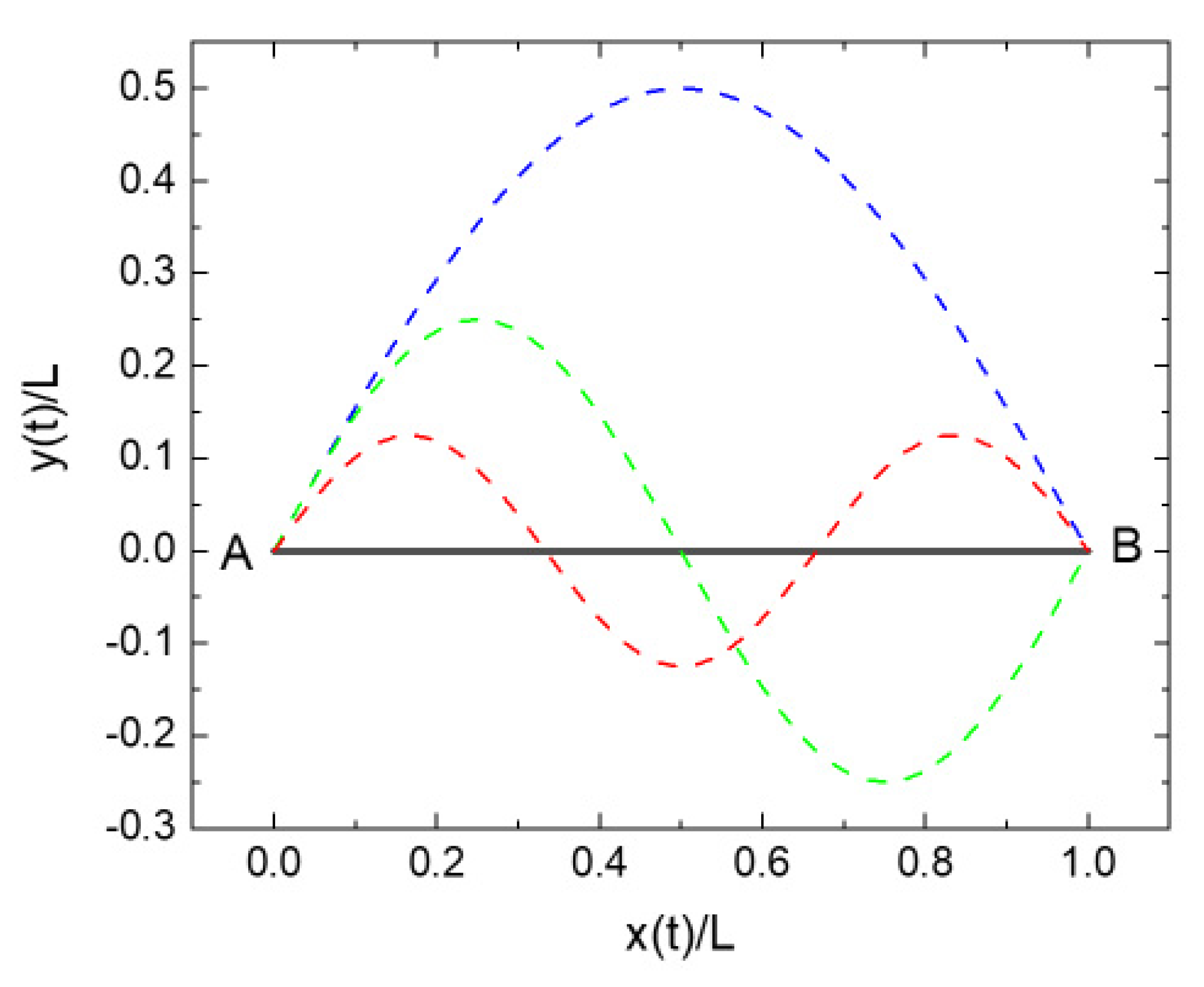
4. Least Action Principles and Observational Overhead
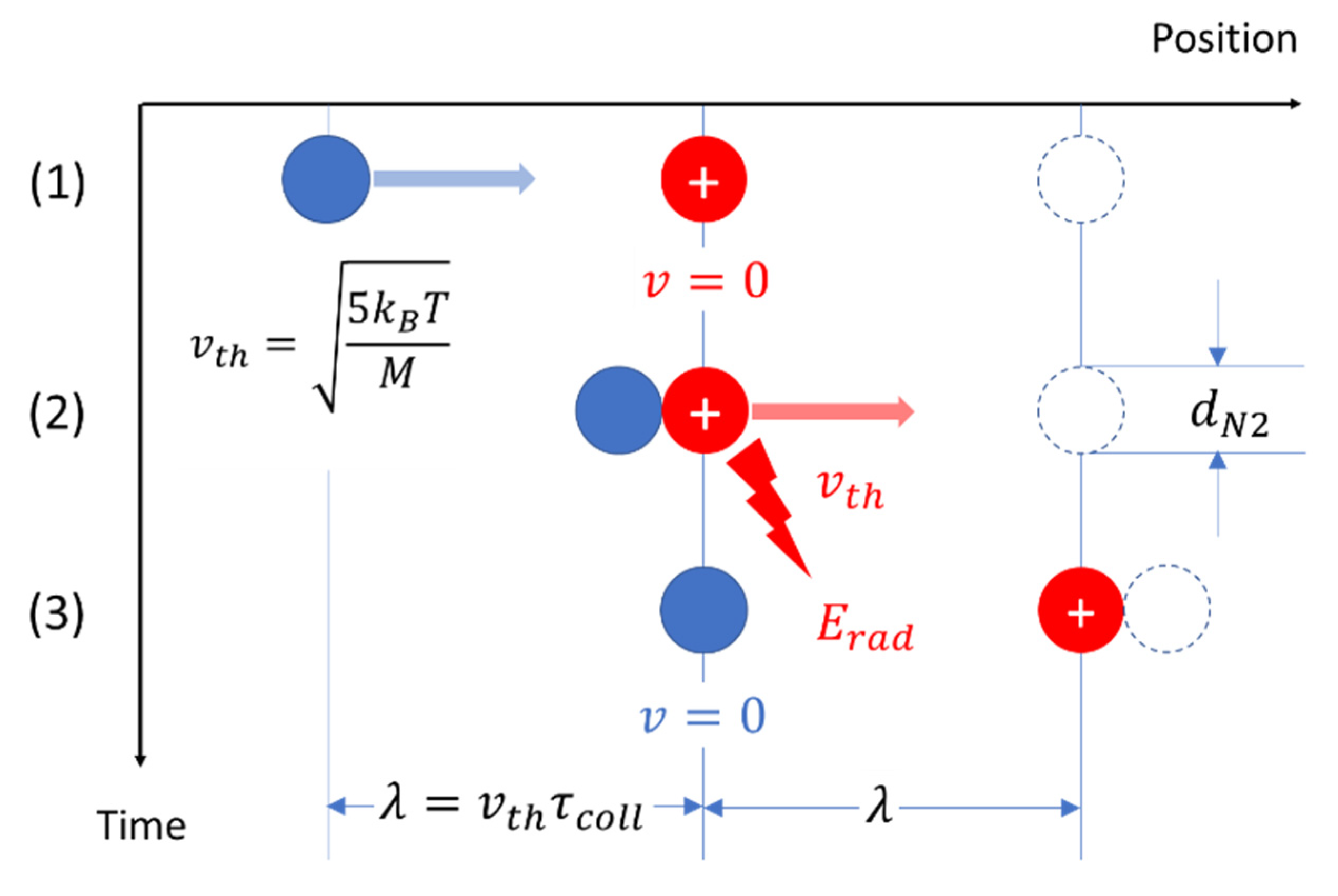
5. Dissipative Overhead and Irreversibility
- (i)
- the fractional loss of mechanical energy, , in each ion–molecule interaction,
- (ii)
- the number of collisions required to transfer the mean thermal energy of the moving ion toward its environment where it becomes dissipated,
- (iii)
- the total time, , required for this energy transfer,
- (iv)
- the length of the diffusion path, , covered in the time .
6. Summary and Conclusions
Funding
Acknowledgments
Conflicts of Interest
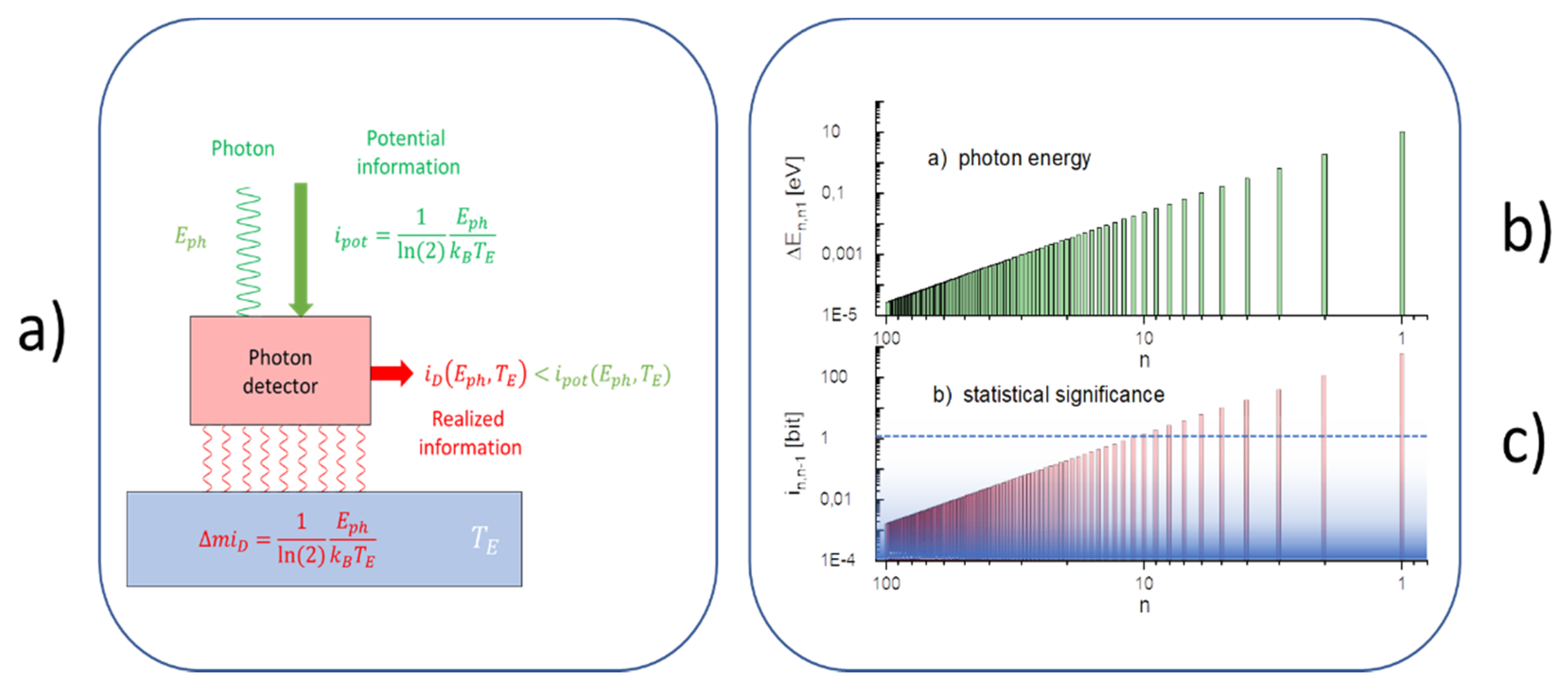
Appendix A. Photon Detection
References
- Goldstein, H.; Poole, C.P.; Safko, J.L. Klassische Mechanik; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2012. [Google Scholar]
- Nolting, W. Grundkurs Theoretische Physik 2—Analytische Mechanik; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2014. [Google Scholar]
- Maxwell, J.C. Theory of Heat; Longmans, Green, and Co.: London, UK, 1871. [Google Scholar]
- Kittel, C.; Krömer, H.; Mitter, M. Physik der Wärme; Oldenbourg Wissenschaftsverlag: München, Germany, 1993. [Google Scholar]
- Nolting, W. Grundkurs Theoretische Physik 5/1; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Leff, H.S.; Rex, A.F. (Eds.) Maxwell’s Demon: Entropy, Information, Computing; Adam Hilger: Bristol, UK; Princeton University Press: Princeton, UK, 1990. [Google Scholar]
- Leff, H.S.; Rex, A.F. (Eds.) Maxwell’s Demon 2: Entropy, Classical and Quantum Information, Computing, 1st ed.; Adam Hilger: Bristol, UK, 2003. [Google Scholar]
- Müller, J.G. Information contained in molecular motion. Entropy 2019, 21, 1052. [Google Scholar] [CrossRef]
- Müller, J.G. Photon detection as a process of information gain. Entropy 2020, 22, 392. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: New York, NY, USA; Chichester, UK; Brisbane, Australia; Toronto, ON, Canada, 1975. [Google Scholar]
- Nolting, W. Grundkurs Theoretische Physik 3—Elektrodynamik; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007. [Google Scholar]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics, 2nd ed.; John Wiley & Sons: New York, NY, USA; Chichester, UK; Brisbane, Australia; Toronto, ON, Canada; Singapore, 1985. [Google Scholar]
- Ben-Naim, A. A Farewell to Entropy: Statistical Thermodynamics Based on Information; World Scientific: Singapore, 2008. [Google Scholar]
- Falk, G.; Ruppel, W. Mechanik, Relativität, Gravitation; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1975. [Google Scholar]
- Falk, G.; Ruppel, W. Energie und Entropie: Eine Einführung in die Thermodynamik; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1976. [Google Scholar]
- Kingston, R.H. Detection of Optical and Infrared Radiation; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Bohr, N. On the constitution of atoms and molecules. Philos. Mag. J. Sci. 1913, 26, 1–25. [Google Scholar] [CrossRef]
- Schpolski, E.W. Atomphysik; VEB Deutscher Verlag der Wissenschaften: Berlin, Germany, 1970. [Google Scholar]
- Reader, J.; Corliss, C.H. Line Spectra of the Elements. In CRC Handbook of Chemistry and Physics; Rumble, J., Ed.; Taylor & Francis: Oxford, UK, 2018; ISBN 978-1-138-56163-2. [Google Scholar]
- Bormashenko, E. The Landauer Principle: Re-Formulation of the Second Thermodynamics Law or a Step to Great Unification? Entropy 2019, 21, 918. [Google Scholar] [CrossRef]
- Bormashenko, E. Informational Reinterpretation of the Mechanics Notions and Laws. Entropy 2020, 22, 631. [Google Scholar] [CrossRef]


| Interaction | ||||
|---|---|---|---|---|
| Gas–ion | ||||
| Gas–electron |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Müller, J.G. Observable and Unobservable Mechanical Motion. Entropy 2020, 22, 737. https://doi.org/10.3390/e22070737
Müller JG. Observable and Unobservable Mechanical Motion. Entropy. 2020; 22(7):737. https://doi.org/10.3390/e22070737
Chicago/Turabian StyleMüller, J. Gerhard. 2020. "Observable and Unobservable Mechanical Motion" Entropy 22, no. 7: 737. https://doi.org/10.3390/e22070737
APA StyleMüller, J. G. (2020). Observable and Unobservable Mechanical Motion. Entropy, 22(7), 737. https://doi.org/10.3390/e22070737





