Optimization Criteria and Efficiency of a Thermoelectric Generator
Abstract
:1. Introduction
2. Thermoelectric Model and Optimal Criteria
2.1. Thermoelectric Generator
2.2. Optimization Criteria
3. Internal Irreversibilities
4. Exoreversible Case
Optimization
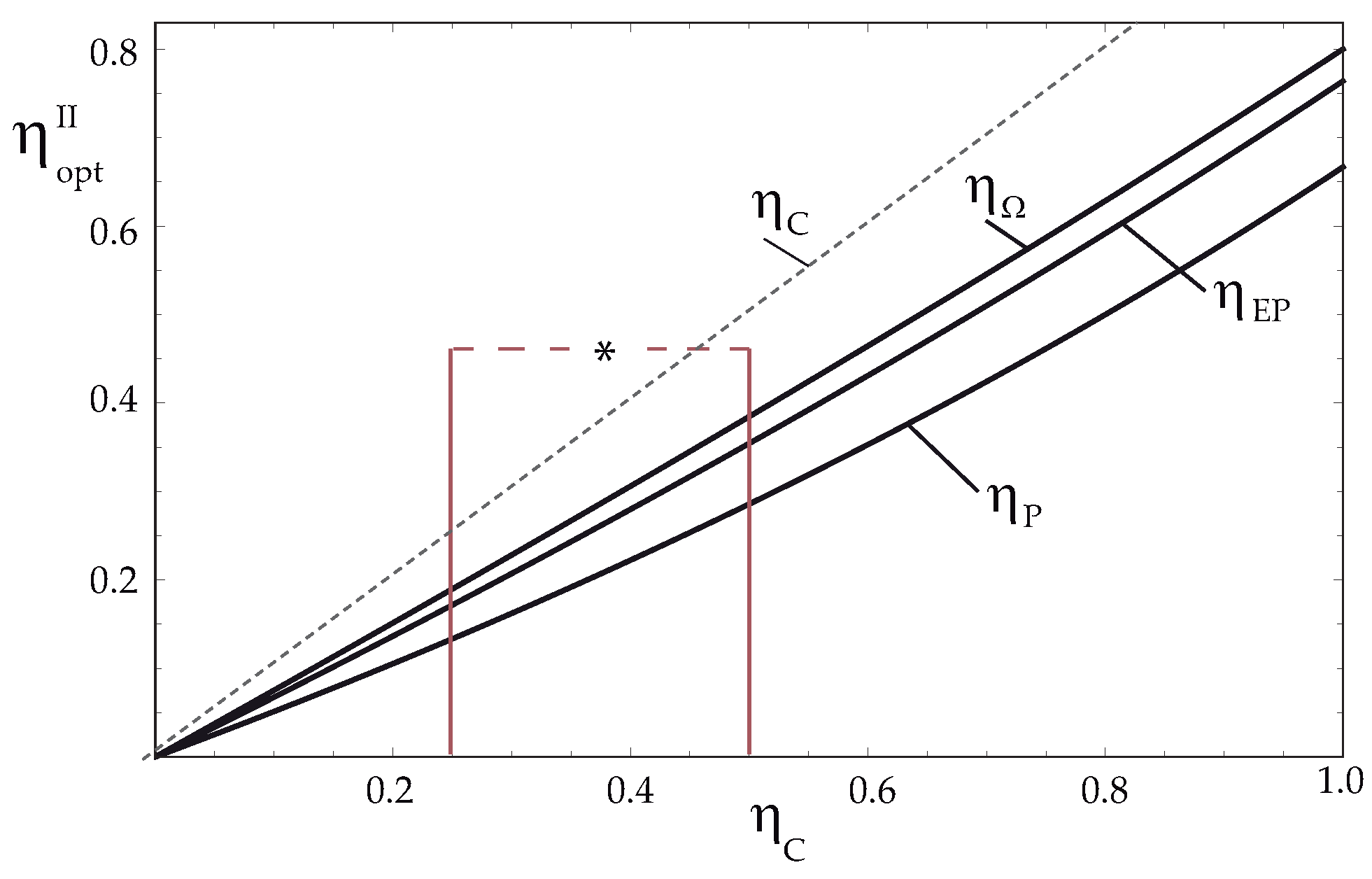
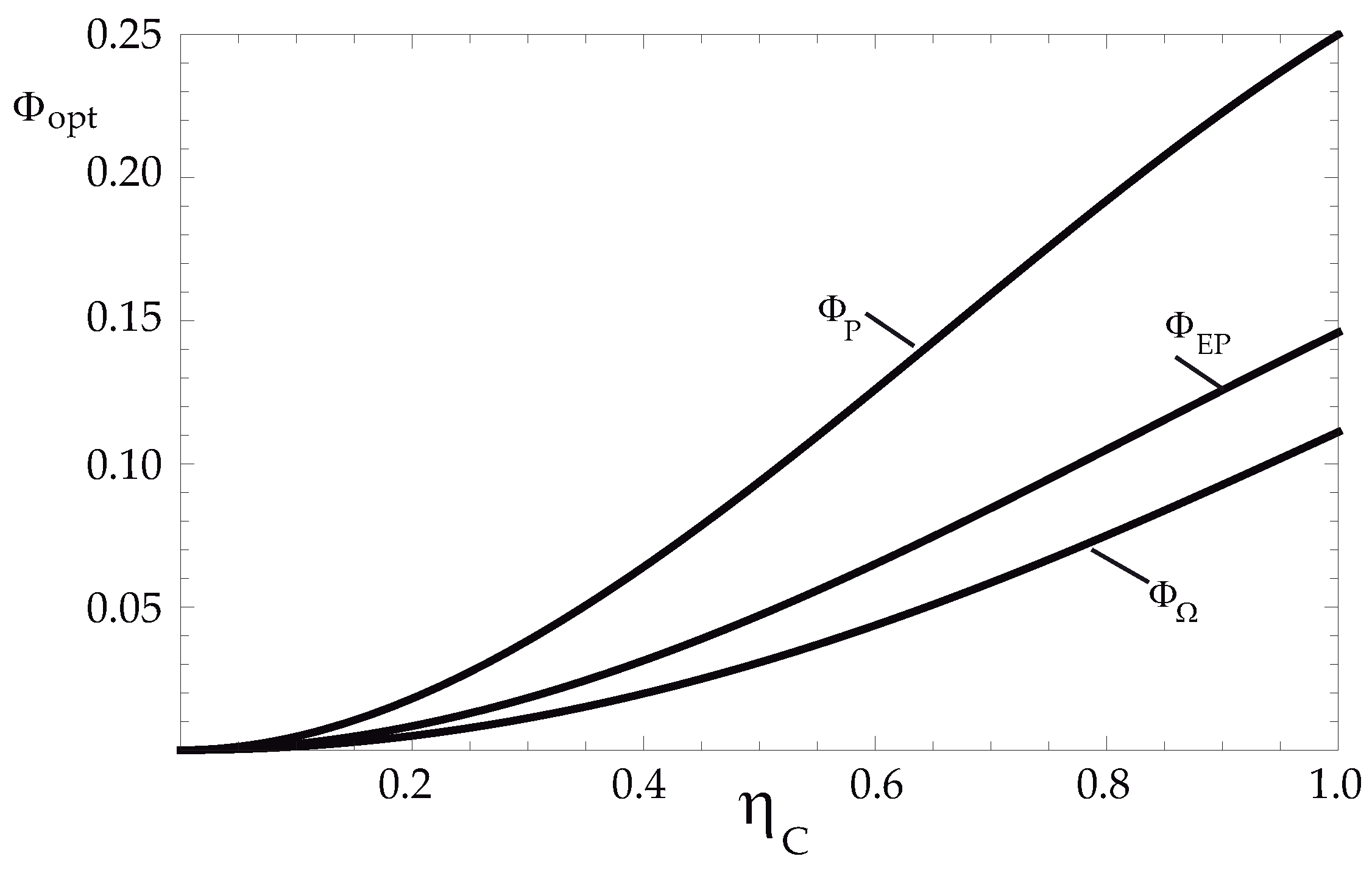
5. Endoreversible Limit
Optimization
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seebeck, T. Über den Magnetismus der Galvanischen Kette Abh k Akad; Wiss: Berlin, Germany, 1820; pp. 289–346. [Google Scholar]
- Seebeck, T.J. Magnetische Polarisation der Metalle und erze Durch Temperatur-Differenz; W. Engelmann: Leipzig, Germany, 1825; Number 70. [Google Scholar]
- Seebeck, T.J. Ueber die Magnetische Polarization der Metalle und Erze durch Temperatur-Differenz. Ann. Phys. Chem. 1826, 6, 1–20, 133–160, 253–286. [Google Scholar] [CrossRef] [Green Version]
- Peltier, J.C.A. Nouvelles expériences sur la caloricité des courants électrique. Ann. Chim. Phys. 1834, 56, 371–386. [Google Scholar]
- Thomson, W. On a Mechanical Theory of Thermo-electric Currents. Proc. R. Soc. Edinb. 1851, 3, 91–98. [Google Scholar] [CrossRef] [Green Version]
- Sieniutycz, S.; Salamon, P. Finite-Time Thermodynamics and Thermoeconomics; Taylor & Francis: New York, NY, USA, 1990. [Google Scholar]
- Calvo Hernández, A.; Roco, J.; Medina, A.; Sánchez-Salas, N. Heat engines and the Curzon-Ahlborn efficiency. Rev. Mex. Fis. 2014, 60, 384–389. [Google Scholar]
- Durmayaz, A.; Sogut, O.S.; Sahin, B.; Yavuz, H. Optimization of thermal systems based on finite-time thermodynamics and thermoeconomics. Prog. Energy Combust. Sci. 2004, 30, 175–217. [Google Scholar] [CrossRef]
- Kaushik, S.C.; Tyagi, S.K.; Kumar, P. Finite Time Thermodynamics of Power and Refrigeration Cycles; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Sieniutycz, S.; Jezowski, J. Energy Optimization in Process Systems and Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Fisher, A.; Hoffmann, K.H. Can a quantitative simulation of an Otto engine be accurately rendered by a simple Novikov model with heat leak? J. Non-Equilib. Thermodyn. 2004, 29, 9–28. [Google Scholar] [CrossRef]
- Curto-Risso, P.L.; Medina, A.; Hernández, A.C. Theoretical and simulated models for an irreversible Otto cycle. J. Appl. Phys. 2008, 104, 094911. [Google Scholar] [CrossRef]
- Curto-Risso, P.; Medina, A.; Calvo Hernández, A. Optimizing the operation of a spark ignition engine: Simulation and theoretical tools. J. Appl. Phys. 2009, 105, 094904. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Sun, F. Advances in Finite Time Thermodynamics, Analysis and Optimization; Nova Science Publishers, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Bejan, A. Entropy generation, minimization: The new thermodynamic of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef] [Green Version]
- Bejan, A. Notes on the History of the Method of Entropy Generation Minimization (Finite Time Thermodynamics). J. Non-Equilib. 1996, 21, 239–242. [Google Scholar]
- Chen, L.; Wu, C.; Sun, F. Finite Time Thermodynamic Optimization or Entropy Generation Minimization of Energy Systems. J. Non-Equilib. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Goupil, C.; Seifert, W.; Zabrocki, K.; Müller, E.; Snyder, G.J. Thermodynamics of Thermoelectric Phenomena and Applications. Entropy 2011, 13, 1481–1517. [Google Scholar] [CrossRef] [Green Version]
- Curzon, F.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Hernández, A.C.; Medina, A.; Roco, J.; White, J.; Velasco, S. Unified optimization criterion for energy converters. Phys. Rev. E 2001, 63, 037102. [Google Scholar] [CrossRef]
- Velasco, S.; Roco, J.; Medina, A.; White, J.; Hernández, A.C. Optimization of heat engines including the saving of natural resources and the reduction of thermal pollution. J. Phys. D Appl. Phys. 2000, 33, 355–359. [Google Scholar] [CrossRef]
- Yilmaz, T. A new performance criterion for heat engines: Efficient power. J. Energy Inst. 2006, 79, 38–41. [Google Scholar] [CrossRef]
- Insinga, A.; Andresen, B.; Salamon, P.; Kosloff, R. Quantum heat engines: Limit cycles and exceptional points. Phys. Rev. E 2018, 97, 062153. [Google Scholar] [CrossRef] [Green Version]
- Kosloff, R. A quantum mechanical open system as a model of a heat engines. J. Chem. Phys. 1984, 80, 1625–1631. [Google Scholar] [CrossRef]
- Stucki, J.W. The optimal efficiency and the economic degrees of coupling of oxidative phosphorylation. Eur. J. Biochem. 1980, 109, 269–283. [Google Scholar] [CrossRef]
- Odum, H.T.; Pinkerton, R.C. Time’s speed regulator: The optimum efficiency for maximum power output in physical and biological systems. Am. Sci. 1955, 43, 331–343. [Google Scholar]
- Santillán, M.; Arias-Hernandez, L.A.; Angulo-Brown, F. Some optimization criteria for biological systems in linear irreversible thermodynamics. Il Nuovo Cim. D 1997, 19, 99–109. [Google Scholar]
- Chimal-Eguia, J.; Paez-Hernandez, R.; Ladino-Luna, D.; Velázquez-Arcos, J.M. Performance of a simple energetic-converting reaction model using linear irreversible thermodynamics. Entropy 2019, 21, 1030. [Google Scholar] [CrossRef] [Green Version]
- Gordon, J.M.; Orlov, V.N. Performance characteristics of endoreversible chemical engines. J. Appl. Phys. 1993, 74, 5303–5309. [Google Scholar] [CrossRef]
- Vos, A.D. Endoreversible thermodynamics and chemical reactions. J. Phys. Chem. 1991, 95, 4534–4540. [Google Scholar] [CrossRef]
- Barranco-Jimenez, M.A.; Sanchez-Salas, N.; Angulo-Brown, F. Finite-Time Thermoeconomic Optimization of a Solar-Driven Heat Engine Model. Entropy 2011, 13, 171–183. [Google Scholar] [CrossRef]
- Sánchez-Salas, N.; Chimal-Eguía, J.C.; Guzmán-Aguilar, F. On the Dynamic Robustness of a Non-Endoreversible Engine Working in Different Operation Regimes. Entropy 2011, 13, 422–436. [Google Scholar] [CrossRef] [Green Version]
- Ha, M.; Park, J.; Lee, Y.; Ko, H. Triboelectric generators and sensors for self-powered wearable electronics. ACS Nano 2015, 9, 3421–3427. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Z.; Li, X.; Lin, Y.; Luo, N.; Long, M.; Zhao, N.; Xu, J.B. Flexible piezoelectric-induced pressure sensors for static measurements based on nanowires/graphene heterostructures. ACS Nano 2017, 11, 4507–4513. [Google Scholar] [CrossRef]
- Freer, R.; Powell, A.V. Realising the potential of thermoelectric technology: A Roadmap. J. Mater. Chem. C 2020, 8, 441–463. [Google Scholar] [CrossRef]
- Soleimani, Z.; Zoras, S.; Ceranic, B.; Cui, Y.; Shahzad, S. A comprehensive review on the output voltage/power of wearable thermoelectric generators concerning their geometry and thermoelectric materials. Nano Energy 2021, 89, 106325. [Google Scholar] [CrossRef]
- Zhu, S.; Fan, Z.; Feng, B.; Shi, R.; Jiang, Z.; Peng, Y.; Gao, J.; Miao, L.; Koumoto, K. Review on Wearable Thermoelectric Generators: From Devices to Applications. Energies 2022, 15, 3375. [Google Scholar] [CrossRef]
- Sattar, M.; Yeo, W.H. Recent Advances in Materials for Wearable Thermoelectric Generators and Biosensing Devices. Materials 2022, 15, 4315. [Google Scholar] [CrossRef] [PubMed]
- Shakouri, A. Recent developments in semiconductor thermoelectric physics and materials. Annu. Rev. Mater. Res. 2011, 41, 399–431. [Google Scholar] [CrossRef]
- Gonzalez-Hernandez, S.; Arias-Hernandez, L.A. Thermoelectric thomson relations revisited for a linear energy converter. J. Non-Equilib. Thermodyn. 2019, 44, 315–332. [Google Scholar] [CrossRef]
- Ouerdane, H.; Apertet, Y.; Goupil, C.; Lecoeur, P. Continuity and boundary conditions in thermodynamics: From Carnot’s efficiency to efficiencies at maximum power. Eur. Phys. J. Spec. Top. 2015, 224, 839–864. [Google Scholar] [CrossRef] [Green Version]
- Gross, E.T. Efficiency of thermoelectric devices. Am. J. Phys. 1961, 29, 729–731. [Google Scholar] [CrossRef]
- Goldsmid, H.J. Introduction to Thermoelectricity; Springer: Berlin/Heidelberg, Germany, 2010; Volume 121. [Google Scholar]
- Gordon, J.M. Generalized power versus efficiency characteristics of heat engines: The thermoelectric generator as an instructive illustration. Am. J. Phys. 1991, 59, 551–555. [Google Scholar] [CrossRef]
- Agrawal, D.C.; Menon, V.J. The thermoelectric generator as an endoreversible Carnot engine. J. Phys. D Appl. Phys. 1997, 30, 357–359. [Google Scholar] [CrossRef]
- Ding, L.C.; Akbarzadeh, A.; Tan, L. A review of power generation with thermoelectric system and its alternative with solar ponds. Renew. Sustain. Energy Rev. 2018, 81, 799–812. [Google Scholar] [CrossRef]
- Kaur, J.; Johal, R.S. Thermoelectric generator at optimal power with external and internal irreversibilities. J. Appl. Phys. 2019, 126, 125111. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, L.; Meng, F.; Sun, F. Thermodynamic analysis of TEG-TEC device including influence of Thomson effect. J. Non-Equilib. Thermodyn. 2018, 43, 75–86. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Yan, Z.; Wu, L. The influence of Thomson effect on the maximum power output and maximum efficiency of a thermoelectric generator. J. Appl. Phys. 1996, 79, 8823–8828. [Google Scholar] [CrossRef]
- Chen, J.; Li, K.; Liu, C.; Li, M.; Lv, Y.; Jia, L.; Jiang, S. Enhanced efficiency of thermoelectric generator by optimizing mechanical and electrical structures. Energies 2017, 10, 1329. [Google Scholar] [CrossRef] [Green Version]
- Ioffe, A. Semiconductor Thermoelements and Thermoelectric Cooling; Infosearch: London, UK, 1957. [Google Scholar]
- Schmiedl, T.; Seifert, U. Efficiency at maximum power: An analytically solvable model for stochastic heat engines. EPL (Europhys. Lett.) 2007, 81, 20003. [Google Scholar] [CrossRef]
- Champier, D. Thermoelectric generators: A review of applications. Energy Convers. Manag. 2017, 140, 167–181. [Google Scholar] [CrossRef]
- Zoui, M.A.; Bentouba, S.; Stocholm, J.G.; Bourouis, M. A review on thermoelectric generators: Progress and applications. Energies 2020, 13, 3606. [Google Scholar] [CrossRef]
- Chen, L.; Yan, Z. The effect of heat-transfer law on performance of a two-heat-source endoreversible cycle. J. Chem. Phys. 1989, 90, 3740–3743. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juárez-Huerta, V.H.; Sánchez-Salas, N.; Chimal-Eguía, J.C. Optimization Criteria and Efficiency of a Thermoelectric Generator. Entropy 2022, 24, 1812. https://doi.org/10.3390/e24121812
Juárez-Huerta VH, Sánchez-Salas N, Chimal-Eguía JC. Optimization Criteria and Efficiency of a Thermoelectric Generator. Entropy. 2022; 24(12):1812. https://doi.org/10.3390/e24121812
Chicago/Turabian StyleJuárez-Huerta, V. H., N. Sánchez-Salas, and J. C. Chimal-Eguía. 2022. "Optimization Criteria and Efficiency of a Thermoelectric Generator" Entropy 24, no. 12: 1812. https://doi.org/10.3390/e24121812





