Investigation of Fluid Characteristic and Performance of an Ejector by a Wet Steam Model
Abstract
:1. Introduction
2. Numerical Modelling
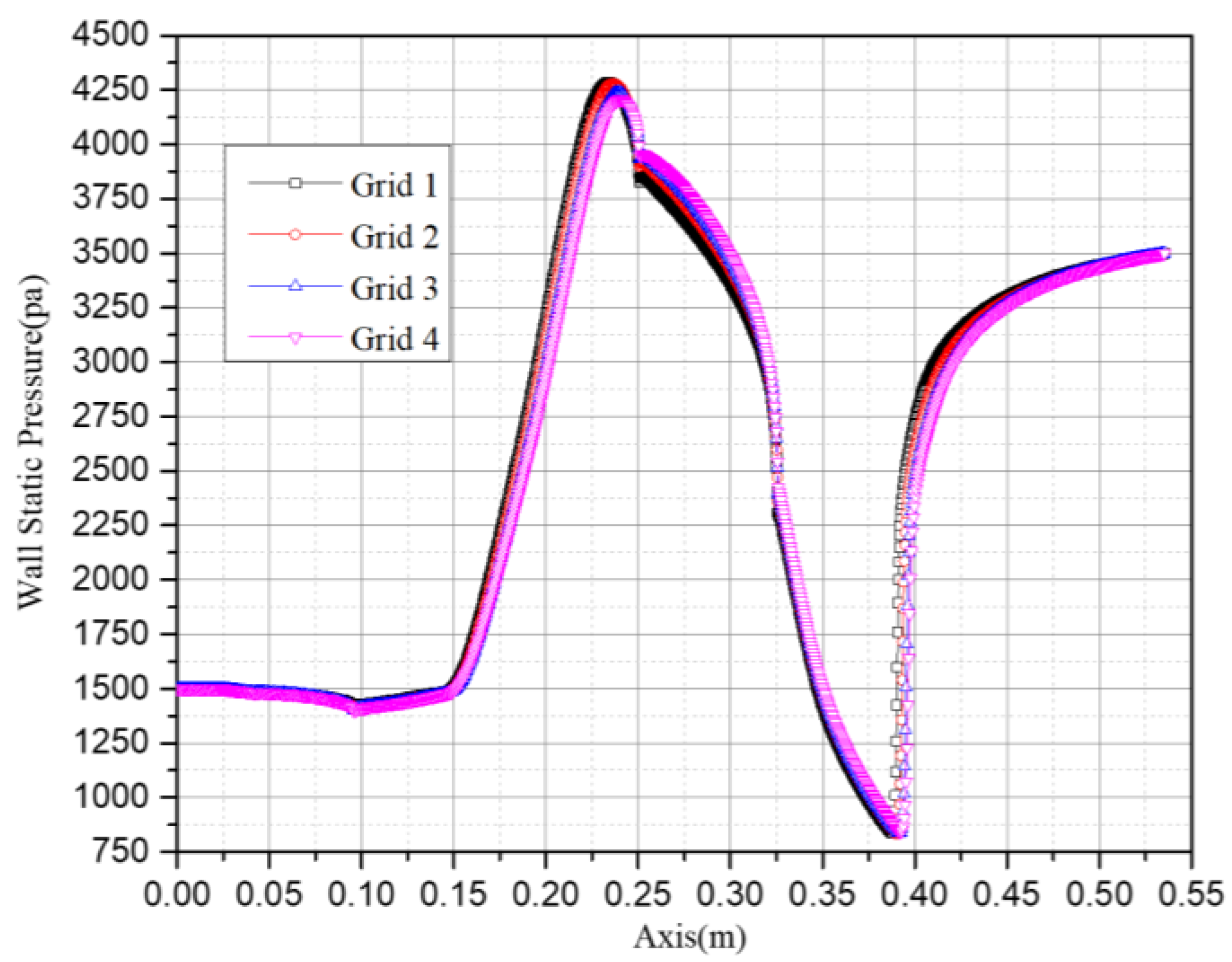
2.1. Grid Generation
2.2. Numerical Formulation
2.2.1. Governing Equations
2.2.2. Wet Steam Flow Equations
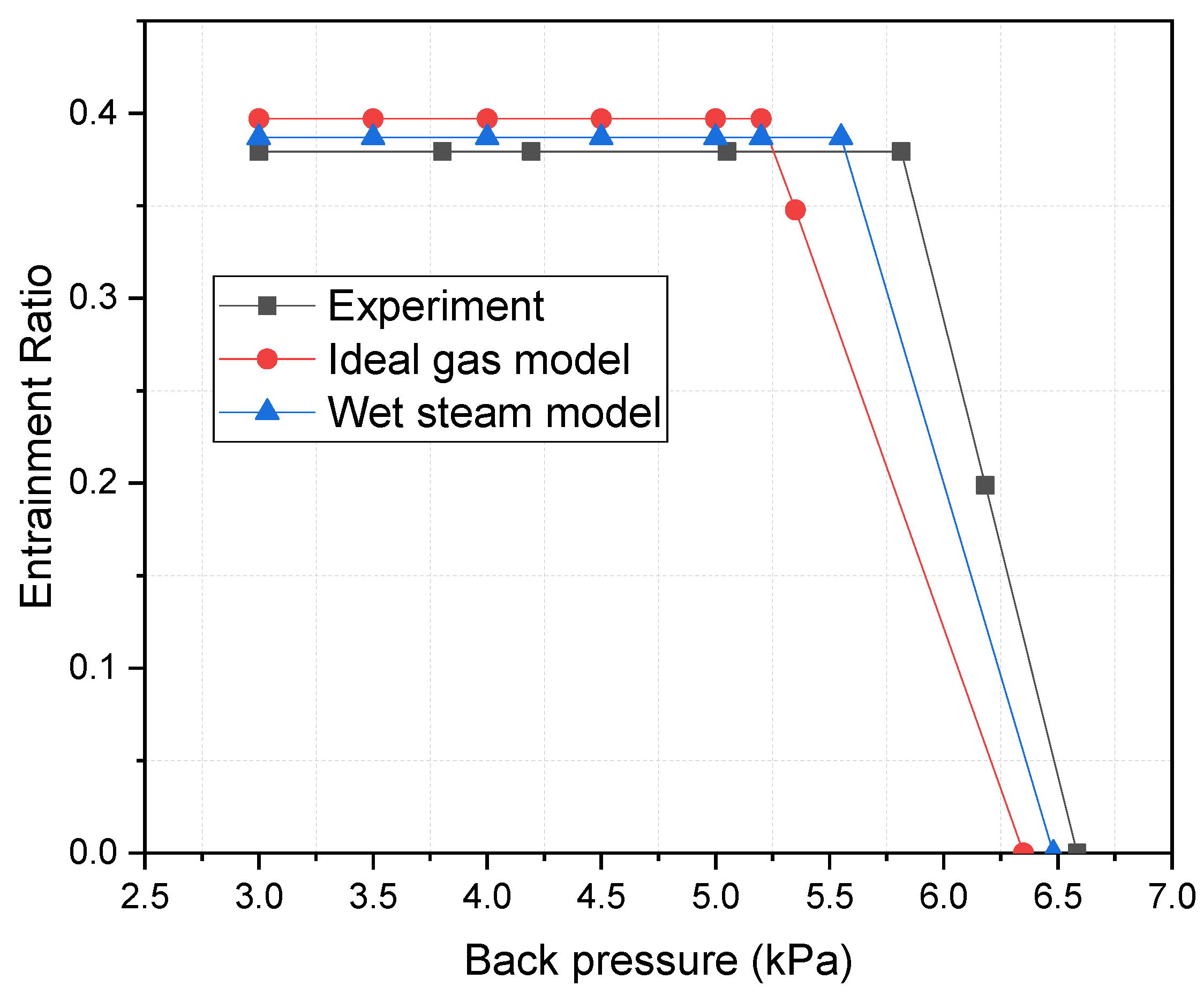
2.3. Model Validation
3. Results and Discussion
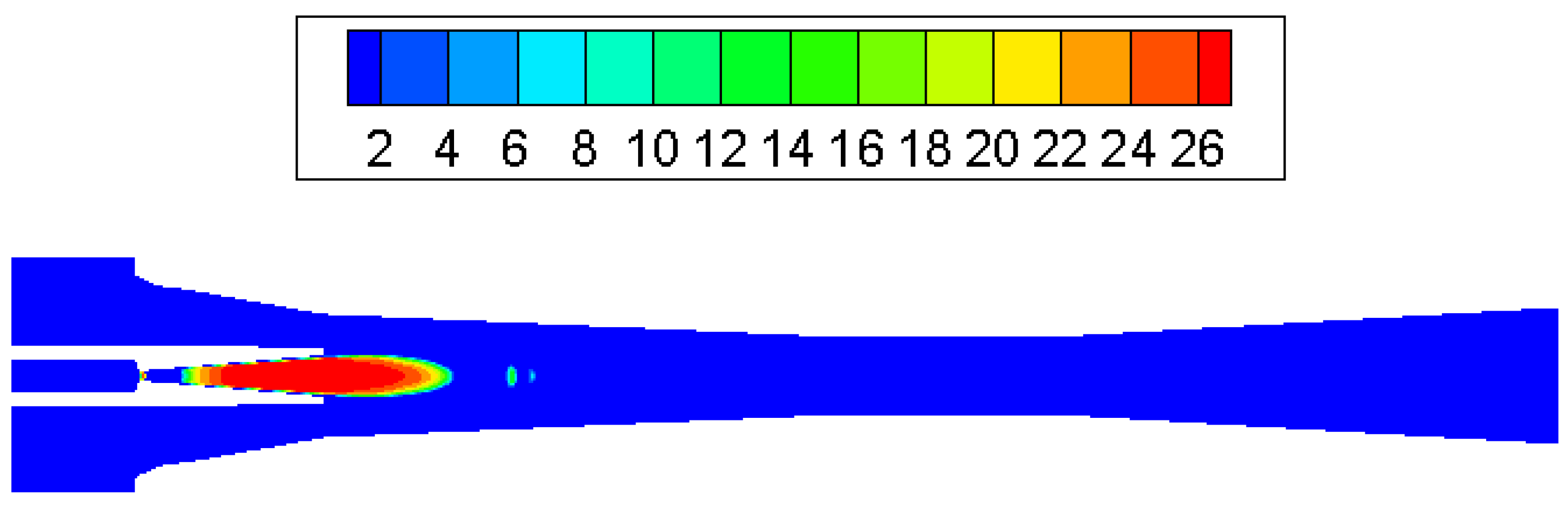
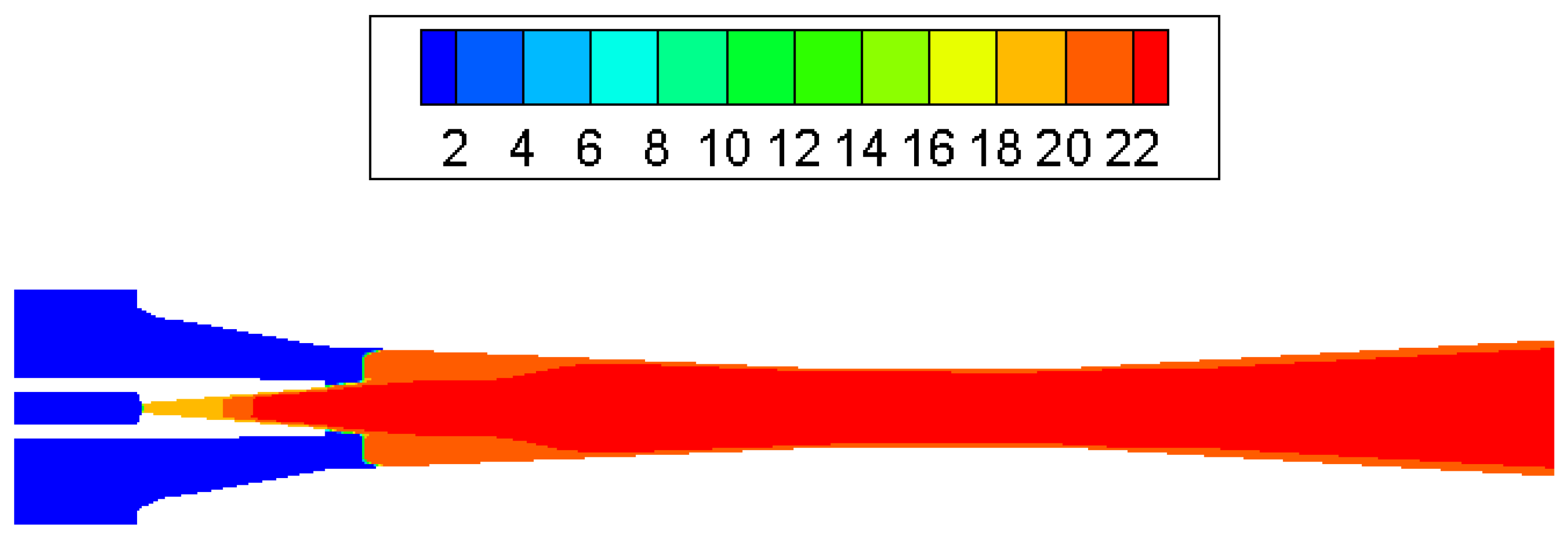
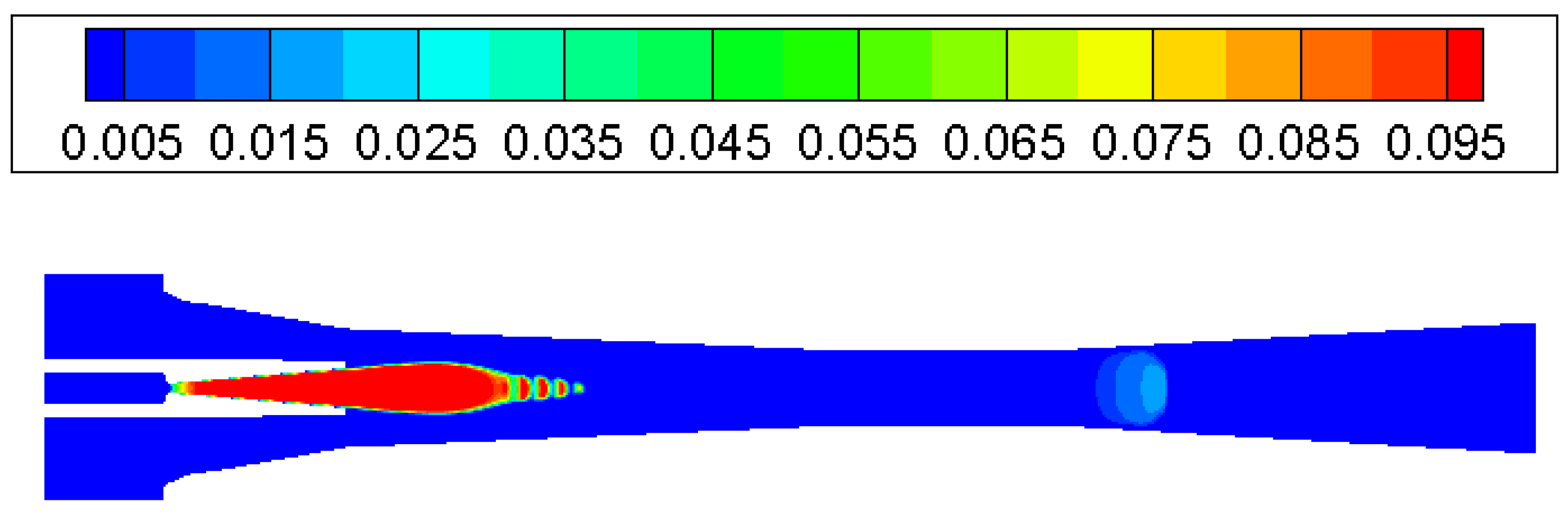
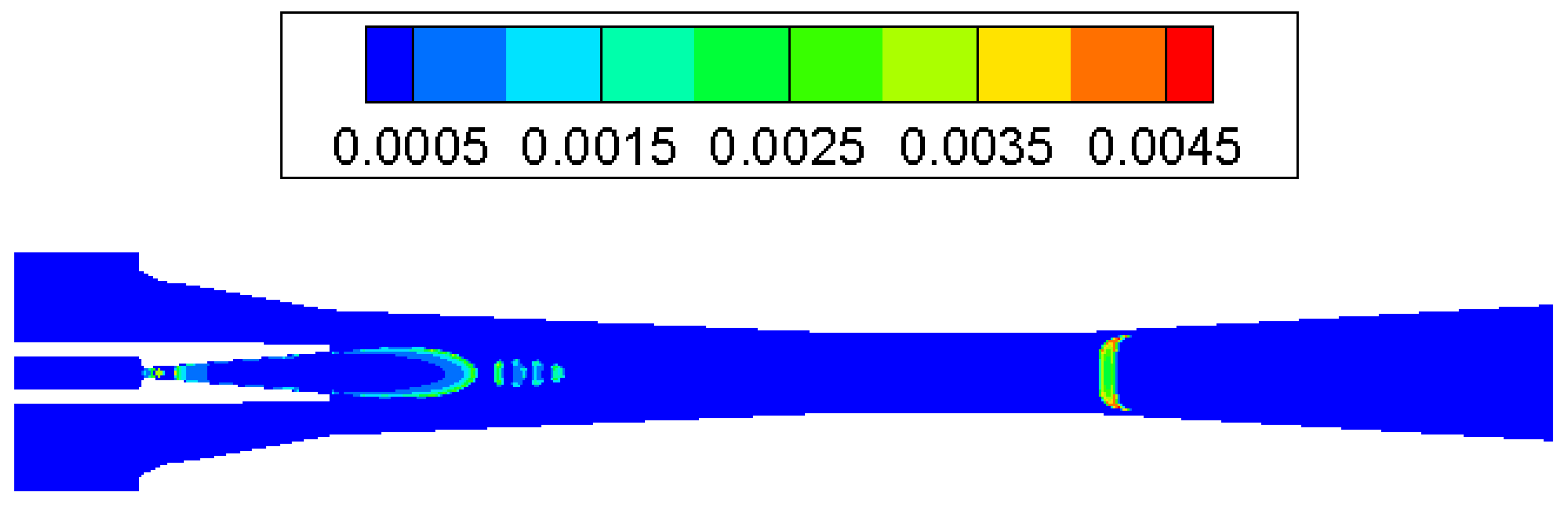
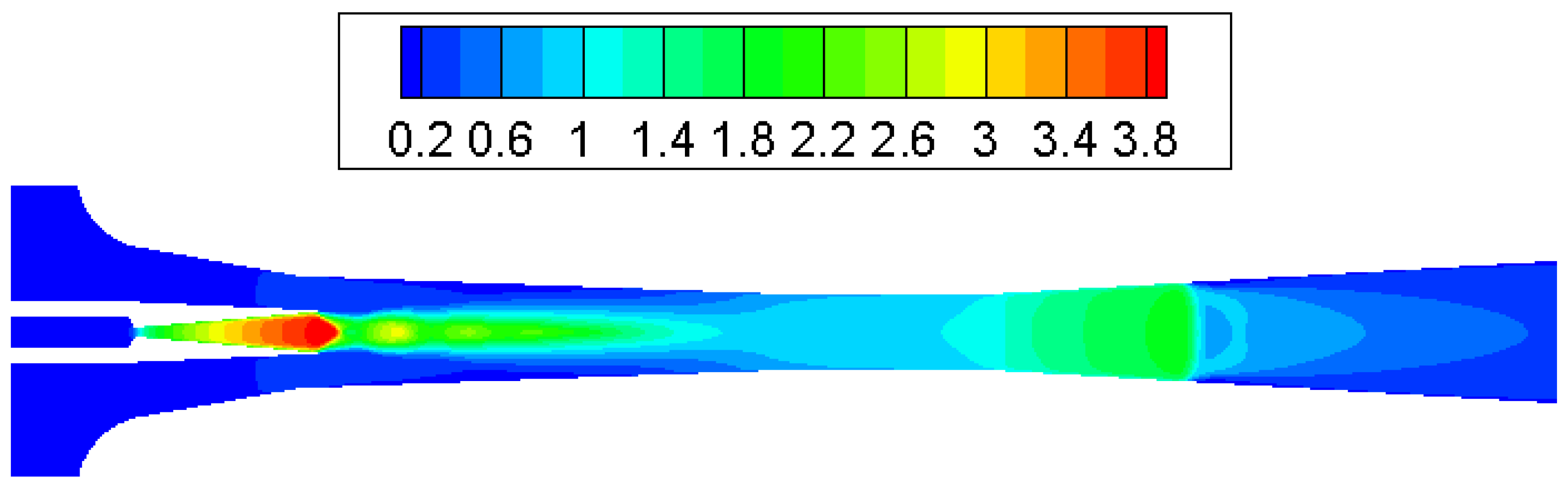
3.1. Condensation Phenomena inside Supersonic Ejector
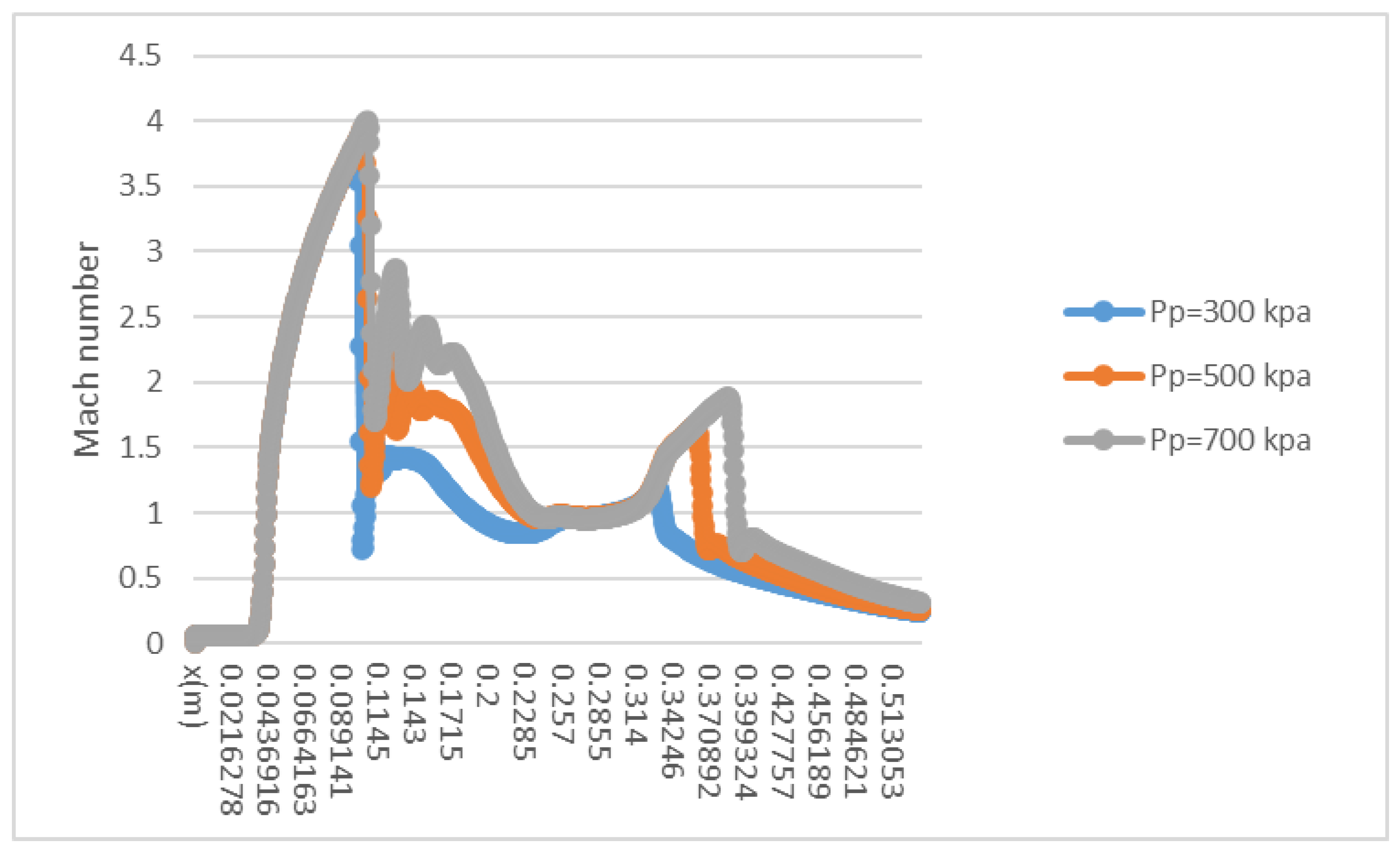
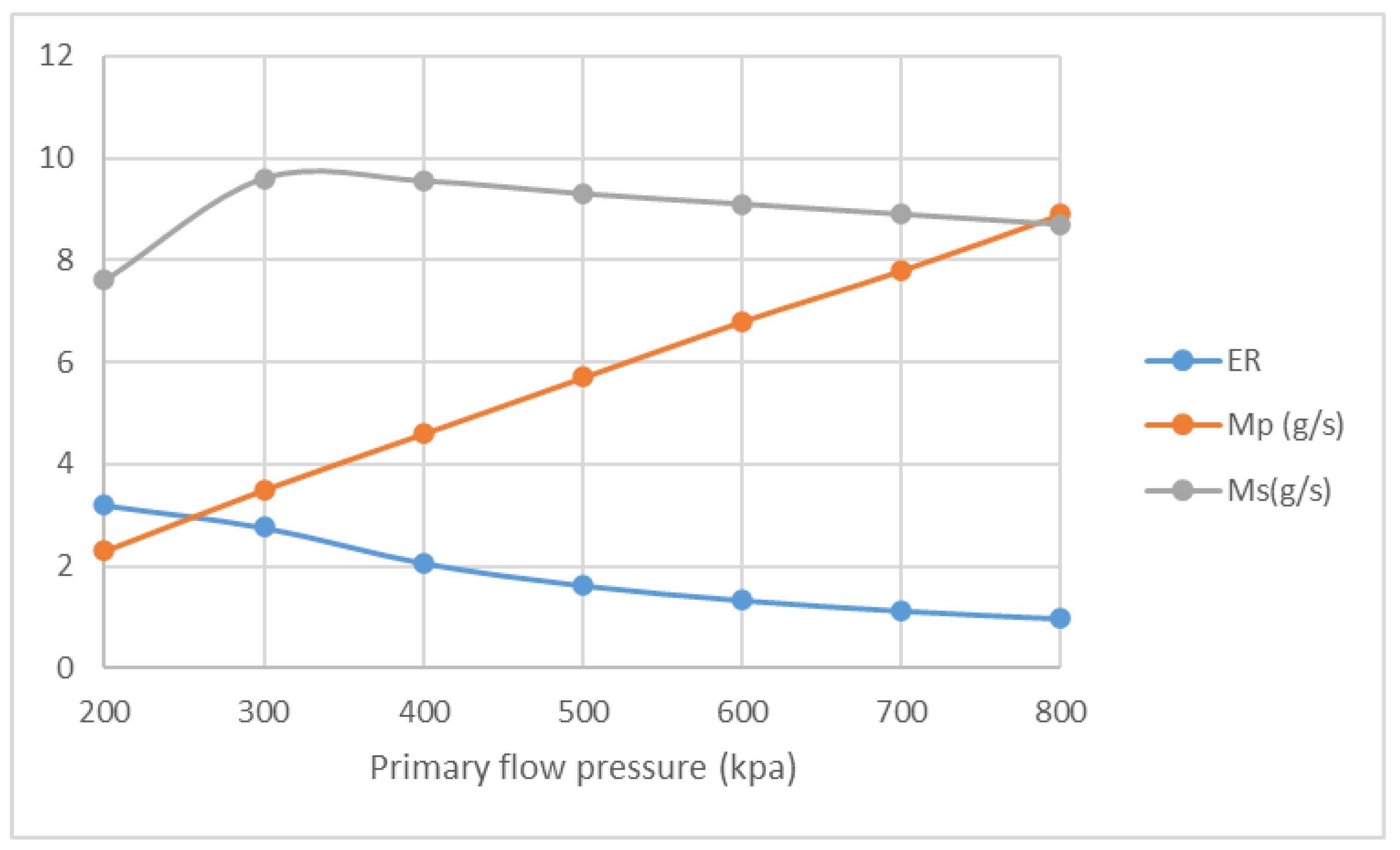
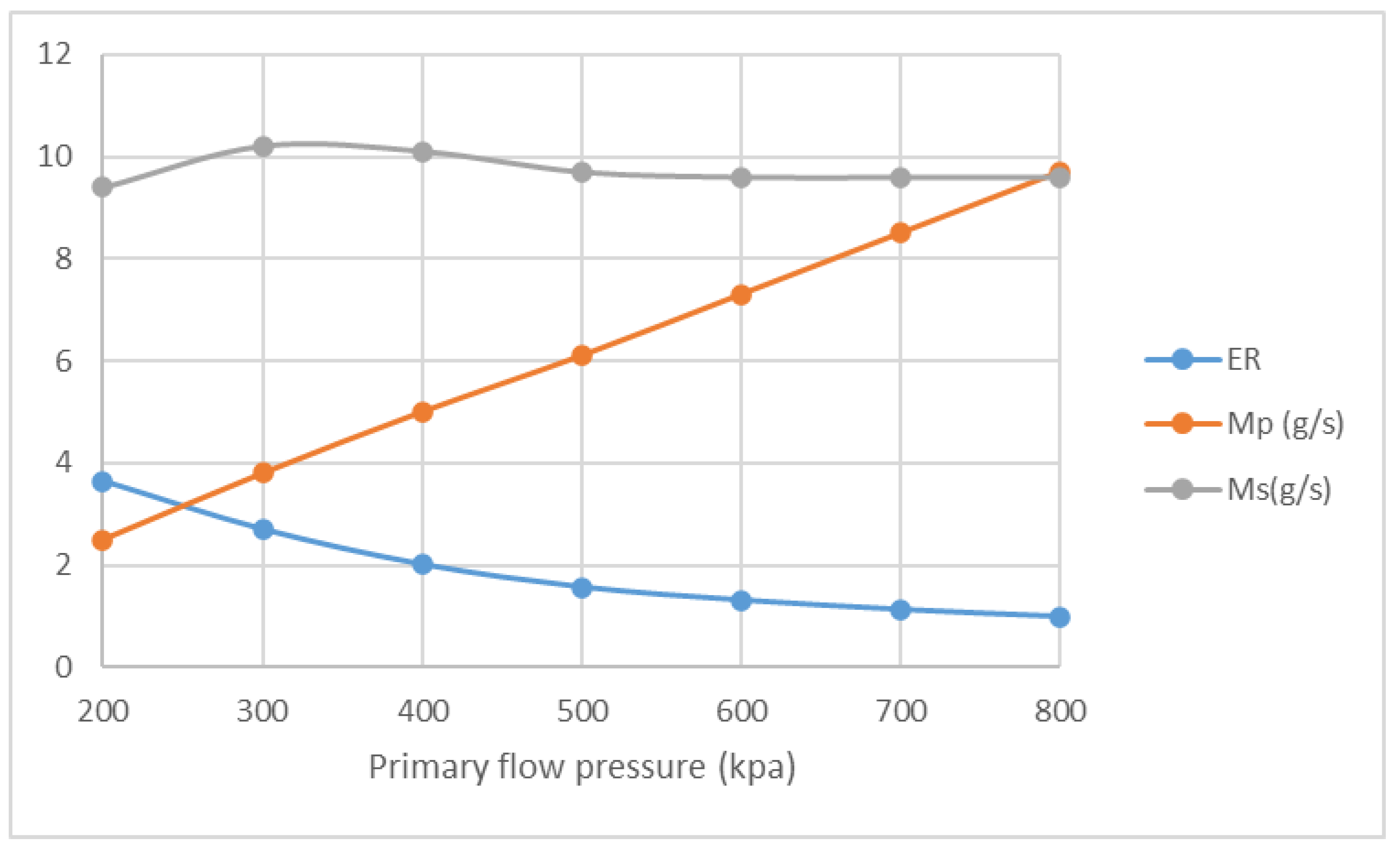
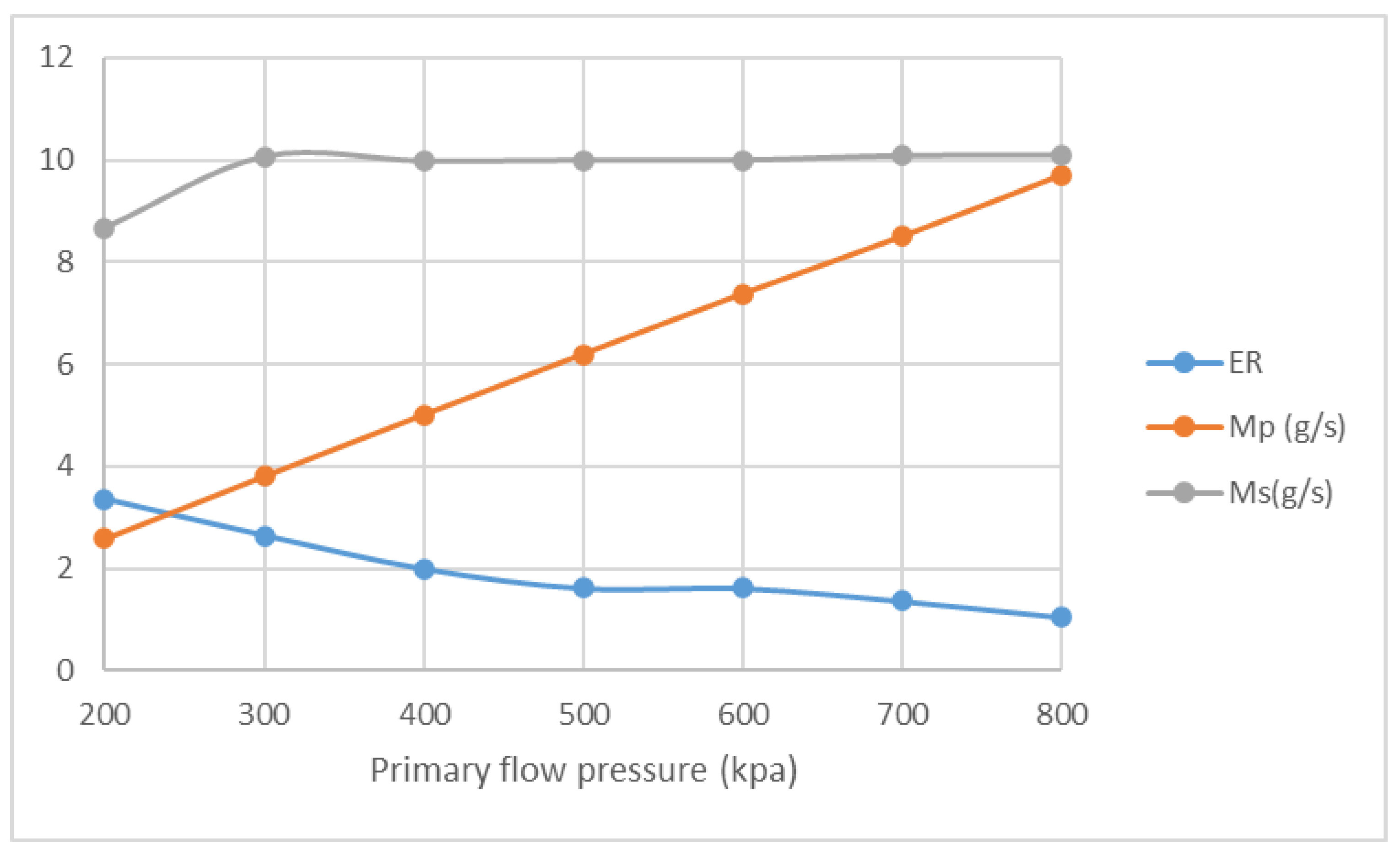
3.2. The Impact of the Primary Flow on Fluid Characteristic
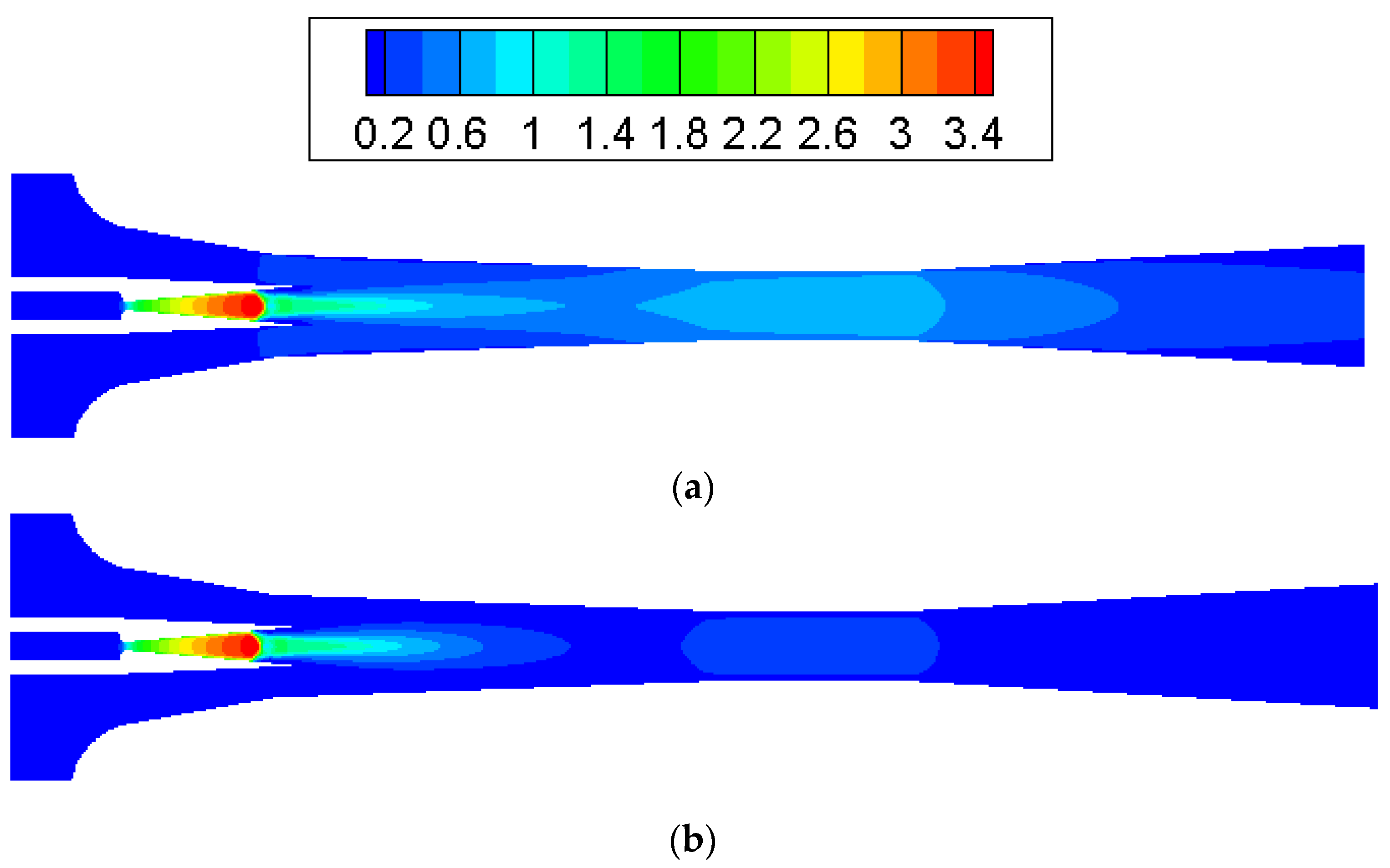
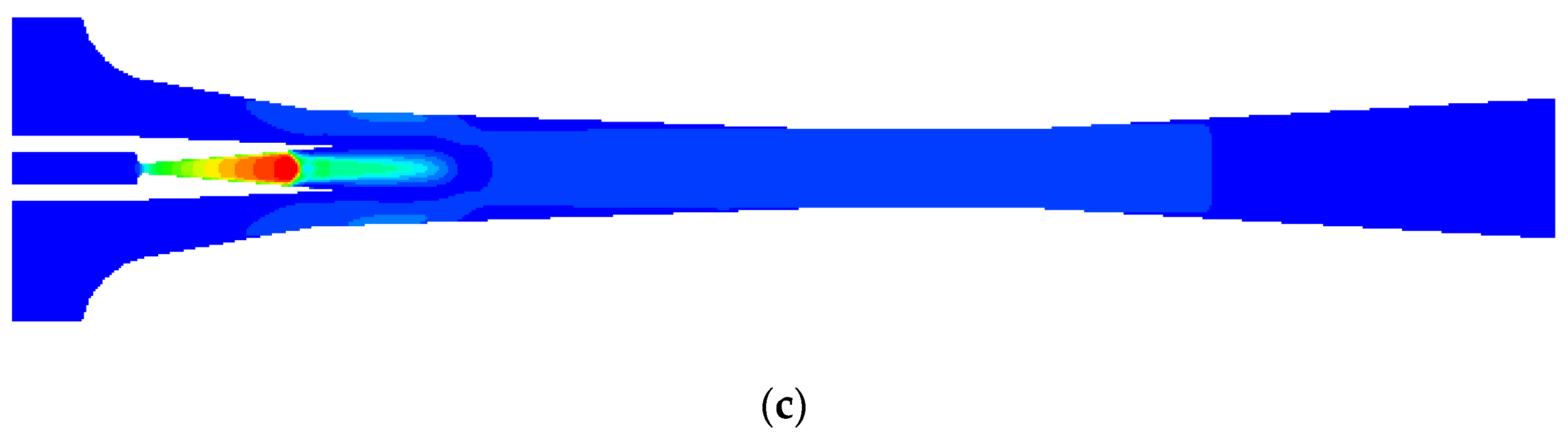
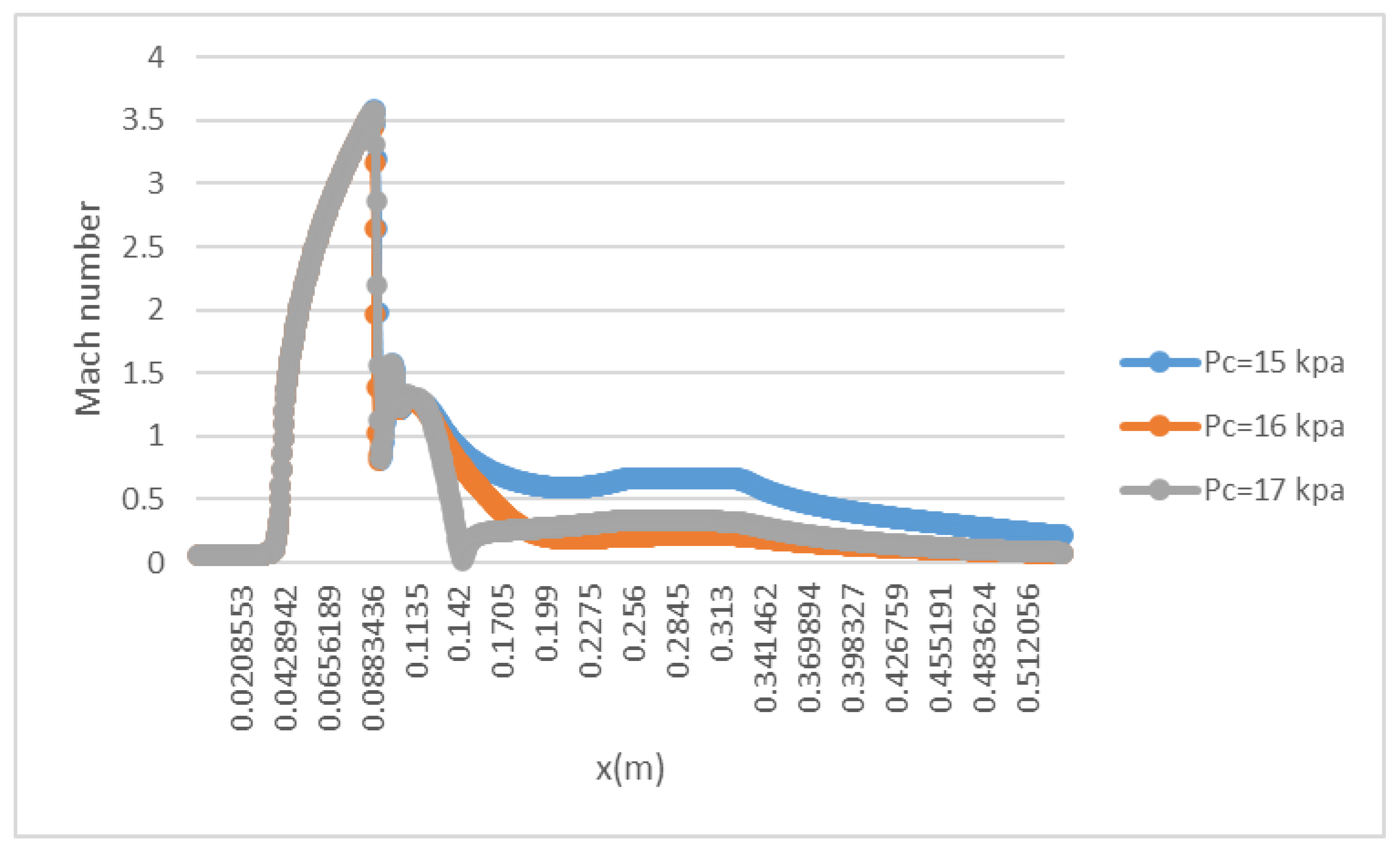
3.3. The Impact of Back Pressure on Fluid Characteristic
3.4. The Impact of Primary Flow and NXP on Supersonic Ejector
4. Conclusions
- (1)
- The most intensive condensation is located around the ejector nozzle downstream, nozzle exit region and the diffuser entrance.
- (2)
- The growth of primary flow pressure will lead to a decline in ER and a downward movement of second chocking position. The ejector may be quite responsive to a tiny change in the back pressure. Measures should be taken to make sure the ejector can work normally.
- (3)
- NXP has different influence on Ms with the change of primary flow pressure while ER drops and Mp increases sharply based on the rise of primary flow pressure at fixed NXP.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, X.; Wang, X.; Wang, L.; Qin, B.; Liu, H.; Jia, L.; Cai, W. Cooperative control of air and fuel feeding for PEM fuel cell with ejector-driven recirculation. Appl. Therm. Eng. 2021, 199, 117590. [Google Scholar] [CrossRef]
- Singer, G.; Gappmayer, G.; Macherhammer, M.; Pertl, P.; Trattner, A. A development toolchain for a pulsed injector-ejector unit for PEM fuel cell applications. Int. J. Hydrogen Energy 2022, 47, 23818–23832. [Google Scholar] [CrossRef]
- Guo, H.; Wang, C.; Wang, L. Optimization of the primary nozzle for design a high entrainment ejector in spacesuit portable life support system. Appl. Therm. Eng. 2022, 217, 119159. [Google Scholar] [CrossRef]
- Yan, J.; Wang, C. Experimental Study on a Multi-Evaporator Refrigeration System Equipped with EEV-Based Ejector. Entropy 2022, 24, 1302. [Google Scholar] [CrossRef] [PubMed]
- Van Nguyen, V.; Varga, S.; Soares, J.; Dvorak, V.; Oliveira, A.C. Applying a variable geometry ejector in a solar ejector refrigeration system. Int. J. Refrig. 2020, 113, 187–195. [Google Scholar] [CrossRef]
- Askalany, A.; Ali, E.S.; Mohammed, R.H. A novel cycle for adsorption desalination system with two stages-ejector for higher water production and efficiency. Desalination 2020, 496, 114753. [Google Scholar] [CrossRef]
- Keenan, J.H.; Neumann, E.P.; Lustwerk, F. An Investigation of Ejector Design by Analysis and Experiment. J. Appl. Mech. 1950, 17, 299–309. [Google Scholar] [CrossRef]
- Munday, J.T.; Bagster, D.F. A new ejector theory applied to steam jet refrigeration. Ind. Eng. Chem. Process Des. Dev. 1977, 16, 442–449. [Google Scholar] [CrossRef]
- Zhu, Y.; Cai, W.; Wen, C.; Li, Y. Shock circle model for ejector performance evaluation. Energy Convers. Manag. 2007, 48, 2533–2541. [Google Scholar] [CrossRef]
- Chen, W.; Liu, M.; Chong, D.; Yan, J.; Little, A.B.; Bartosiewicz, Y. A 1D model to predict ejector performance at critical and sub-critical operational regimes. Int. J. Refrig. 2013, 36, 1750–1761. [Google Scholar] [CrossRef]
- Yan, J.; Lin, C.; Cai, W.; Chen, H.; Wang, H. Experimental study on key geometric parameters of an R134A ejector cooling system. Int. J. Refrig. 2016, 67, 102–108. [Google Scholar] [CrossRef]
- Wang, L.; Yan, J.; Wang, C.; Li, X. Numerical study on optimization of ejector primary nozzle geometries. Int. J. Refrig. 2017, 76, 219–229. [Google Scholar] [CrossRef]
- Yan, J.; Cai, W.; Li, Y. Geometry parameters effect for air-cooled ejector cooling systems with R134a refrigerant. Renew. Energy 2012, 46, 155–163. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Wang, X.; Zhao, H. Design and numerical investigation of an adaptive nozzle exit position ejector in multi-effect distillation desalination system. Energy 2017, 140, 673–681. [Google Scholar] [CrossRef]
- Luiset, B.; Sanchette, F.; Billard, A.; Schuster, D. Mechanisms of stainless steels erosion by water droplets. Wear 2013, 303, 459–464. [Google Scholar] [CrossRef]
- Song, X.-G.; Park, J.-H.; Kim, S.-G.; Park, Y.-C. Performance comparison and erosion prediction of jet pumps by using a numerical method. Math. Comput. Model. 2013, 57, 245–253. [Google Scholar] [CrossRef]
- Zhang, G.; Dykas, S.; Yang, S.; Zhang, X.; Li, H.; Wang, J. Optimization of the primary nozzle based on a modified condensation model in a steam ejector. Appl. Therm. Eng. 2020, 171, 115090. [Google Scholar] [CrossRef]
- Sun, W.; Ma, X.; Ma, S.; Zhang, H.; Zhang, L.; Xue, H.; Jia, L. Effects of surface roughness and temperature on non-equilibrium condensation and entrainment performance in a desalination-oriented steam ejector. Appl. Therm. Eng. 2021, 196, 117264. [Google Scholar] [CrossRef]
- Abadi, S.M.A.N.R.; Kouhikamali, R.; Atashkari, K. Non-equilibrium condensation of wet steam flow within high-pressure thermo-compressor. Appl. Therm. Eng. 2015, 81, 74–82. [Google Scholar] [CrossRef]
- Ariafar, K.; Buttsworth, D.; Sharifi, N.; Malpress, R. Ejector primary nozzle steam condensation: Area ratio effects and mixing layer development. Appl. Therm. Eng. 2014, 71, 519–527. [Google Scholar] [CrossRef]
- Yang, B.; Ma, X.; Zhang, H.; Sun, W.; Jia, L.; Xue, H. Effect of Superheat Steam on Ejector in Distilled Water Preparation System for Medical Injection. Entropy 2022, 24, 960. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Wang, L.; Zou, T.; Zhang, H. Influences of area ratio and surface roughness on homogeneous condensation in ejector primary nozzle. Energy Convers. Manag. 2017, 149, 168–174. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Zhao, H.; Du, Z.; Ding, Z. Effects of superheated steam on non-equilibrium condensation in ejector primary nozzle. Int. J. Refrig. 2016, 67, 214–226. [Google Scholar] [CrossRef]
- Kumar, V.; Singhal, G.; Subbarao, P. Realization of novel constant rate of kinetic energy change (CRKEC) supersonic ejector. Energy 2018, 164, 694–706. [Google Scholar] [CrossRef]
- Ariafar, K.; Buttsworth, D.; Al-Doori, G.; Sharifi, N. Mixing layer effects on the entrainment ratio in steam ejectors through ideal gas computational simulations. Energy 2016, 95, 380–392. [Google Scholar] [CrossRef]
- Rand, C.P.; Croquer, S.; Poirier, M.; Poncet, S. Optimal nozzle exit position for a single-phase ejector (Experimental, numerical and thermodynamic modelling). Int. J. Refrig. 2022, 144, 108–117. [Google Scholar] [CrossRef]
- Poirier, M. Influence of operating conditions on the optimal nozzle exit position for vapor ejector. Appl. Therm. Eng. 2022, 210, 118377. [Google Scholar] [CrossRef]
- Ren, J.; Miao, C.; Wu, Y.; Li, Q.; Xu, J.; Zhang, L. Geometry dimension optimization of a liquid–gas vacuum ejector for MED-TVC system. Appl. Therm. Eng. 2022, 214, 118907. [Google Scholar] [CrossRef]
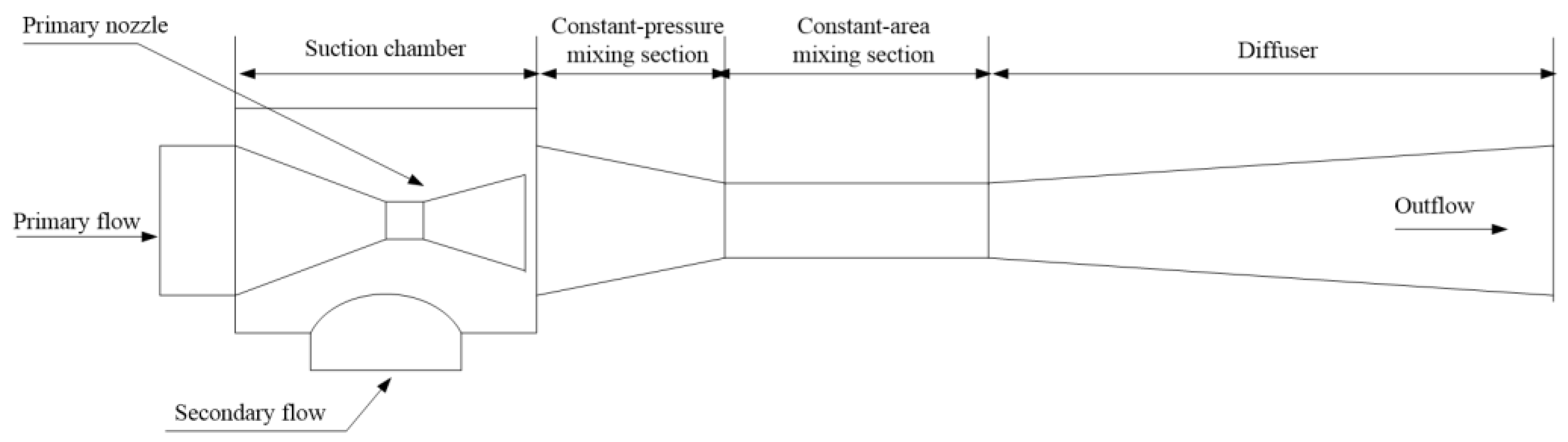

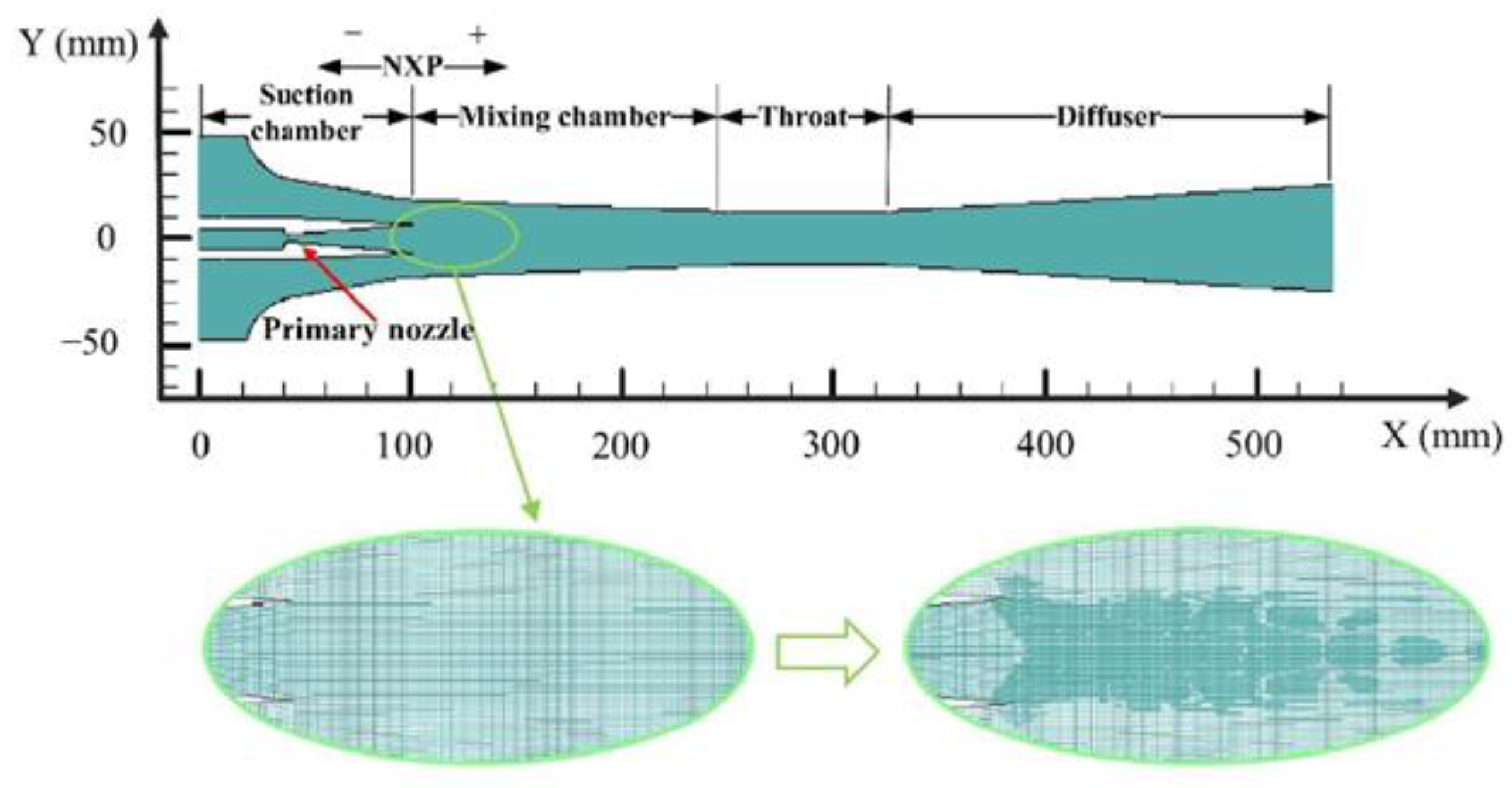



| Geometry Parameters | mm |
|---|---|
| Nozzle throat diameter | 3.2 |
| Nozzle exit position | 6 |
| Mixing chamber length | 155 |
| Throat diameter | 25.4 |
| Throat length | 75 |
| Diffuser length | 210 |
| Diffuser exit diameter | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Wang, L. Investigation of Fluid Characteristic and Performance of an Ejector by a Wet Steam Model. Entropy 2023, 25, 85. https://doi.org/10.3390/e25010085
Wang C, Wang L. Investigation of Fluid Characteristic and Performance of an Ejector by a Wet Steam Model. Entropy. 2023; 25(1):85. https://doi.org/10.3390/e25010085
Chicago/Turabian StyleWang, Chen, and Lei Wang. 2023. "Investigation of Fluid Characteristic and Performance of an Ejector by a Wet Steam Model" Entropy 25, no. 1: 85. https://doi.org/10.3390/e25010085






