High-Temperature Mechanical Properties of NbTaHfTiZrV0.5 Refractory High-Entropy Alloys
Abstract
:1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
- (1)
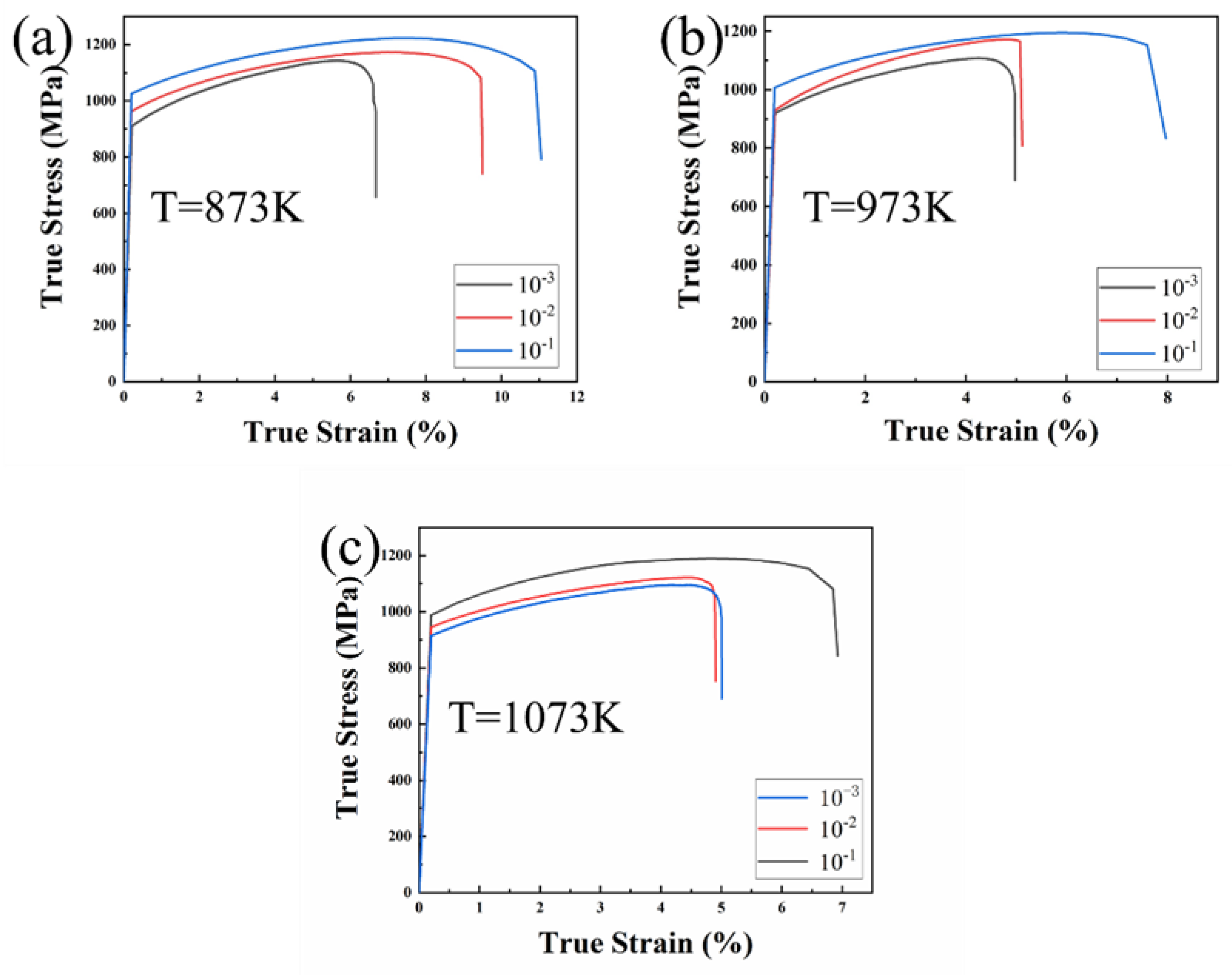
- Over a wide temperature range of RT-1223 K, the studied alloy exhibited excellent tensile mechanical properties. From RT to 678 K, the strength of the alloy was maintained above 1000 MPa; At 878–1078 K, the strength variation was small and no less than 800 MPa, and it nearly exceeded most commercial alloys. Coupled with an excellent cold workability, the alloy has the potential to be used as a new generation of high-temperature materials for the preparation of high-temperature-resistant parts in aerospace.
- (2)
- The true stress–strain curves of the alloy under different deformation conditions showed similar trends at temperatures between 873 K and 1073 K. That is, a work hardening occurred after yielding, and then a gradual softening until fracture. When the strain rate was constant, the yield strength and maximum strength of the alloy dropped as the temperature rose. When the deformation temperature remained constant, the strength grew in proportion to the strain rate.
- (3)
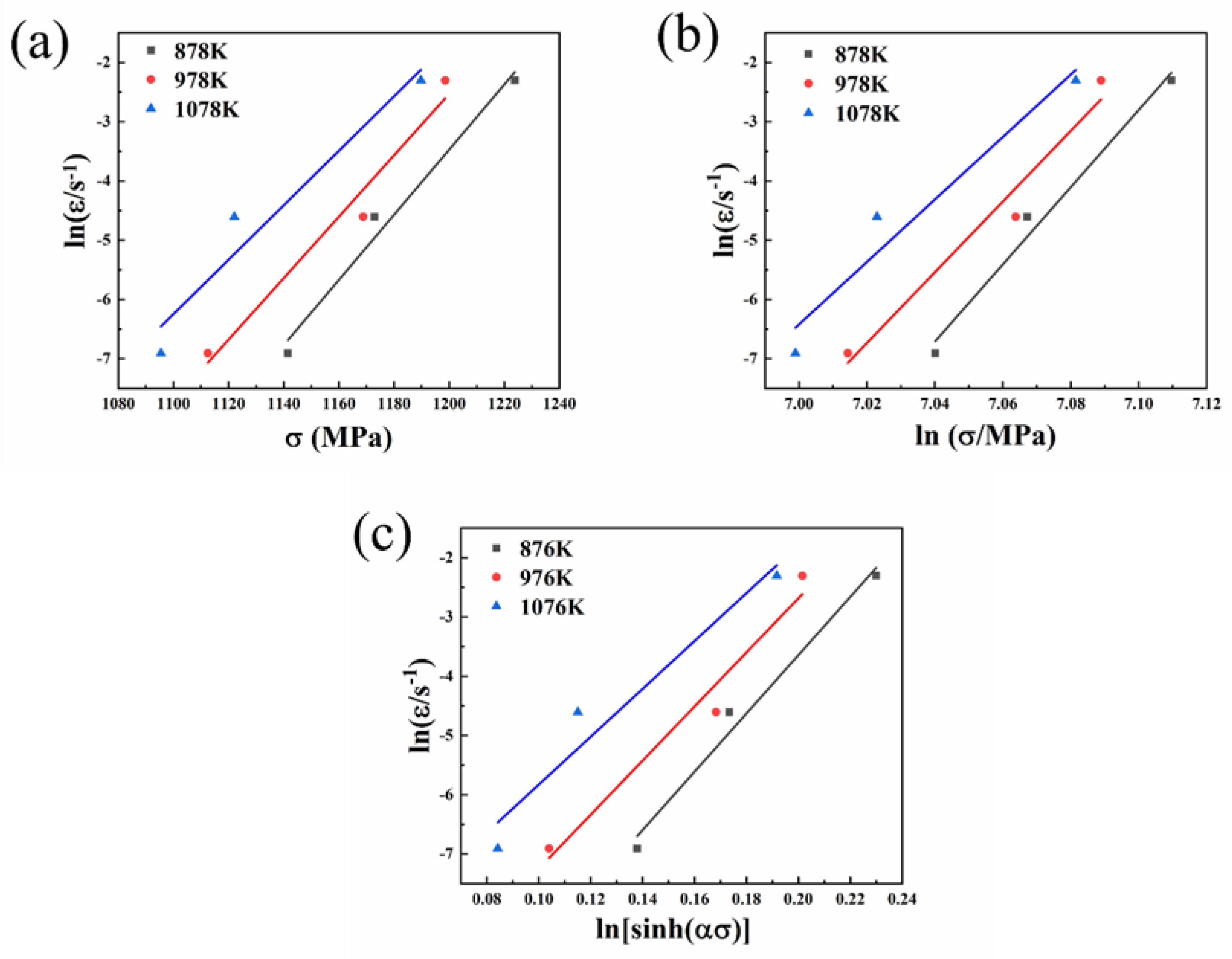
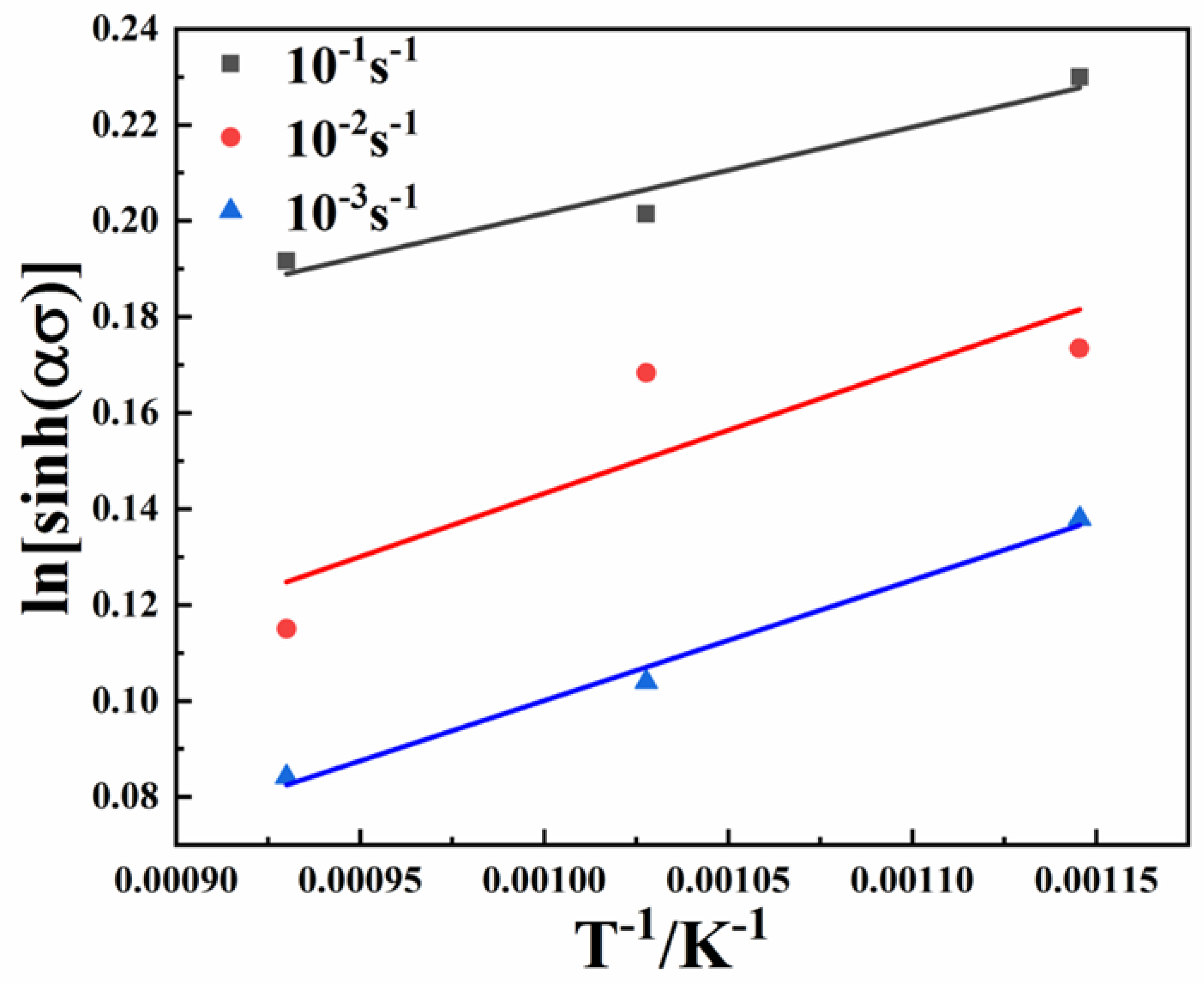
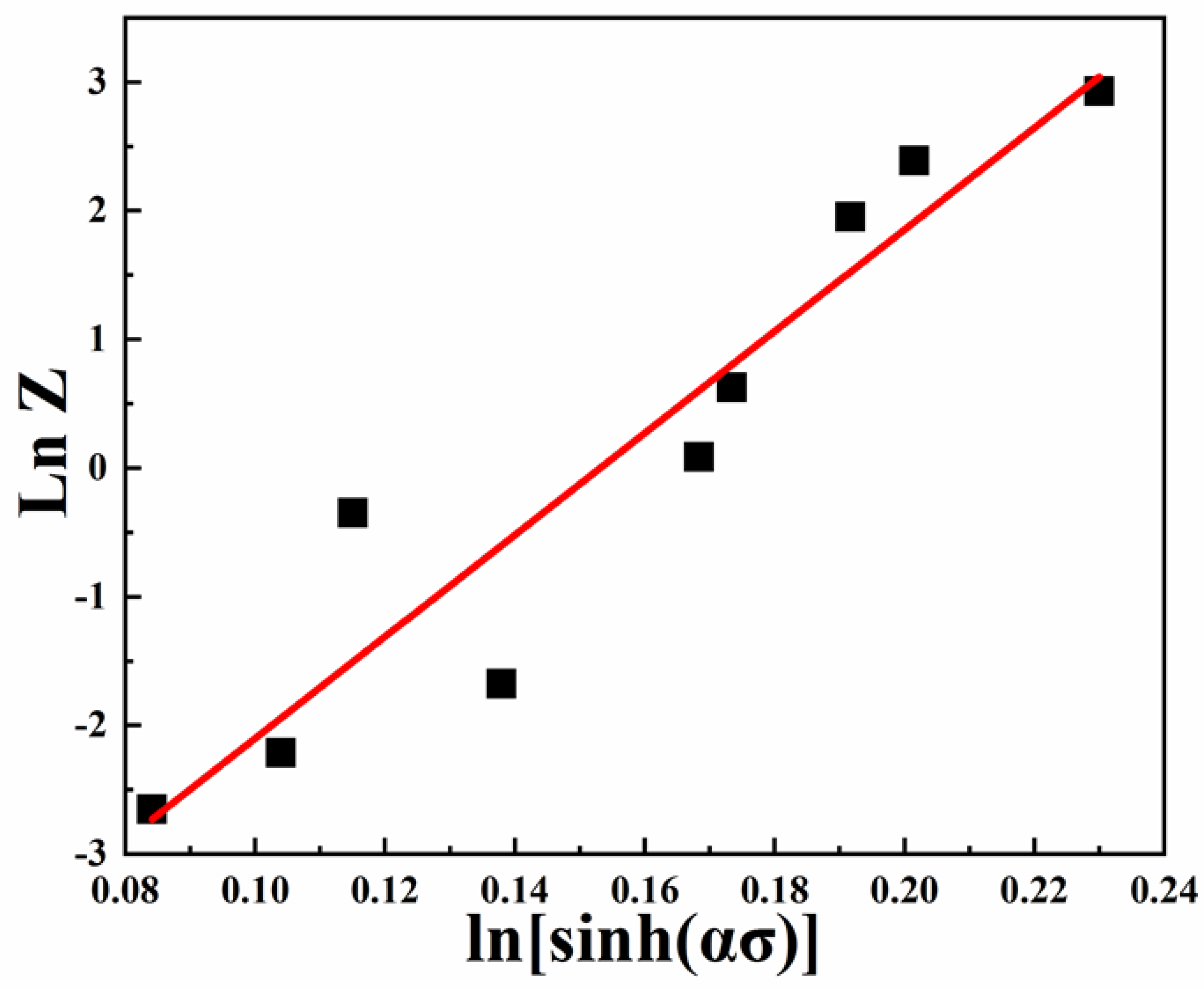
- Strain-dependent constitutive equations based on hyperbolic sine laws were taken into consideration to forecast the flow behavior at various temperatures and strain rates. The stress values predicted by the constitutive equation were in good agreement with the experimental values.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Perrut, M.; Caron, P.; Thomas, M.; Couret, A. High temperature materials for aerospace applications: Ni-based superalloys and γ-TiAl alloys. Comptes Rendus Phys. 2018, 19, 657–671. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Hu, J. Recent advances in the development of aerospace materials. Prog. Aerosp. Sci. 2018, 97, 22–34. [Google Scholar] [CrossRef]
- Zhang, Y. Science and technology in high-entropy alloys. Sci. China Mater. 2017, 61, 2–22. [Google Scholar] [CrossRef] [Green Version]
- Xia, W.; Zhao, X.; Yue, L.; Zhang, Z. A review of composition evolution in Ni-based single crystal superalloys. J. Mater. Sci. Technol. 2020, 44, 76–95. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Zhang, Y.; Zuo, T.T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z.P. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.; Zhao, Y.L.; Tong, Y.; Jiao, Z.B.; Wei, J.; Cai, J.X.; Han, X.D.; Chen, D.; Hu, A.; Kai, J.J.; et al. Multicomponent intermetallic nanoparticles and superb mechanical behaviors of complex alloys. Science 2018, 362, 933–937. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsai, M.-H.; Yeh, J.-W. High-Entropy Alloys: A Critical Review. Mater. Res. Lett. 2014, 2, 107–123. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.J.; Lin, J.P.; Chen, G.L.; Liaw, P.K. Solid-Solution Phase Formation Rules for Multi-component Alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Peng, Z.; Luo, Z.-B.; Li, B.-W.; Li, J.-F.; Luan, H.-W.; Gu, J.-L.; Wu, Y.; Yao, K.-F. Microstructure and mechanical properties of lightweight AlCrTiV0.5Cux high-entropy alloys. Rare Met. 2022, 41, 2016–2020. [Google Scholar] [CrossRef]
- Chen, Y.-T.; Chang, Y.-J.; Murakami, H.; Sasaki, T.; Hono, K.; Li, C.-W.; Kakehi, K.; Yeh, J.-W.; Yeh, A.-C. Hierarchical microstructure strengthening in a single crystal high entropy superalloy. Sci. Rep. 2020, 10, 12163. [Google Scholar] [CrossRef] [PubMed]
- Ming, K.; Bi, X.; Wang, J. Strength and ductility of CrFeCoNiMo alloy with hierarchical microstructures. Int. J. Plast. 2019, 113, 255–268. [Google Scholar] [CrossRef]
- Hasan, M.N.; Liu, Y.F.; An, X.H.; Gu, J.; Song, M.; Cao, Y.; Li, Y.S.; Zhu, Y.T.; Liao, X.Z. Simultaneously enhancing strength and ductility of a high-entropy alloy via gradient hierarchical microstructures. Int. J. Plast. 2019, 123, 178–195. [Google Scholar] [CrossRef]
- Gorsse, S.; Chen, Y.-T.; Hsu, W.-C.; Murakami, H.; Yeh, A.-C. Modeling the precipitation processes and the formation of hierarchical microstructures in a single crystal high entropy superalloy. Scr. Mater. 2021, 193, 147–152. [Google Scholar] [CrossRef]
- He, J.Y.; Wang, H.; Huang, H.L.; Xu, X.D.; Chen, M.W.; Wu, Y.; Liu, X.J.; Nieh, T.G.; An, K.; Lu, Z.P. A precipitation-hardened high-entropy alloy with outstanding tensile properties. Acta Mater. 2016, 102, 187–196. [Google Scholar] [CrossRef] [Green Version]
- Fu, Z.; Jiang, L.; Wardini, J.L.; MacDonald, B.E.; Wen, H.; Xiong, W.; Zhang, D.; Zhou, Y.; Rupert, T.J.; Chen, W.; et al. A high-entropy alloy with hierarchical nanoprecipitates and ultrahigh strength. Sci. Adv. 2018, 4, eaat8712. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef] [Green Version]
- Senkov, O.N.; Miracle, D.B.; Chaput, K.J.; Couzinie, J.-P. Development and exploration of refractory high entropy alloys—A review. J. Mater. Res. 2018, 33, 3092–3128. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Kim, G.; Chou, Y.; Musicó, B.L.; Gao, M.C.; An, K.; Song, G.; Chou, Y.-C.; Keppens, V.; Chen, W.; et al. Temperature dependence of elastic and plastic deformation behavior of a refractory high-entropy alloy. Sci. Adv. 2020, 6, eaaz4748. [Google Scholar] [CrossRef]
- Maresca, F.; Curtin, W.A. Mechanistic origin of high strength in refractory BCC high entropy alloys up to 1900K. Acta Mater. 2020, 182, 235–249. [Google Scholar] [CrossRef]
- Zou, Y.; Ma, H.; Spolenak, R. Ultrastrong ductile and stable high-entropy alloys at small scales. Nat. Commun. 2015, 6, 7748. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Senkov, O.N.; Scott, J.M.; Senkova, S.V.; Meisenkothen, F.; Miracle, D.B.; Woodward, C.F. Microstructure and elevated temperature properties of a refractory TaNbHfZrTi alloy. J. Mater. Sci. 2012, 47, 4062–4074. [Google Scholar] [CrossRef]
- Schuh, B.; Völker, B.; Todt, J.; Schell, N.; Perrière, L.; Li, J.; Couzinié, J.P.; Hohenwarter, A. Thermodynamic instability of a nanocrystalline, single-phase TiZrNbHfTa alloy and its impact on the mechanical properties. Acta Mater. 2018, 142, 201–212. [Google Scholar] [CrossRef]
- Wang, S.; Wu, M.; Shu, D.; Zhu, G.; Wang, D.; Sun, B. Mechanical instability and tensile properties of TiZrHfNbTa high entropy alloy at cryogenic temperatures. Acta Mater. 2020, 201, 517–527. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Z.; Yang, H.J.; Qiao, J.W.; Wang, Z.H.; Wu, Y.C. Ultra-high strain-rate strengthening in ductile refractory high entropy alloys upon dynamic loading. Intermetallics 2020, 121, 106699. [Google Scholar] [CrossRef]
- Lin, D.; Xi, X.; Li, X.; Hu, J.; Xu, L.; Han, Y.; Zhang, Y.; Zhao, L. High-temperature mechanical properties of FeCoCrNi high-entropy alloys fabricated via selective laser melting. Mater. Sci. Eng. A 2022, 832, 142354. [Google Scholar] [CrossRef]
- Smith, L.T.W.; Su, Y.; Xu, S.; Hunter, A.; Beyerlein, I.J. The effect of local chemical ordering on Frank-Read source activation in a refractory multi-principal element alloy. Int. J. Plast. 2020, 134, 102850. [Google Scholar] [CrossRef]
- Foreman, A.J.E.; Makin, M.J. Dislocation movement through random arrays of obstacles. Philos. Mag. J. Theor. Exp. Appl. Phys. 1966, 14, 911–924. [Google Scholar] [CrossRef]
- Eleti, R.R.; Stepanov, N.; Yurchenko, N.; Zherebtsov, S.; Maresca, F. Cross-kink unpinning controls the medium- to high-temperature strength of body-centered cubic NbTiZr medium-entropy alloy. Scr. Mater. 2022, 209, 114367. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, Y.; Cai, J.; Ji, S.; Geng, J.; Sun, X.; Li, D. High-strength NbMoTaX refractory high-entropy alloy with low stacking fault energy eutectic phase via laser additive manufacturing. Mater. Des. 2021, 201, 109462. [Google Scholar] [CrossRef]
- He, S.; Zhou, X.; Mordehai, D.; Marian, J. Thermal super-jogs control the high-temperature strength plateau in Nb-Mo-Ta-W alloys. Acta Mater. 2023, 244, 118539. [Google Scholar] [CrossRef]
- Maresca, F.; Curtin, W.A. Theory of screw dislocation strengthening in random BCC alloys from dilute to “High-Entropy” alloys. Acta Mater. 2020, 182, 144–162. [Google Scholar] [CrossRef]
- Ghafarollahi, A.; Maresca, F.; Curtin, W.A. Solute/screw dislocation interaction energy parameter for strengthening in bcc dilute to high entropy alloys. Modell. Simul. Mater. Sci. Eng. 2019, 27, 085011. [Google Scholar] [CrossRef]
- Ghafarollahi, A.; Curtin, W.A. Screw-controlled strength of BCC non-dilute and high-entropy alloys. Acta Mater. 2022, 226, 117617. [Google Scholar] [CrossRef]
- Lee, C.; Maresca, F.; Feng, R.; Chou, Y.; Ungar, T.; Widom, M.; An, K.; Poplawsky, J.D.; Chou, Y.-C.; Liaw, P.K.; et al. Strength can be controlled by edge dislocations in refractory high-entropy alloys. Nat. Commun. 2021, 12, 5474. [Google Scholar] [CrossRef]
- Robinson, J.S.; Hossain, S.; Truman, C.E.; Paradowska, A.M.; Hughes, D.J.; Wimpory, R.C.; Fox, M.E. Residual stress in 7449 aluminium alloy forgings. Mater. Sci. Eng. A 2010, 527, 2603–2612. [Google Scholar] [CrossRef]
- Anthony Xavior, M.; Manohar, M.; Madhukar, P.M.; Jeyapandiarajan, P. Experimental investigation of work hardening, residual stress and microstructure during machining Inconel 718. J. Mech. Sci. Technol. 2017, 31, 4789–4794. [Google Scholar] [CrossRef]
- Cottrell, A.H. Theory of dislocations. Prog. Met. Phys. 1953, 4, 205–264. [Google Scholar] [CrossRef]
- Brown, L.M. Strengthening Mechanisms in Crystal Plasticity, by Ali Argon. Contemp. Phys. 2013, 54, 306–307. [Google Scholar] [CrossRef]
- Pineau, A.; Benzerga, A.A.; Pardoen, T. Failure of metals I: Brittle and ductile fracture. Acta Mater. 2016, 107, 424–483. [Google Scholar] [CrossRef] [Green Version]
- Jia, J.; Liu, Z.; Li, X.; Du, C.; Li, W. Comparative study on the stress corrosion cracking of a new Ni-advanced high strength steel prepared by TMCP, direct quenching, and quenching & tempering. Mater. Sci. Eng. A 2021, 825, 141854. [Google Scholar] [CrossRef]
- Senkov, O.N.; Wilks, G.B.; Scott, J.M.; Miracle, D.B. Mechanical properties of Nb25Mo25Ta25W25 and V20Nb20Mo20Ta20W20 refractory high entropy alloys. Intermetallics 2011, 19, 698–706. [Google Scholar] [CrossRef]
- Stepanov, N.D.; Yurchenko, N.Y.; Panina, E.S.; Tikhonovsky, M.A.; Zherebtsov, S.V. Precipitation-strengthened refractory Al0.5CrNbTi2V0.5 high entropy alloy. Mater. Lett. 2017, 188, 162–164. [Google Scholar] [CrossRef]
- Senkov, O.N.; Senkova, S.V.; Miracle, D.B.; Woodward, C. Mechanical properties of low-density, refractory multi-principal element alloys of the Cr–Nb–Ti–V–Zr system. Mater. Sci. Eng. A 2013, 565, 51–62. [Google Scholar] [CrossRef]
- Han, Z.D.; Chen, N.; Zhao, S.F.; Fan, L.W.; Yang, G.N.; Shao, Y.; Yao, K.F. Effect of Ti additions on mechanical properties of NbMoTaW and VNbMoTaW refractory high entropy alloys. Intermetallics 2017, 84, 153–157. [Google Scholar] [CrossRef]
- Stepanov, N.D.; Yurchenko, N.Y.; Skibin, D.V.; Tikhonovsky, M.A.; Salishchev, G.A. Structure and mechanical properties of the AlCrxNbTiV (x = 0, 0.5, 1, 1.5) high entropy alloys. J. Alloys Compd. 2015, 652, 266–280. [Google Scholar] [CrossRef]
- Guo, N.N.; Wang, L.; Luo, L.S.; Li, X.Z.; Chen, R.R.; Su, Y.Q.; Guo, J.J.; Fu, H.Z. Microstructure and mechanical properties of in-situ MC-carbide particulates-reinforced refractory high-entropy Mo0.5NbHf0.5ZrTi matrix alloy composite. Intermetallics 2016, 69, 74–77. [Google Scholar] [CrossRef]
- Reed, R. The Superalloys Fundamentals and Applications. In Superalloys: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2006; pp. 1–372. [Google Scholar] [CrossRef]
- Sengupta, A.; Putatunda, S.K.; Bartosiewicz, L.; Hangas, J.; Nailos, P.J.; Peputapeck, M.; Alberts, F.E. Tensile behavior of a new single-crystal nickel-based superalloy (CMSX-4) at room and elevated temperatures. J. Mater. Eng. Perform. 1994, 3, 73–81. [Google Scholar] [CrossRef]
- Wee, S.; Do, J.; Kim, K.; Lee, C.; Seok, C.; Choi, B.-G.; Choi, Y.; Kim, W. Review on Mechanical Thermal Properties of Superalloys and Thermal Barrier Coating Used in Gas Turbines. Appl. Sci. 2020, 10, 5476. [Google Scholar] [CrossRef]
- Prasad, N.E.; Wanhill, R.J. (Eds.) Aerospace Materials and Material Technologies; Springer: Singapore, 2017. [Google Scholar]
- Xiao, Z.; Huang, Y.; Liu, H.; Wang, S. Hot Tensile and Fracture Behavior of 35CrMo Steel at Elevated Temperature and Strain Rate. Metals 2016, 6, 210. [Google Scholar] [CrossRef] [Green Version]
- Senkov, O.N.; Gorsse, S.; Miracle, D.B. High temperature strength of refractory complex concentrated alloys. Acta Mater. 2019, 175, 394–405. [Google Scholar] [CrossRef]
- Hou, J.X.; Liu, S.F.; Cao, B.X.; Luan, J.H.; Zhao, Y.L.; Chen, Z.; Zhang, Q.; Liu, X.J.; Liu, C.T.; Kai, J.J.; et al. Designing nanoparticles-strengthened high-entropy alloys with simultaneously enhanced strength-ductility synergy at both room and elevated temperatures. Acta Mater. 2022, 238, 118216. [Google Scholar] [CrossRef]
- Mills, L.H.; Emigh, M.G.; Frey, C.H.; Philips, N.R.; Murray, S.P.; Shin, J.; Gianola, D.S.; Pollock, T.M. Temperature-dependent tensile behavior of the HfNbTaTiZr multi-principal element alloy. Acta Mater. 2023, 245, 118618. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Liu, B.; Wang, Y.; Cao, Y.; Li, T.; Zhou, R. Flow behavior and microstructures of powder metallurgical CrFeCoNiMo0.2 high entropy alloy during high temperature deformation. Mater. Sci. Eng. A 2017, 689, 233–242. [Google Scholar] [CrossRef]
- Yu, Z.; Xie, B.; Zhu, Z.; Xu, B.; Sun, M. High-temperature deformation behavior and processing maps of a novel AlNbTi3VZr1.5 refractory high entropy alloy. J. Alloys Compd. 2022, 912, 165220. [Google Scholar] [CrossRef]
- Xia, X.; Chen, Q.; Huang, S.; Lin, J.; Hu, C.; Zhao, Z. Hot deformation behavior of extruded Mg–Zn–Y–Zr alloy. J. Alloys Compd. 2015, 644, 308–316. [Google Scholar] [CrossRef]
- Medina, S.F.; Hernandez, C.A. General expression of the Zener-Hollomon parameter as a function of the chemical composition of low alloy and microalloyed steels. Acta Mater. 1996, 44, 137–148. [Google Scholar] [CrossRef]
- Peng, W.; Zeng, W.; Wang, Q.; Yu, H. Characterization of high-temperature deformation behavior of as-cast Ti60 titanium alloy using processing map. Mater. Sci. Eng. A 2013, 571, 116–122. [Google Scholar] [CrossRef]
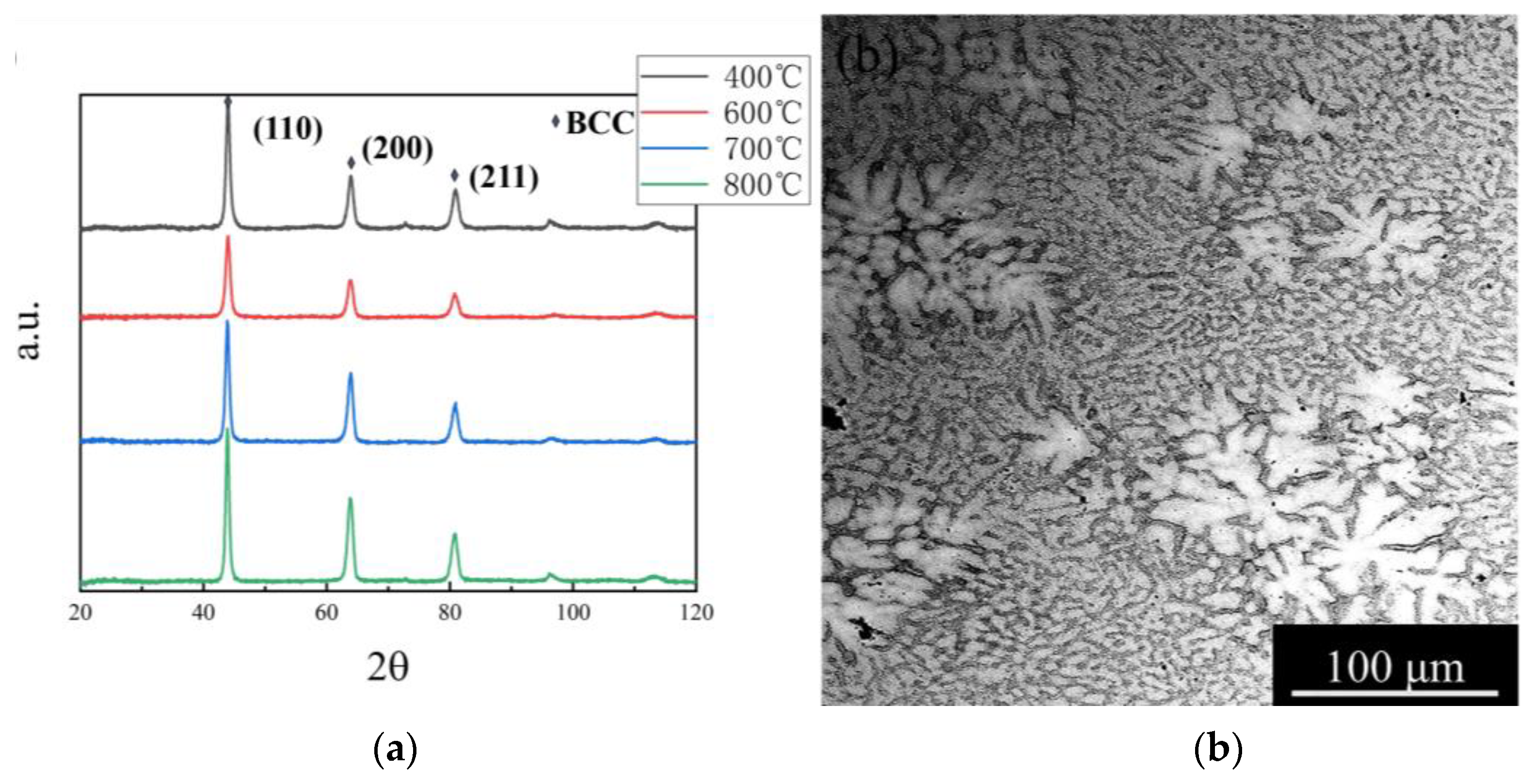
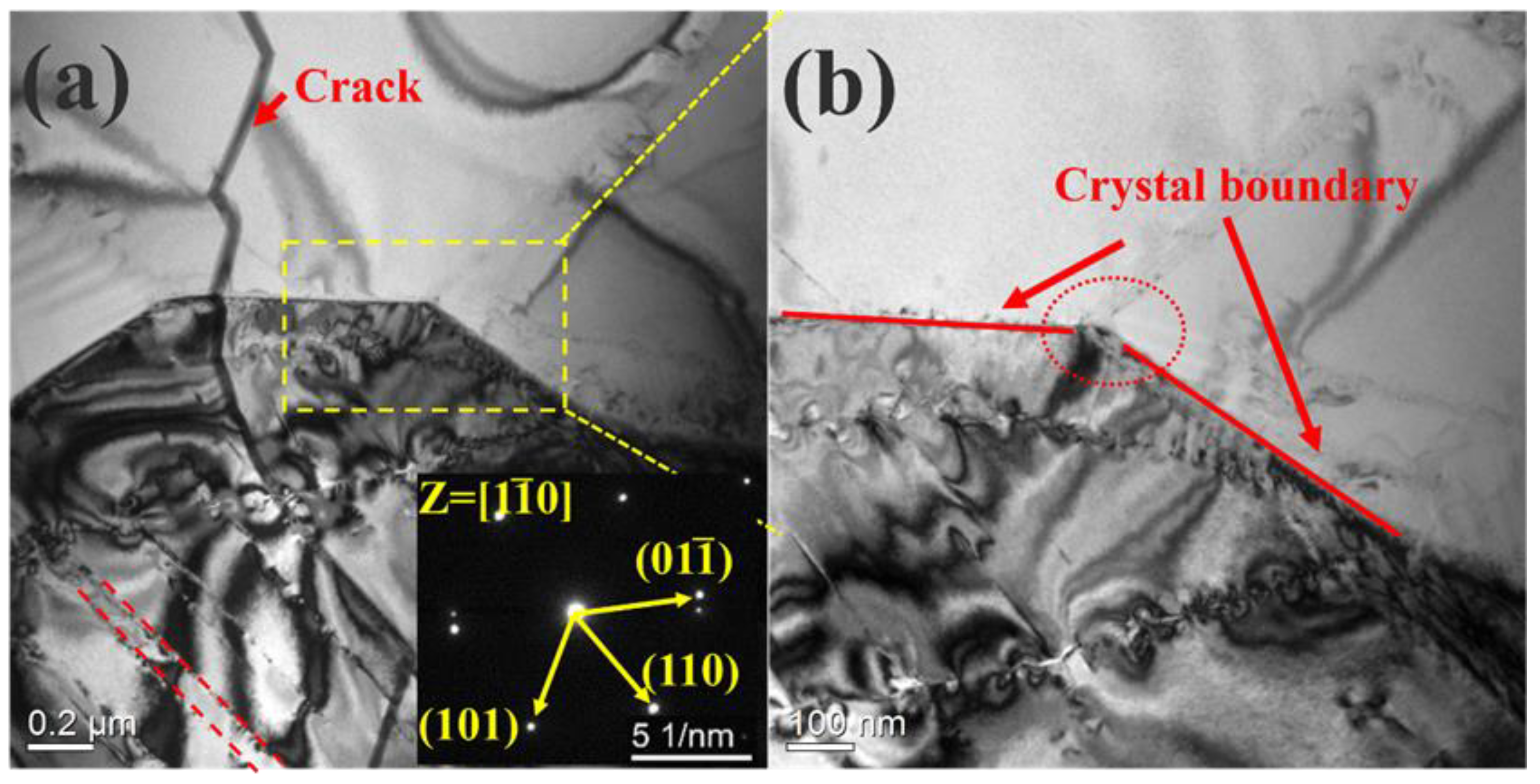

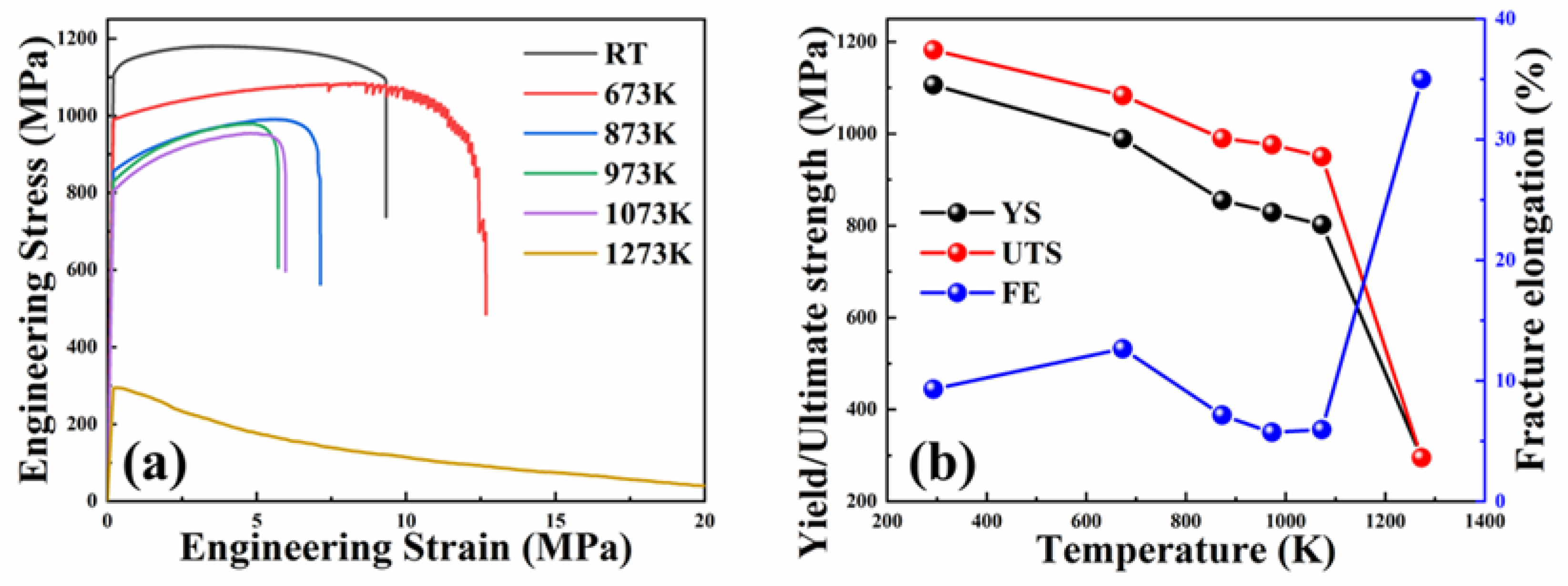


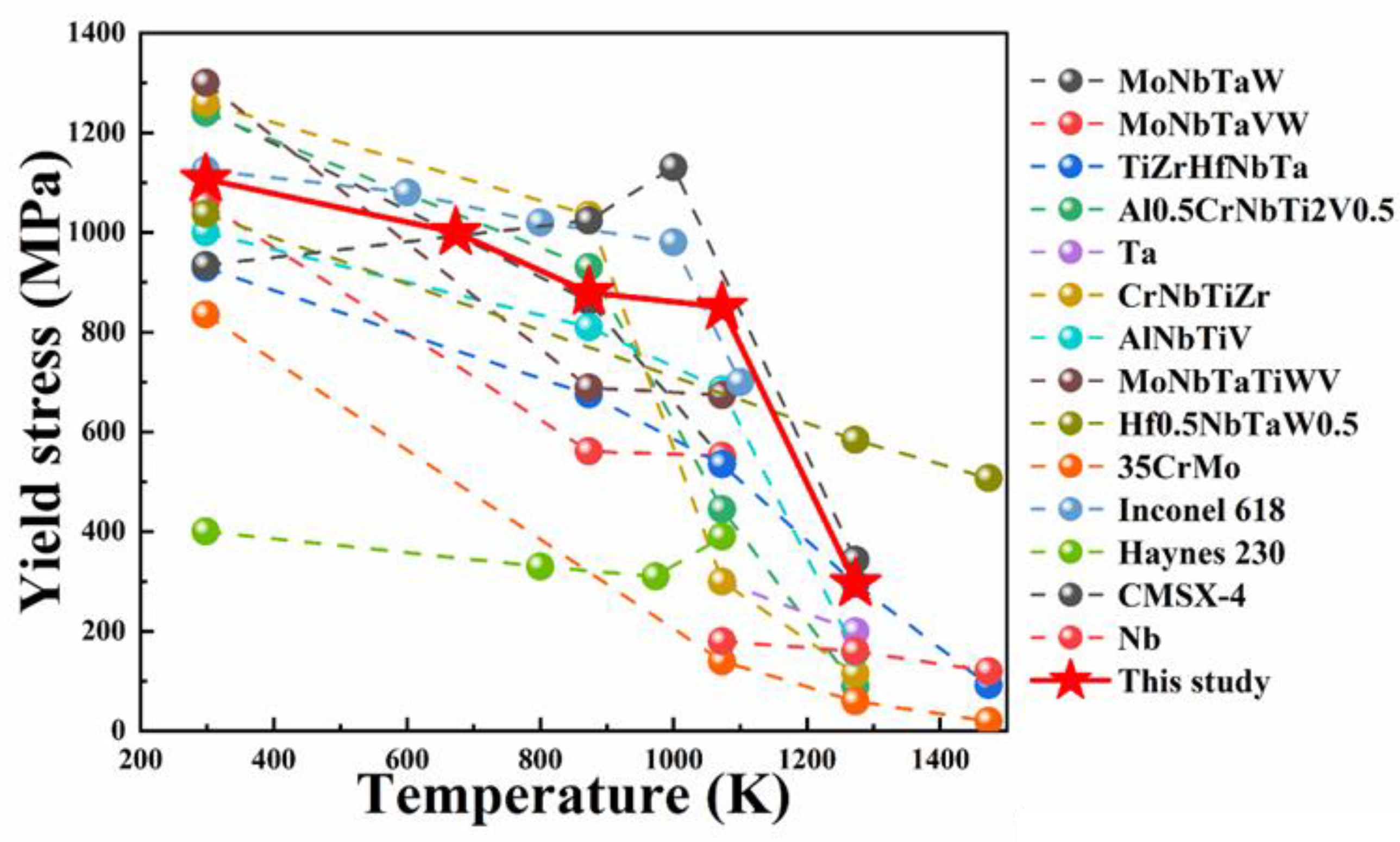

| Alloys | Concentrations (at.%) | Ti | Zr | Nb | Ta | V | Hf |
|---|---|---|---|---|---|---|---|
| TiZrHfNbTaV0.5 | Cexp | 18.09 | 17.54 | 18.33 | 19.13 | 8.95 | 17.99 |
| Cthe | 18.18 | 18.18 | 18.18 | 18.18 | 9.09 | 18.18 |
| Alloys | NbTaHfTiZrV0.5 (RT) | 400 °C | 600 °C | 700 °C | 800 °C |
|---|---|---|---|---|---|
| a (Å) | 3.369 | 3.446 | 3.558 | 3.601 | 3.623 |
| Alloys | NbTaHfTiZrMo0.5 | NbTaHfTiZrMo0.5 | NbTaTiVW | MoNbTaV | MoNbTaTiV |
| a (Å) | 3.383 | 3.218 | 3.224 | 3.208 | 3.224 |
| NbTaHfTiZrV0.5 | 873 K | 973 K | 1073 K | |
|---|---|---|---|---|
| 1 × 10−3 s−1 | Exp | 1141.55 | 1112.50 | 1095.49 |
| Cal | 1019.31 | 994.84 | 975.68 | |
| 1 × 10−2 s−1 | Exp | 1172.89 | 1168.89 | 1122.11 |
| Cal | 1129.86 | 1096.62 | 1080.32 | |
| 1 × 10−1 s−1 | Exp | 1223.76 | 1198.58 | 1189.75 |
| Cal | 1247.42 | 1219.52 | 1195.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Shi, X.; Zhang, M.; Qiao, J. High-Temperature Mechanical Properties of NbTaHfTiZrV0.5 Refractory High-Entropy Alloys. Entropy 2023, 25, 1124. https://doi.org/10.3390/e25081124
Liu Z, Shi X, Zhang M, Qiao J. High-Temperature Mechanical Properties of NbTaHfTiZrV0.5 Refractory High-Entropy Alloys. Entropy. 2023; 25(8):1124. https://doi.org/10.3390/e25081124
Chicago/Turabian StyleLiu, Zhangquan, Xiaohui Shi, Min Zhang, and Junwei Qiao. 2023. "High-Temperature Mechanical Properties of NbTaHfTiZrV0.5 Refractory High-Entropy Alloys" Entropy 25, no. 8: 1124. https://doi.org/10.3390/e25081124
APA StyleLiu, Z., Shi, X., Zhang, M., & Qiao, J. (2023). High-Temperature Mechanical Properties of NbTaHfTiZrV0.5 Refractory High-Entropy Alloys. Entropy, 25(8), 1124. https://doi.org/10.3390/e25081124






