Memory Corrections to Markovian Langevin Dynamics
Abstract
:1. Introduction
2. Model
3. Effective Mass Approach
4. Memory Kernel in the Form of the Prony Series
4.1. First-Order Memory Correction
4.2. Second-Order Memory Correction
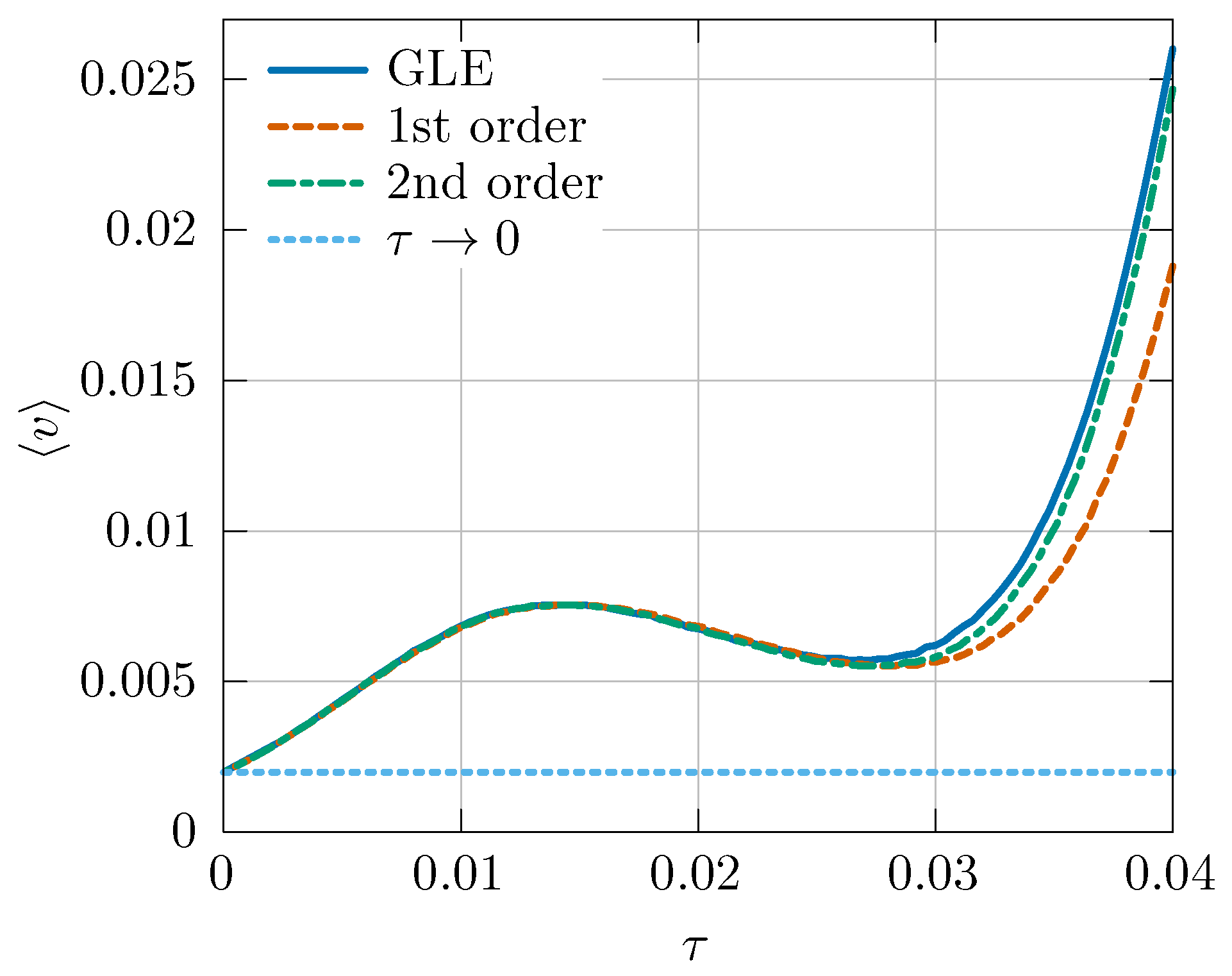
5. Verification of the Memory Corrections
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- van Kampen, N.G. Remarks on Non-Markov Processes. Braz. J. Phys. 1998, 28, 90. [Google Scholar] [CrossRef]
- Hanggi, P.; Jung, P. Colored Noise in Dynamical Systems. Adv. Chem. Phys. 1995, 89, 239. [Google Scholar]
- Milz, S.; Egloff, D.; Taranto, P.; Theurer, T.; Plenio, M.B.; Smirne, A.; Huelga, S.F. When Is a Non-Markovian Quantum Process Classical? Phys. Rev. X 2020, 10, 041049. [Google Scholar] [CrossRef]
- Milz, S.; Modi, K. Quantum Stochastic Processes and Quantum non-Markovian Phenomena. PRX Quantum 2021, 2, 030201. [Google Scholar] [CrossRef]
- White, G.A.L.; Hill, C.D.; Pollock, F.A.; Hollenberg, L.C.L.; Modi, K. Demonstration of non-Markovian process characterisation and control on a quantum processor. Nat. Commun. 2020, 11, 6301. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.D.; Yang, C.; He, R.D.; Gu, M.; Xiang, G.; Li, C.; Guo, G.; Elliott, T.J. Implementing quantum dimensionality reduction for non-Markovian stochastic simulation. Nat. Commun. 2023, 14, 2624. [Google Scholar] [CrossRef] [PubMed]
- Jesi-Baity, M.; Calore, E.; Cruz, A.; Fernandez, L.A.; Gil-Narvion, J.M.; Pemartin, I.G.; Gordillo-Guerrero, A.; Iñiguez, D.; Maiorano, A.; Marinari, E.; et al. Memory and rejuvenation effects in spin glasses are governed by more than one length scale. Nat. Phys. 2023, 19, 978. [Google Scholar] [CrossRef]
- Kanazawa, K.; Sano, T.G.; Cairoli, A.; Baule, A. Loopy Lévy flights enhance tracer diffusion in active suspensions. Nature 2020, 579, 364. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, J.P.; Mandal, R.; Banerjee, D.S.; Thutupalli, S.; Rao, M. Unjamming and emergent nonreciprocity in active ploughing through a compressible viscoelastic fluid. Nat. Commun. 2022, 13, 4533. [Google Scholar] [CrossRef]
- Militaru, A.; Innerbichler, M.; Frimmer, M.; Tebbenjohanns, F.; Novotny, L.; Dellago, C. Escape dynamics of active particles in multistable potentials. Nat. Commun. 2021, 12, 2446. [Google Scholar] [CrossRef]
- Narinder, N.; Bechinger, C.; Gomez-Solano, J.R. Memory-induced transition from a persistent random walk to circular motion for achiral microswimmers. Phys. Rev. Lett. 2018, 121, 078003. [Google Scholar] [CrossRef] [PubMed]
- Tucci, G.; Roldan, E.; Gambassi, A.; Belousov, R.; Berger, F.; Alonso, R.G.; Hudspeth, A.J. Modeling Active Non-Markovian Oscillations. Phys. Rev. Lett. 2022, 129, 030603. [Google Scholar] [CrossRef]
- Cao, X.; Das, D.; Windbacher, N.; Ginot, F.; Krüger, M.; Bechinger, C. Memory-induced Magnus effect. Nat. Phys. 2023, 19, 1904–1909. [Google Scholar] [CrossRef]
- Ayaz, C.; Tepper, L.; Brünig, F.N.; Kappler, J.; Daldrop, J.O.; Netz, R.R. Non-Markovian modeling of protein folding. Proc. Natl. Acad. Sci. USA 2021, 118, e2023856118. [Google Scholar] [CrossRef] [PubMed]
- Vilk, O.; Campos, D.; Mendez, V.; Lourie, E.; Nathan, R.; Assaf, M. Phase transition in a non-markovian animal exploration model with preferential returns. Phys. Rev. Lett. 2022, 128, 148301. [Google Scholar] [CrossRef] [PubMed]
- Ginot, F.; Caspers, J.; Kruger, M.; Bechinger, C. Barrier Crossing in a Viscoelastic Bath. Phys. Rev. Lett. 2022, 128, 028001. [Google Scholar] [CrossRef] [PubMed]
- Ferrer, B.R.; Gomez-Solano, J.R.; Arzola, A.V. Fluid Viscoelasticity Triggers Fast Transitions of a Brownian Particle in a Double Well Optical Potential. Phys. Rev. Lett. 2021, 126, 108001. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Solano, J.R.; Blokhuis, A.; Bechinger, C. Dynamics of Self-Propelled Janus Particles in Viscoelastic Fluids. Phys. Rev. Lett. 2016, 116, 138301. [Google Scholar] [CrossRef] [PubMed]
- Goychuk, I. Viscoelastic Subdiffusion: Generalized Langevin Equation Approach. Adv. Chem. Phys. 2012, 150, 187. [Google Scholar]
- Franosch, T.; Grimm, M.; Belushkin, M.; Mor, F.M.; Foffi, G.; Forró, L.; Jeney, S. Resonances arising from hydrodynamic memory in Brownian motion. Nature 2011, 478, 85. [Google Scholar] [CrossRef]
- Huang, R.; Chavez, I.; Taute, K.; Luki, B.; Jeney, S.; Raizen, M.G.; Florin, E.-L. Direct observation of the full transition from ballistic to diffusive Brownian motion in a liquid. Nat. Phys. 2011, 7, 576. [Google Scholar] [CrossRef]
- Goychuk, I. Fractional Hydrodynamic Memory and Superdiffusion in Tilted Washboard Potentials. Phys. Rev. Lett. 2019, 123, 180603. [Google Scholar] [CrossRef]
- Adelman, S.A. Fokker—Planck equations for simple non-Markovian systems. J. Chem. Phys. 1976, 64, 124. [Google Scholar] [CrossRef]
- Hänggi, P.; Thomas, H.; Grabert, H.; Talkner, P. Note on time evolution of non-Markov processes. J. Stat. Phys. 1978, 18, 155. [Google Scholar] [CrossRef]
- Wiśniewski, M.; Łuczka, J.; Spiechowicz, J. Effective mass approach to memory in non-Markovian systems. Phys. Rev. E 2024, 109, 044116. [Google Scholar] [CrossRef]
- Łuczka, J. Non-Markovian stochastic processes: Colored noise. Chaos 2005, 15, 026107. [Google Scholar] [CrossRef]
- Marchesoni, F.; Grigolini, P. On the extension of the Kramers theory of chemical relaxation to the case of nonwhite noise. J. Chem. Phys. 1983, 78, 6287–6298. [Google Scholar] [CrossRef]
- Straub, J.E.; Borkovec, M.; Berne, B.J. Non-Markovian activated rate processes: Comparison of current theories with numerical simulation data. J. Chem. Phys. 1986, 84, 1788. [Google Scholar] [CrossRef]
- Siegle, P.; Goychuk, I.; Talkner, P.; Hänggi, P. Markovian embedding of non-Markovian superdiffusion. Phys. Rev. E 2010, 81, 011136. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255. [Google Scholar] [CrossRef]
- Dittrich, T.; Hänggi, P.; Ingold, G.-L.; Kramer, B.; Schön, G.; Zwerger, W. Quantum Transport and Dissipation; Wiley: Weinheim, Germany, 1998; Chapter 4. [Google Scholar]
- Córdoba, A.; Indei, T.; Schieber, J.D. Elimination of inertia from a generalized Langevin equation: Applications to microbead rheology modeling and data analysis. J. Rheol. 2012, 56, 185. [Google Scholar] [CrossRef]
- Baczewski, A.D.; Bond, S.D. Numerical Integration of the Extended Variable Generalized Langevin Equation with a Positive Prony Representable Memory Kernel. J. Chem. Phys. 2013, 139, 044107. [Google Scholar] [CrossRef] [PubMed]
- Mauro, J.C.; Mauro, Y.Z. On the prony series representation of stretched exponential relaxation. Phys. A 2018, 506, 75. [Google Scholar] [CrossRef]
- Duong, M.H.; Shang, X. Accurate and robust splitting methods for the generalized Langevin equation with a positive Prony series memory kernel. J. Comput. Phys. 2022, 464, 111332. [Google Scholar] [CrossRef]
- Siegle, P.; Goychuk, I.; Hänggi, P. Origin of hyperdiffusion in generalized Brownian motion. Phys. Rev. Lett. 2010, 105, 100602. [Google Scholar] [CrossRef] [PubMed]
- Spiechowicz, J.; Marchenko, I.G.; Hänggi, P.; Łuczka, J. Diffusion Coefficient of a Brownian Particle in Equilibrium and Nonequilibrium: Einstein Model and Beyond. Entropy 2023, 25, 42. [Google Scholar] [CrossRef] [PubMed]
- Wiśniewski, M.; Spiechowicz, J. Anomalous transport in driven periodic systems: Distribution of the absolute negative mobility effect in the parameter space. New J. Phys. 2022, 24, 063028. [Google Scholar] [CrossRef]
- Wiśniewski, M.; Spiechowicz, J. Paradoxical nature of negative mobility in the weak dissipation regime. Chaos 2023, 33, 063114. [Google Scholar] [CrossRef] [PubMed]
- Spiechowicz, J.; Łuczka, J.; Hänggi, P. Transient anomalous diffusion in periodic systems: Ergodicity, symmetry breaking and velocity relaxation. Sci. Rep. 2016, 6, 30948. [Google Scholar] [CrossRef]
- Platen, E.; Bruti-Liberati, N. Numerical Solution of Stochastic Differential Equations with Jumps in Finance; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Spiechowicz, J.; Kostur, M.; Machura, Ł. GPU accelerated Monte Carlo simulation of Brownian motors dynamics with CUDA. Comp. Phys. Commun. 2015, 191, 140–149. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wiśniewski, M.; Łuczka, J.; Spiechowicz, J. Memory Corrections to Markovian Langevin Dynamics. Entropy 2024, 26, 425. https://doi.org/10.3390/e26050425
Wiśniewski M, Łuczka J, Spiechowicz J. Memory Corrections to Markovian Langevin Dynamics. Entropy. 2024; 26(5):425. https://doi.org/10.3390/e26050425
Chicago/Turabian StyleWiśniewski, Mateusz, Jerzy Łuczka, and Jakub Spiechowicz. 2024. "Memory Corrections to Markovian Langevin Dynamics" Entropy 26, no. 5: 425. https://doi.org/10.3390/e26050425
APA StyleWiśniewski, M., Łuczka, J., & Spiechowicz, J. (2024). Memory Corrections to Markovian Langevin Dynamics. Entropy, 26(5), 425. https://doi.org/10.3390/e26050425





