Internal Structure of Elementary Particle and Possible Deterministic Mechanism of Biological Evolution

Abstract

The possibility of a complicated internal structure of an elementary particle was analyzed. In this case a particle may represent a quantum computer with many degrees of freedom. It was shown that the probability of new species formation by means of random mutations is negligibly small. Deterministic model of evolution is considered. According to this model DNA nucleotides can change their state under the control of elementary particle internal degrees of freedom.

Introduction

The problem is that the Darwin mechanism of the evolution (a random process) cannot explain the known rate of the species evolution. In accordance with the very first estimates, the total number of possible combinations of nucleotides in the DNA is about $4^{2\times {10}^9}$ (because four types of nucleotides are available, while the number of nucleotides in the DNA of higher organisms is about 2 × 10⁹). This figure is much larger than the number of all organisms, which have ever lived on Earth. Therefore, the evolution was not random, but followed deterministic laws. To overcome this contradiction, the present paper hypothesizes the possible existence of a complicated internal structure of elementary particles. An elementary particle can function as a quantum computer (recognize patterns and make decisions), which is capable of controlling the motion of the particle as a whole. Such a control may change the state of genes, considerably accelerating the evolution and explaining the known rate of the species evolution.

1. Estimates of the Biological Evolution Rate

We shall assume first that mutations of various nucleotides are mutually independent and represent a random process (in accordance with the Darwin theory).

Let m be the number of organisms of one species, t the characteristic time of formation of a new species, T the lifetime of one organism, k the number of ecological niches surrounding a given niche (potentially possible close species), and W the probability of mutation of a specific nucleotide during the lifetime of an organism. This probability should depend on the intensity of the external noise (radiation). The lesser the external noise, the smaller the quantity W should be.

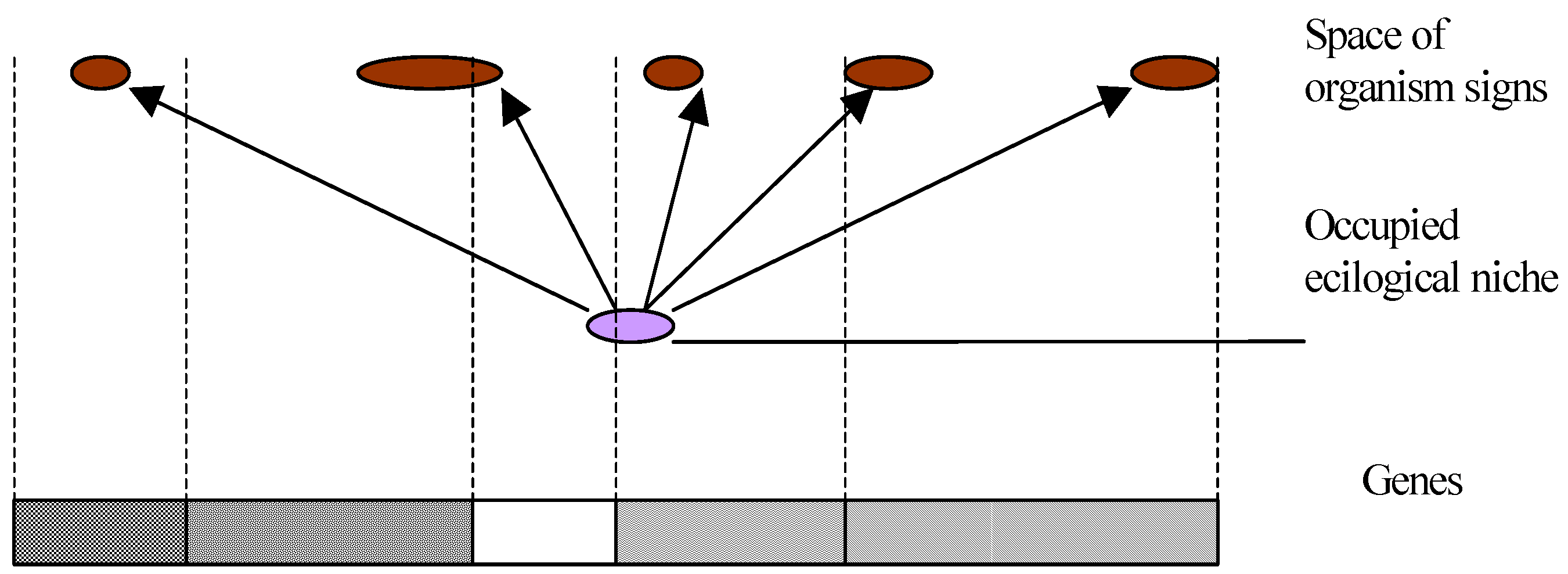
Let N be the total number of nucleotides in the DNA (assume for simplicity that the total number of nucleotides remains unchanged) and N₁ the number of nucleotides in the DNA of a potentially close species, which differ from the nucleotides of the species in question. Take N₂ as the number of nucleotides, which can change, while the organism remains within the given species. In other words, N₂ is the characteristic width of a “potential well” of one species.

In this case, it is possible to determine the number of organisms (or the probability P), which will reach the next niche through random mutations, i.e., will form a new species having quite definite N₁ nucleotides.

Considering what has been said above, we have a formula

$$P=m\frac{t}{T}k{\left(\frac{W}{3}\right)}^{N_1}{4}^{N_2}{[1-W]}^{N-N_1}.$$

Let us determine the upper bound of P. To this end, we shall choose the W value corresponding to a maximum P. In actual fact, this quantity depends on many external factors (temperature, radiation, etc.) and may be far from an optimal value.

To find the maximum, equate the derivative to zero ∂P/∂W = 0. Then we have

$$W=\frac{N_1}{N} \text{and} P=m\frac{t}{T}k{\left(\frac{N_1}{3N}\right)}^{N_1}{4}^{N_2}{(1-\frac{N_1}{N})}^{N-N_1}.$$

(1)

The estimated W value is very large. It corresponds to the situation when the next-generation genetic differences between descendants and their parents are as large as between different species. In this case, the radiation level, for example, must be so high that it would kill all living things. So, if we take W approaching a real value, P will be much smaller too. Let us assume k ≈ 10 (this value is confirmed by anthropologic findings and the description of the morphospace). The characteristic time of the species formation is ≈ 10⁶ years, the mean lifetime of an organism is ≈ 10 years, and m is equal to 10⁸ (of course, this value will be larger for small animals, but, as one will see from the estimates, the main conclusion will not change).

Thus, we have mt/T ≈ 10¹³. The N value for higher organisms is ≈ 2 × 10⁹ (N is smaller for Protozoa, but this fact will have no effect on the general conclusion either). Using the data of comparison biochemistry, estimate N₁ and N₂: N₁ ≈ 0.01N and N₂ = 0.001N. Thus, finally we have P = 10^−57000000. This figure is vanishingly small. Therefore, a conclusion may be drawn that species could not be formed due to random mutations. It is easy to see that this conclusion will not change if most widespread and short-lived species, including bacteria, are considered.

Let us consider an important situation when nucleotides are not independent, but organize themselves as some structures (genes). As a consequence, the number of possible states is reduced considerably.

Whichever self-organization processes, they cannot be pre-oriented to free ecological niches (in terms of the random evolution) and, consequently, cannot accelerate the process of occupying those niches. Indeed, the number of possible combinations of genes is much smaller than the number of nucleotide combinations. However, to calculate the total number of combinations, one has to sum up all possible combinations of nucleotides in each gene! Therefore, the formula (1) holds true. By way of example, we may take a ball of some dimension hitting a target whose position is unknown. Whichever combinations of initial coordinates and speeds of the ball used, the probability of hitting the target will only depend on the ratio between the target and ball areas.

From the viewpoint of the theory of random evolution, all genes are equal (no more or less important genes may exist), because all of them appeared by random mutations. In this case, an organism cannot know beforehand which genes it will need in the distant future.

Thus, either a molecular or some other machine exists deciding on further evolution. However, such a machine will require certain reference samples for its operation establishing what is and what is not important for an organism.

Or this machine does not exist and, then, it is impossible to make a decision. There is no criterion to confirm that a set of nucleotides is the best one in a given situation (Fig.1).

Fig.1.

Fig.1.

In other words, no criteria exist for sampling of genes. Nonequilibrium phase transitions in a system of nucleotides only represent a mechanism of genes sampling and operation of the molecular machine.

To negotiate this contradiction, one has to assume the existence of a decision-making machine with reference samples assigned a priori. Put another way, if we know beforehand the location of a target, the probability of hitting this target may increase considerably. In this case, selection plays a secondary role. It may be compared with a quality inspection department at a factory, which rejects faulty parts, but does not fabricate new ones.

If a molecular machine, which controls the evolution (with reference samples assigned a priori as thermodynamic forces), does not exist, then the Darwin evolution contradicts to the second law, since it represents a macroscopically oriented (from the simple to the complex) fluctuation.

2. Internal Structure of Elementary Particles. Nonlinear Equations of Motion Control

What is the reason why elementary particles are viewed as "simple", i.e. not having a complicated internal structure? The reason is that if a particle represents a macrosystem with many degrees of freedom, then two cases are possible: (a) The interaction between the environment and these degrees of freedom is high. In this case, the energy levels of the particles as a whole will deviate from experimental values (the theory describes them fairly well); (b) The interaction between the environment and internal degrees of freedom is low (such that it falls within the experimental error). In this case, the field will have a vanishingly small effect on the behavior of a particle and deviations will not be detected in experiment.

Still, it is possible that a complex structure of a particle will not contradict experimental data.

Assume that the Schrödinger equation (or a similar expression) represents a linear approximation of a more general nonlinear equation. This nonlinear equation may have both harmonic and nonharmonic solutions. Certain values of control parameters may lead to excitation of internal degrees of freedom (appearance of defects in the structure of elementary particles). This is an analog of quasiparticles like vacancies in a solid, excitons, etc. Defects in an elementary particle have an ordered structure (like, e.g., atoms in a protein molecule). Nonradiative transitions take place when the state of internal degrees of freedom is changed (see for example [1,2]). These effects have long been known for solids.

Let us write a system of nonlinear equations describing the behavior of a particle as a whole and its internal degrees of freedom in the form:

$$\begin{array}{ccc}ih\frac{\partial {\Psi }_j}{\partial t}=\stackrel{⁔}{H}{\Psi }_j+\stackrel{⁔}{u}{\Psi }_j,& & \frac{\partial u_i}{\partial t}=F({\Psi }_k+{\lambda }_m)\end{array}.$$

The subscript i means the number of internal degrees of freedom of a particle The operator $\stackrel{⁔}{u}$ represents a pulsed control of the motion of a particle as a whole.

Thus, a parametric or force control of the behavior of a particle is possible. This may include either a short-time change of the particle properties (for example, the charge) or a short-time application of a field, which renders a rare event highly probable. What is meant here is, for example, climbing of a potential barrier.

Fig.2.

Fig.2.

If the barrier is sufficiently high, the probability of its climbing is small and the time of transition to the adjacent state is long.

If control is present, a compensating field arises. This field may be viewed as a catalyst, whose operation is followed by the return of the energy back to the field:

Fig.3.

Fig.3.

The operation mechanism of a quantum demon may consist in a resonance-induced infiltration through a barrier. Such mechanisms are well known in chemistry and physics. As is known, a catalyst may change the reaction rate by many orders of magnitude (this is especially true of biochemical reactions in a cell). Similarly, the lifetime of an atom in an excited state may change dramatically under some radiation (an induced transition). The operation of lasers is based on this effect. An alternative approach assumes a change in properties of a particle itself, while properties of the field remain unchanged.

Note that one may speak about a transition to one of allowed states of a particle! It is only the probability of this transition that will change (in a pulsed manner).

The structure of internal degrees of freedom is preset so that the behavior of elementary particles is adequate to the environment. Reference samples just correspond to wave eigen-functions of internal degrees of freedom.

One may think that the Pauli principle applies only to a particle as a whole and is invalid for internal degrees of freedom of different particles! That is, all elementary particles differ by their internal degrees of freedom, but they behave themselves absolutely alike outwardly (in the absence of control).

The time behavior of such a particle will look like the operation of a quantum demon. In this case, macroscopic experiments may reveal spontaneous ordering of a system (a decrease in the entropy). However, this violation of the second law of thermodynamics is apparent, because the entropy of a system of such particles will decrease at the expense of an increase in the entropy of their internal degrees of freedom.

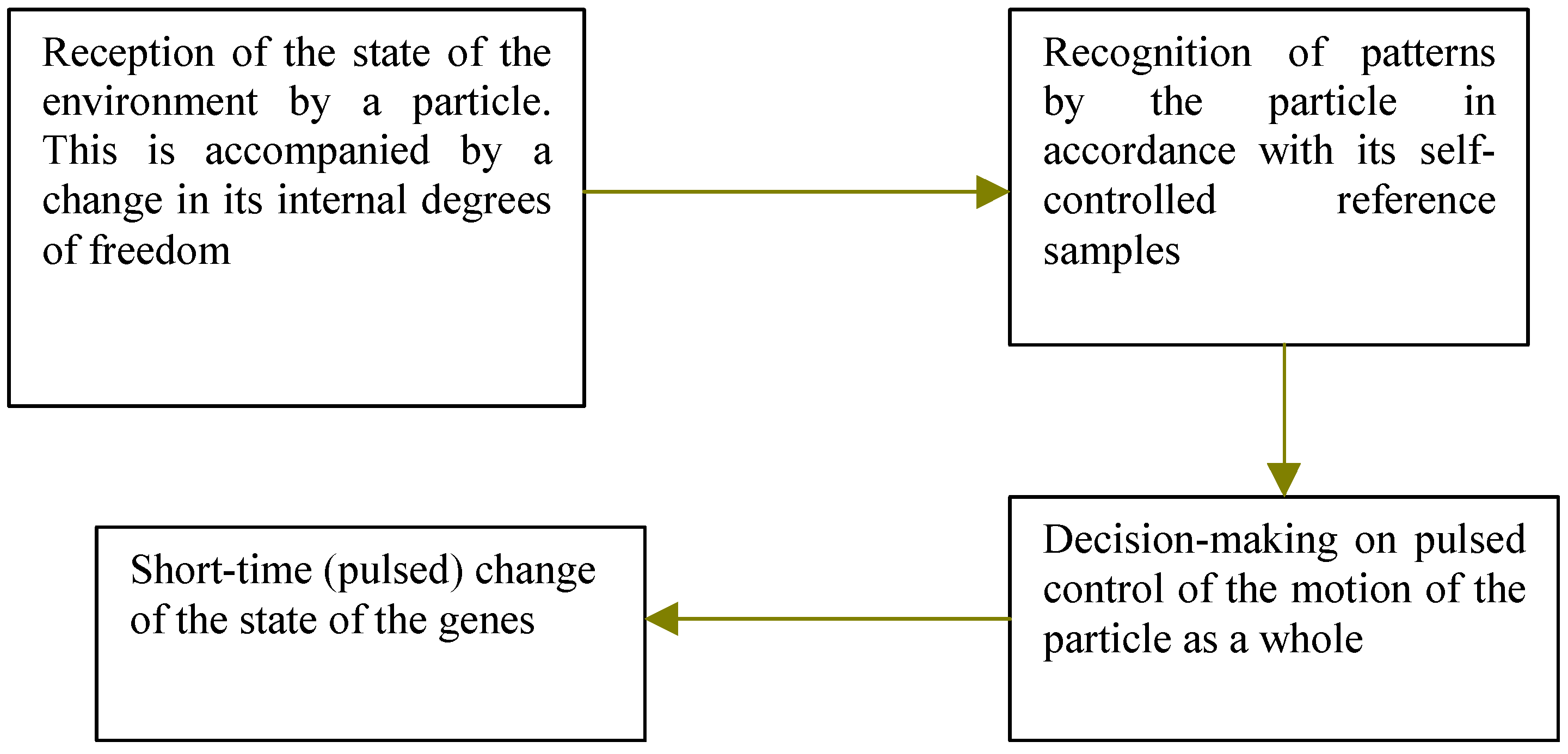
Thus, the sequence of processes taking place in an elementary particle may be schematized as follows:

Fig.4.

Fig.4.

The event at the last stage will appear to us as a post-operation consequence of a demon. For example, this process might lead to sorting of gas molecules:

Fig.5.

Fig.5.

The same considerations apply to genes. Genes could move by chance in a phase space (like gas atoms in a volume). However, if they move very fast (not in a diffusion time), we shall have to assume the operation of a demon pimping molecules from one part to another.

However, if we take into account the entropy (and information) of internal degrees of freedom of a particle, the total entropy of the system will increase.

3. Deterministic Model of the Evolution

Let us discuss how a short-time change of the state of an electron may influence the structure of genes. Experimental data available on today directly specify that, for example, loss of one electron by quite certain nucleotide can result in the directed mutation (see, for example [3,4]). Now we shall imagine, that the electron state as the whole can is directed to vary under action of its internal degrees of freedom. Such mechanism can be started after reception of a signal from an environment. The program of such controlled genome changes can be incorporated in internal degrees of freedom of a particle.

Therefore, the algorithm of movement of an organism from one niche to another can be presented as follows:

• An organism scans the environment in search for nearest free niches.
• If niches are found, the organism decides what niche is the most favorable to move to.
• A step-by-step movement to the nearest niche begins. The space of attributes around the organism (including the presence of other organisms) is measured each step.
• The process continues until the organism occupies the wanted niche. After the number of organisms in the niche reaches a certain value, the transition of other organisms to this niche stops.

The algorithm will be executed until the control system decides that it is more favorable to move to another neighboring niche.

It is significant that such evolution does not require any additional receptors or organs except those, which already exist and are mandatory for vital functions of an organism.

This system will evolve without mutations. Certain programs will be started depending on external conditions. As a result, quite concrete genes will be synthesized and new organisms will appear.

This model allows to explain not only characteristic times of species origin (about millions years), but also cases of fast evolution [5] and so-called adaptive mutations [6,7].

So, this work shows that the Darwin (random) evolution can not explain the organisms evolution rate. A hypothesis has been advanced suggesting a complicated internal structure of elementary particles. This hypothesis removes the said contradictions. However, the operation of such “quantum demon” will not violate the second law of thermodynamics.