On The Use of Entropy to Predict Boundary Layer Stability
Abstract
:Introduction
Primary Factors affecting Transition Onset
Effect of Reynolds Number
Effect of Turbulence Intensity

Effect of Mach Number
Proposed Transition Onset Models
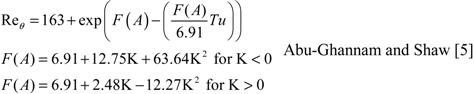
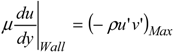
Unification of Transition Onset Parameters
Entropy Generation Rate
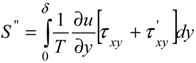
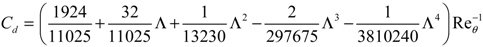


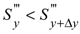

Mach Number
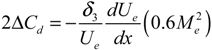
Conclusions and Future Work
- Established transition models are shown to be functions of the entropy generation rate. Further work is required to verify the new criterion with detailed measurements of the Reynolds stresses in laminar boundary layers at transition onset being required.
- For a steady laminar boundary layer, the viscous entropy production per unit volume is independent of the viscosity of the fluid.
- The relationship between Mach number and entropy production was shown to be strongly coupled to the flow field under consideration.
- For future work detailed measurements from pre-transitional laminar boundary layers to allow the implementation of the above hypothesis are needed.
Closure
Acknowledgements
Nomenclature
| Cd | Dimensionless entropy | |
| D | Diameter | m |
| Κ | Form parameter | |
| L | Distance along surface | m |
| M | Mach number | |
| Reθ | Reynolds number | Ueθ/ν |
| ReD | Reynolds number | UmD/ν |
| ReL | Reynolds number | UeL/ν |
| Rex | Reynolds number | UeX/ν |
| S'' | Entropy generation rate per unit area perpendicular to surface | W/m2 K |
| S''' | Entropy generation rate per unit volume | W/m3 K |
| T | Temperature | K |
| Tu | Percentage turbulence intensity based on free-stream conditions | % |
| Ue | Boundary layer edge velocity | m/s |
| Um | Mean Velocity in pipe flow | m/s |
| u | Local velocity in x-direction | m/s |
| v | Local velocity in y-direction | m/s |
| x | Curvilinear streamwise coordinate | m |
| y | Normal distance from wall | m |
Greek
| α | Ratio of specific heats, Cp/Cv | - |
| δ | Boundary layer thickness | m |
| δ3 | Energy thickness | m |
| η | Distance from wall/boundary layer thickness, y/δ | - |
| μ | Dynamic viscosity | kg/ms |
| ρ | Density | kg/m3 |
| τxy | Shear stress | N/m2 |
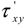 | Fluctuating shear stress | N/m2 |
| θ | Momentum thickness | m |
| υ | Kinematic viscosity | m2/s |
| Λ | Pohlhausen pressure gradient parameter |
Suffices
| ( )C | Chord length |
| ( )ST | Start of transition |
| ( )' | Fluctuating component |
References
- Denton, J.D. Loss Mechanisms in Turbomachines. ASME Journal of Turbomachinery 1993, vol. 115, 621–656. [Google Scholar] [CrossRef]
- Schobeiri, M.T.; Chakka, P. Prediction of Turbine Blade Heat Transfer and Aerodynamics using a new Unsteady Boundary Layer Transition Model. International Journal of Heat and Mass Transfer 2002, 815–829. [Google Scholar] [CrossRef]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures. Wiley: Chichester, U.K, 1998; ISBN 0-471-97394-7. [Google Scholar]
- Prigogine, I. Order Out Of Chaos: Man's New Dialogue With Nature. Heinemann: London, 1984. [Google Scholar]
- Abu-Ghannam, B.J.; Shaw, R. Natural Transition of Boundary Layers – The Effect of Turbulence, Pressure Gradient, and Flow History. IMechE 1980, Vol. 22. No. 5. [Google Scholar] [CrossRef]
- Mayle, R.E. The Role of Laminar-Turbulent Transition in Gas Turbine Engines. Journal of Turbomachinery 1991, vol. 113, 509–537. [Google Scholar] [CrossRef]
- Roach, P.E.; Brierley, D.H. The Influence of a Turbulent Free Stream on Zero Pressure Gradient Transitional Boundary Layer Development. Part 1: Test Cases T3A and T3B. Cambridge University Press, 1990; (Numerical simulation of unsteady flows and transition to turbulence, eds. Pironneau, D. , Rode, W., Ryhming, I.L.). [Google Scholar]
- Mayle, R.E.; Schulz, A. The Path to Predicting Bypass Transition. Journal of Turbomachinery 1997, 119(3), 405–411. [Google Scholar] [CrossRef]
- Moore, F.K. Unsteady, Laminar Boundary-Layer Flow. 1951; NACA TN 2471. [Google Scholar]
- Lighthill, M.J. The Response of Laminar Skin Friction and Heat Transfer to Fluctuations in the Stream Velocity. Proc. Roy. Soc. 1954, A224, 1–23. [Google Scholar] [CrossRef]
- Ackerberg, R.C.; Phillips, J.H. The Unsteady Laminar Boundary Layer on a Semi- Infinite Flat Plate Due to Small Fluctuations in the Magnitude of the Free-Stream. J. Fluid Mech. 1972, 51, 137–157. [Google Scholar] [CrossRef]
- Volino, R.J.; Simon, T.W. Spectral Measurements in Transitional Boundary Layers on a Concave Wall Under High and Low Free-Stream Turbulence. Journal of Turbomachinery 2000, vol. 122, 450–457. [Google Scholar] [CrossRef]
- Walsh, E. The Measurement, Prediction and Minimization of Viscous Entropy Generation in Transitional Boundary Layers. Ph.D. Thesis, Mechanical and Aeronautical Department, University of Limerick, Ireland, 2002. [Google Scholar]
- Narasimha, R. The Laminar Turbulent Transition Zone in the Boundary Layer. Prog. Aerospace Sci. 1985, Vol. 22, 171–176. [Google Scholar] [CrossRef]
- Schook, R.; de Lange, H.C.; van Steenhoven, A.A. Effects of Compressibility and Turbulence Level on Bypass Transition. ASME Congress and Exhibition, Paper No. 98-GT-286. 1998. [Google Scholar]
- Hourmouziadis, J. Aerodynamic Design of Low Pressure Turbines. AGARD Lecture Series, No. 167, 1989. [Google Scholar]
- Liepmann, H.W. Investigations on Laminar Boundary-Layer Stability and Transition on Curved Boundaries. NACA, ACR No. 3H30 (NACA-WR-W-107). 1943. [Google Scholar]
- Schlichting, H. Boundary Layer Theory, 7th Ed. edMc-Graw Hill: New York, 1979. [Google Scholar]
- Launder, B.E.; Sandham, N.D. Closure Strategies for Turbulent and Transitional Flows. Cambridge Univ. Press, 2002; ISBN 0521792088. [Google Scholar]
- O’Donnell, F.K.; Davies, M.R.D. Turbine Blade Entropy Generation Rate – Part II: The Measured Loss. ASME 2000-GT-266. 2000. [Google Scholar]
- Walsh, E.; Myose, R.; Davies, M.R.D. A Prediction Method for the Local Entropy Generation Rate in a Transitional Boundary Layer with a Free Stream Pressure Gradient. In Proceeding of ASME Turbo Expo, GT-2002-30231. Amsterdam, NL, 3-6 June, 2002.
- Thwaites, B. Approximate Calculation of the Laminar Boundary Layer. Aero-Naut. Quart. 1949, 1, 245–280. [Google Scholar]
- Moss, R.W.; Oldfield, M.L.G. Effect of Free-Stream Turbulence on Flat-Plate Heat Flux Signals: Spectra and Eddy Transport Velocities. J. Turbomachinery 1996, Vol. 118, 461–467. [Google Scholar] [CrossRef]
- Pohlhausen, K. Zur näherungsweisen Integration der Differentialgleichung der laminaren Reibungsschicht. ZAMM 1921, 1, 252–268. [Google Scholar] [CrossRef]
- Bejan, A. Shape and Structure from Engineering to Nature. In Shape and Structure from Engineering to Nature; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
© 2004 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Walsh, E.J.; Davies, M.R.D.; McEligot, D.M. On The Use of Entropy to Predict Boundary Layer Stability. Entropy 2004, 6, 375-387. https://doi.org/10.3390/e6040375
Walsh EJ, Davies MRD, McEligot DM. On The Use of Entropy to Predict Boundary Layer Stability. Entropy. 2004; 6(4):375-387. https://doi.org/10.3390/e6040375
Chicago/Turabian StyleWalsh, Ed J., Mark R.D. Davies, and Donald M. McEligot. 2004. "On The Use of Entropy to Predict Boundary Layer Stability" Entropy 6, no. 4: 375-387. https://doi.org/10.3390/e6040375
APA StyleWalsh, E. J., Davies, M. R. D., & McEligot, D. M. (2004). On The Use of Entropy to Predict Boundary Layer Stability. Entropy, 6(4), 375-387. https://doi.org/10.3390/e6040375



