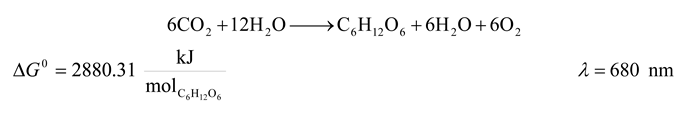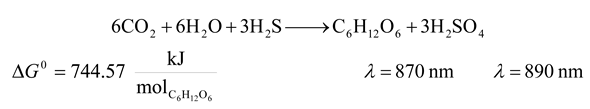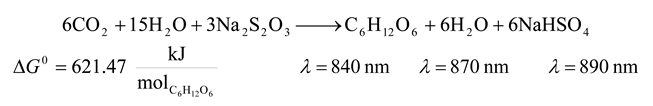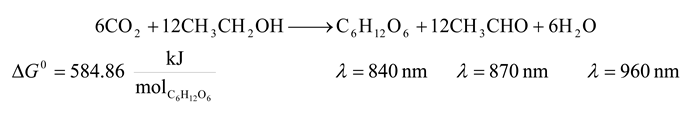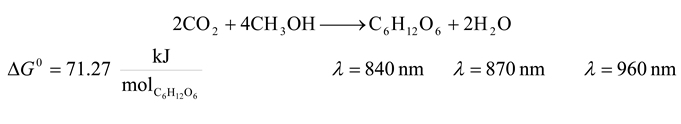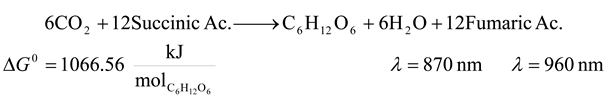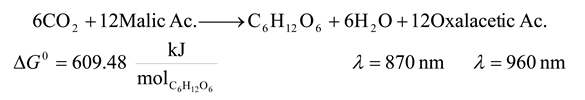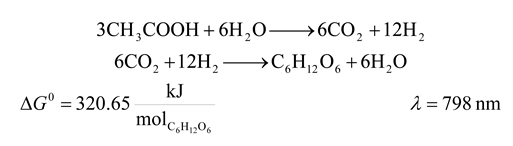A Simple Thermodynamic Analysis of Photosynthesis
Abstract
:1. Introduction
2. Photosynthesis Thermodynamics
- a)
- The Sun, the Earth and the photosynthetic organism (PO) are three different thermodynamic systems.
- b)
- The Sun is a thermal reservoir with constant temperature TS = 5762 K [4].
- c)
- The Sun has constant pressure, volume and chemical composition.
- d)
- Earth behaves as a thermal reservoir at TE = 298.15 K.
- e)
- The Earth is a system with constant pressure, volume and chemical composition.
- f)
- The photosynthetic organism (PO) has constant pressure, volume and temperature, with TPO = TE = 298.15 K.
- g)
- The PO chemical composition is not constant.
- h)
- All photosynthetic reactions are isothermal processes at TPO = 298.15 K.
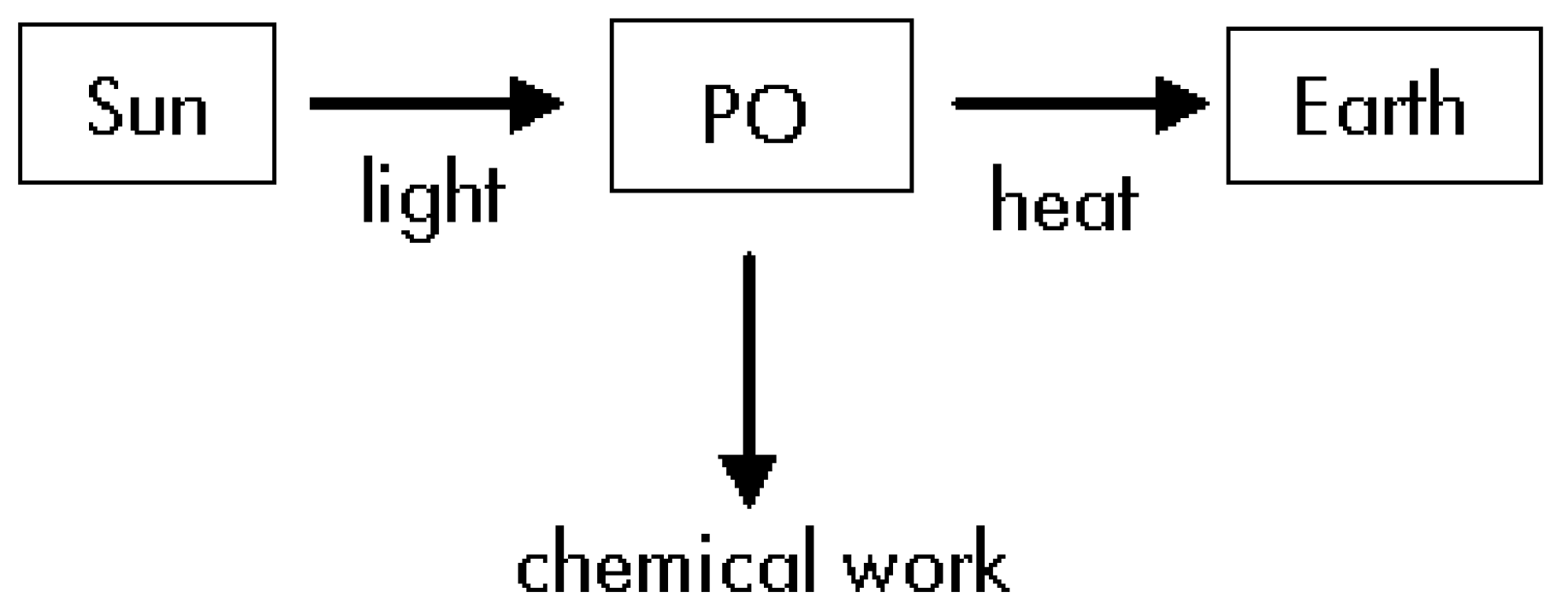
Thermodynamics of Step #1
Thermodynamics of Step #2
Thermodynamics of Step#3
3. Efficiency Calculation
| Reaction | λ [nm] | ΔU [kJ/mol] | ΔG0 [kJ/mol] | η % | ΔSUniverse [kJ/(mol K)] |
|---|---|---|---|---|---|
| 1 | 680 | 10555.287 | 2880.31 | 27.288 | 25.742 |
| 2 | 840 | 8544.756 | 429.64 | 5.028 | 27.218 |
| 2 | 870 | 8250.109 | 429.64 | 5.208 | 26.230 |
| 2 | 890 | 8064.713 | 429.64 | 5.327 | 25.608 |
| 3 | 870 | 8250.109 | 744.57 | 9.025 | 25.174 |
| 3 | 890 | 8064.713 | 744.57 | 9.232 | 24.552 |
| 4 | 840 | 8544.756 | 621.47 | 7.273 | 26.575 |
| 4 | 870 | 8250.109 | 621.47 | 7.533 | 25.587 |
| 4 | 890 | 8064.713 | 621.47 | 7.706 | 24.965 |
| 5 | 840 | 8544.756 | 584.86 | 6.845 | 26.698 |
| 5 | 870 | 8250.109 | 584.86 | 7.089 | 25.709 |
| 5 | 960 | 7476.661 | 584.86 | 7.822 | 23.115 |
| 6 | 840 | 8544.756 | 71.27 | 0.834 | 28.420 |
| 6 | 870 | 8250.109 | 71.27 | 0.864 | 27.432 |
| 6 | 960 | 7476.661 | 71.27 | 0.953 | 24.838 |
| 7 | 870 | 8250.109 | 1066.56 | 12.928 | 24.094 |
| 7 | 960 | 7476.661 | 1066.56 | 14.265 | 21.500 |
| 8 | 870 | 8250.109 | 609.48 | 7.388 | 25.627 |
| 8 | 960 | 7476.661 | 609.48 | 8.152 | 23.033 |
| 9 | 798 | 8994.480 | 320.65 | 3.565 | 29.092 |
4. Comparison of the Photosynthesis Ecological Functions
5. Analyzing the Radiation’s Entropy Change.
| Reaction | λ [nm] | ΔU [kJ/mol] | ΔG0 [kJ/mol] | η % | [kJ/mol] |
|---|---|---|---|---|---|
| 1 | 680 | 10555.287 | 2880.31 | 27.288 | -4794.667 |
| 2 | 840 | 8544.756 | 429.64 | 5.028 | -7685.476 |
| 2 | 870 | 8250.109 | 429.64 | 5.208 | -7390.829 |
| 2 | 890 | 8064.713 | 429.64 | 5.327 | -7205.433 |
| 3 | 870 | 8250.109 | 744.57 | 9.025 | -6760.969 |
| 3 | 890 | 8064.713 | 744.57 | 9.232 | -6575.573 |
| 4 | 840 | 8544.756 | 621.47 | 7.273 | -7301.816 |
| 4 | 870 | 8250.109 | 621.47 | 7.533 | -7007.169 |
| 4 | 890 | 8064.713 | 621.47 | 7.706 | -6821.773 |
| 5 | 840 | 8544.756 | 584.86 | 6.845 | -7375.036 |
| 5 | 870 | 8250.109 | 584.86 | 7.089 | -7080.389 |
| 5 | 960 | 7476.661 | 584.86 | 7.822 | -6306.941 |
| 6 | 840 | 8544.756 | 71.27 | 0.834 | -8402.216 |
| 6 | 870 | 8250.109 | 71.27 | 0.864 | -8107.569 |
| 6 | 960 | 7476.661 | 71.27 | 0.953 | -7334.121 |
| 7 | 870 | 8250.109 | 1066.56 | 12.928 | -6116.989 |
| 7 | 960 | 7476.661 | 1066.56 | 14.265 | -5343.541 |
| 8 | 870 | 8250.109 | 609.48 | 7.388 | -7031.149 |
| 8 | 960 | 7476.661 | 609.48 | 8.152 | -6257.701 |
| 9 | 798 | 8994.480 | 320.65 | 3.565 | -8353.180 |
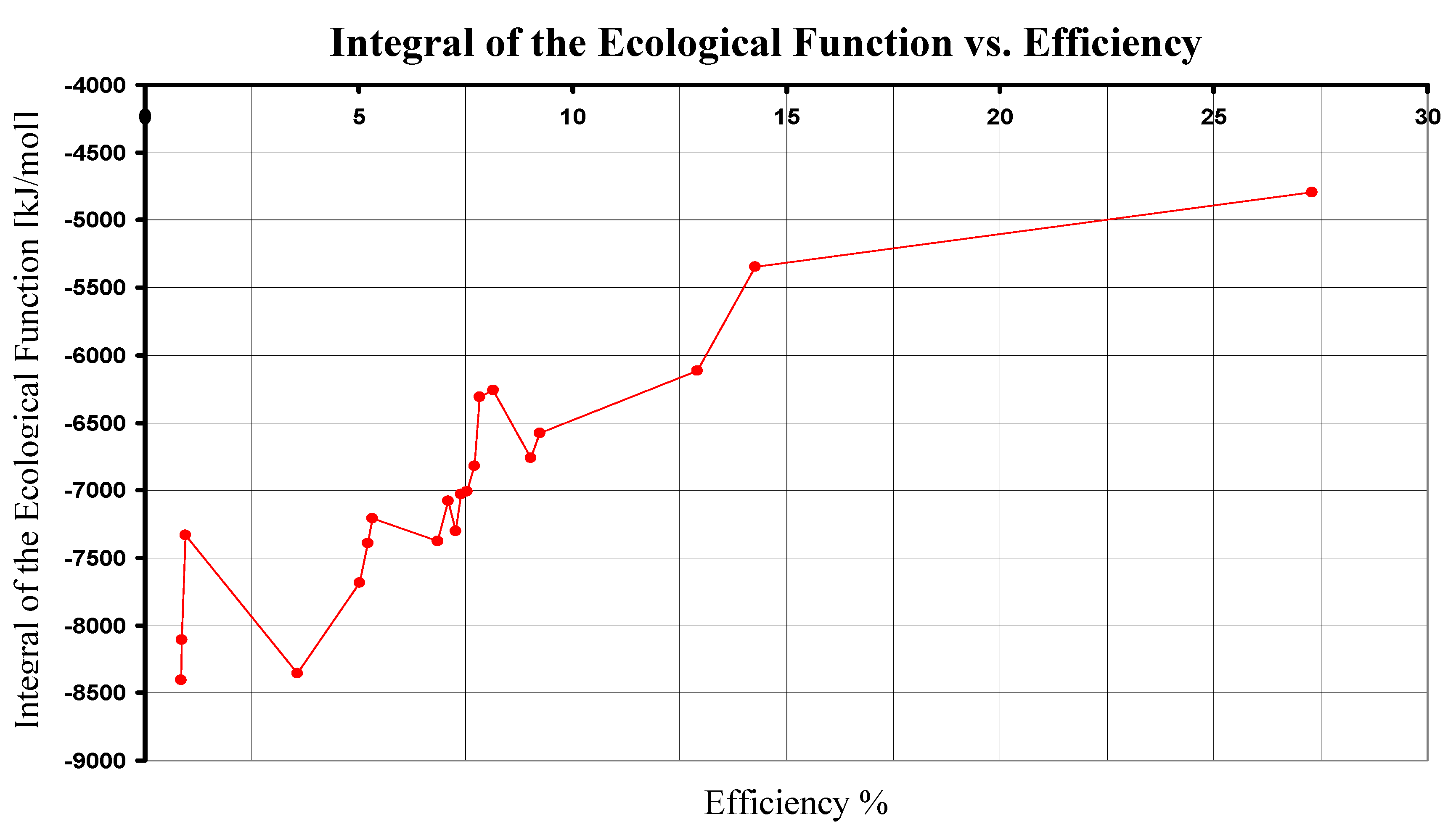

Thermodynamics of Step #1
Thermodynamics of Step #2
Thermodynamics of Step #3
Thermodynamics of Step #4
| Reaction | λ [nm] | ΔU [kJ/mol] | ΔG0 [kJ/mol] | η % | ΔSUniverse [kJ/(mol K)] | [kJ/mol] |
|---|---|---|---|---|---|---|
| 1 | 680 | 10555.287 | 2880.31 | 27.288 | 37.543 | -8313.096 |
| 2 | 840 | 8544.756 | 429.64 | 5.028 | 36.771 | -10533.728 |
| 2 | 870 | 8250.109 | 429.64 | 5.208 | 35.454 | -10140.865 |
| 2 | 890 | 8064.713 | 429.64 | 5.327 | 34.625 | -9893.671 |
| 3 | 870 | 8250.109 | 744.57 | 9.025 | 34.397 | -9511.005 |
| 3 | 890 | 8064.713 | 744.57 | 9.232 | 33.568 | -9263.811 |
| 4 | 840 | 8544.756 | 621.47 | 7.273 | 36.128 | -10150.068 |
| 4 | 870 | 8250.109 | 621.47 | 7.533 | 34.810 | -9757.205 |
| 4 | 890 | 8064.713 | 621.47 | 7.706 | 33.981 | -9510.011 |
| 5 | 840 | 8544.756 | 584.86 | 6.845 | 36.251 | -10223.288 |
| 5 | 870 | 8250.109 | 584.86 | 7.089 | 34.933 | -9830.425 |
| 5 | 960 | 7476.661 | 584.86 | 7.822 | 31.474 | -8799.161 |
| 6 | 840 | 8544.756 | 71.27 | 0.834 | 37.973 | -11250.468 |
| 6 | 870 | 8250.109 | 71.27 | 0.864 | 36.656 | -10857.605 |
| 6 | 960 | 7476.661 | 71.27 | 0.953 | 33.197 | -9826.341 |
| 7 | 870 | 8250.109 | 1066.56 | 12.928 | 33.317 | -8867.025 |
| 7 | 960 | 7476.661 | 1066.56 | 14.265 | 29.859 | -7835.761 |
| 8 | 870 | 8250.109 | 609.48 | 7.388 | 34.850 | -9781.185 |
| 8 | 960 | 7476.661 | 609.48 | 8.152 | 31.392 | -8749.921 |
| 9 | 798 | 8994.480 | 320.65 | 3.565 | 39.148 | -11351.340 |
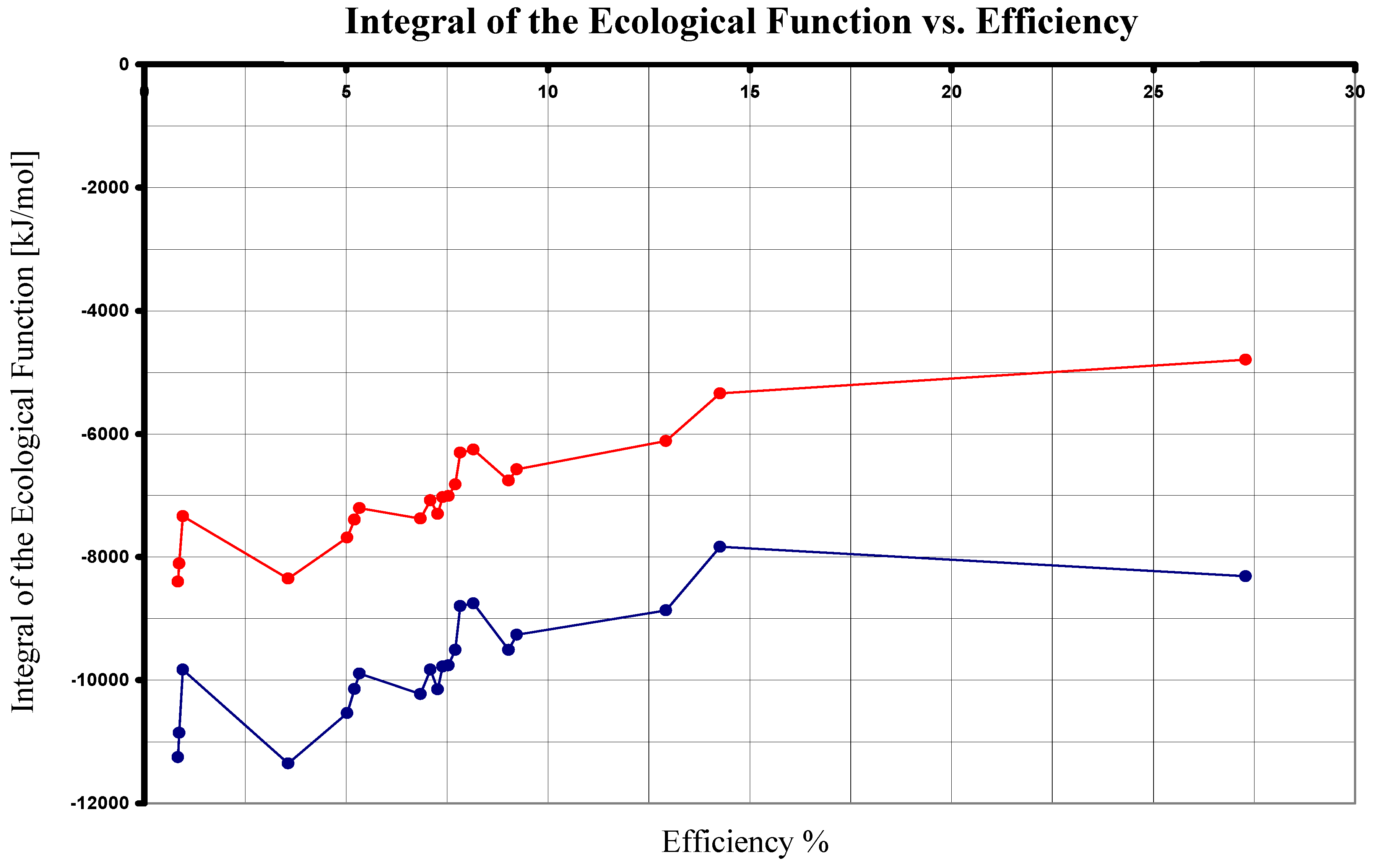
6. Concluding Remarks
Appendix
- 1. Superior Plants and Cyanobacteria
- 2. Sulfur Purple Bacteria and Sulfur Green Bacteria, young bacteria
- 3. Sulfur Purple Bacteria, old bacteria
- 4. Sulfur Purple Bacteria and Sulfur Green Bacteria
- 5. Non Sulfur Purple Bacteria and Non Sulfur Green Bacteria
- 6. Non sulfur Purple Bacteria and Non Sulfur Green Bacteria
- 7. Non Sulfur Purple Bacteria
- 8. Non Sulfur Purple Bacteria
- 9. Heliobacteria
References and Notes
- Schrödinger, E. What is life? Cambridge University Press: Cambridge, 1944. [Google Scholar]
- Andriesse, C.D.; Hollestelle, M.J. Minimum entropy production in photosynthesis. Biophys. Chem. 2001, 90, 249–253. [Google Scholar] [CrossRef]
- van Rotterdam, B.J.; Crielaard, W.; van Stokkum, I.H.M.; Hellingwerf, K.J.; Westerhoff, H.V. FEBS Letters 2002, 510, 105–107. [PubMed]
- De Vos, A. Endoreversible Thermodynamics of Solar Energy Conversion; Oxford University Press: Oxford, U.K, 1992. [Google Scholar]
- Juretic, D.; Zupanovic, P. Photosynthetic models with maximum entropy production in irreversible charge transfer steps. Comp. Biol. Chem. 2003, 27, 541–553. [Google Scholar] [CrossRef]
- Meszena, G.; Westerhoff, H.V. Non-equilibrium thermodynamics of light absorption. J. Phys. A: Math. Gen. 1999, 32, 301–311. [Google Scholar] [CrossRef]
- Stucki, J.W. The optimal efficiency and the economic degrees of coupling of oxidative phosphorylation. Eur. J. Biochem. 1980, 109, 269–283. [Google Scholar] [CrossRef] [PubMed]
- Andersen, B.; Shiner, J.S.; Uehlinger, D.E. Allometric scaling and maximum efficiency in physiological eigen time. Proc. Natl. Acad. Sci. USA 2002, 99, 5822–5824. [Google Scholar] [CrossRef] [PubMed]
- Lavergne, J. Commentary on: “Photosynthesis and negative entropy production” by Jennings and coworkers. Biochim. Biophys. Acta 2006, 1757, 1453–1459. [Google Scholar] [CrossRef] [PubMed]
- Angulo-Brown, F. An ecological optimization criterion for finite time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Lehninger, A.L. Principles of Biochemistry; Worth Publishers: New York, NY, 1982. [Google Scholar]
- Lehninger, A.L. Biochemistry, 2nd Ed. ed; Worth Publishers: New York, NY, 1975. [Google Scholar]
- Hall, D.O.; Rao, K.K. Photosynthesis; Cambridge University Press: Cambridge, 1995; pp. 126–144. [Google Scholar]
- Volkenstein, M.V. Biofísica; MIR: Moscow, 1985; Chapter 14; pp. 478–796. (in Spanish) [Google Scholar]
- Hopkins, W.G. Introduction to Plant Physiology, 2nd Ed. ed; John Wiley & Sons: New York, 1999. [Google Scholar]
- Zemansky, M.W.; Dittman, R.H. Heat and Thermodynamics; Mc Graw Hill: New York, 1981; pp. 212–244. [Google Scholar]
- Brittin, W.; Gamow, G. Negative entropy and photosynthesis. Proc. Natl. Acad. Sci. USA 1961, 47, 724–727. [Google Scholar] [CrossRef] [PubMed]
- Cornish-Bowden, A. Metabolic efficiency: Is it a useful concept? Biochem. Soc. Trans. 1983, 11, 44–45. [Google Scholar] [PubMed]
- Angulo-Brown, F.; Arias-Hernandez, L.; Santillan, M. On some connections between first order irreversible thermodynamics and finite-time thermodynamics. Rev. Mex. Fis. 2002, 48S, 182–192. [Google Scholar]
- Calow, P. Life Cycles; John Wiley & Sons: New York, NY, 1978; p. 29. [Google Scholar]
- Mandl, F. Statistical Physics; John Wiley & Sons: New York, NY, 1988; Chapter 10; pp. 251–259. [Google Scholar]
- Advances in Thermodynamics; Vol. 4, Finite-Time Thermodynamics and Thermoeconomics; Sieniutycz, S.; Salomon, P. (Eds.) Taylor & Francis: New York, NY, 1990.
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79(3), 1191–1218. [Google Scholar] [CrossRef] [Green Version]
- Hoffmann, K.H.; Burzier, J.M.; Schubert, S. Endoreversible Thermodynamics. J. Non-Equilib. Thermodyn. 1997, 22(4), 311–355. [Google Scholar]
- Recent Advances in Finite-Time Thermodynamics; Wu, C.; Chen, L.; Chen, J. (Eds.) Nova Sci. Pub.: New York, NY, 1999.
- Advances in Finite-Time Thermodynamics: Analysis and optimization; Chen, L.; Sun, F. (Eds.) Nova Sci. Pub.: New York, NY, 2004.
- Madigan, M.T.; Martinko, J.M.; Parker, J. Brock, Biology of Microorganisms, 8th Ed. ed; Prentice Hall: Upper Saddle River, NJ, 2000; pp. 635–676, (Spanish Edition). [Google Scholar]
- Dean, J.A. Lange’s Handbook of Chemistry; McGrawHill: New York, NY, 1992. [Google Scholar]
- Conn, E.E.; Stumpf, P.K. Outlines of Biochemistry, 3rd Ed. ed; John Wiley & Sons: New York, NY, 1972; Chapter 15; pp. 401–425, (Spanish Edition). [Google Scholar]
- Parés, R.; Farrás, I.; Jiménez, A.J. Bioquímica de los Microorganismos; Reverté: Barcelona, Spain, 1997; Chapter 23; pp. 304–320. (in Spanish) [Google Scholar]
© 2007 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Albarrán-Zavala, E.; Angulo-Brown, F. A Simple Thermodynamic Analysis of Photosynthesis. Entropy 2007, 9, 152-168. https://doi.org/10.3390/e9040152
Albarrán-Zavala E, Angulo-Brown F. A Simple Thermodynamic Analysis of Photosynthesis. Entropy. 2007; 9(4):152-168. https://doi.org/10.3390/e9040152
Chicago/Turabian StyleAlbarrán-Zavala, E., and F. Angulo-Brown. 2007. "A Simple Thermodynamic Analysis of Photosynthesis" Entropy 9, no. 4: 152-168. https://doi.org/10.3390/e9040152
APA StyleAlbarrán-Zavala, E., & Angulo-Brown, F. (2007). A Simple Thermodynamic Analysis of Photosynthesis. Entropy, 9(4), 152-168. https://doi.org/10.3390/e9040152