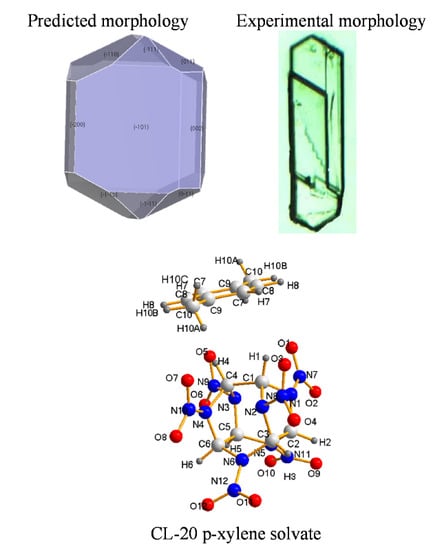
The Crystal Structure and Morphology of 2,4,6,8,10,12-Hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (CL-20) p-Xylene Solvate: A Joint Experimental and Simulation Study
Abstract
:1. Introduction
2. Computational Theoryand Details
2.1. Computational Theory
2.2. Computational Details
3. Results and Discussion
3.1. Crystal Structure
| CCDC | 1022276 |
|---|---|
| Empirical formula | C20H22N24O24 |
| Temperature (K) | 153(2) |
| Wavelength (Å) | 0.71073 Å |
| Space group | Pbca |
| Z | 4 |
| a (Å) | 8.0704(12) |
| b (Å) | 13.410(2) |
| c (Å) | 33.082(5) |
| ɑ(°) | 90 |
| β(°) | 90 |
| γ(°) | 90 |
| Volume (Å3) | 3580.1(9) |
| Density(calculated) (g cm−3) | 1.823 |
| µ (mm−1) | 0.167 |
| F(000) | 2008 |
| Crystal size (mm) | 0.44 × 0.38 × 0.21 |
| θ(°) | 2.81–29.13 |
| Limiting indices | −11 ≤ h ≤ 11 −14 ≤ k ≤ 28 −41 ≤ l ≤ 45 |
| Reflections Collected | 4814 |
| Independent reflections | 4589 |
| Final R indices [I > 2σ(I)] | R1 = 0.0528 ωR2 = 0.1488 |
| Final R indices (all data) | R1 = 0.0566 ωR2 = 0.1528 |


| D–H…A | D–H (Å) | H–A (Å) | <DHA (deg) |
|---|---|---|---|
| Hydrogen Bonds | |||
| C7H7…O1 | 0.9501(1) | 2.8122(3) | 127.893(3) |
| C7H7…O3 | 0.9501(1) | 2.9562(3) | 106.225(7) |
| C8H8…O3 | 0.9499(1) | 2.8723(3) | 148.665(8) |
| C10H10A…O5 | 0.9800(3) | 2.7012(2) | 166.622(8) |
| C10H10B…O3 | 0.9800(1) | 2.7530(3) | 155.673(8) |
| C10H10B…O1 | 0.9800(1) | 2.9322(4) | 96.873(7) |
| C10H10C…O5 | 0.9799(1) | 2.7267(3) | 141.969(8) |
| C10H10C…O1 | 0.9799(1) | 2.8850(3) | 99.801(7) |
| Stacking Interactions (Å) | |||
| O1…C7 | 3.4775(4) | O1…C8 | 3.5569(3) |
| O1…C9 | 3.4060(4) | O1…C10 | 3.2009(3) |
| O3…C7 | 3.3484(3) | O5…C7 | 3.4079(3) |
| O7…C8 | 3.2757(4) | O7…C9 | 3.2217(5) |
| N7…C7 | 3.9333(4) | N7…C8 | 4.0854(4) |
3.2. Solvate Properties


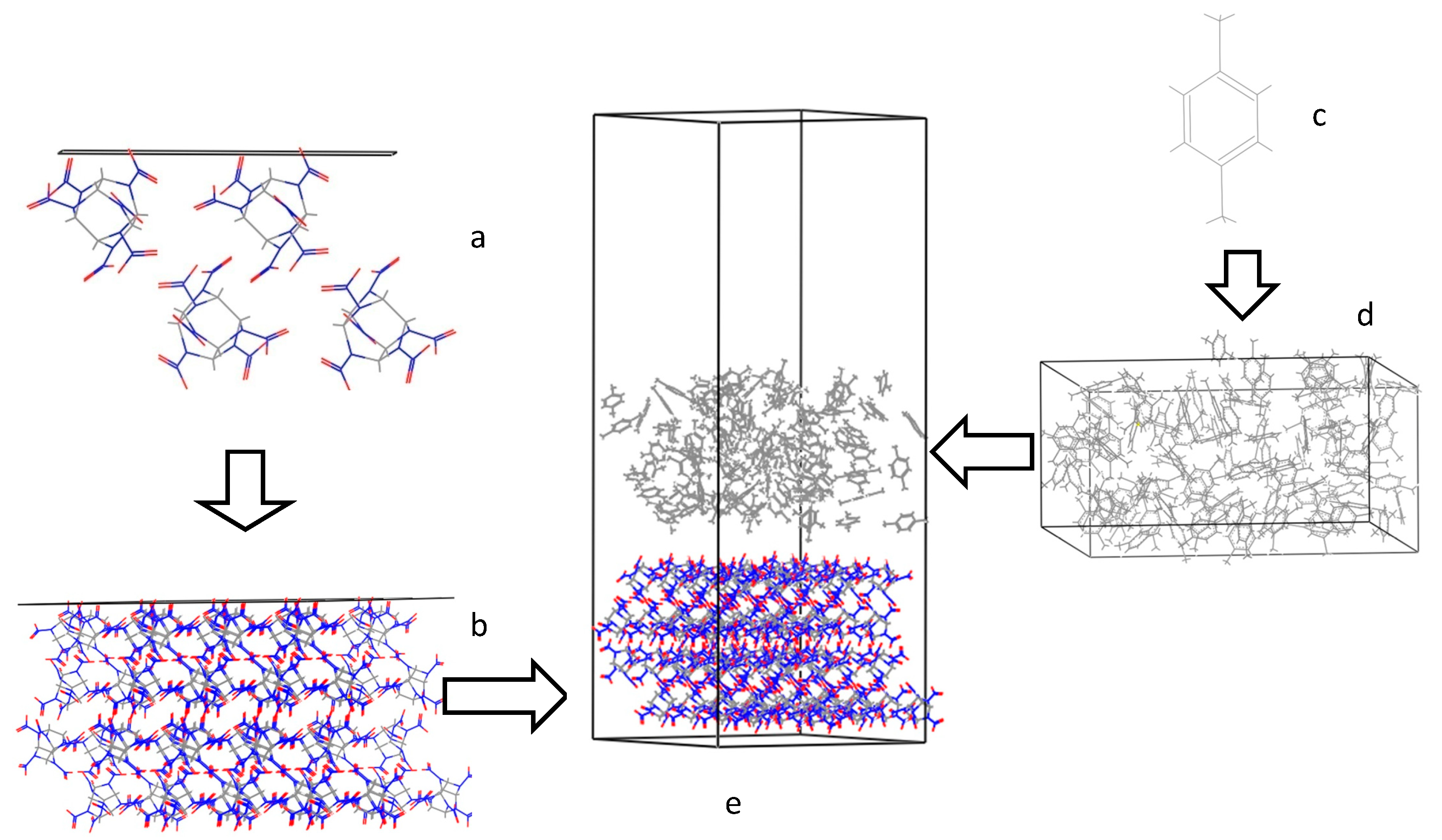
3.3. Crystal Morphology Prediction


| Surface | (10−1) | (101) | (011) | (002) | (110) | (11−1) |
|---|---|---|---|---|---|---|
| Aacc (Å2) | 381.7 | 600.1 | 694.4 | 264.9 | 624.28 | 642.6 |
| Amodel (Å2) | 133.5 | 187.3 | 224.6 | 108.1 | 231.3 | 254.1 |
| S | 2.859 | 3.204 | 3.092 | 2.451 | 2.699 | 2.528 |
| Face | dhkl | Eatt | Rc | Eint | Aacc | Amodel | Es | modelEatt | R'hkl |
|---|---|---|---|---|---|---|---|---|---|
| (10−1) | 11.38 | −56.46 | 1 | −100.874 | 381.7 | 534.09 | −4.505737102 | −43.5736 | 1 |
| (101) | 8.11 | −78.10 | 1.38 | −159.568 | 600.1 | 749.23 | −7.987929119 | −52.5087 | 1.21 |
| (011) | 7.06 | −99.17 | 1.76 | −168.444 | 694.41 | 871.47 | −8.138949579 | −73.9982 | 1.69 |
| (002) | 7.02 | −83.54 | 1.48 | −88.3024 | 264.93 | 432.39 | −3.381490851 | −75.2512 | 1.73 |
| (110) | 6.84 | −87.61 | 1.55 | −183.968 | 624.28 | 875.90 | −7.757439759 | −66.6756 | 1.53 |
| (11−1) | 6.64 | −91.53 | 1.62 | −159.496 | 642.56 | 1017 | −6.501126945 | −75.5951 | 1.73 |
3.4. Radial Distribution Functions of the Interfacial Model

4. Experimental Section
4.1. Crystallization of CL-20 p-Xylene Solvate by Evaporation
4.2. Characterization
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Modi, S.R.; Dantuluri, A.K.R.; Puri, V.; Pawar, Y.B.; Nandekar, P.; Sangamwar, A.T.; Perumalla, S.R.; Sun, C.C.; Bansal, A.K. Impact of crystalhabiton biopharmaceutical performance of celecoxib. Cryst. Growth Des. 2013, 13, 2824–2832. [Google Scholar] [CrossRef]
- Zhang, H.B.; Sun, J.; Kang, B.; Shu, Y.J.; Shu, X.Y.; Liu, Y.; Liu, X.F. Crystalmorphology controlling of TATB by high temperature anti-solvent recrystallization. Propellants Explos. Pyrotech. 2012, 37, 172–178. [Google Scholar] [CrossRef]
- Song, X.L.; Wang, Y.; An, C.W.; Guo, X.D.; Li, F.S. Dependence of particle morphology and size on the mechanical sensitivity and thermal stability of octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine. J. Hazard. Mater. 2008, 159, 222–229. [Google Scholar] [CrossRef] [PubMed]
- Ter Horst, J.H.; Geertman, R.M.; van Rosmalen, G.M. The effect of solvent on crystal morphology. J. Cryst. Growth 2001, 230, 277–284. [Google Scholar] [CrossRef]
- Duan, X.H.; Wei, C.X.; Liu, Y.G.; Pei, C. A molecular dynamics simulation of solvent effects on the crystal morphology of HMX. J. Hazard. Mater. 2010, 174, 175–180. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.X.; Wang, J.K.; Ulrich, J.; Yin, Q.X.; Xue, L.Z. Effect of solvent on the crystal structure and habit of hydrocortisone. J. Cryst. Growth 2008, 8, 1490–1494. [Google Scholar] [CrossRef]
- Aabloo, A.; Klintenberg, M.; Thomas, J.O. Molecular dynamics simulation of a polymer-inorganic interface. Electrochim. Acta 2000, 45, 1425–1429. [Google Scholar] [CrossRef]
- Winn, D.; Doherty, M.F. Modeling crystal shapes of organic materials grown from solution. AIChE J. 2000, 46, 1348–1367. [Google Scholar] [CrossRef]
- Hammond, R.B.; Pencheva, K.; Roberts, K.A. structural-kinetic approach to model face-specific solution/crystal surface energy associated with the crystallization of acetyl salicylic acid from supersaturated aqueous/ethanol solution. Cryst. Growth Des. 2006, 6, 1324–1334. [Google Scholar] [CrossRef]
- Piana, S.; Gale, J.D. Understanding the barriers to crystal growth: Dynamical simulation of the dissolution and growth of urea from aqueous solution. J. Am. Chem. Soc. 2005, 127, 1975–1982. [Google Scholar] [CrossRef] [PubMed]
- Stoica, C.; Verwer, P.; Meekes, H.; van Hoof, P.J.C.M.; Kaspersen, F.M.; Vlieg, E. Understanding the effect of a solvent on the crystal habit. Cryst. Growth Des. 2004, 4, 765–768. [Google Scholar] [CrossRef]
- Li, C.L.; Choi, P. Molecular dynamics study on the effect of solvent adsorption onthe morphology of glycothermallyproduced-Al2O3particles. J. Phys. Chem. C 2008, 112, 10145–10152. [Google Scholar] [CrossRef]
- Bravais, A. Etuldes Cristallographiques; Gthier-Villars: Paris, France, 1866. [Google Scholar]
- Donnay, J.D.H.; Harker, D.A. New law of crystal morphology extending the law of Bravais. Am. Miner. 1937, 22, 446–467. [Google Scholar]
- Liang, Z.Z.; Chen, J.F.; Ma, Y.; Wang, W.; Han, X.L.; Xue, C.Y.; Zhao, H. Qualitative rationalization of the crystal growth morphology of benzoic acid controlled using solvents. CrystEngComm 2014, 16, 5997–6002. [Google Scholar] [CrossRef]
- Harman, P.; Perdok, W.G. Ontherelations between structure and morphology of crystals. Acta Cryst. 1955, 8, 525–530. [Google Scholar] [CrossRef]
- Yi, Q.H.; Che, J.F.; Le, Y.; Wang, J.X.; Xue, C.Y.; Zhao, H. Crystal structure and habit of dirithromycin acetone solvate:A combined experimental and simulative study. J. Cryst. Growth 2013, 372, 193–198. [Google Scholar] [CrossRef]
- Chen, J.; Trout, B.L. Computer-aided solvent selection for improving the morphology of needle-like crystals: Acase study of 2,6-dihydroxybenzoic acid. Cryst. Growth Des. 2010, 10, 4379–4388. [Google Scholar] [CrossRef]
- Nielsen, A.T. Caged polynitramine compound. U.S. Patent 5693794, 2 December 1997. [Google Scholar]
- Tan, J.J.; Ji, G.F.; Chen, X.R.; Li, Z. Structure, equation of state and elasticity of crystalline HNIW by molecular dynamics simulation. Phys. B 2011, 406, 2925–2930. [Google Scholar] [CrossRef]
- Russell, T.P.; Miller, P.J.; Piermarini, G.J.; Block, S. Pressure/temperature phase diagram of hexanitrohexaazaisowurtzitane. J. Phys. Chem. 1993, 97, 1993–1997. [Google Scholar] [CrossRef]
- Millar, D.I.A.; Maynard-Casely, H.E.; Kleppe, A.K.; Marshall, W.G.; Pulham, C.R.; Cumming, A.S. Putting the squeeze on energetic materials-structural charaterisation of a high-pressure phase of CL-20. CrystEngComm 2010, 12, 2524–2527. [Google Scholar] [CrossRef]
- Millar, D.I.A.; Maynard-Casely, H.E.; Allan, D.R. Crystal engineering of energetic materials: Co-crystals of CL-20†. CrystEngComm 2012, 14, 3742–3749. [Google Scholar] [CrossRef]
- Urbelis, J.H.; Swift, J.A. Solvent effects on the growth morphology and phase purity of CL-20. Cryst. Growth Des. 2014, 14, 1642–1649. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Ji, C.L.; Li, H.Z.; Zhou, Y.; Xu, J.J.; Xu, R.J.; Li, J.; Luo, Y.J. Occupancy model for predicting the crystal morphologies influenced by solvents and temperature, and its application tonitroamine explosives. Cryst. Growth Des. 2013, 13, 282–290. [Google Scholar] [CrossRef]
- Hartman, P.; Bennema, P. Theattachment energy as a habit controlling factor: I. Theoretical considerations. J. Cryst. Growth 1980, 49, 145–156. [Google Scholar] [CrossRef]
- Hartman, P.; Chan, H.K. Application of the periodic bond chain (PBC) theory and attachment energy consideration to derive the crystal morphology of hexamethylmelamine. Pharm. Res. 1993, 10, 1052–1058. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.E.; Lee, T.B.; Kim, H.S.; Koo, K.K. Prediction of the growth habit of 7-Amino-4,6-dinitrobenzofuroxan mediated by cosolvents. Cryst. Growth Des. 2010, 10, 618–625. [Google Scholar] [CrossRef]
- Connolly, M.L. Solvent-accessible surface of proteins and nucleic acids. Science 1983, 22, 709–713. [Google Scholar] [CrossRef]
- Liang, Z.Z.; Yi, Q.H.; Wang, W.; Han, X.L.; Chen, J.F.; Le, Y.; Wang, J.X.; Xue, C.Y.; Zhao, H. A systematic study of solvent effect on the crystal habit of dirithromycin solvates by computer simulation. Comput. Chem. Eng. 2014, 62, 56–61. [Google Scholar] [CrossRef]
- Accelrys Software Inc. Accelrys Software Inc. Materials Studio 5.5; Accelrys Inc.: San Diego, CA, USA, 2010. [Google Scholar]
- Nielsen, A.T.; Chafin, A.P.; Christian, S.L.; Moore, D.W.; Nadler, M.P.; Nissan, R.A.; Vanderah, D.J. Synthesis of polyazapolycyclic caged polynitramines. Tetrahedron 1998, 54, 11793–11812. [Google Scholar] [CrossRef]
- Dinesh, K.; Nalini, R.S. Designed isomorphism of Nifedipine: A joint experimental andmolecular simulation study with screened solvents and antisolvents. Cryst. Growth Des. 2014, 14, 326–338. [Google Scholar] [CrossRef]
- Yellin, Z.B. Toward an ab Initio Derivation of Crystal Morphology. J. Am. Chem. Soc. 1985, 107, 8239–8253. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab initio force-field optimized for condensed-phaseapplications-overview with details onalkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Hammond, R.B.; Pencheva, K.; Ramachandran, V.; Roberts, K.J. Application of grid-based molecular methods for modeling solvent-dependent crystal growth morphology: Aspirin crystallization from aqueous ethanolic solution. Cryst. Growth Des. 2007, 7, 1571–1574. [Google Scholar] [CrossRef]
- Shim, H.M.; Kim, J.W.; Koo, K.K. Molecular interaction of solvent with crystal surfaces in the crystallization of ammonium sulfate. J. Cryst. Growth 2013, 373, 64–68. [Google Scholar] [CrossRef]
- Turcotte, R.; Vachon, M.; Queenie, S.M.K.; Wang, R.P.; Jones, D.E.G. Thermal study of HNIW (CL-20). Thermochim. Acta 2005, 433, 105–115. [Google Scholar] [CrossRef]
- Guo, C.Y.; Zhang, H.B.; Wang, X.C.; Xu, J.J.; Liu, Y.; Liu, X.F.; Huang, H.; Sun, J. Crystal structure and explosive performance of a new CL-20/ caprolactam cocrystal. J. Mol. Struct. 2013, 1048, 267–273. [Google Scholar] [CrossRef]
- Kholod, Y.; Okovytyy, S.; Kuramshina, G.; Qasim, M.; Gorb, L.; Leszczynski, J. An analysis of stable forms of CL-20: A DFT study of conformational transitions, infrared and Raman spectra. J. Mol. Struct. 2007, 843, 14–25. [Google Scholar] [CrossRef]
- Chen, G.; Xia, M.Z.; Wu, L.; Wang, F.Y.; Gong, X.D. A study of the solvent effect on the morphology of RDX crystalby molecular modeling method. J. Mol. Model. 2013, 19, 5397–5406. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.Y.; Xia, M.Z.; Wu, L.; Wang, F.Y. Solvent effect on the crystal morphology of 2,6-diamino-3,5-dinitropyridine-1-oxide: A molecular dynamics simulation study. J. Mol. Graph. Model. 2014, 50, 71–77. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. SHELXTL: Structure Determination Software Program; Bruker Analytic X-Ray Systerm Inc.: Madison, WI, USA, 1997. [Google Scholar]
- Sample Availability: Samples of the compounds 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaiso-wurtzitane (CL-20) p-xylene solvate are available from the authors.
© 2014 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, F.; Lv, P.; Sun, C.; Zhang, R.; Pang, S. The Crystal Structure and Morphology of 2,4,6,8,10,12-Hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (CL-20) p-Xylene Solvate: A Joint Experimental and Simulation Study. Molecules 2014, 19, 18574-18589. https://doi.org/10.3390/molecules191118574
Shen F, Lv P, Sun C, Zhang R, Pang S. The Crystal Structure and Morphology of 2,4,6,8,10,12-Hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (CL-20) p-Xylene Solvate: A Joint Experimental and Simulation Study. Molecules. 2014; 19(11):18574-18589. https://doi.org/10.3390/molecules191118574
Chicago/Turabian StyleShen, Fanfan, Penghao Lv, Chenghui Sun, Rubo Zhang, and Siping Pang. 2014. "The Crystal Structure and Morphology of 2,4,6,8,10,12-Hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (CL-20) p-Xylene Solvate: A Joint Experimental and Simulation Study" Molecules 19, no. 11: 18574-18589. https://doi.org/10.3390/molecules191118574
APA StyleShen, F., Lv, P., Sun, C., Zhang, R., & Pang, S. (2014). The Crystal Structure and Morphology of 2,4,6,8,10,12-Hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (CL-20) p-Xylene Solvate: A Joint Experimental and Simulation Study. Molecules, 19(11), 18574-18589. https://doi.org/10.3390/molecules191118574