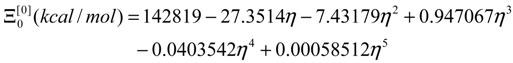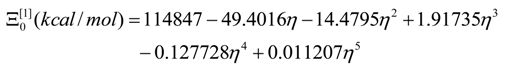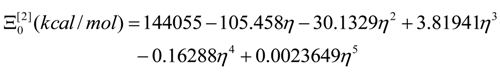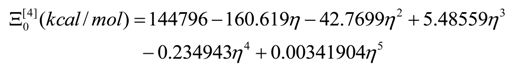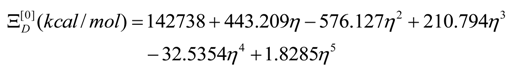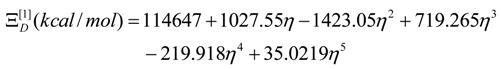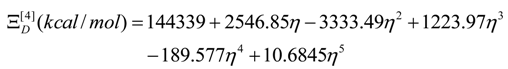Bondonic Effects in Group-IV Honeycomb Nanoribbons with Stone-Wales Topological Defects
Abstract
:1. Introduction
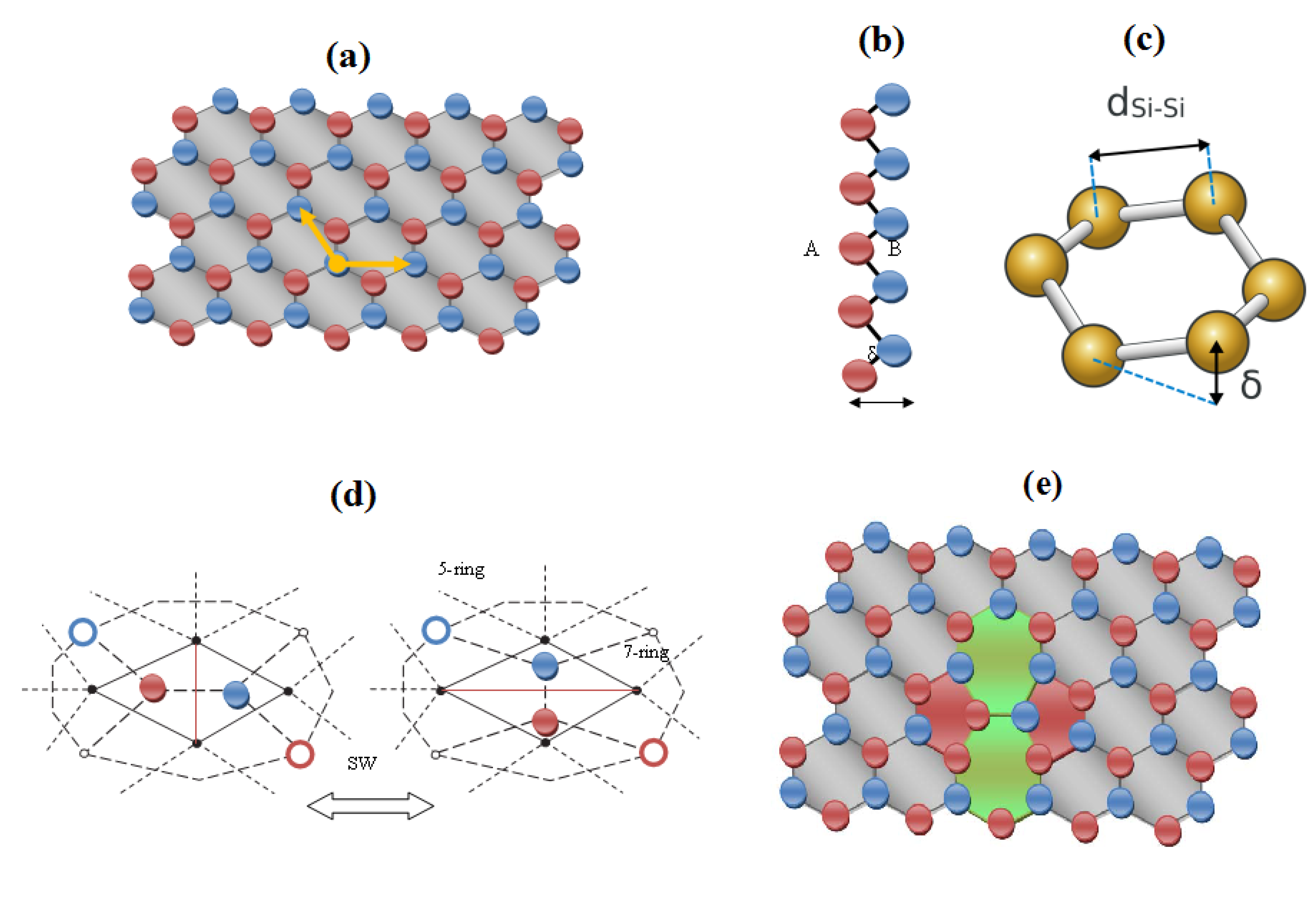
2. Structure and Topology of Honeycomb Nanoribbons
3. The Computational Method
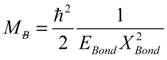

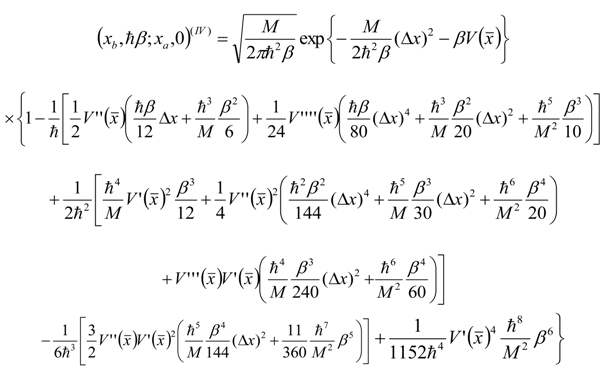
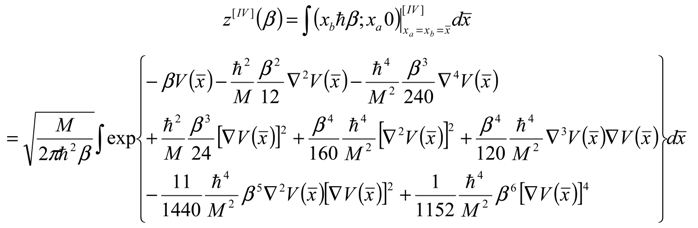
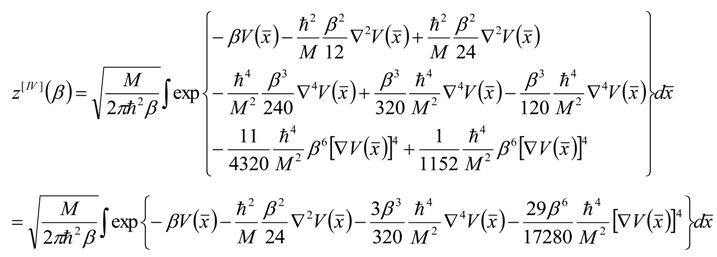
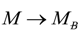 , thus turning Equation (5) into the actual bonding related one:
, thus turning Equation (5) into the actual bonding related one:
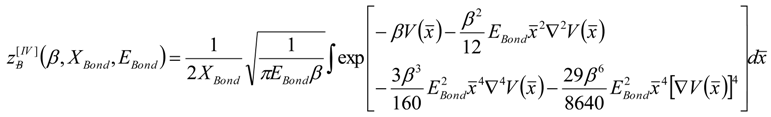
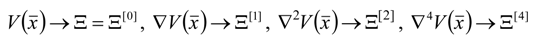




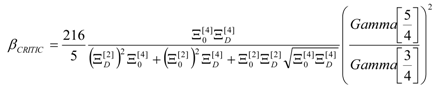
4. Results and Discussion
4.1. Topological Wiener Polynomials
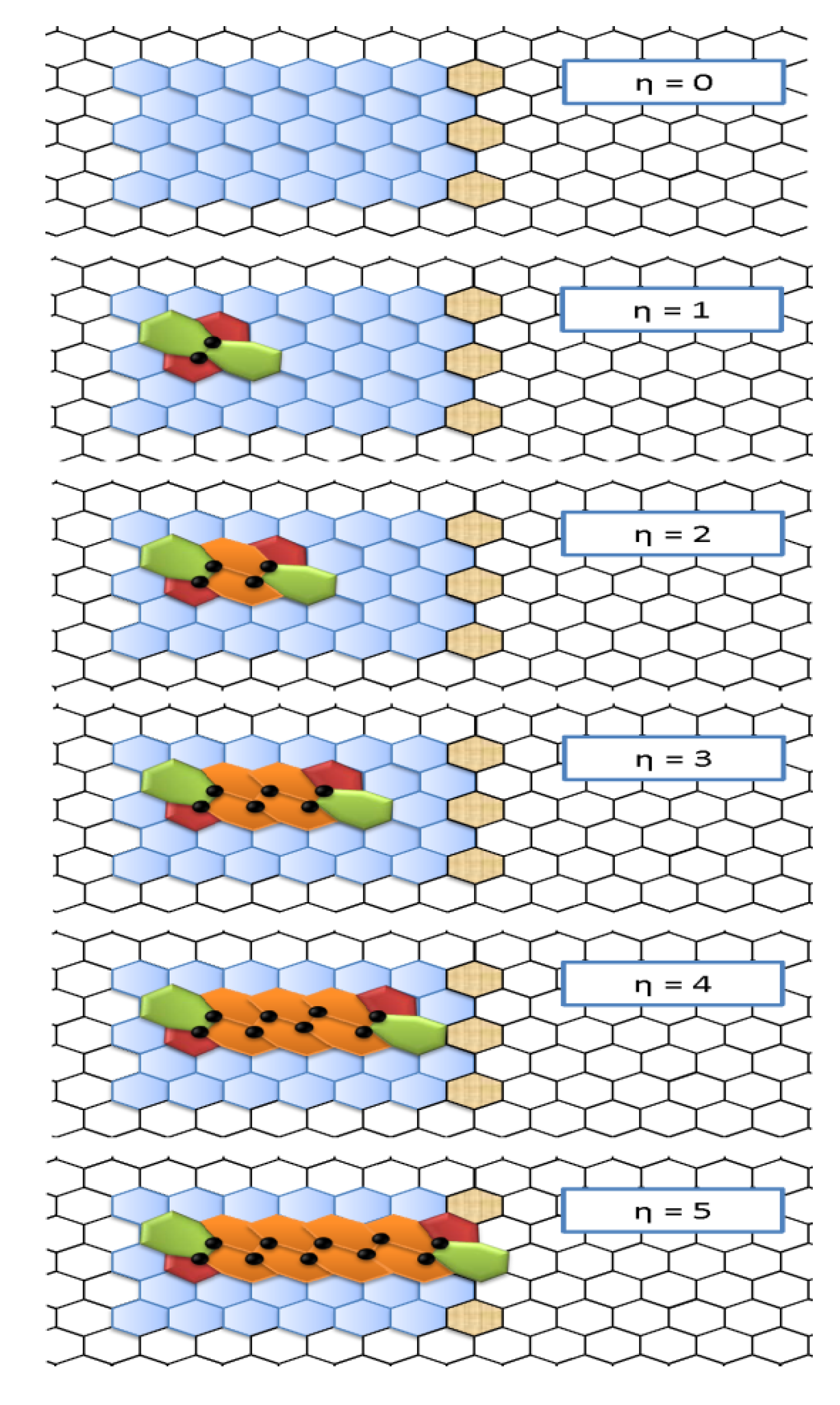
- First, the two 5|7 pentagon-heptagon units SW constituting the SW defect, also called 5|7|7|5 dipole, are considered free to migrate in the hexagonal lattice by inserting η-1 pairs of hexagons 6|6.
- The evolution of the nanoribbon defective structure is controlled by a pure topological potentials Ξ expressing the long-range, collective effects of the network on the network stability itself in terms of distance-based topological invariants computed on the nanoribbon chemical graph composed by n nodes.
- (i)
- physically, the topological potential Ξ considers by definition the collective long-range effects produced by the mutual interactions of all atoms pairs of the chemical system;
- (ii)
- numerically, Ξ features an easily-manageable polynomial behavior in term of the parameter expressing the size of the system (that parameter may be n or even η) with the leading coefficient of the respective polynomial only depending from the dimensionality D of the system–see the recent review on topological modeling methods and results [33].
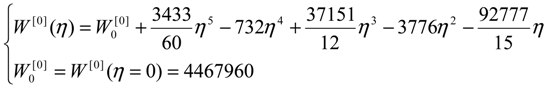
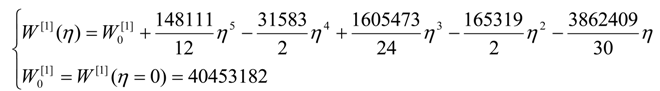
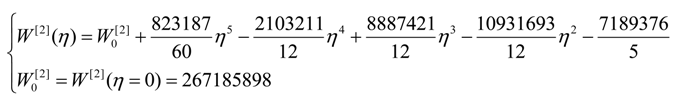
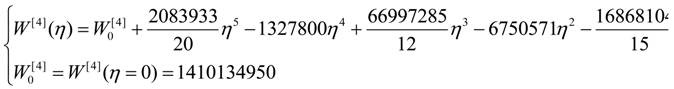
| η | W[°] | W[1] | W[2] | W[4] |
|---|---|---|---|---|
| 0 | 4,467,960 | 40,453,200 | 267,186,000 | 1,410,130,000 |
| 0.2 | 4,466,600 | 40,424,600 | 266,868,000 | 1,407,660,000 |
| 0.4 | 4,465,060 | 40,392,500 | 266,508,000 | 1,404,880,000 |
| 0.6 | 4,463,470 | 40,359,500 | 266,134,000 | 1,402,000,000 |
| 0.8 | 4,461,900 | 40,329,100 | 265,764,000 | 1,399,170,000 |
| 1 | 4,460,420 | 40,305,200 | 265,416,000 | 1,396,500,000 |
| 2 | 4,455,370 | 40,542,500 | 264,226,000 | 1,387,400,000 |
| 3 | 4,453,620 | 42,849,300 | 263,807,000 | 1,384,160,000 |
| 4 | 4,452,140 | 51,493,100 | 263,439,000 | 1,381,240,000 |
| 5 | 4,450,930 | 74,805,700 | 263,132,000 | 1,378,770,000 |
| Defect Step | Instant Structure | Electronic Energy (eV) | Total Energy (eV) | Binding Energy (eV) | Parabolic Energy (eV) |
|---|---|---|---|---|---|
| η = 0 |  | 2858.69979 | 2595.306 | 7308.17 | 13,063.1207 |
| η = 1 |  | 2425.90314 | 2409.47 | 7494.0069 | 102,344.109 |
| η = 2 |  | 2641.35644 | 2410.023 | 7493.4534 | 100,091.3384 |
| η = 3 |  | 90063.404 | 10331.43 | −427.9522 | 6770.427006 |
| η = 4 |  | 2428.23769 | 2408.129 | 7495.3472 | 102,353.338 |
| η = 5 |  | 2484.84517 | 2468.133 | 7676.8912 | 107,394.1399 |
| Correlation Slope, α in Equation (18) | W[0](η) | 0.00384593 | 0.000846 | 0.0013853 | 0.01614977 |
| W[1](η) | 0.00029961 | 7.01 × 10−5 | 0.000123 | 0.001488221 | |
| W[2](η) | 6.4681 × 10−5 | 1.42 × 10−5 | 2.335 × 10−5 | 0.000271766 | |
| W[4](η) | 1.2299 × 10−5 | 2.71 × 10−6 | 4.445 × 10−6 | 5.16926 × 10−5 | |
| Correlation Factor R2 | W[0](η) | 0.21643315 | 0.622413 | 0.813889 | 0.727612957 |
| W[1](η) | 0.16519269 | 0.538169 | 0.8067669 | 0.777077187 | |
| W[2](η) | 0.21568411 | 0.621567 | 0.8144879 | 0.725935217 | |
| W[4](η) | 0.21522938 | 0.621048 | 0.8148337 | 0.724864925 |
4.2. Topo-Reactivity Wiener Polynomials
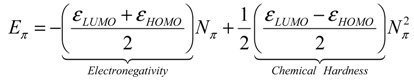

- the pro-argument, largely advocated by Parr works in last decades of conceptual chemistry research with application in inorganic and organic reactivity alike [41,42,43,44], while being recently employed by present authors in “coloring” chemical topology with chemical reactivity electronic frontier information of atoms in molecules
- the contra-argument, defended by late Szentpaly works on various inorganic systems [46], according which the parabolic description is slightly non-realistic neither for ground nor for valence state of atoms and molecules since actually not having the minimum of the parabola on the right realm of exchanged electrons in bonding or in ionization-affinity processed; this limitation was also conceptually discussed by one of the present authors in a recent paper advancing the cubic form of chemical reactivity as a better framework for conceptual treatment for electronic exchange as driven by electronegativity and chemical hardness, with an universal (and also Bohmian) value [47].
- the energetically calibrated topological potentials for the forming SW defect instance (still corresponding to the “0” structure) within [0-1] range of the η “steps”:
- The polynomials for the topological potentials describing the SW waves still corresponding to the defective “D” structures) within [0-5] range of the ; steps
4.3. Bondonic Effects on Topological Defects in Group IV-Honeycomb Nanoribbons

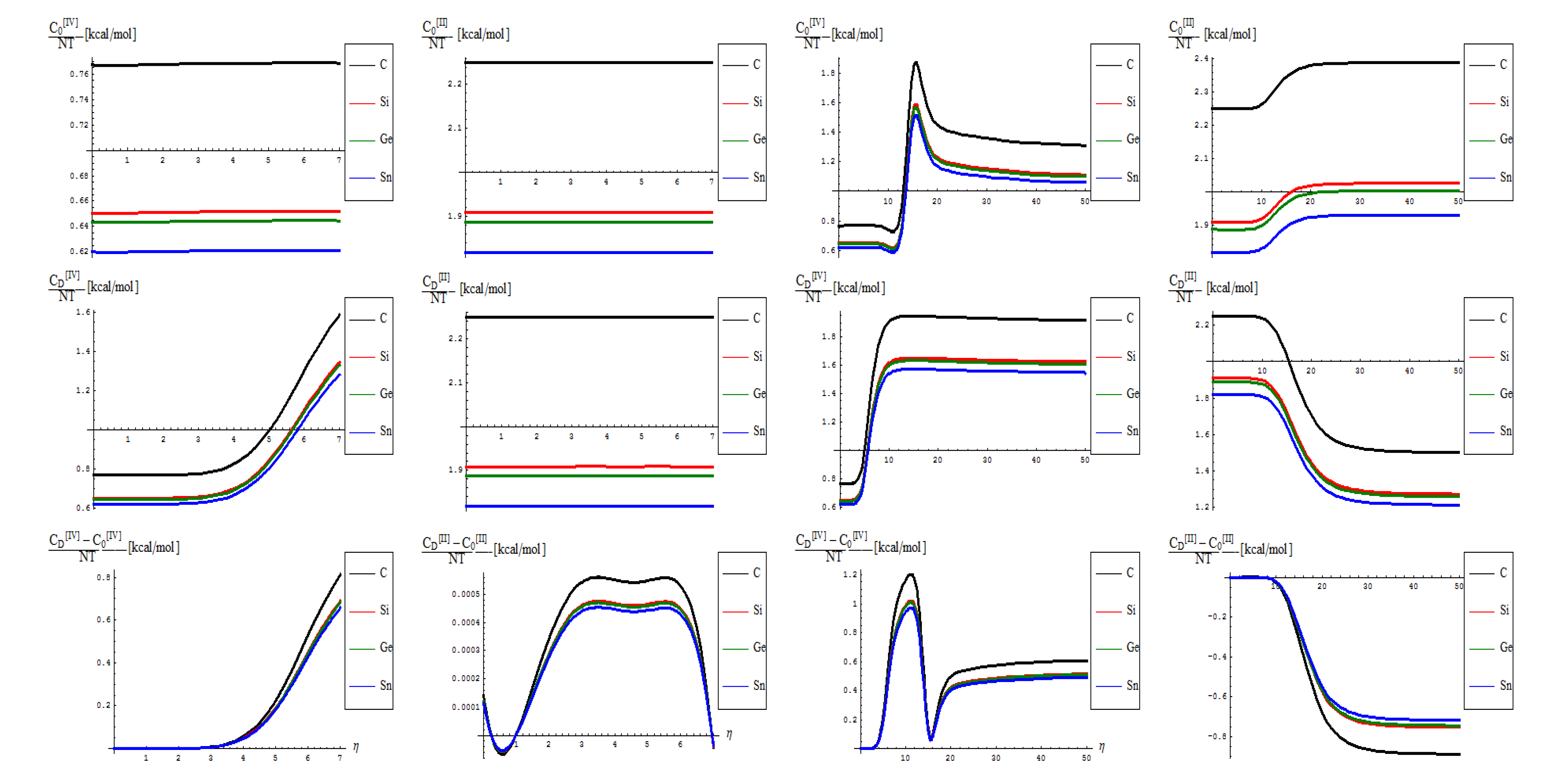
- The topological potentials modeling the forming (“0-to-1”) step of SWw are all monotonically descending, meaning their eventual release into defective structures;
- The topological defective potentials have quite constant behavior over the entire computational η = 0-5 plateau, while recording quasi-critical rise for the potential “echo” spanning the long range behavior, meaning the rising of the defective potential barrier in fact (with more emphasize for the first order potential, as expected from previous discussion, see Table 1, for instance); this strongly suggest the real finite range for the defective SWw, i.e., the annihilation long-range stage that came after their creation on the short-range realm;
- The D-to-0 difference shows some short range fluctuations for all potentials unless the first order one, yet ending into the D-potential definite rising barrier on the long range behavior; the difference for the first order potential displays such energetic barrier rise just from the short range, paralleling the defective “D” shape;
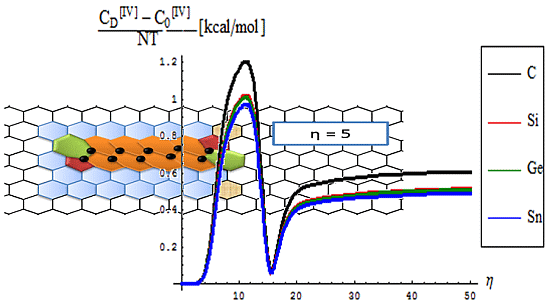
- Concerning the C > Si > Ge > Sn potential (paralleling the electronegativity) hierarchy, one sees that the C-to-Si large energetic gap for pristine “0” structure is considerably attenuated for the “D” propagation of the SWw defect, manifested especially for second and 4th order, while the Si-to-Ge energetic curves almost coincides for these orders; even more, all Si, Ge, and Sn shapes are practically united under first order defective potential “D1”.

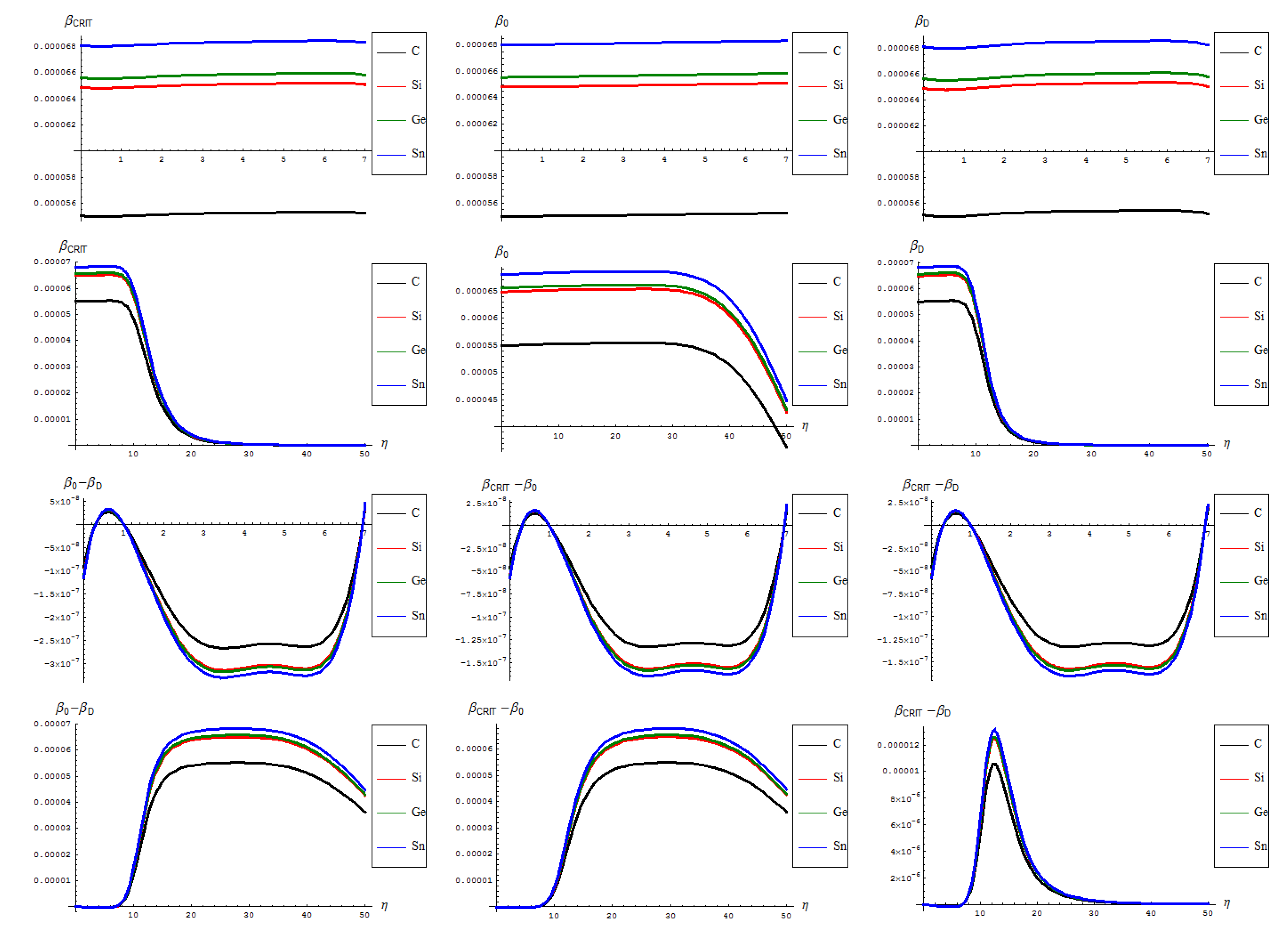
- The general feature for the β signals is that it is constantly for the short range in phase transition (critical curve) between forming (“0-to-1”) and transforming “D” of SW waves and along the predicted inverse C < Si < Ge < Sn signal (pulse) hierarchy;
- The situation changes on the long range “echo” when the critical signal may be recorded closer to the defective than to the pristine structures, when one should record also a shrink signal pulses gap between the C-to-Si-to-Ge-to-Sn;
- The differences between the critical-to-defective-to-pristine structures’ pulses shapes follows on a short range the generally recorded topological potential difference in that range, while noticing definite cupolas for the long range behavior–especially on the critical regime, meaning that indeed the SWw echo is disappearing after about 50 isomeric topological transformation of the considered honey-comb nanosystem (see the right bottom line picture of Figure 4).
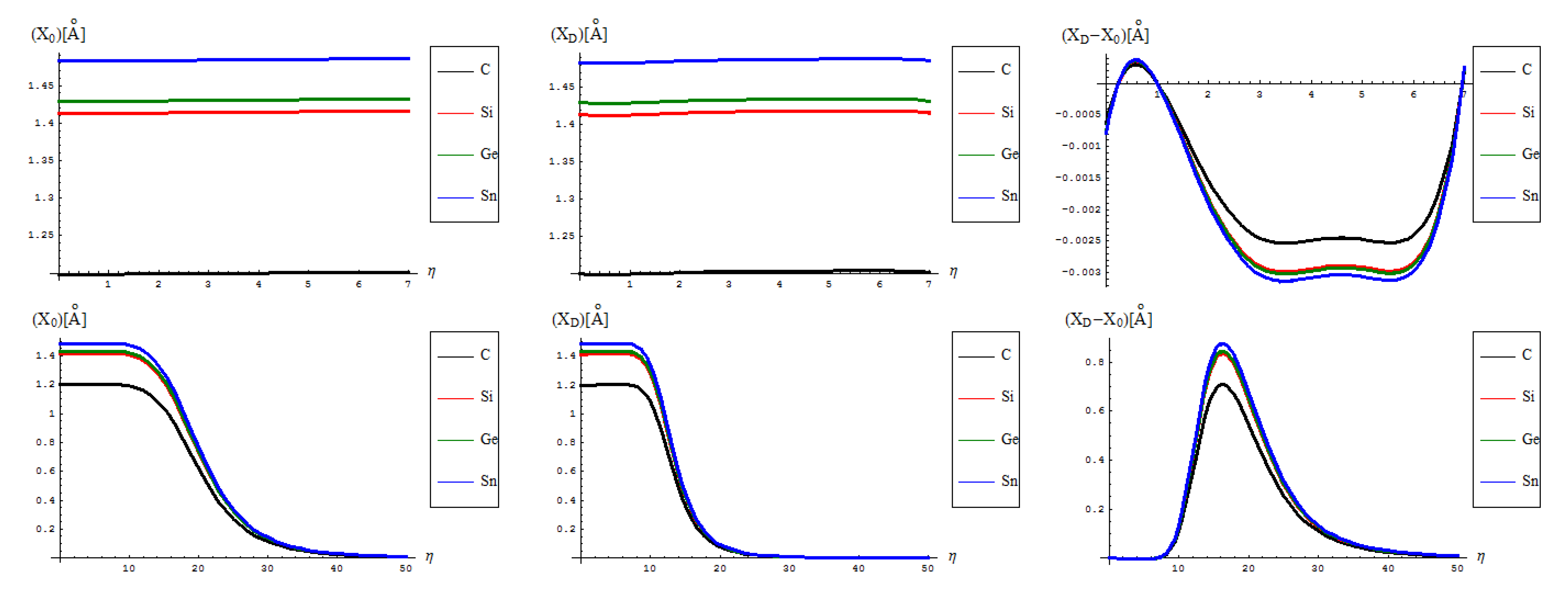
- The identical boning length for pristine and defective structures on the short range transformations (up to seven topological rearrangements paralleling the SW wave propagation into extended lattice); notably, the bondonic lengths are correctly shorter than the detected or previously estimated bonding length for C-C bond (in graphene) and elongated in Si-Si bond (in silicene), see the Introduction, since the bondonic agent nature, in assuring the bonding action for the basic atomic pairing in honey-comb nanoribbons.
- The decrease of boning length and of the consequent action on the long range dynamics, paralleling the decreasing of the inter-elongation difference in bonding for C-to-Si-to-Ge-to-Sn;
- The prediction on the bondonic longest “echo” in an extended lattice, limited to 50 transformations, or dipole extensions steps continuing the Figure 2; this information has a practical consequence in predicting the longest nano-fragment still chemically stabilized by the bondonic “echo” by its long range action (sustained by its inner Bohmian nature, see reference [9]);
- The D-to-0 bondonic length differences parallels those recorded for the critical-to-D one found for the β signal in Figure 4, this way confirming the finite (non-zero nor infinite) physical length over which the phase transition from pristine to Stone-Wales topological isomer is taking place; it also offers an spatial alternative to temporal (quasi-inaccessible) scale of measuring and detecting the bondonic effects on topological transformations and isomeric rearrangements.
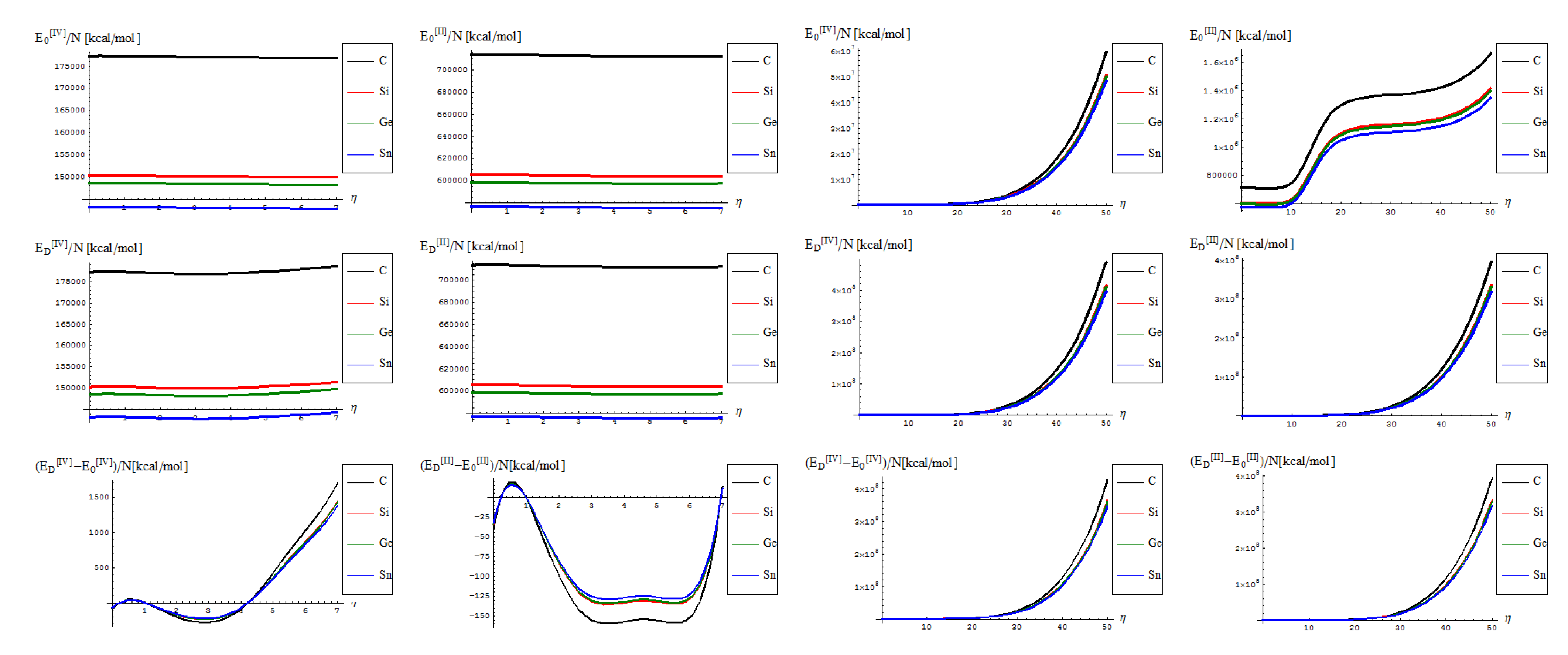
- No shape differences other than the overall scales along a quasi invariant energy-gap between C-to-Si-to-Ge-to-Sn related lattices are recorded between the [II] and [IV] order path-integral bondonic formalisms, with natural higher energetic records for the later approach since more interaction/interconnection effects are included, for the internal energies of honeycomb lattice without and with topological defects as triggered on the short range as in Figure 2;
- The previous situation changes for the long range SW dipole transformations, noticing the same type of energetic increase as for the forth order topological potential/barrier in Figure 3, together with quasi-unifying the C with Si-to-Ge-to-Sn behaviors (being the last three atomic based lattices quite unified in total bondonic energetic shape); the peculiar behavior is noted just to [II] order treatment and in the long range pristine super cell self-arranging, when the energy rising displays two plateaus as well as still a C respecting Si-to-Ge-to-Sn energetic gaps for their honeycomb lattices; however, the energetic rising even for the so called pristine structures is in accordance with the bohemian quantum nature of the bondon which accounts for the self-arrangements of a quantum structure even when self-symmetric, being this in accordance with quantum vacuum energy which is non-zero due to the energy required for internal self-symmetry eventually broken in the spring isomerisations of space, here represented by the SW topological defects and of their (also finite) propagations.
- The D-to-0 differences are nevertheless replicating the defective behavior for both the [II] and [IV] order analysis on the long range, while showcasing some different types of fluctuations and inversions along the C-to-Si-to-Ge-to-Sn honeycomb nanosystems for the short-range of SW dipole evolution;
- with special reference to [IV] short range behavior one notes the the pristine “0” state is still present as an “echo” over the defective “D” state, due to its energetic dominance, that nevertheless has the contribution in replicating “the learning” mechanism of generating SW defects in between each short range steps as was the case in between η = 0 and η = 1; remarkably, this may have future exciting consequences in better understanding the cellular morphogenesis by “replicating the learning” machinery of the Stone-Wales transformation, found to be present also at the cell-life-cycle phenomenology, see [28].
- from the scale values, one obtains actual quite impressive accordance with the previously calculated or predicted values for the graphene and silicone networks: take for instance just the pristine “0” output, in [IV] other environment; for it one notes the constant results about
/(NT)[kcal/mol] ~ 0.77 for graphene and
/(NT)[kcal/mol] ~ 0.65 for silicene; when taking account of the units transformations [49] such as 1 [kcal/mol] = 503.228 [K], one arrives that, for instance, for room temperature of T~300 K, and for short range transformation (say N = 7 bondons involved, one created per each step of topological transformation) one gets
(C)[hartree] ~ 0.185 and respectively
(Si)[hartree] ~ 0.156, which in [eV] will respectively give about
(C)[eV] ~ 5.09 and
(Si)[eV] ~ 4.24 which nevertheless are quite close with previous estimations for SW rotation barriers as Eb ≈ 5 eV for graphene and Eb ≈ 2.8 eV for silicene (see Introduction); the discrepancy may be nevertheless avoided while considering the semiconductor properties of Si which requires more bondons being involved such that the SW rotational barrier to be passed and the defective dipole triggered; as such for N = 10 created bondons for Si–SW super cell one refines the above result to
(Si,N = 10)[eV] ~ 2.96 which fits quite well with literature results, see reference [25]. On the other hand, it is also apparent that for [II] order treatment the data of Figure 7 implies that more bondons are required to fit with the right observed or by other means estimated data, which leaves with the important conceptual lesson: more bondons–less connectivity relationship, very useful in addressing other fundamental chemical problems like crystal field theory and aromatic compounds, just to name a few.
- As previously noted the “D” effect is to shrink the energetic gap between C-to-Si-to-Ge-to-Sn lattice structural behavior, respecting the “0” pristine or defect forming transition state;
- The short range D-to-O differences closely follow the previous internal energy shapes of Figure 6, yet with less oscillations for the [IV] treatment, thus in accordance with more observable character of the caloric capacity;
- For the long range behavior, instead, what was previously a parabolic increase in internal energy acquires now a plateau behavior in all [IV] and [II] order representations: “0”, “D”, and their “D-to-0” differences; nevertheless it seems that the “echo”/signal about η = 10 is particularly strong in [IV] order modeling of D-to-0 differences in caloric capacities, while we notice for the “D” state the graphenic apex curvature about η = 7 followed by that of silicone at η = 10, in full consistency with above bondonic energetic analysis (N = 7 for C-lattice, and N = 10 for Si lattice), thus confirming it. Further signals are also visible, for accumulation of bondons (as the SW dipole evolve and extends over the nanostructure) at η = 15 in pristine structure, as well as for the further plateaus within the [II] order analysis, again in accordance with the above discovered rule of more bondons being required for acquiring the same effect with less connectivity (long-range-bonding neighboring) analysis.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
Appendix 1: Derivation of the 4th Order Path Integral Based Quantum Propagator
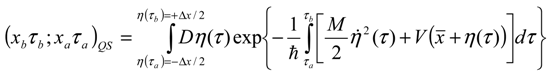

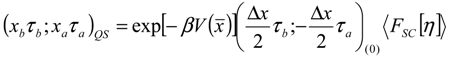
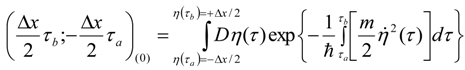

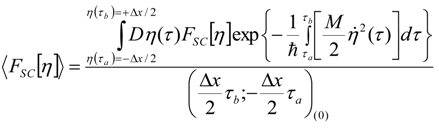
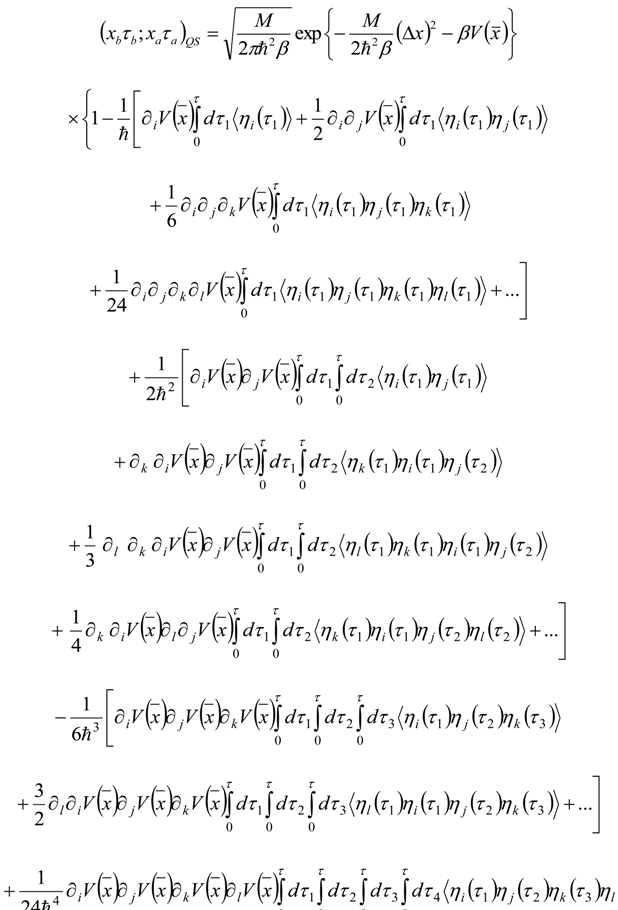


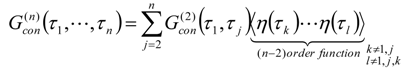

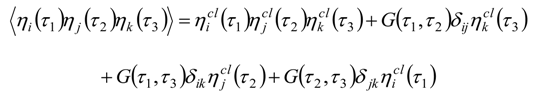



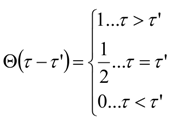
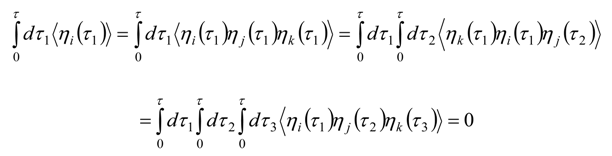

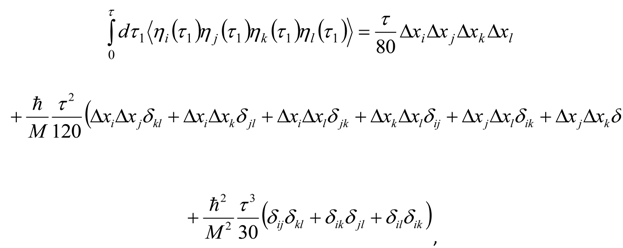
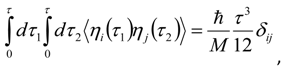
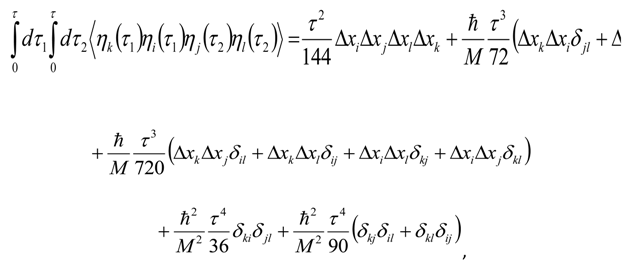
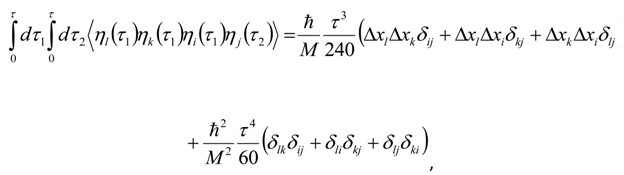
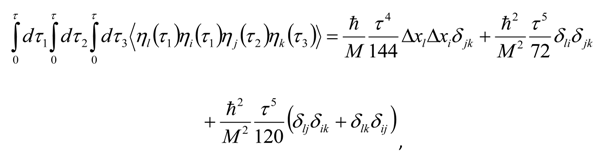
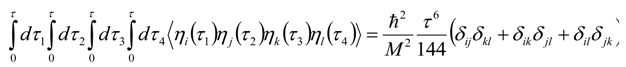
Appendix 2: Gauss Type Relationships for Higher Order Integrals
 ), successively as:
), successively as:
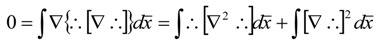
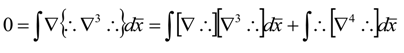

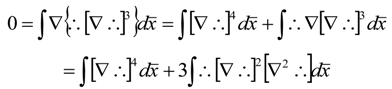

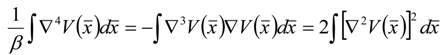

References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Falko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
- Butler, S.Z.; Hollen, S.M.; Cao, L.; Cui, Y.; Gupta, J.A.; Gutiérrez, H.R.; Heinz, T.F.; Hong, S.S.; Huang, J.; Ismach, A.F.; et al. Progress, challenges, and opportunities in two-dimensional materials beyond graphene. ACS Nano 2013, 7, 2898–2926. [Google Scholar] [CrossRef]
- Britnell, L.; Gorbachev, R.V.; Jalil, R.; Belle, B.D.; Schedin, F.; Mishchenko, A.; Georgiou, T.; Katsnelson, M.I.; Eaves, L.; Morozov, S.V.; et al. Field-effect tunneling transistor based on vertical graphene heterostructures. Science 2012, 335, 947–950. [Google Scholar] [CrossRef]
- Takeda, K.; Shiraishi, K. Theoretical possibility of stage corrugation in Si and Ge analogs of graphite. Phys. Rev. B 1994, 50, 14916–14922. [Google Scholar] [CrossRef]
- Guzman-Verri, G.G.; Lew Yan Voon, L.C. Electronic structure of silicon-based nanostructures. Phys. Rev. B 2007, 76, 075131. [Google Scholar] [CrossRef]
- Nakano, H.; Mitsuoka, T.; Harada, M.; Horibuchi, K.; Nozaki, H.; Takahashi, N.; Nonaka, T.; Seno, Y.; Nakamura, H. Soft synthesis of single-crystal silicon monolayer sheets. Angew. Chem. Int. Ed. 2006, 45, 6303–6306. [Google Scholar] [CrossRef]
- Putz, M.V. The Bondons: The quantum particles of the chemical bond. Int. J. Mol. Sci. 2010, 11, 4227–4256. [Google Scholar] [CrossRef]
- Putz, M.V. Beyond quantum nonlocality: Chemical bonding field. Int. J. Environ. Sci. 2010, 1, 25–31. [Google Scholar]
- Putz, M.V. Hidden Side of Chemical Bond: The Bosonic Condensate. In Advances in Chemistry Research. Volume 10; Taylor, J.C., Ed.; NOVA Science Publishers, Inc.: New York, NY, USA, 2011; Chapter 8; pp. 261–298. [Google Scholar]
- Putz, M.V. Nanoroots of Quantum Chemistry: Atomic Radii, Periodic Behavior, and Bondons. In Nanoscience and Advancing Computational Methods in Chemistry: Research Progress; Castro, E.A., Haghi, A.K., Eds.; IGI Global (formerly Idea Group Inc.): Hershey, PA, USA, 2012; pp. 103–143. [Google Scholar]
- Putz, M.V. Quantum Theory: Density, Condensation, and Bonding; Apple Academics: Oakville, ON, Canada, 2012. [Google Scholar]
- Putz, M.V. Chemical Orthogonal Spaces; Kragujevac University: Kragujevac, Serbia, 2012; Mathematical Chemistry Monographs; Volume 14. [Google Scholar]
- Putz, M.V. Density functional theory of Bose-Einstein condensation: Road to chemical bonding quantum condensate. Struct. Bond. 2012, 149, 1–50. [Google Scholar] [CrossRef]
- Putz, M.V.; Ori, O. Bondonic Characterization of extended nanosystems: Application to graphene’s nanoribbons. Chem. Phys. Lett. 2012, 548, 95–100. [Google Scholar] [CrossRef]
- Leandri, C.; le Lay, G.; Aufray, B.; Girardeaux, C.; Avila, J.; Dávila, M.E.; Asensio, M.C.; Ottaviani, C.; Cricenti, A. Self-aligned silicon quantum wires on Ag(110). Surface Sci. 2005, 574, L9–L15. [Google Scholar] [CrossRef]
- Aufray, B.; Kara, A.; Vizzini, S.; Oughaddou, H.; Léandri, C.; Ealet, B.; le Lay, G. Graphene-like silicon nanoribbons on Ag(110): A possible formation of silicone. Appl. Phys. Lett. 2010, 96, 183102. [Google Scholar]
- Sahaf, H.; Masson, L.; Léandri, C.; Aufray, B.; le Lay, G.; Ronci, F. Formation of a one-dimensional grating at the molecular scale by selfassembly of straight silicon nanowires. Appl. Phys. Lett. 2007, 90, 263110. [Google Scholar] [CrossRef]
- Vogt, P.; de Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M.C.; Resta, A.; Ealet, B.; le Lay, G. Silicene: Compelling experimental evidence for graphenelike two-dimensional silicon. Phys. Rev. Lett. 2012, 108, 155501. [Google Scholar] [CrossRef]
- Cahangirov, S.; Topsakal, M.; Aktürk, E.; Sahin, H.; Ciraci, S. Two- and one-dimensional honeycomb structures of silicon and germanium. Phys. Rev. Lett. 2009, 102, 236804. [Google Scholar] [CrossRef]
- Davydov, S.Y. On the elastic characteristics of graphene and silicone. Phys. Solid State 2010, 52, 184–187. [Google Scholar] [CrossRef]
- Zhang, R.Q.; Lee, S.T.; Law, C.-K.; Li, W.-K.; Teo, B.K. Silicon nanotubes: Why not? Chem. Phys. Lett. 2002, 364, 251–258. [Google Scholar] [CrossRef]
- Ma, J.; Alfè, D.; Michaelides, A.; Wang, E. Stone-Wales defects in graphene and other planar sp2-bonded materials. Phys. Rev. B 2007, 80, 075131. [Google Scholar]
- Sahin, H.; Sivek, J.; Li, S.; Partoens, B.; Peeters, F.M. Stone-Wales defects in silicene: Formation, stability, and reactivity of defect sites. Phys. Rev. B 2013, 88, 045434. [Google Scholar]
- De Padova, P.; Quaresima, C.; Ottaviani, C.; Sheverdyaeva, P.M.; Moras, P.; Carbone, C.; Topwal, D.; Olivieri, B.; Kara, A.; Oughaddou, H.; et al. Evidence of graphene-like electronic signature in silicene nanoribbons. Appl. Phys. Lett. 2010, 96, 261905. [Google Scholar] [CrossRef]
- Kara, A.; Léandri, C.; Dávila, M.E.; de Padova, P.; Ealet, B.; Oughaddou, H.; Aufray, B.; le Lay, G. Physics of silicene stripes. J. Supercond. Nov. Magn. 2009, 22, 259–263. [Google Scholar] [CrossRef]
- Guillot, C.; Lecuit, T. Mechanics of epithelial tissue homeostasis and morphogenesis. Science 2013, 34, 1185–1189. [Google Scholar] [CrossRef]
- Putz, M.V. Semiclassical electronegativity and chemical hardness. J. Theor. Comput. Chem. 2007, 6, 33–47. [Google Scholar] [CrossRef]
- Putz, M.V. Electronegativity and chemical hardness: Different patterns in quantum chemistry. Curr. Phys. Chem. 2011, 1, 111–139. [Google Scholar] [CrossRef]
- Ori, O.; Cataldo, F.; Putz, M.V. Topological anisotropy of Stone-Wales waves in graphenic fragments. Int. J. Mol. Sci. 2011, 12, 7934–7949. [Google Scholar] [CrossRef]
- Samsonidze, Ge.G.; Samsonidze, G.G.; Yakobson, B.I. Energetics of Stone–Wales defects in deformations of monoatomic hexagonal layers. Comput. Mater. Sci. 2002, 23, 62–72. [Google Scholar] [CrossRef]
- Iranmanesh, A.; Ashrafi, A.R.; Graovac, A.; Cataldo, F.; Ori, O. Wiener Index Role in Topological Modeling of Hexagonal Systems-From Fullerenes to Graphene. In Distance in Molecular Graphs-Applications; Gutman, I., Furtula, B., Eds.; University of Kragujevac: Kragujevac, Serbia, 2012; Mathematical Chemistry Monographs Series; Volume 13, pp. 135–155. [Google Scholar]
- De Corato, M.; Bernasconi, M.; D’Alessio, L.; Ori, O.; Putz, M.V.; Benedek, G. Topological Versus Physical and Chemical Properties of Negatively Curved Carbon Surfaces. In Topological Modelling of Nanostructures and Extended Systems; Ashrafi, A.R., Cataldo, F., Iranmanesh, A., Ori, O., Eds.; Springer Science+Business Media: Dordrecht, The Netherland, 2013; pp. 105–136. [Google Scholar]
- Putz, M.V. Quantum Parabolic Effects of Electronegativity and Chemical Hardness on Carbon π-Systems. In Carbon Bonding and Structures: Advances in Physics and Chemistry; Putz, M.V., Ed.; Springer Science+Business Media: London, UK, 2011; Chapter 1, Carbon Materials: Chemistry and Physics; Volume 5, pp. 1–32. [Google Scholar]
- Putz, M.V. Chemical Reactivity and Biological Activity Criteria from DFT Parabolic Dependency E = E(N). In Theoretical and Computational Developments in Modern Density Functional Theory; Roy, A.K., Ed.; NOVA Science Publishers, Inc.: New York, NY, USA, 2012; Chapter 17; pp. 449–484. [Google Scholar]
- Putz, M.V. Absolute and Chemical Electronegativity and Hardness; NOVA Science Publishers: New York, NY, USA, 2008. [Google Scholar]
- Putz, M.V. Koopmans’ analysis of chemical hardness with spectral like resolution. Sci. World J. 2013, 2013, 348415. [Google Scholar]
- HyperChem 7.01 [Program Package]; Hypercube, Inc.: Gainesville, FL, USA, 2002.
- Kleinert, H.; Pelster, A.; Putz, M.V. Variational perturbation theory for Markov processes. Phys. Rev. E 2002, 65, 066128:1–066128:7. [Google Scholar]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Parr, R.G. Density functional theory. Annu. Rev. Phys. Chem. 1983, 34, 631–656. [Google Scholar] [CrossRef]
- Parr, R.G.; Pearson, R.G. Absolute hardness: Companion parameter to absolute electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [CrossRef]
- Chattaraj, P.K.; Parr, R.G. Density functional theory of chemical hardness. Struct. Bond. 1993, 80, 11–25. [Google Scholar] [CrossRef]
- Putz, M.V.; Ori, O.; Cataldo, F.; Putz, A.M. Parabolic reactivity <<coloring>> molecular topology. Application on carcinogenic PAHs. Curr. Org. Chem. 2013, 17, 2816–2830. [Google Scholar] [CrossRef]
- Von Szentpály, L. Modeling the charge dependence of total energy and its relevance to electrophilicity. Int. J. Quant. Chem. 2000, 76, 222–234. [Google Scholar] [CrossRef]
- Putz, M.V. Valence atom with bohmian quantum potential: The golden ratio approach. Chem. Cent. J. 2012, 6, 135. [Google Scholar] [CrossRef]
- Parr, R.G.; Bartolotti, L.J. On the geometric mean principle of electronegativity equalization. J. Am. Chem. Soc. 1982, 104, 3801–3803. [Google Scholar] [CrossRef]
- Physical Units’ Transformations: Web. Available online: http://users.mccammon.ucsd.edu/~blu/Research-Handbook/physical-constant.html (accessed on 10 August 2013).
- Novoselov, K.S. Nobel lecture-Graphene: Materials in the flatland. Rev. Mod. Phys. 2011, 83, 837–849. [Google Scholar] [CrossRef]
- Ori, O.; Putz, M.V.; Gutman, I.; Schwerdtfeger, P. Generalized Stone-Wales transformations for fullerene graphs derived from Berge’s switching theorem. In Ante Graovac–Life and Works; Gutman, I., Pokrić, B., Vukičević, D., Eds.; University of Kragujevac: Kragujevac, Serbia, 2014; Mathematical Chemistry Monographs No. 16; pp. 259–272. [Google Scholar]
- Kleinert, H. Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 3rd ed.; World Scientific: Singapore, 2004. [Google Scholar]
- Putz, M.V. Path integrals for electronic densities, reactivity indices, and localization functions in quantum systems. Int. J. Mol. Sci. 2009, 10, 4816–4940. [Google Scholar] [CrossRef]
- Sample Availability: Not available.
© 2014 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Putz, M.V.; Ori, O. Bondonic Effects in Group-IV Honeycomb Nanoribbons with Stone-Wales Topological Defects. Molecules 2014, 19, 4157-4188. https://doi.org/10.3390/molecules19044157
Putz MV, Ori O. Bondonic Effects in Group-IV Honeycomb Nanoribbons with Stone-Wales Topological Defects. Molecules. 2014; 19(4):4157-4188. https://doi.org/10.3390/molecules19044157
Chicago/Turabian StylePutz, Mihai V., and Ottorino Ori. 2014. "Bondonic Effects in Group-IV Honeycomb Nanoribbons with Stone-Wales Topological Defects" Molecules 19, no. 4: 4157-4188. https://doi.org/10.3390/molecules19044157
APA StylePutz, M. V., & Ori, O. (2014). Bondonic Effects in Group-IV Honeycomb Nanoribbons with Stone-Wales Topological Defects. Molecules, 19(4), 4157-4188. https://doi.org/10.3390/molecules19044157