Experimental Investigation and Simplistic Geochemical Modeling of CO2 Mineral Carbonation Using the Mount Tawai Peridotite
Abstract
:1. Introduction
2. Results and Discussion
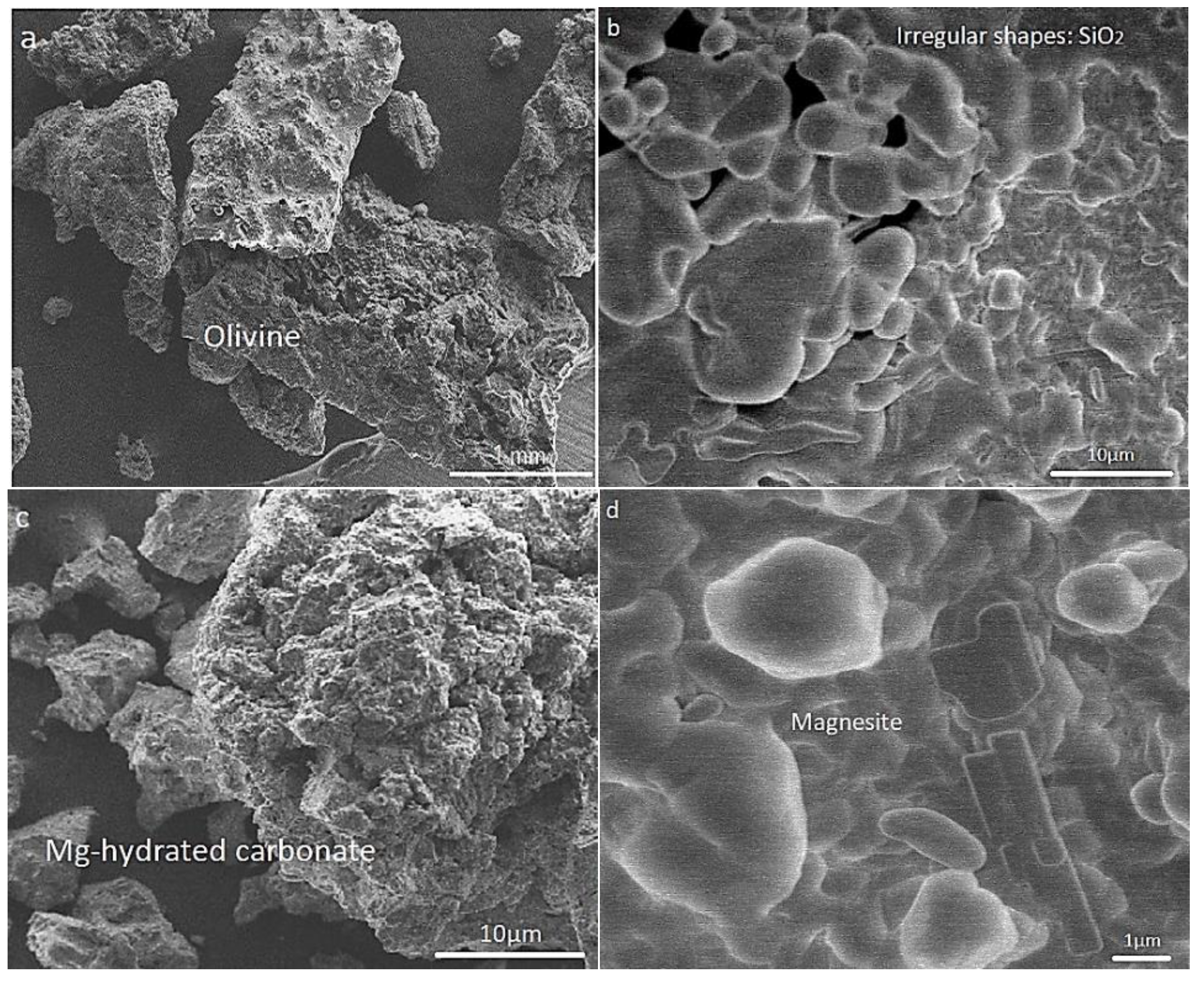
2.1. Mineral Characterization
2.2. Effect of Particle Size on the Carbonation of Olivine
2.3. Effect of Temperature on the Carbonation of Olivine
2.4. Effect of Water Concentration
2.5. Kinetic Analysis of Mg Extraction by HCl
2.6. Thermodynamic Considerations on the Mineral Carbonation
2.7. Geochemical Modeling
3. Experimental and Modeling Section
3.1. Materials
3.2. Experimental Apparatus
3.3. Experimental Procedure
3.4. Estimation of Carbonation Yield
3.5. Modeling System and Kinetic Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rahmani, O.; Junin, R.; Tyrer, M.; Mohsin, R. Mineral carbonation of red gypsum for CO2 sequestration. Energy Fuels 2014, 28, 5953–5958. [Google Scholar] [CrossRef]
- Sanderson, B.M.; O’Neill, B.C.; Kiehl, J.T.; Meehl, G.A.; Knutti, R.; Washington, W.M. The response of the climate system to very high greenhouse gas emission scenarios. Environ. Res. Lett. 2011, 6, 034005. [Google Scholar] [CrossRef]
- Bodman, R.W.; Rayner, P.J.; Karoly, D.J. Uncertainty in temperature projections reduced using carbon cycle and climate observations. Nat. Clim. Chang. 2013, 3, 725–729. [Google Scholar] [CrossRef]
- Bachu, S.; Gunter, W.D.; Perkins, E.H. Aquifer disposal of CO2: Hydrodynamic and mineral trapping. Energy Convers. Manag. 1994, 35, 269–279. [Google Scholar] [CrossRef]
- Sanna, A.; Uibu, M.; Caramanna, G.; Kuusik, R.; Maroto-Valer, M.M. A review of mineral carbonation technologies to sequester CO2. Chem. Soc. Rev. 2014, 43, 8049–8080. [Google Scholar] [CrossRef] [PubMed]
- Kaszuba, J.P.; Janecky, D.R.; Snow, M.G. Carbon dioxide reaction processes in a model brine aquifer at 200 °C and 200 bars: Implications for geologic sequestration of carbon. Appl. Geochem. 2003, 18, 1065–1080. [Google Scholar] [CrossRef]
- Xu, T.F.; Apps, J.A.; Pruess, K. Numerical simulation of CO2 disposal by mineral trapping in deep aquifers. Appl. Geochem. 2004, 19, 917–936. [Google Scholar] [CrossRef]
- Maroto-Valer, M.M.; Fauth, D.J.; Kuchta, M.E.; Zhang, Y.; Andrésen, J.M. Activation of magnesium rich minerals as carbonation feedstock materials for CO2 sequestration. Fuel Process. Technol. 2005, 86, 1627–1645. [Google Scholar] [CrossRef]
- Palandri, J.L.; Kharaka, Y.K. Ferric iron-bearing sediments as a mineral trap for CO2 sequestration: Iron reduction using sulfur-bearing waste gas. Chem. Geol. 2005, 217, 351–364. [Google Scholar] [CrossRef]
- Flaathen, T.K.; Gislason, S.R.; Oelkers, E.H.; Sveinbjörnsdóttir, A.E. Chemical evolution of the Mt. Hekla, Iceland, groundwaters: A natural analogue for CO2 sequestration in basaltic rocks. Appl. Geochem. 2009, 24, 463–474. [Google Scholar] [CrossRef]
- Gislason, S.R.; Wolff-Boenisch, D.; Stefansson, A.; Oelkers, E.H.; Gunnlaugsson, E.; Sigurdardottir, H.; Sigfusson, B.; Broecker, W.S.; Matter, J.M.; Stute, M.; et al. Mineral sequestration of carbon dioxide in basalt: A pre-injection overview of the CarbFix project. Int. J. Greenh. Gas Control 2010, 4, 537–545. [Google Scholar] [CrossRef]
- King, H.E.; Plümper, O.; Putnis, A. Effect of Secondary Phase Formation on the Carbonation of Olivine. Environ. Sci. Technol. 2010, 44, 6503–6509. [Google Scholar] [CrossRef] [PubMed]
- Qafoku, O.; Kovarik, L.; Kukkadapu, R.K.; Ilton, E.S.; Arey, B.W.; Tucek, J.; Felmy, A.R. Fayalite dissolution and siderite formation in water-saturated supercritical CO2. Chem. Geol. 2012, 332, 124–135. [Google Scholar] [CrossRef]
- Rahmani, O.; Tyrer, M.; Junin, R. Calcite precipitation from by-product red gypsum in aqueous carbonation process. RSC Adv. 2014, 4, 45548–45557. [Google Scholar] [CrossRef]
- Lackner, K.S.; Wendt, C.H.; Butt, D.P.; Joyce, E.L.; Sharp, D.H. Carbon dioxide disposal in carbonate minerals. Energy 1995, 20, 1153–1170. [Google Scholar] [CrossRef]
- Olsson, J.; Bovet, N.; Makovicky, E.; Bechgaard, K.; Balogh, Z.; Stipp, S.L.S. Olivine reactivity with CO2 and H2O on a microscale: Implications for carbon sequestration. Geochim. Cosmochim. Acta 2012, 77, 86–97. [Google Scholar] [CrossRef]
- Lackner, K.S.; Butt, D.P.; Wendt, C.H. Progress on binding CO2 in mineral substrates. Energy Convers. Mgmt. 1997, 38, S259–S264. [Google Scholar] [CrossRef]
- Kwon, S.; Fan, M.H.; DaCosta, H.M.D.; Russell, A.G.; Armistead, G.R. Factors affecting the direct mineralization of CO2 with olivine. J. Environ Sci. 2011, 23, 1233–1239. [Google Scholar] [CrossRef]
- Larachi, F.; Gravel, J.P.; Grandjean, B.P.A.; Beaudoin, G. Role of steam, hydrogen and pretreatment in chrysotile gas–solid carbonation: Opportunities for pre-combustion CO2 capture. Int. J. Greenh. Gas Control 2012, 6, 69–76. [Google Scholar] [CrossRef]
- Fricker, K.J.; Park, A.H.A. Effect of H2O on Mg(OH)2 carbonation pathways for combined CO2 capture and storage. Chem. Eng. Sci. 2013, 100, 332–341. [Google Scholar] [CrossRef]
- Fagerlund, J.; Zevenhoven, R. An experimental study of Mg(OH)2 carbonation. Int. J. Greenh. Gas Control 2011, 5, 1406–1412. [Google Scholar] [CrossRef]
- McGrail, B.P.; Schaef, H.T.; Ho, A.M.; Chien, Y.J.; Dooley, J.J.; Davidson, C.L. Potential for carbon dioxide sequestration in flood basalts. J. Geophys. Res. 2006, 111, 12201–12213. [Google Scholar] [CrossRef]
- Oelkers, E.H.; Cole, D.R. Carbon Dioxide Sequestration A Solution to a Global Problem. Elements 2008, 4, 305–310. [Google Scholar] [CrossRef]
- Matter, J.M.; Broecker, W.S.; Stute, M.; Gislason, S.R.; Oelkers, E.H.; Stefansson, A.; Wolff-Boenisch, D.; Gunnlaugsson, E.; Axelsson, G.; Bjornsson, G. Permanent Carbon Dioxide Storage into Basalt: The CarbFix Pilot Project, Iceland. Energy Procedia 2009, 1, 3641–3646. [Google Scholar] [CrossRef]
- Schaef, H.T.; McGrail, B.P.; Owen, A.T. Basalt- CO2–H2O interactions and variability in carbonate mineralization rates. Energy Procedia 2009, 1, 4899–4906. [Google Scholar] [CrossRef]
- Tian, S.; Jiang, J.; Li, K.; Yan, F.; Chen, X. Performance of steel slag in carbonation–calcination looping for CO2capture from industrial flue gas. RSC Adv. 2014, 4, 6858–6862. [Google Scholar] [CrossRef]
- Highfield, J.; Lim, H.Q.; Fagerlund, J.; Zevenhoven, R. Activation of serpentine for CO2 mineralization by flux extraction of soluble magnesium salts using ammonium sulphate. RSC Adv. 2012, 2, 6535–6541. [Google Scholar] [CrossRef]
- Chu, D.H.; Vinoba, M.; Bhagiyalakshmi, M.; Baek, I.H.; Nam, S.C.; Yoon, Y.; Kim, S.H.; Jeong, S.K. CO2 mineralization into different polymorphs of CaCO3 using an aqueous-CO2 system. RSC Adv. 2013, 3, 21722–21729. [Google Scholar] [CrossRef]
- Gulliver, D.M.; Lowry, G.V.; Gregory, K.B. CO2 concentration and pH alters subsurface microbial ecology at reservoir temperature and pressure. RSC Adv. 2014, 4, 17443–17453. [Google Scholar] [CrossRef]
- Bearat, H.M.J.; McKelvy, M.J.; Chizmeshya, A.V.G.; Gormley, D.; Nunez, R.; Carpenter, R.W.; Squires, K.; Wolf, G.H. Carbon sequestration via aqueous olivine mineral carbonation: Role of passivating layer formation. Environ. Sci. Technol. 2006, 40, 4802–4808. [Google Scholar] [CrossRef] [PubMed]
- Fagerlund, J.; Highfield, J.; Zevenhoven, R. Kinetics studies on wet and dry gas-solid carbonation of MgO and Mg(OH)2 for CO2 sequestration. RSC Adv. 2012, 2, 10380. [Google Scholar] [CrossRef]
- Garcia, B.; Beaumont, V.; Perfetti, E.; Rouchon, V.; Blanchet, D.; Oger, P.; Dromart, G.; Huc, A.Y.; Haeseler, F. Experiments and geochemical modelling of CO2 sequestration by olivine: Potential, quantification. Appl. Geochem. 2010, 25, 1383–1396. [Google Scholar] [CrossRef]
- Pokrovsky, O.S.; Golubev, S.V.; Schott, J.; Castillo, A. Calcite, dolomite and magnesite dissolution kinetics in aqueous solutions at acid to circumneutral pH, 25 to 150 °C and 1 to 55 atm pCO2: New constraints on CO2 sequestration in sedimentary basins. Chem. Geol. 2009, 265, 20–32. [Google Scholar] [CrossRef]
- Saldi, G.D.; Jordan, G.; Schott, J.; Oelkers, E. Magnesite growth rates as a function of temperature and saturation state. Geochim. Cosmochim. Acta 2009, 73, 5646–5657. [Google Scholar] [CrossRef]
- Highfield, J.; Chen, J.; Bu, J.; Åbacka, J.; Fagerlund, J.; Zevenhoven, R. Steam-promoted gas-solid carbonation of magnesia and brucite below 200 °C. In Proceedings of the 4th International Conference on Accelerated Carbonation for Environmental and Materials Engineering (ACEME 2013), Leuven, Belgium, 9–12 April 2013.
- Chen, Z.Y.; O’Connor, W.K.; Gerdemann, S.J. Chemistry of aqueous mineral carbonation for carbon sequestration and explanation of experimental results. Environ. Prog. 2006, 25, 161–166. [Google Scholar] [CrossRef]
- Saldi, G.D.; Daval, D.; Morvan, G.; Knauss, K.G. The role of Fe and redox conditions in olivine carbonation rates: An experimental study of the rate limiting reactions at 90 and 150 °C in open and closed systems. Geochim. Cosmochim. Acta 2013, 118, 157–183. [Google Scholar] [CrossRef]
- Highfield, J.; Åbacka, J.; Chen, J.; Nduagu, E.; Zevenhoven, R. Overview of the ÅAU/ICES collaboration in ex-situ CO2 mineralization. In Proceedings of the 13th International Conference on Carbon Dioxide Utilization (ICCDU 2015), Singapore, Singapore, 5–9 July 2015. paper 251.
- Felmy, A.R.; Qafoku, O.; Arey, B.W.; Hu, J.Z.; Hu, M.; Schaef, H.T.; Ilton, E.S.; Hess, N.J.; Pearce, C.I.; Feng, J.; et al. Reaction of water-saturated supercritical CO2 with forsterite: Evidence for magnesite formation at low temperatures. Geochim. Cosmochim. Acta 2012, 91, 271–282. [Google Scholar] [CrossRef]
- Loring, J.S.; Thompson, C.J.; Wang, Z.; Joly, A.G.; Sklarew, D.S.; Schaef, H.T.; Ilton, E.S.; Rosso, K.M.; Felmy, A.R. In situ infrared spectroscopic study of forsterite carbonation in wet supercritical CO2. Environ. Sci. Technol. 2011, 45, 6204–6210. [Google Scholar] [CrossRef] [PubMed]
- Schaef, H.T.; McGrail, B.P.; Loring, J.L.; Bowden, M.E.; Arey, B.W.; Rosso, K.M. Forsterite [Mg2SiO4)] carbonation in wet supercritical CO2: An in situ high-pressure X-ray diffraction study. Environ. Sci. Technol. 2013, 47, 174–181. [Google Scholar] [CrossRef] [PubMed]
- Schaef, H.T.; Windisch, C.F., Jr.; McGrail, B.P.; Martin, P.F.; Rosso, K.M. Brucite [Mg(OH2)] carbonation in wet supercritical CO2: An in situ high pressure X-ray diffraction study. Geochim. Cosmochim. Acta 2011, 75, 7458–7471. [Google Scholar] [CrossRef]
- Loring, J.S.; Thompson, C.J.; Zhang, C.Y.; Wang, Z.M.; Schaef, H.T.; Rosso, K.M. In situ infrared spectroscopic study of brucite carbonation in dry to water-saturated supercritical carbon dioxide. J. Phys. Chem. A 2012, 116, 4768–4777. [Google Scholar] [CrossRef] [PubMed]
- Kwak, J.H.; Hu, J.Z.; Turcu, R.V.F.; Rosso, K.M.; Ilton, E.S.; Wang, C.; Sears, J.A.; Engelhard, M.H.; Felmy, A.R.; Hoyt, D.W. The role of H2O in the carbonation of forsterite in supercritical CO2. Int. J. Greenh. Gas Control 2011, 5, 1081–1092. [Google Scholar] [CrossRef]
- Vitillo, J.G. Magnesium-based systems for carbon dioxide capture, storage and recycling: From leaves to synthetic nanostructured materials. RSC Adv. 2015, 5, 36192–36239. [Google Scholar] [CrossRef]
- Siriwardane, R.V.; Stevens, R.W., Jr. Novel regenerable magnesium hydroxide sorbents for CO2 capture at warm gas temperatures. Ind. Eng. Chem. Res. 2009, 48, 2135–2141. [Google Scholar] [CrossRef]
- Gharabaghi, M.; Irannajad, M.; Azadmehr, A.R. Leaching kinetics of nickel extraction from hazardous waste by sulphuric acid and optimization dissolution conditions. Chem. Eng. Res. Des. 2013, 91, 325–331. [Google Scholar] [CrossRef]
- Pokrovsky, O.S.; Schott, J. Forsterite surface composition in aqueous solutions: A combined potentiometric, electrokinetic, and spectroscopic approach. Geochim. Cosmochim. Acta 2000, 64, 3299–3312. [Google Scholar] [CrossRef]
- O’Connor, W.K.; Dahlin, D.C.; Rush, G.E.; Dahlin, C.L.; Collins, W.K. Carbon dioxide sequestration by direct mineral carbonation: Process mineralogy of feed and products. Miner. Metall. Process. 2002, 19, 95–101. [Google Scholar]
- Na, B.K.; Koo, K.K.; Eum, H.M.; Lee, H.; Song, H.K. CO2 recovery from flue gas by PSA process using activated carbon. Korean J. Chem. Eng. 2001, 18, 220–227. [Google Scholar] [CrossRef]
- Yong, Z.; Mata, V.; Rodriguez, A.E. Adsorption of carbon dioxide onto hydrotalcite-like compounds (HTlcs) at high temperatures. Ind. Eng. Chem. Res. 2001, 40, 204–209. [Google Scholar] [CrossRef]
- Ko, D.; Siriwardane, R.V.; Biegler, L.T. Optimization of pressure swing adsorption and fractionated vacuum pressure swing adsorption processes for CO2 capture. Ind. Eng. Chem. Res. 2005, 44, 8084–8094. [Google Scholar] [CrossRef]
- Reynolds, S.P.; Ebner, A.D.; Ritter, J.A. New pressure swing adsorption cycles for carbon dioxide sequestration. Adsorption 2005, 11, 531–536. [Google Scholar] [CrossRef]
- Xu, X.C.; Song, C.S.; Miller, B.G.; Scaroni, A.W. Adsorption separation of carbon dioxide from flue gas of natural gas-fired boiler by a novel nanoporous “molecular basket” adsorbent. Fuel Process. Technol. 2005, 86, 1457–1472. [Google Scholar] [CrossRef]
- Hicks, J.C.; Drese, J.H.; Fauth, D.J.; Gray, M.L.; Qi, G.G.; Jones, C.W. Designing adsorbents for CO2 capture from flue gas-hyperbranched aminosilicas capable of capturing CO2 reversibly. J. Am. Chem. Soc. 2008, 130, 2902–2903. [Google Scholar] [CrossRef] [PubMed]
- Hänchen, M.; Prigiobbe, V.; Storti, G.; Seward, T.M.; Mazzotti, M. Dissolution kinetics of forsteritic olivine at 90–150 °C including effects of the presence of CO2. Geochim. Cosmochim. Acta 2006, 70, 4403–4416. [Google Scholar] [CrossRef]
- Hänchen, M.; Prigiobbe, V.; Baciocchi, R.; Mazzotti, M. Precipitation in the Mg-carbonate system—effects of temperature andCO2 pressure. Chem. Eng. Sci. 2008, 63, 1012–1028. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. User’s Guide to PHREEQC (Version 2) a Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; Water-Resources Investigations Report 99–4259; U.S. Geological Survey: Reston, WV, USA, 1999; p. 312.
- Konigsberger, E.; Konigsberger, L.C.; Ager, H.G. Low-temperature thermodynamic model for the system Na2CO3–MgCO3–CaCO3–H2O. Geochim. Cosmochim. Acta 1999, 63, 3105–3119. [Google Scholar] [CrossRef]
- Power, I.M.; Harrison, A.L.; Dipple, G.M.; Wilson, S.A.; Kelemen, P.B.; Hitch, M.; Southam, G. Carbon mineralization: From natural analogues to engineered systems. Rev. Miner. Geochem. 2013, 77, 305. [Google Scholar] [CrossRef]
- Wollast, R.; Mackenzie, F.T.; Bricker, O.P. Experimental precipitation and genesis of sepiolite at earth-surface conditions. Am. Miner. 1968, 53, 1645–1662. [Google Scholar]
- Christ, C.L.; Hostetler, B.P.; Siebert, R.M. Studies in the system MgO–SiO2–CO2–H2O: III. Am. J. Sci. 1973, 273, 65–83. [Google Scholar] [CrossRef]
- Birsoy, R. Formation of sepiolite-palygorskite and related minerals from solution. Clays Clay Miner. 2002, 50, 736–745. [Google Scholar] [CrossRef]
- Gadikota, G.; Matter, J.; Kelemen, P.; Park, A.H.A. Chemical and morphological changes during olivine carbonation for CO2 storage in the presence of NaCl and NaHCO3. Phys. Chem. Chem. Phys. 2014, 16, 4679. [Google Scholar] [CrossRef] [PubMed]
- Levenspiel, O. Chemical Reaction Engineering, 2nd ed.; John Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Dri, M.; Sanna, A.; Maroto-Valer, M.M. Dissolution of steel slag and recycled concrete aggregate in ammonium bisulphate for CO2 mineral carbonation. Fuel Process. Technol. 2013, 113, 114–122. [Google Scholar] [CrossRef]
- Sample Availability: Not available.












| Al2O3 | CaO | FeO | MgO | K2O | SiO2 | Na2O | Cr2O3 | Volatiles | |
|---|---|---|---|---|---|---|---|---|---|
| C + CO2 | H2O | ||||||||
| 0.204 | 0.061 | 5.969 | 51.921 | 0.005 | 41.072 | 0.083 | 0.034 | <0.352 | 0.291 |
| Number of ions on the basis of O | |||||||||
| Al | Ca | Fe | Na | Mg | K | Si | Na | Cr | - |
| 0.001 | 0.004 | 0.161 | 0.001 | 1.812 | 0.004 | 0.995 | 0.008 | - | - |
| Kinetic Analysis | k | ln k | T (°C) | T (K) | 1/T |
|---|---|---|---|---|---|
| Combination of chemical reaction control and product layer diffusion | 9.0243 × 10−5 | −9.313 | 175 | 448.15 | 0.00223 |
| 5.0135 × 10−5 | −9.9007 | 125 | 398.15 | 0.00251 | |
| 3.0101 × 10−5 | −10.4109 | 75 | 348.15 | 0.00287 | |
| 1.0028 × 10−5 | −11.5101 | 25 | 298.15 | 0.00335 | |
| Product layer diffusion | 9.0635 × 10−5 | −9.3086 | 175 | 448.15 | 0.00223 |
| 4.0244 × 10−5 | −10.1205 | 125 | 398.15 | 0.00251 | |
| 2.0153 × 10−5 | −10.8121 | 75 | 348.15 | 0.00287 | |
| 1.0014 × 10−5 | −11.5115 | 25 | 298.15 | 0.00335 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahmani, O.; Highfield, J.; Junin, R.; Tyrer, M.; Pour, A.B. Experimental Investigation and Simplistic Geochemical Modeling of CO2 Mineral Carbonation Using the Mount Tawai Peridotite. Molecules 2016, 21, 353. https://doi.org/10.3390/molecules21030353
Rahmani O, Highfield J, Junin R, Tyrer M, Pour AB. Experimental Investigation and Simplistic Geochemical Modeling of CO2 Mineral Carbonation Using the Mount Tawai Peridotite. Molecules. 2016; 21(3):353. https://doi.org/10.3390/molecules21030353
Chicago/Turabian StyleRahmani, Omeid, James Highfield, Radzuan Junin, Mark Tyrer, and Amin Beiranvand Pour. 2016. "Experimental Investigation and Simplistic Geochemical Modeling of CO2 Mineral Carbonation Using the Mount Tawai Peridotite" Molecules 21, no. 3: 353. https://doi.org/10.3390/molecules21030353
APA StyleRahmani, O., Highfield, J., Junin, R., Tyrer, M., & Pour, A. B. (2016). Experimental Investigation and Simplistic Geochemical Modeling of CO2 Mineral Carbonation Using the Mount Tawai Peridotite. Molecules, 21(3), 353. https://doi.org/10.3390/molecules21030353







