Energy of Intramolecular Hydrogen Bonding in ortho-Hydroxybenzaldehydes, Phenones and Quinones. Transfer of Aromaticity from ipso-Benzene Ring to the Enol System(s)
Abstract
:1. Introduction
2. Computational Methods
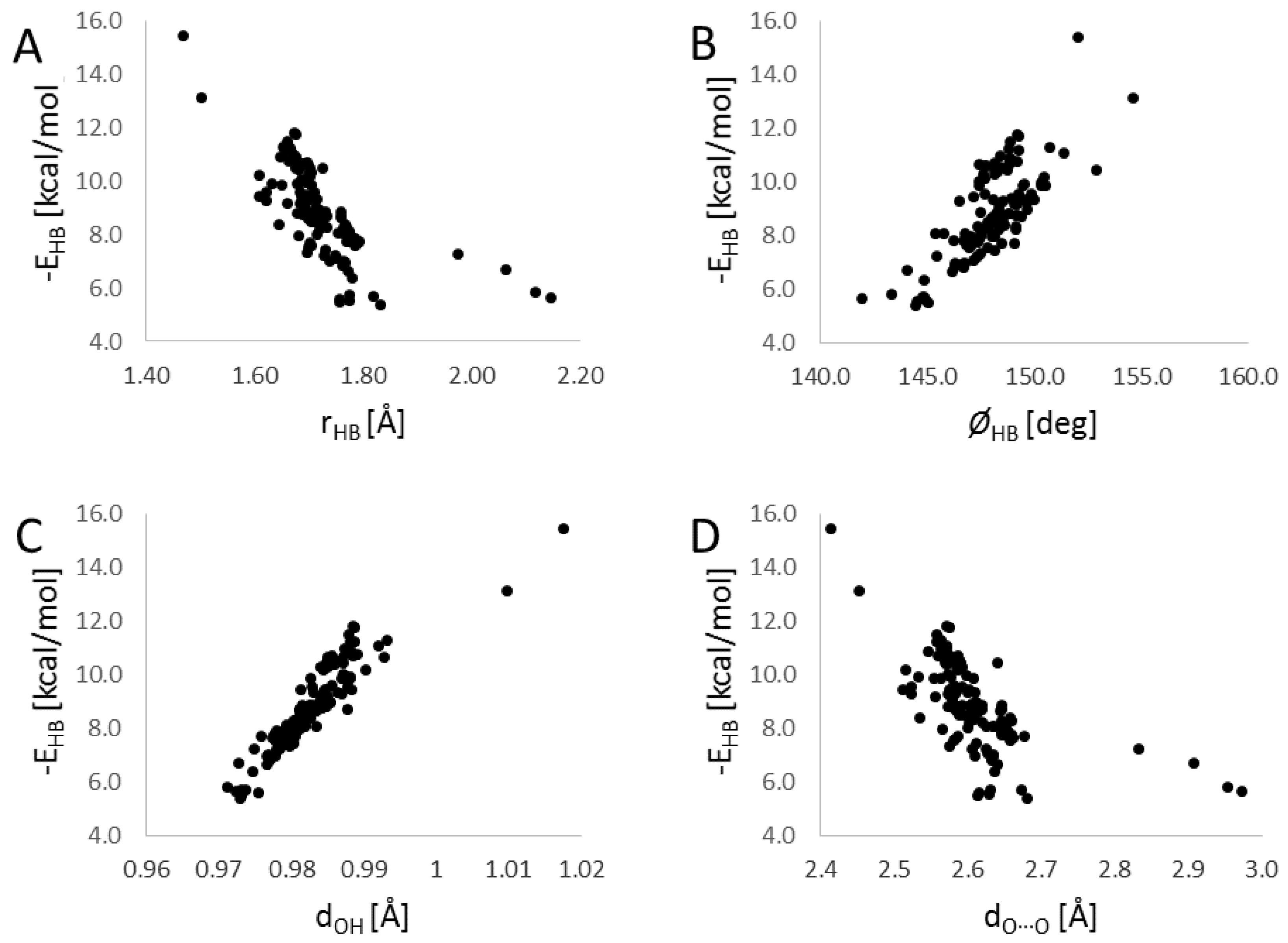
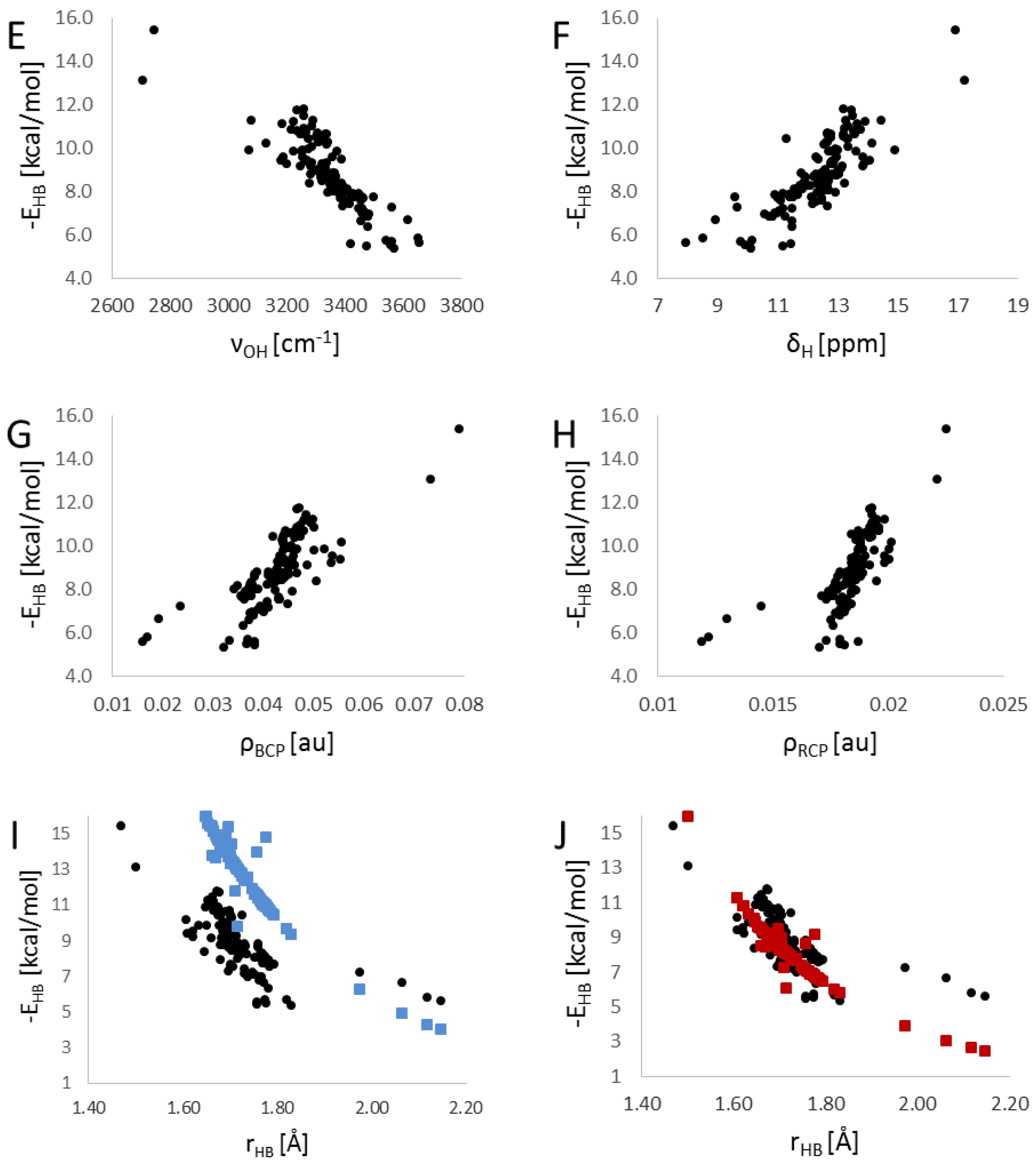
3. Results
4. Summary and Discussion
Supplementary Materials
Acknowledgments
Conflicts of Interest
References
- Jeffrey, G.A.; Saenger, W. Hydrogen Bonding in Biological Structures; Springer-Verlag: Berlin, Germany, 1994. [Google Scholar]
- Desiraju, G.; Steiner, T. The Weak Hydrogen Bond–In Structural Chemistry and Biology; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Bilton, C.; Allen, F.H.; Shields, G.P.; Howard, J.A.K. Intramolecular Hydrogen Bonds: Common Motifs, Probabilities of Formation and Implications for Supramolecular Organization. Acta Crystallogr. 2000, B56, 849–856. [Google Scholar] [CrossRef] [PubMed]
- Gilli, G.; Bellucci, F.; Ferretti, V.; Bertolasi, V. Evidence for Resonance-Assisted Hydrogen Bonding from Crystal-Structure Correlations on the Enol form of the β-Diketone Fragment. J. Am. Chem. Soc. 1989, 111, 1023–1028. [Google Scholar] [CrossRef]
- Gilli, P.; Bertolasi, V.; Ferretti, V.; Gilli, G. Covalent Nature of the Strong Homonuclear Hydrogen Bond. Study of the O-H∙∙∙O System by Crystal Structure Correlation Methods. J. Am. Chem. Soc. 1994, 116, 909–915. [Google Scholar] [CrossRef]
- Gilli, G.; Gilli, P. The Nature of the Hydrogen Bond–Outline of a Comprehensive Hydrogen Bond Theory; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Scheiner, S. Relative Strengths of NH∙∙∙O and CH∙∙∙O Hydrogen Bonds between Polypeptide Chain Segment. J. Phys. Chem. B 2005, 109, 16132–16141. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S.; Kar, T. Red- versus Blue-Shifting Hydrogen Bonds: Are there Fundamental Distinctions? J. Phys. Chem. A 2002, 106, 1784–1789. [Google Scholar] [CrossRef]
- Sigalov, M.V.; Doronina, E.P.; Sidorkin, V.F. CAr-H∙∙∙O Hydrogen Bonds in Substituted Isobenzofuranone Derivatives: Geometric, Topological, and NMR Characterization. J. Phys. Chem. A 2012, 116, 7718–7725. [Google Scholar] [CrossRef] [PubMed]
- Sobczyk, L.; Grabowski, S.J.; Krygowski, T.M. Interrelation between H-Bond and Pi-Electron Delocalization. Chem. Rev. 2005, 105, 3513–3560. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Assessment of the Presence and Strangth of H-Bonds By Means of Corrected NMR. Molecules 2016, 21, 1426. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M.; Zachara, J.E.; Ośmiałowski, B.; Gawinecki, R. Topology-Driven Physicochemical Properties of π-Electron Systems. 1. Does the Clar Rule Work in Cyclic π-Electron Systems with the Intramolecular Hydrogen or Lithium Bond? J. Org. Chem. 2006, 71, 7678–7682. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. Hydrogen Bonding Strength-Measures Based on Geometrical and Topological Parameters. J. Phys. Org. Chem. 2004, 17, 18–31. [Google Scholar] [CrossRef]
- Jabłoński, M. Energetic and Geometrical Evidence of Nonbonding Character of Some Intramolecular Halogen∙∙∙Oxygen and Other Y∙∙∙Y Interactions. J. Phys. Chem. A 2012, 116, 3753–3764. [Google Scholar] [CrossRef] [PubMed]
- Parra, R.D.; Ohlssen, J. Cooperativity in Intramolecular Bifurcated Hydrogen Bonds: An Ab Initio Study. J. Phys. Chem. A 2008, 112, 3492–3498. [Google Scholar] [CrossRef] [PubMed]
- Jabłoński, M. Full vs. Constrain Geometry Optimization in the Open-closed Method in Estimating the Energy of Intramolecular Charge-inverted Hydrogen Bonds. Chem. Phys. 2010, 376, 76–83. [Google Scholar] [CrossRef]
- Deshmukh, M.M.; Suresh, C.H.; Gadre, S.R. Intramolecular Hydrogen Bond Energy in Polyhydroxy Systems: A Critical Comparison of Molecular Tailoring and Isodesmic Approaches. J. Phys. Chem. A 2007, 111, 6472–6480. [Google Scholar] [CrossRef] [PubMed]
- Jabłoński, M.; Monaco, G. Different Zeroes of Interaction Energies as the Cause of Opposite Results on the Stabilizing Nature of C−H···O Intramolecular Interaction. J. Chem. Inf. Model. 2013, 53, 1661–1675. [Google Scholar] [CrossRef] [PubMed]
- Rozas, I. On the Nature of Hydrogen Bonds: An Overview on Computational Studies and a Word about Patterns. Phys. Chem. Chem. Phys. 2007, 9, 2782–2790. [Google Scholar] [CrossRef] [PubMed]
- Fuster, F.; Grabowski, S.J. Intramolecular Hydrogen Bonds: the QTAIM and ELF Characteristics. J. Phys. Chem. A 2011, 115, 10078–10086. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, M.M.; Gadre, S.R.; Bartolotti, L.J. Estimation of Intramolecular Hydrogen Bond Energy via Molecular Tailoring Approach. J. Phys. Chem. A 2006, 110, 12519–12523. [Google Scholar] [CrossRef] [PubMed]
- Mo, Y. Can QTAIM Topological Parameters Be a Measure of Hydrogen Bonding Strength? J. Phys. Chem. A 2012, 116, 5240–5246. [Google Scholar] [CrossRef] [PubMed]
- Parra, R.D.; Streu, K. Cooperative Effects in Regular and Bifurcated Intramolecular OH∙∙∙O=C Interactions: A Computational Study. Comput. Theor. Chem. 2011, 977, 181–187. [Google Scholar] [CrossRef]
- Grabowski, S.J. п-Electron Delocalisation for Intramolecular Resonance Assisted Hydrogen Bonds. J. Phys. Org. Chem. 2003, 16, 797–802. [Google Scholar] [CrossRef]
- Rusinska-Roszak, D. Intramolecular O−H···O=C Hydrogen Bond Energy via the Molecular Tailoring Approach to RAHB Structures. J. Phys. Chem. A 2015, 119, 3674–3687. [Google Scholar] [CrossRef] [PubMed]
- Palusiak, M.; Krygowski, T.M. Application of AIM Parameters at Ring Critical Points for Estimation of π-Electron Delocalization in Six-Membered Aromatic and Quasi-Aromatic Rings. Chem. Eur. J. 2007, 13, 7996–8006. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen Bond Strenght Revealed by Topological Analyses of Experimentally Observed Electron Densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Afonin, A.V.; Vashchenko, A.V.; Sigalov, M.V. Estimating the Energy of Intramolecular Hydrogen Bonds from 1H NMR and QTAIM Calculations. Org. Biomol. Chem. 2016, 14, 11199–11211. [Google Scholar] [CrossRef] [PubMed]
- Gadre, S.R.; Shirsat, R.N.; Limaye, A.C. Molecular Tailoring Approach for Simulation of Electrostatic Properties. J. Phys. Chem. 1994, 98, 9165–9169. [Google Scholar] [CrossRef]
- Rusinska-Roszak, D.; Sowinski, G. Estimation of the Intramolecular O-H∙∙∙O=C Hydrogen Bond Energy via the Molecular Tailoring Approach: Part I Aliphatic Structures. J. Chem. Inf. Model. 2014, 54, 1963–1977. [Google Scholar] [CrossRef] [PubMed]
- Alvareda, E.; Denis, P.A.; Iribarne, F.; Paulino, M. Bond Dissociation Energies and Enthalpies of Formation of Flavonoids: A G4 and 06-2X Investigation. Comput. Theor. Chem. 2016, 1091, 18–23. [Google Scholar] [CrossRef]
- Mammino, L.; Kabanda, M.M. A Computational Study of the Effects of Different Solvents on the Characteristics of the Intramolecular Hydrogen Bond in Acylphloroglucinols. J. Phys. Chem. A 2009, 113, 15064–15077. [Google Scholar] [CrossRef] [PubMed]
- Mammino, L.; Kabanda, M.M. Computational Study of the Patterns of Weaker Computational Intramolecular Hydrogen Bond Stabilizing Acylphloroglucinols. Int. J. Quantum Chem. 2012, 112, 2650–2658. [Google Scholar] [CrossRef]
- Galasso, V. Probing the Molecular and Electronic Structure of the Lichen Metabolite Usinic Acid: A DFT Study. Chem. Phys. 2010, 374, 138–145. [Google Scholar] [CrossRef]
- Zheng, Y.-J.; Basarab, G.S.; Jordan, D.B. Roles of Substrate Distortion and Intramolecular Hydrogen Bonding in Enzymatic Catalysis by Scytalone Dehydratase. Biochemistry 2002, 41, 820–826. [Google Scholar] [CrossRef] [PubMed]
- Da Rocha, D.R.; de Souza, A.C.G.; Resende, J.A.L.C.; Santos, W.C.; dos Santos, E.A.; Pessoa, C.; de Moraes, M.O.; Costa-Lotufo, L.V.; Montenegro, R.C.; Vereira, V.F. Synthesis of New 9-hydroxy-α- and 7-hydroxy-β-pyranNaphtoquinones and Cytotoxicity against Cancer Cell Lines. Org. Biomol. Chem. 2011, 9, 4315–4322. [Google Scholar] [CrossRef] [PubMed]
- Musin, R.N.; Mariam, Y.H. An Integrated Approach to the Study of Intramolecular Hydrogen Bonds in Malonaldehyde Enol Derivatives and Naphtharizin: Trend in Energetic versus Geometrical Consequences. J. Phys. Org. Chem. 2006, 19, 425–444. [Google Scholar] [CrossRef]
- Jacquemin, D.; Brémond, E.; Planchat, A.; Ciofini, I.; Adamo, C. TD-DFT Vibronic Couplings in Anthraquinones: From Basis Set and Functional Benchmarks to Applications for Industrial Dyes. J. Chem. Theory Comput. 2011, 7, 1882–1892. [Google Scholar] [CrossRef] [PubMed]
- Palusiak, M.; Simon, S.; Sola, M. Interplay between Intramolecular Resonance-Assisted Hydrogen Bonding and Aromaticity in o-Hydroxyaryl Aldehydes. J. Org. Chem. 2006, 71, 5241–5248. [Google Scholar] [CrossRef] [PubMed]
- Lenain, P.; Mandado, M.; Mosquera, R.A.; Bultinck, P. Interplay between Hydrogen-Bond formation and Multicenter π-Electron Delocalization: Intramolecular Hydrogen Bonds. J. Phys. Chem. A 2008, 112, 10689–10696. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision B.01; Gaussian, Inc.: Wallingford, TC, USA, 2010. [Google Scholar]
- Catalán, J.; Palomar, J.; de Paz, J.L.G. Intramolecular Proton or Hydrogen-Atom Transfer in the Ground and Excited States of 2-Hydroxybenzoyl Compounds. J. Phys. Chem. A 1997, 101, 7914–7921. [Google Scholar]
- Wolinski, K.; Hilton, J.F.; Pulay, P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Biegler-Kӧnig, F.; Schӧnbohm, J.; Bayles, D. Software News and Updates AIM2000─A program to Analyze and Visualize Atoms in Molecules. J. Comput. Chem. 2001, 22, 545–559. [Google Scholar]
- Keith, T.A. AIMAll; Version 13.01.27; TK Gristmill Software: Overland Park, KS, USA, 2013. [Google Scholar]
- Palusiak, M.; Simon, S.; Sola, M. Interplay between Intramolecular Resonance-Assisted Hydrogen Bonding and Local Aromaticity. II. 1,3-Dihydroxyaryl-2-Aldehydes. J. Org Chem. 2009, 74, 2059–2066. [Google Scholar] [CrossRef] [PubMed]
- Jezierska-Mazzarello, A.; Panek, J.J.; Szatyłowicz, H.; Krygowski, T.M. Hydrogen Bonding as A Modulator of Aromaticity and Electronic Structure of Selected ortho-Hydroxybenzaldehyde Derivatives. J. Phys. Chem. A 2012, 116, 460–475. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M. Crystallographic Studies of Inter- and Intramolecular Interactions Reflected In Aromatic Character of π-Electron Systems. J. Chem. Inf. Comput. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Cyrański, M.K. Two Faces of the Structural Aspects of Aromaticity. Phys. Chem. Chem. Phys. 2004, 6, 249–255. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Cyrański, M. Separation of the Energetic and Geometric Contributions to the Aromaticity of π-Electron Carbocyclics. Tetrahedron 1996, 52, 1713–1722. [Google Scholar] [CrossRef]
- Jezierska-Mazzarello, A.; Szatyłowicz, H.; Krygowski, T.M. Interference of H-Bonding and Subsituent Effects in Nitro- and Hydroxy-Substituted Salicylaldehydes. J. Mol. Model. 2012, 18, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, A.; Khorasani, S.M.H.; Neyband, R.S. The O∙∙∙H Intramolecular Hydrogen Bond in 4-X-Hydroxybenzaldehydes: The Relationships Between Geometrical Parameters, Estimated Binding Energies, and NMR Data. Int. J. Quantum Chem. 2010, 110, 1871–1879. [Google Scholar] [CrossRef]
- Grabowski, S.J. Properties of a Ring Critical Points Measures of Intramolecular H-Bond Strength. Monatsh. Chem. 2002, 133, 1373–1380. [Google Scholar] [CrossRef]
- Lapinski, L.; Rostkowska, H.; Reva, I.; Fausto, R.; Nowak, M.J. Positive Identification of UV-Generated, Non-Hydrogen-Bonded Isomers of o-Hydroxybenzaldehyde and o-Hydroxyacetophenone. J. Phys. Chem. A 2010, 114, 5588–5595. [Google Scholar] [CrossRef] [PubMed]
- Fedorov, E.E.; Makarov, O.E.; Pankratov, A.N.; Grinev, V.S. Gas-Liquid Chromatography-Obtained Differences In the Dissolution Enthalpy between Two Positional Isomers in a Polar Stationary Phase: A Measure of the Inter- or Intramolecular Hydrogen Bond Energy? J. Chromatogr. A 2012, 1241, 76–83. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, C.-S. Estimation on Intramolecular Hydrogen-Bonding Energy via the Substitution Method JIEGO HUAXUE. Chin. J. Struct. Chem. 2008, 27, 829–835. [Google Scholar]
- Ebrahimi, A.; Habibi, S.M.; Neyband, R.S. Substituent Effect on Intramolecular Hydrogen Bonding in 2-Hydroxybenzaldehyde. Int. J. Quantum Chem. 2009, 109, 1274–1282. [Google Scholar] [CrossRef]
- Davalos, J.Z.; Guerrero, A.; Herrero, R.; Jimenez, P.; Chana, A.; Abboud, J.L.M.; Lima, C.F.R.A.C.; Santos, L.N.B.F.; Lago, A.F. Neutral, Ion Gas-Phase Energetics and Structural Properties of Hydroxybenzophenones. J. Org. Chem. 2010, 75, 2564–2571. [Google Scholar] [CrossRef] [PubMed]
- Ganguly, A.; Paul, B.K.; Ghosh, S.; Guchhait, N. A Computational Acumen into the Relative Applicability of Geometrical and Quantum Chemical Criteria in Assessing Intramolecular Hydrogen Bonding (IMHB) Interaction: 5-Halosalicylic Acids as Representative Examples. Comput. Theor. Chem. 2013, 1018, 103–114. [Google Scholar] [CrossRef]
- Shigorin, D.N. Hydrogen Bond in π-Electron Systems. In Hydrogen Bond; Sokolov, N.D., Chulanovsky, A.D., Eds.; Nauka: Moscow, Russia, 1964; pp. 195–219. [Google Scholar]
- Kopteva, T.S.; Shigorin, D.N. Nature of Intramolecular Hydrogen Bonding in Molecules with P-Electrons and Its Effects on the IR Vibrational Spectra. Zh. Fiz. Khim. 1974, 48, 532–536. [Google Scholar]
- Lago, A.F.; Jimenez, P.; Herrero, R.; Davalos, J.Z.; Abboud, J.-L.M. Thermochemistry and Gas-Phase Ion Energetics of 2-Hydroxy-4-Methoxy-Benzophenone (Oxybenzone). J. Phys. Chem. A 2008, 112, 3201–3208. [Google Scholar] [CrossRef] [PubMed]
- Wiberg, K.B. Application of the Pople-Santry-Segal CNDO Method to the Cyclopropylcarbinyl and Cyclobutyl Cation and to Bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]
- Randić, M. Aromaticity of Polycyclic Conjugated Hydrocarbons. Chem. Rev. 2003, 103, 3449–3605. [Google Scholar] [CrossRef] [PubMed]
- Solà, M. Forty Years of Clar'sAromatic π-Sekstet Rule. Front. Chem. 2013, 2, 1–8. [Google Scholar]
- Ramondo, F.; Bencivenni, L. Ab Initio HF-SCF Study of Naphthazarin: Geometries, Isomerism, Hydrogen Bond, and Vibrational Spectrum. Struct. Chem. 1994, 5, 211–224. [Google Scholar] [CrossRef]
- Zahedi-Tabrizi, M.; Tayyari, S.F.; Tayyari, F.; Behforouz, M. Fourierr Transform Infrared and Raman Spectra, Vibrational Assignment and Density Functional Theory Calculations of Naphthazarin. Spectrochim. Acta. A 2004, 60, 111–120. [Google Scholar] [CrossRef]
- Zahedi-Tabrizi, M.; Farahati, R. Calculation of Intramolecular Hydrogen Bonding Strength and Natural Bond Orbital (NBO) Analysis of Naphthazarin with Chlorine Substitution. Comput. Theor. Chem. 2011, 977, 195–200. [Google Scholar] [CrossRef]
- Sørensen, J.; Clausen, H.F.; Poulsen, R.D.; Overgaard, J.; Schiøt, B. Short Strong Hydrogen Bonds in 2-Acetyl-1,8-Dihydroxy-3,6-Dimethylnaphthalene: An Outlier to Current Hydrogen Bond Theory? J. Phys. Chem. A 2007, 111, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Pakiari, A.H.; Eskandari, K. The Chemical Nature of Very Strong Hydrogen Bonds in Some Categories of Compounds. J. Mol. Struct. (Theochem) 2006, 759, 51–60. [Google Scholar] [CrossRef]
- Siskos, M.G.; Tzakos, A.G.; Gerothanassis, I.O. Accurate Ab Initio Calculations of O-H∙∙∙O and O-H∙∙∙-O Proton Chemical Shifts: Towards Elucidation of the Nature of the Hydrogen Bond and Prediction of Hydrogen Bond Distances. Org. Biomol. Chem. 2015, 13, 8852–8868. [Google Scholar] [CrossRef] [PubMed]
- Sample Availability: Coordinates of the compounds 1–129 are available from the author.
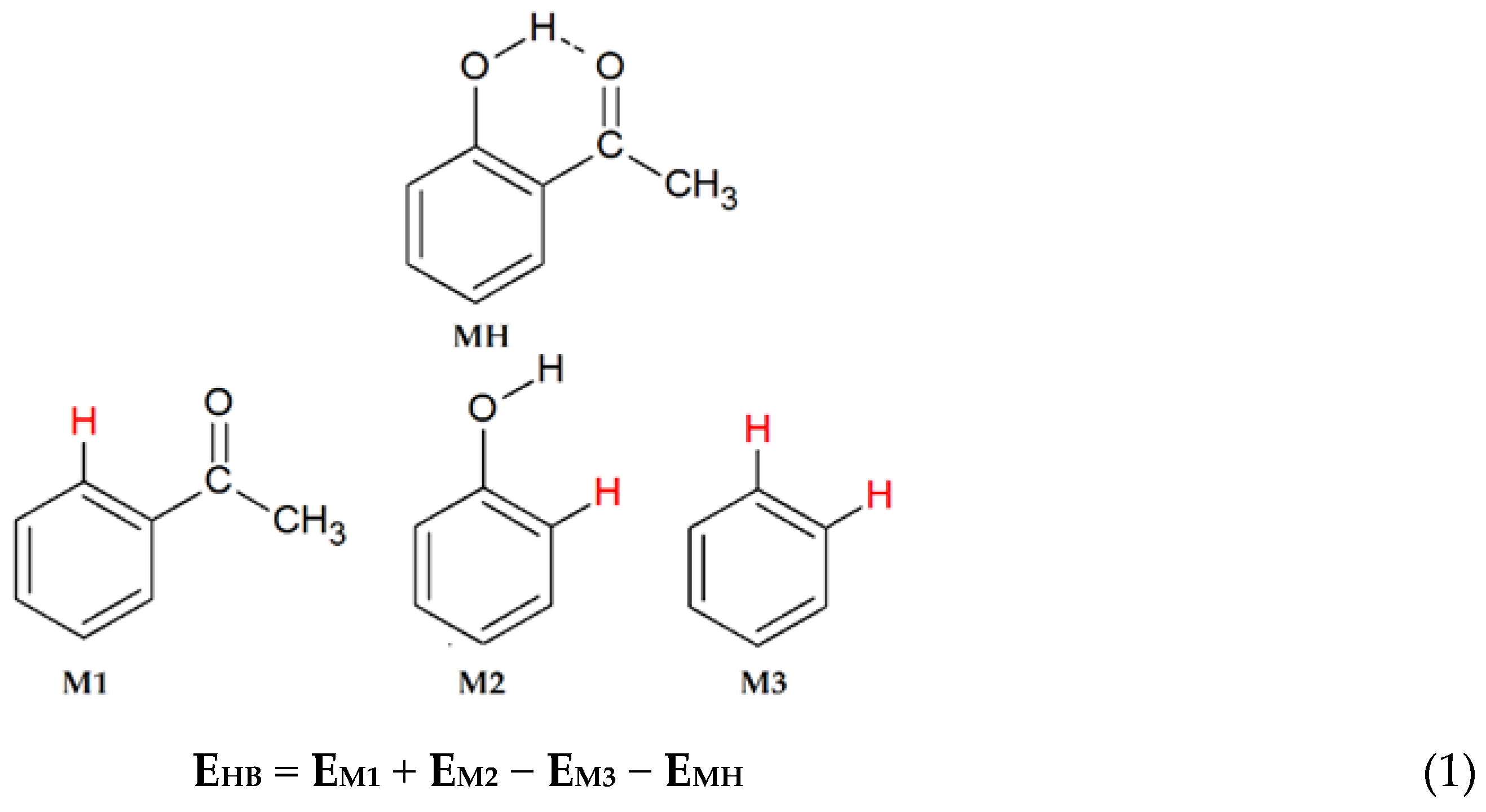
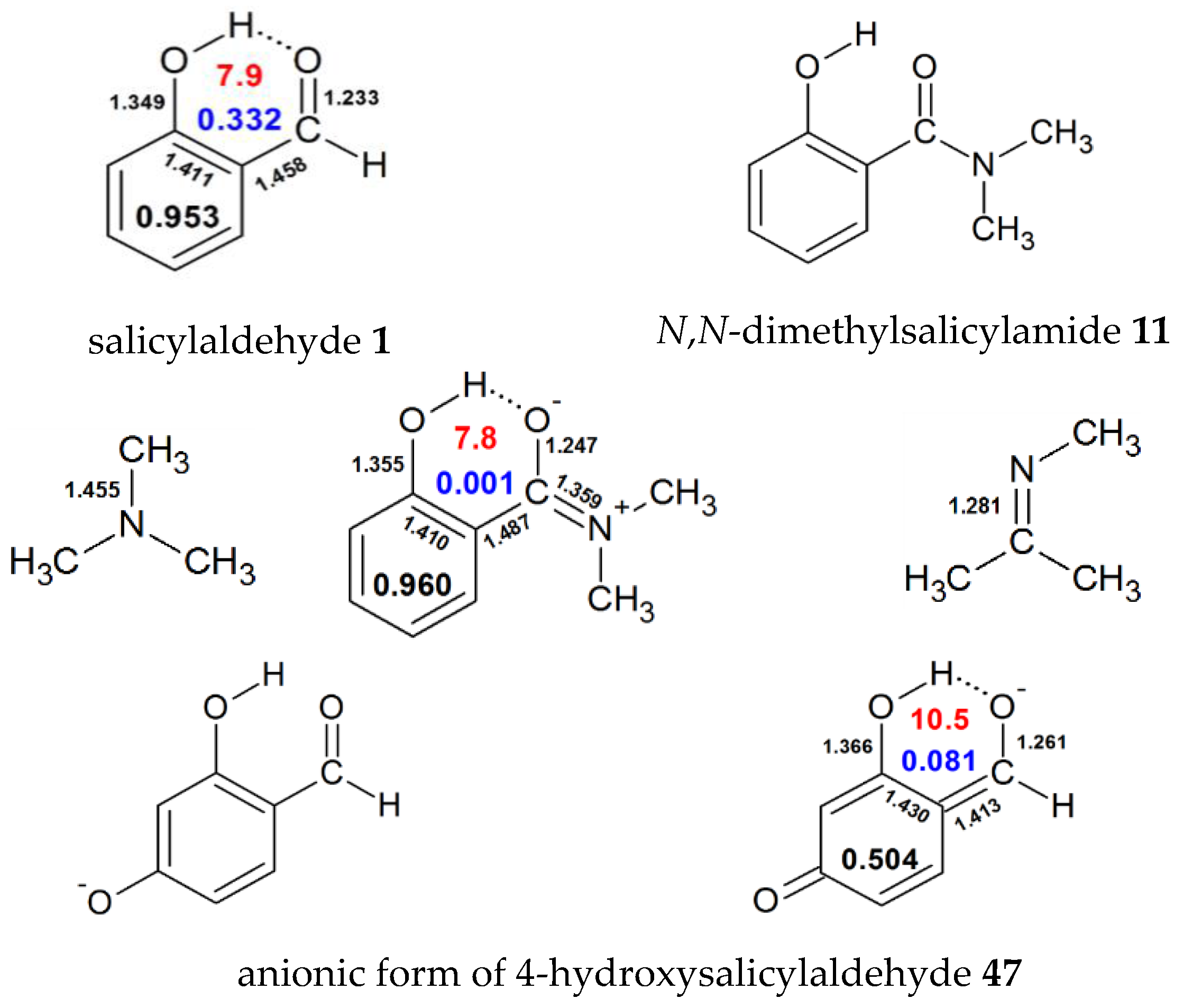
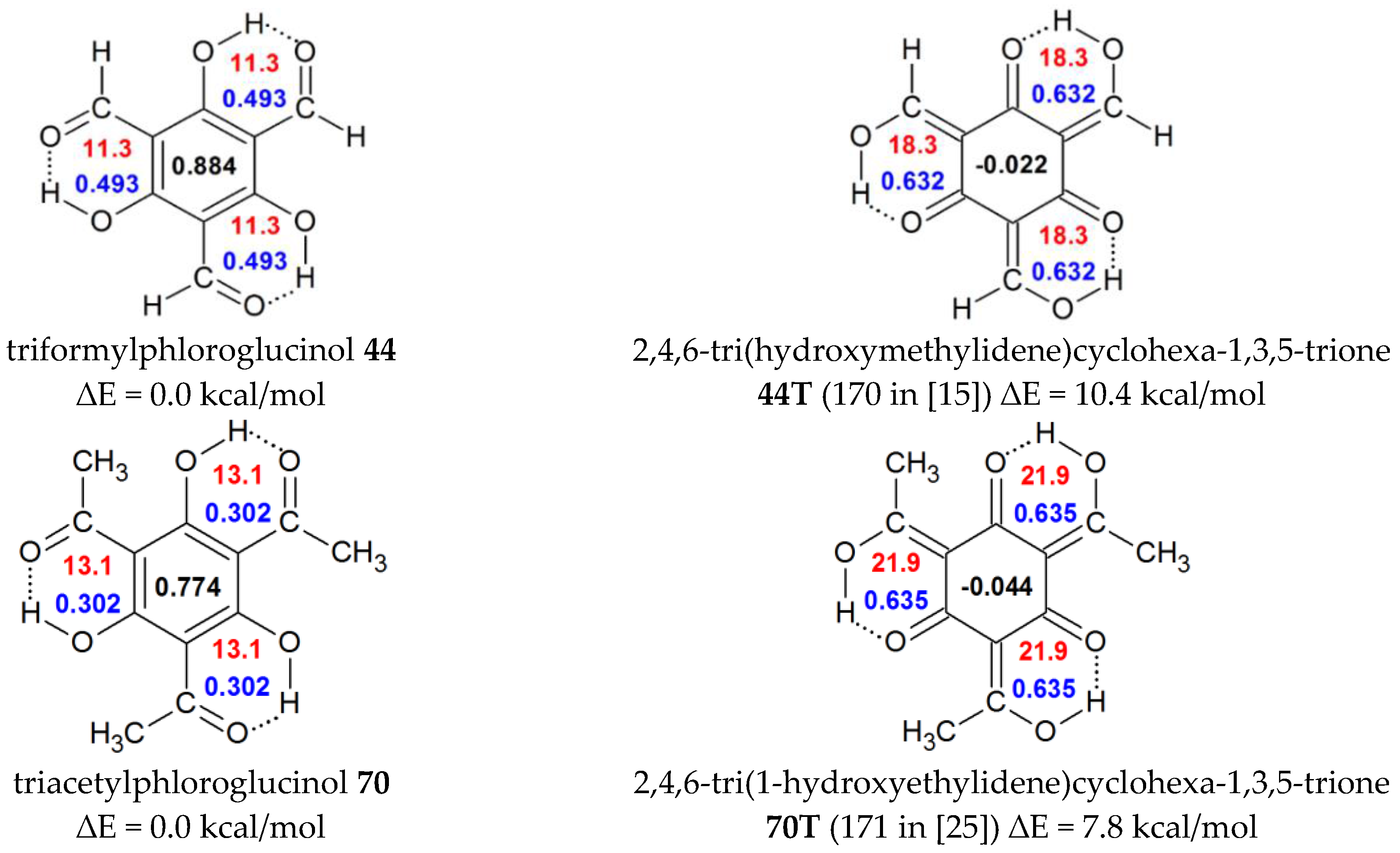

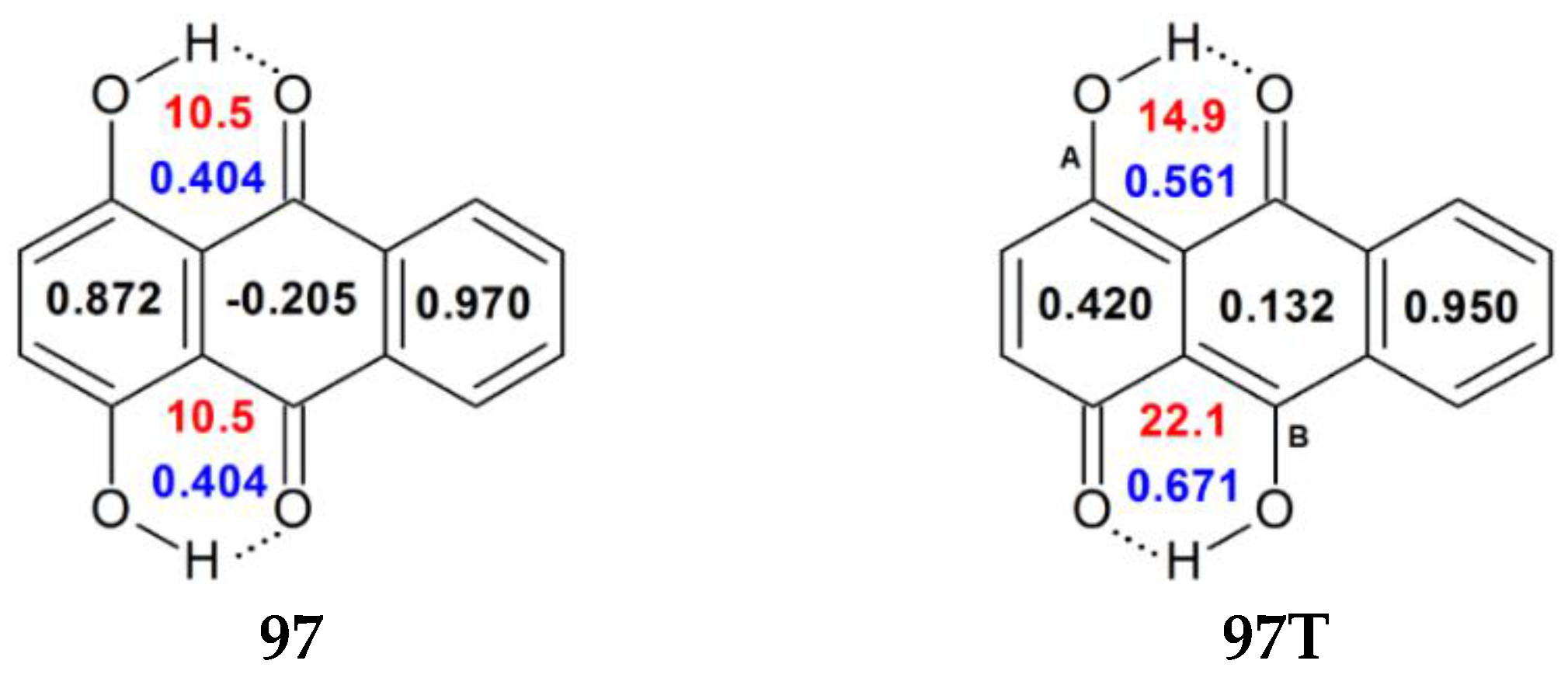
 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
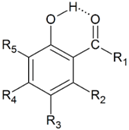
| Unsubstituted o-Hydroxycarbonyl Compounds | |||||||||
| No | R1 | HOMA | quasiHOMA | EHB a | Ref. | ||||
| 1 | H | 0.953 | 0.332 | 7.9 | 8.37 [53], 10.61 [54], 9.62 [55], 12.66 [56],11.08 [40],10.9 [37], 11.07 [39], 5.64 [57], 12.33 [44], 10.33 [58], 15.60 [59], 7.1 [28] | ||||
| 2 | Me | 0.940 | 0.180 | 8.6 | 16.4 [34], 14.23 [44], 10.55 [54] ,9.5 [28] | ||||
| 3 | Ph | 0.937 | 0.187 | 8.2 | 6.52, 5.64, 5.47 [60] | ||||
| 4 | OH | 0.953 | 0.211 | 6.8 | 10.95 [61], 12.17 [44], 11.66 [58], 5.8 [62] | ||||
| 5 | OMe | 0.954 | 0.160 | 7.1 | 12.28 [44], 6.8 [63], 7.1 [28] | ||||
| 6 | OEt | 0.954 | 0.151 | 7.2 | |||||
| 7 | OPh | 0.952 | 0.174 | 7.0 | 6.4 [62] | ||||
| 8 | NH2 | 0.950 | 0.090 | 8.6 | 15.42 [44] | ||||
| 9 | NHMe | 0.956 | 0.047 | 8.1 | 16.0 [44] | ||||
| 10 | NHPh | 0.949 | 0.035 | 8.0 | |||||
| 11 | N(Me)2 | 0.960 | 0.001 | 7.8 | |||||
| 12 | SH | 0.947 | 0.200 | 7.0 | 11.34 [48], 11.96 [44] | ||||
| 13 | SMe | 0.946 | 0.175 | 7.2 | 12.39 [44] | ||||
| 14 | F | 0.952 | 0.204 | 5.7 | 10.13 [44] | ||||
| 15 | Cl | 0.937 | 0.189 | 5.7 | 9.64 [44] | ||||
| 16 | Br | 0.934 | 0.176 | 5.5 | |||||
| 17 | CN | 0.935 | 0.369 | 6.6 | 10.97 [44] | ||||
| 18 | NO2 | 0.942 | 0.347 | 5.4 | 9.68 [44] | ||||
| Substituted o-Hydroxyaldehydes | |||||||||
| No | R1 | R2 | R3 | R4 | R5 | HOMA | quasiHOMA | EHB a | Ref. |
| 19 | H | H | Me | H | H | 0.948 | 0.339 | 7.9 | 15.00 [59] |
| 20 | H | H | OHtrans | H | H | 0.956 | 0.300 | 7.6 | 8.17 [53], 14.37 [59] |
| 21 | H | H | OHcis | H | H | 0.952 | 0.332 | 7.9 | 8.69 [53] |
| 22 | H | H | NH2 | H | H | 0.948 | 0.321 | 7.7 | 14.15 [59] |
| 23 | H | H | N(Me)2 | H | H | 0.929 | 0.323 | 7.7 | 14.85 [59] |
| 24 | H | H | F | H | H | 0.954 | 0.310 | 7.8 | 9.650 [55], 14.84 [59] |
| 25 | H | H | Cl | H | H | 0.959 | 0.314 | 7.8 | 15.23 [59] |
| 26 | H | H | Br | H | H | 0.959 | 0.402 | 7.8 | 15.31 [59] |
| 27 | H | H | C(O)H | H | H | 0.951 | 0.294 | 7.7 | |
| 28 | H | H | H | C(O)H | H | 0.942 | 0.321 | 7.9 | |
| 29 | H | H | NO2 | H | H | 0.960 | 0.302 | 8.0 | 8.28 [53], 16.48 [59] |
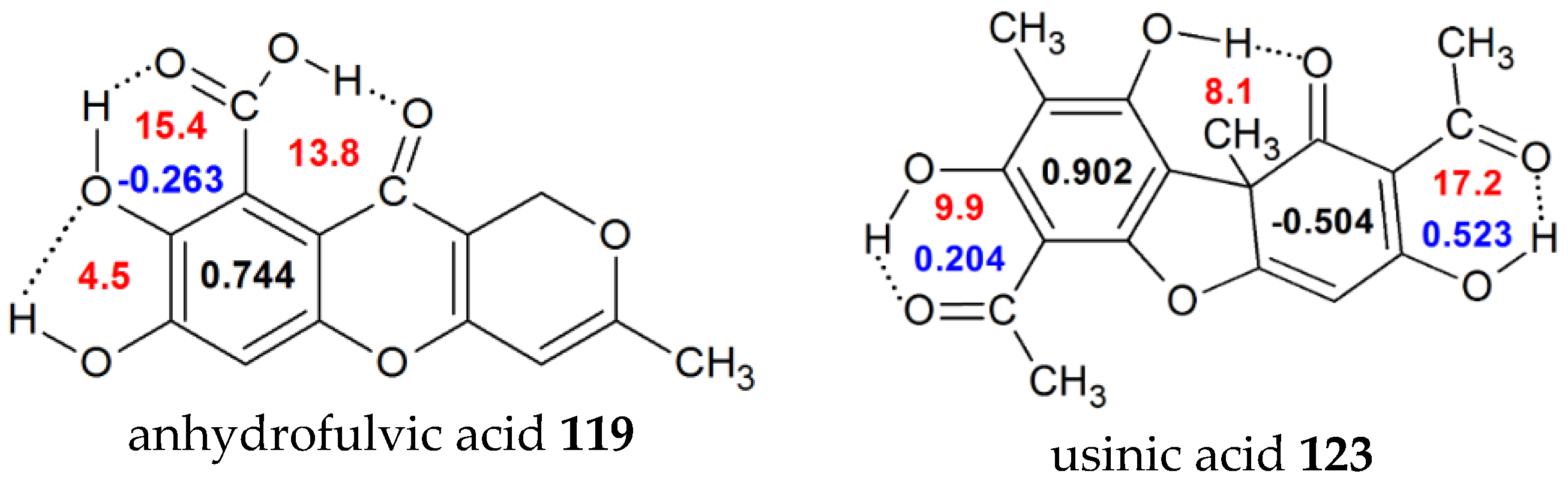
| 30 | H | H | H | Me | H | 0.948 | 0.352 | 8.1 | 10.679 [54] |
| 31 | H | H | H | OH | H | 0.953 | 0.399 | 8.7 | 8.55 [53], 10.867 [54] |
| 32 | H | H | H | OMe | H | 0.948 | 0.371 | 8.1 | |
| 33 | H | H | H | NH2 | H | 0.938 | 0.412 | 8.7 | 11.276 [54] |
| 34 | H | H | H | N(Me)2 | H | 0.897 | 0.427 | 8.8 | 11.13 [54] |
| 35 | H | H | H | F | H | 0.958 | 0.365 | 8.3 | 9.93 [55], 10.895 [54] |
| 36 | H | H | H | Cl | H | 0.957 | 0.359 | 8.1 | 10.722 [54] |
| 37 | H | H | H | Br | H | 0.957 | 0.357 | 8.0 | 10.685 [54] |
| 38 | H | H | H | NO2 | H | 0.953 | 0.330 | 7.9 | 7.91 [53], 10.393 [54] |
| 39 | H | H | F | H | F | 0.953 | 0.334 | 7.8 | 6.38 [55] |
| 40 | H | F | H | F | H | 0.950 | 0.369 | 8.9 | 10.47 [55] |
| 41 | H | OH | H | OH | 0.944 | 0.418 | 9.4 | ||
| 42 | H | OH trans | H | H | H | 0.945 | 0.339 | 8.6 | 12.57 [48] |
| 43 | H | -O-(CO)-CH=CH- | H | H | 0.929 | 0.339 | 8.9 | ||
| 44 | H | OH | C(O)H | OH | C(O)H | 0.884 | 0.494 | 11.3 | triformylphloroglucinol |
| 45 | H | H | H | NH3+ | H | 0.954 | 0.224 | 8.1 | |
| 46 | H | H | NH3+ | H | H | 0.946 | 0.257 | 8.1 | 16.88 [59], 10.7 [54] |
| 47 | H | H | H | O- | H | 0.504 | 0.081 | 10.5 | |
| 48 | H | H | O- | H | H | 0.696 | 0.263 | 7.7 | 12.36 [59], 12.05 [54] |
| 44T | H | enolic tautomer of 44 b | -0.022 | 0.631 | 18.3 | ||||
| Substituted Hydroxyketones and Acids | |||||||||
| No | R1 | R2 | R3 | R4 | R5 | HOMA | quasiHOMA | EHB a | Ref. and/or Common Name |
| 49 | Me | OHcis | H | H | H | 0.881 | 0.128 | 8.4 | |
| 50 | Me | OHtrans | H | H | H | 0.906 | 0.086 | 9.3 | |
| 51 | Me | OMetrans | H | H | H | 0.887 | 0.099 | 9.4 | |
| 52 | Me | OH | H | Me | H | 0.909 | 0.130 | 9.6 | |
| 53 | Me | H | H | OHtrans | H | 0.942 | 0.267 | 9.4 | |
| 54 | Me | H | H | OMecis | H | 0.938 | 0.234 | 8.8 | |
| 55 | Me | H | H | -CH2CH=CHCH2- | 0.928 | 0.215 | 9.2 | ||
| 56 | Ph | H | H | OMecis | H | 0.933 | 0.250 | 8.5 | 7.19, 7.8, 8.5 [64] |
| 57 | Ph | H | Cl | Me | H | 0.942 | 0.194 | 8.3 | |
| 58 | CH=CH-Ph | H | H | H | H | 0.927 | 0.164 | 9.2 | |
| 59 | CH=CH-Ph | OMe | H | OMe | H | 0.891 | 0.256 | 9.9 | chalcone |
| 60 | CH=C(OH)Ph | H | H | H | H | 0.931 | 0.184 | 8.0 | |
| 61 | (o-OH)Ph | H | H | H | H | 0.939 | 0.176 | 6.4 | |
| 62 | -CH2-CH2- | H | H | H | 0.978 | 0.314 | 7.2 | ||
| 63 | -CH2-CH(OH)-CH2‑ | H | H | H | 0.929 | 0.220 | 8.8 | vermelone c | |
| 64 | -CH=CH-O- | H | H | H | 0.948 | 0.328 | 9.0 | ||
| 65 | -CH2-CH(OH)-CH2- | H | OH | H | 0.935 | 0.345 | 9.4 | scytalone c | |
| 66 | -CH2-CH(OH)-CH2- | H | OH | H | 0.932 | 0.312 | 9.6 | scytalone c | |
| 67 | -CH2-CH2-C=O | OH | H | H | 0.875 | 0.327 | 9.6 | ||
| 68 | -(CH=CH)-C=CH2 | OH | H | H | 0.920 | 0.239 | 8.8 | ||
| 69 | Me | OH | H | OH | H | 0.906 | 0.192 | acetylphloroglucinol | |
| 70 | Me | OH | C(O)Me | OH | C(O)Me | 0.774 | 0.303 | 13.1 | triacetylphloroglucinol |
| 71 | OH | H | F | H | H | 0.955 | 0.196 | 7.0 | 10.89 [61] |
| 72 | OH | H | Cl | H | H | 0.959 | 0.197 | 6.9 | 10.76 [61] |
| 73 | OH | H | Br | H | H | 0.959 | 0.198 | 6.9 | 10.94 [61] |
| 70T | enolic tautomer of 70 d | −0.044 | 0.635 | 21.9 | |||||
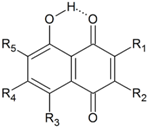 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| No | R1 | R2 | R3 | R4 | R5 | HOMA | quasiHOMA | EHB | Common Name and Ref. |
| 74 | H | H | H | H | H | 0.938 | 0.313 | 8.3 | juglone |
| 75 | H | CH3 | H | H | H | 0.943 | 0.317 | 8.7 | plumbagin |
| 76 | H | (CH2)3COOH | H | H | H | 0.942 | 0.322 | 8.5 | |
| 77 | H | NH(CH2)2COOH | H | H | H | 0.946 | 0.207 | 9.9 a | juglonbutin |
| 78a | CH2-COOH | OH | H | H | H | 0.944 | 0.290 | 8.5 b | grecoketide |
| 78b | CH2-COOH | OH | H | H | H | 0.945 | 0.283 | 8.5 c | grecoketide |
| 78c | CH2-COOH | OH | H | H | H | 0.936 | 0.253 | 8.8 d | grecoketide |
| 79 | CH2CH=C(CH3)2 | OH | H | H | H | 0.943 | 0.226 | 9.3 e | hydroxylapachol |
| 80 | CH2CH=C(CH3)2 | OH | H | H | H | 0.945 | 0.260 | 8.7 f | hydroxylapachol |
| 81 | H | (1,3-diOH)Ph | H | H | H | 0.946 | 0.330 | 8.9 | juglone |
| 82 | -O-C(CH3)2-(CH2)2- | H | H | H | 0.942 | 0.325 | 8.4 | caryopterone | |
| 83 | H | H | OH | H | H | 0.885 | 0.429 | 10.5 | naphthazarin 13.0 [37], 19.36 [68], 13.15 [69], 14.5 [70] |
| 84 | CH2-CO-CH3 | CH3 | OH | H | OCH3 | 0.868 | 0.524 | 11.7 g | javanicin |
| 0.868 | 0.543 | 11.8 | |||||||
| 85 | Cl | H | OH | H | H | 0.883 | 0.437 | 10.3 g | 13.5, 14.0 [70] |
| 0.883 | 0.450 | 10.7 | |||||||
| 86 | H | H | OH | Cl | H | 0.883 | 0.450 | 10.3 g | 13.9, 11.2 [70] |
| 0.883 | 0.441 | 10.7 | |||||||
| 87 | Cl | Cl | OH | H | H | 0.884 | 0.466 | 10.6 | 12.8 [70] |
| 88 | H | H | OH | Cl | Cl | 0.823 | 0.453 | 10.6 | 11.8 [70] |
| 89 | Cl | H | OH | H | Cl | 0.881 | 0.451 | 10.4 g | 10.6, 13.8 [70] |
| 0.881 | 0.474 | 10.6 | |||||||
| 90 | H | Cl | OH | H | Cl | 0.880 | 0.461 | 10.9 g | 13.3, 11.2 [70] |
| 0.880 | 0.464 | 10.2 | |||||||
| 91 | Cl | Cl | OH | Cl | H | 0.880 | 0.489 | 10.6 g | 10.7, 13.4 [70] |
| 0.880 | 0.481 | 11.0 | |||||||
| 92 | Cl | H | OH | Cl | Cl | 0.874 | 0.490 | 10.5 g | 10.6, 11.3 [70] |
| 0.874 | 0.497 | 10.8 | |||||||
| 93 | Cl | Cl | OH | Cl | Cl | 0.874 | 0.513 | 10.7 | 11.2 [70] |
| 83T | 4,8-dihydroxynaphtho-1,5-quinone | 0.513 | 0.622 | 19.32 | |||||
 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No | R1 | R2 | R3 | R4 | R5 | R6 | R7 | HOMA | quasiHOMA | EHB |
| 94 | H | H | H | H | H | H | H | 0.929 | 0.301 | 8.8 a |
| 95 | H | H | H | H | H | H | OH | 0.939 | 0.310 | 10.0 |
| 96 | H | H | H | OH | H | H | H | 0.933 | 0.316 | 9.1 b |
| 97 | H | H | H | H | OH | H | H | 0.872 | 0.404 | 10.5 c |
| 98 | OH | H | H | H | H | H | H | 0.927 | 0.344 | 7.6 |
| 99 | OH | H | H | OH | OH | H | H | 0.870 | 0.448 | 9.9 |
| 100 | OH | OH | H | H | OH | H | H | 0.740 | 0.366 | 9.3 d |
| 0.870 | 0.458 | 9.5 d | ||||||||
| 0.870 | 0.388 | 11.5 d | ||||||||
| 101 | H | OH | COOH | CH3 | OH | H | OH | 0.871 | 0.518 | 11.6 e |
| 0.871 | 0.448 | 10.9 e | ||||||||
| 0.881 | 0.024 | 5.6 e | ||||||||
| 97T | H | H | H | H | R5=O, R10=OH | H | H | 0.420 | 0.561 | 14.9 |
| 0.132 | 0.671 | 22.1 | ||||||||
| No | Name (Customary Name) | HOMA | quasiHOMA | EHB | Ref. |
|---|---|---|---|---|---|
| 102 | 2-hydroxy-6-methyl [(1R)-2-oxo-(5R,6R)-5,6-dihydroxy-3-methyl)cyclohex-3-enoic]benzoate | 0.914 | 0.163 | 5.5 che | |
| 103 | 5-hydroxy-2,2-dimethyl-8H-furo[3,4-g]chromen-6-one (salfredin B) | 0.990 | 0.205 | 5.6 | |
| 104 | 1,8-dihydroxyfluoren-9-one | 0.954 | 0.218 | 5.8 che | |
| 105 | 1-hydroxyfluoren-9-one | 0.960 | 0.169 | 6.7 | |
| 106 | 1,8-dihydroxy-9,10-dihydroanthracen-9-one (dithranol) | 0.930 | 0.286 | 7.3 che | |
| 107 | 1,8-dihydroxy-9H-xanthen-9-one | 0.939 | 0.422 | 7.4 che | |
| 108 | 8-hydroxy-2-(1-hydroxyethylene)-3,6-dimethyl-1(2H)-naphthalenone | 0.900 | 0.412 | 7.6 che | 9.5 [71] |
| 109 | 8-hydroxy-2-(1-hydroxyethylene)-1(2H)-naphthalenone | 0.885 | 0.397 | 7.7 che | |
| 110 | 2,3-dihydro-2,5-dihydroxy-4H-benzopyran-4-one (DDBO in [35]) | 0.939 | 0.310 | 8.2 | |
| 111 | 3,5,7-trihydroxy-2-(4-hydroxyphenyl)-3,5,7-trihydroxy-4H-chromen-4-one (kemferol) | 0.943 | 0.529 | 8.3 che | |
| 112 | 2-(3,4-dihydroxyphenyl)-3,5,7-trihydroxy-4H-chromen-4-one (quercetin) | 0.944 | 0.528 | 8.4 | |
| 113 | (1S*,3aR*,9aS*)-1,8-dihydroxy-1,2,3,3a-tetrahydrocyclopenta-[b]chromen-9(9aH)-one (diaporteone B) | 0.937 | 0.385 | 8.7 che | |
| 114 | 1-hydroxy-9H-xanthen-9-one | 0.788 | 0.366 | 8.7 | |
| 115 | 9(10H)-1,8-dihydroxyacridinone | 0.921 | 0.452 | 8.8 che | 4.97 [23] |
| 116 | 7-hydroxy-2,2-dimethyl-3,4-dihydro-2H-benzo[h]chromene-5,6-dione (7-hydroxylapachone) | 0.933 | 0.363 | 9.3 | |
| 117 | 5-hydroxy-4H-chromen-4-one | 0.952 | 0.347 | 9.3 | |
| 118 | 2-(3,4-dihydroxyphenyl)-5,7-dihydroxy-4-chromenone (luteolin) | 0.944 | 0.398 | 9.8 | |
| 119 | 7,8-dihydroxy-3-methyl-10-oxo-1H,10H-pyrano[4,3-b]chromene-9-carboxylic acid (anhydrofulvicacid) | 0.744 | -0.263 | 15.4 | |
| 120 | 5,7-dihydroxy-3-(4-hydroxyphenyl)chromen-4-one (genistein) | 0.941 | 0.392 | 10.0 | |
| 121 | 5-hydroxy-4-quinolon | 0.921 | 0.299 | 11.1 | 5.7 [23] |
| 122 | 2,3-dihydro-9,10-dihydroxy-1,4-anthracenedione (leucoquinizarin) | 0.692 | 0.434 | 11.2 | |
| 123 | 2,6-diacetyl-7,9-dihydroxy-8,9b-dimethyl-1,3(2H,9bh) (usinicacid) | 0.902 | 0.204 | 9.9 | 20.1 [34] |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rusinska-Roszak, D. Energy of Intramolecular Hydrogen Bonding in ortho-Hydroxybenzaldehydes, Phenones and Quinones. Transfer of Aromaticity from ipso-Benzene Ring to the Enol System(s). Molecules 2017, 22, 481. https://doi.org/10.3390/molecules22030481
Rusinska-Roszak D. Energy of Intramolecular Hydrogen Bonding in ortho-Hydroxybenzaldehydes, Phenones and Quinones. Transfer of Aromaticity from ipso-Benzene Ring to the Enol System(s). Molecules. 2017; 22(3):481. https://doi.org/10.3390/molecules22030481
Chicago/Turabian StyleRusinska-Roszak, Danuta. 2017. "Energy of Intramolecular Hydrogen Bonding in ortho-Hydroxybenzaldehydes, Phenones and Quinones. Transfer of Aromaticity from ipso-Benzene Ring to the Enol System(s)" Molecules 22, no. 3: 481. https://doi.org/10.3390/molecules22030481
APA StyleRusinska-Roszak, D. (2017). Energy of Intramolecular Hydrogen Bonding in ortho-Hydroxybenzaldehydes, Phenones and Quinones. Transfer of Aromaticity from ipso-Benzene Ring to the Enol System(s). Molecules, 22(3), 481. https://doi.org/10.3390/molecules22030481





