In Silico Prediction of O6-Methylguanine-DNA Methyltransferase Inhibitory Potency of Base Analogs with QSAR and Machine Learning Methods
Abstract
1. Introduction
2. Results and Discussions
2.1. QSAR Models
2.1.1. Model Validation
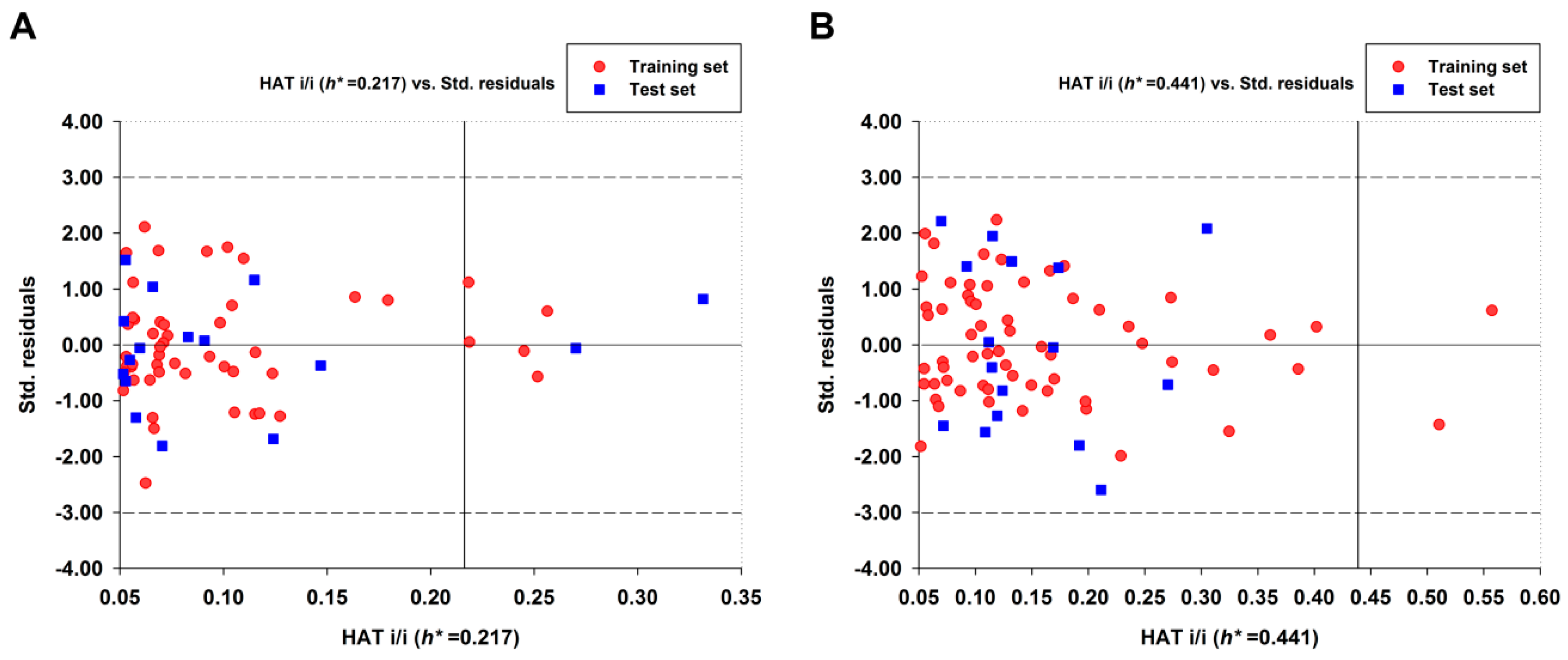
2.1.2. Outliers Analysis and Applicability Domain of QSAR Models
2.1.3. Mechanism Interpretation
2.2. Classification Models
2.2.1. Data Set Analysis
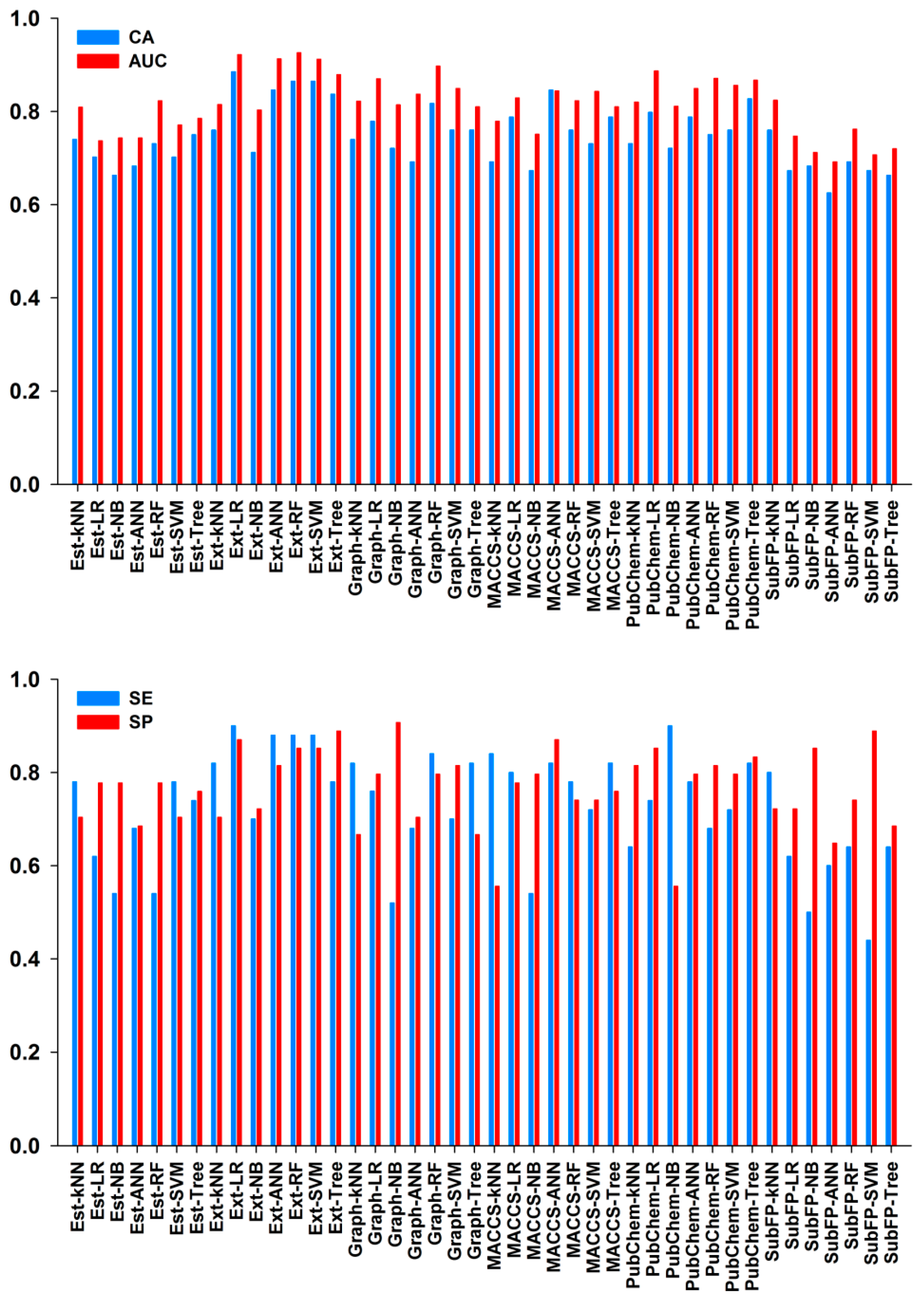
2.2.2. Performances of 10-Fold Cross-Validation
2.2.3. Performances of External Test Set
2.2.4. Identification and Analysis of Privileged Substructures
3. Materials and Methods
3.1. QSAR Study
3.1.1. Data Set
3.1.2. Calculation of Molecular Descriptors
3.1.3. Model Development and Evaluation
3.1.4. Applicability Domain
3.2. Classification Study
3.2.1. Data Collection and Preparation
3.2.2. Molecular Fingerprints
3.2.3. Machine Learning Methods
3.2.4. Model Performance Evaluation
3.2.5. Privileged Substructure Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Gnewuch, C.T.; Sosnovsky, G. A critical appraisal of the evolution of N-nitrosoureas as anticancer drugs. Chem. Rev. 1997, 97, 829–1013. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.H.; Zhao, L.J.; Zhong, R.G.; Peng, Y.Z. The specific role of O6-methylguanine-DNA methyltransferase inhibitors in cancer chemotherapy. Future Med. Chem. 2018, 10, 1971–1996. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.H.; Zhao, L.J.; Zhong, R.G. The induction and repair of DNA interstrand crosslinks and implications in cancer chemotherapy. Anti-Cancer Agents Med. Chem. 2016, 16, 221–246. [Google Scholar]
- Sun, G.H.; Fan, T.J.; Zhao, L.J.; Zhou, Y.; Zhong, R.G. The potential of combi-molecules with DNA-damaging function as anticancer agents. Future Med. Chem. 2017, 9, 403–435. [Google Scholar] [CrossRef] [PubMed]
- Roos, W.P.; Kaina, B. DNA damage-induced cell death: From specific DNA lesions to the DNA damage response and apoptosis. Cancer Lett. 2013, 332, 237–248. [Google Scholar] [CrossRef] [PubMed]
- Middleton, M.R.; Margison, G.P. Improvement of chemotherapy efficacy by inactivation of a DNA-repair pathway. Lancet Oncol. 2003, 4, 37–44. [Google Scholar] [CrossRef]
- Rajski, S.R.; Williams, R.M. DNA cross-linking agents as antitumor drugs. Chem. Rev. 1998, 98, 2723–2795. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, M.; Kastan, M.B. The DNA damage response: Implications for tumor responses to radiation and chemotherapy. Annu. Rev. Med. 2015, 66, 129–143. [Google Scholar] [CrossRef] [PubMed]
- Kaina, B.; Margison, G.P.; Christmann, M. Targeting O6-methylguanine-DNA methyltransferase with specific inhibitors as a strategy in cancer therapy. Cell. Mol. Life Sci. 2010, 67, 3663–3681. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.H.; Zhao, L.J.; Fan, T.J.; Li, S.S.; Zhong, R.G. Investigations on the effect of O6-benzylguanine on the formation of dG-dC interstrand cross-links induced by chloroethylnitrosoureas in human glioma cells using stable isotope dilution high-performance liquid chromatography electrospray ionization tandem mass spectrometry. Chem. Res. Toxicol. 2014, 27, 1253–1262. [Google Scholar] [PubMed]
- Sun, G.H.; Zhang, N.; Zhao, L.J.; Fan, T.J.; Zhang, S.F.; Zhong, R.G. Synthesis and antitumor activity evaluation of a novel combi-nitrosourea prodrug: Designed to release a DNA cross-linking agent and an inhibitor of O6-alkylguanine-DNA alkyltransferase. Bioorg. Med. Chem. 2016, 24, 2097–2107. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.J.; Ma, X.Y.; Zhong, R.G. A density functional theory investigation on the formation mechanisms of DNA interstrand crosslinks induced by chloroethylnitrosoureas. Int. J. Quantum Chem. 2013, 113, 1299–1306. [Google Scholar] [CrossRef]
- Pegg, A.E. Multifaceted roles of alkyltransferase and related proteins in DNA repair, DNA damage, resistance to chemotherapy, and research tools. Chem. Res. Toxicol. 2011, 24, 618–639. [Google Scholar] [CrossRef] [PubMed]
- Fahrer, J.; Kaina, B. O6-methylguanine-DNA methyltransferase in the defense against N-nitroso compounds and colorectal cancer. Carcinogenesis 2013, 34, 2435–2442. [Google Scholar] [CrossRef] [PubMed]
- Belanich, M.; Pastor, M.; Randall, T.; Guerra, D.; Kibitel, J.; Alas, L.; Li, B.; Citron, M.; Wasserman, P.; White, A.; et al. Retrospective study of the correlation between the DNA repair protein alkyltransferase and survival of brain tumor patients treated with carmustine. Cancer Res. 1996, 56, 783–788. [Google Scholar] [PubMed]
- Gerson, S.L. Clinical relevance of MGMT in the treatment of cancer. J. Clin. Oncol. 2002, 20, 2388–2399. [Google Scholar] [CrossRef] [PubMed]
- Hegi, M.E.; Liu, L.L.; Herman, J.G.; Stupp, R.; Wick, W.; Weller, M.; Mehta, M.P.; Gilbert, M.R. Correlation of O6-methylguanine methyltransferase (MGMT) promoter methylation with clinical outcomes in glioblastoma and clinical strategies to modulate MGMT activity. J. Clin. Oncol. 2008, 26, 4189–4199. [Google Scholar] [CrossRef] [PubMed]
- Tropsha, A.; Gramatica, P.; Gombar, V.K. The importance of being earnest: Validation is the absolute essential for successful application and interpretation of QSPR models. QSAR Comb. Sci. 2003, 22, 69–77. [Google Scholar] [CrossRef]
- Todeschini, R.; Consonni, V.; Maiocchi, A. The K correlation index: Theory development and its application in chemometrics. Chemometr. Intell. Lab. Syst. 1999, 46, 13–29. [Google Scholar] [CrossRef]
- Golbraikh, A.; Tropsha, A. Beware of q2! J. Mol. Graph. 2002, 20, 269–276. [Google Scholar] [CrossRef]
- Tropsha, A. Best practices for QSAR model development, validation, and exploitation. Mol. Inform. 2010, 29, 476–488. [Google Scholar] [CrossRef] [PubMed]
- Gramatica, P.; Chirico, N.; Papa, E.; Cassani, S.; Kovarich, S. QSARINS: A new software for the development, analysis, and validation of QSAR MLR models. J. Comput. Chem. 2013, 34, 2121–2132. [Google Scholar] [CrossRef]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; Wiley-VCH: Weinheim, Germany, 2008; Volume 11. [Google Scholar]
- Galvez, J.; Garciadomenech, R.; Dejulianortiz, J.V.; Soler, R. Topological approach to drug design. J. Chem. Inf. Comput. Sci. 1995, 35, 272–284. [Google Scholar] [CrossRef] [PubMed]
- Galvez, J.; Garcia, R.; Salabert, M.T.; Soler, R. Charge indexes—New topological descriptors. J. Chem. Inf. Comp. Sci. 1994, 34, 520–525. [Google Scholar] [CrossRef]
- Mota, S.G.R.; Barros, T.F.; Castilho, M.S. In vitro screening and chemometrics analysis on a series of azole derivatives with fungicide activity against Moniliophthora perniciosa. J. Braz. Chem. Soc. 2010, 21, 510–519. [Google Scholar] [CrossRef]
- Cassotti, M.; Ballabio, D.; Consonni, V.; Mauri, A.; Tetko, I.V.; Todeschini, R. Prediction of acute aquatic toxicity toward daphnia magna by using the GA-kNN method. Atla-Altern. Lab. Anim. 2014, 42, 31–41. [Google Scholar]
- Pauly, G.T.; Loktionova, N.A.; Fang, Q.M.; Vankayala, S.L.; Guida, W.C.; Pegg, A.E. Substitution of aminomethyl at the meta-position enhances the inactivation of O6-alkylguanine-DNA alkyltransferase by O6-benzylguanine. J. Med. Chem. 2008, 51, 7144–7153. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.H.; Fan, T.J.; Zhang, N.; Ren, T.; Zhao, L.J.; Zhong, R.G. Identification of the structural features of guanine derivatives as MGMT inhibitors using 3D-QSAR modeling combined with molecular docking. Molecules 2016, 21, 823. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.X.; Liu, Y.H. Quantitative structure-toxicity relationship for predicting acute toxicity of alkylbenzenes. AMM 2014, 665, 571–574. [Google Scholar] [CrossRef]
- Belka, M.; Konieczna, L.; Kawczak, P.; Ciesielski, T.; Slawinski, J.; Baczek, T. The chemometric evaluation of antitumor activity of novel benzensulfonamide derivatives based on their physiochemical properties. Lett. Drug Des. Discov. 2012, 9, 288–294. [Google Scholar] [CrossRef]
- Alberca, L.N.; Sbaraglini, M.L.; Balcazar, D.; Fraccaroli, L.; Carrillo, C.; Medeiros, A.; Benitez, D.; Comini, M.; Talevi, A. Discovery of novel polyamine analogs with anti-protozoal activity by computer guided drug repositioning. J. Comput.-Aided Mol. Des. 2016, 30, 305–321. [Google Scholar] [CrossRef] [PubMed]
- Fan, T.J.; Sun, G.H.; Zhao, L.J.; Cui, X.; Zhong, R.G. QSAR and classification study on prediction of acute oral toxicity of N-nitroso compounds. Int. J. Mol. Sci. 2018, 19, 3015. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Cai, Y.; Yang, H.; Zhang, H.; Xue, Y.; Liu, G.; Tang, Y.; Li, W. In silico prediction of chemicals binding to aromatase with machine learning methods. Chem. Res. Toxicol. 2017, 30, 1209–1218. [Google Scholar] [CrossRef] [PubMed]
- Sawada, R.; Kotera, M.; Yamanishi, Y. Benchmarking a wide range of chemical descriptors for drug-target interaction prediction using a chemogenomic approach. Mol. Inform. 2014, 33, 719–731. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.J.; Cheng, F.X.; Sun, L.; Li, W.H.; Liu, G.X.; Tang, Y. Computational models to predict endocrine-disrupting chemical binding with androgen or oestrogen receptors. Ecotoxicol. Environ. Saf. 2014, 110, 280–287. [Google Scholar] [CrossRef] [PubMed]
- Simeon, S.; Anuwongcharoen, N.; Shoombuatong, W.; Malik, A.A.; Prachayasittikul, V.; Wikberg, J.E.S.; Nantasenamat, C. Probing the origins of human acetylcholinesterase inhibition via QSAR modeling and molecular docking. PeerJ 2016, 4, e2322. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Li, X.; Yang, H.B.; Cai, Y.C.; Wang, Y.Y.; Wang, Z.; Li, W.H.; Tang, Y.; Liu, G.X. In silico prediction of serious eye irritation or corrosion potential of chemicals. RSC Adv. 2017, 7, 6697–6703. [Google Scholar] [CrossRef]
- Reinhard, J.; Hull, W.E.; von der Lieth, C.W.; Eichhorn, U.; Kliem, H.C.; Kaina, B.; Wiessler, M. Monosaccharide-linked inhibitors of O6-methylguanine-DNA methyltransferase (MGMT): Synthesis, molecular modeling, and structure-activity relationships. J. Med. Chem. 2001, 44, 4050–4061. [Google Scholar] [CrossRef] [PubMed]
- Terashima, I.; Kohda, K. Inhibition of human O6-alkylguanine-DNA alkyltransferase and potentiation of the cytotoxicity of chloroethylnitrosourea by 4(6)-(benzyloxy)-2,6(4)-diamino-5-(nitro or nitroso)pyrimidine derivatives and analogues. J. Med. Chem. 1998, 41, 503–508. [Google Scholar] [CrossRef] [PubMed]
- Moschel, R.C.; McDougall, M.G.; Dolan, M.E.; Stine, L.; Pegg, A.E. Structural features of substituted purine derivatives compatible with depletion of human O6-alkylguanine-DNA alkyltransferase. J. Med. Chem. 1992, 35, 4486–4491. [Google Scholar] [CrossRef] [PubMed]
- Chae, M.Y.; McDougall, M.G.; Dolan, M.E.; Swenn, K.; Pegg, A.E.; Moschel, R.C. Substituted O6-benzylguanine derivatives and their inactivation of human O6-alkylguanine-DNA alkyltransferase. J. Med. Chem. 1994, 37, 342–347. [Google Scholar] [CrossRef] [PubMed]
- Chae, M.Y.; Swenn, K.; Kanugula, S.; Dolan, M.E.; Pegg, A.E.; Moschel, R.C. 8-Substituted O6-benzylguanine, substituted 6(4)-(benzyloxy)pyrimidine, and related derivatives as inactivators of human O6-alkylguanine-DNA alkyltransferase. J. Med. Chem. 1995, 38, 359–365. [Google Scholar] [CrossRef] [PubMed]
- McElhinney, R.S.; Donnelly, D.J.; McCormick, J.E.; Kelly, J.; Watson, A.J.; Rafferty, J.A.; Elder, R.H.; Middleton, M.R.; Willington, M.A.; McMurry, T.B.H.; et al. Inactivation of O6-alkylguanine-DNA alkyltransferase. 1. Novel O6-(hetarylmethyl)guanines having basic rings in the side chain. J. Med. Chem. 1998, 41, 5265–5271. [Google Scholar] [CrossRef] [PubMed]
- Griffin, R.J.; Arris, C.E.; Bleasdale, C.; Boyle, F.T.; Calvert, A.H.; Curtin, N.J.; Dalby, C.; Kanugula, S.; Lembicz, N.K.; Newell, D.R.; et al. Resistance-modifying agents. 8. Inhibition of O6-alkylguanine-DNA alkyltransferase by O6-alkenyl-, O6-cycloalkenyl-, and O6-(2-oxoalkyl)guanines and potentiation of temozolomide cytotoxicity in vitro by O6-(1-cyclopentenylmethyl)guanine. J. Med. Chem. 2000, 43, 4071–4083. [Google Scholar] [CrossRef] [PubMed]
- Reinard, J.; Eichhorn, U.; Wiessler, M.; Kaina, B. Inactivation of O6-methylguanine-DNA methyltransferase by glucose-conjugated inhibitors. Int. J. Cancer 2001, 93, 373–379. [Google Scholar] [CrossRef] [PubMed]
- Wei, G.P.; Loktionova, N.A.; Pegg, A.E.; Moschel, R.C. β-Glucuronidase-cleavable prodrugs of O6-benzylguanine and O6-benzyl-21-deoxyguanosine. J. Med. Chem. 2005, 48, 256–261. [Google Scholar] [CrossRef] [PubMed]
- Mineura, K.; Fukuchi, M.; Kowada, M.; Terashima, I.; Kohda, K. Differential inactivation of O6-methylguanine-DNA methyltransferase activity by O6-arylmethylguanines. Int. J. Cancer 1995, 63, 148–151. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision A.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Kode Srl. Dragon Software for Molecular Descriptor Calculation V 7.0.6. Available online: https://chm.kode-solutions.net/ (accessed on 3 September 2017).
- Onlu, S.; Turker, S.M. Impact of geometry optimization methods on QSAR modelling: A case study for predicting human serum albumin binding affinity. SAR QSAR Environ. Res. 2017, 28, 491–509. [Google Scholar] [CrossRef] [PubMed]
- Gramatica, P.; Cassani, S.; Chirico, N. QSARINS-chem: Insubria datasets and new QSAR/QSPR models for environmental pollutants in QSARINS. J. Comput. Chem. 2014, 35, 1036–1044. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Zhang, Q.; Hu, J. QSAR study of the acute toxicity to fathead minnow based on a large dataset. SAR QSAR Environ. Res. 2016, 27, 147–164. [Google Scholar] [CrossRef] [PubMed]
- Gramatica, P. Principles of QSAR models validation: Internal and external. QSAR Comb. Sci. 2007, 26, 694–701. [Google Scholar] [CrossRef]
- Shi, L.M.; Fang, H.; Tong, W.D.; Wu, J.; Perkins, R.; Blair, R.M.; Branham, W.S.; Dial, S.L.; Moland, C.I.; Sheehan, D.M. QSAR models using a large diverse set of estrogens. J. Chem. Inf. Comput. Sci. 2001, 41, 186–195. [Google Scholar] [CrossRef] [PubMed]
- Schueuermann, G.; Ebert, R.; Chen, J.; Wang, B.; Kuehne, R. External validation and prediction employing the predictive squared correlation coefficient-test set activity mean vs training set activity mean. J. Chem. Inf. Model. 2008, 48, 2140–2145. [Google Scholar] [CrossRef] [PubMed]
- Consonni, V.; Ballabio, D.; Todeschini, R. Comments on the definition of the q(2) parameter for QSAR validation. J. Chem. Inf. Model. 2009, 49, 1669–1678. [Google Scholar] [CrossRef] [PubMed]
- Consonni, V.; Ballabio, D.; Todeschini, R. Evaluation of model predictive ability by external validation techniques. J. Chemometr. 2010, 24, 194–201. [Google Scholar] [CrossRef]
- Lin, L. A concordance correlation-coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef] [PubMed]
- Lin, L. Assay validation using the concordance correlation-coefficient. Biometrics 1992, 48, 599–604. [Google Scholar] [CrossRef]
- Chirico, N.; Gramatica, P. Real external predictivity of QSAR models: How to evaluate it? Comparison of different validation criteria and proposal of using the concordance correlation coefficient. J. Chem. Inf. Model. 2011, 51, 2320–2335. [Google Scholar] [CrossRef] [PubMed]
- Chirico, N.; Gramatica, P. Real external predictivity of QSAR models. Part 2. New intercomparable thresholds for different validation criteria and the need for scatter plot inspection. J. Chem. Inf. Model. 2012, 52, 2044–2058. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Cheng, F.; Xu, Y.; Li, W.; Tang, Y. Estimation of ADME properties with substructure pattern recognition. J. Chem Inf. Model. 2010, 50, 1034–1041. [Google Scholar] [CrossRef] [PubMed]
- Yap, C.W. PaDEL-Descriptor: An open source software to calculate molecular descriptors and fingerprints. J. Comput. Chem. 2011, 32, 1466–1474. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Cox, D. The regression analysis of binary sequences. J. R. Stat. Soc. 1958, 2, 215–242. [Google Scholar]
- Walker, S.H.; Duncan, D.B. Estimation of the probability of an event as a function of several independent variables. Biometrika 1967, 54, 167–179. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.M. A naive Bayes classifier for prediction of multidrug resistance reversal activity on the basis of atom typing. J. Med. Chem. 2005, 48, 4031–4039. [Google Scholar] [CrossRef] [PubMed]
- Watson, P. Naive Bayes classification using 2D pharmacophore feature triplet vectors. J. Chem Inf. Model. 2008, 48, 166–178. [Google Scholar] [CrossRef] [PubMed]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chang, C.; Lin, C. LIBSVM: A library for support vector machines. ACM. Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Plewczynski, D.; Spieser, S.; Koch, U. Assessing different classification methods for virtual screening. J. Chem. Inf. Model. 2006, 46, 1098–1106. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Garrido, A.; Helguera, A.M.; Borges, F.; Cordeiro, M.N.D.S.; Rivero, V.; Escudero, A.G. Two new parameters based on distances in a receiver operating characteristic chart for the selection of classification models. J. Chem. Inf. Model. 2011, 51, 2746–2759. [Google Scholar] [CrossRef] [PubMed]
- Cheng, F.X.; Yu, Y.; Shen, J.; Yang, L.; Li, W.H.; Liu, G.X.; Lee, P.W.; Tang, Y. Classification of cytochrome P450 inhibitors and noninhibitors using combined classifiers. J. Chem Inf. Model. 2011, 51, 996–1011. [Google Scholar] [CrossRef] [PubMed]
- Jensen, B.F.; Vind, C.; Brockhoff, P.B.; Refsgaard, H.H.F. In silico prediction of cytochrome P450 2D6 and 3A4 inhibition using gaussian kernel weightedk-nearest neighbor and extended connectivity fingerprints, including structural fragment analysis of inhibitors versus noninhibitors. J. Med. Chem. 2007, 50, 501–511. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: No samples of the compounds mentioned in this study are available from the authors. |



| Descriptor | Type | Chemical Meaning |
|---|---|---|
| VE3sign_X | 2D matrix-based descriptors | logarithmic coefficient sum of the last eigenvector from chi matrix |
| J_Dz(p) | 2D matrix-based descriptors | balaban-like index from Barysz matrix weighted by polarizability |
| SpPosA_B(p) | 2D matrix-based descriptors | normalized spectral positive sum from Burden matrix weighted by polarizability |
| VE3sign_B(s) | 2D matrix-based descriptors | logarithmic coefficient sum of the last eigenvector from Burden matrix weighted by I-State |
| MATS1i | 2D autocorrelations | Moran autocorrelation of lag 1 weighted by ionization potential |
| JGI4 | 2D autocorrelations | mean topological charge index of order 4 |
| B09[C-C] | 2D Atom Pairs Binary | presence/absence of C-C at topological distance 9 |
| nArNH2 | Functional group counts | number of primary amines (aromatic) |
| CATS2D_07_DA | CATS 2D | CATS2D Donor-Acceptor at lag 07 |
| Data Set | Model | CA | AUC | SE | SP | TP | TN | FP | FN |
|---|---|---|---|---|---|---|---|---|---|
| Training set | Ext-RF | 0.865 | 0.926 | 0.88 | 0.85 | 44 | 46 | 8 | 6 |
| Ext-LR | 0.885 | 0.922 | 0.90 | 0.87 | 45 | 47 | 7 | 5 | |
| Ext-ANN | 0.846 | 0.913 | 0.88 | 0.81 | 44 | 44 | 10 | 6 | |
| Ext-SVM | 0.865 | 0.912 | 0.88 | 0.85 | 44 | 46 | 8 | 6 | |
| Graph-RF | 0.817 | 0.897 | 0.84 | 0.80 | 42 | 43 | 11 | 8 | |
| PubChem-LR | 0.798 | 0.887 | 0.74 | 0.85 | 37 | 46 | 8 | 13 | |
| Ext-Tree | 0.837 | 0.879 | 0.78 | 0.89 | 39 | 48 | 6 | 11 | |
| PubChem-RF | 0.750 | 0.871 | 0.68 | 0.81 | 34 | 44 | 10 | 16 | |
| Graph-LR | 0.779 | 0.870 | 0.76 | 0.80 | 38 | 43 | 11 | 12 | |
| PubChem-Tree | 0.827 | 0.867 | 0.82 | 0.83 | 41 | 45 | 9 | 9 | |
| External test set | Ext-RF | 0.840 | 0.930 | 0.75 | 0.92 | 9 | 12 | 1 | 3 |
| Ext-LR | 0.840 | 0.974 | 0.75 | 0.92 | 9 | 12 | 1 | 3 | |
| Ext-ANN | 0.800 | 0.962 | 0.67 | 0.92 | 8 | 12 | 1 | 4 | |
| Ext-SVM | 0.880 | 0.904 | 0.83 | 0.92 | 10 | 12 | 1 | 2 | |
| Graph-RF | 0.880 | 0.920 | 0.92 | 0.85 | 11 | 11 | 2 | 1 | |
| PubChem-LR | 0.840 | 0.936 | 0.92 | 0.77 | 11 | 10 | 3 | 1 | |
| Ext-Tree | 0.880 | 0.901 | 0.83 | 0.92 | 10 | 12 | 1 | 2 | |
| PubChem-RF | 0.800 | 0.917 | 0.75 | 0.85 | 9 | 11 | 2 | 3 | |
| Graph-LR | 0.840 | 0.936 | 0.75 | 0.92 | 9 | 12 | 1 | 3 | |
| PubChem-Tree | 0.640 | 0.667 | 0.67 | 0.62 | 8 | 8 | 5 | 4 |
| No. | Privileged Substructures | General Substructures | Representative Compounds | IG | FP | FN |
|---|---|---|---|---|---|---|
| FP297 | C-Br |  |  | 0.096 | 2.08(11) | 0(0) |
| FP327 | C(~Br)(~C) 1 | 0.087 | 2.08(11) | 0(0) | ||
| FP328 | C(~Br)(~C)(~C) | 0.087 | 2.08(11) | 0(0) | ||
| FP330 | C(~Br)(:C) 2 | 0.087 | 2.08(11) | 0(0) | ||
| FP43 | ≥1 Br | 0.096 | 2.08(11) | 0(0) | ||
| FP509 | Br-C:C-C | 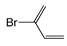 | 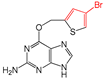 | 0.078 | 2.08(9) | 0(0) |
| FP554 | Br-C-C-C | 0.078 | 2.08(9) | 0(0) | ||
| FP670 | Br-C:C:C-C | 0.078 | 2.08(9) | 0(0) | ||
| FP421 | C=S |  | 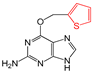 | 0.078 | 2.08(9) | 0(0) |
| FP471 | S:C:C:C | 0.078 | 2.08(9) | 0(0) | ||
| FP480 | C:S:C-C | 0.078 | 2.08(9) | 0(0) | ||
| FP513 | S:C:C-[#1] | 0.078 | 2.08(9) | 0(0) | ||
| FP532 | S-C:C-[#1] | 0.078 | 2.08(9) | 0(0) | ||
| FP699 | O-C-C-C-C-C(C)-C | 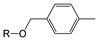 | 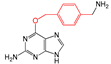 | 0.096 | 2.08(11) | 0(0) |
| FP776 | CC1CCC(C)CC1 | 0.064 | 2.08(11) | 0(0) | ||
| FP188 | ≥2 saturated or aromatic heteroatom-containing ring size 6 |  | 0.081 | 1.93(13) | 0.14(1) | |
| FP648 | O=N-C:C-N | 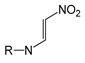 | 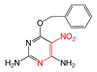 | 0.073 | 1.92(12) | 0.15(1) |
| FP260 | ≥3 hetero-aromatic rings | 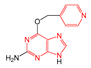 | 0.056 | 1.89(10) | 0.18(1) | |
| FP713 | Cc1ccc(C)cc1 | 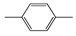 | 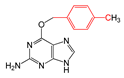 | 0.056 | 1.89(10) | 0.18(1) |
| FP697 | C-C-C-C-C-C(C)-C |  | 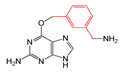 | 0.048 | 1.87(9) | 0.19(1) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, G.; Fan, T.; Sun, X.; Hao, Y.; Cui, X.; Zhao, L.; Ren, T.; Zhou, Y.; Zhong, R.; Peng, Y. In Silico Prediction of O6-Methylguanine-DNA Methyltransferase Inhibitory Potency of Base Analogs with QSAR and Machine Learning Methods. Molecules 2018, 23, 2892. https://doi.org/10.3390/molecules23112892
Sun G, Fan T, Sun X, Hao Y, Cui X, Zhao L, Ren T, Zhou Y, Zhong R, Peng Y. In Silico Prediction of O6-Methylguanine-DNA Methyltransferase Inhibitory Potency of Base Analogs with QSAR and Machine Learning Methods. Molecules. 2018; 23(11):2892. https://doi.org/10.3390/molecules23112892
Chicago/Turabian StyleSun, Guohui, Tengjiao Fan, Xiaodong Sun, Yuxing Hao, Xin Cui, Lijiao Zhao, Ting Ren, Yue Zhou, Rugang Zhong, and Yongzhen Peng. 2018. "In Silico Prediction of O6-Methylguanine-DNA Methyltransferase Inhibitory Potency of Base Analogs with QSAR and Machine Learning Methods" Molecules 23, no. 11: 2892. https://doi.org/10.3390/molecules23112892
APA StyleSun, G., Fan, T., Sun, X., Hao, Y., Cui, X., Zhao, L., Ren, T., Zhou, Y., Zhong, R., & Peng, Y. (2018). In Silico Prediction of O6-Methylguanine-DNA Methyltransferase Inhibitory Potency of Base Analogs with QSAR and Machine Learning Methods. Molecules, 23(11), 2892. https://doi.org/10.3390/molecules23112892








