Thermal Decomposition Behavior of Hydroxytyrosol (HT) in Nitrogen Atmosphere Based on TG-FTIR Methods
Abstract
:1. Introduction
2. Results and Discussion
2.1. Thermal Decomposition Behavior
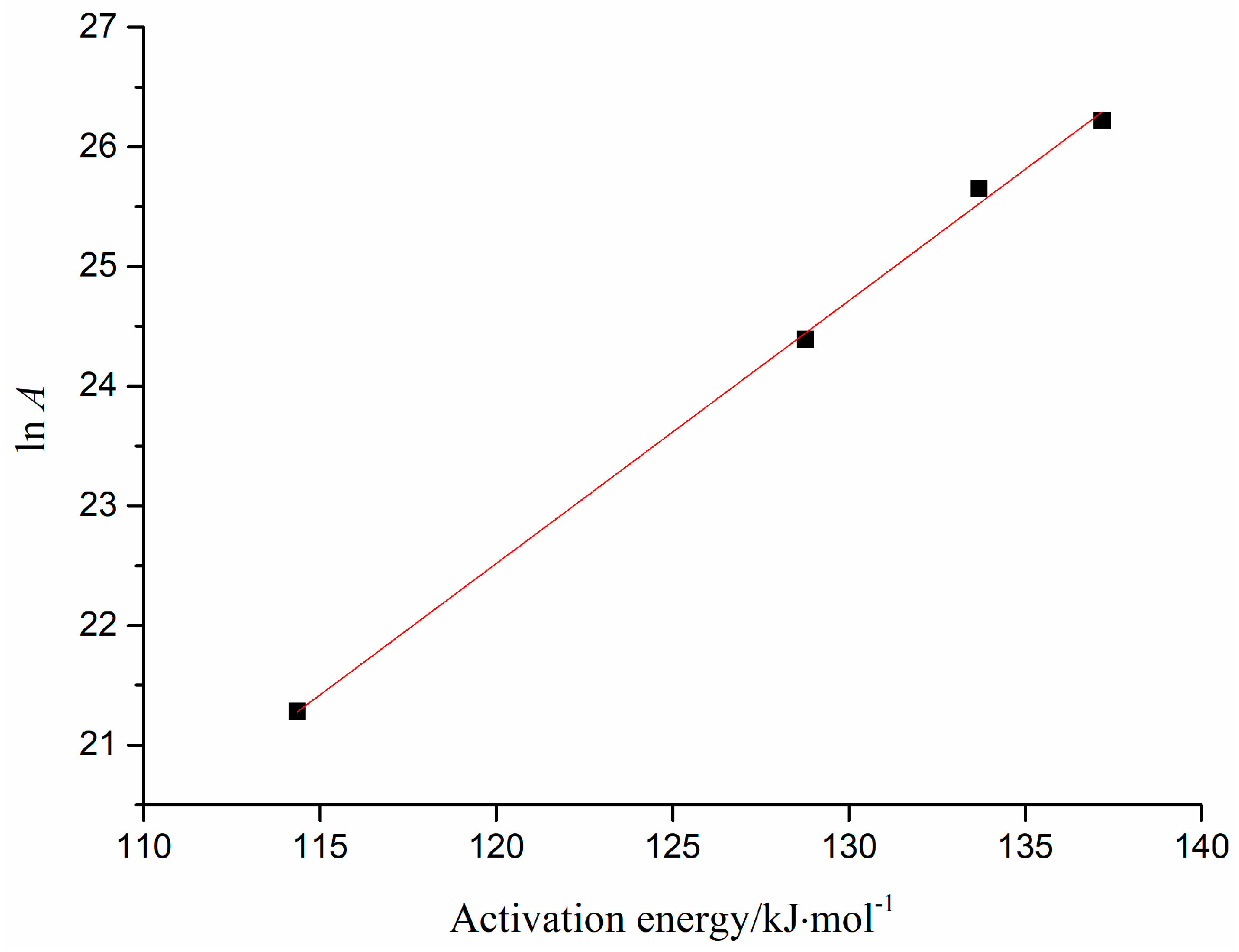
2.2. Nonisothermal Kinetics of HT
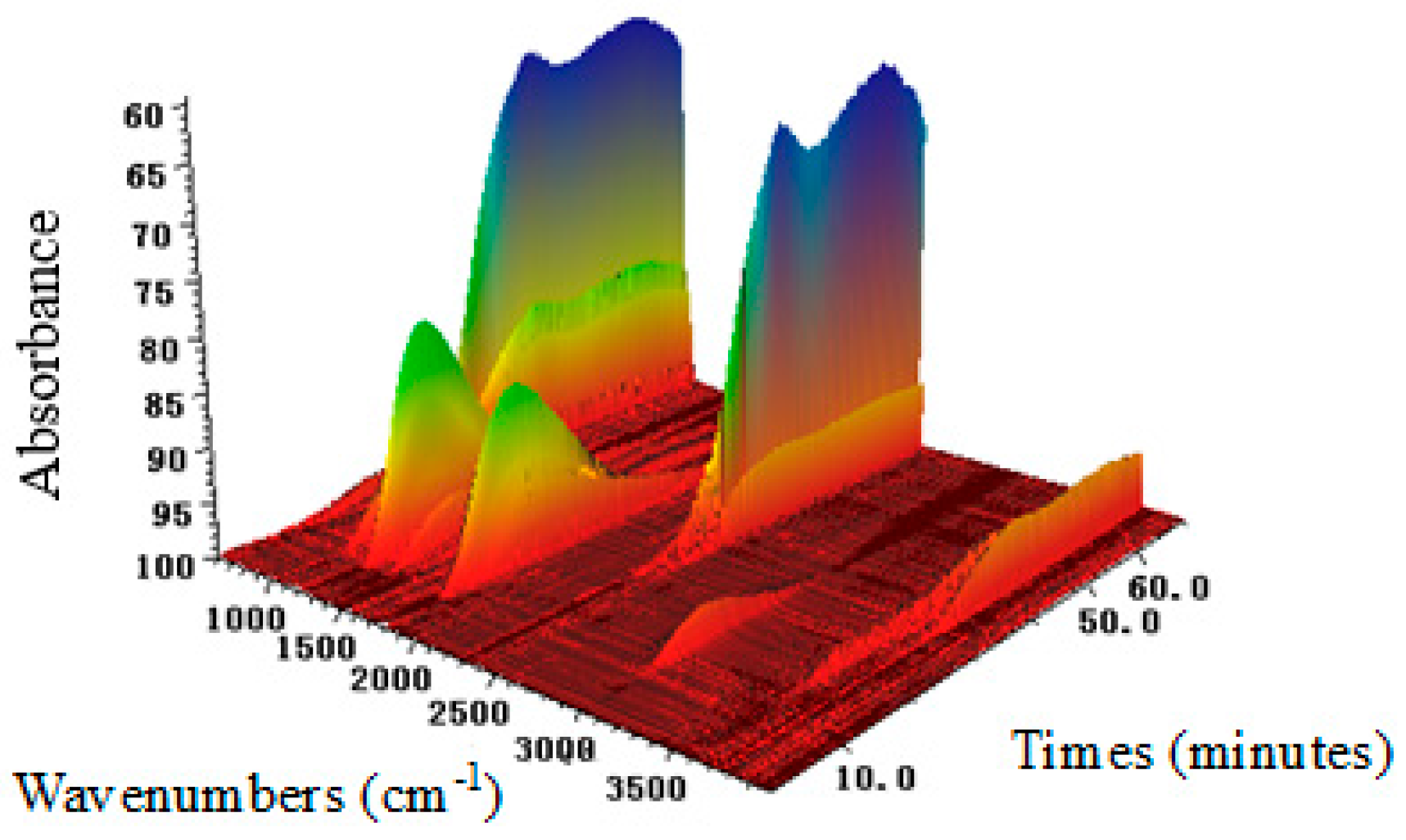
2.3. Chemical Bond Change by TG-FTIR
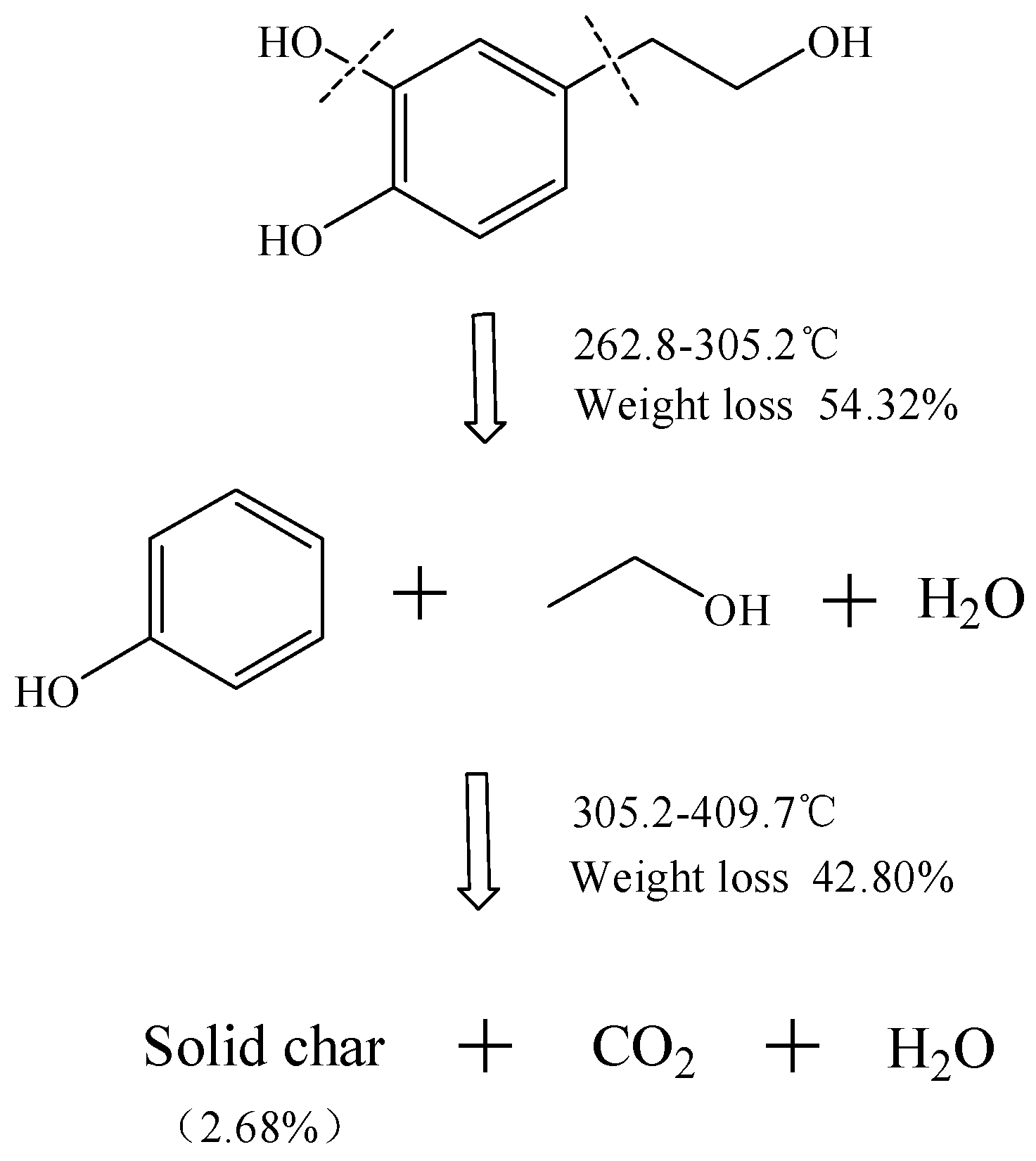
2.4. Proposed Mechanism of HT Thermal Decomposition
3. Materials and Methods
3.1. Material
3.2. Methods
3.3. Theoretical Analysis
3.3.1. Kissinger Method
3.3.2. Flynn-Wall-Ozawa Method
3.3.3. Friedman Method
3.3.4. Most Probable Reaction Mechanism and Mathematical Model
3.3.5. Calculation of ln A
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| dx/dt | stands for a rate of conversion; |
| x | stands for the conversion of the reaction, which is defined as x =(w0 − wt)/(w0 − wf), where w0 and wf stand for the initial and final masses of the sample at each stage of decomposition (mg), respectively, and wt stands for the mass of the sample at time t (mg); |
| f(x) | stands for a differential mathematical model function of kinetics, which depends on the reaction type and mechanism; |
| g(x) | stands for an integral mechanism model function of kinetics, which depends on the reaction type and mechanism; |
| k(T) | stands for the temperature-dependent rate constant, which can be described by the Arrhenius equation; |
| A | stands for the preexponential factor (min−1); |
| R | stands for the gas constant 8.314 J·(mol·K)−1; |
| E | stands for the apparent activation energy (kJ·mol−1); |
| T | stands for the absolute temperature (K); |
| Β | stands for the heating rate (K·min−1); |
| Tp | stands for the absolute thermodynamic temperature at which the weight loss rate reaches a maximum value (K). |
References
- Adhami, H.R.; Zehl, M.; Dangl, C.; Dorfmeister, D.; Stadler, M.; Urban, E.; Hewitson, P.; Ignatova, S.; Krenn, L. Preparative isolation of oleocanthal, tyrosol, and hydroxytyrosol from olive oil by HPCCC. Food Chem. 2015, 170, 154–159. [Google Scholar] [CrossRef] [PubMed]
- Ozkan, M.; Muftuler, F.B.; Kilcar, A.Y.; Medine, E.I.; Unak, P. Isolation of hydroxytyrosol from olive leaves extract, radioiodination and investigation of bioaffinity using in vivo/in vitro methods. Radiochim. Acta 2013, 101, 585–593. [Google Scholar]
- Visioli, F.; Caruso, D.; Plasmati, E.; Patelli, R.; Mulinacci, N.; Romani, A.; Galli, G.; Galli, C. Hydroxytyrosol, as a component of olive mill waste water, is dose-dependently absorbed and increases the antioxidant capacity of rat plasma. Free Radic. Res. 2001, 34, 301–305. [Google Scholar] [CrossRef] [PubMed]
- Owen, R.W.; Giacosa, A.; Hull, W.E.; Haubner, R.; Spiegelhalder, B.; Bartsch, H. The antioxidant/anticancer potential of phenolic compounds isolated from olive oil. Eur. J. Cancer 2000, 36, 1235–1247. [Google Scholar] [CrossRef]
- Bisignano, G.; Tomaino, A.; Lo, C.R.; Crisafi, G.; Uccella, N.; Saija, A. On the in vitro antimicrobial activity of oleuropein and hydroxytyrosol. J. Pharm. Pharmacol. 1999, 51, 971–974. [Google Scholar] [CrossRef] [PubMed]
- Medinamartínez, M.S.; Truchado, P.; Castroibáñez, I.; Allende, A. Antimicrobial activity of hydroxytyrosol: A current controversy. Biosci. Biotechnol. Biochem. 2016, 80, 801–810. [Google Scholar] [CrossRef] [PubMed]
- Killeen, M.J.; Pontoniere, P.; Crea, R. Hydroxytyrosol: An examination of its potential role in cardiovascular disease, inflammation, and longevity. Agro Food Ind. Hi-Tech 2011, 22, 16–19. [Google Scholar]
- Fabiani, R.; De, B.A.; Rosignoli, P.; Servili, M.; Selvaggini, R.; Montedoro, G.F.; Di, S.C.; Morozzi, G. Virgin olive oil phenols inhibit proliferation of human promyelocytic leukemia cells (HL60) by inducing apoptosis and differentiation. J. Nutr. 2006, 136, 614–619. [Google Scholar] [CrossRef] [PubMed]
- Bernini, R.; Crisante, F.; Merendino, N.; Molinari, R.; Soldatelli, M.C.; Velotti, F. Synthesis of a Novel Ester of Hydroxytyrosol and α-Lipoic Acid Exhibiting an Antiproliferative Effect on Human Colon Cancer HT-29 Cells. Eur. J. Med. Chem. 2011, 46, 439–446. [Google Scholar] [CrossRef] [PubMed]
- Bouallagui, Z.; Han, J.; Isoda, H.; Sayadi, S. Hydroxytyrosol rich extract from olive leaves modulates cell cycle progression in MCF-7 human breast cancer cells. Food Chem. Toxicol. 2011, 49, 179–184. [Google Scholar] [CrossRef] [PubMed]
- Trujillo, M.; Gallardo, E.; Madrona, A.; Bravo, L.; Sarriá, B.; González-Correa, J.A.; Mateos, R.; Espartero, J.L. Synthesis and antioxidant activity of nitrohydroxytyrosol and its acyl derivatives. J. Agric. Food Chem. 2014, 62, 10297–10303. [Google Scholar] [CrossRef] [PubMed]
- Mateos, R.; Madrona, A.; Pereiracaro, G.; Cert, R.M.; Parrado, J.; Bravo, L.; Espartero, J.L. Synthesis and antioxidant evaluation of isochroman-derivatives of hydroxytyrosol: Structure-activity relationship. Food Chem. 2015, 173, 313–320. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Luo, C.; Liu, J. Hydroxytyrosol induces apoptosis in human colon cancer cells through ROS generation. Food Funct. 2014, 5, 1909–1914. [Google Scholar] [CrossRef] [PubMed]
- D’Angelo, S.; Manna, C.; Migliardi, V.; Mazzoni, O.; Morrica, P.; Capasso, G.; Pontoni, G.; Galletti, P.; Zappia, V. Pharmacokinetics and Metabolism of Hydroxytyrosol, a Natural Antioxidant from Olive Oil. Drug Metab. Dispos. 2001, 29, 1492–1498. [Google Scholar] [PubMed]
- Luo, C.; Liu, J.K. Advances in Anti-Cancer Mechanisms of Hydroxytyrosol. Sci. China Earth Sci. 2014, 44, 14–20. [Google Scholar]
- Zhu, X.M. Thermal Stability and Thermal Decomposition Kinetics of Ofloxacin. Chem. World 2008, 49, 333–328. [Google Scholar]
- Xiao, Z.B.; Guo, M.M.; Guo, R.K.; Xiong, L.Z. Thermal stability, decomposition kinetics and storage time of gutta-percha. Chem. Ind. For. Prod. 2013, 13, 664–666. [Google Scholar]
- Gallo, R.C.; Ferreira, A.P.G.; Castro, R.E.A.; Cavalheiro, E.T.G. Studying the thermal decomposition of carvedilol by coupled TG-FTIR. J. Therm. Anal. Calorim. 2016, 123, 2307–2312. [Google Scholar] [CrossRef]
- Zhang, C.W.; Wang, C.Z.; Tao, R. Thermal Decomposition Kinetics of Ginkgo biloba Leaves Polyprenol in Nitrogen Atmosphere. Int. J. Chem. Kinet. 2016, 48, 671–678. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Chen, Z.; Chai, Q.; Liao, S.; He, Y.; Li, Y.; Bo, X.; Wu, W.; Li, B. Application of isoconversional calculation procedure to non-isothermal kinetic study: III. Thermal decomposition of ammonium cobalt phosphate hydrate. Thermochim. Acta 2012, 543, 205–210. [Google Scholar] [CrossRef]
- Lopez-Velazquez, M.A.; Santes, V.; Balmaseda, J.; Torres-Garcia, E. Pyrolysis of orange waste: A thermo-kinetic study. J. Anal. Appl. Pyrolysis 2013, 99, 170–177. [Google Scholar] [CrossRef]
- Salehi, M.; Clemens, F.; Graule, T.; Grobéty, B. Kinetic analysis of the polymer burnout in ceramic thermoplastic processing of the YSZ thin electrolyte structures using model free method. Appl. Energy 2012, 95, 147–155. [Google Scholar] [CrossRef]
- Aburto, J.; Moran, M.; Galano, A.; Torres-García, E. Non-isothermal pyrolysis of pectin: A thermochemical and kinetic approach. J. Anal. Appl. Pyrolysis 2015, 112, 94–104. [Google Scholar] [CrossRef]
- Rotaru, A.; Moanţă, A.; Rotaru, P.; Segal, E. Thermal decomposition kinetics of some aromatic azomonoethers. J. Therm. Anal. Calorim. 2009, 92, 233–238. [Google Scholar] [CrossRef]
- Venkatesh, M.; Ravi, P.; Tewari, S.P. Isoconversional Kinetic Analysis of Decomposition of Nitroimidazoles: Friedman method vs. Flynn–Wall–Ozawa Method. J. Phys. Chem. A 2013, 117, 10162–10169. [Google Scholar] [CrossRef] [PubMed]
- Corradini, E.; Teixeira, E.M.; Paladin, P.D.; Agnelli, J.A.; Silva, O.R.R.F.; Mattoso, L.H.C. Thermal stability and degradation kinetic study of white and colored cotton fibers by thermogravimetric analysis. J. Therm. Anal. Calorim. 2009, 97, 415–419. [Google Scholar] [CrossRef]
- Hao, Y.R. Study on Pyrolysis Kinetic of Biomass Residue. Master’s Thesis, Nanjing University of Science and Technology, Nanjing, China, 2012. [Google Scholar]
- Naqvi, S.R.; Uemura, Y.; Osman, N.; Yusup, S. Kinetic study of the catalytic pyrolysis of paddy husk by use of thermogravimetric data and the Coats–Redfern model. Res. Chem. Intermed. 2015, 41, 9743–9755. [Google Scholar] [CrossRef]
Sample Availability: Not available. |
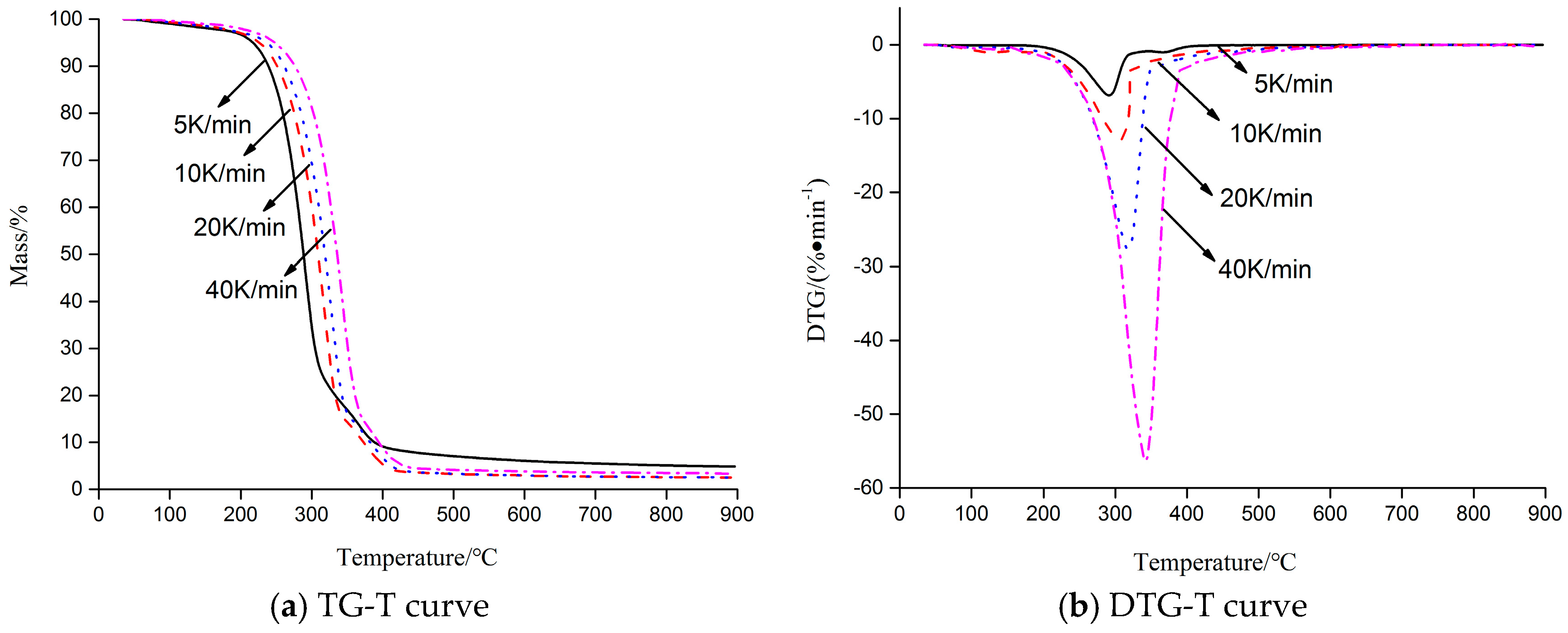

| Heating Rate (K·min−1) | Beginning Temperature (°C) | End Temperature (°C) | Tm (°C) | Maximum Loss Ratio (%·min−1) | Solid Char (%) |
|---|---|---|---|---|---|
| 5 | 252.9 | 395.1 | 291.4 | −6.85 | 4.85 |
| 10 | 262.8 | 409.7 | 305.2 | −12.91 | 2.68 |
| 20 | 273.6 | 415.3 | 314.8 | −27.71 | 2.53 |
| 40 | 298.7 | 418.9 | 341.9 | −56.35 | 3.34 |
| Conversion | Friedman Method | F-W-O Method | ||
|---|---|---|---|---|
| E (kJ·mol−1) | R2 | E (kJ·mol−1) | R2 | |
| 0.1 | 121.36 | 0.9329 | 125.71 | 0.9950 |
| 0.2 | 118.89 | 0.9744 | 118.41 | 0.9894 |
| 0.3 | 124.24 | 0.9903 | 118.56 | 0.9858 |
| 0.4 | 126.51 | 0.9815 | 119.64 | 0.9815 |
| 0.5 | 127.05 | 0.9673 | 120.19 | 0.9783 |
| 0.6 | 133.66 | 0.9317 | 123.37 | 0.9784 |
| 0.7 | 249.99 | 0.9 | 174.39 | 0.9503 |
| Mean | 143.1 | — | 128.61 | — |
| No. | β = 5 K·min−1 | β = 10 K·min−1 | β = 20 K·min−1 | β = 40 K·min−1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | ln A | R2 | E | ln A | R2 | E | ln A | R2 | E | ln A | R2 | |
| F1 | 71.80 | 12.91 | 0.9782 | 79.79 | 14.90 | 0.9937 | 82.91 | 15.97 | 0.9934 | 85.04 | 16.56 | 0.9911 |
| F2 | 96.65 | 18.86 | 0.987 | 104.83 | 20.97 | 0.9682 | 109.56 | 22.14 | 0.968 | 112.36 | 22.72 | 0.9654 |
| F3 | 126.61 | 26.15 | 0.9779 | 136.33 | 28.15 | 0.9349 | 141.52 | 29.45 | 0.9348 | 145.14 | 29.99 | 0.9323 |
| D1 | 114.36 | 21.28 | 0.9489 | 128.77 | 24.39 | 0.9976 | 133.69 | 25.65 | 0.9975 | 137.18 | 26.22 | 0.9961 |
| D2 | 125.43 | 23.27 | 0.9616 | 140.43 | 26.43 | 0.9991 | 145.77 | 27.74 | 0.9989 | 149.57 | 28.30 | 0.9972 |
| D3 | 138.74 | 24.97 | 0.9732 | 154.32 | 28.16 | 0.998 | 160.17 | 29.53 | 0.9978 | 164.33 | 30.08 | 0.9958 |
| D4 | 129.83 | 22.83 | 0.9660 | 145.03 | 26.00 | 0.9991 | 150.54 | 27.33 | 0.9989 | 154.45 | 27.88 | 0.9971 |
| A2 | 31.30 | 3.64 | 0.9707 | 35.21 | 5.03 | 0.9924 | 36.69 | 5.92 | 0.9921 | 37.62 | 6.55 | 0.9892 |
| A3 | 17.80 | 0.27 | 0.959 | 20.35 | 1.47 | 0.9906 | 21.28 | 2.30 | 0.9902 | 21.81 | 2.93 | 0.9865 |
| R1 | 52.58 | 8.11 | 0.9392 | 59.70 | 10.07 | 0.9971 | 62.08 | 11.05 | 0.997 | 63.69 | 11.66 | 0.9954 |
| R2 | 61.49 | 9.66 | 0.9629 | 69.05 | 11.64 | 0.9988 | 71.77 | 12.66 | 0.9986 | 73.62 | 13.27 | 0.9965 |
| R3 | 64.77 | 10.07 | 0.9689 | 72.48 | 12.06 | 0.9978 | 75.32 | 13.09 | 0.9976 | 77.26 | 13.82 | 0.9954 |
| P2 | 21.69 | 1.04 | 0.9107 | 25.17 | 2.42 | 0.9956 | 26.27 | 3.27 | 0.9954 | 26.94 | 3.91 | 0.9933 |
| P3 | 11.39 | −1.67 | 0.8598 | 13.65 | −0.45 | 0.9927 | 14.34 | 0.36 | 0.9926 | 14.69 | 1.01 | 0.9895 |
| P4 | 6.24 | −3.31 | 0.7605 | 7.90 | −2.12 | 0.9867 | 8.37 | −1.33 | 0.9868 | 8.57 | −0.69 | 0.982 |
| Wavenumber (cm−1) | Vibration of Corresponding Bond | Functional Group |
|---|---|---|
| 3964–3500, 1300–1800 | O–H stretching | H2O |
| 2313–2361, 669 | C=O stretching, C=O bending | CO2 |
| 1684–1745, 2822–2915 | C=O stretching, C–H stretching | R–CHO |
| 1000–1300, 3585–3650 | C–O stretching, O–H stretching | R–OH |
| 2900–3000 | C–H stretching | –CH3 (saturation) |
| 3066 | C–H stretching (aromatic ring) | 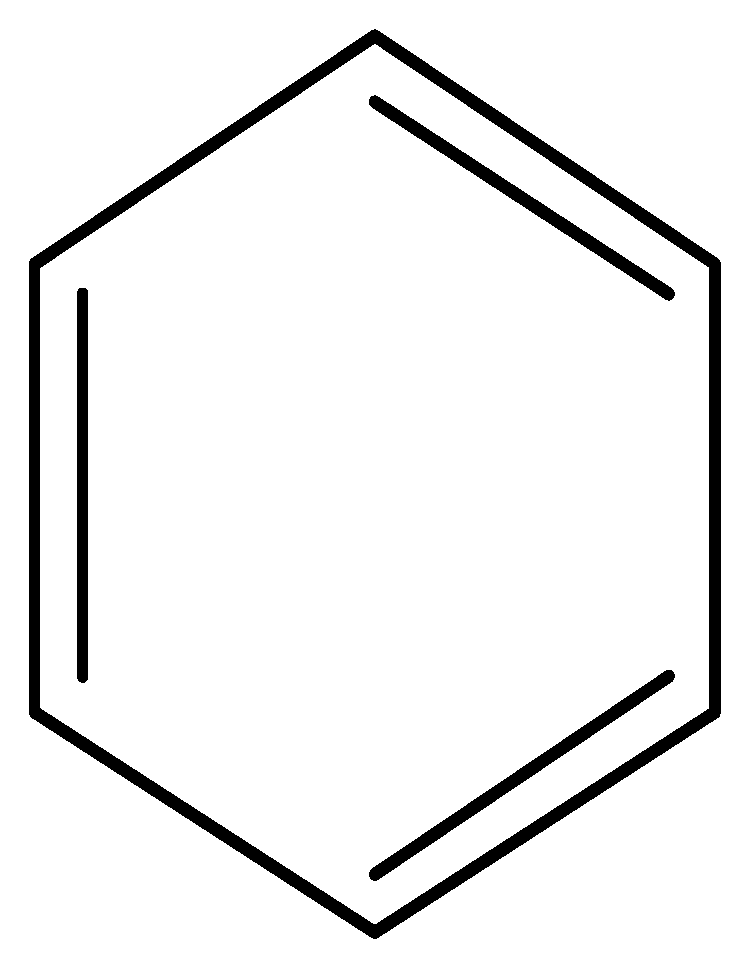 |
| 1600 | =C–C=C– (aromatic ring) | |
| 1715 | C=C stretching | –C=C |
| 3200–3650 | O–H stretching | –OH |
| 1000–1300 | C–O stretching | –C–O |
| Number | Model | Reaction Mechanism | g(x) |
|---|---|---|---|
| 1 (F1) | Chemical reaction | n = 1 | −ln(1 − x) |
| 2 (F2) | n = 2 | (1 − x)−1 − 1 | |
| 3 (F3) | n = 3 | [(1 − x)−2 − 1]/2 | |
| 4 (D1) | Diffusion | One-dimensional diffusion | x2 |
| 5 (D2) | Two-dimensional diffusion | (1 − x)ln(1 − x) + x | |
| 6 (D3) | Three-dimensional diffusion (Jander equation) | [1 − (1 − x)1/3]2 | |
| 7 (D4) | Three-dimensional diffusion (Ginstling-Brounshtein equation) | (1 − 2x/3) − (1 − x)2/3 | |
| 8 (A2) | Random nucleation and growth | Two-dimensional | [−ln(1 − x)]1/2 |
| 9 (A3) | Three-dimensional | [−ln(1 − x)]1/3 | |
| 10 (R1) | Interfacial reaction | One-dimensional | x |
| 11 (R2) | Cylindrical symmetry | [1 − (1 − x)1/2] | |
| 12 (R3) | Spherical symmetry | [1 − (1 − x)1/3] | |
| 13 (P2) | Exponential nucleation | Power function, n = 1/2 | x1/2 |
| 14 (P3) | Power function, n = 1/3 | x1/3 | |
| 15 (P4) | Power function, n = 1/4 | x1/4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, J.-L.; Yuan, J.-J. Thermal Decomposition Behavior of Hydroxytyrosol (HT) in Nitrogen Atmosphere Based on TG-FTIR Methods. Molecules 2018, 23, 404. https://doi.org/10.3390/molecules23020404
Tu J-L, Yuan J-J. Thermal Decomposition Behavior of Hydroxytyrosol (HT) in Nitrogen Atmosphere Based on TG-FTIR Methods. Molecules. 2018; 23(2):404. https://doi.org/10.3390/molecules23020404
Chicago/Turabian StyleTu, Jun-Ling, and Jiao-Jiao Yuan. 2018. "Thermal Decomposition Behavior of Hydroxytyrosol (HT) in Nitrogen Atmosphere Based on TG-FTIR Methods" Molecules 23, no. 2: 404. https://doi.org/10.3390/molecules23020404
APA StyleTu, J.-L., & Yuan, J.-J. (2018). Thermal Decomposition Behavior of Hydroxytyrosol (HT) in Nitrogen Atmosphere Based on TG-FTIR Methods. Molecules, 23(2), 404. https://doi.org/10.3390/molecules23020404





