An Explanation about the Use of (S)-Citronellal as a Chiral Derivatizing Agent (CDA) in 1H and 13C NMR for Sec-Butylamine, Methylbenzylamine, and Amphetamine: A Theoretical-Experimental Study
Abstract
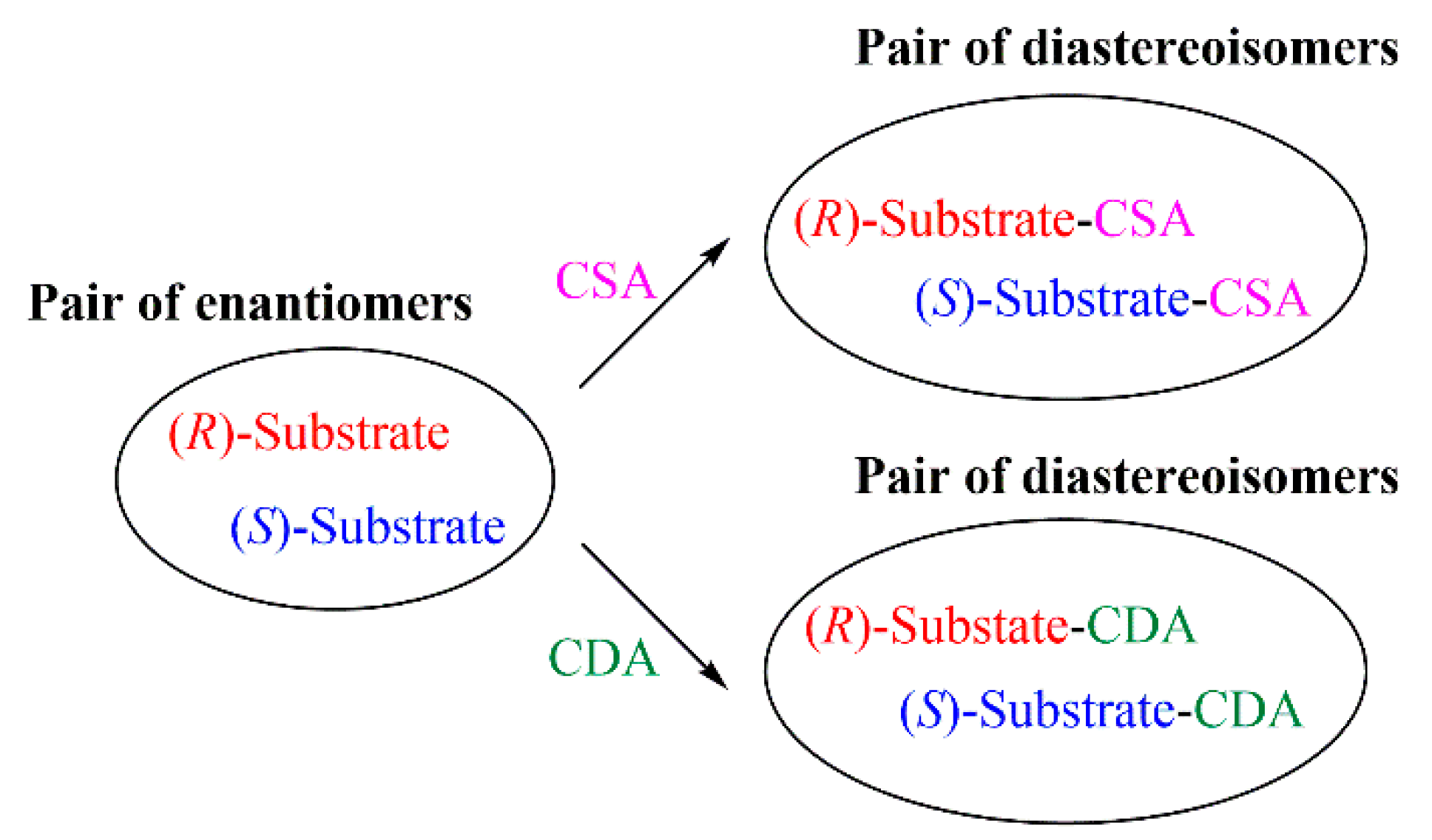
:1. Introduction
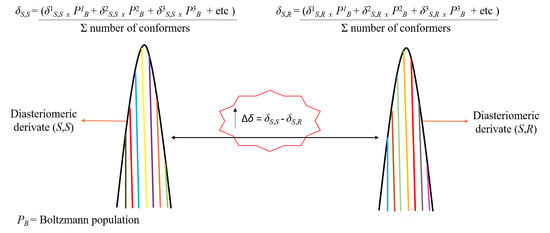
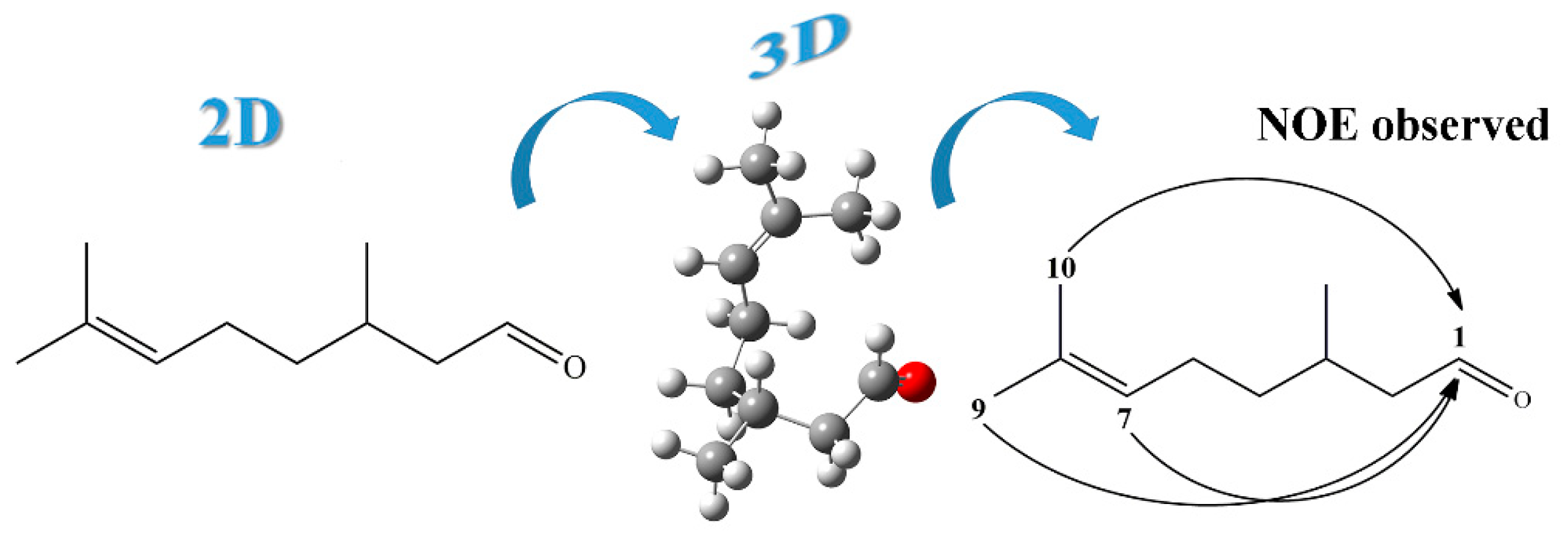
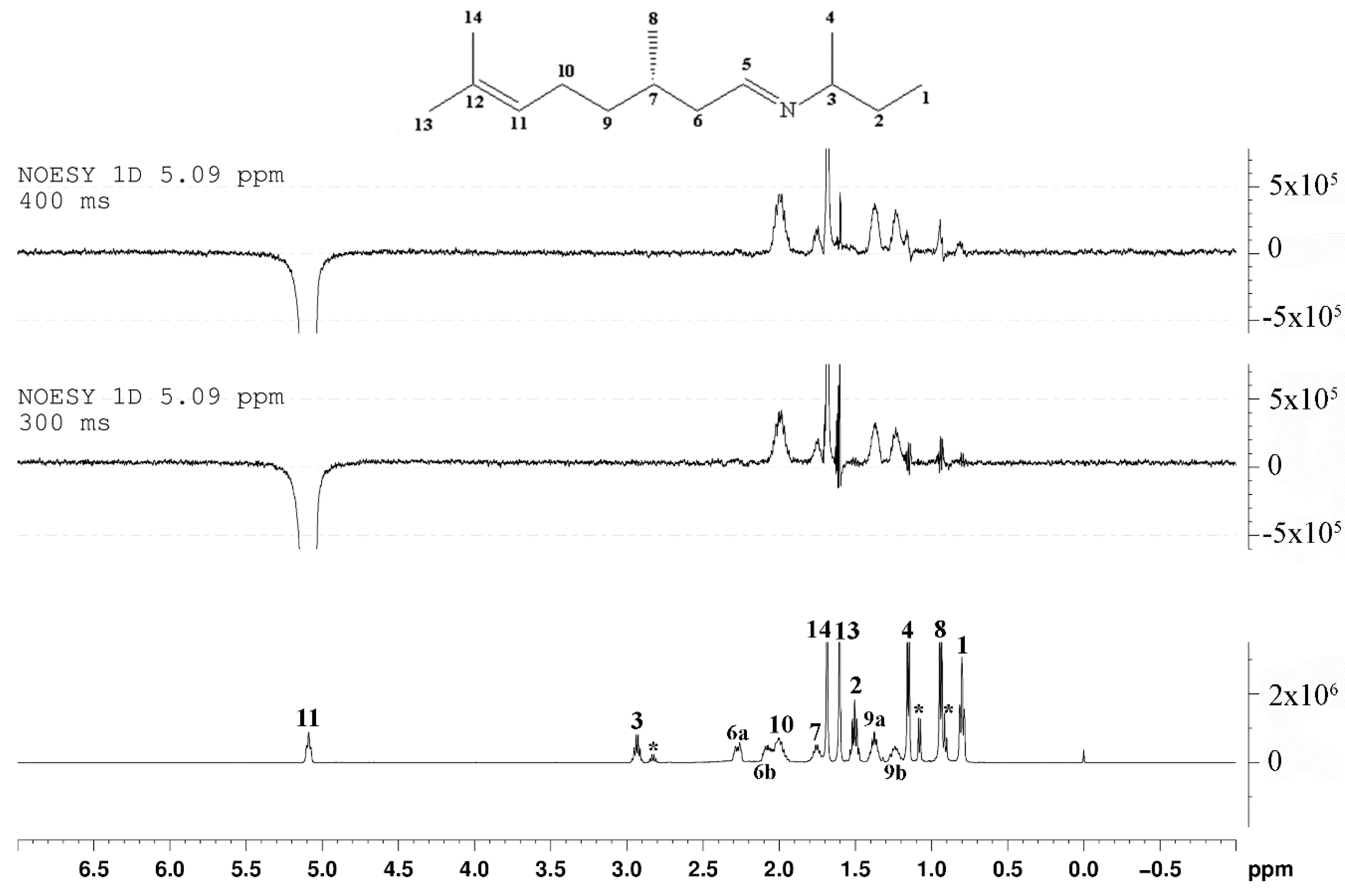
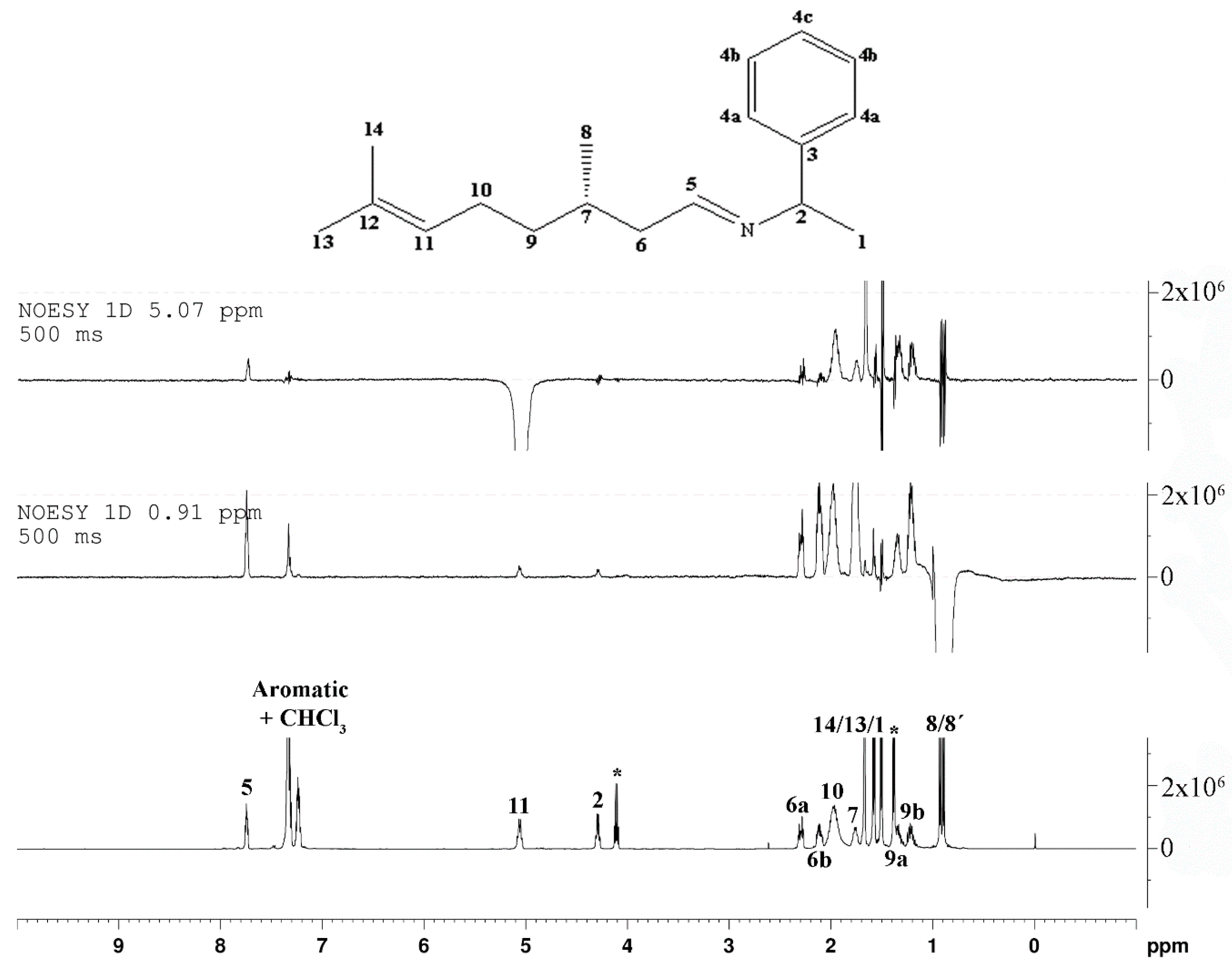
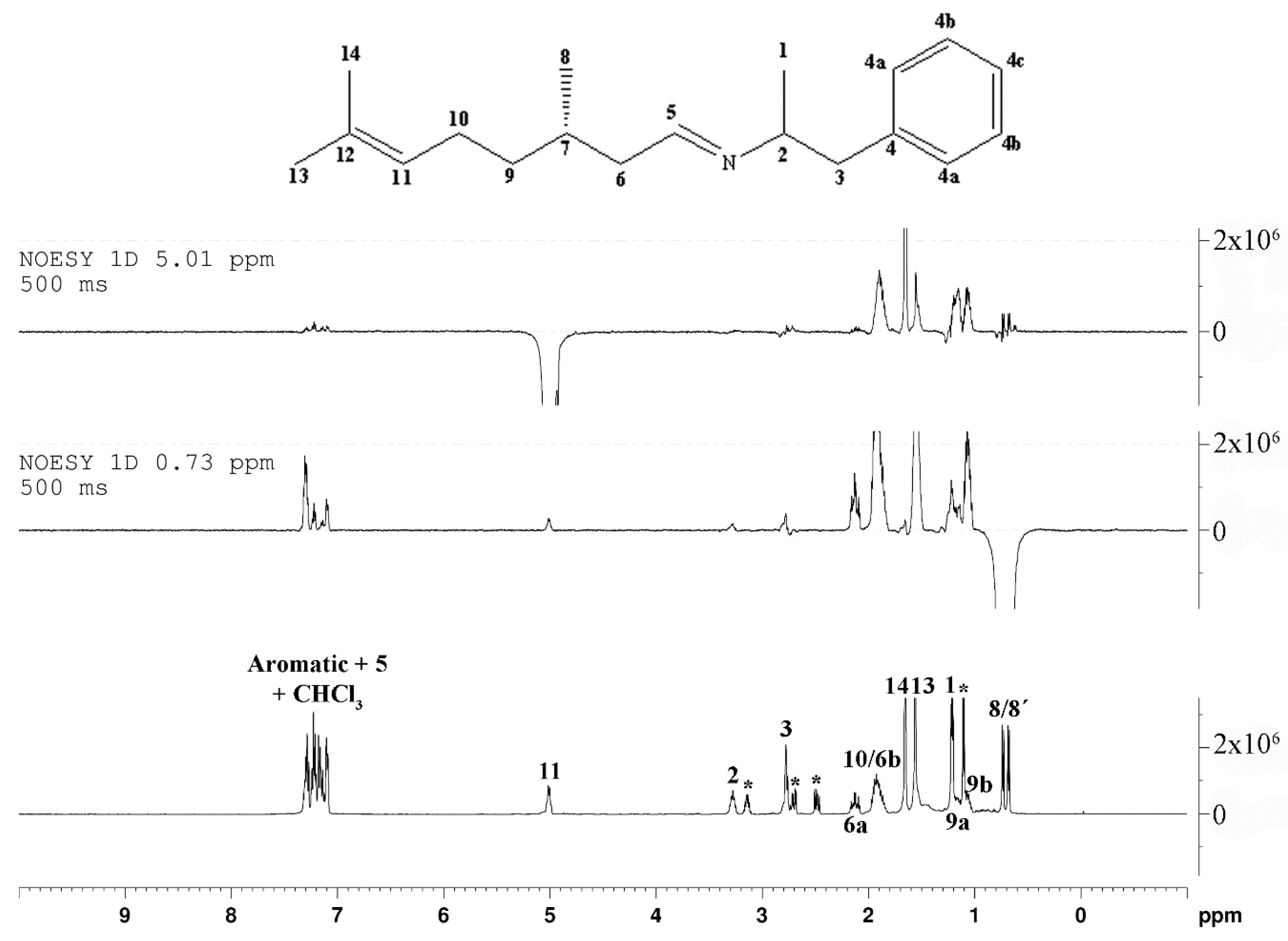
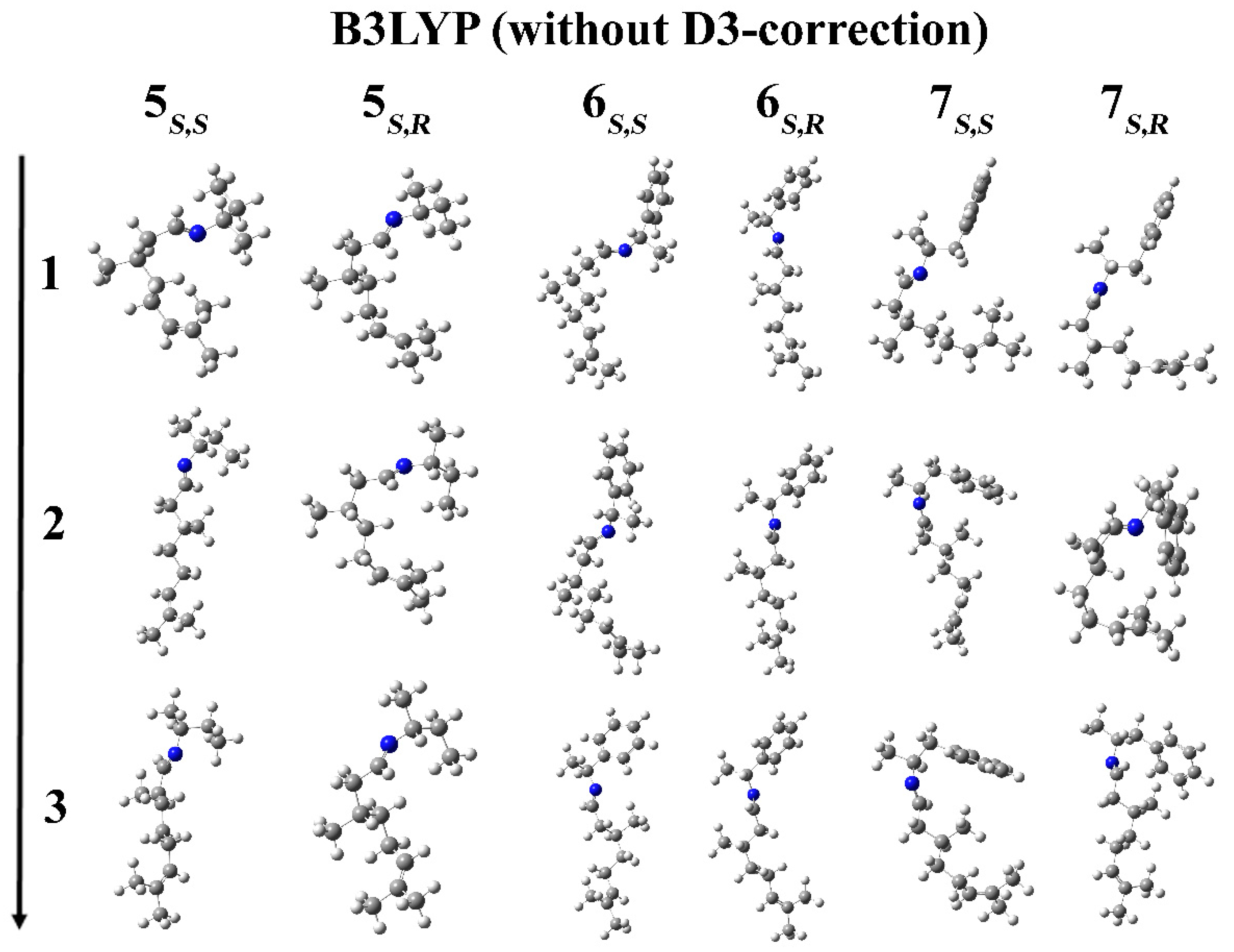
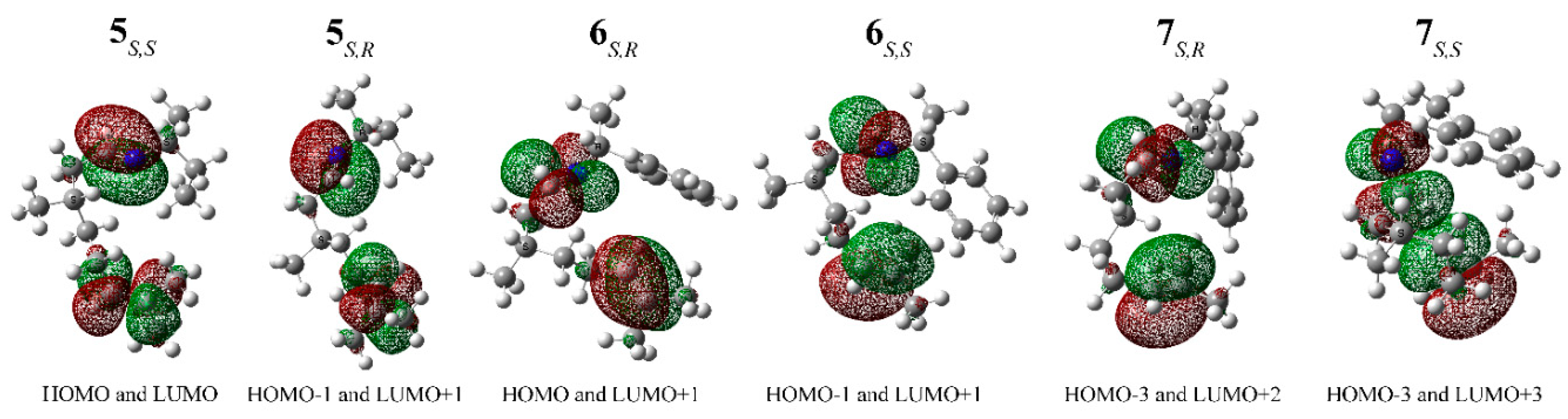
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seco, J.M.; Quiñoá, E.; Riguera, R. The Assignment of Absolute Configuration by NMR. Chem. Rev. 2004, 104, 7–118. [Google Scholar] [CrossRef]
- Dale, J.A.; Mosher, H.S. Nuclear magnetic resonance enantiomer regents. Configurational correlations via nuclear magnetic resonance chemical shifts of diastereomeric mandelate, O-methylmandelate, and α-methoxy-α-trifluoromethylphenylacetate (MTPA) esters. J. Am. Chem. Soc. 1973, 95, 512–519. [Google Scholar] [CrossRef]
- Seco, J.M.; Quiñoá, E.; Riguera, R. The Assignment of the Absolute Configuration by NMR Using Chiral Derivatizing Agents: A Practical Guide, 1st ed.; E.U.A Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Willoughby, P.H.; Jansma, M.J.; Hoye, T.R. A guide to small-molecule structure assignment through computation of (1H and 13C) NMR chemical shifts. Nat. Protoc. 2014, 9, 643–660. [Google Scholar] [CrossRef] [PubMed]
- Ahn, H.C.; Choi, K. Determination of the absolute configuration of primary amines in polar NMR solvents. Chem. Lett. 2007, 36, 1330–1331. [Google Scholar] [CrossRef]
- du Boullay, O.T.; Alba, A.; Oukhatar, F.; Martin-Vaca, B.; Bourissou, D. (1-Naphthyl)(trifluoromethyl) O-Carboxy Anhydride as a Chiral Derivatizing Agent: Eclipsed Conformation Enforced by Hydrogen Bonding. Org. Lett. 2008, 10, 4669–4672. [Google Scholar] [CrossRef] [PubMed]
- Cozzi, P.G. Metal–Salen Schiff base complexes in catalysis: Practical aspects. Chem. Soc. Rev. 2004, 33, 410–421. [Google Scholar] [CrossRef] [PubMed]
- da Silva, C.M.; da Silva, D.L.; Modolo, L.V.; Alves, R.B.; de Resende, M.A.; Martins, C.V.B.; de Fátima, A. Schiff bases: A short review of their antimicrobial activities. J. Adv. Res. 2011, 2, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Nardini, V.; Palaretti, V.; Da Silva, G.V.J. Enantiomeric quantification of amines by 1H and 13C NMR: First report of S-citronellal as chiral derivatization agent (CDA). Microchem. J. 2017, 133, 208–215. [Google Scholar] [CrossRef]
- Nardini, V.; Dias, L.G.; Palaretti, V.; Da Silva, G.V.J. Citronellal assumes a folded conformation in solution due to dispersion interactions: A joint NMR-DFT analysis. J. Mol. Struct. 2017, 1157, 401–407. [Google Scholar] [CrossRef]
- Claridge, T.D.W. High-Resolution in NMR Techniques in Organic Chemistry—Tetrahedron Organic Chemistry, 2nd ed.; Elservier: Amsterdam, The Netherlands, 2009; Volume 27. [Google Scholar]
- Kaiser, C.R. RMN 2D: Detecção Inversa e Gradiente de Campo na Determinação Estrutural de Compostos Orgânicos Quím. Nova 2000, 23, 231–236. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Phys. Chem. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Steinmetz, M. Effects of London dispersion correction in density functional theory on the structures of organic molecules in the gas phase. Phys. Chem. Chem. Phys. 2013, 15, 16031–16042. [Google Scholar] [CrossRef]
- Fukui, K. Role of frontier orbitals in chemical-reactions. Science 1982, 218, 747–754. [Google Scholar] [CrossRef]
- Fukui, K.; Yonezawa, T.; Nagata, C.; Shingu, H. Molecular Orbital Theory of Orientation in Aromatic, Heteroaromatic, and Other Conjugated Molecules. J. Chem. Phys. 1954, 22, 1433–1442. [Google Scholar] [CrossRef] [Green Version]
- Fukui, K.; Yonezawa, T.; Shingu, H. A molecular orbital theory of reactivity in aromatic hydrocarbons. J. Chem. Phys. 1952, 20, 722–725. [Google Scholar] [CrossRef]
- da Silva, R.R.; Ramalho, T.C.; Santos, J.M.; Figueroa-Villar, J.D. On the Limits of Highest-Occupied Molecular Orbital Driven Reactions: The Frontier Effective-for-Reaction Molecular Orbital Concept. J. Chem. Phys. A 2006, 110, 1031–1040. [Google Scholar] [CrossRef]
- da Silva, R.R.; Santos, J.M.; Ramalho, T.C.; Figueroa-Villar, J.D. Concerning the FERMO Concept and Pearson’s Hard and Soft Acid-Base Principle. J. Braz. Chem. Soc. 2006, 17, 223–226. [Google Scholar] [CrossRef]
- Pereira, D.H.; La Porta, F.A.; Santiago, R.T.; Garcia, D.R.; Ramalho, T. Novas Perspectivas sobre o Papel dos Orbitais Moleculares de Fronteira no Estudo Da Reatividade Química: Uma Revisão. Rev. Virtual Quim. 2016, 8, 425–453. [Google Scholar] [CrossRef]
- Gille, A.L.; Dutmer, B.C.; Gilbert, T.M. PCMODEL 9.2. J. Am. Chem. Soc. 2009, 131, 5714. [Google Scholar] [CrossRef]
- Bjorgo, J.; Boyd, D.R.; Watson, C.G.; Jennings, W.B.; Jerina, D.M. E–Z-isomerism in aldimines. J. Chem. Soc. Perkin Trans. 1974, 2, 1081–1084. [Google Scholar] [CrossRef]
- Blanco, F.; Alkorta, I.; Elguero, J. Barriers about Double Carbon-Nitrogen Bond in Imine Derivatives (Aldimines, Oximes, Hydrazones, Azines). Croat. Chem. Acta 2009, 82, 173–183. [Google Scholar]
- Raban, M.; Carlson, E. Syn-anti isomerism in an N-benzenesulfonylimine. Mechanism of stereomutation at the carbon-nitrogen double bond. J. Am. Chem. Soc. 1970, 93, 685–691. [Google Scholar] [CrossRef]
- Neese, F. The ORCA Program System. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchang. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Weitao, Y.; Robert, G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Schaefer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Phys. Chem. 1994, 108, 5829–5835. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Gemmer, J.; Michel, M.; Mahler, G. Quantum Thermodynamics: Emergence of Thermodynamic Behavior within Composite Quantum Systems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Demailly, G.; Solladie, G. Biomimetic polyene cyclizations. asymmetric induction during the acid-catalyzed cyclization of chiral imines. J. Org. Chem. 1981, 46, 3102–3108. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds 5, 6 and 7 are available from the authors. |



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nardini, V.; Palaretti, V.; Dias, L.G.; da Silva, G.V.J. An Explanation about the Use of (S)-Citronellal as a Chiral Derivatizing Agent (CDA) in 1H and 13C NMR for Sec-Butylamine, Methylbenzylamine, and Amphetamine: A Theoretical-Experimental Study. Molecules 2019, 24, 2830. https://doi.org/10.3390/molecules24152830
Nardini V, Palaretti V, Dias LG, da Silva GVJ. An Explanation about the Use of (S)-Citronellal as a Chiral Derivatizing Agent (CDA) in 1H and 13C NMR for Sec-Butylamine, Methylbenzylamine, and Amphetamine: A Theoretical-Experimental Study. Molecules. 2019; 24(15):2830. https://doi.org/10.3390/molecules24152830
Chicago/Turabian StyleNardini, Viviani, Vinicius Palaretti, Luis Gustavo Dias, and Gil Valdo José da Silva. 2019. "An Explanation about the Use of (S)-Citronellal as a Chiral Derivatizing Agent (CDA) in 1H and 13C NMR for Sec-Butylamine, Methylbenzylamine, and Amphetamine: A Theoretical-Experimental Study" Molecules 24, no. 15: 2830. https://doi.org/10.3390/molecules24152830
APA StyleNardini, V., Palaretti, V., Dias, L. G., & da Silva, G. V. J. (2019). An Explanation about the Use of (S)-Citronellal as a Chiral Derivatizing Agent (CDA) in 1H and 13C NMR for Sec-Butylamine, Methylbenzylamine, and Amphetamine: A Theoretical-Experimental Study. Molecules, 24(15), 2830. https://doi.org/10.3390/molecules24152830