Key Electronic, Linear and Nonlinear Optical Properties of Designed Disubstituted Quinoline with Carbazole Compounds
Abstract
:1. Introduction
2. Results and Discussion
2.1. Modeling and Designing of Compounds
2.2. Frontier Molecular Orbital (FMO) Analysis
2.3. Global Reactivity Parameters (GRPs)
2.4. Natural Bond Orbital (NBO) Analysis
2.5. Nonlinear Optical (NLO) Properties
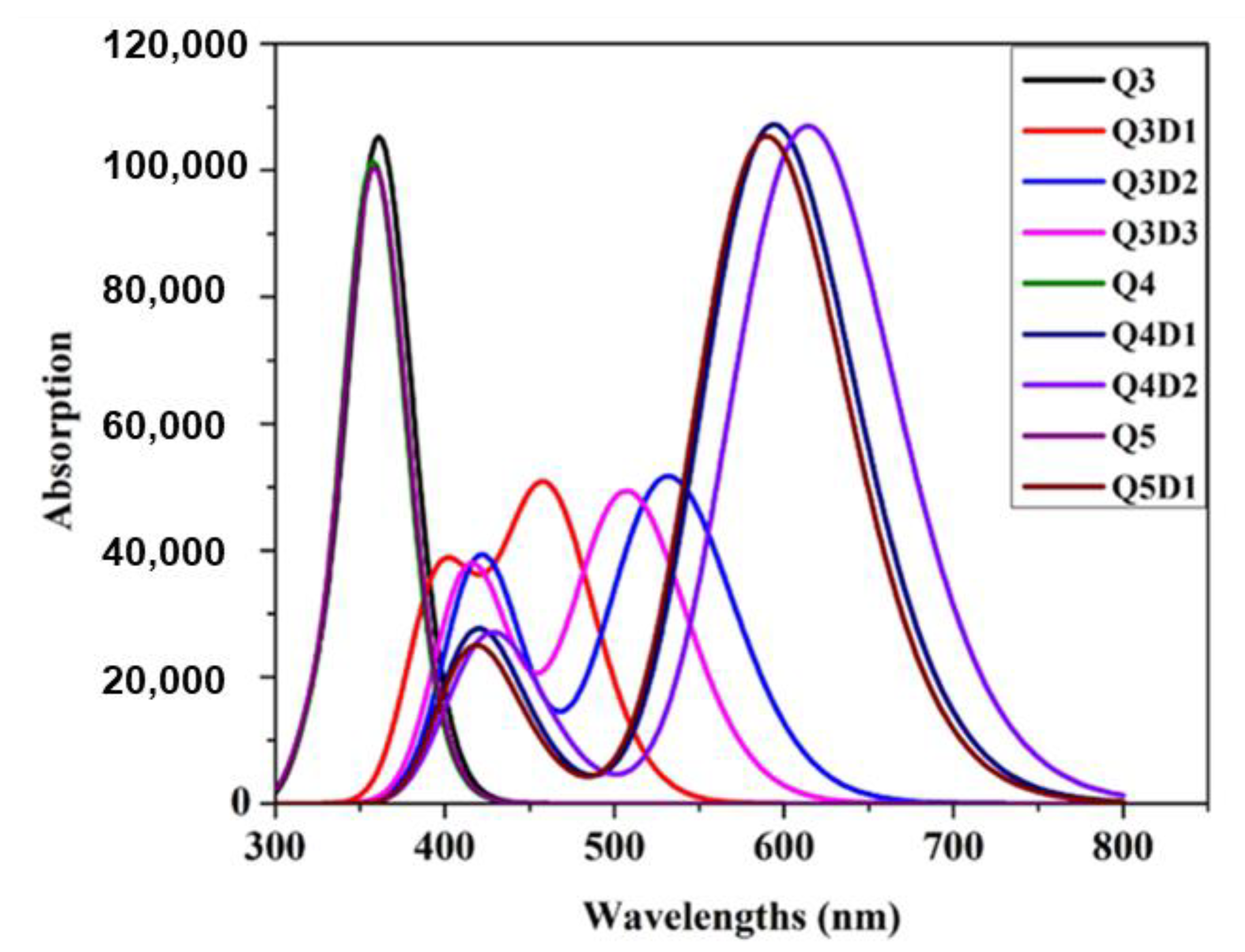
2.6. UV–Vis Spectra Analysis
3. Computational Procedure
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Ghiasuddin; Akram, M.; Adeel, M.; Khalid, M.; Tahir, M.N.; Khan, M.U.; Asghar, M.A.; Ullah, M.A.; Iqbal, M. A combined experimental and computational study of 3-bromo-5-(2,5-difluorophenyl) pyridine and 3,5-bis(naphthalen-1-yl)pyridine: Insight into the synthesis, spectroscopic, single crystal XRD, electronic, nonlinear optical and biological properties. J. Mol. Struct. 2018, 1160, 129–141. [Google Scholar] [CrossRef]
- Ahmad, M.S.; Khalid, M.; Shaheen, M.A.; Tahir, M.N.; Khan, M.U.; Braga, A.A.C.; Shad, H.A. Synthesis and XRD, FT-IR vibrational, UV–vis, and nonlinear optical exploration of novel tetra substituted imidazole derivatives: A synergistic experimental-computational analysis. J. Phys. Chem. Solids 2018, 115, 265–276. [Google Scholar] [CrossRef]
- Shahid, M.; Salim, M.; Khalid, M.; Tahir, M.N.; Khan, M.U.; Braga, A.A.C. Synthetic, XRD, non-covalent interactions and solvent dependent nonlinear optical studies of Sulfadiazine-Ortho-Vanillin Schiff base: (E)-4-((2-hydroxy-3-methoxy- benzylidene) amino)-N-(pyrimidin-2-yl)benzene-sulfonamide. J. Mol. Struct. 2018, 1161, 66–75. [Google Scholar] [CrossRef]
- Jawaria, R.; Hussain, M.; Khalid, M.; Khan, M.U.; Tahir, M.N.; Naseer, M.M.; Braga, A.A.C.; Shafiq, Z. Synthesis, crystal structure analysis, spectral characterization and nonlinear optical exploration of potent thiosemicarbazones based compounds: A DFT refine experimental study. Inorg. Chim. Acta 2019, 486, 162–171. [Google Scholar] [CrossRef]
- Khalid, M.; Ullah, M.A.; Adeel, M.; Khan, M.U.; Tahir, M.N.; Braga, A.A.C. Synthesis, crystal structure analysis, spectral IR, UV–Vis, NMR assessments, electronic and nonlinear optical properties of potent quinoline based derivatives: Interplay of experimental and DFT study. J. Saudi Chem. Soc. 2019, 23, 546–560. [Google Scholar] [CrossRef]
- Tahir, M.N.; Mirza, S.H.; Khalid, M.; Ali, A.; Khan, M.U.; Braga, A.A.C. Synthesis, single crystal analysis and DFT based computational studies of 2,4-diamino-5-(4-chlorophenyl)-6-ethylpyrim idin-1-ium 3,4,5-trihydroxybenzoate -methanol (DETM). J. Mol. Struct. 2019, 1180, 119–126. [Google Scholar] [CrossRef]
- Hales, J.M.; Cozzuol, M.; Screen, T.E.O.; Anderson, H.L.; Perry, J.W. Metalloporphyrin polymer with temporally agile, broadband nonlinear absorption for optical limiting in the near infrared. Opt. Express 2009, 17, 18478–18488. [Google Scholar] [CrossRef] [PubMed]
- He, G.S.; Tan, L.-S.; Zheng, A.Q.; Prasad, P.N. Multiphoton Absorbing Materials: Molecular Designs, Characterizations, and Applications. Chem. Rev. 2008, 108, 1245–1330. [Google Scholar] [CrossRef]
- Pawlicki, M.; Collins, H.A.; Denning, R.G.; Anderson, H.L. Two-Photon Absorption and the Design of Two-Photon Dyes. Angew. Chem. Int. Ed. 2009, 48, 3244–3266. [Google Scholar] [CrossRef]
- Jiang, D.; Chen, S.; Xue, Z.; Li, Y.; Liu, H.; Yang, W.; Li, Y. Donor–acceptor molecules based on benzothiadiazole: Synthesis, X-ray crystal structures, linear and third-order nonlinear optical properties. Dye. Pigment. 2016, 125, 100–105. [Google Scholar] [CrossRef]
- Tang, C.; Zheng, Q.; Zhu, H.; Wang, L.; Chen, S.-C.; Ma, E.; Chen, X. Two-photon absorption and optical power limiting properties of ladder-type tetraphenylene cored chromophores with different terminal groups. J. Mater. Chem. C 2013, 1, 1771–1780. [Google Scholar] [CrossRef]
- Garmire, E. Nonlinear optics in daily life. Opt. Express 2013, 21, 30532–30544. [Google Scholar] [CrossRef]
- Halasyamani, P.S.; Zhang, W. Viewpoint: Inorganic Materials for UV and Deep-UV Nonlinear-Optical Applications. Inorg. Chem. 2017, 56, 12077–12085. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Shi, G.; Yang, Z.; Zhang, F.; Pan, S. Fluorooxoborates: Beryllium-Free Deep-Ultraviolet Nonlinear Optical Materials without Layered Growth. Angew. Chem. Int. Ed. 2017, 56, 3916–3919. [Google Scholar] [CrossRef]
- Yamashita, S. A Tutorial on Nonlinear Photonic Applications of Carbon Nanotube and Graphene. J. Light. Technol. 2011, 30, 427–447. [Google Scholar] [CrossRef]
- Guo, L.; Guo, Z.; Li, X. Design and preparation of side chain electro-optic polymeric materials based on novel organic second order nonlinear optical chromophores with double carboxyl groups. J. Mater. Sci. Mater. Electron. 2017, 29, 2577–2584. [Google Scholar] [CrossRef]
- Fonseca, R.D.; Vivas, M.G.; Silva, D.L.; Eucat, G.; Bretonnière, Y.; Andraud, C.; De Boni, L.; Mendonça, C.R. First-Order Hyperpolarizability of Triphenylamine Derivatives Containing Cyanopyridine: Molecular Branching Effect. J. Phys. Chem. C 2018, 122, 1770–1778. [Google Scholar] [CrossRef]
- Chen, W.; Tian, K.; Song, X.; Zhang, Z.; Ye, K.; Yu, G.; Wang, Y. Large π-Conjugated Quinacridone Derivatives: Syntheses, Characterizations, Emission, and Charge Transport Properties. Org. Lett. 2015, 17, 6146–6149. [Google Scholar] [CrossRef] [PubMed]
- Sung, P.-H.; Hsu, T.-F. Thermal stability of NLO sol—gel networks with reactive chromophores. Polymer 1998, 39, 1453–1459. [Google Scholar] [CrossRef]
- Hochberg, M.; Baehr-Jones, T.; Wang, G.; Shearn, M.; Harvard, K.; Luo, J.; Chen, B.; Shi, Z.; Lawson, R.; Sullivan, P.; et al. Terahertz all-optical modulation in a silicon–polymer hybrid system. Nat. Mater. 2006, 5, 703–709. [Google Scholar] [CrossRef] [Green Version]
- Zych, D.; Slodek, A.; Matussek, M.; Filapek, M.; Szafraniec-Gorol, G.; Krompiec, S.; Kotowicz, S.; Siwy, M.; Schab-Balcerzak, E.; Bednarczyk, K. Highly Luminescent 4′-(4-ethynylphenyl)-2, 2′: 6′, 2″-Terpyridine Derivatives as Materials for Potential Applications in Organic Light Emitting Diodes. ChemistrySelect 2017, 2, 8221–8233. [Google Scholar] [CrossRef]
- Khalid, M.; Hussain, R.; Hussain, A.; Ali, B.; Jaleel, F.; Imran, M.; Assiri, M.A.; Khan, M.U.; Ahmed, S.; Abid, S.; et al. Electron Donor and Acceptor Influence on the Nonlinear Optical Response of Diacetylene-Functionalized Organic Materials (DFOMs): Density Functional Theory Calculations. Molecules 2019, 24, 2096. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khan, M.U.; Khalid, M.; Ibrahim, M.; Braga, A.A.C.; Safdar, M.; Al-Saadi, A.A.; Janjua, M.R.S.A. First Theoretical Framework of Triphenylamine–Dicyanovinylene-Based Nonlinear Optical Dyes: Structural Modification of π-Linkers. J. Phys. Chem. C 2018, 122, 4009–4018. [Google Scholar] [CrossRef]
- Janjua, M.R.S.A.; Khan, M.U.; Bashir, B.; Iqbal, M.A.; Song, Y.; Naqvi, S.A.R.; Khan, Z.A. Effect of π-conjugation spacer (C C) on the first hyperpolarizabilities of polymeric chain containing polyoxometalate cluster as a side-chain pendant: A DFT study. Comput. Theor. Chem. 2012, 994, 34–40. [Google Scholar] [CrossRef]
- Janjua, M.R.S.A.; Amin, M.; Ali, M.A.; Bashir, B.; Khan, M.U.; Iqbal, M.A.; Guan, W.; Yan, L.; Su, Z.-M. A DFT Study on The Two-Dimensional Second-Order Nonlinear Optical (NLO) Response of Terpyridine-Substituted Hexamolybdates: Physical Insight on 2D Inorganic-Organic Hybrid Functional Materials. Eur. J. Inorg. Chem. 2012, 2012, 705–711. [Google Scholar] [CrossRef]
- Khan, M.U.; Ibrahim, M.; Khalid, M.; Qureshi, M.S.; Gulzar, T.; Zia, K.M.; Al-Saadi, A.A.; Janjua, M.R.S.A. First theoretical probe for efficient enhancement of nonlinear optical properties of quinacridone based compounds through various modifications. Chem. Phys. Lett. 2019, 715, 222–230. [Google Scholar] [CrossRef]
- Khan, M.U.; Ibrahim, M.; Khalid, M.; Braga, A.A.C.; Ahmed, S.; Sultan, A. Prediction of Second-Order Nonlinear Optical Properties of D–π–A Compounds Containing Novel Fluorene Derivatives: A Promising Route to Giant Hyperpolarizabilities. J. Clust. Sci. 2019, 30, 415–430. [Google Scholar] [CrossRef]
- Khan, B.; Khalid, M.; Shah, M.R.; Tahir, M.N.; Khan, M.U.; Ali, A.; Muhammad, S. Efficient Synthesis by Mono-Carboxy Methylation of 4, 4′-Biphenol, X-ray Diffraction, Spectroscopic Characterization and Computational Study of the Crystal Packing of Ethyl 2-((4′-hydroxy-[1,1′-biphenyl]-4-yl) oxy) acetate. ChemistrySelect 2019, 4, 9274–9284. [Google Scholar] [CrossRef]
- Roy, R.S.; Nandi, P.K. Exploring bridging effect on first hyperpolarizability. RSC Adv. 2015, 5, 103729–103738. [Google Scholar] [CrossRef]
- Wielopolski, M.; Kim, J.-H.; Jung, Y.-S.; Yu, Y.-J.; Kay, K.-Y.; Holcombe, T.W.; Zakeeruddin, S.M.; Grätzel, M.; Moser, J.-E. Position-Dependent Extension of π-Conjugation in D-π-A Dye Sensitizers and the Impact on the Charge-Transfer Properties. J. Phys. Chem. C 2013, 117, 13805–13815. [Google Scholar] [CrossRef] [Green Version]
- Katono, M.; Wielopolski, M.; Marszalek, M.; Bessho, T.; Moser, J.-E.; Humphry-Baker, R.; Zakeeruddin, S.M.; Grätzel, M. Effect of extended π-conjugation of the donor structure of organic D–A− π–A dyes on the photovoltaic performance of dye-Sensitized solar cells. J. Phys. Chem. C 2014, 118, 16486–16493. [Google Scholar] [CrossRef] [Green Version]
- Panneerselvam, M.; Kathiravan, A.; Solomon, R.V.; Jaccob, M. The role of π-linkers in tuning the optoelectronic properties of triphenylamine derivatives for solar cell applications—A DFT/TDDFT study. Phys. Chem. Chem. Phys. 2017, 19, 6153–6163. [Google Scholar] [CrossRef] [PubMed]
- Namuangruk, S.; Fukuda, R.; Ehara, M.; Meeprasert, J.; Khanasa, T.; Morada, S.; Kaewin, T.; Jungsuttiwong, S.; Sudyoadsuk, T.; Promarak, V. D–D−π–A-Type Organic Dyes for Dye-Sensitized Solar Cells with a Potential for Direct Electron Injection and a High Extinction Coefficient: Synthesis, Characterization, and Theoretical Investigation. J. Phys. Chem. C 2012, 116, 25653–25663. [Google Scholar] [CrossRef]
- Khalid, M.; Ali, A.; Jawaria, R.; Asghar, M.A.; Asim, S.; Khan, M.U.; Hussain, R.; Rehman, M.F.U.; Ennis, C.J.; Akram, M.S. First principles study of electronic and nonlinear optical properties of A–D–π–A and D–A–D–π–A configured compounds containing novel quinoline–carbazole derivatives. RSC Adv. 2020, 10, 22273–22283. [Google Scholar] [CrossRef]
- Sych, G.; Volyniuk, D.; Bezvikonnyi, O.; Lytvyn, R.; Grazulevicius, J.V. Dual Interface Exciplex Emission of Quinoline and Carbazole Derivatives for Simplified Nondoped White OLEDs. J. Phys. Chem. C 2019, 123, 2386–2397. [Google Scholar] [CrossRef]
- Mao, M.; Zhang, X.; Zhu, B.; Wang, J.; Wu, G.; Yin, Y.; Song, Q. Comparative studies of organic dyes with a quinazoline or quinoline chromophore as π-conjugated bridges for dye-sensitized solar cells. Dye. Pigment. 2016, 124, 72–81. [Google Scholar] [CrossRef]
- Aivali, S.; Tsimpouki, L.; Anastasopoulos, C.; Kallitsis, J.K. Synthesis and Optoelectronic Characterization of Perylene Diimide-Quinoline Based Small Molecules. Molecules 2019, 24, 4406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeyada, H.; El-Nahass, M.; El-Shabaan, M. Photovoltaic properties of the 4H-pyrano[3,2-c]quinoline derivatives and their applications in organic–inorganic photodiode fabrication. Synth. Met. 2016, 220, 102–113. [Google Scholar] [CrossRef]
- Kotowicz, S.; Siwy, M.; Filapek, M.; Malecki, J.G.; Smolarek, K.; Grzelak, J.; Mackowski, S.; Slodek, A.; Schab-Balcerzak, E. New donor-acceptor-donor molecules based on quinoline acceptor unit with Schiff base bridge: Synthesis and characterization. J. Lumin. 2017, 183, 458–469. [Google Scholar] [CrossRef]
- Bhattacharjee, I.; Acharya, N.; Bhatia, H.; Ray, D. Dual Emission through Thermally Activated Delayed Fluorescence and Room-Temperature Phosphorescence, and Their Thermal Enhancement via Solid-State Structural Change in a Carbazole-Quinoline Conjugate. J. Phys. Chem. Lett. 2018, 9, 2733–2738. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, C.; Peng, J.; Li, M. Copper(II)-Catalyzed Three-Component Cascade Annulation of Diaryliodoniums, Nitriles, and Alkynes: A Regioselective Synthesis of Multiply Substituted Quinolines. Angew. Chem. Int. Ed. 2013, 52, 5323–5327. [Google Scholar] [CrossRef] [PubMed]
- Ji, X.; Huang, H.; Li, Y.; Chen, H.; Jiang, H. Palladium-Catalyzed Sequential Formation of C-C Bonds: Efficient Assembly of 2-Substituted and 2, 3-Disubstituted Quinolines. Angew. Chem. Int. Ed. 2012, 51, 7292–7296. [Google Scholar] [CrossRef]
- Al-Busafi, S.N.; Suliman, F.O.; Al-Alawi, Z.R. Synthesis, characterization and electronic effects investigations of new 5,7-disubstituted tris(8-quinolinolate)Al(III) complexes. Dye. Pigment. 2014, 103, 138–144. [Google Scholar] [CrossRef]
- Kiymaz, D.; Sezgin, M.; Sefer, E.; Zafer, C.; Koyuncu, S. Carbazole based DA-π-A chromophores for dye sensitized solar cells: Effect of the side alkyl chain length on device performance. Int. J. Hydrogen Energy 2017, 42, 8569–8575. [Google Scholar] [CrossRef]
- Slodek, A.; Zych, D.; Maroń, A.; Malecki, J.G.; Golba, S.; Szafraniec-Gorol, G.; Pajak, M. Does the length matter?—Synthesis, photophysical, and theoretical study of novel quinolines based on carbazoles with different length of alkyl chain. Dye. Pigment. 2019, 160, 604–613. [Google Scholar] [CrossRef]
- Khan, M.U.; Iqbal, J.; Khalid, M.; Hussain, R.; Braga, A.A.C.; Hussain, M.; Muhammad, S. Designing triazatruxene-based donor materials with promising photovoltaic parameters for organic solar cells. RSC Adv. 2019, 9, 26402–26418. [Google Scholar] [CrossRef] [Green Version]
- Janjua, M.R.S.A.; Khan, M.U.; Khalid, M.; Ullah, N.; Kalgaonkar, R.; Alnoaimi, K.; Baqader, N.; Jamil, S. Theoretical and Conceptual Framework to Design Efficient Dye-Sensitized Solar Cells (DSSCs): Molecular Engineering by DFT Method. J. Clust. Sci. 2021, 32, 243–253. [Google Scholar] [CrossRef]
- Amiri, S.S.; Makarem, S.; Ahmar, H.; Ashenagar, S. Theoretical studies and spectroscopic characterization of novel 4-methyl-5-((5-phenyl-1,3,4-oxadiazol-2-yl)thio)benzene-1,2-diol. J. Mol. Struct. 2016, 1119, 18–24. [Google Scholar] [CrossRef]
- Klopman, G. Chemical reactivity and the concept of charge- and frontier-controlled reactions. J. Am. Chem. Soc. 1968, 90, 223–234. [Google Scholar] [CrossRef]
- Hussain, A.; Khan, M.U.; Ibrahim, M.; Khalid, M.; Ali, A.; Hussain, S.; Saleem, M.; Ahmad, N.; Muhammad, S.; Al-Sehemi, A.G.; et al. Structural parameters, electronic, linear and nonlinear optical exploration of thiopyrimidine derivatives: A comparison between DFT/TDDFT and experimental study. J. Mol. Struct. 2020, 1201, 127183. [Google Scholar] [CrossRef]
- Qin, C.; Clark, A.E. DFT characterization of the optical and redox properties of natural pigments relevant to dye-sensitized solar cells. Chem. Phys. Lett. 2007, 438, 26–30. [Google Scholar] [CrossRef]
- Khalid, M.; Ali, A.; Rehman, M.F.; Mustaqeem, M.; Ali, S.; Khan, M.U.; Asim, S.; Ahmad, N.; Saleem, M. Exploration of Noncovalent Interactions, Chemical Reactivity, and Nonlinear Optical Properties of Piperidone Derivatives: A Concise Theoretical Approach. ACS Omega 2020, 5, 13236–13249. [Google Scholar] [CrossRef]
- Kanis, D.R.; Ratner, M.A.; Marks, T.J. Design and construction of molecular assemblies with large second-order optical nonlinearities. Quantum chemical aspects. Chem. Rev. 1994, 94, 195–242. [Google Scholar] [CrossRef]
- Nalwa, H.S. Handbook of Advanced Electronic and Photonic Materials and Devices: Semiconductors; Academic Press: Cambridge, MA, USA, 2001; Volume 1. [Google Scholar]
- Oudar, J.L.; Chemla, D.S. Hyperpolarizabilities of the nitroanilines and their relations to the excited state dipole moment. J. Chem. Phys. 1977, 66, 2664–2668. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.; et al. D. 0109, Revision D. 01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Dennington, R.D.; Keith, T.A.; Millam, J.M. GaussView 5.0. 8; Gaussian Inc.: Wallingford, CT, USA, 2008. [Google Scholar]
- Karakaş, A.; Elmali, A.; Ünver, H. Linear optical transmission measurements and computational study of linear polarizabilities, first hyperpolarizabilities of a dinuclear iron(III) complex. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2007, 68, 567–572. [Google Scholar] [CrossRef] [PubMed]
- Parr, R.G.; Szentpály, L.V.; Liu, S. Electrophilicity Index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Parr, R.G.; Donnelly, R.A.; Levy, M.; Palke, W.E. Electronegativity: The density functional viewpoint. J. Chem. Phys. 1978, 68, 3801–3807. [Google Scholar] [CrossRef]
- Chattaraj, P.K.; Sarkar, A.U.; Roy, D.R. Electrophilicity Index. Chem. Rev. 2006, 106, 2065–2091. [Google Scholar] [CrossRef]
- Lesar, A.; Milošev, I. Density functional study of the corrosion inhibition properties of 1,2,4-triazole and its amino derivatives. Chem. Phys. Lett. 2009, 483, 198–203. [Google Scholar] [CrossRef]
- Sheela, N.; Muthu, S.; Sampathkrishnan, S. Molecular orbital studies (hardness, chemical potential and electrophilicity), vibrational investigation and theoretical NBO analysis of 4-4′-(1H-1,2,4-triazol-1-yl methylene) dibenzonitrile based on abinitio and DFT methods. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2014, 120, 237–251. [Google Scholar] [CrossRef]


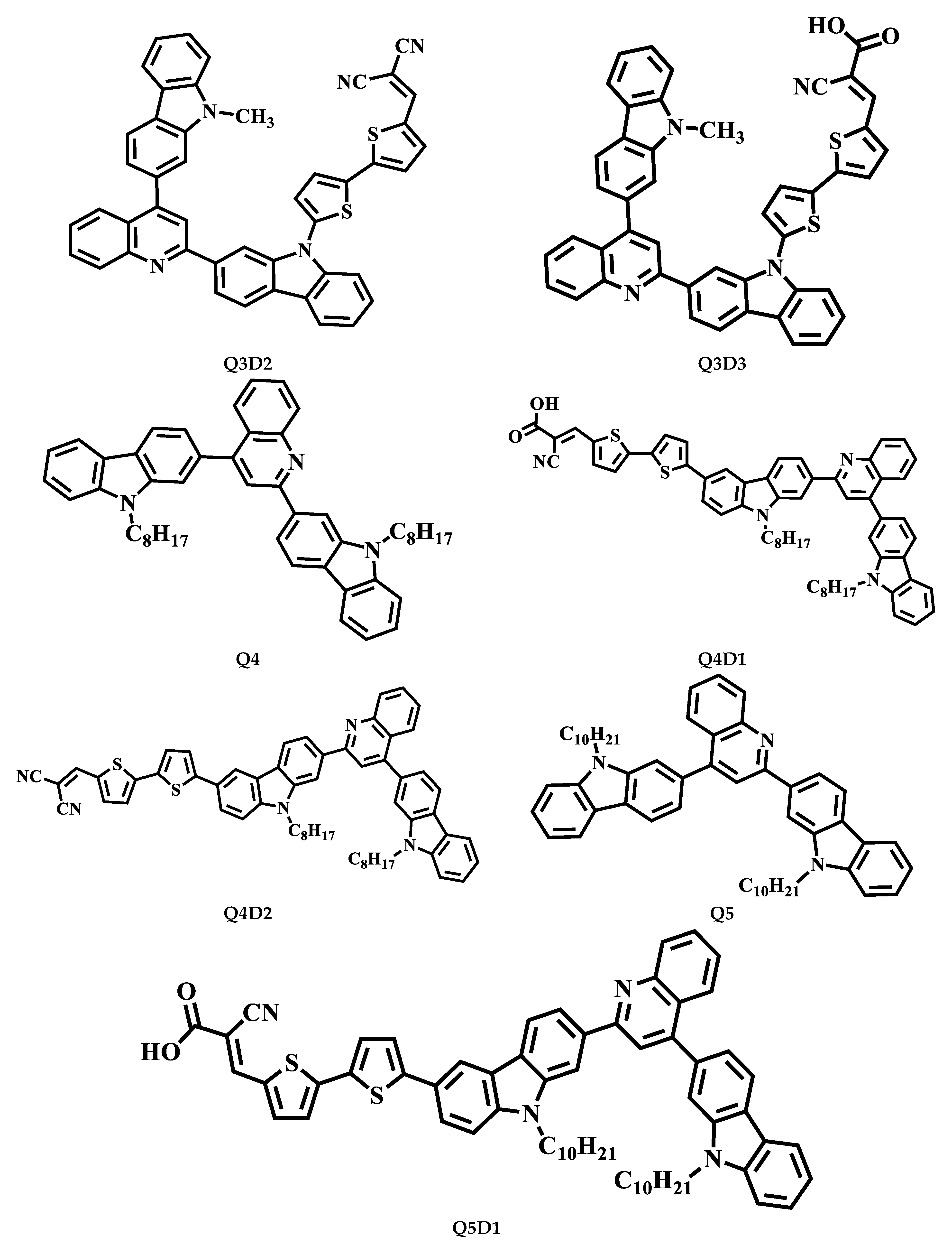
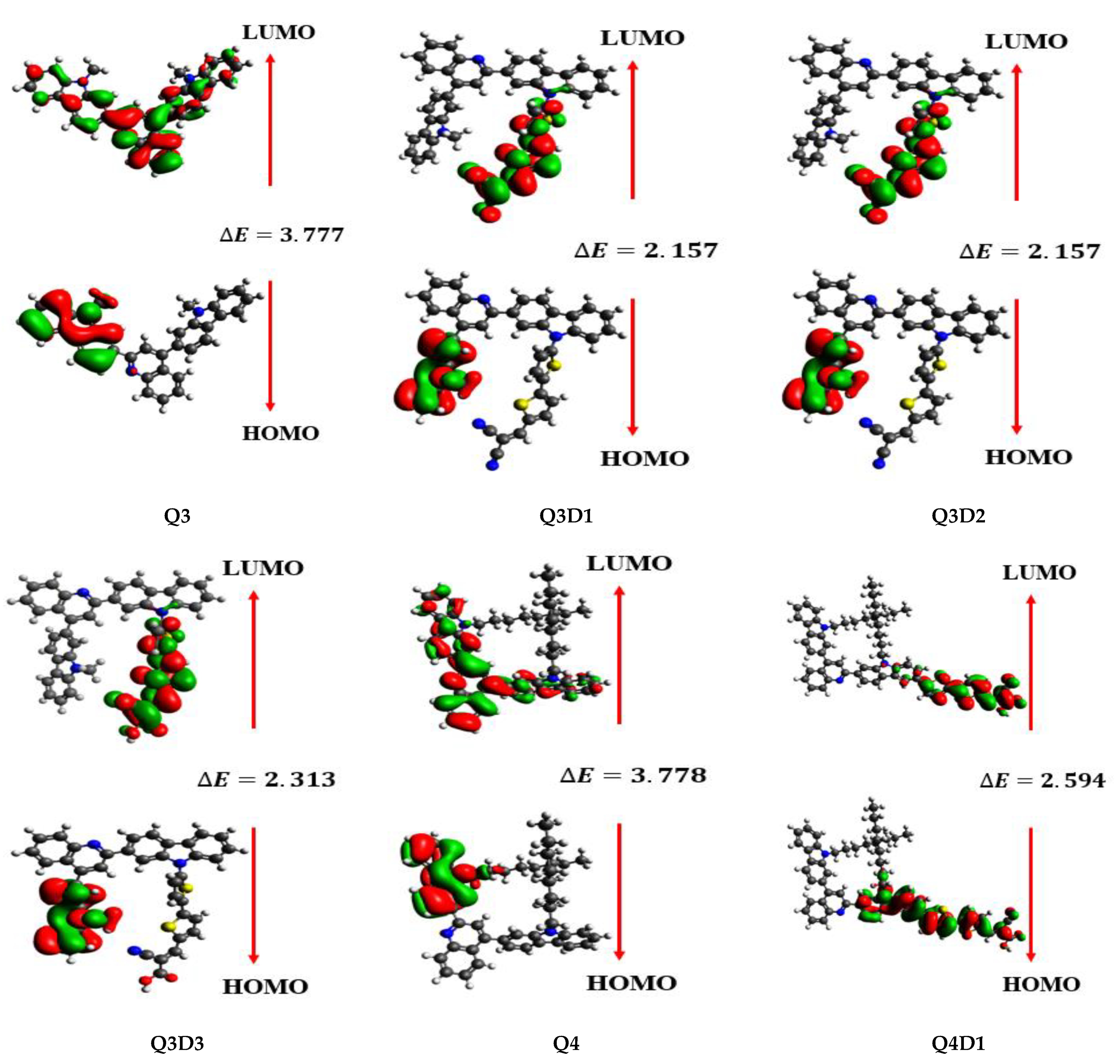
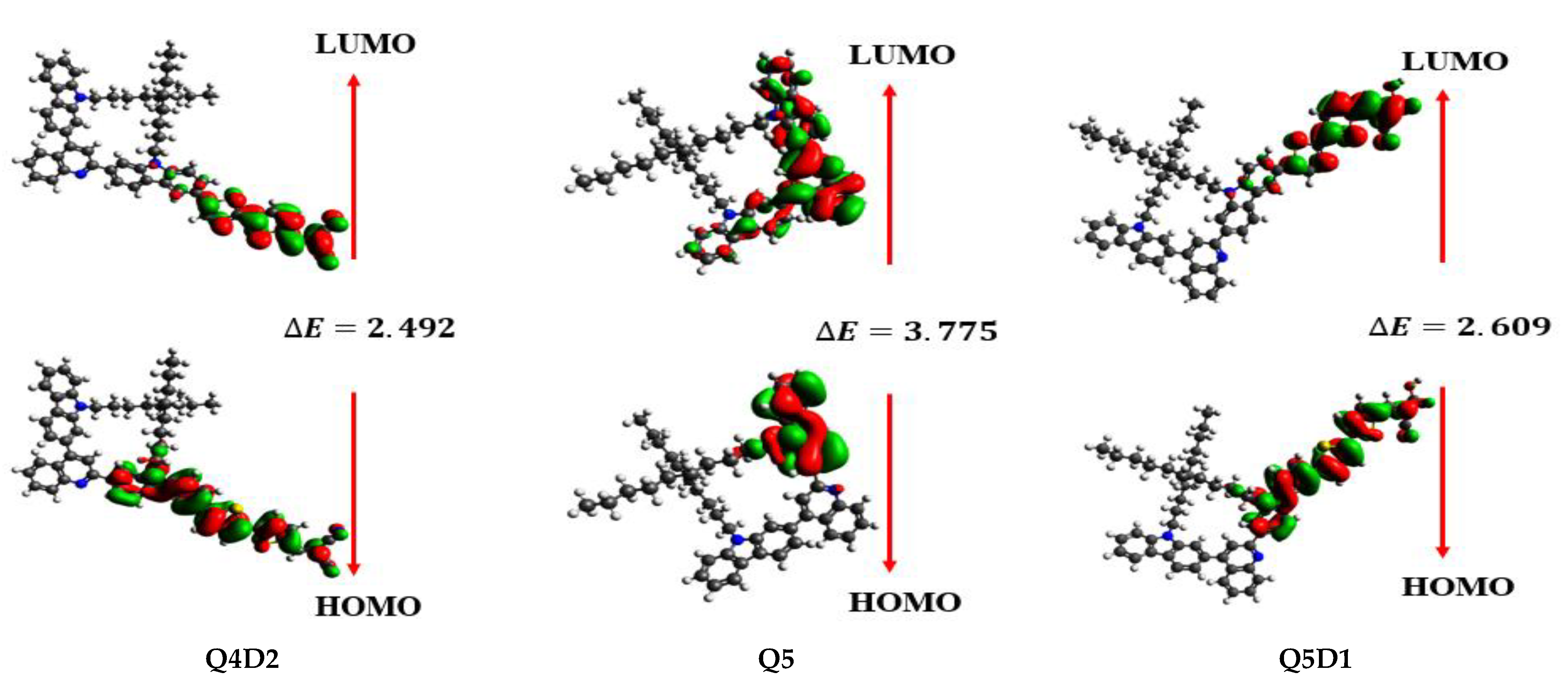
| Compounds | E(HOMO) | E(LUMO) | Bandgap (ELUMO–EHOMO) |
|---|---|---|---|
| Q3 | -5.593 | −1.816 | 3.777 |
| Q3D1 | −5.828 | −2.781 | 3.047 |
| Q3D2 | −5.598 | −3.441 | 2.157 |
| Q3D3 | −5.535 | −3.222 | 2.313 |
| Q4 | −5.546 | −1.768 | 3.778 |
| Q4D1 | −5.522 | −2.928 | 2.594 |
| Q4D2 | −5.618 | −3.126 | 2.492 |
| Q5 | −5.540 | −1.765 | 3.775 |
| Q5D1 | −5.488 | −2.879 | 2.609 |
| Compounds | I | A | X | η | μ | ω | S |
|---|---|---|---|---|---|---|---|
| Q3 | 5.593 | 1.816 | 3.704 | 1.888 | −3.704 | 3.633 | 0.2647 |
| Q3D1 | 5.828 | 2.781 | 4.304 | 1.523 | −4.304 | 6.080 | 0.3280 |
| Q3D2 | 5.598 | 3.441 | 4.519 | 1.078 | −4.519 | 9.469 | 0.4630 |
| Q3D3 | 5.535 | 3.222 | 4.378 | 1.156 | −4.378 | 8.288 | 0.4320 |
| Q4 | 5.546 | 1.768 | 3.655 | 1.889 | −3.657 | 3.539 | 0.2646 |
| Q4D1 | 5.522 | 2.928 | 4.225 | 1.297 | −4.225 | 6.881 | 0.3850 |
| Q4D2 | 5.618 | 3.126 | 4.372 | 1.246 | −4.372 | 7.670 | 0.4010 |
| Q5 | 5.540 | 1.765 | 3.652 | 1.887 | −3.652 | 3.533 | 0.2649 |
| Q5D1 | 5.488 | 2.879 | 4.183 | 1.304 | −4.183 | 6.708 | 0.3830 |
| Systems | αxx | αyy | αzz | <α> |
|---|---|---|---|---|
| Q3 | 672.576 | 539.206 | 221.601 | 477.794 |
| Q3D1 | 993.607 | 751.135 | 324.147 | 689.629 |
| Q3D2 | 1055.229 | 741.468 | 312.972 | 703.223 |
| Q3D3 | 1019.920 | 750.156 | 319.464 | 696.513 |
| Q4 | 798.885 | 687.857 | 419.76 | 635.500 |
| Q4D1 | 1673.744 | 875.709 | 481.294 | 1010.249 |
| Q4D2 | 1707.951 | 868.809 | 482.809 | 1019.856 |
| Q5 | 730.898 | 855.859 | 467.796 | 684.851 |
| Q5D1 | 1688.74 | 930.010 | 526.738 | 1048.496 |
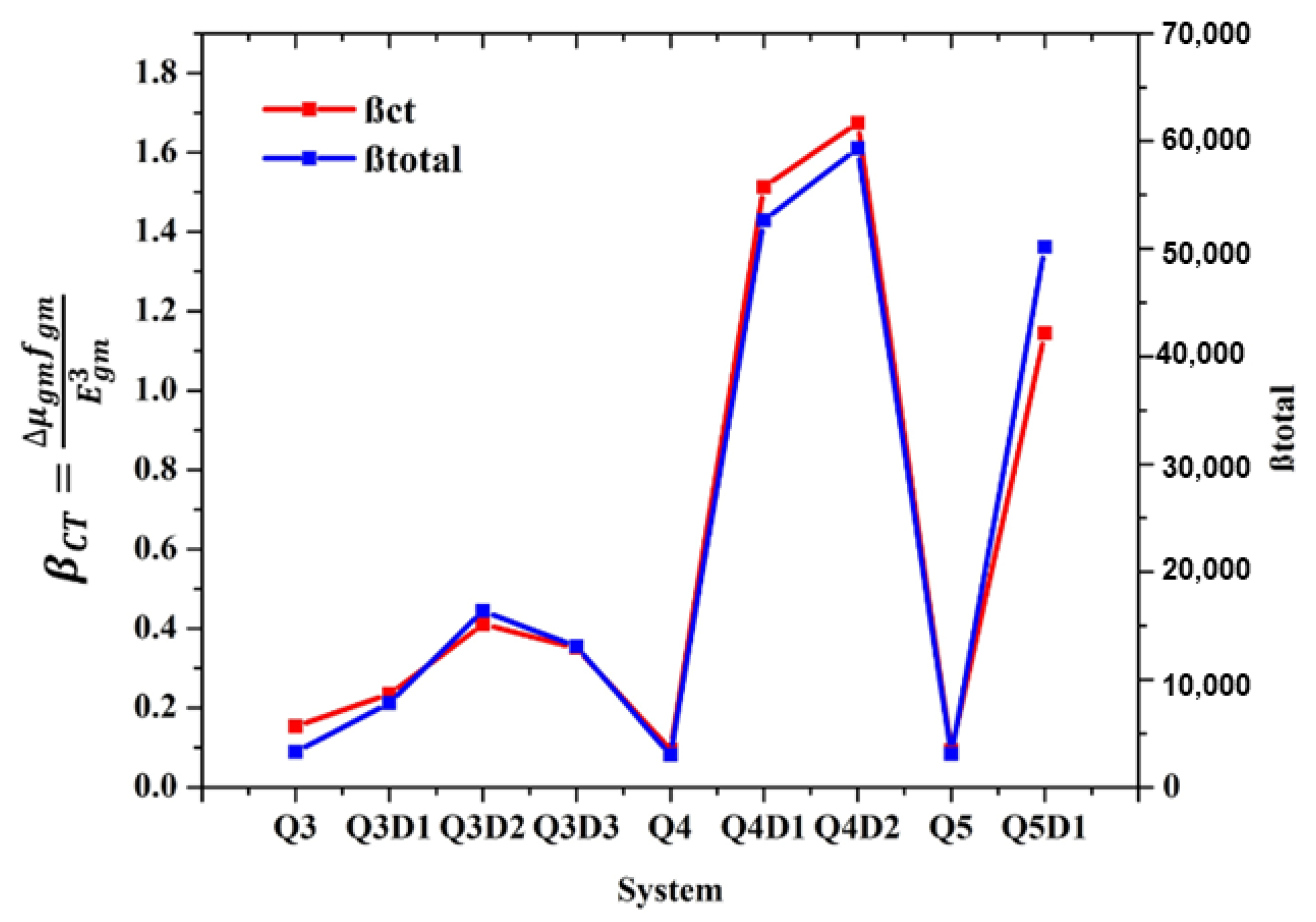
| System | βxxx | βxxy | βxyy | βyyy | βxzz | βyzz | βzzz | βtotal |
|---|---|---|---|---|---|---|---|---|
| Q3 | −1530.726 | 1871.795 | −474.090 | 730.504 | −51.232 | −50.945 | −77.808 | 3277.62 |
| Q3D1 | 7134.938 | −602.979 | 413.750 | 2310.371 | 38.201 | 17.561 | −3.128 | 7811.75 |
| Q3D2 | 15,811.353 | −3037.588 | 490.217 | 1138.007 | −38.279 | −15.314 | −44.940 | 16,375.60 |
| Q3D3 | 13,250.577 | −884.401 | −113.490 | 1410.887 | −51.728 | −14.813 | −47.341 | 13,095.90 |
| Q4 | 1303.257 | −1614.86 | 461.9083 | −732.367 | 94.1197 | 16.408 | −3.3530 | 3000.35 |
| Q4D1 | −50,840.435 | 4690.332 | −737.360 | −762.310 | −469.516 | 105.223 | 63.545 | 52,662.1 |
| Q4D2 | −56,982.727 | 5969.852 | −1009.638 | −703.564 | −573.947 | 143.688 | 56.811 | 59,316.4 |
| Q5 | −595.429 | −141.705 | −1439.05 | −1813.59 | −43.2138 | −228.978 | 57.493 | 3103.51 |
| Q5D1 | −48,440.596 | 5639.601 | −697.923 | −541.280 | −337.387 | 120.393 | 26.346 | 50,156.00 |
| Compounds | Ege (eV) | λmax (nm) | ƒos | LHE | ∆μgm (a.u) | Major MO Transitions |
|---|---|---|---|---|---|---|
| Q3 | 3.397 | 364.97 (349) | 1.026 | 0.905 | 5.842 | H-2→LUMO (92%) |
| Q3D1 | 2.699 | 459.35 | 0.652 | 0.777 | 7.088 | H-1→LUMO (95%) |
| Q3D2 | 2.332 | 531.57 | 0.707 | 0.803 | 7.366 | H-1→LUMO (98%) |
| Q3D3 | 2.445 | 507.09 | 0.673 | 0.788 | 7.611 | H-1→LUMO (98%) |
| Q4 | 3.435 | 360.90 (347) | 1.005 | 0.901 | 3.854 | H-2→LUMO (92%) |
| Q4D1 | 2.087 | 593.82 | 1.479 | 0.966 | 9.309 | HOMO→LUMO (99%) |
| Q4D2 | 2.019 | 613.87 | 1.476 | 0.966 | 9.345 | HOMO→LUMO (99%) |
| Q5 | 3.428 | 361.67 (323) | 1.025 | 0.905 | 3.658 | H-2→LUMO (93%) |
| Q5D1 | 2.102 | 589.61 | 1.454 | 0.964 | 7.317 | HOMO→LUMO (99%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, B.; Khalid, M.; Asim, S.; Usman Khan, M.; Iqbal, Z.; Hussain, A.; Hussain, R.; Ahmed, S.; Ali, A.; Hussain, A.; et al. Key Electronic, Linear and Nonlinear Optical Properties of Designed Disubstituted Quinoline with Carbazole Compounds. Molecules 2021, 26, 2760. https://doi.org/10.3390/molecules26092760
Ali B, Khalid M, Asim S, Usman Khan M, Iqbal Z, Hussain A, Hussain R, Ahmed S, Ali A, Hussain A, et al. Key Electronic, Linear and Nonlinear Optical Properties of Designed Disubstituted Quinoline with Carbazole Compounds. Molecules. 2021; 26(9):2760. https://doi.org/10.3390/molecules26092760
Chicago/Turabian StyleAli, Bakhat, Muhammad Khalid, Sumreen Asim, Muhammad Usman Khan, Zahid Iqbal, Ajaz Hussain, Riaz Hussain, Sarfraz Ahmed, Akbar Ali, Amjad Hussain, and et al. 2021. "Key Electronic, Linear and Nonlinear Optical Properties of Designed Disubstituted Quinoline with Carbazole Compounds" Molecules 26, no. 9: 2760. https://doi.org/10.3390/molecules26092760








