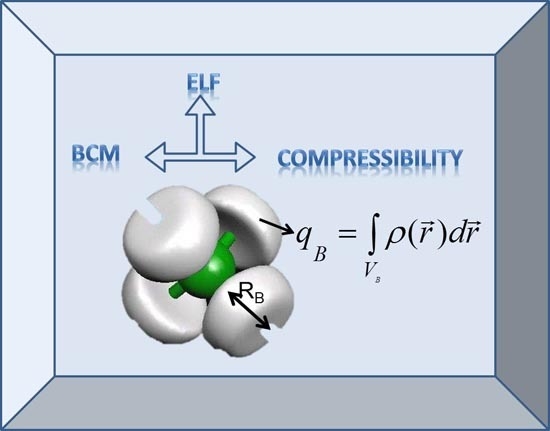
From ELF to Compressibility in Solids
Abstract
:1. Introduction
2. Theoretical Backgroud
2.1. The Bond Charge Model: Original Definition
2.1.1. Homo and Heteronuclear Diatomic Molecules
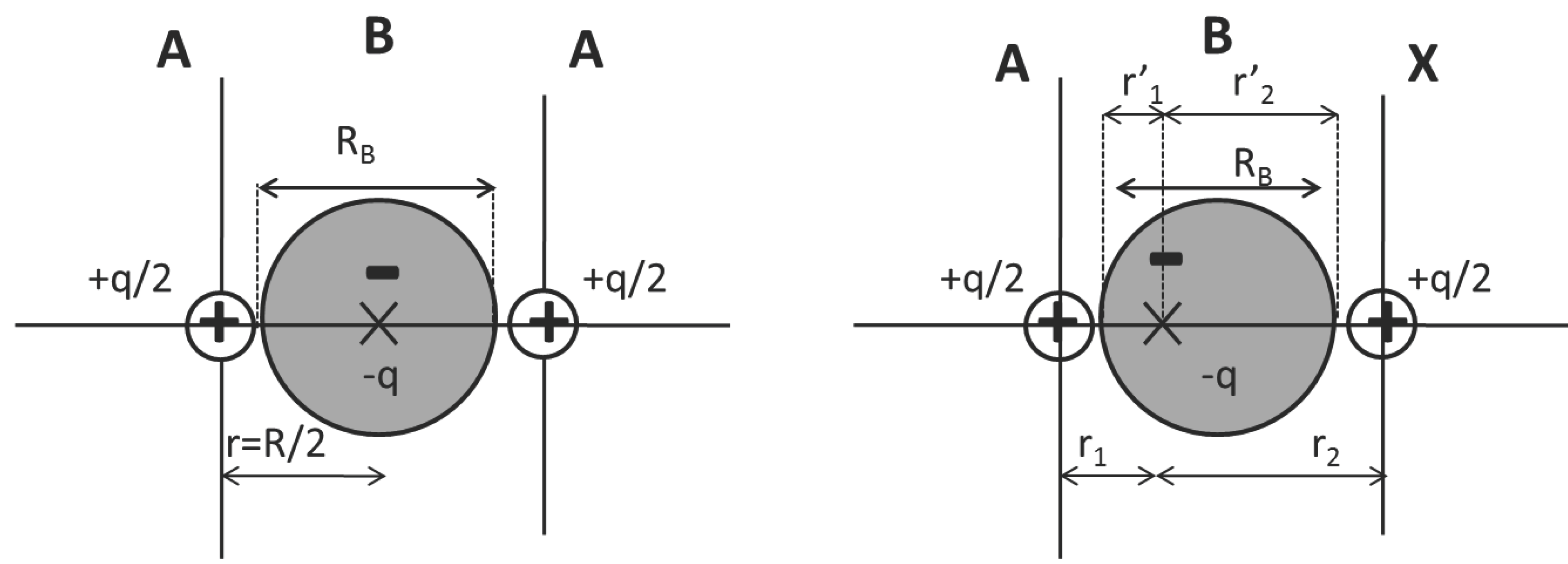
2.1.2. Binary Covalent Solids
| AX | a | ∆χ | r1/r2 | RB | qB | M | EB | δ | |
|---|---|---|---|---|---|---|---|---|---|
| C | 3.557 | 0.0 | 1.00 | 1.00 | 0.938 | 1.950 | 10.856 | −11.644 | 0.000 |
| Si | 5.431 | 0.0 | 1.00 | 1.00 | 1.132 | 1.950 | 8.577 | −7.623 | 0.000 |
| Ge | 5.658 | 0.0 | 1.00 | 1.00 | 1.003 | 2.100 | 7.414 | −8.625 | 0.000 |
| SiC | 4.360 | 0.7 | 1.17 | 0.75 | 0.985 | 1.950 | 9.356 | −9.556 | 0.000 |
| BN | 3.616 | 1.0 | 1.07 | 0.86 | 0.936 | 1.975 | 11.006 | −12.136 | 0.241 |
| BP | 4.538 | 0.1 | 0.96 | 1.21 | 1.050 | 2.000 | 9.662 | −9.739 | 0.250 |
| BAs | 4.777 | 0.0 | 0.70 | 0.82 | 1.023 | 2.050 | 8.711 | −9.468 | 0.268 |
| BSb | 5.156 | 0.1 | 0.62 | 0.88 | 0.999 | 1.988 | 8.554 | −8.954 | 0.245 |
| AlP | 5.464 | 0.6 | 1.14 | 0.97 | 1.122 | 1.975 | 8.925 | −8.206 | 0.266 |
| AlAs | 5.661 | 0.5 | 0.96 | 0.83 | 1.080 | 2.025 | 8.028 | −8.068 | 0.284 |
| AlSb | 6.136 | 0.4 | 0.81 | 0.77 | 1.093 | 1.963 | 7.304 | −6.810 | 0.261 |
| GaAs | 5.653 | 0.4 | 1.19 | 1.18 | 0.992 | 2.100 | 7.662 | −9.008 | 0.238 |
| GaSb | 6.096 | 0.3 | 1.00 | 1.12 | 0.986 | 2.038 | 6.764 | −7.538 | 0.215 |
| InP | 5.869 | 0.4 | 1.64 | 1.38 | 1.012 | 1.970 | 8.494 | −8.615 | 0.269 |
| InAs | 6.058 | 0.3 | 1.35 | 1.11 | 0.958 | 2.020 | 7.268 | −8.187 | 0.287 |
| CdS | 5.818 | 0.8 | 1.89 | 1.48 | 0.976 | 1.975 | 10.016 | −10.512 | 0.494 |
| CdSe | 6.077 | 0.7 | 1.56 | 1.27 | 0.938 | 2.025 | 8.591 | −9.697 | 0.506 |
| ZnS | 5.410 | 0.9 | 1.67 | 1.50 | 1.001 | 2.025 | 10.130 | −10.976 | 0.457 |
| ZnSe | 5.668 | 0.8 | 1.37 | 1.30 | 0.970 | 2.075 | 8.631 | −10.134 | 0.470 |
| ZnTe | 6.104 | 0.5 | 1.15 | 1.25 | 0.971 | 2.038 | 7.415 | −8.389 | 0.460 |
2.2. ELF Topology
3. Computational Details
3.1. Bond Length: RB, r1/r2

4. Defining the Parameters from First Principles
4.1. Bond Charge: qB
5. Testing the Model: Response to Pressure
5.1. Bulk Modulus


5.2. From Micro- to Macroscopic: Understanding Compressibility
- α, β and ν are constant upon compression for the various types of bonding considered. Further analysis shows that α, β and ν can certainly be related to hardness, since they determine which ion compresses the most. Indeed a look at Figure 5 shows that in the case of BN, where the hardness of atoms is more similar, r1 and r2 compress at similar rates, whereas in BAs, the compression of As overcomes that of B.
- As a consequence of the previous observation and from Equation (19), we can consider that the charge transfer is also constant upon compression for the ranges considered.

- Perfectly covalent case (diamond): in this case A = X (or ∆χ = 0), so that all lengths are the same.
- Polar case (BN): in this case A ≠ X (∆χ ≠ 0). However, a relationship holds between the core and the bond location displacement. It is found that the cores differential size, ϵ = rX− rA for ϵ > 0 is equivalent to the displacement of the bond location from the center toward the smaller atom A, (remember that r1 = + rA and r2 = + rX). In BN, a good combination of atomic sizes and polarity compensate to provide r1/r2 = 1.03.
6. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gilman, J.J. Electronic Basis of the Strength of Materials; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Gilman, J.J. Why silicon is hard. Science 1993, 261, 1436–1439. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; He, J.; Wu, E.; Liu, S.; Yu, D.; Li, D.; Zhang, S.; Tian, Y. Hardness of covalent crystals. Phys. Rev. Lett. 2003, 91, 015502. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Wang, X.; Zhang, F.; Xue, D. Electronegativity identification of novel superhard materials. Phys. Rev. Lett. 2008, 100, 235504. [Google Scholar] [CrossRef] [PubMed]
- Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef] [PubMed]
- Lyakhov, A.O.; Oganov, A.R. Evolutionary search for superhard materials: Methodology and applications to forms of carbon and TiO2. Phys. Rev. B 2011, 84, 092103–1. [Google Scholar] [CrossRef]
- Parr, R.; Pearson, R.G. Absolute hardness: Companion parameter to absolute electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [CrossRef]
- Putz, M.V. Electronegativity: Quantum observable. Int. J. Quantum Chem 2009, 109, 733–738. [Google Scholar] [CrossRef]
- Putz, M.V. Chemical action and chemical bonding. J. Mol. Stru.: Theochem 2009, 900, 64–70. [Google Scholar] [CrossRef]
- Putz, M.V. The Bondons: The quantum particles of the chemical bond. Int. J. Mol. Sci. 2010, 11, 4227–4256. [Google Scholar] [CrossRef] [PubMed]
- Putz, M.V. Density functional theory of bose-einstein condensation: Road to chemical bonding quantum condensate. Struc. Bond. 2012, 149, 1–50. [Google Scholar]
- Bader, R.F.W. Atoms in Moleculess, A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Martín Pendás, A.; Costales, A.; Luaña, V. The topology of the electron density in ionic materials. III. Geometry and ionic radii. J. Phys. Chem. B 1998, 102, 6937–6948. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Savin, A.; Jepsen, O.; Flad, J.; Andersen, L.K.; Preuss, H.; von Schnering, H.G. Electron localization in solid-state structures of the elements: The diamond structure. Angew. Chem. Int. Ed. Engl. 1992, 31, 187–188. [Google Scholar] [CrossRef]
- Borkman, R.F.; Parr, R.G. Toward an understanding of potential-energy functions for diatomic Molecules. J. Chem. Phys. 1968, 48, 1116–1126. [Google Scholar] [CrossRef]
- Parr, R.G.; Borkman, R.F. Simple bond-charge model for potential-energy curves of homonuclear diatomic molecules. J. Chem. Phys. 1968, 49, 1055–1058. [Google Scholar] [CrossRef]
- Borkman, R.F.; Simons, G.; Parr, R. Simple bond-charge model for potential-energy curves of heteronuclear diatomic molecules. J. Chem. Phys. 1969, 50, 58–65. [Google Scholar] [CrossRef]
- Parr, R.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Ray, N.K.; Samuels, L.; Parr, R.G. Studies of electronegativity equalization. J. Chem. Phys. 1979, 70, 3680–3684. [Google Scholar] [CrossRef]
- Martin, R.M. A simple bond charge model for vibrations in covalent crystals. Chem. Phys. Lett. 1968, 2, 268–270. [Google Scholar] [CrossRef]
- Oviedo’s Quantum Chemistry Group. Available online: http://azufre.quimica.uniovi.es/software.html (accessed on 8 April 2015).
- Pauling, L. The Nature of the Chemical Bond, 3rd ed.; Cornell Univ. Press: Ithaca, NY, USA, 1960. [Google Scholar]
- Putz, M.V. Markovian approach of the electron localization functions. Int. J. Quantum Chem. 2005, 105, 1–11. [Google Scholar] [CrossRef]
- Putz, M.V. Density functionals of chemical bonding. Int. J. Mol. Sci. 2008, 9, 1050–1095. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, R.J.; Nyholm, R.S. Inorganic stereo-chemistry. Quart. Rev. 1957, 11, 339–380. [Google Scholar] [CrossRef]
- ELK Code. Available online: http://elk.sourceforge.net/ (accessed on 8 April 2015).
- Drief, F.; Tadjer, A.; Mesri, D.; Aourag, H. First principles study of structural, electronic, elastic and optical properties of MgS, MgSe and MgTe. Catal. Today 2004, 89, 343–355. [Google Scholar] [CrossRef]
- Semiconductors information web-site. Available online: www.semiconductors.co.uk (accessed on 8 April 2015).
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke K., *!!! REPLACE !!!*; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Contreras-García, J.; Martin Pendás, A.; Silvi, B.; Recio, J.M. Useful applications of the electron localization function in high-pressure crystal chemistry. J. Phys. Chem. Solids 2008, 69, 2204–2207. [Google Scholar] [CrossRef]
- Contreras-García, J.; Silvi, B.; Martín Pendás, A.; Recio, J.M. Computation of local and global properties of the electron localization function topology in crystals. J. Chem. Theory Comput. 2009, 5, 164–173. [Google Scholar] [CrossRef]
- Kohout, M.; Savin, A. Atomic shell structure and electron numbers. Int. J. Quant. Chem. 1996, 60, 875–882. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03, Revision C.02; Gaussian, Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. TopMoD Package; Universite Pierre et Marie Curie: Paris, France, 1997. [Google Scholar]
- Otero-de-la-Roza, A.; Blanco, M.A.; Martín Pendás, A.; Luaña, V. Critic: A new program for the topological analysis of solid-state electron densities. Comput. Phys. Commun. 2009, 180, 157–166. [Google Scholar] [CrossRef]
- Kohout, M.; Savin, A.; Preuss, H. Contribution to electron density analysis. I. Shell structure of atoms. J. Chem. Phys. 1991, 95, 1928–1942. [Google Scholar] [CrossRef]
- Ackland, G.J.; Marqués, M.; Contreras-García, J.; McMahon, M.I. Origin of incommensurate modulations in the high-pressure phosphorus IV phase. Phys. Rev. B 2008, 78, 054120. [Google Scholar] [CrossRef]
- Marqués, M.; Ackland, G.J.; Lundegaard, L.F.; Contreras-García, J.; McMahon, M.I. Potassium under pressure: A pseudobinary ionic compound. Phys. Rev. Lett. 2009, 103, 115501. [Google Scholar] [CrossRef] [PubMed]
- Marqués, M.; Santoro, M.; Guillaume, C. L.; Gorelli, F.; Contreras-García, J.; Howie, R.; Goncharov, A.F.; Gregoryanz, E. Optical and electronic properties of dense sodium. Phys. Rev. B 2011, 83, 184106. [Google Scholar] [CrossRef]
- Anderson, D.L.; Anderson, O.L.J. The bulk modulus-volume relationship for oxides. J. Geophys. Res. 1970, 75, 3494–3500. [Google Scholar]
- Contreras-García, J.; Mori-Sánchez, P.; Silvi, B.; Recio, J.M.A. Quantum chemical interpretation of compressibility in solids. J. Chem. Theory Comput. 2009, 5, 2108–2114. [Google Scholar] [CrossRef]
- Glasser, L. Volume-based thermoelasticity: Compressibility of inorganic solids. Inorg. Chem. 2010, 49, 3424–3427. [Google Scholar] [CrossRef] [PubMed]
- Glasser, L. Volume-based thermoelasticity: Compressibility of mineral-structured materials. J. Phys. Chem. C 2010, 114, 11248–11251. [Google Scholar] [CrossRef]
- Glasser, L.; Jenkins, H.D.B. Internally consistent ion volumes and their application in volume-based thermodynamics. Inorg. Chem. 2008, 47, 6195–6202. [Google Scholar] [CrossRef] [PubMed]
- Martín Pendás, A.; Costales, A.; Blanco, M.A.; Recio, J.M.; Luaña, V. Local compressibilities in crystals. Phys. Rev. B 2000, 62, 13970–13978. [Google Scholar] [CrossRef]
- Ouahrani, T.; Menendez, J.M.; Marqués, M.; Contreras-García, J.; Baonza, V.G.; Recio, J.M. Local pressures in Zn chalcogenide polymorphs. Europhys. Lett. 2012, 98, 56002. [Google Scholar] [CrossRef]
- Contreras-García, J.; Recio, J.M. On bonding in ionic crystals. J. Phys. Chem. C 2011, 115, 257–263. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contreras-García, J.; Marqués, M.; Menéndez, J.M.; Recio, J.M. From ELF to Compressibility in Solids. Int. J. Mol. Sci. 2015, 16, 8151-8167. https://doi.org/10.3390/ijms16048151
Contreras-García J, Marqués M, Menéndez JM, Recio JM. From ELF to Compressibility in Solids. International Journal of Molecular Sciences. 2015; 16(4):8151-8167. https://doi.org/10.3390/ijms16048151
Chicago/Turabian StyleContreras-García, Julia, Miriam Marqués, José Manuel Menéndez, and José Manuel Recio. 2015. "From ELF to Compressibility in Solids" International Journal of Molecular Sciences 16, no. 4: 8151-8167. https://doi.org/10.3390/ijms16048151