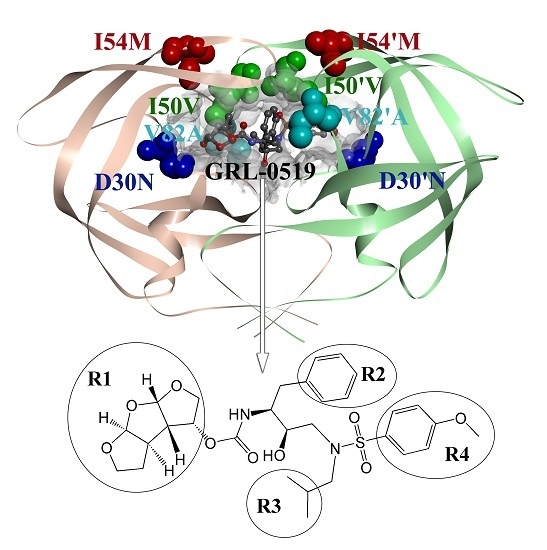
Computational Studies of a Mechanism for Binding and Drug Resistance in the Wild Type and Four Mutations of HIV-1 Protease with a GRL-0519 Inhibitor
Abstract
:1. Introduction
2. Results and Discussion
2.1. The Flexibility of WT and Mutated Complexes
2.2. Analysis of Binding Free Energy
2.3. Identification of the Key Residues Responsible for the Binding of Inhibitor
2.4. Mutations’ Influence on the Binding of Inhibitor
3. Materials and Methods
3.1. System Setups
3.2. Molecular Dynamics Simulations
3.3. MM-PBSA Calculations
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hu, G.; Zhang, S.L.; Zhang, Q. Molecular iynamics simulations and free energy calculation of FKBP12 protein and its inhibitors. Acta Chim. Sin. 2009, 67, 1019–1025. [Google Scholar]
- Oroszlan, S.; Luftig, R.B. Retroviral proteinases. Curr. Top. Microbiol. Immunol. 1990, 157, 153–185. [Google Scholar] [PubMed]
- Richman, D.D.; Morton, S.C.; Wrin, T.; Hellmann, N.; Berry, S.; Shapiro, M.F.; Bozzette, S.A. The prevalence of antiretroviral drug resistance in the United States. Aids 2004, 18, 1393–1401. [Google Scholar] [CrossRef] [PubMed]
- Barbaro, G.; Scozzafava, A.; Mastrolorenzo, A.; Supuran, C.T. Highly active antiretroviral therapy: Current state of the art, new agents and their pharmacological interactions useful for improving therapeutic outcome. Curr. Pharm. Des. 2005, 11, 1805–1843. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Quinones-Mateu, M.E.; Mansky, L.M. Drug resistance, virus fitness and HIV-1 mutagenesis. Curr. Pharm. Des. 2004, 10, 4065–4070. [Google Scholar] [CrossRef] [PubMed]
- Miller, V. International perspectives on antiretroviral resistance. Resistance to protease inhibitors. J. Acquir. Immune Defic. Syndr. 2001, 26 (Suppl. S1), S34–S50. [Google Scholar] [CrossRef] [PubMed]
- Weber, I.T.; Agniswamy, J. HIV-1 protease: Structural perspectives on drug resistance. Viruses 2009, 1, 1110–1136. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.K.; Kincaid, J.F.; Cho, W.; Walters, D.E.; Krishnan, K.; Hussain, K.A.; Koo, Y.; Cho, H.; Rudall, C.; Holland, L.; et al. Potent HIV protease inhibitors incorporating high-affinity P2-ligands and (R)-(hydroxyethylamino)sulfonamide isostere. Bioorg. Med. Chem. Lett. 1998, 8, 687–690. [Google Scholar] [CrossRef]
- Surleraux, D.L.; Tahri, A.; Verschueren, W.G.; Pille, G.M.; de Kock, H.A.; Jonckers, T.H.; Peeters, A.; de Meyer, S.; Azijn, H.; Pauwels, R.; et al. Discovery and selection of TMC114, a next generation HIV-1 protease inhibitor. J. Med. Chem. 2005, 48, 1813–1822. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Wang, Y.F.; Shen, C.H.; Agniswamy, J.; Rao, K.V.; Xu, C.X.; Ghosh, A.K.; Harrison, R.W.; Weber, I.T. Novel P2 tris-tetrahydrofuran group in antiviral compound 1 (GRL-0519) fills the S2 binding pocket of selected mutants of HIV-1 protease. J. Med. Chem. 2013, 56, 1074–1083. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.K.; Xu, C.X.; Rao, K.V.; Baldridge, A.; Agniswamy, J.; Wang, Y.F.; Weber, I.T.; Aoki, M.; Miguel, S.G.; Amano, M.; et al. Probing multidrug-resistance and protein-ligand interactions with oxatricyclic designed ligands in HIV-1 protease inhibitors. Chem. Med. Chem. 2010, 5, 1850–1854. [Google Scholar] [CrossRef] [PubMed]
- Mahalingam, B.; Wang, Y.F.; Boross, P.I.; Tozser, J.; Louis, J.M.; Harrison, R.W.; Weber, I.T. Crystal structures of HIV protease V82A and L90M mutants reveal changes in the indinavir-binding site. Eur. J. Biochem. 2004, 271, 1516–1524. [Google Scholar] [CrossRef] [PubMed]
- Clavel, F.; Hance, A.J. HIV drug resistance. New Engl. J. Med. 2004, 350, 1023–1035. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, B.; Faulds, D. Nelfinavir. A review of its therapeutic efficacy in HIV infection. Drugs 1998, 56, 147–167. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Cao, Z.; Xu, S.; Wang, W.; Wang, J. Revealing the binding modes and the unbinding of 14-3-3σ proteins and inhibitors by computational methods. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Hou, T.; Wang, J.; Li, Y.; Wang, W. Assessing the performance of the MM/PBSA and MM/GBSA methods. 1. The accuracy of binding free energy calculations based on molecular dynamics simulations. J. Chem. Inf. Model. 2011, 51, 69–82. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, J.; Cheatham, T.E.; Cieplak, P.; Kollman, P.A.; Case, D.A. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate-DNA helices. J. Am. Chem. Soc. 1998, 120, 9401–9409. [Google Scholar] [CrossRef]
- Genheden, S.; Ryde, U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discov. 2015, 10, 449–461. [Google Scholar] [CrossRef] [PubMed]
- Reblova, K.; Strelcova, Z.; Kulhanek, P.; Besseova, I.; Mathews, D.H.; Nostrand, K.V.; Yildirim, I.; Turner, D.H.; Sponer, J. An RNA molecular switch: Intrinsic flexibility of 23s rRNA helices 40 and 68 5′-UAA/5′-GAN internal loops studied by molecular dynamics methods. J. Chem. Theory Comput. 2010, 2010, 910–929. [Google Scholar] [CrossRef] [PubMed]
- Gohlke, H.; Kiel, C.; Case, D.A. Insights into protein-protein binding by binding free energy calculation and free energy decomposition for the Ras-Raf and Ras-RalGDS complexes. J. Mol. Biol. 2003, 330, 891–913. [Google Scholar] [CrossRef]
- Gohlke, H.; Case, D.A. Converging free energy estimates: MM-PB(GB)SA studies on the protein–protein complex RAS-RAF. J. Comput. Chem. 2004, 25, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Sirin, S.; Kumar, R.; Martinez, C.; Karmilowicz, M.J.; Ghosh, P.; Abramov, Y.A.; Martin, V.; Sherman, W. A computational approach to enzyme design: Predicting ω-aminotransferase catalytic activity using docking and MM-GBSA scoring. J. Chem. Inf. Model. 2014, 54, 2334–2346. [Google Scholar] [CrossRef] [PubMed]
- Hou, T.; Wang, J.; Li, Y.; Wang, W. Assessing the performance of the molecular mechanics/poisson boltzmann surface area and molecular mechanics/generalized born surface area methods. II. The accuracy of ranking poses generated from docking. J. Comput. Chem. 2011, 32, 866–877. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Li, Y.; Shen, M.; Tian, S.; Xu, L.; Pan, P.; Guan, Y.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 5. Improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring. Phys. Chem. Chem. Phys. 2014, 16, 22035–22045. [Google Scholar] [CrossRef] [PubMed]
- Wright, D.W.; Hall, B.A.; Kenway, O.A.; Jha, S.; Coveney, P.V. Computing clinically relevant binding free energies of HIV-1 protease inhibitors. J. Chem. Theory Comput. 2014, 10, 1228–1241. [Google Scholar] [CrossRef] [PubMed]
- Tzoupis, H.; Leonis, G.; Mavromoustakos, T.; Papadopoulos, M.G. A comparative molecular dynamics, MM-PBSA and thermodynamic integration study of saquinavir complexes with wild-type HIV-1 PR and L10I, G48V, L63P, A71V, G73S, V82A and I84V single mutants. J. Chem. Theory Comput. 2013, 9, 1754–1764. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Srivastava, H.K.; Sastry, G.N. Molecular dynamics investigation on a series of HIV protease inhibitors: Assessing the performance of MM-PBSA and MM-GBSA approaches. J. Chem. Inf. Model. 2012, 52, 3088–3098. [Google Scholar] [CrossRef] [PubMed]
- Kar, P.; Knecht, V. Energetic basis for drug resistance of HIV-1 protease mutants against amprenavir. J. Comput. Aided Mol. Des. 2012, 26, 215–232. [Google Scholar] [CrossRef] [PubMed]
- Stoica, I.; Sadiq, S.K.; Coveney, P.V. Rapid and accurate prediction of binding free energies for saquinavir-bound HIV-1 proteases. J. Am. Chem. Soc. 2008, 130, 2639–2648. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liang, Z.; Wang, W.; Yi, C.; Zhang, S.; Zhang, Q. Revealing origin of decrease in potency of darunavir and amprenavir against HIV-2 relative to HIV-1 protease by molecular dynamics simulations. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, X.; Zhu, T.; Zhang, Q.; Zhang, J.Z. A comparative insight into amprenavir resistance of mutations V32I, G48V, I50V, I54V, and I84V in HIV-1 protease based on thermodynamic integration and MM-PBSA methods. J. Chem. Inf. Model. 2015, 55, 1903–1913. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Morin, P.; Wang, W.; Kollman, P.A. Use of MM-PBSA in reproducing the binding free energies to HIV-1 RT of TIBO derivatives and predicting the binding mode to HIV-1 RT of efavirenz by docking and MM-PBSA. J. Am. Chem. Soc. 2001, 123, 5221–5230. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Sun, H.; Li, Y.; Wang, J.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 3. The impact of force fields and ligand charge models. J. Phys. Chem. B 2013, 117, 8408–8421. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Shen, Y.; Liu, H.; Yao, X. Molecular dynamics simulation and free energy calculation studies of the binding mechanism of allosteric inhibitors with p38αMAP kinase. J. Chem. Inf. Model. 2011, 51, 3235–3246. [Google Scholar] [CrossRef] [PubMed]
- Genheden, S.; Ryde, U. How to obtain statistically converged MM/GBSA results. J. Comput. Chem. 2010, 31, 837–846. [Google Scholar] [CrossRef] [PubMed]
- Wu, E.L.; Han, K.L.; Zhang, J.Z.H. Selectivity of neutral/weakly basic P1 group inhibitors of thrombin and trypsin by a molecular dynamics study. Chem. Eur. J. 2008, 14, 8704–8714. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, J.; Zhu, W.; Li, G. A computational analysis of binding modes and conformation changes of MDM2 induced by p53 and inhibitor bindings. J. Comput. Aided Mol. Des. 2013, 27, 965–974. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.X.; Freedberg, D.I.; Wingfield, P.T.; Stahl, S.J.; Kaufman, J.D.; Kiso, Y.; Bhat, T.N.; Erickson, J.W.; Torchia, D.A. Bound water molecules at the interface between the HIV-1 protease and a potent inhibitor, KNI-272, determined by NMR. J. Am. Chem. Soc. 1996, 118, 12287–12290. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, C.Y.; Wang, S. Binding free energy contributions of interfacial waters in HIV-1 protease/inhibitor complexes. J. Am. Chem. Soc. 2006, 128, 11830–11839. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Zhu, T.; Zhang, S.L.; Wang, D.; Zhang, Q. Some insights into mechanism for binding and drug resistance of wild type and I50VV82A and I84V mutations in HIV-1 protease with GRL-98065 inhibitor from molecular dynamic simulations. Eur. J. Med. Chem. 2010, 45, 227–235. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Kollman, P.A. Free energy calculations on dimer stability of the HIV protease using molecular dynamics and a continuum solvent model. J. Mol. Biol. 2000, 303, 567–582. [Google Scholar] [CrossRef] [PubMed]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 2002, 117, 5179–5197. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03, Revision c.02; Gaussian, Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Cieplak, P.; Cornell, W.D.; Bayly, C.; Kollman, P.A. Application of the multimolecule and multiconformational RESP methodology to biopolymers: Charge derivation for DNA, RNA, and proteins. J. Comput. Chem. 1995, 16, 1357–1377. [Google Scholar] [CrossRef]
- Wang, J.M.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Case, D.A.; Darden, T.A.; Cheatham, T.E., III; Simmerling, C.L.; Wang, J.; Duke, R.E.; Luo, R.; Walker, R.C.; Zhang, W.; Merz, K.M; et al. Amber 12; University of California: San Francisco, CA, USA, 2012. [Google Scholar]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical-integration of cartesian equations of motion of a system with constraints: Molecular-dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Izaguirre, J.A.; Catarello, D.P.; Wozniak, J.M.; Skeel, R.D. Langevin stabilization of molecular dynamics. J. Chem. Phys. 2001, 114, 2090–2098. [Google Scholar] [CrossRef]
- Swanson, J.M.; Henchman, R.H.; McCammon, J.A. Revisiting free energy calculations: A theoretical connection to MM/PBSA and direct calculation of the association free energy. Biophys. J. 2004, 86, 67–74. [Google Scholar] [CrossRef]
- Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins: Struct. Funct. Bioinform. 2004, 55, 383–394. [Google Scholar] [CrossRef] [PubMed]
- Weiser, J.; Shenkin, P.S.; Still, W.C. Approximate atomic surfaces from linear combinations of pairwise overlaps (LCPO). J. Comput. Chem. 1999, 20, 217–230. [Google Scholar] [CrossRef]
- Pearlman, D.A. Evaluating the molecular mechanics poisson-boltzmann surface area free energy method using a congeneric series of ligands to p38 MAP kinase. J. Med. Chem. 2005, 48, 7796–7807. [Google Scholar] [CrossRef] [PubMed]








| Residues | Chains | WT | Mutation | ||
|---|---|---|---|---|---|
| (°) | ψ (°) | (°) | ψ (°) | ||
| 30 | A | −115.63 | 149.32 | −125.53 | 153.97 |
| B | −127.02 | 152.80 | −135.51 | 150.64 | |
| 50 | A | −66.61 | −31.90 | −66.88 | −24.81 |
| B | −69.57 | 133.36 | −56.66 | −42.28 | |
| 54 | A | −135.28 | 152.63 | −134.94 | 139.37 |
| B | −132.16 | 147.75 | −141.02 | 137.87 | |
| 82 | A | −144.86 | 149.19 | −149.81 | 152.56 |
| B | −145.22 | 152.89 | −148.01 | 150.60 | |
| Compounds | WT | D30N | I50V | I54M | V82A | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Items a | Mean | σ b | Mean | σ b | Mean | σ b | Mean | σ b | Mean | σ b |
| ΔEele | −58.49 | 0.19 | −41.66 | 0.21 | −49.89 | 0.26 | −56.59 | 0.20 | −58.12 | 0.21 |
| ΔEvdw | −69.18 | 0.12 | −73.02 | 0.11 | −70.99 | 0.13 | −70.06 | 0.13 | −68.84 | 0.13 |
| ΔGnonpol | −7.44 | 0.00 | −7.55 | 0.00 | −7.36 | 0.00 | −7.54 | 0.00 | −7.51 | 0.00 |
| ΔGpol | 84.09 | 0.18 | 74.23 | 0.17 | 79.47 | 0.18 | 86.11 | 0.16 | 85.72 | 0.17 |
| ΔGele+pol | 25.60 | 0.19 | 32.57 | 0.19 | 29.58 | 0.22 | 29.52 | 0.18 | 27.60 | 0.19 |
| ΔGvdw+nonpol | −76.62 | 0.06 | −80.57 | 0.06 | −78.35 | 0.06 | −77.60 | 0.07 | −76.35 | 0.06 |
| ΔH | −51.02 | 0.15 | −48.00 | 0.15 | −48.77 | 0.17 | −48.08 | 0.16 | −48.75 | 0.15 |
| TΔS | −27.23 | 0.48 | −27.28 | 0.40 | −29.12 | 0.41 | −26.90 | 0.46 | −26.89 | 0.46 |
| ΔGbind | −23.79 | – | −20.72 | – | −19.65 | – | −21.18 | – | −21.86 | – |
| ΔGexp c | −12.77 | – | −11.05 | – | −10.31 | – | −11.61 | – | −11.66 | – |
| ΔΔGbind | – | – | −3.07 | – | −4.14 | – | −2.61 | – | −1.93 | – |
| ΔΔGexp | – | – | −1.72 | – | −2.46 | – | −1.16 | – | −1.11 | – |
| Hydrogen Bond a | WT | D30N | I50V | I54M | V82A | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Occ (%) | Dist (Å) | Occ (%) | Dist (Å) | Occ (%) | Dist (Å) | Occ (%) | Dist (Å) | Occ (%) | Dist (Å) | |
| Asp25′@OD1···GRL@H17–O3 | 100.00 | 2.62 | 59.54 | 2.65 | 46.43 | 2.65 | 49.60 | 3.14 | 53.26 | 3.03 |
| Asp25′@OD2···GRL@H17–O3 | 50.57 | 3.07 | 37.11 | 2.71 | 63.17 | 2.78 | 100.00 | 2.62 | 99.40 | 2.64 |
| GRL@O3···Asp25@HD2–OD2 | 99.97 | 2.64 | – | – | 31.86 | 2.75 | 99.80 | 2.65 | 96.37 | 2.64 |
| Wat@O···Ile50′@H–N | 81.83 | 3.09 | 84.46 | 3.02 | 43.03 | 3.07 | 86.63 | 3.04 | 78.63 | 3.13 |
| Wat@O···Ile50@H–N | 98.94 | 2.97 | 94.86 | 3.09 | 91.89 | 3.08 | 99.17 | 2.96 | 98.91 | 2.98 |
| GRL@O4···Wat@H1–O | 95.37 | 2.76 | 79.03 | 2.75 | 88.94 | 2.75 | 99.23 | 2.75 | 78.94 | 2.78 |
| GRL@O2···Wat@H2–O | 89.23 | 2.82 | 77.69 | 2.79 | 88.57 | 2.85 | 96.43 | 2.77 | 68.40 | 2.87 |
| Gly27@O···GRL@H19–N2 | 38.63 | 3.21 | 21.91 | 3.23 | 60.54 | 3.15 | 34.80 | 3.19 | 50.11 | 3.12 |
| GRL@O5···Ala@HA-CA | 40.40 | 3.39 | 27.83 | 3.39 | – | – | 40.09 | 3.39 | 36.37 | 3.39 |
| GRL@O7···Asp29@H–N | 98.74 | 2.96 | 71.11 | 2.99 | 96.71 | 2.99 | 99.00 | 2.98 | 96.97 | 3.00 |
| GRL@O6···Asp29@H–N | 76.29 | 3.10 | 29.06 | 3.20 | 88.54 | 3.05 | 56.09 | 3.15 | 75.63 | 3.10 |
| GRL@O8···Asp30′@H–N | 27.37 | 3.24 | 26.14 | 3.28 | 33.80 | 3.27 | – | – | 46.83 | 3.21 |
| GRL@O6···Asp30@H–N | 90.40 | 3.14 | 77.40 | 3.17 | 80.34 | 3.16 | 75.20 | 3.20 | 71.94 | 3.19 |
| Residues | Distance (Å) | Energy (kcal/mol) | ||
|---|---|---|---|---|
| WT | I50V | WT | I50V | |
| Ile(Val)50′-Ile84 | 4.33 | 3.98 | −0.54 | −0.55 |
| Ile(Val)50′-Ile47 | 4.24 | 3.98 | −0.59 | −0.40 |
| Ile(Val)50-Ile84′ | 4.48 | 5.11 | −0.38 | −0.17 |
| Ile(Val)50-Ile47′ | 4.18 | 4.59 | −0.60 | −0.44 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Ma, A.; Dou, X.; Zhao, L.; Wang, J. Computational Studies of a Mechanism for Binding and Drug Resistance in the Wild Type and Four Mutations of HIV-1 Protease with a GRL-0519 Inhibitor. Int. J. Mol. Sci. 2016, 17, 819. https://doi.org/10.3390/ijms17060819
Hu G, Ma A, Dou X, Zhao L, Wang J. Computational Studies of a Mechanism for Binding and Drug Resistance in the Wild Type and Four Mutations of HIV-1 Protease with a GRL-0519 Inhibitor. International Journal of Molecular Sciences. 2016; 17(6):819. https://doi.org/10.3390/ijms17060819
Chicago/Turabian StyleHu, Guodong, Aijing Ma, Xianghua Dou, Liling Zhao, and Jihua Wang. 2016. "Computational Studies of a Mechanism for Binding and Drug Resistance in the Wild Type and Four Mutations of HIV-1 Protease with a GRL-0519 Inhibitor" International Journal of Molecular Sciences 17, no. 6: 819. https://doi.org/10.3390/ijms17060819
APA StyleHu, G., Ma, A., Dou, X., Zhao, L., & Wang, J. (2016). Computational Studies of a Mechanism for Binding and Drug Resistance in the Wild Type and Four Mutations of HIV-1 Protease with a GRL-0519 Inhibitor. International Journal of Molecular Sciences, 17(6), 819. https://doi.org/10.3390/ijms17060819