Role of Carbonic Anhydrases and Inhibitors in Acid–Base Physiology: Insights from Mathematical Modeling
Abstract
:1. Introduction
2. Role of Carbonic Anhydrases in Acid–Base Buffering
2.1. Role of Buffers in Acid–Base Homeostasis
2.2. The CO2/HCO3− Buffer System and Related Species
2.3. Competition among Buffers
2.4. CO2/HCO3− Buffering in Closed vs. Open Systems
3. Role of Carbonic Anhydrases in the Facilitated Diffusion of CO2 and Other Buffers
3.1. Role of CA in the Facilitated Diffusion of CO2
3.2. Role of CA in the Facilitated Diffusion of Solutes Other Than CO2
3.3. Role of CA in the Diffusion of CO2 across Artificial Membranes
- CO2, HCO3− and CO3= are in chemical equilibrium, that is, the reactions among these solutes occur very rapidly (i.e., CA is present), at a rate much faster than the rate of solute diffusion across the ULs and the membrane;
- only HCO3− and CO3= carry the tracer and diffuse through the ULs; and
- only CO2 moves across the membrane,
3.4. Role of CA in the Diffusion of CO2 across the Membrane of a Living Cell
- The oocyte, a sphere that comprises the cell membrane and intracellular fluid. Within the ICF, reactions among buffers and diffusion of solutes occur. Surrounding the oocyte is…
- The extracellular unconvected fluid (EUF), a spherical annulus that is concentric with the oocyte. Within the EUF, reactions among buffers and diffusion of solutes occur. Conceptually, the EUF is similar to the classical unstirred layer (a steady-state concept, with a characteristic value for each solute), except that the EUF has meaning even before the establishment of a steady state, and the EUF has the same thickness for each solute [59]. Surrounding the EUF is…
- The bECF, an infinite reservoir of pre-equilibrated solution that mimics the composition of the bath solution used in the physiological experiments. No reaction or diffusion occurs in the bECF.
4. Role of Carbonic Anhydrases in Whole-Body Acid–Base Homeostasis: Transport of HCO3− and CO2
4.1. The Renal System: H+ Secretion and HCO3− Reabsorption
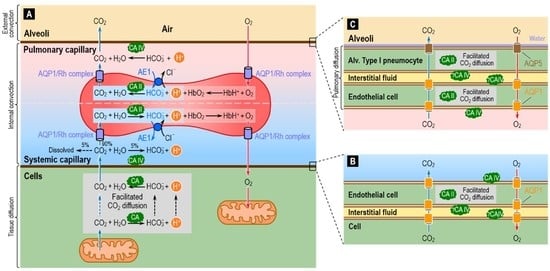
4.2. The Respiratory System: CO2 Removal from the Human Body
5. Conclusions
Funding
Conflicts of Interest
References
- Meldrum, N.U.; Roughton, F.J. Carbonic anhydrase. Its preparation and properties. J. Physiol. 1933, 80, 113–142. [Google Scholar] [CrossRef] [PubMed]
- Del Prete, S.; Vullo, D.; Fisher, G.M.; Andrews, K.T.; Poulsen, S.-A.; Capasso, C.; Supuran, C.T. Discovery of a new family of carbonic anhydrases in the malaria pathogen Plasmodium falciparum—The η-carbonic anhydrases. Bioorg. Med. Chem. Lett. 2014, 24, 4389–4396. [Google Scholar] [CrossRef] [PubMed]
- Kikutani, S.; Nakajima, K.; Nagasato, C.; Tsuji, Y.; Miyatake, A.; Matsuda, Y. Thylakoid luminal θ-carbonic anhydrase critical for growth and photosynthesis in the marine diatom Phaeodactylum tricornutum. Proc. Natl. Acad. Sci. USA 2016, 113, 9828–9833. [Google Scholar] [CrossRef] [PubMed]
- Frost, S.C.; McKenna, R. Carbonic Anhydrase: Mechanism, Regulation, Links to Disease, and Industrial Applications; Subcellular Biochemistry; Springer: Dordrecht, The Netherlands; Heidelberg, Germany; New York, NY, USA; London, UK, 2014; ISBN 978-94-007-7358-5. [Google Scholar]
- Lomelino, C.L.; Andring, J.T.; McKenna, R. Crystallography and Its Impact on Carbonic Anhydrase Research. Int. J. Med. Chem. 2018, 2018. [Google Scholar] [CrossRef] [PubMed]
- Silverman, D.N.; Lindskog, S. The catalytic mechanism of carbonic anhydrase: Implications of a rate-limiting protolysis of water. Acc. Chem. Res. 1988, 21, 30–36. [Google Scholar] [CrossRef]
- Imtaiyaz Hassan, M.; Shajee, B.; Waheed, A.; Ahmad, F.; Sly, W.S. Structure, function and applications of carbonic anhydrase isozymes. Bioorg. Med. Chem. 2013, 21, 1570–1582. [Google Scholar] [CrossRef]
- Supuran, C.T. Carbonic anhydrases—An overview. Curr. Pharm. Des. 2008, 14, 603–614. [Google Scholar] [CrossRef]
- Esbaugh, A.J.; Tufts, B.L. The structure and function of carbonic anhydrase isozymes in the respiratory system of vertebrates. Respir. Physiol. Neurobiol. 2006, 154, 185–198. [Google Scholar] [CrossRef]
- Tashian, R.E.; Hewett-Emmett, D.; Carter, N.; Bergenhem, N.C. Carbonic anhydrase (CA)-related proteins (CA-RPs), and transmembrane proteins with CA or CA-RP domains. In The Carbonic Anhydrases; Springer: Berlin/Heidelberg, Germany, 2000; pp. 105–120. [Google Scholar]
- Aspatwar, A.; Tolvanen, M.E.; Parkkila, S. Phylogeny and expression of carbonic anhydrase-related proteins. BMC Mol. Biol. 2010, 11, 25. [Google Scholar] [CrossRef]
- Aspatwar, A.; Tolvanen, M.E.E.; Ortutay, C.; Parkkila, S. Carbonic anhydrase related proteins: Molecular biology and evolution. Subcell. Biochem. 2014, 75, 135–156. [Google Scholar]
- Aspatwar, A.; Tolvanen, M.E.E.; Parkkila, S. An update on carbonic anhydrase-related proteins VIII, X and XI. J. Enzyme Inhib. Med. Chem. 2013, 28, 1129–1142. [Google Scholar] [CrossRef] [PubMed]
- Sjöblom, B.; Elleby, B.; Wallgren, K.; Jonsson, B.H.; Lindskog, S. Two point mutations convert a catalytically inactive carbonic anhydrase-related protein (CARP) to an active enzyme. FEBS Lett. 1996, 398, 322–325. [Google Scholar] [CrossRef] [Green Version]
- Picaud, S.S.; Muniz, J.R.C.; Kramm, A.; Pilka, E.S.; Kochan, G.; Oppermann, U.; Yue, W.W. Crystal structure of human carbonic anhydrase-related protein VIII reveals the basis for catalytic silencing. Proteins 2009, 76, 507–511. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nishimori, I.; Vullo, D.; Minakuchi, T.; Scozzafava, A.; Capasso, C.; Supuran, C.T. Restoring catalytic activity to the human carbonic anhydrase (CA) related proteins VIII, X and XI affords isoforms with high catalytic efficiency and susceptibility to anion inhibition. Bioorg. Med. Chem. Lett. 2013, 23, 256–260. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Skelton, L.A.; Xu, L.; Chandler, M.P.; Berthiaume, J.M.; Boron, W.F. Role of receptor protein tyrosine phosphatase γ in sensing extracellular CO2 and HCO3−. J. Am. Soc. Nephrol. 2016, 27, 2616–2621. [Google Scholar] [CrossRef] [PubMed]
- Patrikainen, M.; Pan, P.; Kulesskaya, N.; Voikar, V.; Parkkila, S. The role of carbonic anhydrase VI in bitter taste perception: Evidence from the Car6−/− mouse model. J. Biomed. Sci. 2014, 21, 82. [Google Scholar] [CrossRef] [PubMed]
- Dodgson, S.J. Liver Mitochondrial Carbonic Anhydrase (CA V), Gluconeogenesis, and Ureagenesis in the Hepatocyte. In The Carbonic Anhydrases: Cellular Physiology and Molecular Genetics; Dodgson, S.J., Tashian, R.E., Gros, G., Carter, N.D., Eds.; Springer: Boston, MA, USA, 1991; pp. 297–306. ISBN 978-1-4899-0750-9. [Google Scholar]
- Lehenkari, P.; Hentunen, T.A.; Laitala-Leinonen, T.; Tuukkanen, J.; Väänänen, H.K. Carbonic anhydrase II plays a major role in osteoclast differentiation and bone resorption by effecting the steady state intracellular pH and Ca2+. Exp. Cell Res. 1998, 242, 128–137. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.H.; Muhammad, E.; Zheng, C.; Hershkovitz, E.; Alkrinawi, S.; Loewenthal, N.; Parvari, R.; Muallem, S. Essential role of carbonic anhydrase XII in secretory gland fluid and HCO3− secretion revealed by disease causing human mutation. J. Physiol. 2015, 593, 5299–5312. [Google Scholar] [CrossRef] [PubMed]
- Maren, T.H.; Broder, L.E. The Role of Carbonic Anhydrase in Anion Secretion into Cerebrospinal Fluid. J. Pharmacol. Exp. Ther. 1970, 172, 197–202. [Google Scholar] [PubMed]
- Sly, W.S.; Hewett-Emmett, D.; Whyte, M.P.; Yu, Y.S.; Tashian, R.E. Carbonic anhydrase II deficiency identified as the primary defect in the autosomal recessive syndrome of osteopetrosis with renal tubular acidosis and cerebral calcification. Proc. Natl. Acad. Sci. USA 1983, 80, 2752–2756. [Google Scholar] [CrossRef]
- Nagelhus, E.A.; Mathiisen, T.M.; Bateman, A.C.; Haug, F.-M.; Ottersen, O.P.; Grubb, J.H.; Waheed, A.; Sly, W.S. Carbonic anhydrase XIV is enriched in specific membrane domains of retinal pigment epithelium, Muller cells, and astrocytes. Proc. Natl. Acad. Sci. USA 2005, 102, 8030–8035. [Google Scholar] [CrossRef] [PubMed]
- Kivelä, A.-J.; Kivelä, J.; Saarnio, J.; Parkkila, S. Carbonic anhydrases in normal gastrointestinal tract and gastrointestinal tumours. World J. Gastroenterol. 2005, 11, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Kivelä, A.J.; Parkkila, S.; Saarnio, J.; Karttunen, T.J.; Kivelä, J.; Parkkila, A.K.; Pastoreková, S.; Pastorek, J.; Waheed, A.; Sly, W.S.; et al. Expression of transmembrane carbonic anhydrase isoenzymes IX and XII in normal human pancreas and pancreatic tumours. Histochem. Cell Biol. 2000, 114, 197–204. [Google Scholar] [PubMed]
- Mboge, M.Y.; Kota, A.; McKenna, R.; Frost, S.C. Biophysical, Biochemical, and Cell Based Approaches Used to Decipher the Role of Carbonic Anhydrases in Cancer and to Evaluate the Potency of Targeted Inhibitors. Int. J. Med. Chem. 2018, 2018. [Google Scholar] [CrossRef] [PubMed]
- Swietach, P.; Patiar, S.; Supuran, C.T.; Harris, A.L.; Vaughan-Jones, R.D. The role of carbonic anhydrase 9 in regulating extracellular and intracellular pH in three-dimensional tumor cell growths. J. Biol. Chem. 2009, 284, 20299–20310. [Google Scholar] [CrossRef] [PubMed]
- Supuran, C.T. Carbonic anhydrases: Novel therapeutic applications for inhibitors and activators. Nat. Rev. Drug Discov. 2008, 7, 168–181. [Google Scholar] [CrossRef] [PubMed]
- Supuran, C.T. Applications of carbonic anhydrases inhibitors in renal and central nervous system diseases. Expert Opin. Ther. Pat. 2018, 28, 713–721. [Google Scholar] [CrossRef] [PubMed]
- Supuran, C.T. Carbonic anhydrase inhibitors as emerging agents for the treatment and imaging of hypoxic tumors. Expert Opin. Investig. Drugs 2018, 27, 963–970. [Google Scholar] [CrossRef]
- Scozzafava, A.; Supuran, C.T. Glaucoma and the applications of carbonic anhydrase inhibitors. Subcell. Biochem. 2014, 75, 349–359. [Google Scholar]
- Henry, R.P. Multiple roles of carbonic anhydrase in cellular transport and metabolism. Annu. Rev. Physiol. 1996, 58, 523–538. [Google Scholar] [CrossRef]
- Chegwidden, W.W.R.; Carter, N.N.D.; Edwards, Y.Y.H. The Carbonic Anhydrases; Springer: Berlin/Heidelberg, Germany, 2000; ISBN 3-7643-5670-7. [Google Scholar]
- Gilmour, K.M. Perspectives on carbonic anhydrase. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2010, 157, 193–197. [Google Scholar] [CrossRef] [PubMed]
- Tripp, B.C.; Smith, K.; Ferry, J.G. Carbonic Anhydrase: New Insights for an Ancient Enzyme. J. Biol. Chem. 2001, 276, 48615–48618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maren, T.H. Carbonic anhydrase: Chemistry, physiology, and inhibition. Physiol. Rev. 1967, 47, 595–781. [Google Scholar] [CrossRef] [PubMed]
- Bauer, C.; Gros, G.; Bartels, H. Biophysics and Physiology of Carbon Dioxide; Springer: Berlin/Heidelberg, Germany, 1980; ISBN 978-3-642-67572-0. [Google Scholar]
- Dodgson, S.J.; Gros, G.; Carter, N.D. The Carbonic Anhydrases: Cellular Physiology and Molecular Genetics; Springer: Boston, MA, USA, 1991; ISBN 978-1-4899-0750-9. [Google Scholar]
- Geers, C.; Gros, G. Carbon dioxide transport and carbonic anhydrase in blood and muscle. Physiol. Rev. 2000, 80, 681–715. [Google Scholar] [CrossRef] [PubMed]
- Purkerson, J.M.; Schwartz, G.J. The role of carbonic anhydrases in renal physiology. Kidney Int. 2007, 71, 103–115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adamson, R.; Swenson, E.R. Acetazolamide Use in Severe Chronic Obstructive Pulmonary Disease. Pros and Cons. Ann. Am. Thorac. Soc. 2017, 14, 1086–1093. [Google Scholar] [PubMed]
- Sly, W.S.; Hu, P.Y. Human carbonic anhydrases and carbonic anhydrase deficiencies. Annu. Rev. Biochem. 1995, 64, 375–401. [Google Scholar] [CrossRef]
- Bidani, A.; Crandall, E.D. Velocity of CO2 exchanges in the lungs. Annu. Rev. Physiol. 1988, 50, 639–652. [Google Scholar] [CrossRef]
- Boron, W.F. Evaluating the role of carbonic anhydrases in the transport of HCO3−-related species. Biochim. Biophys. Acta 2010, 1804, 410–421. [Google Scholar] [CrossRef]
- Swietach, P.; Vaughan-Jones, R.D.; Harris, A.L. Regulation of tumor pH and the role of carbonic anhydrase 9. Cancer Metastasis Rev. 2007, 26, 299–310. [Google Scholar] [CrossRef]
- Waheed, A.; Sly, W.S. Carbonic anhydrase XII functions in health and disease. Gene 2017, 623, 33–40. [Google Scholar] [CrossRef] [PubMed]
- Maren, T.H. Carbonic anhydrase: General perspective and advances in glaucoma research. Drug Dev. Res. 1987, 10, 255–276. [Google Scholar] [CrossRef]
- Lindskog, S. Structure and mechanism of carbonic anhydrase. Pharmacol. Ther. 1997, 74, 1–20. [Google Scholar] [CrossRef]
- Boron, W.F. Regulation of intracellular pH. Adv. Physiol. Educ. 2004, 28, 160–179. [Google Scholar] [CrossRef] [PubMed]
- Boron, W.F. Acid-base physiology. In Medical Physiology: A Cellular and Molecular Approach; Boron, W.F., Boulpaep, E.L., Eds.; Saunders Elsevier: Philadelphia, PA, USA, 2016; pp. 628–646. ISBN 978-1-4557-4377-3. [Google Scholar]
- Bevensee, M.O.; Boron, W.F. Control of intracellular pH. In Seldin and Giebisch’s The Kidney: Physiology & Pathophysiology; Academic Press: Cambridge, MA, USA, 2013; Volume 2, pp. 1773–1835. [Google Scholar]
- Roos, A.; Boron, W.F. Intracellular pH. Physiol. Rev. 1981, 61, 296–434. [Google Scholar] [CrossRef] [PubMed]
- Occhipinti, R.; Boron, W.F. Mathematical modeling of acid-base physiology. Prog. Biophys. Mol. Biol. 2015, 117, 43–58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Forster, R.E.; Dodgson, S.J. Membrane transport and provision of substrates for carbonic anhydrase: In vertebrates. In The Carbonic Anhydrases; Springer: Berlin/Heidelberg, Germany, 2000; pp. 263–280. [Google Scholar]
- Lee, S.-K.; Grichtchenko, I.I.; Boron, W.F. Distinguishing HCO3− from CO32− transport by NBCe1-A. FASEB J. 2011, 25, 656.9. [Google Scholar]
- Zhao, P.; Geyer, R.R.; Boron, W.F. A novel stopped-flow assay for quantitating carbonic-anhydrase activity and assessing red-blood-cell hemolysis. Front. Physiol. 2017, 8, 169. [Google Scholar] [CrossRef] [PubMed]
- Davenport, H.W. The ABC of Acid-Base Chemistry: The Elements of Physiological Blood-Gas Chemistry for Medical Students and Physicians; Sixth, Revised; University of Chicago Press: Chicago, IL, USA, 1974; ISBN 978-0-226-13703-2. [Google Scholar]
- Somersalo, E.; Occhipinti, R.; Boron, W.F.; Calvetti, D. A reaction-diffusion model of CO2 influx into an oocyte. J. Theor. Biol. 2012, 309, 185–203. [Google Scholar] [CrossRef] [PubMed]
- Occhipinti, R.; Lee, S.-K.; Boron, W.F. Mathematical modeling of bicarbonate versus carbonate transport by the electrogenic Na+/HCO3− cotransporter. IUPS 2013 2013, 543P. [Google Scholar]
- Calvetti, D.; Prezioso, J.; Occhipinti, R.; Boron, W.F.; Somersalo, E. Computational model of electrode-induced microenvironmental effects on pH measurements near a cell membrane. Submitted.
- Boron, W.F. Sharpey-Schafer lecture: Gas channels. Exp. Physiol. 2010, 95, 1107–1130. [Google Scholar] [CrossRef] [PubMed]
- Longmuir, I.S.; Forster, R.E.; Woo, C.-Y. Diffusion of Carbon Dioxide through Thin Layers of Solution. Nature 1966, 209, 393–394. [Google Scholar] [CrossRef]
- Enns, T.; Sham, G.B.; Anderson, S. Carbonic anhydrase diffusion of CO2 in whole blood. Physiologist 1966, 9, 176. [Google Scholar]
- Moll, W.; Gros, G. Untersuchungen uber den gasaustausch der erythrocyten. In Pflugers Archiv Fur Die Gesamte Physiologie des Menschen und Der Tiere; Springer: New York, NY, USA, 1966; Volume 291, p. R54. [Google Scholar]
- Enns, T. Facilitation by carbonic anhydrase of carbon dioxide transport. Science 1967, 155, 44–47. [Google Scholar] [CrossRef] [PubMed]
- Gros, G.; Moll, W. Facilitated diffusion of CO2 across albumin solutions. J. Gen. Physiol. 1974, 64, 356–371. [Google Scholar] [CrossRef] [PubMed]
- Gros, G.; Moll, W.; Hoppe, H.; Gros, H. Proton transport by phosphate diffusion—A mechanism of facilitated CO2 transfer. J. Gen. Physiol. 1976, 67, 773–790. [Google Scholar] [CrossRef] [PubMed]
- Gros, G.; Gros, H.; Lavalette, D.; Amand, B.; Pochon, F. Mechanisms of facilitated CO2 and H+ diffusion in protein solutions. In Biophysics and Physiology of Carbon Dioxide; Springer: Berlin/Heidelberg, Germany, 1980; pp. 36–48. [Google Scholar]
- Spitzer, K.W.; Skolnick, R.L.; Peercy, B.E.; Keener, J.P.; Vaughan-Jones, R.D. Facilitation of intracellular H+ ion mobility by CO2/HCO3− in rabbit ventricular myocytes is regulated by carbonic anhydrase. J. Physiol. 2002, 541, 159–167. [Google Scholar] [CrossRef]
- Cooper, G.J.; Boron, W.F. Effect of pCMBS on CO2 permeability of Xenopus oocytes expressing aquaporin 1 or its C189S mutant. Am. J. Physiol. 1998, 275, C1481–C1486. [Google Scholar] [CrossRef] [PubMed]
- Endeward, V.; Cartron, J.-P.; Ripoche, P.; Gros, G. RhAG protein of the Rhesus complex is a CO2 channel in the human red cell membrane. FASEB J. 2008, 22, 64–73. [Google Scholar] [CrossRef]
- Geyer, R.R.; Musa-Aziz, R.; Qin, X.; Boron, W.F. Relative CO2/NH3 selectivities of mammalian Aquaporins 0–9. Am. J. Physiol. Cell Physiol. 2013, 304, C985–C994. [Google Scholar] [CrossRef]
- Musa-Aziz, R.; Chen, L.-M.; Pelletier, M.F.; Boron, W.F. Relative CO2/NH3 selectivities of AQP1, AQP4, AQP5, AmtB, and RhAG. Proc. Natl. Acad. Sci. USA 2009, 106, 5406–5411. [Google Scholar] [CrossRef] [PubMed]
- Nakhoul, N.L.; Davis, B.A.; Romero, M.F.; Boron, W.F. Effect of expressing the water channel aquaporin-1 on the CO2 permeability of Xenopus oocytes. Am. J. Physiol. 1998, 274, C543–C548. [Google Scholar] [CrossRef] [PubMed]
- Geyer, R.R.; Parker, M.D.; Toye, A.M.; Boron, W.F.; Musa-Aziz, R. Relative CO2/NH3 permeabilities of human RhAG, RhBG and RhCG. J. Membr. Biol. 2013, 246, 915–926. [Google Scholar] [CrossRef] [PubMed]
- Musa-Aziz, R.; Occhipinti, R.; Boron, W.F. Evidence from simultaneous intracellular- and surface-pH transients that Carbonic Anhydrase IV enhances CO2 fluxes across Xenopus oocyte plasma membranes. Am. J. Physiol. Cell Physiol. 2014, 307, C814–C840. [Google Scholar] [CrossRef] [PubMed]
- Musa-Aziz, R.; Occhipinti, R.; Boron, W.F. Evidence from simultaneous intracellular- and surface-pH transients that Carbonic Anhydrase II enhances CO2 fluxes across Xenopus oocytes plasma membranes. Am. J. Physiol. Cell Physiol. 2014, 307, C791–C813. [Google Scholar] [CrossRef] [PubMed]
- Occhipinti, R.; Musa-Aziz, R.; Boron, W.F. Evidence from mathematical modeling that Carbonic Anhydrase II and IV enhance CO2 fluxes across Xenopus oocytes plasma membranes. Am. J. Physiol. Cell Physiol. 2014, 307, C841–C858. [Google Scholar] [CrossRef] [PubMed]
- Broun, G.; Selegny, E.; Minh, C.T.; Thomas, D. Facilitated transport of CO(2) across a membrane bearing carbonic anhydrase. FEBS Lett. 1970, 7, 223–226. [Google Scholar] [CrossRef]
- Broun, G.; Tran-Minh, C.; Thomas, D.; Domurado, D.; Selegny, E. The use of proteic and enzymatic coatins and/or membranes for oxygenators. ASAIO J. 1971, 17, 341–349. [Google Scholar]
- Gutknecht, J.; Bisson, M.A.; Tosteson, F.C. Diffusion of carbon dioxide through lipid bilayer membranes: Effects of carbonic anhydrase, bicarbonate, and unstirred layers. J. Gen. Physiol. 1977, 69, 779–794. [Google Scholar] [CrossRef]
- Gutknecht, J.; Tosteson, D.C. Diffusion of weak acids across lipid bilayer membranes: Effects of chemical reactions in the unstirred layers. Science 1973, 182, 1258–1261. [Google Scholar] [CrossRef]
- Gutknecht, J.; Bruner, L.J.; Tosteson, D.C. The permeability of thin lipid membranes to bromide and bromine. J. Gen. Physiol. 1972, 59, 486–592. [Google Scholar] [CrossRef] [PubMed]
- Purkerson, J.M.; Kittelberger, A.M.; Schwartz, G.J. Basolateral carbonic anhydrase IV in the proximal tubule is a glycosylphosphatidylinositol-anchored protein. Kidney Int. 2007, 71, 407–416. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parkkila, S.; Parkkila, A.K.; Saarnio, J.; Kivelä, J.; Karttunen, T.J.; Kaunisto, K.; Waheed, A.; Sly, W.S.; Türeci, O.; Virtanen, I.; et al. Expression of the membrane-associated carbonic anhydrase isozyme XII in the human kidney and renal tumors. J. Histochem. Cytochem. 2000, 48, 1601–1608. [Google Scholar] [CrossRef] [PubMed]
- Giebisch, G.; Windhager, E.E.; Aronson, P.S. Transport of acids and bases. In Medical Physiology. A Cellular and Molecular Approach; Boron, W.F., Boulpaep, E.L., Eds.; Elsevier Saunders: Philadelphia, PA, USA, 2016; pp. 821–835. ISBN 978-1-4557-4377-3. [Google Scholar]
- Agre, P.; Sasaki, S.; Chrispeels, M.J. Aquaporins: A family of water channel proteins. Am. J. Physiol. 1993, 265, F461. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Bouyer, P.; Boron, W.F. Evidence that AQP1 is a functional CO2 channel in proximal tubules. FASEB J. 2006, 20, A1225–A1226. [Google Scholar]
- Guo, Y.-M.; Liu, Y.; Liu, M.; Wang, J.-L.; Xie, Z.-D.; Chen, K.-J.; Wang, D.-K.; Occhipinti, R.; Boron, W.F.; Chen, L.-M. Na+/HCO3− Cotransporter NBCn2 Mediates HCO3− Reclamation in the Apical Membrane of Renal Proximal Tubules. J. Am. Soc. Nephrol. 2017, 28, 2409–2419. [Google Scholar] [CrossRef]
- Parker, M.D.; Musa-Aziz, R.; Rojas, J.D.; Choi, I.; Daly, C.M.; Boron, W.F. Characterization of human SLC4A10 as an electroneutral Na/HCO3 cotransporter (NBCn2) with Cl− self-exchange activity. J. Biol. Chem. 2008, 283, 12777–12788. [Google Scholar] [CrossRef]
- Gilmour, K.M. The Disequilibrium pH: A Tool for the Localization of Carbonic Anhydrase. Comp. Biochem. Physiol. Part A. Mol. Integr. Physiol 1998, 119, 243–254. [Google Scholar] [CrossRef]
- Rector, F.C.; Carter, N.W.; Seldin, D.W. The Mechanism of Bicarbonate Reabsorption in the Proximal and Distal Tubules of the Kidney. J. Clin. Investig. 1965, 44, 278–290. [Google Scholar] [CrossRef]
- Vieira, F.L.; Malnic, G. Hydrogen ion secretion by rat renal cortical tubules as studied by an antimony microelectrode. Am. J. Physiol. 1968, 214, 710–718. [Google Scholar] [CrossRef] [Green Version]
- DuBose, T.D.; Pucacco, L.R.; Seldin, D.W.; Carter, N.W.; Kokko, J.P. Microelectrode determination of pH and PCO2 in rat proximal tubule after benzolamide: Evidence for hydrogen ion secretion. Kidney Int. 1979, 15, 624–629. [Google Scholar] [CrossRef] [PubMed]
- DuBose, T.D.; Lucci, M.S. Effect of carbonic anhydrase inhibition on superficial and deep nephron bicarbonate reabsorption in the rat. J. Clin. Investig. 1983, 71, 55–65. [Google Scholar] [CrossRef] [PubMed]
- Lucci, M.S.; Tinker, J.P.; Weiner, I.M.; DuBose, T.D. Function of proximal tubule carbonic anhydrase defined by selective inhibition. Am. J. Physiol.-Ren. Physiol. 1983, 245, F443–F449. [Google Scholar] [CrossRef] [PubMed]
- Sly, W.S.; Whyte, M.P.; Sundaram, V.; Tashian, R.E.; Hewett-Emmett, D.; Guibaud, P.; Vainsel, M.; Baluarte, H.J.; Gruskin, A.; Al-Mosawi, M.; et al. Carbonic Anhydrase II Deficiency in 12 Families with the Autosomal Recessive Syndrome of Osteopetrosis with Renal Tubular Acidosis and Cerebral Calcification. N. Engl. J. Med. 1985, 313, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Lewis, S.E.; Erickson, R.P.; Barnett, L.B.; Venta, P.J.; Tashian, R.E. N-ethyl-N-nitrosourea-induced null mutation at the mouse Car-2 locus: An animal model for human carbonic anhydrase II deficiency syndrome. Proc. Natl. Acad. Sci. USA 1988, 85, 1962–1966. [Google Scholar] [CrossRef] [PubMed]
- Soleimani, M.; Aronson, P.S. Effects of acetazolamide on Na+-HCO-3 cotransport in basolateral membrane vesicles isolated from rabbit renal cortex. J. Clin. Investig. 1989, 83, 945–951. [Google Scholar] [CrossRef] [PubMed]
- Henderson, R.M.; Bell, P.B.; Cohen, R.D.; Browning, C.; Iles, R.A. Measurement of intracellular pH with microelectrodes in rat kidney in vivo. Am. J. Physiol.-Ren. Physiol. 1986, 250, F203–F209. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, G.J.; Weinstein, A.M.; Steele, R.E.; Stephenson, J.L.; Burg, M.B. Carbon dioxide permeability of rabbit proximal convoluted tubules. Am. J. Physiol. 1981, 240, F231–F244. [Google Scholar] [CrossRef] [PubMed]
- Krahn, T.A.; Weinstein, A.M. Acid/base transport in a model of the proximal tubule brush border: Impact of carbonic anhydrase. Am. J. Physiol.-Ren. Physiol. 1996, 270, F344–F355. [Google Scholar] [CrossRef]
- Endeward, V.; Musa-Aziz, R.; Cooper, G.J.; Chen, L.-M.; Pelletier, M.F.; Virkki, L.V.; Supuran, C.T.; King, L.S.; Boron, W.F.; Gros, G. Evidence that aquaporin 1 is a major pathway for CO2 transport across the human erythrocyte membrane. FASEB J. 2006, 20, 1974–1981. [Google Scholar] [CrossRef]
- Jennings, M.L. Structure and function of the red blood cell anion transport protein. Annu. Rev. Biophys. Biophys. Chem. 1989, 18, 397–430. [Google Scholar] [CrossRef] [PubMed]
- Parker, M.D.; Boron, W.F. The divergence, actions, roles, and relatives of sodium-coupled bicarbonate transporters. Physiol. Rev. 2013, 93, 803–959. [Google Scholar] [CrossRef] [PubMed]
- Boron, W. Transport of oxygen and carbon dioxide in the blood. In Medical Physiology; Boron, W., Boulpaep, E., Eds.; Elsevier: Philadelphia, PA, USA, 2017; pp. 647–659. ISBN 978-1-4557-4377-3. [Google Scholar]
- Zhao, P.; Geyer, R.R.; Sim, E.S.; Salameh, A.I.; Meyerson, H.; Wass, A.B.; Moss, F.J.; Boron, W.F. Oxygen channels in red blood cells. FASEB J. 2016, 30, 1224.24. [Google Scholar]
- Verkman, A.S. Role of aquaporins in lung liquid physiology. Respir. Physiol. Neurobiol. 2007, 159, 324–330. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swenson, E.R. Respiratory and renal roles of carbonic anhydrase in gas exchange and acid-base regulation. In The Carbonic Anhydrases; Birkhäuser: Basel, Switzerland, 2000; pp. 281–341. [Google Scholar]
- Forster, R.E.; Itada, N. Carbonic Anhydrase Activity in Intact Red Cells as Measured by Means of 18O Exchange between CO2 and Water. In Biophysics and Physiology of Carbon Dioxide; Bauer, C., Gros, G., Bartels, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1980; pp. 177–183. [Google Scholar]
- Al-Samir, S.; Papadopoulos, S.; Scheibe, R.J.; Meißner, J.D.; Cartron, J.-P.; Sly, W.S.; Alper, S.L.; Gros, G.; Endeward, V. Activity and distribution of intracellular carbonic anhydrase II and their effects on the transport activity of anion exchanger AE1/SLC4A1. J. Physiol. 2013, 591, 4963–4982. [Google Scholar] [CrossRef] [PubMed]
- Endeward, V.; Gros, G. Low carbon dioxide permeability of the apical epithelial membrane of guinea-pig colon. J. Physiol. 2005, 567, 253–265. [Google Scholar] [CrossRef] [PubMed]
- Effros, R.M.; Chang, R.S.; Silverman, P. Acceleration of plasma bicarbonate conversion to carbon dioxide by pulmonary carbonic anhydrase. Science 1978, 199, 427–429. [Google Scholar] [CrossRef]
- Klocke, R.A. Catalysis of CO2 reactions by lung carbonic anhydrase. J. Appl. Physiol. 1978, 44, 882–888. [Google Scholar] [CrossRef]
- Ryan, U.S.; Whitney, P.L.; Ryan, J.W. Localization of carbonic anhydrase on pulmonary artery endothelial cells in culture. J. Appl. Physiol. 1982, 53, 914–919. [Google Scholar] [CrossRef]
- Fleming, R.E.; Crouch, E.C.; Ruzicka, C.A.; Sly, W.S. Pulmonary carbonic anhydrase IV: Developmental regulation and cell-specific expression in the capillary endothelium. Am. J. Physiol. 1993, 265, L627–L635. [Google Scholar] [CrossRef]
- Zhu, X.L.; Sly, W.S. Carbonic anhydrase IV from human lung. Purification, characterization, and comparison with membrane carbonic anhydrase from human kidney. J. Biol. Chem. 1990, 265, 8795–8801. [Google Scholar] [PubMed]
- Henry, R.P.; Dodgson, S.J.; Forster, R.E.; Storey, B.T. Rat lung carbonic anhydrase: Activity, localization, and isozymes. J. Appl. Physiol. 1986, 60, 638–645. [Google Scholar] [CrossRef] [PubMed]
- Nioka, S.; Henry, R.P.; Forster, R.E. Total CA activity in isolated perfused guinea pig lung by 18O-exchange method. J. Appl. Physiol. 1988, 65, 2236–2244. [Google Scholar] [CrossRef] [PubMed]
- Nioka, S.; Forster, R.E. Lung Carbonic Anhydrase. In The Carbonic Anhydrases: Cellular Physiology and Molecular Genetics; Dodgson, S.J., Tashian, R.E., Gros, G., Carter, N.D., Eds.; Springer: Boston, MA, USA, 1991; pp. 333–340. ISBN 978-1-4899-0750-9. [Google Scholar]
- Weibel, E.R. Lung morphometry: The link between structure and function. Cell Tissue Res. 2017, 367, 413–426. [Google Scholar] [CrossRef] [PubMed]
- Gehr, P.; Bachofen, M.; Weibel, E.R. The normal human lung: Ultrastructure and morphometric estimation of diffusion capacity. Respir. Physiol. 1978, 32, 121–140. [Google Scholar] [CrossRef]
- Crapo, J.D.; Barry, B.E.; Gehr, P.; Bachofen, M.; Weibel, E.R. Cell Number and Cell Characteristics of the Normal Human Lung. Am. Rev. Respir. Dis. 1982, 126, 332–337. [Google Scholar] [PubMed]
- Fleming, R.E.; Moxley, M.A.; Waheed, A.; Crouch, E.C.; Sly, W.S.; Longmore, W.J. Carbonic anhydrase II expression in rat type II pneumocytes. Am. J. Respir. Cell Mol. Biol. 1994, 10, 499–505. [Google Scholar] [CrossRef]
- Chen, J.; Lecuona, E.; Briva, A.; Welch, L.C.; Sznajder, J.I. Carbonic anhydrase II and alveolar fluid reabsorption during hypercapnia. Am. J. Respir. Cell Mol. Biol. 2008, 38, 32–37. [Google Scholar] [CrossRef]
- Effros, R.M.; Mason, G.; Silverman, P. Role of perfusion and diffusion in 14CO2 exchange in the rabbit lung. J. Appl. Physiol. 1981, 51, 1136–1144. [Google Scholar] [CrossRef]
- Effros, R.M. Carbonic Anhydrase and Alveolar Fluid Absorption. Am. J. Respir. Cell Mol. Biol. 2008, 39, 124. [Google Scholar] [CrossRef]
- Ridderstråle, Y.; Wistrand, P.J.; Holm, L.; Carter, N.D. Use of carbonic anhydrase II-deficient mice in uncovering the cellular location of membrane-associated isoforms. In The Carbonic Anhydrases; Birkhäuser: Basel, Switzerland, 2000; pp. 143–155. [Google Scholar]
- Swenson, E.R. Carbonic anhydrase inhibitors and high altitude illnesses. Subcell. Biochem. 2014, 75, 361–386. [Google Scholar] [PubMed]
- Forster, R.E.; Crandall, E.D. Time course of exchanges between red cells and extracellular fluid during CO2 uptake. J. Appl. Physiol. 1975, 38, 710–718. [Google Scholar] [CrossRef] [PubMed]
- Hill, E.P.; Power, G.G.; Longo, L.D. Mathematical simulation of pulmonary O2 and CO2 exchange. Am. J. Physiol. 1973, 224, 904–917. [Google Scholar] [CrossRef] [PubMed]
- Bidani, A.; Crandall, E.D.; Forster, R.E. Analysis of postcapillary pH changes in blood in vivo after gas exchange. J. Appl. Physiol. 1978, 44, 770–781. [Google Scholar] [CrossRef] [PubMed]
- Tyrrell, H.J.V. The origin and present status of Fick’s diffusion law. J. Chem. Educ. 1964, 41, 397. [Google Scholar] [CrossRef]
- Alvarez, O.; Latorre, R. The enduring legacy of the “constant-field equation” in membrane ion transport. J. Gen. Physiol. 2017, 149, 911–920. [Google Scholar] [CrossRef]
- Crandall, E.D.; O’Brasky, J.E. Direct evidence of participation of rat lung carbonic anhydrase in CO2 reactions. J. Clin. Investig. 1978, 62, 618–622. [Google Scholar] [CrossRef] [PubMed]
- Heming, T.A.; Geers, C.; Gros, G.; Bidani, A.; Crandall, E.D. Effects of dextran-bound inhibitors on carbonic anhydrase activity in isolated rat lungs. J. Appl. Physiol. 1986, 61, 1849–1856. [Google Scholar] [CrossRef]
- Heming, T.A.; Vanoye, C.G.; Stabenau, E.K.; Roush, E.D.; Fierke, C.A.; Bidani, A. Inhibitor sensitivity of pulmonary vascular carbonic anhydrase. J. Appl. Physiol. 1993, 75, 1642–1649. [Google Scholar] [CrossRef]
- Enns, T.; Hill, E.P. CO2 diffusing capacity in isolated dog lung lobes and the role of carbonic anhydrase. J. Appl. Physiol. 1983, 54, 483–490. [Google Scholar] [CrossRef]
- DeCoursey, T.E. Hypothesis: Do voltage-gated H(+) channels in alveolar epithelial cells contribute to CO(2) elimination by the lung? Am. J. Physiol. Cell Physiol. 2000, 278, C1–C10. [Google Scholar] [CrossRef] [PubMed]
- Boron, W.F.; De Weer, P. Intracellular pH transients in squid giant axons caused by CO2, NH3, and metabolic inhibitors. J. Gen. Physiol. 1976, 67, 91–112. [Google Scholar] [CrossRef] [PubMed]









© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Occhipinti, R.; Boron, W.F. Role of Carbonic Anhydrases and Inhibitors in Acid–Base Physiology: Insights from Mathematical Modeling. Int. J. Mol. Sci. 2019, 20, 3841. https://doi.org/10.3390/ijms20153841
Occhipinti R, Boron WF. Role of Carbonic Anhydrases and Inhibitors in Acid–Base Physiology: Insights from Mathematical Modeling. International Journal of Molecular Sciences. 2019; 20(15):3841. https://doi.org/10.3390/ijms20153841
Chicago/Turabian StyleOcchipinti, Rossana, and Walter F. Boron. 2019. "Role of Carbonic Anhydrases and Inhibitors in Acid–Base Physiology: Insights from Mathematical Modeling" International Journal of Molecular Sciences 20, no. 15: 3841. https://doi.org/10.3390/ijms20153841
APA StyleOcchipinti, R., & Boron, W. F. (2019). Role of Carbonic Anhydrases and Inhibitors in Acid–Base Physiology: Insights from Mathematical Modeling. International Journal of Molecular Sciences, 20(15), 3841. https://doi.org/10.3390/ijms20153841