Temperature Dependence of Interfacial Bonding and Configuration Transition in Graphene/Hexagonal Boron Nitride Containing Grain Boundaries and Functional Groups
Abstract
:1. Introduction
2. Results and Discussion
2.1. Validation
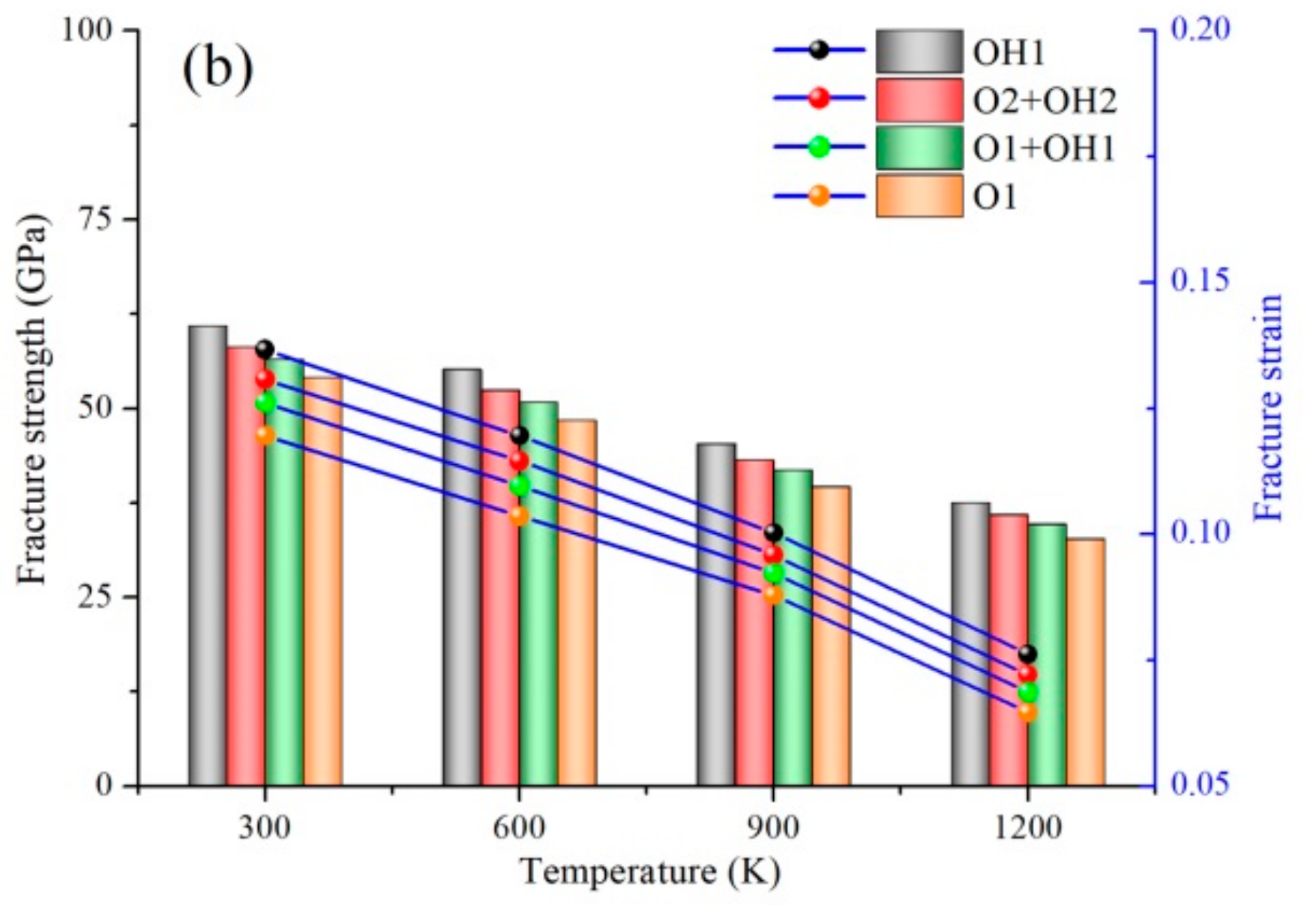
2.2. Coupling Effect of GBs and FGs at High Temperature
2.3. Coupling Effect of GBs and FGs at Different Strain
2.4. Interfacial Distance Effect
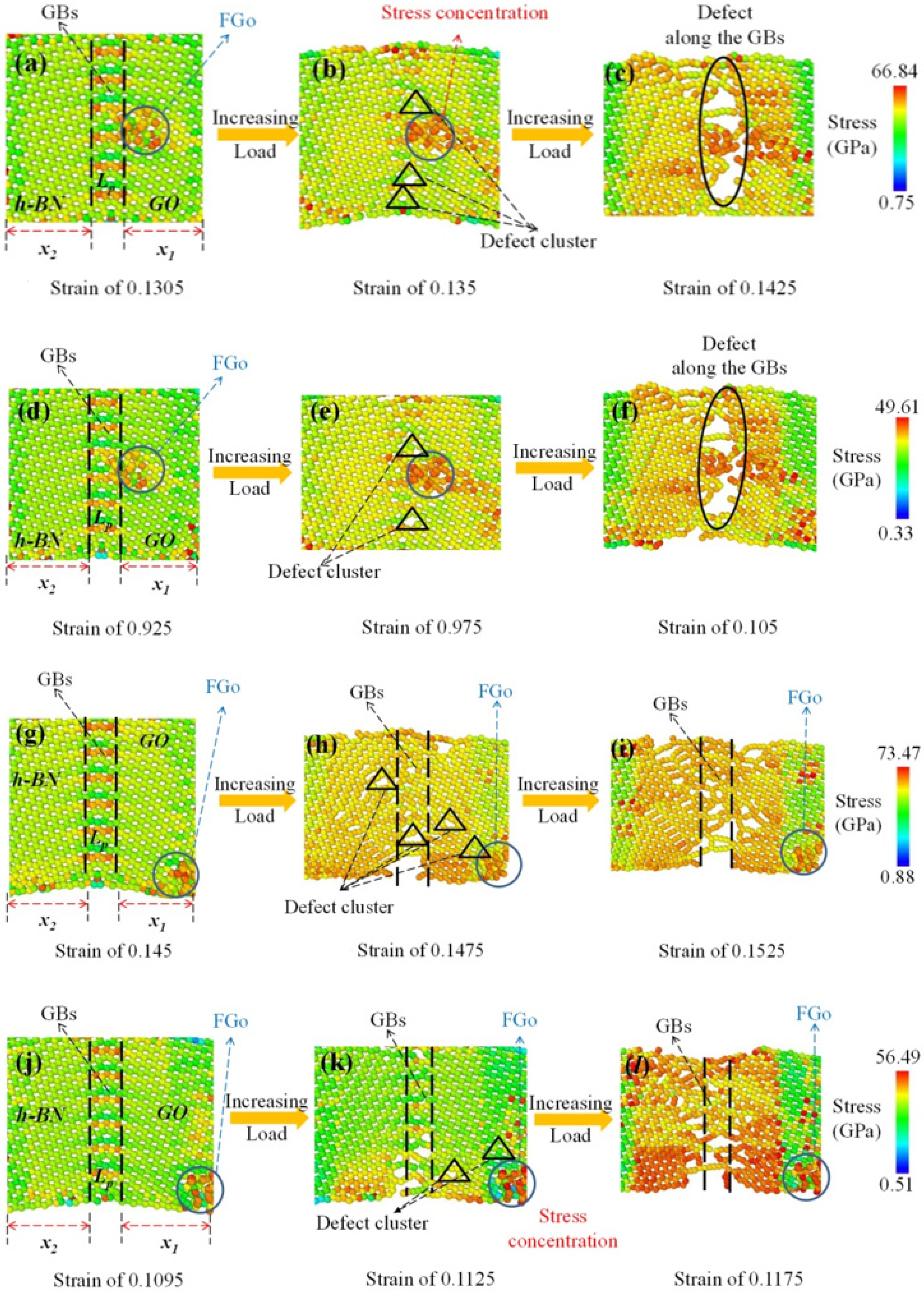
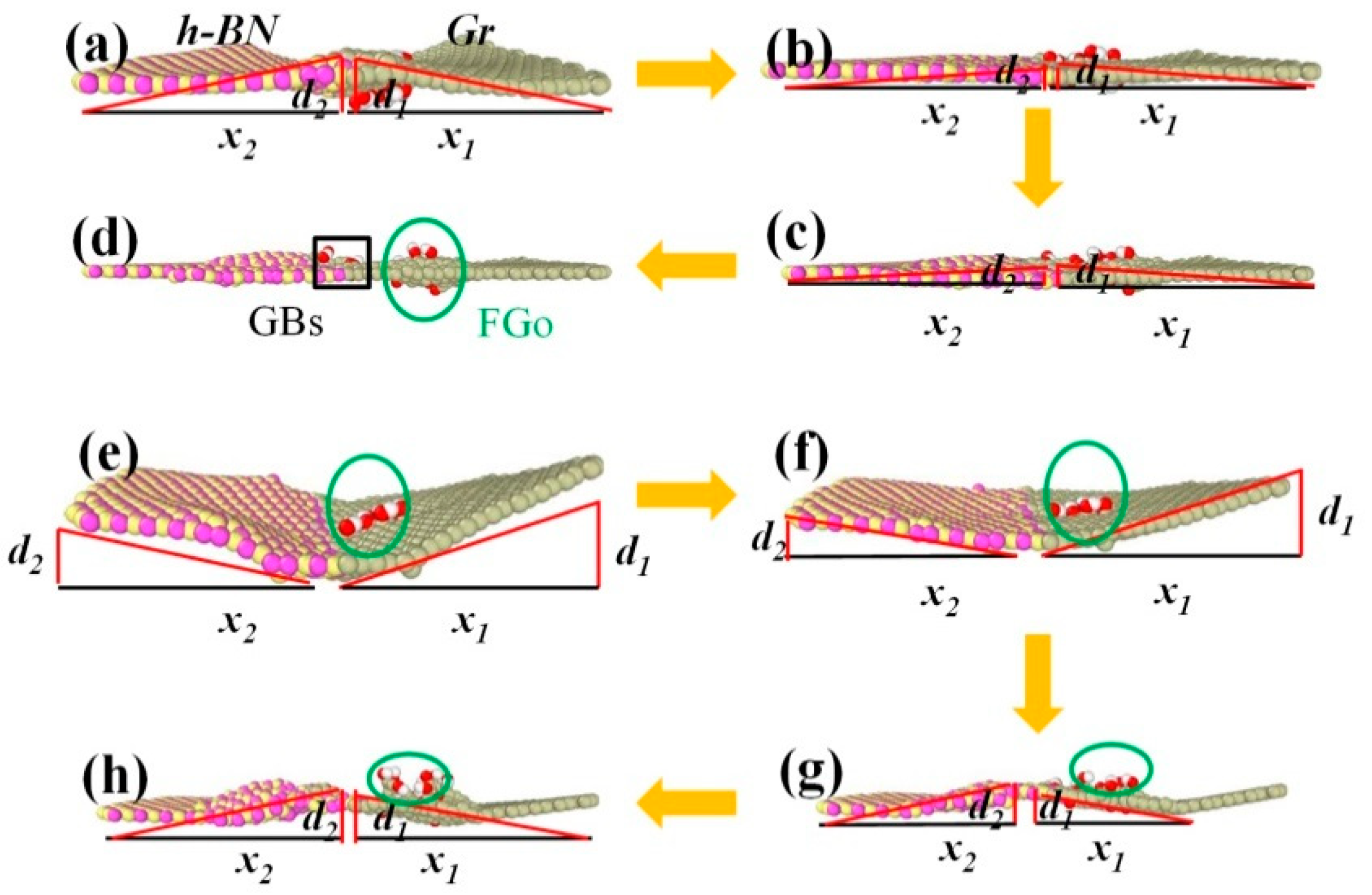
2.5. Stress Distribution and Configuration Transition
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Gr | graphene |
| h-BN | hexagonal boron nitride |
| G-BN | graphene/boron nitride heterostructures |
| G-BN-GB | graphene/h-BN with grain boundaries |
| G-BN-GO | graphene/h-BN with functional groups |
| FGo | functional groups |
| GBs | grain boundary |
| GrO-BN-GBs | graphene/h-BN with FGo and GBs |
| MD | molecular dynamics |
| –O | epoxy |
| –OH | hydroxyl |
References
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.S.; Zhao, Y.; Jang, H.; Lee, S.Y.; Kim, J.M.; Kim, K.S.; Ahn, J.H.; Kim, P.; Choi, J.Y.; Hong, B.H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706–710. [Google Scholar] [CrossRef] [PubMed]
- Bae, S.K.; Kim, H.; Lee, Y.B.; Xu, X.F.; Park, J.S.; Zheng, Y.; Balakrishnan, J.; Lei, T.; Kim, H.R.; Song, Y.I.; et al. Roll-to-roll production of 30-inch graphene films for transparent electrodes. Nat. Nanotechnol. 2010, 5, 574–578. [Google Scholar] [CrossRef] [Green Version]
- Singh, V.; Joung, D.; Zhai, L.; Das, S.; Khondaker, S.I.; Seal, S. Graphene based materials: Past, present and future. Prog. Mater. Sci. 2011, 56, 1178–1271. [Google Scholar] [CrossRef]
- Sun, Z.X.; Fang, S.Y.; Hu, Y.H. 3D Graphene materials: From understanding to design and synthesis control. Chem. Rev. 2020, 120, 10336–10453. [Google Scholar] [CrossRef] [PubMed]
- Bahiraei, M.; Heshmatian, S. Graphene family nanofluids: A critical review and future research directions. Energy Convers. Manag. 2019, 196, 1222–1256. [Google Scholar] [CrossRef]
- Zeng, M.Q.; Xiao, Y.; Liu, J.X.; Yang, K.; Fu, L. Exploring two-dimensional materials toward the next-generation circuits: From monomer design to assembly control. Chem. Rev. 2018, 118, 6236–6296. [Google Scholar] [CrossRef] [PubMed]
- Song, H.F.; Liu, J.M.; Liu, B.L.; Wu, J.Q.; Cheng, H.M.; Kang, F.Y. Two-dimensional materials for thermal management applications. Joule 2018, 2, 442–463. [Google Scholar] [CrossRef] [Green Version]
- Khan, K.; Tareen, A.K.; Aslam, M.; Wang, R.H.; Zhang, Y.P.; Mahmood, A.; Ouyang, Z.B.; Zhang, H.; Guo, Z.Y. Recent developments in emerging two-dimensional materials and their applications. J. Mater. Chem. C 2020, 8, 387–440. [Google Scholar] [CrossRef]
- Moreno, C.; Vilas-Varela, M.; Kretz, B.; Garcia-Lekue, A.; Costache, M.V.; Paradinas, M.; Panighel, M.; Ceballos, G.; Valenzuela, S.O.; Pena, D.; et al. Bottom-up synthesis of multifunctional nanoporous graphene. Science 2009, 360, 199–203. [Google Scholar] [CrossRef] [Green Version]
- Rocha, J.F.; Hostert, L.; Bejarano, M.L.M.; Cardoso, R.M.; Santos, M.D.; Maroneze, C.M.; Gongora-Rubio, M.R.; Silva, C.D.C. Graphene oxide fibers by microfluidics assembly: A strategy for structural and dimensional control. Nanoscale 2021, 13, 6752–6758. [Google Scholar] [CrossRef] [PubMed]
- Tarcan, R.; Todor-Boer, O.; Petrovai, I.; Leordean, C.; Astilean, S.; Botiz, I. Reduced graphene oxide today. J. Mater. Chem. C 2020, 8, 1198–1224. [Google Scholar] [CrossRef]
- Li, Q.C.; Liu, M.X.; Zhang, Y.F.; Liu, Z.F. Hexagonal boron nitride-graphene heterostructures: Synthesis and interfacial properties. Small 2016, 12, 32–50. [Google Scholar] [CrossRef]
- Yao, W.J.; Fan, L. Defects in graphene/h-BN planar heterostructures: Insights into the interfacial thermal transport properties. Nanomaterials 2021, 11, 500. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Yao, W.J. Reduction of interfacial thermal transport of bilayer in-plane graphene/hexagonal boron nitride heterostructures via interlayer sp3 bonds, defects and stacking angle. Diam. Relat. Mater. 2021, 118, 108521. [Google Scholar] [CrossRef]
- Ren, W.J.; Ouyang, Y.L.; Jiang, P.F.; Yu, C.Q.; He, J.; Chen, J. The Impact of interlayer rotation on thermal transport across graphene/hexagonal boron nitride van der Waals heterostructure. Nano Lett. 2021, 21, 2634–2641. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, Y.; Duan, X. Van der Waals integration before and beyond two-dimensional materials. Nature 2019, 567, 323–333. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.Q.; Feng, W.; Lei, Y.; Wang, Z.X.; Wen, Y.; Shifa, T.A.; He, J. High-performance, multifunctional devices based on asymmetric van der Waals heterostructures. Nat. Electron. 2018, 1, 356–361. [Google Scholar] [CrossRef]
- Tran, K.; Moody, G.; Wu, F.C.; Lu, X.B.; Choi, J.; Kim, K.; Rai, A.; Sanchez, D.A.; Quan, J.M.; Singh, A.; et al. Evidence for moire excitons in van der Waals heterostructures. Nature 2019, 567, 71. [Google Scholar] [CrossRef] [Green Version]
- Lu, G.Y.; Wu, T.R.; Yang, P.; Yang, Y.C.; Jin, Z.H.; Chen, W.B.; Jia, S.; Wang, H.M.; Zhang, G.H.; Sun, J.L.; et al. Synthesis of high-quality graphene and hexagonal boron nitride monolayer in-plane heterostructure on Cu-Ni alloy. Adv. Sci. 2017, 4, 1700076. [Google Scholar] [CrossRef] [Green Version]
- Wei, W.; Pan, J.Q.; Euaruksakul, C.; Yang, Y.; Cui, Y.; Fu, Q.; Bao, X.H. Dynamic observation of in-plane h-BN/graphene heterostructures growth on Ni(111). Nano Res. 2020, 13, 1789–1794. [Google Scholar] [CrossRef]
- Li, M.Y.; Zheng, B.; Duan, K.; Zhang, Y.; Huang, Z.G.; Zhou, H.M. Effect of defects on the thermal transport across the graphene/hexagonal boron nitride interface. J. Phys. Chem. C 2018, 122, 14945–14953. [Google Scholar] [CrossRef]
- Fan, L.; Yao, W.J. Effect of defects on mechanical properties of planar h-BN-graphene heterostructure. Mater. Res. Express 2019, 6, 105613. [Google Scholar] [CrossRef]
- Li, Y.F.; Wei, A.R.; Ye, H.; Yao, H.M. Mechanical and thermal properties of grain boundary in a planar heterostructure of graphene and hexagonal boron nitride. Nanoscale 2018, 10, 3497. [Google Scholar] [CrossRef]
- Liu, X.J.; Zhang, G.; Zhang, Y.W. Topological defects at the graphene/h-BN interface abnormally enhance its thermal conductance. Nano Lett. 2016, 16, 4954–4959. [Google Scholar] [CrossRef] [PubMed]
- Yazyev, V.; Chen, Y.P. Polycrystalline graphene and other two-dimensional materials. Nat. Nanotechnol. 2014, 9, 755–767. [Google Scholar] [CrossRef]
- Cao, Q.; Geng, X.; Wang, H.P.; Wang, P.J.; Liu, A.; Lan, Y.C.; Peng, Q. A Review of current development of graphene mechanics. Crystals 2018, 8, 357. [Google Scholar] [CrossRef] [Green Version]
- Eshkalak, K.E.; Sadeghzadeh, S.; Jalaly, M. Mechanical properties of defective hybrid graphene-boron nitride nanosheets: A molecular dynamics study. Comput. Mater. Sci. 2018, 149, 170–181. [Google Scholar] [CrossRef]
- Song, Z.G.; Artyukhov, V.I.; Wu, J.; Yakobson, B.I.; Xu, Z.P. Defect-detriment to graphene strength is concealed by local probe: The topological and geometrical effects. ACS Nano 2015, 9, 401–408. [Google Scholar] [CrossRef]
- Yao, W.J.; Fan, L. Research on the correlation of mechanical properties of BN–graphene–BN/BN verticallystacked nanostructures in the presence of interlayer sp3 bonds and nanopores with temperature. Phys. Chem. Chem. Phys. 2020, 22, 5920–5928. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Min, K.; Aluru, N.R. Size and chirality dependent elastic properties of graphene nanoribbons under uniaxial tension. Nano Lett. 2009, 9, 3012–3015. [Google Scholar] [CrossRef]
- Bosak, A.; Serrano, J.; Krisch, M.; Watanabe, K.; Taniguchi, T.; Kanda, H. Elasticity of hexagonal boron nitride: Inelastic X-ray scattering measurements. Phys. Rev. B 2006, 73, 041402. [Google Scholar] [CrossRef]
- Vinod, S.; Tiwary, C.S.; Samanta, A.; Ozden, S.; Narayanan, T.N.; Vajtai, R.; Agarwal, V.; Singh, A.K.; John, G.; Ajarwal, P.M. Graphene oxide epoxy (GO-xy): GO as epoxy adhesive by interfacial reaction of functionalities. Adv. Mater. Interfaces 2018, 5, 1700657. [Google Scholar] [CrossRef]
- Fan, L.; Yao, W.J. Mechanical properties of a G/h-BN heterobilayer nanosheets coupled by interlayer sp3 bonds and defects. Mater. Res. Express 2019, 6, 095075. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, T.J.; Jia, Y.T.; Hou, D.S.; Li, H.B.; Jiang, J.Y.; Zhang, J.R. Molecular dynamics study on the weakening effect of moisture content on graphene oxide reinforced cement composite. Chem. Phys. Lett. 2018, 708, 177–182. [Google Scholar] [CrossRef]
- Fan, L.; Yao, W.J. Effect of transverse and longitudinal defects on mechanical properties of graphene-h-BN/copper vertically-stacked heterostructure. Comput. Mater. Sci. 2020, 183, 109810. [Google Scholar] [CrossRef]
- Akarsh, V.; Avinash, P. Molecular dynamics based simulations to study the fracture strength of monolayer graphene oxide. Nanotechnology 2018, 29, 115706. [Google Scholar]
- Verma, A.; Parashar, A. Molecular dynamics based simulations to study failure morphology of hydroxyl and epoxide functionalised graphene. Comput. Mater. Sci. 2018, 143, 15–26. [Google Scholar] [CrossRef]
- Deng, L.; Du, J.C. Development of boron oxide potentials for computer simulations of multicomponent oxide glasses. J. Am. Ceram. Soc. 2019, 102, 2482–2505. [Google Scholar] [CrossRef]
- Liang, T.; Shan, T.R.; Cheng, Y.T.; Devine, B.D.; Noordhoek, M.; Li, Y.Z.; Lu, Z.Z.; Phillpot, S.R.; Sinnott, S.B. Classical atomistic simulations of surfaces and heterogeneous interfaces with the charge-optimized many body (COMB) potentials. Mater. Sci. Eng. R-Rep. 2013, 74, 255–279. [Google Scholar] [CrossRef]
- Sharma, B.B.; Parashar, A. Atomistic simulations to study the effect of water molecules on the mechanical behavior of functionalized and non-functionalized boron nitride nanosheets. Comput. Mater. Sci. 2019, 169, 109092. [Google Scholar] [CrossRef]
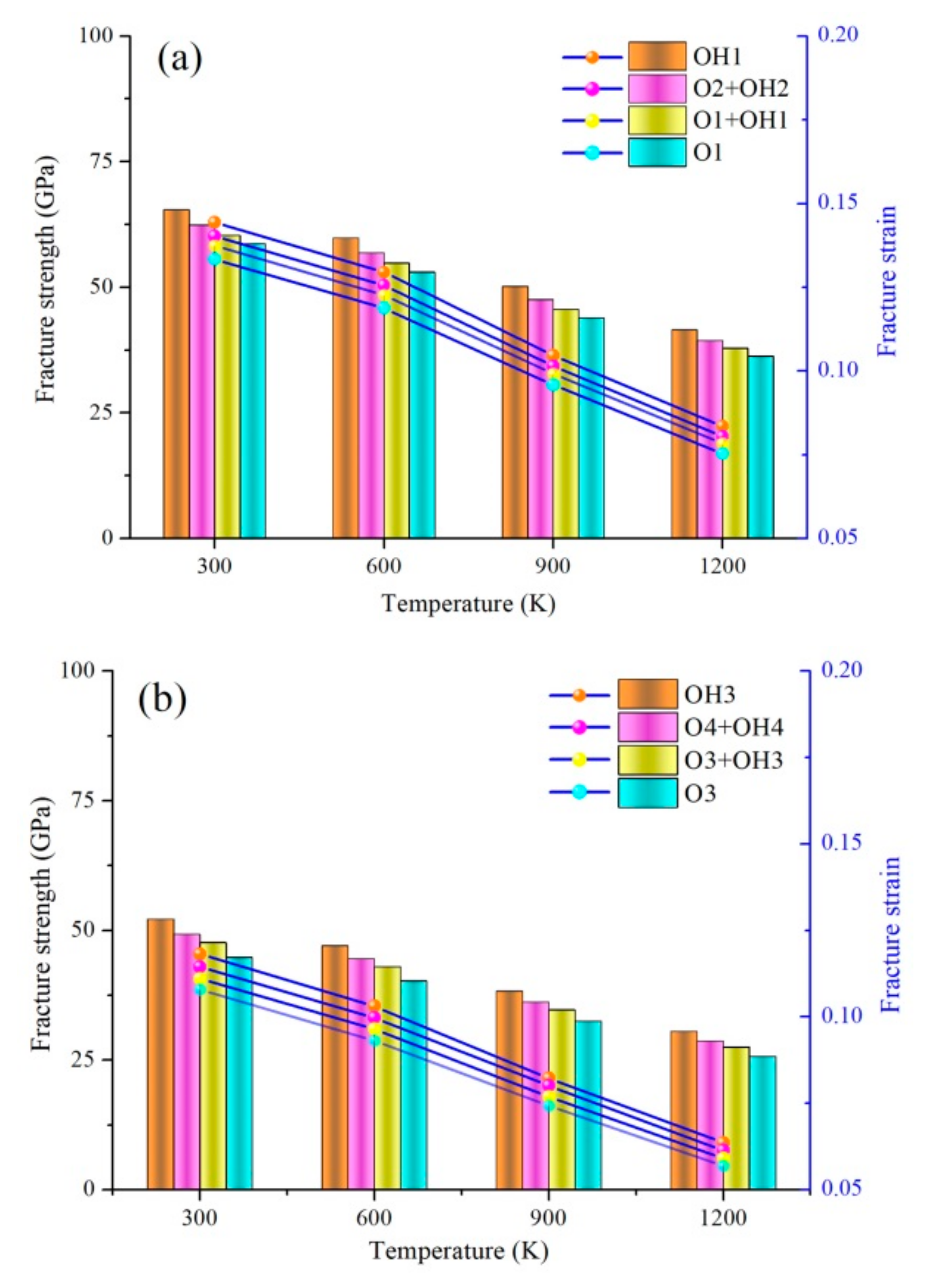
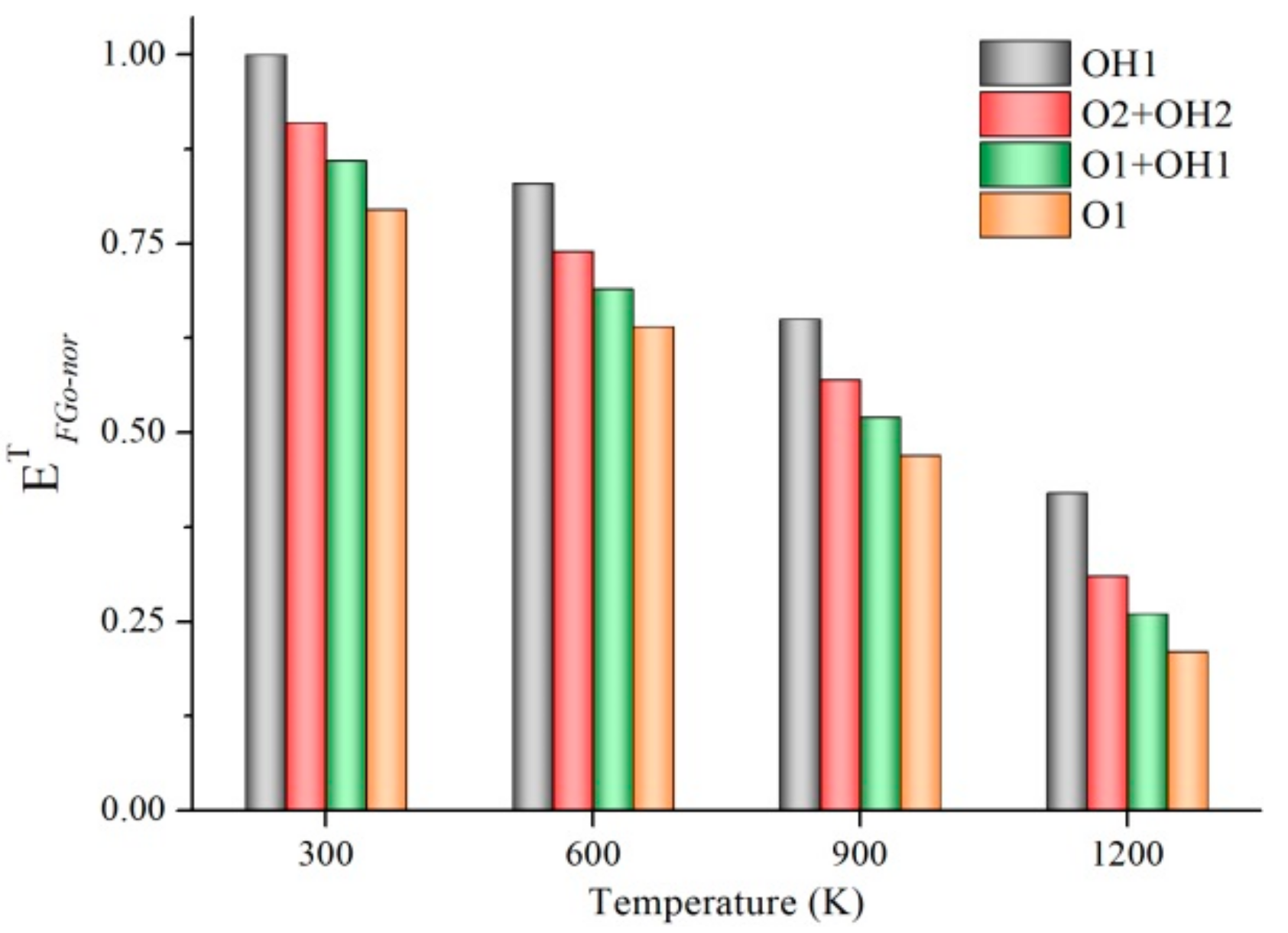



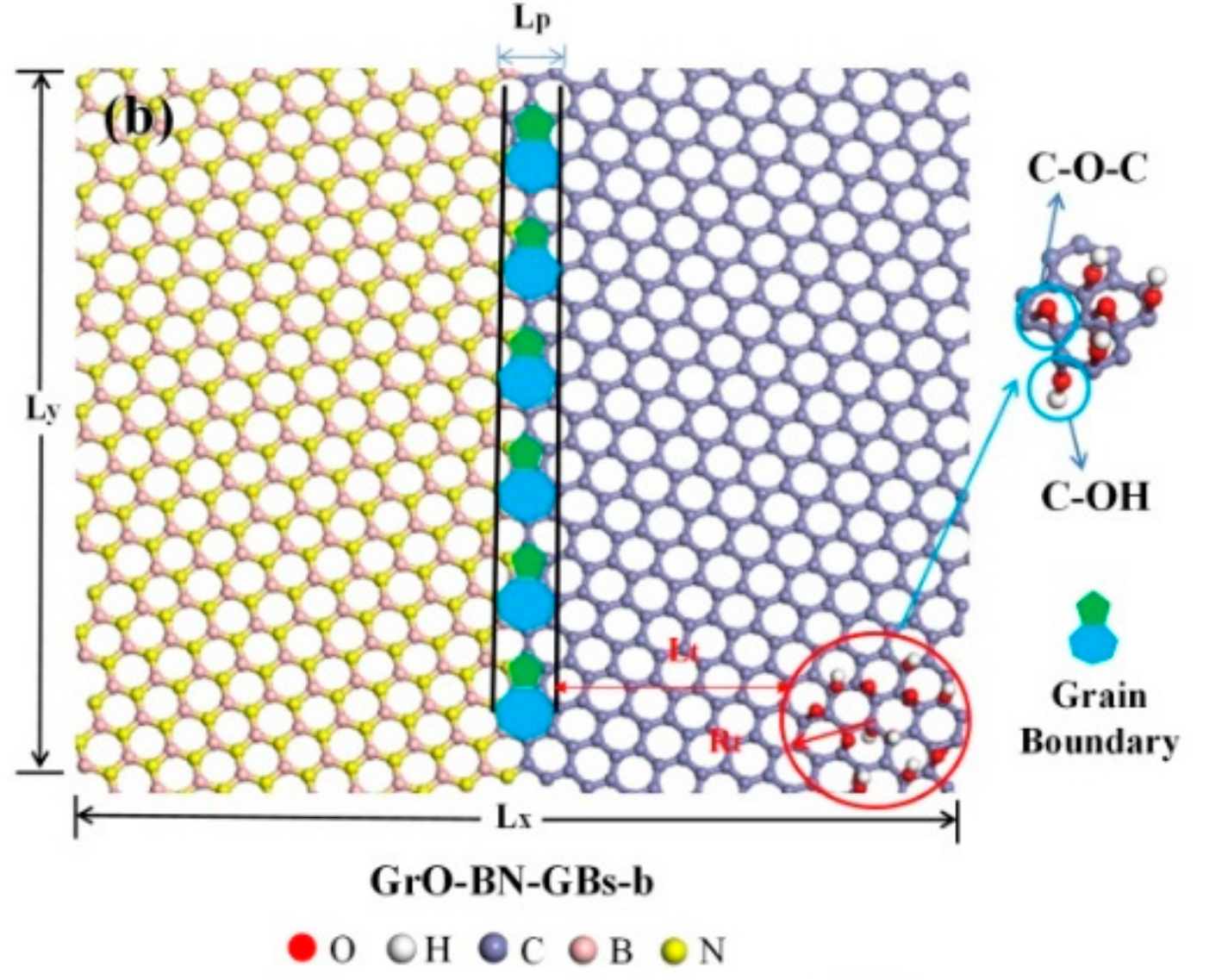
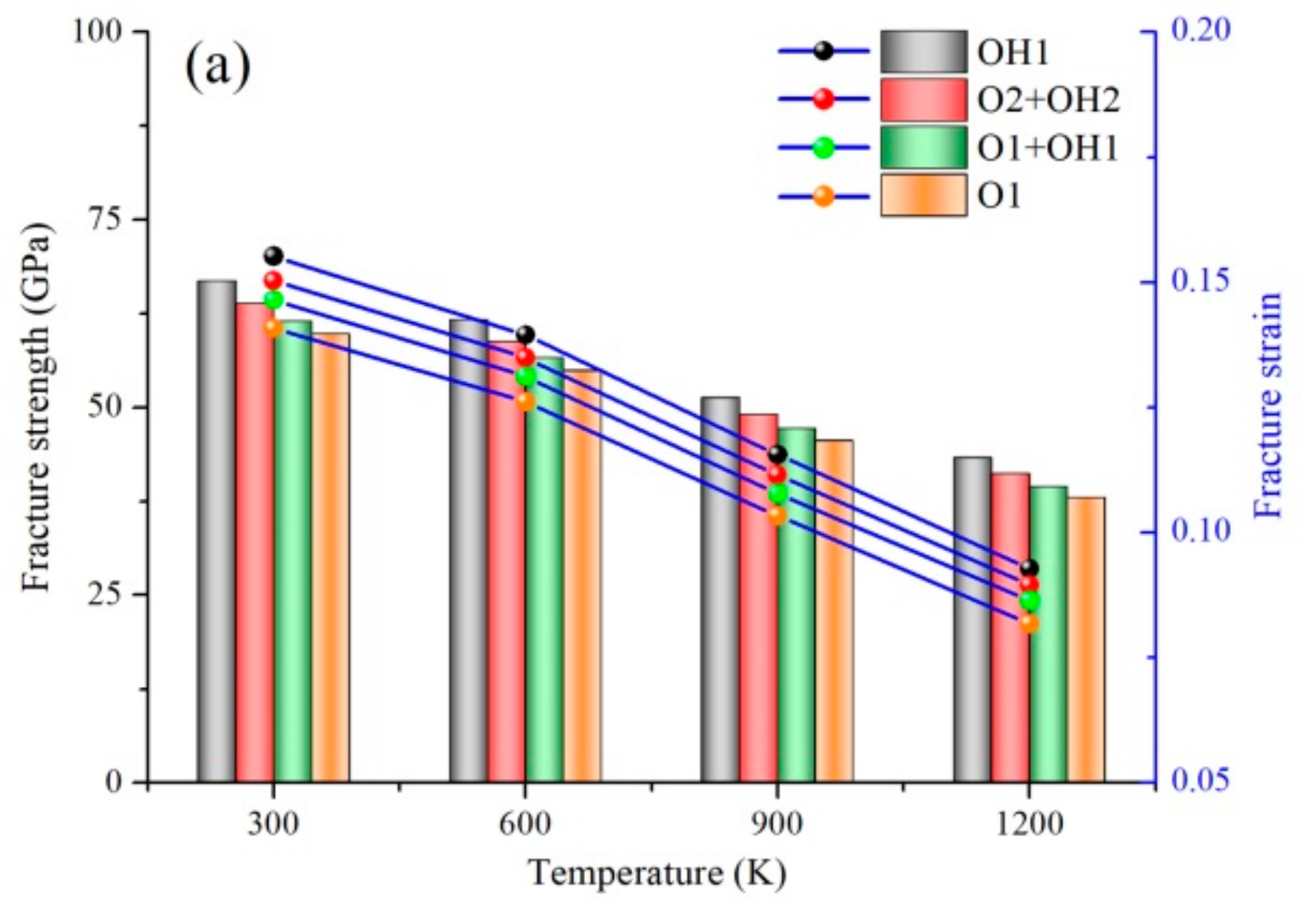


| Various Types | Assessment Method (Potential) | Failure Strain | Failure Strength (GPa) | Young’s Modulus (GPa) | References |
|---|---|---|---|---|---|
| Single-layer | MD (Tersoff) | 0.204 | 123 | 919 | Present study |
| Single-layer | MD (Tersoff) | 0.201 | 131 | 930 | Eshkalak et al. [28] |
| Single-layer | MD (Tersoff) | 0.208 | 127 | 925 | Fan et al. [33] |
| Experimental | 0.130 | 90 | 1000 | Zhao et al. [31] |
| Various Types | Assessment Method (Potential) | Failure Strain | Failure Strength (GPa) | Young’s Modulus (GPa) | References |
|---|---|---|---|---|---|
| Single-layer | MD (Tersoff) | 0.207 | 125 | 921 | Present study |
| Single-layer | MD (Tersoff) | 0.200 | 131 | 930 | Eshkalak et al. [28] |
| Single-layer | MD (Tersoff) | 0.210 | 128 | 923 | Fan et al. [33] |
| Experimental | - | - | 881 | Bosak et al. [32] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, L.; Yao, W. Temperature Dependence of Interfacial Bonding and Configuration Transition in Graphene/Hexagonal Boron Nitride Containing Grain Boundaries and Functional Groups. Int. J. Mol. Sci. 2022, 23, 1433. https://doi.org/10.3390/ijms23031433
Fan L, Yao W. Temperature Dependence of Interfacial Bonding and Configuration Transition in Graphene/Hexagonal Boron Nitride Containing Grain Boundaries and Functional Groups. International Journal of Molecular Sciences. 2022; 23(3):1433. https://doi.org/10.3390/ijms23031433
Chicago/Turabian StyleFan, Lei, and Wenjuan Yao. 2022. "Temperature Dependence of Interfacial Bonding and Configuration Transition in Graphene/Hexagonal Boron Nitride Containing Grain Boundaries and Functional Groups" International Journal of Molecular Sciences 23, no. 3: 1433. https://doi.org/10.3390/ijms23031433
APA StyleFan, L., & Yao, W. (2022). Temperature Dependence of Interfacial Bonding and Configuration Transition in Graphene/Hexagonal Boron Nitride Containing Grain Boundaries and Functional Groups. International Journal of Molecular Sciences, 23(3), 1433. https://doi.org/10.3390/ijms23031433





