Molecule Clustering Dynamics in the Molecular Doping Process of Si(111) with Diethyl-propyl-phosphonate
Abstract
:1. Introduction
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ho, J.C.; Yerushalmi, R.; Jacobson, Z.A.; Fan, Z.; Alley, R.L.; Javey, A. Controlled nanoscale doping of semiconductors via molecular monolayers. Nat. Mater. 2008, 7, 62–67. [Google Scholar] [CrossRef] [PubMed]
- Voorthuijzen, W.P.; Yilmaz, M.D.; Naber, W.J.M.; Huskens, J.; van der Wiel, W.G. Local Doping of Silicon Using Nanoimprint Lithography and Molecular Monolayers. Adv. Mater. 2011, 23, 1346–1350. [Google Scholar] [CrossRef] [PubMed]
- Doran, J. Monolayer doping (MLD) for ultra-shallow junction MOSFET fabrication. J. Microelectron. Eng. Conf. 2018, 24, 16. [Google Scholar]
- Puglisi, R.A.; Caccamo, S.; D’Urso, L.; Fisichella, G.; Giannazzo, F.; Italia, M.; La Magna, A. A comprehensive study on the physicochemical and electrical properties of Si doped with the molecular doping method. Phys. Status Solidi (A) 2015, 212, 1685–1694. [Google Scholar] [CrossRef]
- Caccamo, S.; Puglisi, R.A. Carbon-Free Solution-Based Doping for Silicon. Nanomaterials 2021, 11, 2006. [Google Scholar] [CrossRef] [PubMed]
- Caccamo, S.; Puglisi, R.A.; Di Franco, S.; D’Urso, L.; Indelicato, V.; Italia, M.; Pannitteri, S.; La Magna, A. Silicon doped by molecular doping technique: Role of the surface layers of doped Si on the electrical characteristics. Mat. Sci. Semic. Proc. 2016, 42, 200–203. [Google Scholar] [CrossRef]
- Yi, R.; Mao, Y.; Shen, Y.; Chen, L. Self-assembled monolayers for batteries. J. Am. Chem. Soc. 2021, 143, 12897–12912. [Google Scholar] [CrossRef]
- Paniagua, S.A.; Giordano, A.J.; Smith, O.L.; Barlow, S.; Li, H.; Armstrong, N.R.; Pemberton, J.E.; Bredas, J.L.; Ginger, D.; Marder, S.R. Phosphonic acids for interfacial engineering of transparent conductive oxides. Chem. Rev. 2016, 116, 7117–7158. [Google Scholar] [CrossRef]
- Ulman, A. An Introduction to Ultrathin Organic Films: From Langmuir–Blodgett to Self–Assembly; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Schreiber, F. Self-assembled monolayers: From ‘simple’ model systems to biofunctionalized interfaces. J. Phys. Condens. Matter 2004, 16, R881. [Google Scholar] [CrossRef]
- Campbell, I.; Kress, J.; Martin, R.; Smith, D.; Barashkov, N.; Ferraris, J. Controlling charge injection in organic electronic devices using self-assembled monolayers. Appl. Phys. Lett. 1997, 71, 3528–3530. [Google Scholar] [CrossRef]
- Braun, S.; Salaneck, W.R.; Fahlman, M. Energy-level alignment at organic/metal and organic/organic interfaces. Adv. Mater. 2009, 21, 1450–1472. [Google Scholar] [CrossRef]
- Mirkin, C.A.; Ratner, M.A. Molecular electronics. Annu. Rev. Phys. Chem. 1992, 43, 719–754. [Google Scholar] [CrossRef]
- Garozzo, C.; Giannazzo, F.; Italia, M.; La Magna, A.; Privitera, V.; Puglisi, R.A. Radial junctions formed by conformal chemical doping for innovative hole-based solar cells. Mater. Sci. Eng. B 2013, 178, 686–690. [Google Scholar] [CrossRef]
- Park, C.J.; Jung, S.M.; Kim, J.H.; Shin, M.W. Conformal doping strategy for fin structures: Tailoring of dopant profile through multiple monolayer doping and capping layer control. Semicond. Sci. Technol. 2020, 35, 055028. [Google Scholar] [CrossRef]
- Puglisi, R.A.; Caccamo, S.; Bongiorno, C.; Fisicaro, G.; Genovese, L.; Goedecker, S.; Mannino, G.; La Magna, A. Direct observation of single organic molecules grafted on the surface of a silicon nanowire. Sci. Rep. 2019, 9, 5647. [Google Scholar] [CrossRef] [Green Version]
- Ho, J.C.; Yerushalmi, R.; Smith, G.; Majhi, P.; Bennett, J.; Halim, J.; Faifer, V.N.; Javey, A. Wafer-Scale, Sub-5 nm Junction Formation by Monolayer Doping and Conventional Spike Annealing. Nano Lett. 2009, 9, 725–730. [Google Scholar] [CrossRef] [Green Version]
- Ang, K.W.; Barnett, J.; Loh, W.Y.; Huang, J.; Min, B.G.; Hung, P.Y.; Ok, I.; Yum, J.H.; Bersuker, G.; Rodgers, M.; et al. 300 mm FinFET results utilizing conformal, damage free, ultra shallow junctions (Xj∼5 nm) formed with molecular monolayer doping technique. In Proceedings of the 2011 International Electron Devices Meeting, Washington, DC, USA, 5–7 December 2011; pp. 35.5.1–35.5.4. [Google Scholar] [CrossRef]
- Puglisi, R.A.; Garozzo, C.; Bongiorno, C.; Di Franco, S.; Italia, M.; Mannino, G.; Scalese, S.; La Magna, A. Molecular doping applied to Si nanowires array based solar cells. Sol. Energy Mater. Sol. Cells 2015, 132, 118–122. [Google Scholar] [CrossRef]
- Tzaguy, A.; Karadan, P.; Killi, K.; Hazut, O.; Amit, I.; Rosenwaks, Y.; Yerushalmi, R. Boron Monolayer Doping: Role of Oxide Capping Layer, Molecular Fragmentation, and Doping Uniformity at the Nanoscale. Adv. Mater. Interfaces 2020, 7, 1902198. [Google Scholar] [CrossRef]
- Pizzone, M.; Grimaldi, M.G.; La Magna, A.; Rahmani, N.; Scalese, S.; Adam, J.; Puglisi, R.A. Study of the Molecule Adsorption Process during the Molecular Doping. Nanomaterials 2021, 11, 1899. [Google Scholar] [CrossRef]
- Ye, L.; Pujari, S.P.; Zuilhof, H.; Kudernac, T.; de Jong, M.P.; van der Wiel, W.G.; Huskens, J. Controlling the Dopant Dose in Silicon by Mixed-Monolayer Doping. ACS Appl. Mater. Interfaces 2015, 7, 3231–3236. [Google Scholar] [CrossRef]
- Eberhardt, A.; Fenter, P.; Eisenberger, P. Growth kinetics in self-assembling monolayers: A unique adsorption mechanism. Surf. Sci. 1998, 397, L285–L290. [Google Scholar] [CrossRef]
- Doudevski, I.; Hayes, W.A.; Schwartz, D.K. Submonolayer Island Nucleation and Growth Kinetics during Self-Assembled Monolayer Formation. Phys. Rev. Lett. 1998, 81, 4927–4930. [Google Scholar] [CrossRef]
- Holmes, S.; Palmer, R.E.; Guo, Q. Diffusion of Au(CH3S)2 on Au(111) Observed with the Scanning Tunneling Microscope. J. Phys. Chem. C 2019, 123, 24104–24110. [Google Scholar] [CrossRef]
- Schwartz, D.K. Mechanisms and kinetics of self-assembled monolayer formation. Annu. Rev. Phys. Chem. 2001, 52, 107–137. [Google Scholar] [CrossRef] [PubMed]
- Valiokas, R.; Klenkar, G.; Tinazli, A.; Reichel, A.; Tampé, R.; Piehler, J.; Liedberg, B. Self-assembled monolayers containing terminal mono-, bis-, and tris-nitrilotriacetic acid groups: Characterization and application. Langmuir 2008, 24, 4959–4967. [Google Scholar] [CrossRef]
- Folkers, J.P.; Laibinis, P.E.; Whitesides, G.M.; Deutch, J. Phase behavior of two-component self-assembled monolayers of alkanethiolates on gold. J. Phys. Chem. 1994, 98, 563–571. [Google Scholar] [CrossRef]
- Yamada, R.; Wano, H.; Uosaki, K. Effect of temperature on structure of the self-assembled monolayer of decanethiol on Au (111) surface. Langmuir 2000, 16, 5523–5525. [Google Scholar] [CrossRef]
- Parikh, A.N.; Allara, D.L.; Azouz, I.B.; Rondelez, F. An intrinsic relationship between molecular structure in self-assembled n-alkylsiloxane monolayers and deposition temperature. J. Phys. Chem. 1994, 98, 7577–7590. [Google Scholar] [CrossRef]
- Veerbeek, J.; Ye, L.; Vijselaar, W.; Kudernac, T.; van der Wiel, W.G.; Huskens, J. Highly doped silicon nanowires by monolayer doping. Nanoscale 2017, 9, 2836–2844. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change. I General Theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change. II Transformation-Time Relations for Random Distribution of Nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Avrami, M. Granulation, Phase Change, and Microstructure Kinetics of Phase Change. III. J. Chem. Phys. 1941, 9, 177–184. [Google Scholar] [CrossRef]
- Khanna, Y.; Taylor, T. Comments and recommendations on the use of the Avrami equation for physico-chemical kinetics. Polym. Eng. Sci. 1988, 28, 1042–1045. [Google Scholar] [CrossRef]
- Herrero, C.; Scalliet, C.; Ediger, M.; Berthier, L. Two-step devitrification of ultrastable glasses. arXiv 2022, arXiv:2210.04775. [Google Scholar]
- Lelito, J. Crystallization kinetics analysis of the amorphouse Mg72Zn24Ca4 alloy at the isothermal annealing temperature of 507 K. Materials 2020, 13, 2815. [Google Scholar] [CrossRef] [PubMed]
- Malekan, M.; Rashidi, R. Effective role of minor silicon addition on crystallization kinetics of Cu50Zr43Al7 bulk metallic glass. Appl. Phys. A 2021, 127, 1–9. [Google Scholar] [CrossRef]
- Sinha, I.; Mandal, R. Avrami exponent under transient and heterogeneous nucleation transformation conditions. J. -Non-Cryst. Solids 2011, 357, 919–925. [Google Scholar] [CrossRef] [Green Version]
- Kisuuk, P. The sticking probabilities of gases chemisorbed on the surfaces of solids—II. J. Phys. Chem. Solids 1958, 5, 78–84. [Google Scholar] [CrossRef]
- von Keudell, A. Surface processes during thin-film growth. Plasma Sources Sci. Technol. 2000, 9, 455. [Google Scholar] [CrossRef]
- Pimpinelli, A.; Tumbek, L.; Winkler, A. Scaling and exponent equalities in island nucleation: Novel results and application to organic films. J. Phys. Chem. Lett. 2014, 5, 995–998. [Google Scholar] [CrossRef]
- Mulheran, P.; Blackman, J. Capture zones and scaling in homogeneous thin-film growth. Phys. Rev. B 1996, 53, 10261. [Google Scholar] [CrossRef]
- Körner, M.; Einax, M.; Maass, P. Capture numbers and island size distributions in models of submonolayer surface growth. Phys. Rev. B 2012, 86, 085403. [Google Scholar] [CrossRef] [Green Version]
- Shelemin, A.; Pleskunov, P.; Kousal, J.; Drewes, J.; Hanuš, J.; Ali-Ogly, S.; Nikitin, D.; Solař, P.; Kratochvíl, J.; Vaidulych, M.; et al. Nucleation and growth of magnetron-sputtered Ag nanoparticles as witnessed by time-resolved small angle X-ray scattering. Part. Part. Syst. Charact. 2020, 37, 1900436. [Google Scholar] [CrossRef]
- Sabbar, E.H.; Poddar, N.N.; Amar, J.G. Irreversible island nucleation and growth with anomalous diffusion in d > 2. Phys. A Stat. Mech. Its Appl. 2018, 508, 567–576. [Google Scholar] [CrossRef]
- Oliveira, T.; Reis, F.A. Scaling of island size and capture zone distributions in submonolayer growth. Phys. Rev. B 2011, 83, 201405. [Google Scholar] [CrossRef] [Green Version]
- Puglisi, R.A.; Nicotra, G.; Lombardo, S.; Spinella, C.; Ammendola, G.; Bileci, M.; Gerardi, C. Exclusion zone surrounding silicon nanoclusters formed by rapid thermal chemical vapour deposition on SiO2. Surf. Sci. 2004, 550, 119. [Google Scholar] [CrossRef]
- Puglisi, R.A.; Nicotra, G.; Lombardo, S.; Spinella, C.; Ammendola, G.; Gerardi, C. Partial self-ordering observed in silicon nanoclusters deposited on silicon oxide substrates by chemical vapor deposition. Phys. Rev. B 2005, 71, 125322. [Google Scholar] [CrossRef]
- Venables, J.; Spiller, G. Nucleation and growth of thin films. In Surface Mobilities on Solid Materials; Springer: Berlin/Heidelberg, Germany, 1983; pp. 341–404. [Google Scholar]

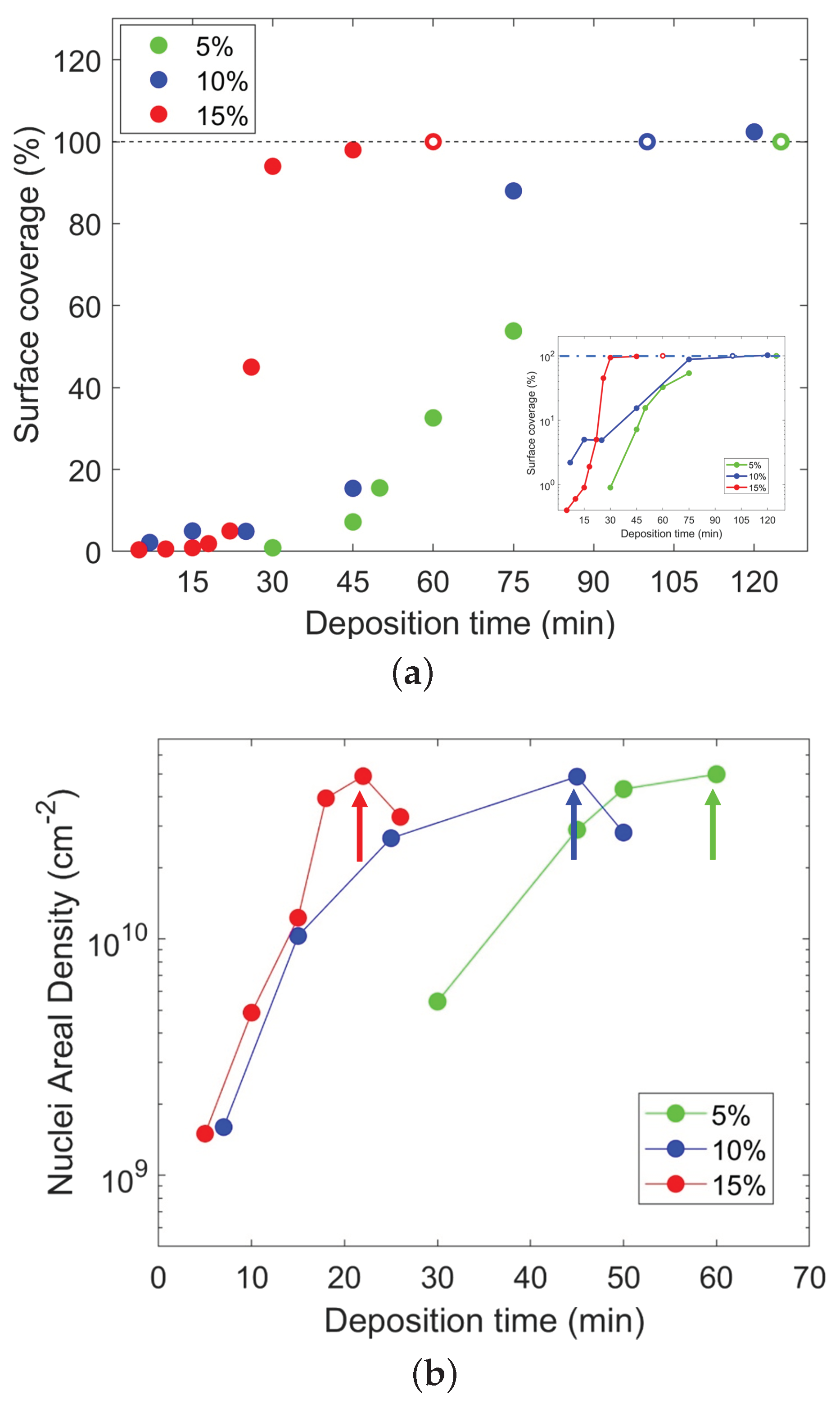


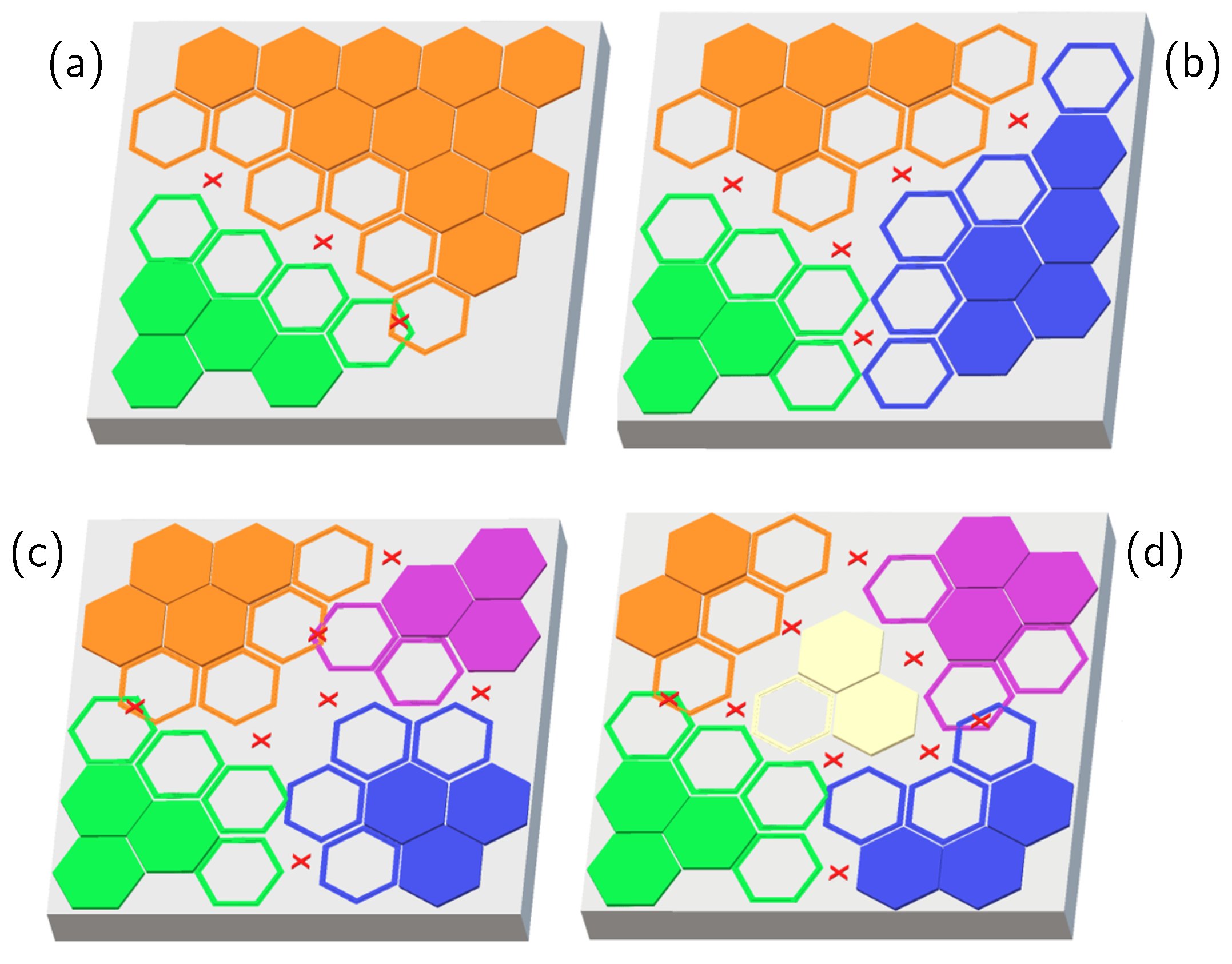
| Percentage [%] | [min] | k [a.u.] | n [a.u.] | LS Error [a.u.] |
|---|---|---|---|---|
| 5 | 6.53 | 68.18 | 3.86 | 9.70 × 10 |
| 10 | 0.00 | 64.45 | 4.94 | 8.59 × 10 |
| 15 | 11.50 | 15.73 | 6.66 | 5.99 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pizzone, M.; Grimaldi, M.G.; La Magna, A.; Scalese, S.; Adam, J.; Puglisi, R.A. Molecule Clustering Dynamics in the Molecular Doping Process of Si(111) with Diethyl-propyl-phosphonate. Int. J. Mol. Sci. 2023, 24, 6877. https://doi.org/10.3390/ijms24086877
Pizzone M, Grimaldi MG, La Magna A, Scalese S, Adam J, Puglisi RA. Molecule Clustering Dynamics in the Molecular Doping Process of Si(111) with Diethyl-propyl-phosphonate. International Journal of Molecular Sciences. 2023; 24(8):6877. https://doi.org/10.3390/ijms24086877
Chicago/Turabian StylePizzone, Mattia, Maria Grazia Grimaldi, Antonino La Magna, Silvia Scalese, Jost Adam, and Rosaria A. Puglisi. 2023. "Molecule Clustering Dynamics in the Molecular Doping Process of Si(111) with Diethyl-propyl-phosphonate" International Journal of Molecular Sciences 24, no. 8: 6877. https://doi.org/10.3390/ijms24086877
APA StylePizzone, M., Grimaldi, M. G., La Magna, A., Scalese, S., Adam, J., & Puglisi, R. A. (2023). Molecule Clustering Dynamics in the Molecular Doping Process of Si(111) with Diethyl-propyl-phosphonate. International Journal of Molecular Sciences, 24(8), 6877. https://doi.org/10.3390/ijms24086877











