Flavonoid Oxidation Potentials and Antioxidant Activities-Theoretical Models Based on Oxidation Mechanisms and Related Changes in Electronic Structure
Abstract
1. Introduction
| Flavonoids | A Site | Ep1/V (pH = 3) | Ep1/V (pH = 7) | AOSPRad | ΔNACCat-Neut (var. 1) | ΔNACRad-Anion (var. 2) | ΔNACRad-Neut (var. 3) | Mean of var. 1–3 | ΔNACCat.-Neut. (on active O) | % var.1 (on C) | % var.1 (on O) | % var.1 (on H) | NOH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3,3′,4′THF | 4′ | 0.456 b | 0.197 b | 0.527 | 0.353 | 0.333 | 0.249 | 0.312 | 0.222 | 0.454 | 0.337 | 0.209 | 3 |
| 2 | 3′,4′DHF | 4′ | 0.513 b | 0.283 b | 0.631 | 0.373 | 0.387 | 0.272 | 0.344 | 0.222 | 0.479 | 0.311 | 0.209 | 2 |
| 3 | 3HF | 3 | 0.751 b | 0.566 b | 0.697 | 0.428 | 0.44 | 0.239 | 0.369 | 0.257 | 0.576 | 0.243 | 0.181 | 1 |
| 4 | 5HF | 5 | 1.164 b | 0.909 b | 0.845 | 0.516 | 0.493 | 0.358 | 0.456 | 0.287 | 0.724 | 0.098 | 0.178 | 1 |
| 5 | 7,8DHF | 8 | 0.456 b | 0.225 b | 0.538 | 0.339 | 0.361 | 0.217 | 0.306 | 0.275 | 0.468 | 0.29 | 0.242 | 2 |
| 6 | Apigenin | 4′ | 0.928 c | 0.696 g | 0.792 | 0.467 | 0.46 | 0.335 | 0.421 | 0.258 | 0.629 | 0.135 | 0.235 | 3 |
| 7 | Chrysin | 5 | 1.162 c | 0.956 g | 0.923 | 0.508 | 0.493 | 0.375 | 0.459 | 0.286 | 0.711 | 0.169 | 0.119 | 2 |
| 8 | Galangin | 3 | 0.655 c | 0.430 b | 0.733 | 0.437 | 0.444 | 0.244 | 0.375 | 0.253 | 0.585 | 0.257 | 0.158 | 3 |
| 9 | Luteolin | 4′ | 0.513 b | 0.288 g | 0.631 | 0.366 | 0.38 | 0.266 | 0.337 | 0.222 | 0.47 | 0.327 | 0.202 | 4 |
| 10 | Quercetin | 4′ | 0.435 c | 0.180 g | 0.519 | 0.350 | 0.325 | 0.248 | 0.308 | 0.224 | 0.451 | 0.343 | 0.206 | 5 |
| 11 | Myricetin | 4′ | 0.351 c | 0.089 d | 0.364 | 0.281 | 0.253 | 0.229 | 0.254 | 0.263 | 0.381 | 0.425 | 0.194 | 6 |
| 12 | EGC | 4′ | 0.307 e | 0.028 e | 0.471 | 0.283 | 0.293 | 0.248 | 0.275 | 0.278 | 0.392 | 0.353 | 0.255 | 6 |
| 13 | EC | 4′ | 0.390 f | 0.150 f | 0.621 | 0.372 | 0.374 | 0.28 | 0.342 | 0.206 | 0.469 | 0.293 | 0.239 | 5 |
| 14 | Morin | 3 | 0.458 c | 0.227 g | 0.591 | 0.380 | 0.335 | 0.239 | 0.318 | 0.214 | 0.483 | 0.354 | 0.163 | 5 |
| 15 | EGCG | 4′ | 0.367 c | 0.051 e | 0.472 | 0.298 | 0.294 | 0.248 | 0.28 | 0.273 | 0.374 | 0.341 | 0.285 | 5 |
| 16 | ECG | 4′ | 0.477 c | 0.162 f | 0.622 | 0.362 | 0.374 | 0.276 | 0.337 | 0.207 | 0.456 | 0.284 | 0.259 | 4 |
| 17 | Naringenin | 4′ | 0.929 c | 0.704 h | 0.790 | 0.480 | 0.462 | 0.356 | 0.433 | 0.279 | 0.666 | 0.049 | 0.285 | 3 |
| 18 | Kaempferid | 3 | 0.584 c | 0.369 h | 0.654 | 0.414 | 0.407 | 0.233 | 0.351 | 0.193 | 0.513 | 0.297 | 0.19 | 3 |
| 19 | Dyhidromyricetin | 4′ | 0.354 d | 0.098 d | 0.470 | 0.305 | 0.302 | 0.245 | 0.284 | 0.276 | 0.421 | 0.362 | 0.217 | 6 |
| 20 | Rutin | 4′ | 0.504 c | 0.267 h | 0.610 | 0.361 | 0.367 | 0.271 | 0.333 | 0.225 | 0.466 | 0.325 | 0.209 | 4 |
| 21 | Hesperetin | 3’ | 0.737 i | 0.510 i | 0.751 | 0.423 | 0.429 | 0.322 | 0.391 | 0.288 | 0.594 | 0.095 | 0.311 | 3 |
| 22 | Daidzein | 4’ | 0.795 i | 0.592 i | 0.772 | 0.451 | 0.432 | 0.328 | 0.404 | 0.236 | 0.59 | 0.098 | 0.312 | 2 |
| 23 | Kaempferol | 3 | 0.498 i | 0.235 i | 0.659 | 0.419 | 0.409 | 0.234 | 0.354 | 0.202 | 0.525 | 0.293 | 0.182 | 4 |
| 24 | Acacetin | 5 | 1.174 i | 0.952 i | 0.925 | 0.509 | 0.491 | 0.374 | 0.458 | 0.284 | 0.711 | 0.187 | 0.103 | 2 |
| 25 | Naringin | 4’ | 0.959 i | 0.732 i | 0.791 | 0.466 | 0.463 | 0.348 | 0.426 | 0.275 | 0.643 | 0.065 | 0.292 | 2 |
| 26 | Neohesperidin | 3’ | 0.766 i | 0.549 i | 0.750 | 0.424 | 0.424 | 0.322 | 0.39 | 0.287 | 0.595 | 0.09 | 0.315 | 2 |
| 27 | Hesperidin | 3’ | 0.739 i | 0.542 i | 0.750 | 0.424 | 0.424 | 0.322 | 0.39 | 0.287 | 0.595 | 0.09 | 0.315 | 2 |
| 28 | Quercitrin | 4’ | 0.500 i | 0.270 i | 0.610 | 0.361 | 0.367 | 0.271 | 0.333 | 0.225 | 0.466 | 0.325 | 0.209 | 4 |
| 29 | Gossypin | 4’ | 0.416 i | 0.132 i | 0.515 | 0.349 | 0.328 | 0.244 | 0.307 | 0.212 | 0.443 | 0.356 | 0.201 | 5 |
| 30 | 567THF | 6 | 0.411 a | 0.162 a | 0.409 | 0.304 | 0.293 | 0.233 | 0.277 | 0.276 | 0.42 | 0.388 | 0.192 | 3 |
| 31 | Fisetin | 4’ | 0.435 a | 0.183 a | 0.524 | 0.355 | 0.331 | 0.252 | 0.313 | 0.223 | 0.457 | 0.328 | 0.215 | 4 |
| 32 | 37DHF | 3 | 0.643 a | 0.474 a | 0.726 | 0.436 | 0.448 | 0.246 | 0.377 | 0.255 | 0.585 | 0.243 | 0.172 | 2 |
| 33 | 4′7DHF | 4’ | 0.948 a | 0.692 a | 0.793 | 0.474 | 0.466 | 0.339 | 0.426 | 0.257 | 0.638 | 0.121 | 0.241 | 2 |
| 34 | Genistein | 4’ | 0.809 a | 0.613 a | 0.773 | 0.450 | 0.433 | 0.328 | 0.404 | 0.239 | 0.591 | 0.103 | 0.306 | 3 |
| 35 | 6HF | 6 | 0.975 a | 0.751 a | 0.742 | 0.449 | 0.467 | 0.322 | 0.413 | 0.264 | 0.61 | 0.187 | 0.202 | 1 |
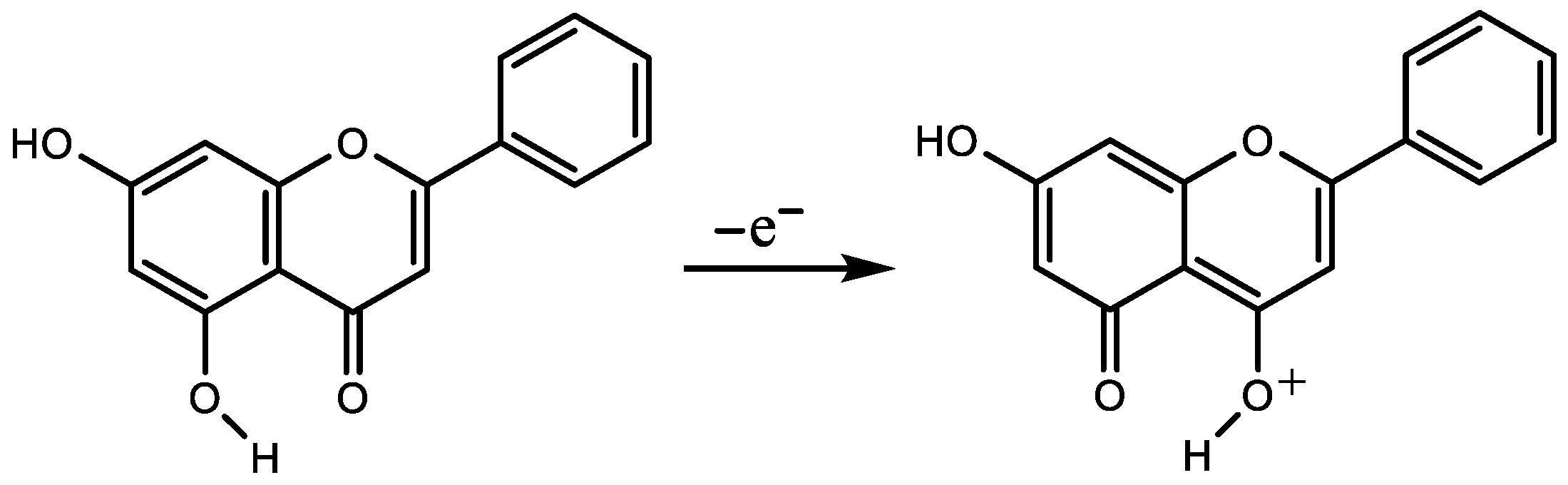
2. Determination of an Active OH Group
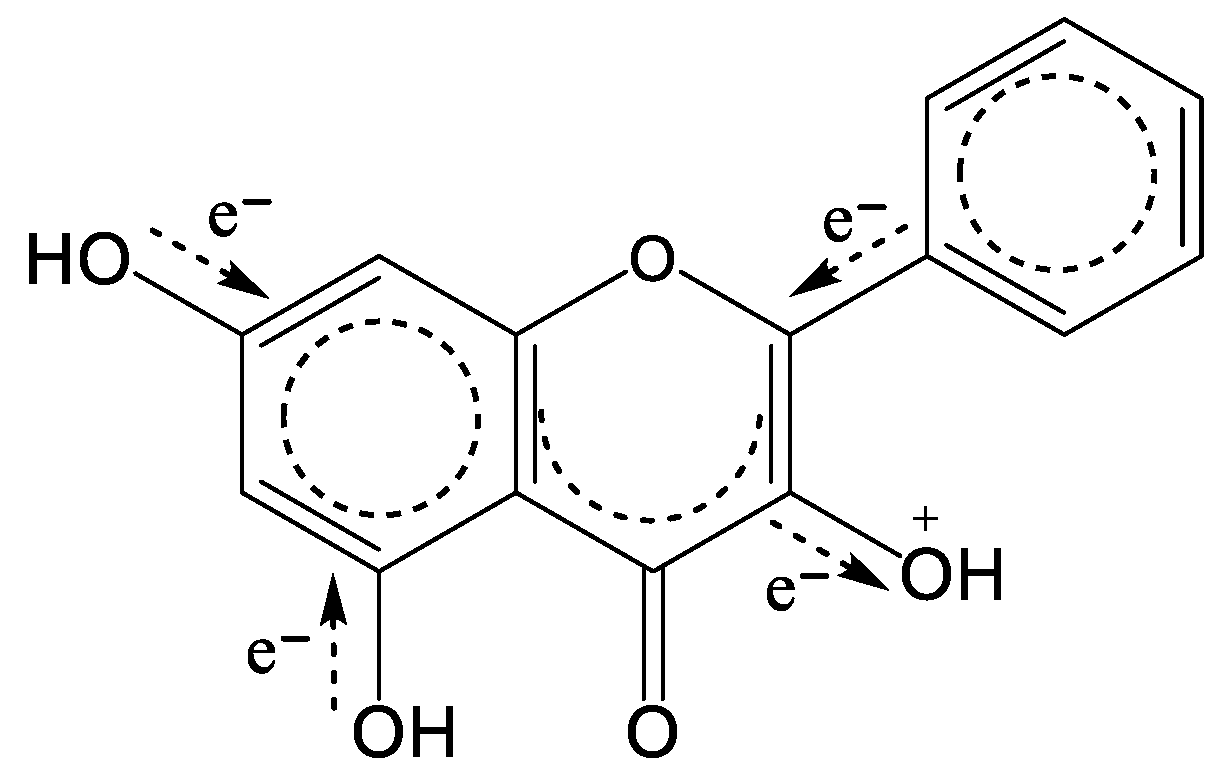
3. Quantification of Changes in Electronic Structure upon Electrochemical Oxidation
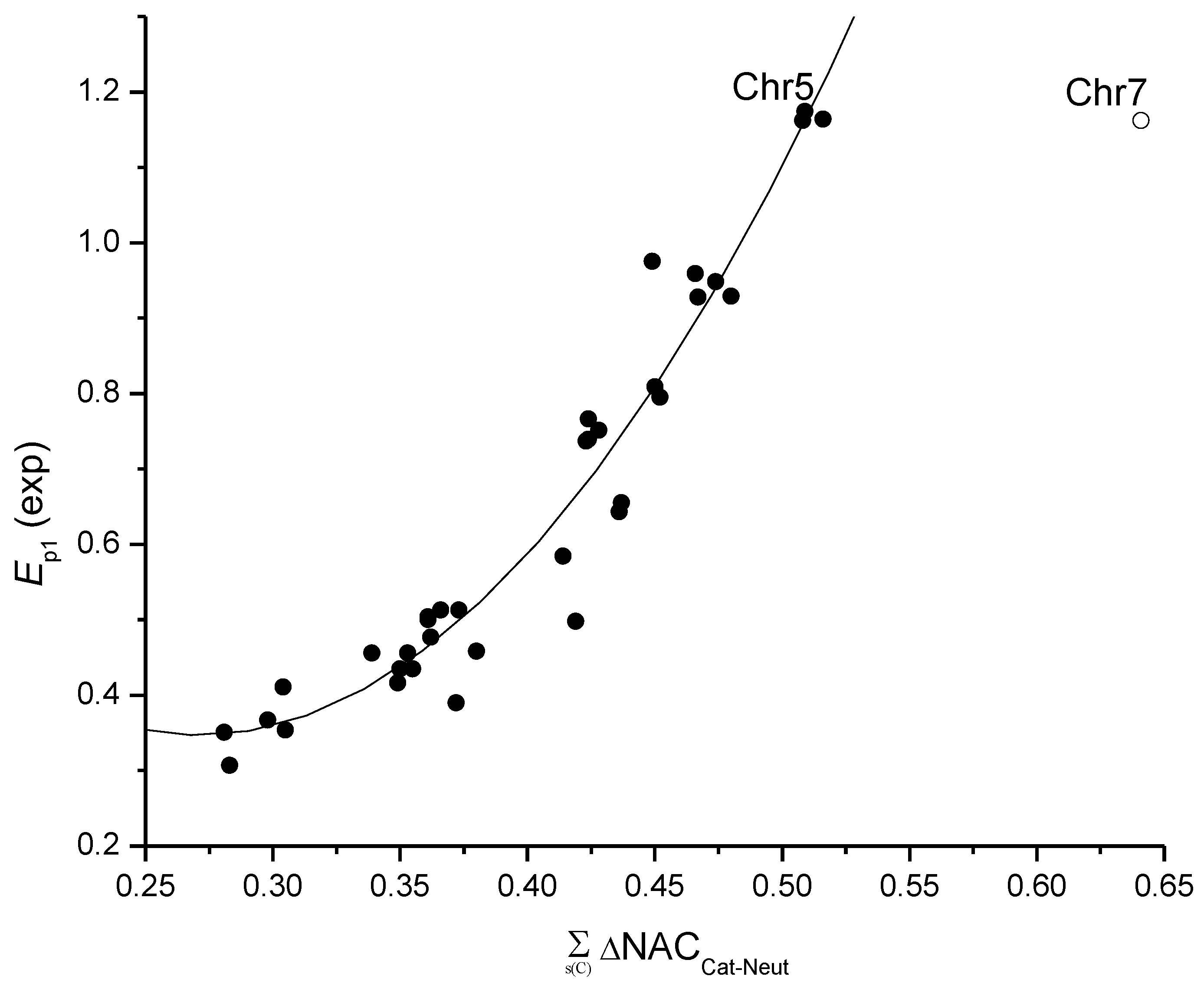
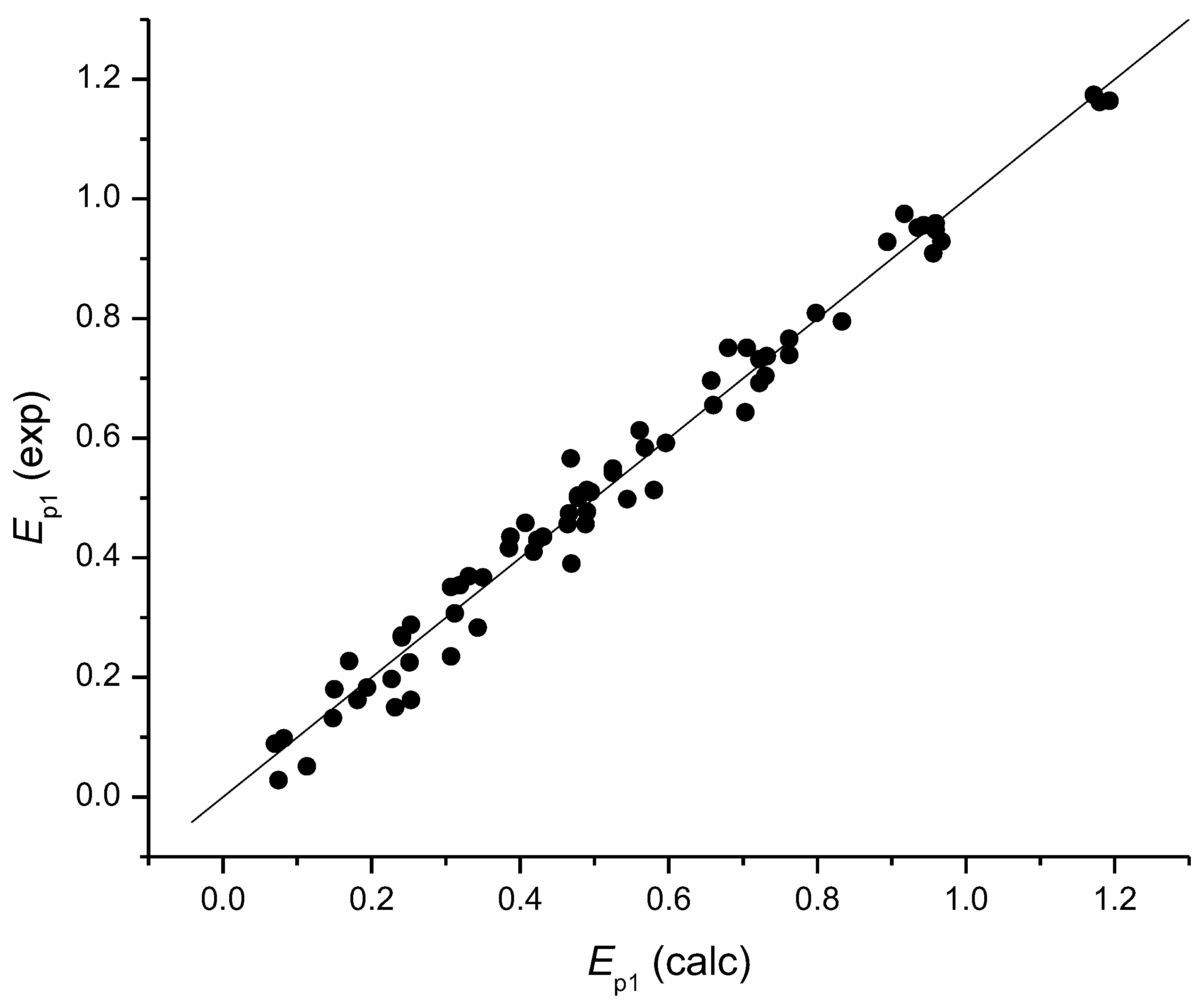
4. The Models for the Estimation of the First Electrochemical Oxidation Potential Ep1
5. Calculation of Variables

6. Antioxidant Activity and the First Oxidation Potential
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Jovanović, S.V.; Steenken, S.; Tošić, M.; Marjanović, B.; Šimić, M.G. Flavonoids as Antioxidants. J. Am. Chem. Soc. 1994, 116, 4846–4851. [Google Scholar] [CrossRef]
- Jovanović, S.V.; Steenken, S.; Hara, Y.; Šimić, M.G. Reduction potentials of flavonoid and model phenoxyl radicals. Which ring in flavonoids is responsible for antioxidant activity? J. Chem. Soc. Perkin Trans. 1996, 2, 2497–2504. [Google Scholar] [CrossRef]
- Leopoldini, M.; Russo, N.; Toscano, M. The molecular basis of working mechanism of natural polyphenolic antioxidants. Food Chem. 2011, 125, 288–306. [Google Scholar] [CrossRef]
- Cai, Q.; Rahn, R.O.; Zhang, R. Dietary flavonoids, quercetin, luteolin and genistein, reduce oxidative DNA damage and lipid peroxidation and quench free radicals. Cancer Lett. 1997, 119, 99–107. [Google Scholar] [CrossRef] [PubMed]
- Santos, A.C.; Uyemura, S.A.; Lopes, J.L.C.; Bazon, J.N.; Mingatto, F.E.; Curti, C. Effect of naturally occurring flavonoids on lipid peroxidation and membrane permeability transition in mitochondria. Free Radic. Biol. Med. 1998, 24, 1455–1461. [Google Scholar] [CrossRef] [PubMed]
- Plaza, M.; Batista, Â.G.; Cazarin, C.B.B.; Sandahl, M.; Turner, C.; Östman, E.; Júnior, M.R.M. Characterization of antioxidant polyphenols from Myrciaria jaboticaba peel and their effects on glucose metabolism and antioxidant status: A pilot clinical study. Food Chem. 2016, 211, 185–197. [Google Scholar] [CrossRef] [PubMed]
- Ravishankar, D.; Rajora, A.K.; Greco, F.; Osborn, H.M.I. Flavonoids as prospective compounds for anti-cancer therapy. Int. J. Biochem. Cell Biol. 2013, 45, 2821–2831. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Suo, W.; Zhang, X.; Yang, Y.; Zhao, W.; Li, H.; Ni, Q. Targeting epigenetics in diabetic cardiomyopathy: Therapeutic potential of flavonoids. Biomed. Pharmacother. 2023, 157, 114025. [Google Scholar] [CrossRef] [PubMed]
- Miličević, A.; Jovanović, I.N.; Miletić, G.I. Changes in electronic structures of flavonoids upon electrochemical oxidation and a theoretical model for the estimation of the first oxidation potential. Electrochim. Acta 2018, 284, 742–750. [Google Scholar] [CrossRef]
- Miličević, A.; Miletić, G.I.; Jovanović, I.N. Electrochemical oxidation of flavonoids: PM6 and DFT for elucidating electronic changes and modelling oxidation potential. J. Mol. Liq. 2019, 285, 551–556. [Google Scholar] [CrossRef]
- Miličević, A.; Miletić, G.I.; Jovanović, I.N. Electrochemical oxidation of flavonoids: PM6 and DFT for elucidating electronic changes and modelling oxidation potential (part II). J. Mol. Liq. 2019, 295, 111730. [Google Scholar] [CrossRef]
- Miličević, A.; Jovanović, I.N. The relationship between the first oxidation potential and changes in electronic structures upon the electrochemical oxidation of flavonoids: Approach to O-glycosyl, galloyl and methoxy substituents. J. Mol. Liq. 2021, 335, 116223. [Google Scholar] [CrossRef]
- Jovanović, I.N.; Miličević, A. A new, simplified model for the estimation of polyphenol oxidation potentials based on the number of OH groups. Arch. Ind. Hyg. Toxicol. 2017, 68, 93–98. [Google Scholar] [CrossRef]
- Jadreško, D.; Miličević, A.; Jovanović, I.N. Reactivity of flavonoids toward superoxide radical: An electrochemical approach. Electrochim. Acta 2022, 421, 140501. [Google Scholar] [CrossRef]
- Komorsky-Lovrić, Š.; Novak, I. Abrasive stripping voltammetry of myricetin and dihydromyricetin. Electrochim. Acta 2013, 98, 153–156. [Google Scholar] [CrossRef]
- Novak, I.; Šeruga, M.; Komorsky-Lovric, Š. Electrochemical Characterization of Epigallocatechin Gallate Using Square-Wave Voltammetry. Electroanalysis 2009, 21, 1019–1025. [Google Scholar] [CrossRef]
- Novak, I.; Šeruga, M.; Komorsky-Lovrić, Š. Square-wave and cyclic voltammetry of epicatechin gallate on glassy carbon electrode. J. Electroanal. Chem. 2009, 631, 71–75. [Google Scholar] [CrossRef]
- Jovanović, I.N.; Miličević, A. A model for the estimation of oxidation potentials of polyphenols. J. Mol. Liq. 2017, 241, 255–259. [Google Scholar] [CrossRef]
- Miličević, A. Application of Changes in Atomic Charges Resulting from Different Electrochemical Oxidation Mechanisms for the Estimation of the First Oxidation Potential of Flavonoids. MATCH Commun. Math. Comput. Chem. 2022, 88, 67–78. [Google Scholar] [CrossRef]
- Miličević, A. Estimating flavonoid oxidation potentials: Mechanisms and charge-related regression models. Arh. Hig. Rada Toksikol. 2023, 74, 99–105. [Google Scholar] [CrossRef]
- Miličević, A. The relationship between antioxidant activity, first electrochemical oxidation potential, and spin population of flavonoid radicals. Arh. Hig. Rada Toksikol. 2019, 70, 134–139. [Google Scholar] [CrossRef] [PubMed]
- Van Acker, S.A.B.E.; Van Den Berg, D.J.; Tromp, M.N.J.L.; Griffioen, D.H.; Van Bennekom, W.P.; Van Der Vijgh, W.J.F. Bast, Structural aspects of antioxidant activity of flavonoids. Free Radic. Biol. Med. 1996, 20, 331–342. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Kotani, A.; Arai, K.; Kusu, F. Estimation of the Antioxidant Activities of Flavonoids from Their Oxidation Potentials. Anal. Sci. 2001, 17, 599–604. [Google Scholar] [CrossRef] [PubMed]
- Hotta, H.; Nagano, S.; Ueda, M.; Tsujino, Y.; Koyama, J.; Osakai, T. Higher radical scavenging activities of polyphenolic antioxidants can be ascribed to chemical reactions following their oxidation. Biochim. Biophys. Acta Gen. Subj. 2002, 1572, 123–132. [Google Scholar] [CrossRef] [PubMed]
- Arteaga, J.F.; Ruiz-Montoya, M.; Palma, A.; Alonso-Garrido, G.; Pintado, S.; Rodríguez-Mellado, J.M. Comparison of the Simple Cyclic Voltammetry (CV) and DPPH Assays for the Determination of Antioxidant Capacity of Active Principles. Molecules 2012, 17, 5126–5138. [Google Scholar] [CrossRef]
- Zhang, D.; Chu, L.; Liu, Y.; Wang, A.; Ji, B.; Wu, W.; Zhou, F.; Wei, Y.; Cheng, Q.; Cai, S.; et al. Analysis of the antioxidant capacities of flavonoids under different spectrophotometric assays using cyclic voltammetry and density functional theory. J. Agric. Food Chem. 2011, 59, 10277–10285. [Google Scholar] [CrossRef] [PubMed]
- Gil, E.S.; Couto, R.O. Flavonoid electrochemistry: A review on the electroanalytical applications. Braz. J. Pharmacogn. 2013, 23, 542–558. [Google Scholar] [CrossRef]
- Alov, P.; Tsakovska, I.; Pajeva, I. Computational Studies of Free Radical-Scavenging Properties of Phenolic Compounds. Curr. Top. Med. Chem. 2015, 15, 85–104. [Google Scholar] [CrossRef]
- Amić, D.; Davidović-Amić, D.; Bešlo, D.; Rastija, V.; Lučić, B.; Trinajstić, N. SAR and QSAR of the Antioxidant Activity of Flavonoids. Curr. Med. Chem. 2007, 14, 827–845. [Google Scholar] [CrossRef]
- Amić, A.; Marković, Z.; Marković, J.M.D.; Stepanić, V.; Lučić, B.; Amić, D. Towards an improved prediction of the free radical scavenging potency of flavonoids: The significance of double PCET mechanisms. Food Chem. 2014, 152, 578–585. [Google Scholar] [CrossRef]
- Amić, D.; Lučić, B.; Kovačević, G.; Trinajstić, N. Bond dissociation enthalpies calculated by the PM3 method confirm activity cliffs in radical scavenging of flavonoids. Mol. Divers. 2009, 13, 27–36. [Google Scholar] [CrossRef] [PubMed]
- Nikolić, K.M. Theoretical study of phenolic antioxidants properties in reaction with oxygen-centered radicals. J. Mol. Struct. Theochem 2006, 774, 95–105. [Google Scholar] [CrossRef]
- Tabart, J.; Kevers, C.; Pincemail, J.; Defraigne, J.O.; Dommes, J. Comparative antioxidant capacities of phenolic compounds measured by various tests. Food Chem. 2009, 113, 1226–1233. [Google Scholar] [CrossRef]
- Foti, M.C. Use and Abuse of the DPPH• Radical. J. Agric. Food Chem. 2015, 63, 8765–8776. [Google Scholar] [CrossRef] [PubMed]
- Speisky, H.; Shahidi, F.; de Camargo, A.C.; Fuentes, J. Revisiting the Oxidation of Flavonoids: Loss, Conservation or Enhancement of Their Antioxidant Properties. Antioxidants 2022, 11, 133. [Google Scholar] [CrossRef] [PubMed]
- Pietta, P.-G. Flavonoids as Antioxidants. J. Nat. Prod. 2000, 63, 1035–1042. [Google Scholar] [CrossRef] [PubMed]
- Atala, E.; Fuentes, J.; Wehrhahn, M.J.; Speisky, H. Quercetin and related flavonoids conserve their antioxidant properties despite undergoing chemical or enzymatic oxidation. Food Chem. 2017, 234, 479–485. [Google Scholar] [CrossRef] [PubMed]
- Heřmánková, E.; Zatloukalová, M.; Biler, M.; Sokolová, R.; Bancířová, M.; Tzakos, A.G.; Křen, V.; Kuzma, M.; Trouillas, P.; Vacek, J. Redox properties of individual quercetin moieties. Free Radic. Biol. Med. 2019, 143, 240–251. [Google Scholar] [CrossRef] [PubMed]
- Martinez, S.; Valek, L.; Petrović, Ž.; Metikoš-Huković, M.; Piljac, J. Catechin antioxidant action at various pH studied by cyclic voltammetry and PM3 semi-empirical calculations. J. Electroanal. Chem. 2005, 584, 92–95. [Google Scholar] [CrossRef]
- Lemańska, K.; Szymusiak, H.; Tyrakowska, B.; Zieliński, R.; Soffers, A.E.M.F.; Rietjens, I.M.C.M. The influence of pH on antioxidant properties and the mechanism of antioxidant action of hydroxyflavones. Free Radic. Biol. Med. 2001, 31, 869–881. [Google Scholar] [CrossRef]
- Woldu, A.S.; Mai, J. Computation of the bond dissociation enthalpies and free energies of hydroxylic antioxidants using the ab initio Hartree-Fock method. Redox Rep. 2012, 17, 252–274. [Google Scholar] [CrossRef] [PubMed]
- Parker, V.D. Homolytic bond (H-A) dissociation free energies in solution. Applications of the standard potential of the (H+/H.bul.) couple. J. Am. Chem. Soc. 1992, 114, 7458–7462. [Google Scholar] [CrossRef]
- Bizarro, M.M.; Cabral, B.J.C.; Santos, R.M.B.D.; Simões, J.A.M. Substituent effects on the O–H bond dissociation enthalpies in phenolic compounds: Agreements and controversies + erratum. Pure Appl. Chem. 1999, 71, 1249–1256. [Google Scholar] [CrossRef]
- Marković, Z.; Milenković, D.; Đorović, J.; Marković, J.M.D.; Stepanić, V.; Lučić, B.; Amić, D. PM6 and DFT study of free radical scavenging activity of morin. Food Chem. 2012, 134, 1754–1760. [Google Scholar] [CrossRef] [PubMed]
- Janeiro, P.; Brett, A.M.O. Solid State Electrochemical Oxidation Mechanisms Of Morin in Aqueous Media. Electroanalysis 2005, 17, 733–738. [Google Scholar] [CrossRef]
- Musialik, M.; Kuzmicz, R.; Pawłowski, T.S.; Litwinienko, G. Acidity of Hydroxyl Groups: An Overlooked Influence on Antiradical Properties of Flavonoids. J. Org. Chem. 2009, 74, 2699–2709. [Google Scholar] [CrossRef] [PubMed]
- Gerson, F.; Huber, W. Electron Spin Resonance Spectroscopy of Organic Radicals; Wiley-VCH: Weinheim, Germany, 2003. [Google Scholar]
- Arroyo-Currás, N.; Rosas-García, V.; Videa, M. Substituent Inductive Effects on the Electrochemical Oxidation of Flavonoids Studied by Square Wave Voltammetry and Ab Initio Calculations. Molecules 2016, 21, 1422. [Google Scholar] [CrossRef] [PubMed]
- De Almeida, W.B.; Taguchi, A.T.; Dikanov, S.A.; Wraight, C.A.; O’Malley, P.J. The 2-Methoxy Group Orientation Regulates the Redox Potential Difference between the Primary (Q A) and Secondary (Q B) Quinones of Type II Bacterial Photosynthetic Reaction Centers. J. Phys. Chem. Lett. 2014, 5, 2506–2509. [Google Scholar] [CrossRef] [PubMed]
- Robinson, H.H.; Kahn, S.D. Interplay of Substituent Conformation and Electron Affinity in Quinone Models of Quinone Reductases. J. Am. Chem. Soc. 1990, 112, 4728–4731. [Google Scholar] [CrossRef]
- Miličević, A. A follow-up on the hesperetin issue in modelling the first electrochemical oxidation potential and antioxidant activity of flavonoids. Arch. Ind. Hyg. Toxicol. 2024, 75, 85–86. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miličević, A. Flavonoid Oxidation Potentials and Antioxidant Activities-Theoretical Models Based on Oxidation Mechanisms and Related Changes in Electronic Structure. Int. J. Mol. Sci. 2024, 25, 5011. https://doi.org/10.3390/ijms25095011
Miličević A. Flavonoid Oxidation Potentials and Antioxidant Activities-Theoretical Models Based on Oxidation Mechanisms and Related Changes in Electronic Structure. International Journal of Molecular Sciences. 2024; 25(9):5011. https://doi.org/10.3390/ijms25095011
Chicago/Turabian StyleMiličević, Ante. 2024. "Flavonoid Oxidation Potentials and Antioxidant Activities-Theoretical Models Based on Oxidation Mechanisms and Related Changes in Electronic Structure" International Journal of Molecular Sciences 25, no. 9: 5011. https://doi.org/10.3390/ijms25095011
APA StyleMiličević, A. (2024). Flavonoid Oxidation Potentials and Antioxidant Activities-Theoretical Models Based on Oxidation Mechanisms and Related Changes in Electronic Structure. International Journal of Molecular Sciences, 25(9), 5011. https://doi.org/10.3390/ijms25095011






