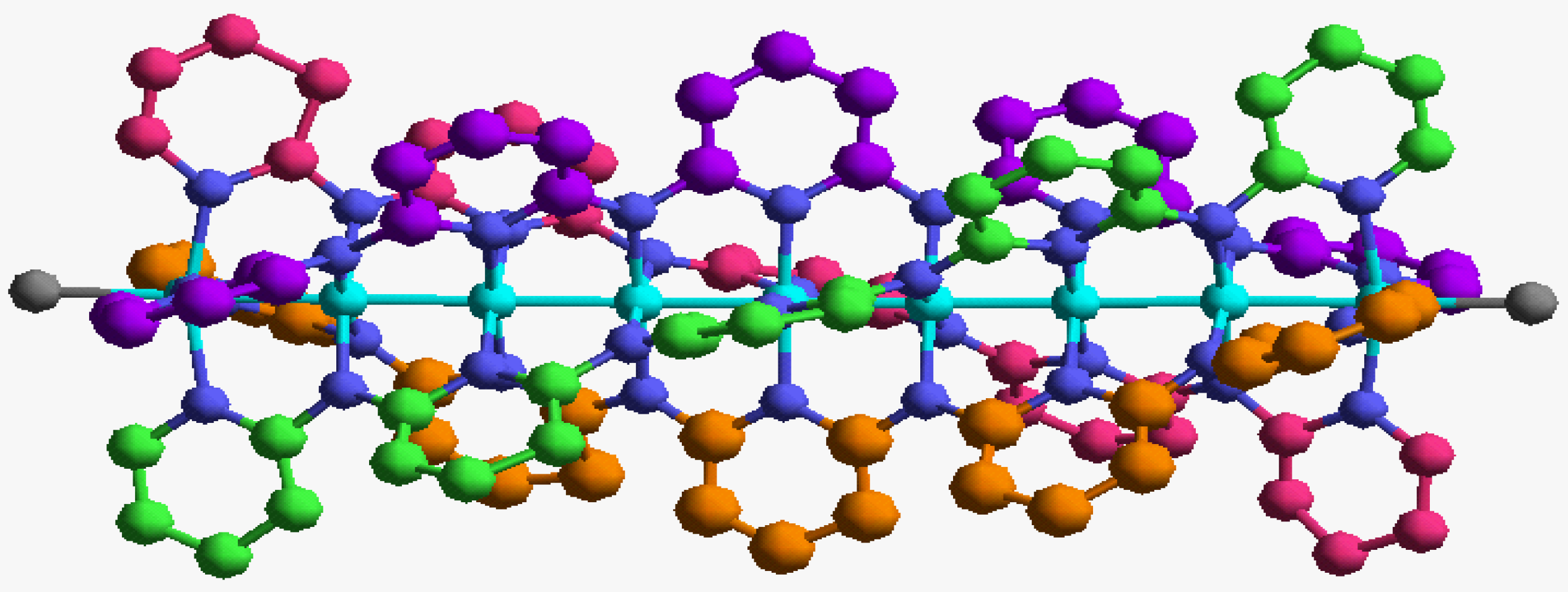
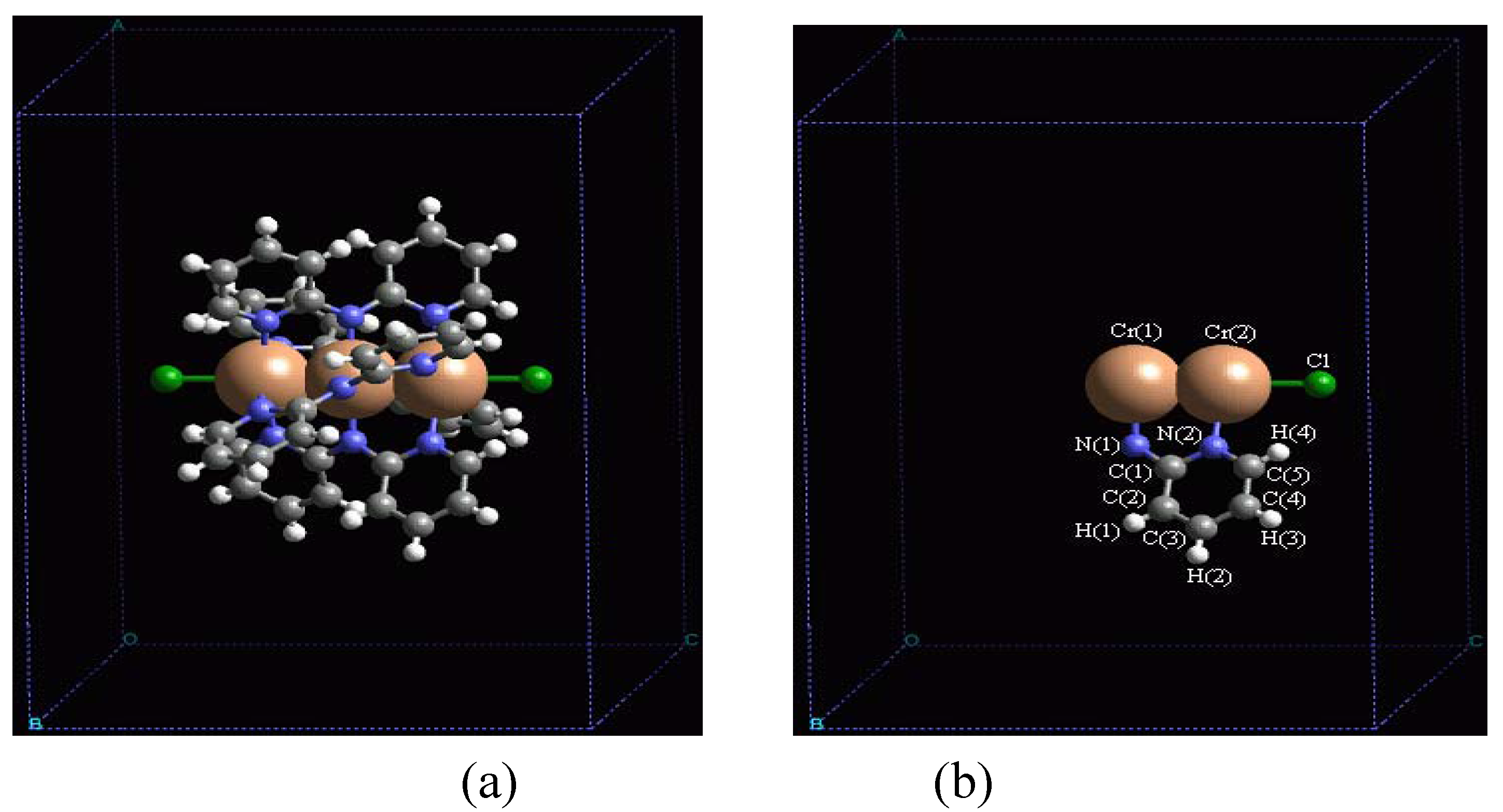
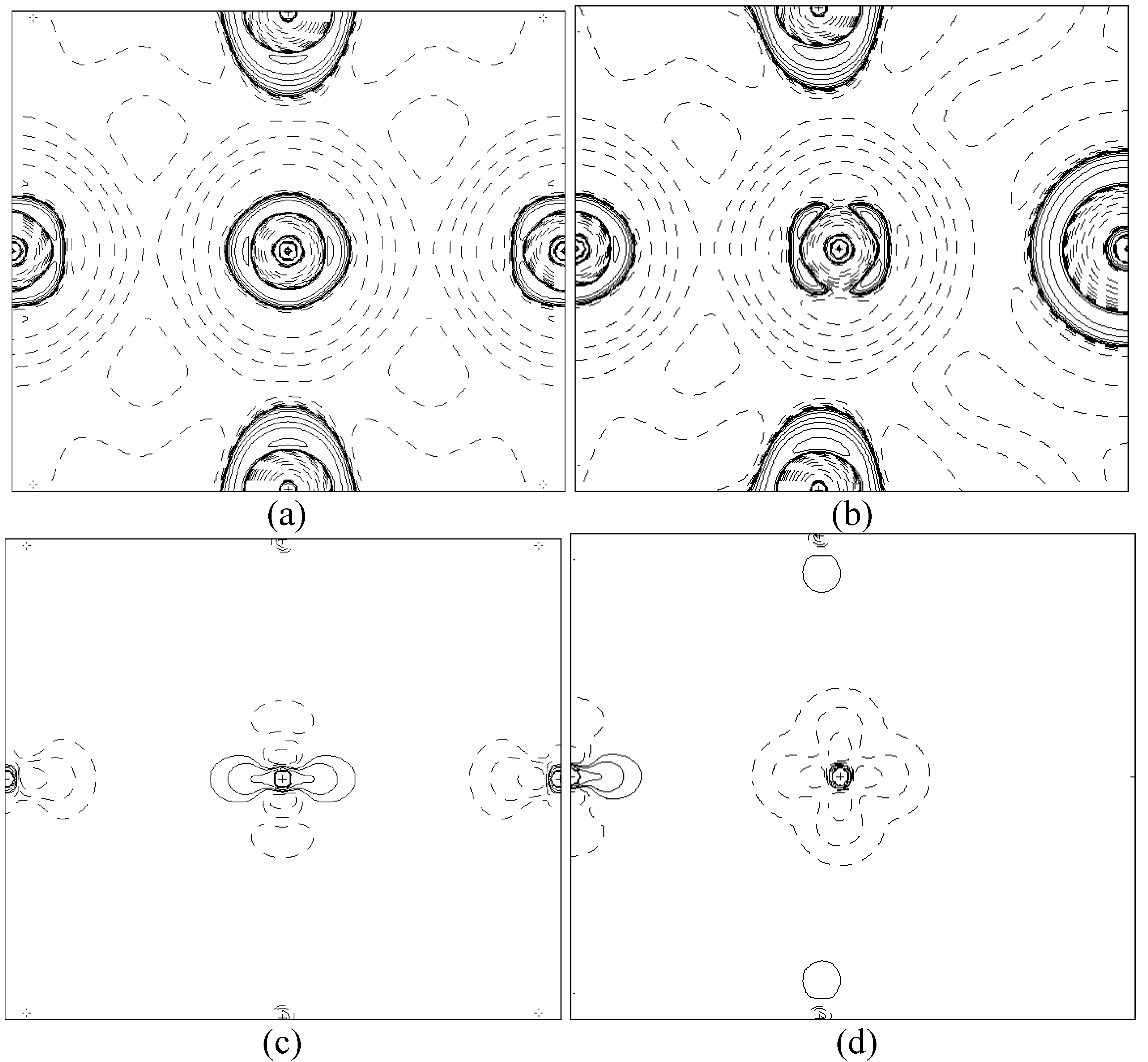
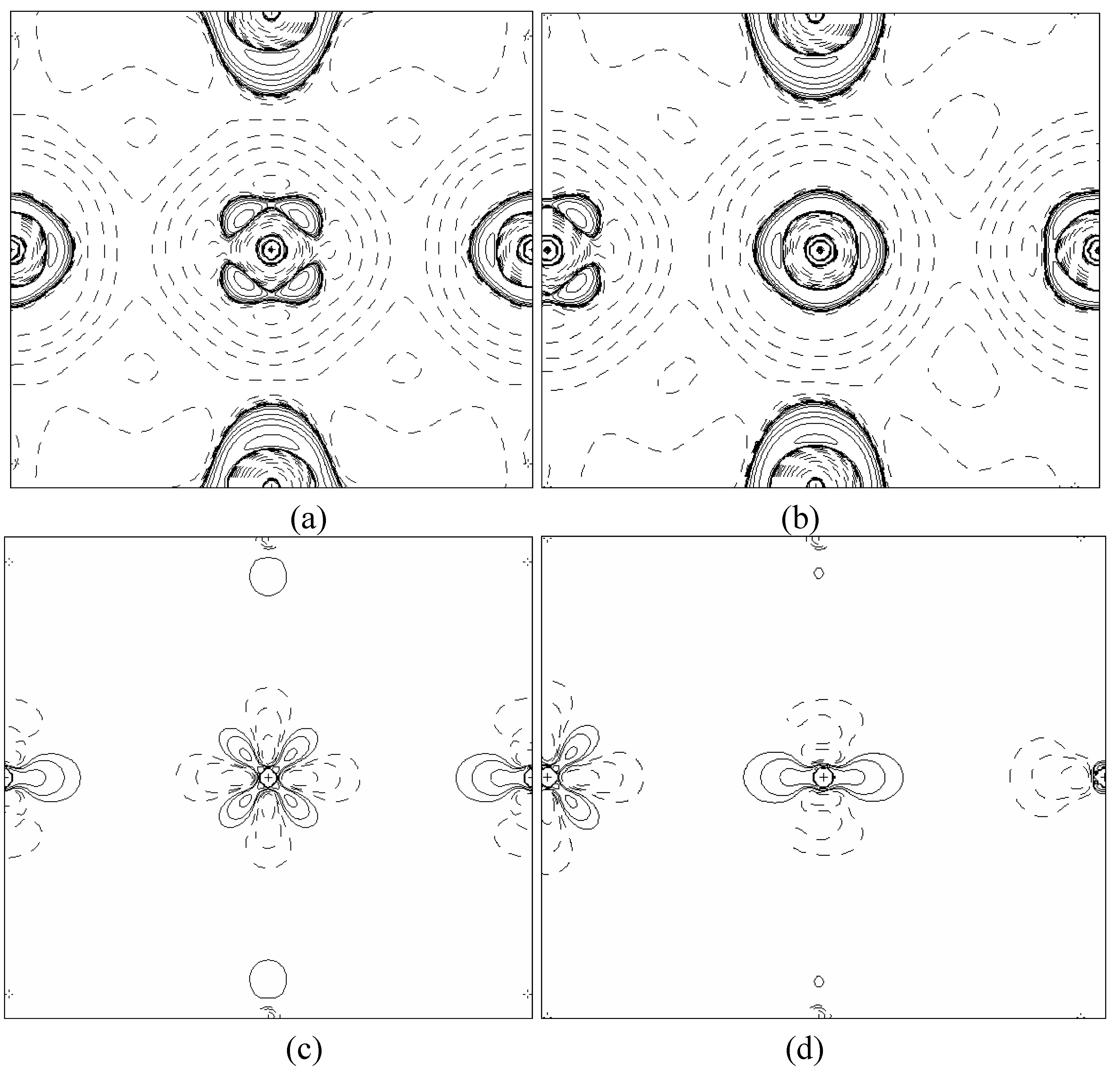
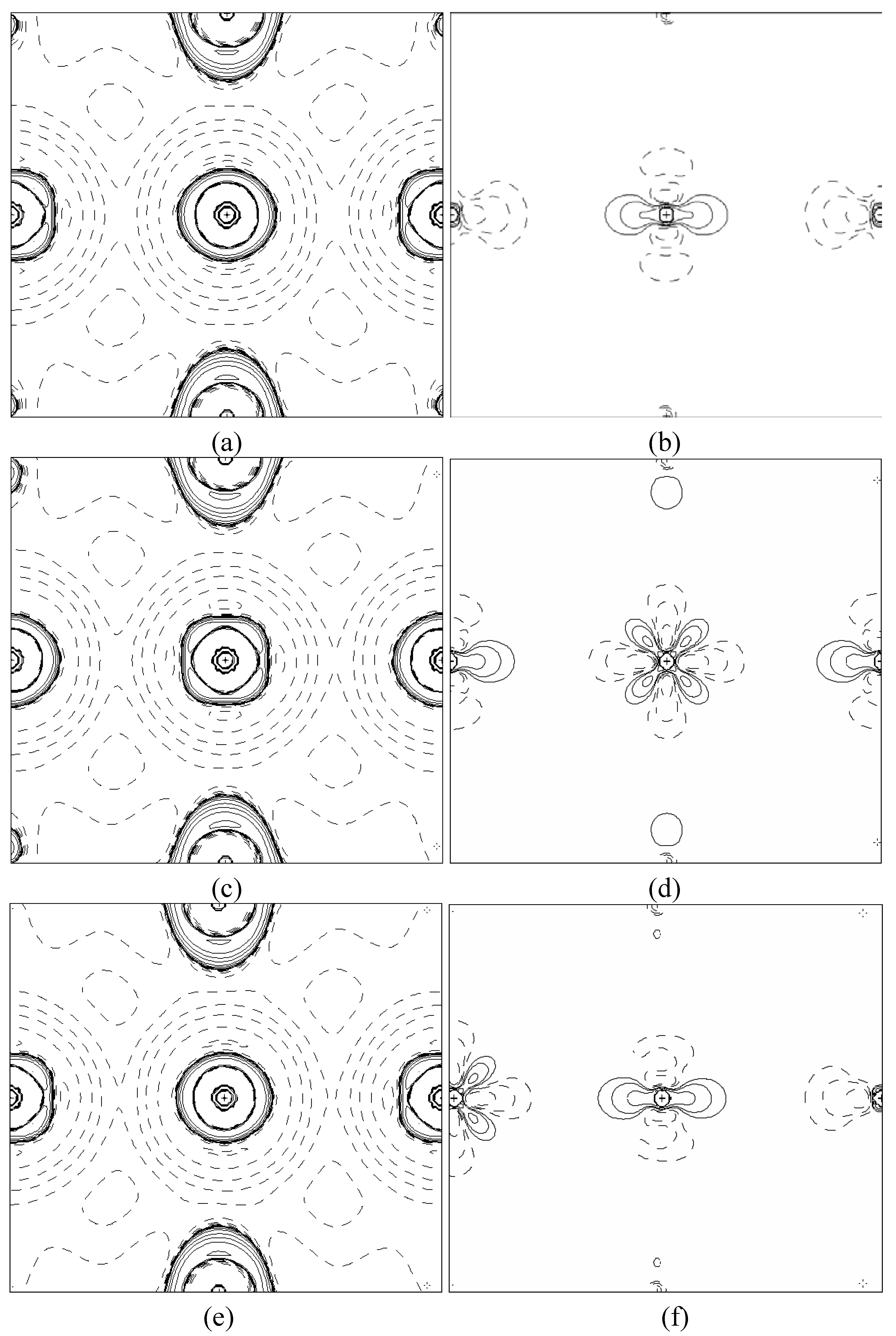
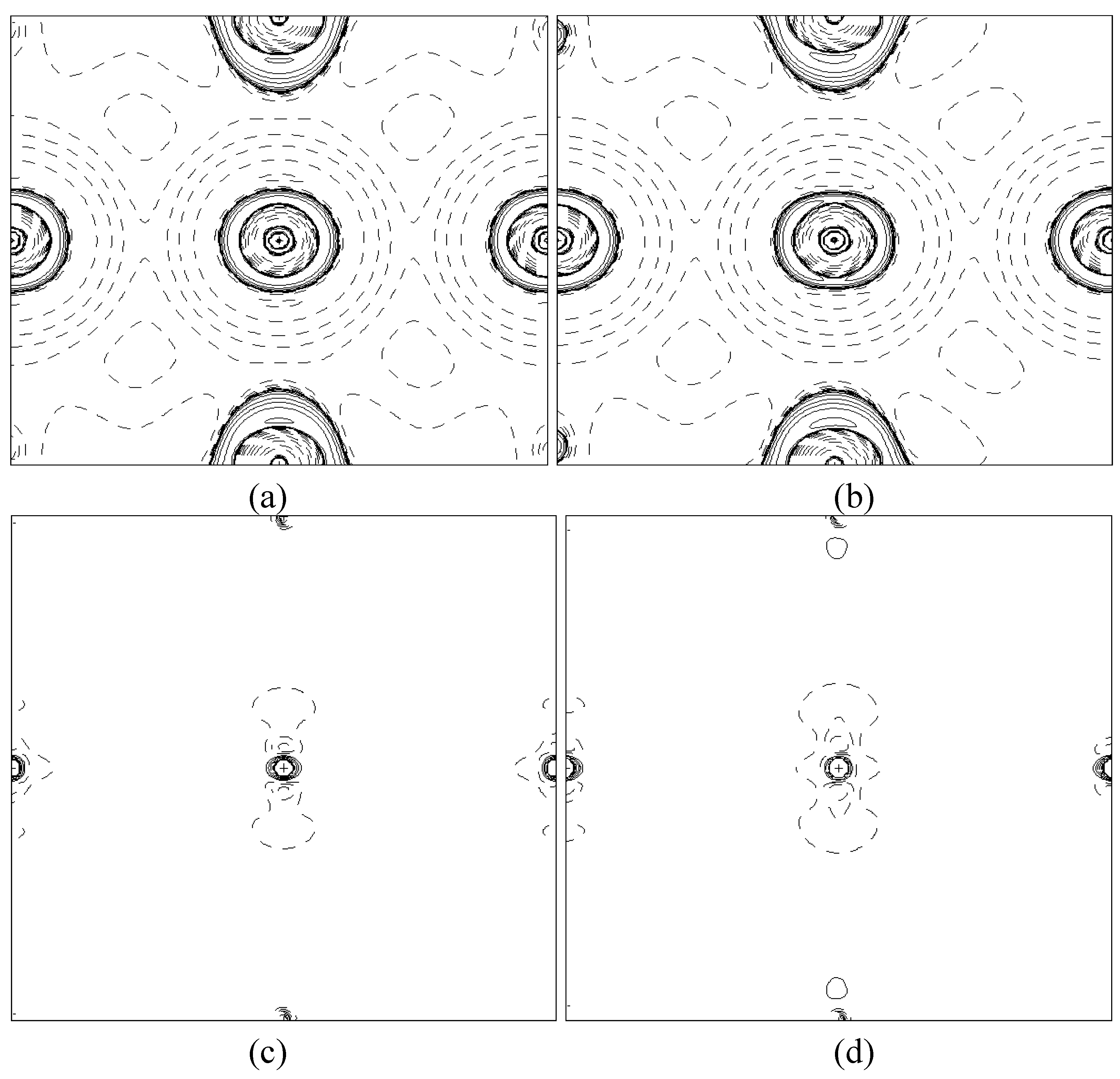
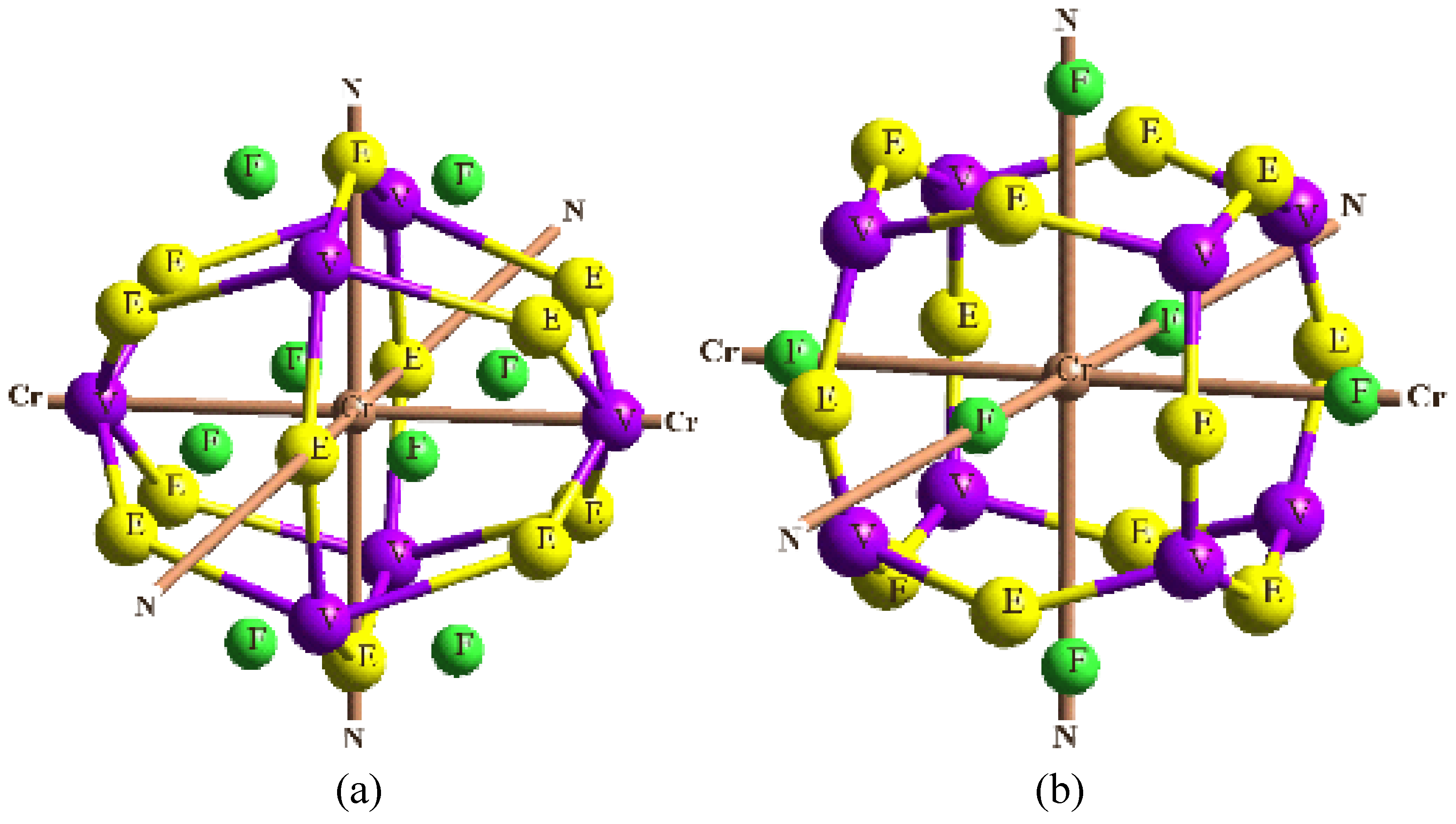
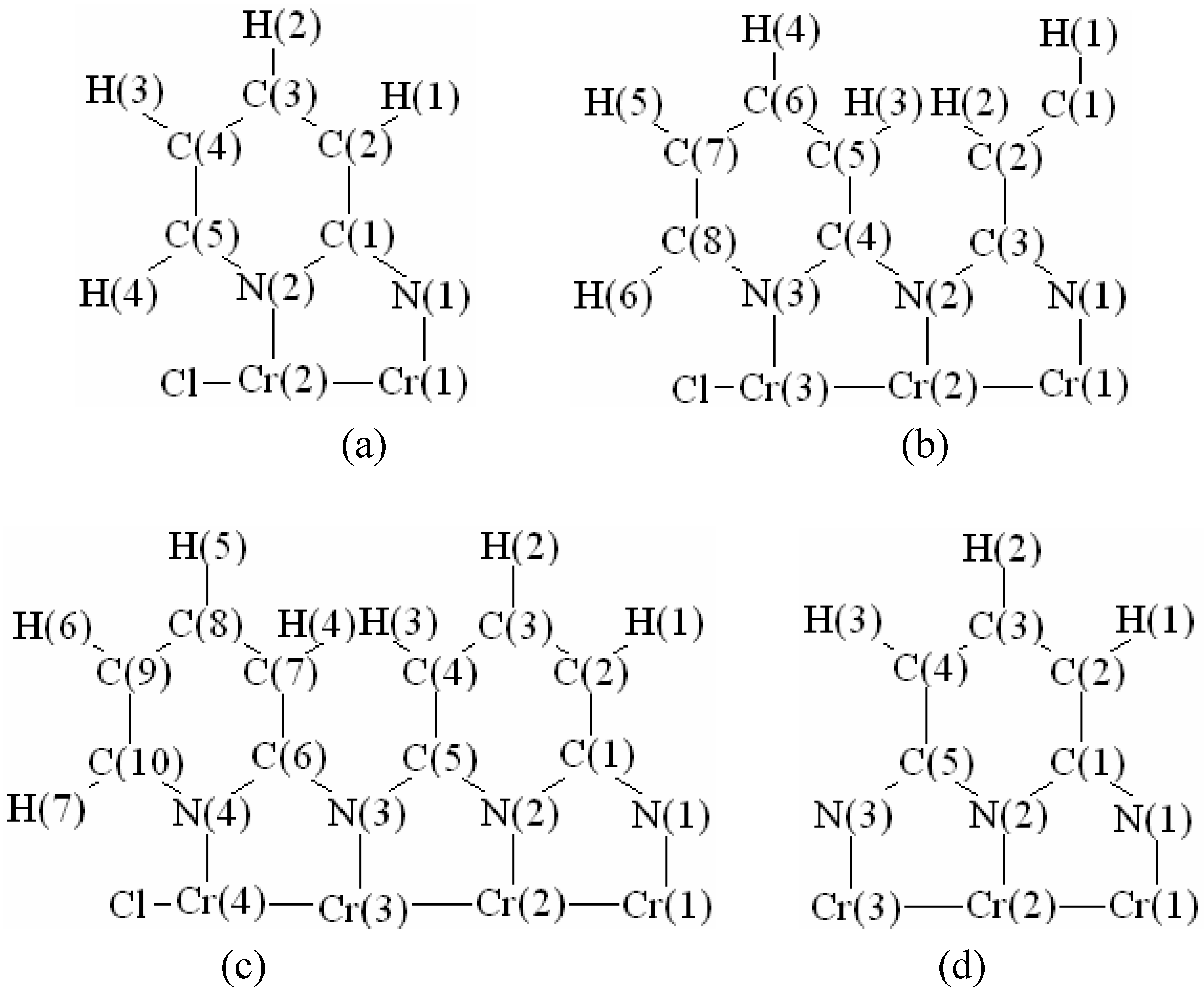In order to validate our model-construction of the HILOM nanowire, we employ the topological analysis of the electron density to investigate the general pattern of the electron density shared by the Cr LOM complexes with various number of Cr ions. This tool is based on the atoms in molecules (AIM) theory developed by Bader [
20,
21,
22]. The topological properties of the electron distribution of a molecular or crystalline system are based on the gradient vector field of the electron density ∇ρ(
r), and on the Laplacian of the electron density ∇
2ρ(
r). The electron density distribution of the HILOM nanowires is described by ρ(
r), where
r is a vector in ordinary three-dimensional space and
X represents a particular set of the nuclear coordinates in space corresponding to the nuclear configurations of the HILOM nanowires. An Atom in molecule is defined as region of real three-dimensional space bounded by a zero-flux surface. The points on this surface satisfy ∇ρ(
r)∇
n(
r)=0 where
n(
r) is the unit vector normal to this surface at
r. Two interacting atoms in a molecule form a critical point in the electron density, where ∇ρ(
r)=0, called a bond critical point (BCP) and abbreviated as
rb. The pairs of gradient paths, which originate at a BCP and terminate at neighboring nuclei, define a line, through which electron distribution, ρ(
r), is a maximum with respect to any lateral displacement. Linking two nuclei in a molecule with a nuclear equilibrium configuration, this kind of lines are called atomic interaction lines implying that two atoms are bonded to one another and in this instance this line is called a bond path. The network of bond paths for a molecule in a given nuclear configuration
X defines the molecular graph. Such a topological graph usually corresponds to the commonly drawn chemical bond network. The electron density at the BCP, ρ(
r b) ≡ρ
b, is related to the bond order and therefore the bond strength [
23]. The eigenvalues (λ
i, i = 1,3) of the Hessian matrix of ρ
b, whose sum equals ∇
2ρ(
r), indicate how rapidly the electron density changes on moving away from the BCP and represent the curvatures of the electron density along the principal axes of curvature. The critical point is labeled by two values, rank and signature. The rank of a critical point, denoted by ω, is equal to the number of non-zero eigenvalues of ρ at the critical point. The signature, denoted by σ, is simply the algebraic sum of the signs of the eigenvalues. For a normal single bond, such as the C-C bond in ethane, the two negative curvatures (λ
1 and λ
2), which are perpendicular to bond line, are equal. However, in the case of a double bond, one curvature (in the direction of the π bond) will be much smaller than the other two. The difference may be described by the ellipticity, ε, of the bond which is defined as ε=(λ
1/λ
2)-1, in which λ
2 is the curvature of smallest magnitude. For a single bond λ
1 ≈ λ
2 and therefore ε ≈ 0. For a double bond |λ
1| > |λ
2| and therefore ε > 0. For the CC bond in an aromatic system, in, general, ε is in between a typical single and typical double bond. For symmetrical triple bonds, since λ
1 ≈ λ
2, ε is equal or close to zero. One can also determine the regions of space wherein the electron density is locally concentrated or depleted by inspecting the Laplacian of the electron density, ∇
2ρ(
r). ρ(
r) is greater than the average of its values over an infinitesimal sphere centered on
r, where ∇
2ρ(
r) < 0, and ρ(
r) is less than its average when ∇
2ρ(
r) > 0. The quantum shells of an atom are divided into an inner region (core) and outer one (valence). The portion of the valence shell over which ∇
2ρ(
r) < 0 is called the valence shell charge concentration (VSCC). Within this shell is the sphere over whose surface the valence electronic charge is maximally and uniformly concentrated. The structure of the Laplacian of charge density for atoms in molecules is most easily visualized in terms of the minimum in ∇
2ρ(
r), a polyhedron whose numbers of vertexes (
V), edges (
E), faces (
F) and the only cage critical point within the sphere obey the Poincare-Hopf relationship [
24]. As a peculiar case, this is easily transformed into Euler’s polyhedral formula [
25]
V-E+F=2. Extrema in the Lapacian of ρ are classified by rank and signature in the same way as are critical points in the charge density. The local minimum (charge concentration, CC) in valence shell of an atom defines the vertexes,
V. The unique pair of trajectories of the gradient of ∇
2ρ(
r) that originate at a (3,-1) critical point or saddle point between two minima and terminate at neighboring vertexes defines
E of the polyhedron. The set of trajectories that arise at a (3,+1) critical point define the faces F of the polyhedron. The face critical points are where ∇
2ρ(
r) attains a local maximum (charge depletion). This is called an atomic graph. [
26] Another important parameter to characterize the atomic interaction is the total energy density
H(
r), which is defined as
H(
r)=
G(
r)+
V(
r) where
G(
r) is a local kinetic energy density and
V(
r) is the average field experienced by one electron in a many-particle system (or the local potential energy density). The sign of
H(
r) determines whether the accumulation of charge at a point
r is stabilization [
H(
r)<0] or destabilization [
H(
r) >0]. Investigation of a variety of chemical bonds revealed [
27,
28] that the covalent bonding feature (shared interaction) also can be characterized by a predominance of local potential energy density
V(
r) at the BCP reflected by
H(
rb)≡
Hb <0. The larger the minus
Hb value is, the stronger the covalent bond is. On the other hand, the closed shell interactions, van der Waals interactions or ionic bonds are characterized by a positive
Hb.[
21,
27,
28] Therefore, it is reasonable to say that the sign of
Hb can provide bonding characterization in addition to the properties of ρ
b, ∇
2ρ
b and ε. We choose TOPOND98 [
29] because it takes molecular symmetry and periodicity in proper account, at variance with other software packages for the electron density topological analysis. This peculiarity makes TOPOND98 a unique tool to perform the topological analysis of the electron density in crystals and in large molecular systems.