Experimental Determination of Pseudorotation Potentials for Disubstituted Cyclopentanes Based on Spin–Spin Coupling Constants

Abstract

Complete analysis of ¹H-NMR spectra of trans-1,2-dichlorocyclopentane and trans-1,2-dibromocyclopentane was performed with use of our total lineshape fitting algorithm VALISA. The resulting high precision spin-spin coupling constants were then applied to the problem of conformational analysis, yielding a continuos potential of pseudorotation for the studied compounds in CDCl₃, CCl₄, and CD₃CN solutions.

Introduction

Modern development of NMR is centered on new, more powerful, spectrometers, and multi-dimensional techniques, which aid greatly in analysis of complex first-order NMR systems [1]. However, obtaining spin-spin coupling constants (SSCCs) from strongly coupled systems remains a non-trivial problem. Knowledge of SSCCs is vital for conformational analysis of organic molecules, but this problem hinders its experimental study even for systems as simple as cyclopentanes. To this day, there has been no experimental study of substituted cyclopentane pseudorotation in isotropic liquid phase, based on NMR data. Early attempts to analyse the spectra of these compounds [2] produced limited information, which was insufficient for accurate conformational description.

The problem of complete analysis of tightly coupled NMR spin systems, i.e. determination of chemical shifts and SSCCs, has been addressed in a number of ways, each having its own strengths and weaknesses. One is the approach first introduced by Castellano and Bothner-By [3], where observable peak frequencies f_i are compared to theoretical transition frequencies ψ_i, and the resulting functional (1) is iteratively minimized:

$${\chi }_{laocoon}^2(\overline{p})={\displaystyle \sum _{i=1}^N}{\left(f_i-{\psi }_i(\overline{p})\right)}^2.$$

(1)

The well-known major drawback of this approach is the requirement of spectral assignment – manual procedure to establish which experimental peak corresponds to which theoretical transition. There have been successful attempts of turning the assignment procedure automatic, most promising probably being PAREMUS [4], where it was done with help of pattern recognition theory. Another problem associated with Castellano and Bothner-By approach is the loss of spectral information. Of all data points received from the spectrometer, only a few dozens, rarely more than a hundred are actually used in the functional (1). This problem is dealt with by a group of methods known as integral transform (IT) analysis, introduced by Diel et al [5], and developed currently by Laatikainen [6,7]. Here instead of discrete frequency values, the minimized functional χ² is built upon special functionals, known as ITs, each dependant on a fragment of spectral lineshape, surrounding a given peak.

The other classical approach is the total line shape fitting analysis, first developed by Heinzer [8], where from the very beginning the entire NMR spectrum is treated as a single entity, without any assignments or deconvolution procedures. The minimized functional (2) depends on every data point in a uniform manner:

$${\chi }_{lineshape}^2(\overline{p})={\displaystyle \sum _f}{\left(y^{\exp }(f)-y^{calc}(f;\overline{p})\right)}^2,$$

(2)

where y(f) is spectral amplitude at frequency f, and p is parameter vector, which includes both common spectral parameters (chemical shifts and SSCCs) and specific lineshape parameters (scaling and linewidth, in the simplest case). We believe that the total lineshape approach is the key to the automated analysis of complex strongly coupled NMR spectra, because it does not discard any spectral information. However, being formally a typical task of multivariable function optimization, this method suffers from all relevant problems. The global minimum of the functional (2) is extremely hard to locate. Previous attempts to solve this problem, most notably algorithm DAVINS [9] were based on complex mathematical transformations of spectral lineshape and found little use.

We found, however, that simple broadening of an NMR spectrum, performed by exponential multiplication of the FID, can eliminate local minima efficiently. Once a global minimum on such broadened spectrum has been reached, the degree of broadening can be decreased, and the procedure repeated. This approach has been implemented in our algorithm VALISA [10], which proved to be capable of dealing with many spectral analysis problems, ranging from four to nine-spin tightly coupled systems.

VALISA, like any total lineshape analysis, produces spectral parameters with a very high degree of precision – average values for standard error of SSCCs fall into 10^-2-10^-3 Hz. This precision gave us a possibility to approach the important problem of conformational analysis of substituted cyclopentanes at a whole new level of theory.

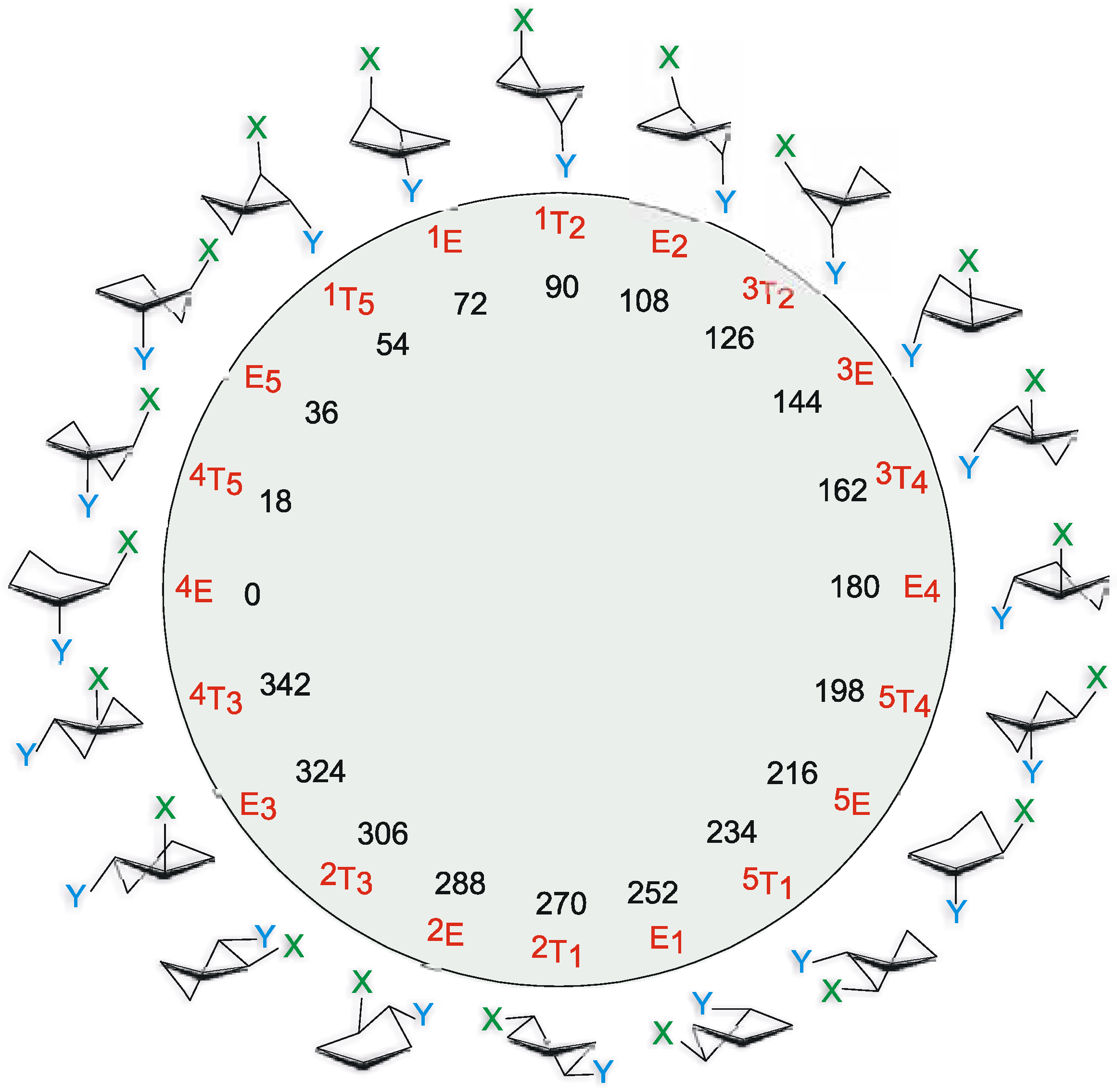
Conformational analysis of five-membered rings has been described theoretically in great detail with the advent of Cremer-Pople[11] puckering coordinates. These coordinates, ring puckering q and phase angle of pseudorotation φ, form a basis in a two-dimensional space so that every possible conformation of a five-membered ring can be represented as a point in this space. Substituted cyclopentanes undergo a process called pseudorotation, where the most puckered part of the ring travels from one carbon to another, in a circle (Figure 1).

Figure 1. Pseudorotation in disubstituted cyclopentanes. Numbers in black inside the circle are values of the phase angle of pseudorotation, numbers and letters in red are the names of the basis conformations.

Figure 1. Pseudorotation in disubstituted cyclopentanes. Numbers in black inside the circle are values of the phase angle of pseudorotation, numbers and letters in red are the names of the basis conformations.

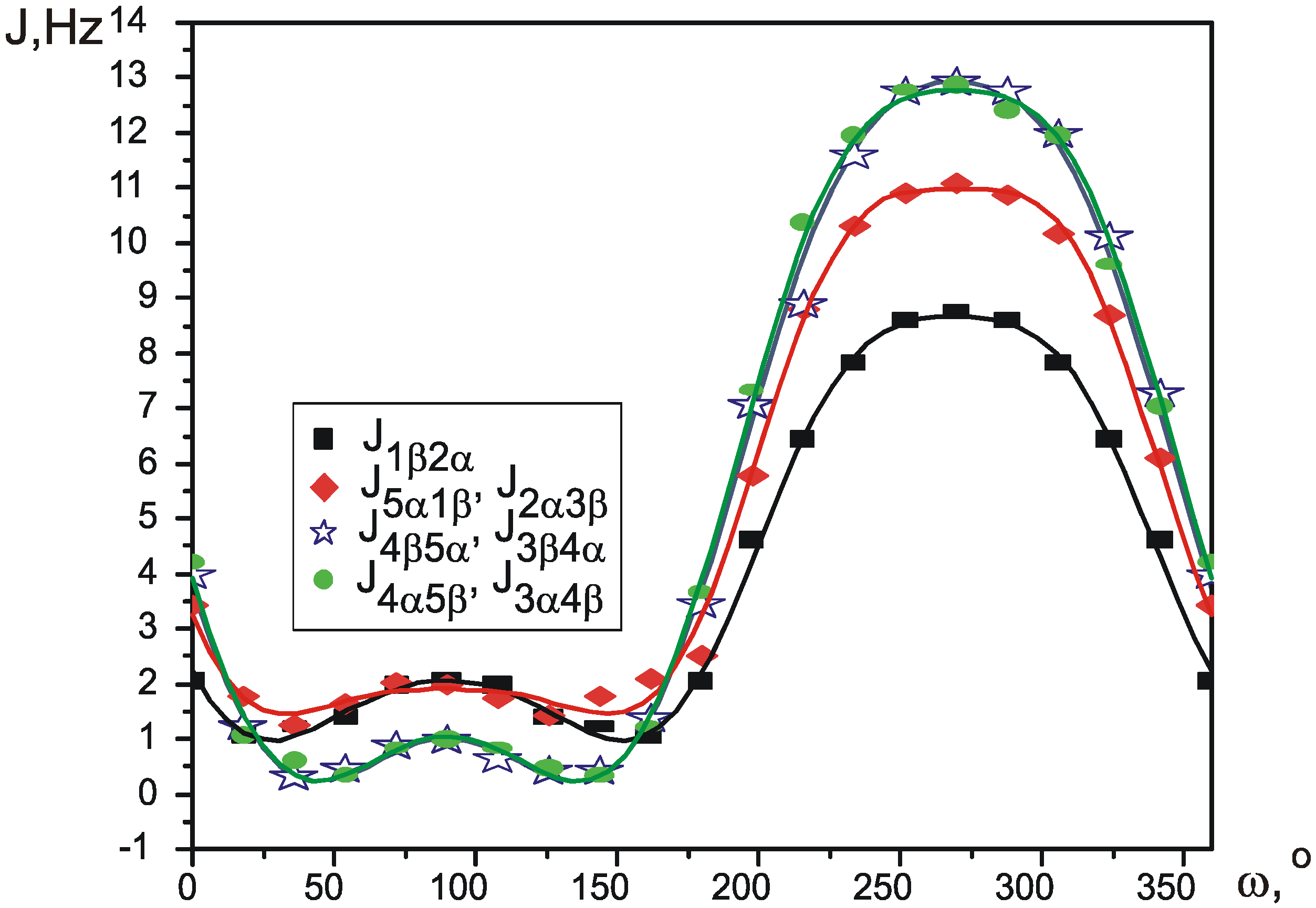
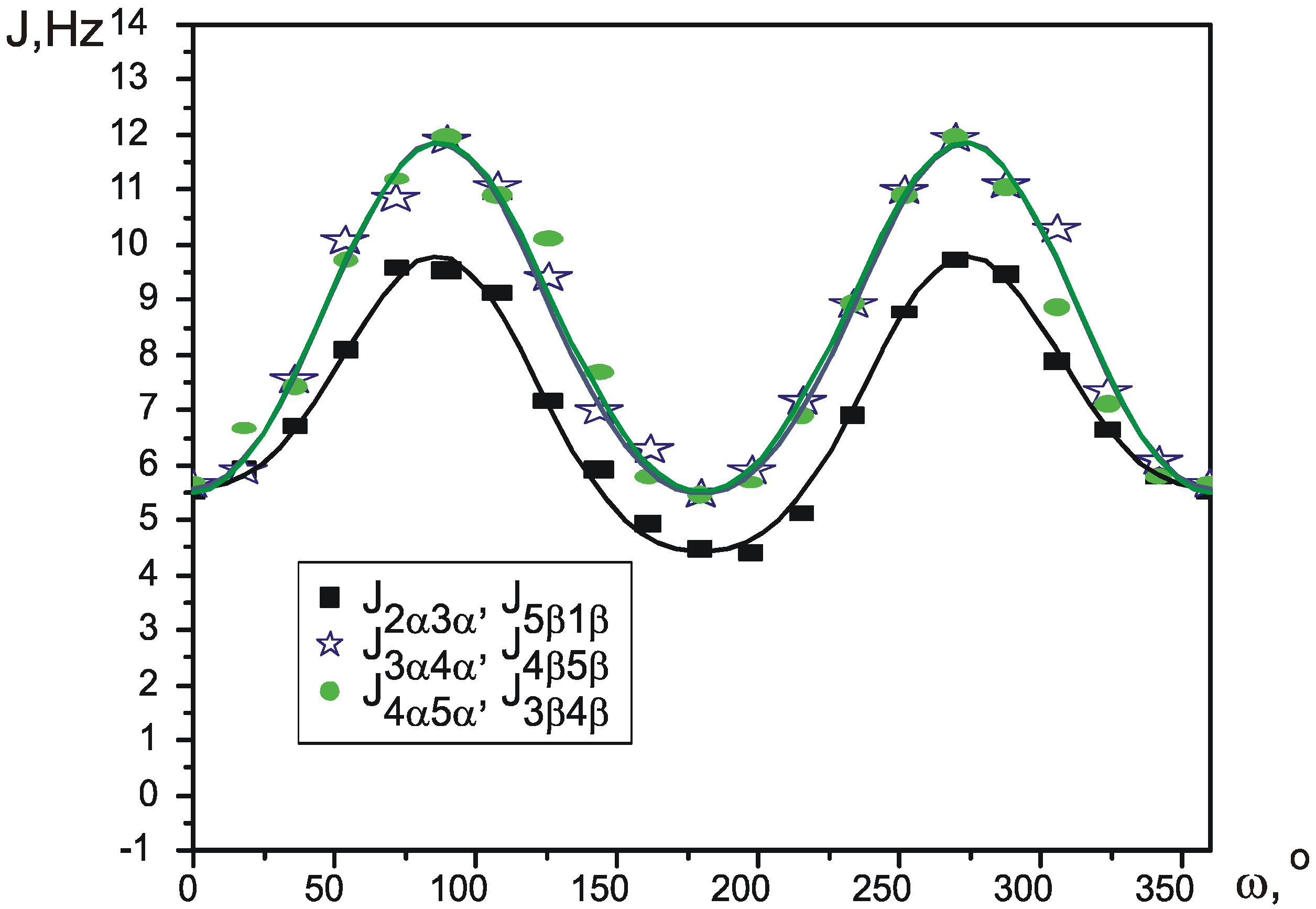
Pseudorotation is a low-energy process, which occurs fast in NMR timescale, so that normally it is only possible to measure averaged values of the spectral parameters. Wu et al. [12] recently proposed a simple way to calculate the values of average SSCCs. Each coupling constant is parameterized as a function of Cremer-Pople pseudorotation angle φ, thus giving a different function J_i(φ) for every different SSCC. Knowing the potential of pseudorotation V(φ), an average value for each coupling constant at a given temperature can be calculated using Boltzman distribution:

$$\langle J_i\rangle =\frac{{\displaystyle \underset{0}{\overset{2\pi }{\int }}}{J}_i\left(\phi \right)e^{-V(\phi )/RT}}{{\displaystyle \underset{0}{\overset{2\pi }{\int }}}{e}^{-V(\phi )/RT}}$$

(3)

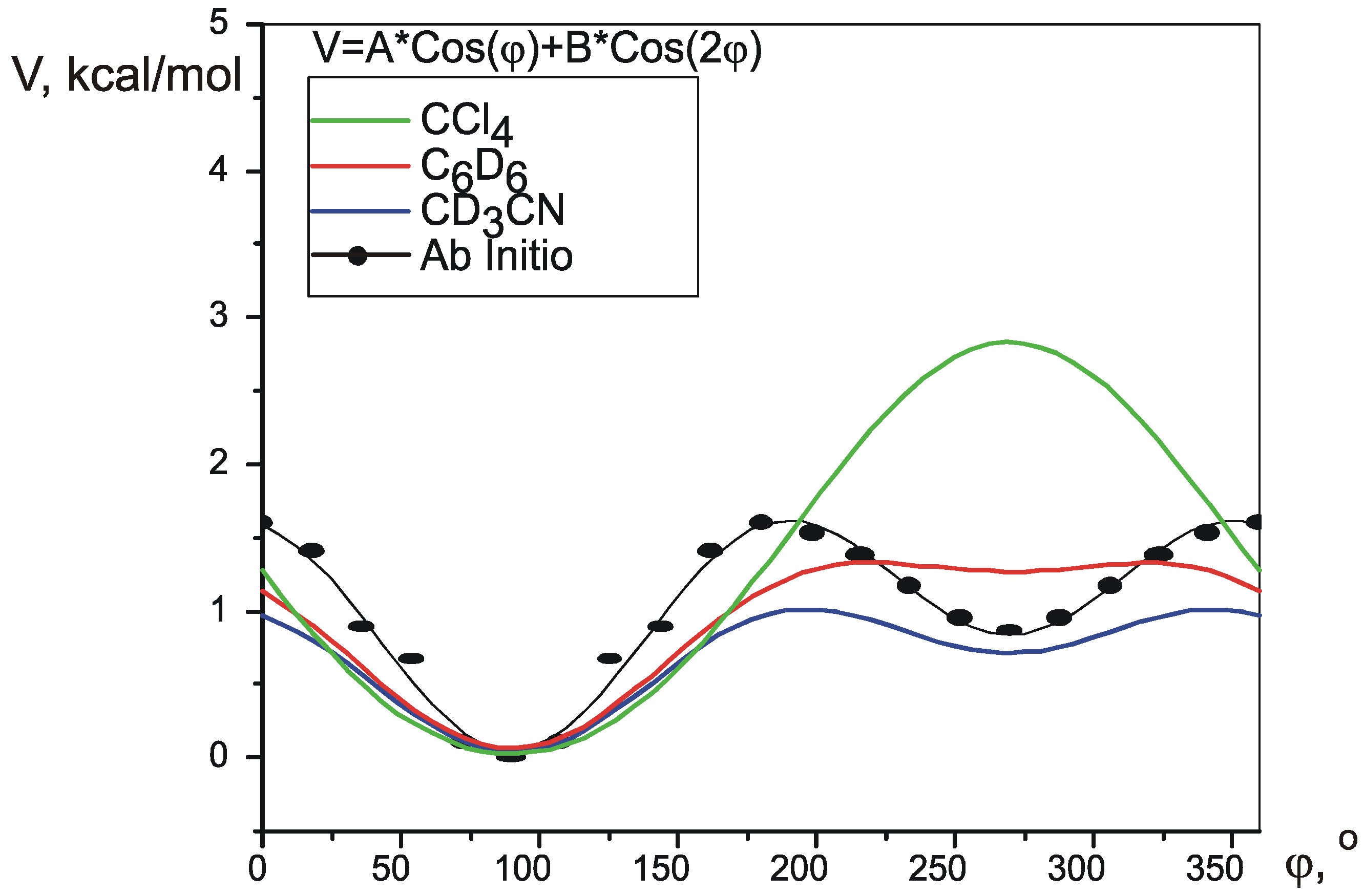
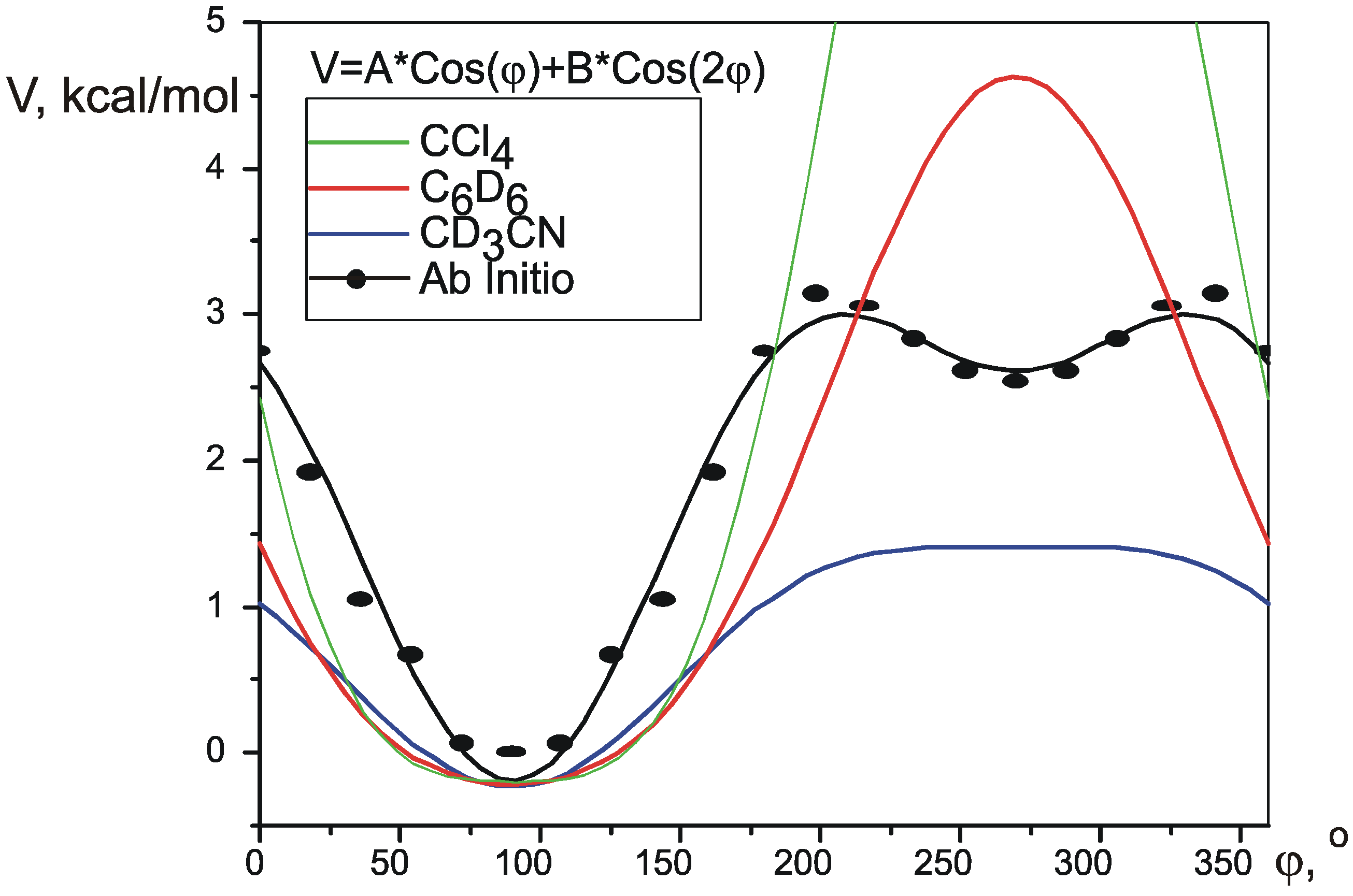
Functions J_i(φ) can be produced by theoretical calculation of SSCCs in conformations, corresponding to different values of φ. The potential V(φ) can be created using one of many quantum theory methods.

Experimental studies of five-membered ring conformation seem to be lagging behind theory. 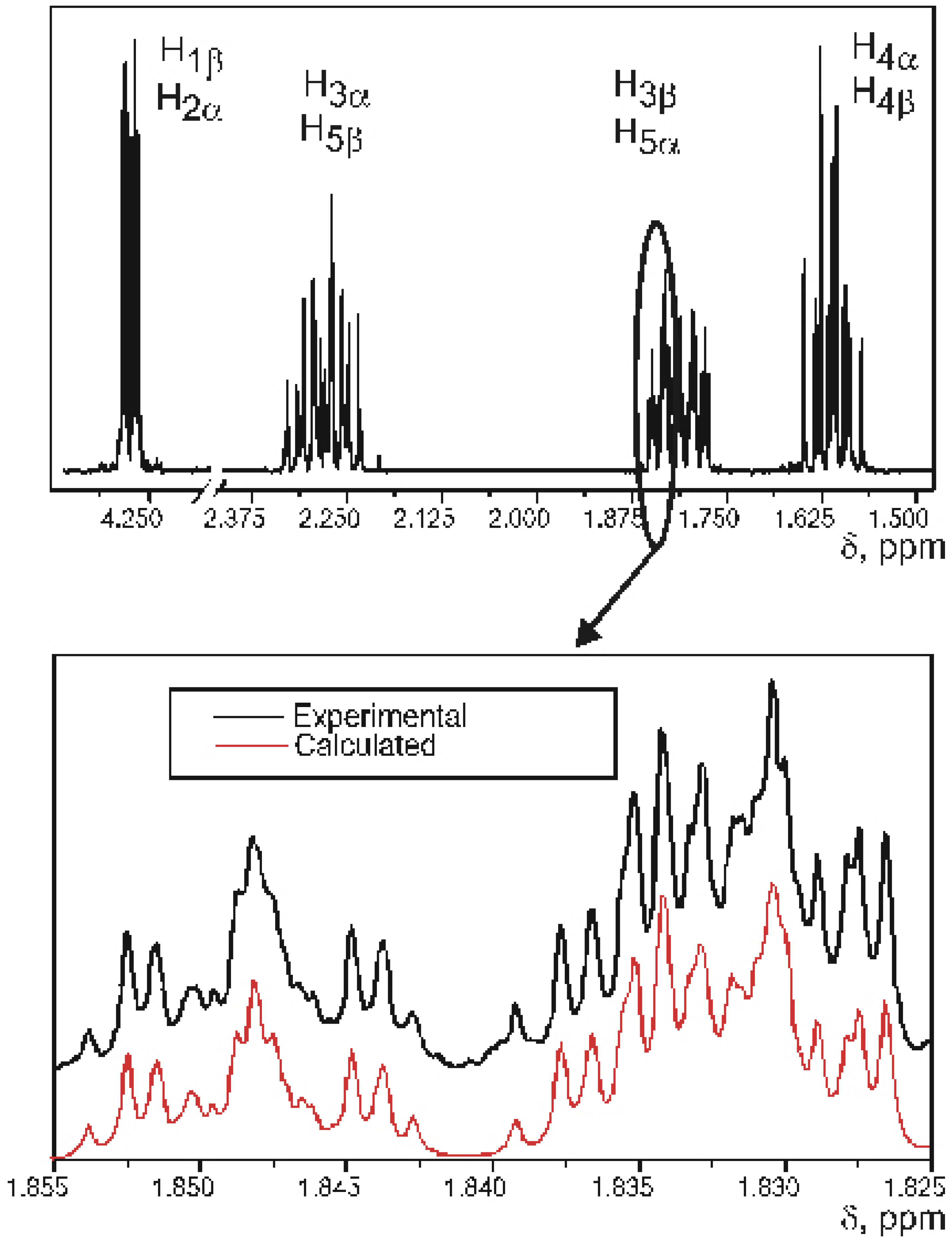In the classical works [2] the process was reduced to an equilibrium of two fixed conformations, which was shown to be an erroneous approach later [13], but even the most recent studies in anisotropic liquid crystal phase [14] have been unable to give an answer more detailed than stating that the pseudorotation is limited to a sector of the Figure 1 circle. Apparently, the reason for this is that a correct experimental description of such process requires many independent experimental parameters to be measured with sufficient precision. Ideally this could be the proton-proton coupling constants, but, for example, a disubstituted cyclopentane represents an eight-spin system of type AA’BB’CC’DD’ and contains several hundred spectral components. Complete analysis of such system could not be performed directly, without first developing a new method of spectral analysis.

The aim of this paper is to close the gap between theoretical and experimental description of substituted cyclopentane pseudorotation and to demonstrate how a continuos potential of pseudorotation can be built, based on single measurement of vicinal proton-proton coupling constants at room temperature.

Experimental

In order to achieve the highest possible resolution, the samples of trans-1,2-dichlorocyclopentane and trans-1,2-dibromocyclopentane (2M solutions in CDCl₃, CCl₄ and CD₃CN) were degassed and sealed in 5mm tubes. ¹H-NMR spectra were acquired on a Varian VXR-400 spectrometer at 303K with acquisition time from 10 to 30 seconds. No resolution enhancement windowing functions were used, digital resolution after Fourrier transform was typically 0.05 Hz/point. Resulting line width at half height equaled 0.1-0.2 Hz.

Calculation and Results

Experimental SSCCs

The analysis of ¹H-NMR spectra of trans-1,2-dichlorocyclopentane and trans-1,2-dibromocyclopentane was carried out using total line shape fitting procedure VALISA [10] with additional broadenings of 0.5, 0.3, 0.2, and 0.1 Hz. Complete analysis of one 8-spin system took several hours on 500 MHz Pentium-II PC. One of the spectrums analyzed is displayed at Figure 2. The number of visible peaks in these spectrums is approximately 300-400, which means full assignment of every transition is virtually impossible.

Figure 2. Experimental (top) ¹H-NMR spectrum of trans-1,2-dibromocyclopentane (2M solution in CD₃CN, 303K, 400 MHz) and an inset (bottom) of experimental (black) and calculated (red) spectra.

Figure 2. Experimental (top) ¹H-NMR spectrum of trans-1,2-dibromocyclopentane (2M solution in CD₃CN, 303K, 400 MHz) and an inset (bottom) of experimental (black) and calculated (red) spectra.

Visual correspondence between the calculated spectrum (in red) and the experimental is practically perfect. Value of standard error calculated using the same method as in [8] totaled 8000 for this case. For example, a change of two of long-range coupling constants by 0.2 Hz, which does not create easily noticeable differences, caused the error to raise more than twice. As a result of the iterations, every SSCC was obtained with a level of precision 0.002 – 0.008 Hz (Table 1 and Table 2), which is average for total line shape fitting procedures.

Table 1. Vicinal proton-proton coupling constants in trans-1,2-dichlorocyclopentane

	J1β2α	J1β5β, J2α3α	J2α3β, J1β5α	J3α4α, J5β4β	J3α4β, J5β4α	J3β4α, J5α4β	J3β4β, J5α4α
C6D6	2.860(6)	6.610(6)	3.280(6)	9.830(7)	7.080(8)	4.210(7)	9.090(5)
CCl4	2.510(5)	5.980(6)	2.080(5)	10.030(7)	7.470(8)	4.040(8)	8.880(7)
CD3CN	3.340(7)	6.310(6)	3.910(8)	9.810(6)	6.540(6)	5.030(9)	9.140(9)

Table 1. Vicinal proton-proton coupling constants in trans-1,2-dichlorocyclopentane

	J1β2α	J1β5β, J2α3α	J2α3β, J1β5α	J3α4α, J5β4β	J3α4β, J5β4α	J3β4α, J5α4β	J3β4β, J5α4α
C6D6	2.860(6)	6.610(6)	3.280(6)	9.830(7)	7.080(8)	4.210(7)	9.090(5)
CCl4	2.510(5)	5.980(6)	2.080(5)	10.030(7)	7.470(8)	4.040(8)	8.880(7)
CD3CN	3.340(7)	6.310(6)	3.910(8)	9.810(6)	6.540(6)	5.030(9)	9.140(9)

Table 2. Vicinal proton-proton coupling constants in trans-1,2-dibromocyclopentane

	J1β2α	J1β5β, J2α3α	J2α3β, J1β5α	J3α4α, J5β4β	J3α4β, J5β4α	J3β4α, J5α4β	J3β4β, J5α4α
C6D6	1.631(1)	5.615(1)	1.912(1)	10.173(1)	7.400(1)	3.93(1)	8.951(1)
CCl4	1.171(2)	5.446(1)	1.395(2)	10.314(3)	7.594(3)	3.635(2)	8.918(2)
CD3CN	2.352(3)	5.877(1)	2.685(2)	10.002(4)	7.087(4)	4.346(4)	9.053(4)

Table 2. Vicinal proton-proton coupling constants in trans-1,2-dibromocyclopentane

	J1β2α	J1β5β, J2α3α	J2α3β, J1β5α	J3α4α, J5β4β	J3α4β, J5β4α	J3β4α, J5α4β	J3β4β, J5α4α
C6D6	1.631(1)	5.615(1)	1.912(1)	10.173(1)	7.400(1)	3.93(1)	8.951(1)
CCl4	1.171(2)	5.446(1)	1.395(2)	10.314(3)	7.594(3)	3.635(2)	8.918(2)
CD3CN	2.352(3)	5.877(1)	2.685(2)	10.002(4)	7.087(4)	4.346(4)	9.053(4)

Naming of protons in these tables and everywhere throughout this article is done similar to [15]: numbers correspond to carbon atom numbers in the cycle, letter α stands for a proton being above mean plane, β - below mean plane. Molecule is oriented so that the substituent at atom C₁ is located above the plane (Figure 3).

Figure 3. Proton numbering scheme for trans-1,2-disubstituted cyclopentanes.

Figure 3. Proton numbering scheme for trans-1,2-disubstituted cyclopentanes.

Theoretical SSCCs

Geometry of each basic symmetrical conformation (6 twists and 5 envelopes) was optimized at RHF/6-31G(d) level of theory with Gaussian 94 [16]. All these conformations except two (diaxial twist ¹T₂ at φ=90^o and diequatorial twist ²T₁ at φ=270^o) are not stable, and the optimization was performed using potential scan technique [17] One of the molecule’s torsion angles was fixed, which resulted in energy optimization with only a small deviation from the ideal value of φ. The energy profile, at the first impression, seemed to agree with widely known fact that such disubstituted compounds have two favorable conformations: more stable diaxial ¹T₂ and less stable diequatorial ²T₁. We found that simple expression (4) satisfied ab initio calculated V(φ) with R.M.S. of 0.023 (dichlorocyclopentane) and 0.005 (dibromocyclopentane) kcal.

V(φ) = V₀ + V₁cos(φ + π/2) + V₂cos(2[φ+π/2]),

(4)

where parameters V₀, V₁, V₂ are the unknowns and their numerical estimates are discussed in pseudorotation potential subsection.

For each of the optimized theoretical conformation values of vicinal proton-proton coupling constants were estimated using the Haasnoot’s extension of the Karplus [18] equation. Each vicinal SSCC was then parameterized as a function of the pseudorotation angle, using the equations similar to those introduced by Wu et al [12].

$${}^{3}J_{HH}^{trans}=J_o+J_1\cos \left(2\omega \right)+J_2\cos \left(4\omega \right)+J_3\sin \left(\omega \right)+J_4\sin \left(3\omega \right)$$

(5)

$${}_{3}J_{HH}^{cis}=J_0+J_1\cos \left(\omega \right)+J_2\cos \left(2\omega \right)+J_3\cos \left(3\omega \right)+J_4\cos \left(4\omega \right),$$

(6)

$$\omega =\phi +s$$

(7)

where J_i are empirical parameters, φ is the phase angle of pseudorotation, and s is a fixed value, different for each SSCC and defined by the ring symmetry. For trans-constants s is a multiple of π/5, for cis-constants it is a multiple of π/10. A set of parameters J₀-J₄ was obtained for each of the 13 SSCCs. The standard error of this fitting varied from 0.02 to 0.09 Hz (Table 3, Table 4).

Table 3. Pseudorotation angle dependency parameters for vicinal SSCCs in trans-1,2-dichloro-cyclopentane

	J0	J1	J2	J3	J4	s	χ2	R
J1β2α	4.040	-1.575	-0.248	-3.802	-0.498	0	0.031	0.997
J5α1β, J2α3β	5.225	-1.618	-0.383	-5.127	-0.619	+0.2π, -0.2π	0.072	0.996
J3α4β, J4α5β	5.540	-1.536	-0.167	-6.792	-0.921	+0.6π, -0.6π	0.051	0.998
J4β5α, J3β4α	5.459	-1.612	-0.093	-6.745	-0.789	+0.4π, -0.4π	0.091	0.997
J2α3α, J5β1β	7.067	0.675	-2.385	-0.105	0.325	0.3π, 0.7π	0.047	0.987
J3α4α, J4β5β	8.524	0.173	-3.192	-0.206	0.115	0.1π, 0.9π	0.083	0.988
J4α5α, J3β4β	8.472	0.272	-3.158	-0.222	0.205	0.1π, -0.1π	0.065	0.991

Table 3. Pseudorotation angle dependency parameters for vicinal SSCCs in trans-1,2-dichloro-cyclopentane

	J0	J1	J2	J3	J4	s	χ2	R
J1β2α	4.040	-1.575	-0.248	-3.802	-0.498	0	0.031	0.997
J5α1β, J2α3β	5.225	-1.618	-0.383	-5.127	-0.619	+0.2π, -0.2π	0.072	0.996
J3α4β, J4α5β	5.540	-1.536	-0.167	-6.792	-0.921	+0.6π, -0.6π	0.051	0.998
J4β5α, J3β4α	5.459	-1.612	-0.093	-6.745	-0.789	+0.4π, -0.4π	0.091	0.997
J2α3α, J5β1β	7.067	0.675	-2.385	-0.105	0.325	0.3π, 0.7π	0.047	0.987
J3α4α, J4β5β	8.524	0.173	-3.192	-0.206	0.115	0.1π, 0.9π	0.083	0.988
J4α5α, J3β4β	8.472	0.272	-3.158	-0.222	0.205	0.1π, -0.1π	0.065	0.991

Table 4. Pseudorotation angle dependency parameters for vicinal SSCCs in trans-1,2-dibromocyclo-pentane

	J0	J1	J2	J3	J4	S	χ2	R
J1β2α	4.292	-1.677	-0.233	-4.077	-0.552	0	0.016	0.999
J5α1β, J2α3β	5.241	-1.678	-0.340	-5.283	-0.666	+0.2π, -0.2π	0.041	0.998
J3α4β, J4α5β	5.555	-1.554	-0.186	-6.796	-0.933	+0.6π, -0.6π	0.048	0.998
J4β5α, J3β4α	5.520	-1.527	-0.039	-6.741	-0.847	+0.4π, -0.4π	0.086	0.997
J2α3α, J5β1β	7.127	0.717	-2.466	-0.166	0.342	0.3π, 0.7π	0.058	0.987
J3α4α, J4β5β	8.392	0.151	-3.183	-0.103	0.204	0.1π, 0.9π	0.045	0.993
J4α5α, J3β4β	8.402	0.283	-3.181	-0.241	0.207	0.1π, -0.1π	0.050	0.993

Table 4. Pseudorotation angle dependency parameters for vicinal SSCCs in trans-1,2-dibromocyclo-pentane

	J0	J1	J2	J3	J4	S	χ2	R
J1β2α	4.292	-1.677	-0.233	-4.077	-0.552	0	0.016	0.999
J5α1β, J2α3β	5.241	-1.678	-0.340	-5.283	-0.666	+0.2π, -0.2π	0.041	0.998
J3α4β, J4α5β	5.555	-1.554	-0.186	-6.796	-0.933	+0.6π, -0.6π	0.048	0.998
J4β5α, J3β4α	5.520	-1.527	-0.039	-6.741	-0.847	+0.4π, -0.4π	0.086	0.997
J2α3α, J5β1β	7.127	0.717	-2.466	-0.166	0.342	0.3π, 0.7π	0.058	0.987
J3α4α, J4β5β	8.392	0.151	-3.183	-0.103	0.204	0.1π, 0.9π	0.045	0.993
J4α5α, J3β4β	8.402	0.283	-3.181	-0.241	0.207	0.1π, -0.1π	0.050	0.993

There are only four different trans-SSCCs and three cis-SSCCs observable in trans-1,2-disubstituted cyclopentanes, due to averaging. However, most of the constants are present in the molecule twice. It became obvious from our calculations that for every such pair, both participant SSCCs have identical pseudorotation angle dependency, except it is shifted by the phase angle. The parameter s we introduced makes it possible to express such pairs of SSCCs uniformly. Every such pair is represented by one line in the Table 3 and Table 4, and by a single plot on Figure 4 and Figure 5.

Figure 4. Pseudorotation angle dependency parameters for vicinal trans-SSCCs in trans-1,2-dichlorocyclopentane.

Figure 4. Pseudorotation angle dependency parameters for vicinal trans-SSCCs in trans-1,2-dichlorocyclopentane.

Figure 5. Pseudorotation angle dependency parameters for vicinal cis-SSCCs in trans-1,2-dichlorocyclopentane.

Figure 5. Pseudorotation angle dependency parameters for vicinal cis-SSCCs in trans-1,2-dichlorocyclopentane.

As can be seen on both plots, the values of SSCCs are influenced by the closeness of substituents. The pair of constants farthest from the substituents is almost identical on this plot. For example, J_3α4α is almost identical to J_3β4β. This happens because the torsion angle H_3αC₃C₄H_4α is equal to H_3βC₃C₄H_4β and torsion angle dependency defines vicinal SSCCs to a very large degree.

It is interesting to compare our results to the ab initio parameterization for nonsubstituted cyclopentane in [12]. The values of J_i are similar, except that some of them have wrong signs. This is a result of a fact that the basis we are using allows every constant to be described by two different equivalent sets of parameters {J₀, J₁, J₂, J₃, J₄, s}:

$${}^{3}J_{HCCH}^{trans}\left(J_0,J_1,J_2,J_3,J_4,s\right)\iff {}^{3}J_{HCCH}^{trans}\left(J_0,J_1,J_2,-J_3,-J_4,s+\pi \right)$$

(8)

$${}^{3}J_{HCCH}^{cis}\left(J_0,J_1,J_2,J_3,J_4,s\right)\iff {}^{3}J_{HCCH}^{cis}\left(J_0,-J_1,-J_2,-J_3,J_4,s+\pi /2\right)$$

(9)

Changing the signs with (8) and (9) brings our parameters closer to those calculated by Wu et al, but there still is noticeable difference. It diminishes, as can be expected, when proceeding from the SSCCs close to the substituents, such as J_1β2α to those on the opposite side of the ring, such as J_3β4α. However, it remains large (above 1 Hz) for the parameter J₁. This can be explained both by potential deficiencies of the semi-empirical equation [18] we used, and also by the fact that SSCCs are dependant not only on the phase angle φ, but also on the ring puckering q. In case of nonsubstituted cyclopentane the change of ring puckering during pseudorotation is negligible, but with trans-1,2-disubstituted cyclopentanes, as our calculations have shown, q varies from 0.342 to 0.420 between diaxial (φ=90^o) and diequatorial (φ=270^o) twist conformations.

A more accurate conclusion will be possible when these calculations are performed at a higher level of theory, but they appear to be sufficient for our current purpose of demonstrating the technique of building pseudorotation potentials from spin-spin coupling constants.

Pseudorotation potential.

Now, having obtained experimental values of average SSCCs <J_i> and theoretical functions J_i(φ), we could finally determine the pseudorotation potential. We performed a simple iterative procedure to produce the unknown V(φ) from the equations (3). We solved these equations for given parameters V₁ and V₂ from (4), compared the resulting SSCCs with the experimental data, changed V₁ and V₂ and repeated the procedure until the best fit was reached. The results of this optimization are presented in Table 5, Table 6 and Figure 6, Figure 7.

Table 5. Results of pseudorotational potential optimization for trans-1,2-dichlorocyclopentane.

	V1	V2	RMS, Hz			Vmax-Vmin	V(2T1)-V(1T2)	precision*
			CD3CN	C6D6	CCl4
ab initio	0.394	-0.5678	0.58	0.56	0.97	1.563	0.788	n/a
CD3CN	0.3393	-0.2942	0.45			0.976	0.679	0.01
C6D6	0.6028	-0.2341		0.41		1.264	1.206	0.03
CCl4	1.4035	0.07861			0.59	2.807	2.807	0.7

* change in V(²T₁)-V(¹T₂) if experimental SSCCs are varied by 0.01 Hz

Table 5. Results of pseudorotational potential optimization for trans-1,2-dichlorocyclopentane.

	V1	V2	RMS, Hz			Vmax-Vmin	V(2T1)-V(1T2)	precision*
			CD3CN	C6D6	CCl4
ab initio	0.394	-0.5678	0.58	0.56	0.97	1.563	0.788	n/a
CD3CN	0.3393	-0.2942	0.45			0.976	0.679	0.01
C6D6	0.6028	-0.2341		0.41		1.264	1.206	0.03
CCl4	1.4035	0.07861			0.59	2.807	2.807	0.7

* change in V(²T₁)-V(¹T₂) if experimental SSCCs are varied by 0.01 Hz

Table 6. Results of pseudorotational potential optimization for trans-1,2-dibromocyclopentane.

	V1	V2	RMS, Hz			Vmax-Vmin	V(2T1)-V(1T2)	precision
			CD3CN	C6D6	CCl4
ab initio	1.403	-0.721	0.96	0.83	0.86	3.191	2.806	n/a
CD3CN	0.8205	-0.2174	0.53			1.642	1.641	0.06
C6D6	2.4222	0.3886		0.61		4.844	4.844	2.0
CCl4	4.9797	1.1819			0.72	9.959	9.959	5.8

Table 6. Results of pseudorotational potential optimization for trans-1,2-dibromocyclopentane.

	V1	V2	RMS, Hz			Vmax-Vmin	V(2T1)-V(1T2)	precision
			CD3CN	C6D6	CCl4
ab initio	1.403	-0.721	0.96	0.83	0.86	3.191	2.806	n/a
CD3CN	0.8205	-0.2174	0.53			1.642	1.641	0.06
C6D6	2.4222	0.3886		0.61		4.844	4.844	2.0
CCl4	4.9797	1.1819			0.72	9.959	9.959	5.8

Figure 6. Pseudorotation potential for trans-1,2-dichlorocyclopentane.

Figure 6. Pseudorotation potential for trans-1,2-dichlorocyclopentane.

Figure 7. Pseudorotation potential for trans-1,2-dibromocyclopentane.

Figure 7. Pseudorotation potential for trans-1,2-dibromocyclopentane.

There are a number of interesting things to be noted about the potentials we have obtained. First of all, they show that polar solvents stabilize the less stable dipolar conformation ²T₁, which agrees with general knowledge. Indeed, unlike cyclohexanes, where axial position is hindered by 1-4 diaxial interaction, there are no other axial protons or subsituents on the same side of the ring. Moreover, axial position takes the substituent out of plane, and decrements the number of hydrogens it interacts with. However, not everything is perfect with the plot. In some cases, especially in case of dibromocyclopentane in CCl₄, our potential assigns unbelievably high energy for this conformation.

Looking at the precision column in the table 5 and table 6, one can also see that in all cases of extremely high barrier, the height of this barrier is far from being accurate. We believe that this happens because high energy fragments of V(φ) cannot be efficiently accounted for with our simple Boltzman model. Once their share into overall distribution becomes comparable or smaller than the influence of higher-order harmonics of V, our optimization procedure assigns wrong energy values to high-energy fragments of the potential, if this can change the shape of low-energy parts towards its correct form.

Apparently, our approach works, and works well, only for low-barrier processes. Which is exactly what we have been looking for – an ability to describe a fast low-barrier pseudorotation in terms of continuos distribution of conformations, based on a single NMR spectrum taken.