Acidity Study on 3-Substituted Pyridines
Abstract
:
Introduction
Computational methods



Results and discussion
Conformation and tautomerism
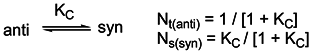
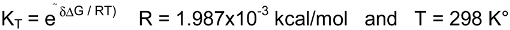
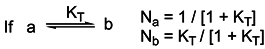
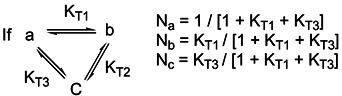
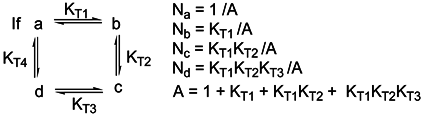
Basicity
| Compound | ΔHf (kcal/mol) | ΔS (cal/mol K) | ΔGf a (kcal/mol) | Mol fractions of conformers or tautomersb | Weighted average ΔGf c (kcal/mol) |
|---|---|---|---|---|---|
| 1 | 23.81 | 67.41 | 3.72 | ||
| 2 | 15.82 | 75.27 | -6.61 | ||
| 3 | 9.99 | 84.08 | -15.07 | ||
| 4 | 5.94 | 90.20 | -20.94 | ||
| 6s | -35.14 | 78.17 | -58.43 | N6s = 0.08 | -59.74 |
| 6t | -35.12 | 83.00 | -59.85 | N6t = 0.92 | |
| 11 | -48.81 | 101.49 | -79.05 | ||
| 13a | -24.83 | 74.70 | -47.10 | N13a = 1.00 | -47.10 |
| 13b | -21.69 | 73.35 | -43.55 | N13b = 0.00 | |
| 14s | -17.00 | 81.44 | -41.27 | N14s = 0.49 | -41.28 |
| 14t | -16.82 | 82.11 | -41.29 | N14t = 0.51 | |
| 15a | 23.47 | 79.34 | -0.17 | N15a = 0.00 | -9.62 |
| 15b | 13.15 | 76.40 | -9.62 | N15b = 1.00 | |
| 16a | -138.95 | 90.49 | -165.92 | N16a = 0.99 | -165.89 |
| 16b | -135.16 | 94.22 | -163.24 | N16b = 0.01 | |
| 17 | -21.00 | 73.05 | -42.77 | ||
| 18 | 16.94 | 75.78 | -5.64 | ||
| 19 | 27.89 | 78.72 | 4.43 | ||
| 20 | 39.32 | 80.62 | 15.30 | ||
| 21 | 17.16 | 84.73 | -8.09 | ||
| 22a | 15.58 | 74.66 | -6.67 | N22a = 1.00 | -6.67 |
| 22b | 39.53 | 76.79 | 16.65 | N22b = 0.00 | |
| 23 | 28.09 | 90.57 | 1.10 | ||
| 24a | -25.52 | 88.95 | -52.03 | N24a = 0.10 | -52.72 |
| 24b | -24.92 | 91.95 | -51.60 | N24b = 0.05 | |
| 24c | -25.04 | 93.73 | -52.97 | N24c = 0.52 | |
| 24d | -25.35 | 91.78 | -52.70 | N24d = 0.33 | |
| 25a | -16.06 | 100.30 | -45.95 | N25a = 0.32 | -45.82 |
| 25b | -15.62 | 100.88 | -45.68 | N25b = 0.20 | |
| 25c | -15.67 | 100.63 | -45.66 | N25c = 0.20 | |
| 25d | -16.00 | 100.25 | -45.87 | N25d = 0.28 | |
| 28s | -14.56 | 80.42 | -38.53 | N28s = 0.51 | -38.52 |
| 28t | -14.58 | 80.26 | -38.50 | N28t = 0.49 | |
| 29s | -20.40 | 91.34 | -47.62 | N29s = 0.82 | -47.46 |
| 29t | -20.34 | 88.53 | -46.73 | N29t = 0.18 | |
| 31a | -77.03 | 86.63 | -102.84 | N31a = 0.84 | -102.62 |
| 31bs | -75.82 | 85.56 | -101.32 | N31b = 0.05 | |
| 31bt | -74.81 | 85.85 | -100.39 | N31c = 0.11 | |
| 31cs | -75.84 | 86.97 | -101.76 | ||
| 31ct | -74.62 | 86.45 | -100.38 | ||
| 32 | -173.27 | 86.39 | -199.01 | ||
| 33ss | -66.86 | 98.59 | -96.24 | N33ss = 0.98 | -96.21 |
| 33st | -64.15 | 93.94 | -92.14 | N33st = 0.00 | |
| 33ts | -66.89 | 90.99 | -94.01 | N33ts = 0.02 | |
| 33tt | -64.07 | 94.50 | -92.23 | N33tt = 0.00 | |
| 34ss | -72.52 | 103.66 | -103.41 | N34ss = 0.68 | -103.22 |
| 34st | -69.89 | 105.79 | -101.42 | N34st = 0.02 | |
| 34ts | --72.56 | 101.89 | -102.92 | N34ts = 0.30 | |
| 34tt | -69.84 | 102.97 | -100.53 | N34tt = 0.00 | |
| 35s | -28.56 | 85.54 | -54.06 | N35s = 0.54 | -54.01 |
| 35t | -28.50 | 85.45 | -53.96 | N35t = 0.46 | |
| 36 | 52.35 | 77.61 | 29.22 | ||
| H2O | -68.89 | 45.11 | -82.31 |
| Compound | ΔHf (kcal/mol) | ΔS (cal/mol K) | ΔGfa (kcal/mol | Mol fractions of conformers or tautomersb | Weighted average ΔGf c (kcal/mol) |
|---|---|---|---|---|---|
| 37 | 118.38 | 67.77 | 98.18 | ||
| 38 | 111.04 | 80.48 | 87.06 | ||
| 39 | 105.20 | 85.55 | 79.71 | ||
| 40 | 101.20 | 92.26 | 73.71 | ||
| 42s | 60.17 | 78.45 | 36.81 | N42s = 0.04 | 35.07 |
| 42t | 60.09 | 84.19 | 35.00 | N42t = 0.96 | |
| 47 | 44.81 | 100.39 | 14.89 | ||
| 49 | 71.25 | 75.35 | 48.80 | ||
| 50s | 79.85 | 83.70 | 54.91 | N50s = 0.25 | 54.43 |
| 50t | 80.03 | 86.45 | 54.27 | N50t = 0.75 | |
| 51 | 119.55 | 80.48 | 95.57 | ||
| 52 | -40.25 | 96.02 | -68.86 | ||
| 53 | 75.96 | 73.50 | 54.06 | ||
| 54 | 113.65 | 76.24 | 90.93 | ||
| 55 | 124.49 | 79.15 | 100.90 | ||
| 56 | 135.60 | 81.00 | 111.46 | ||
| 57a | 115.06 | 84.23 | 89.96 | N57a = 1.00 | 89.96 |
| 57b | 141.24 | 84.66 | 116.01 | N57b = 0.00 | |
| 57c | 141.23 | 83.44 | 116.36 | N57c = 0.00 | |
| 58a | 112.39 | 75.87 | 89.79 | N58a = 0.00 | 80.59 |
| 58b | 103.51 | 76.92 | 80.59 | N58b = 1.00 | |
| 59a | 124.79 | 92.13 | 97.34 | N59a = 1.00 | 97.34 |
| 59b | 128.49 | 90.59 | 101.49 | N59b = 0.00 | |
| 60a | 71.08 | 88.65 | 44.68 | N60a = 0.01 | 42.39 |
| 60b | 71.27 | 94.16 | 43.21 | N60b = 0.13 | |
| 60c | 70.99 | 92.11 | 43.54 | N60c = 0.07 | |
| 60d | 70.76 | 96.12 | 42.12 | N60d = 0.79 | |
| 61a | 80.63 | 96.86 | 51.77 | N61a = 0.08 | 50.84 |
| 61b | 80.77 | 101.54 | 50.51 | N61b = 0.70 | |
| 61c | 80.58 | 97.09 | 51.65 | N61c = 0.10 | |
| 61d | 80.46 | 96.54 | 51.69 | N61d = 0.11 | |
| 64s | 81.23 | 80.93 | 57.11 | N64s = 0.41 | 56.99 |
| 64t | 80.96 | 80.74 | 56.90 | N64t = 0.59 | |
| 65s | 75.63 | 89.30 | 49.02 | N65s = 0.56 | 49.08 |
| 65t | 75.60 | 88.73 | 49.16 | N65t = 0.44 | |
| 67ss | 20.19 | 86.90 | -5.71 | N67ss = 0.50 | -5.47 |
| 67st | 21.06 | 86.73 | -4.79 | N67st = 0.11 | |
| 67ts | 20.05 | 85.75 | -5.50 | N67ts = 0.35 | |
| 67tt | 21.00 | 84.54 | -4.19 | N67tt = 0.04 | |
| 68ss | 29.32 | 95.36 | 0.90 | N68ss = 0.82 | 1.06 |
| 68st | 32.03 | 94.92 | 3.74 | N68st = 0.00 | |
| 68ts | 29.13 | 91.75 | 1.79 | N68ts = 0.18 | |
| 68tt | 32.03 | 95.30 | 3.63 | N68tt = 0.01 | |
| 69ss | 23.79 | 96.89 | -5.08 | N69ss = 0.03 | -6.80 |
| 69st | 26.93 | 97.75 | -2.20 | N69st = 0.00 | |
| 69ts | 23.58 | 102.34 | -6.92 | N69ts = 0.96 | |
| 69tt | 26.25 | 103.35 | -4.55 | N69tt = 0.01 | |
| 70s | 67.66 | 85.71 | 42.12 | N70s = 0.49 | 42.10 |
| 70t | 67.38 | 85.73 | 42.09 | N70t = 0.51 | |
| 71 | 148.47 | 78.16 | 125.18 | ||
| H3O+ | 33.13 | 46.13 | 19.38 |
| Conjugate base (B) | ΔGf Kcal/mol | Conjugate acid (BH+) | ΔGf Kcal/mol | δΔGfa Kcal/mol | pKa(BH+)b | Exp. pKa(BH+)c | Absolute error between pKa(calc.) and pKa(exp.) | Referencesc |
|---|---|---|---|---|---|---|---|---|
| 1 | 3.72 | 37 | 98.18 | 7.23 | 5.30 | 5.27, 5.28 | 0.03, 0.02 | 23, 24, 25 |
| 2 | -6.61 | 38 | 87.06 | 8.02 | 5.88 | 5.67, 5.70, 5.75 | 0.21, 0.18, 0.13 | 26, 27, 28, 29 |
| 3 | -15.07 | 39 | 79.71 | 6.91 | 5.07 | 5.70 | 0.63 | 30 |
| 4 | -20.94 | 40 | 73.71 | 7.04 | 5.16 | 5.72 | -0.56 | 30 |
| 6 | -59.74 | 42 | 35.07 | 6.88 | 5.05 | 4.90, 4.95 | 0.15, 0.10 | 31, 32 |
| 11 | -79.05 | 47 | 14.89 | 7.75 | 5.68 | 5.47 | 0.21 | 31 |
| 13 | -47.10 | 49 | 48.80 | 5.79 | 4.25 | 4.80, 4.86 | -0.55, -0.61 | 27, 38, 39, 40 |
| 14 | -41.28 | 50 | 54.43 | 5.98 | 4.39 | 4.78, 4.88, 4.90 | -0.39, -0.49, -0.51 | 26, 40, 38, 27 |
| 15 | -9.62 | 51 | 95.57 | -3.5 | -2.57 | 2.28 | -4.85 | 19 |
| 16 | -165.89 | 52 | -68.86 | 4.66 | 3.42 | 3.22 | 0.20 | 41 |
| 17 | -42.77 | 53 | 54.06 | 4.86 | 3.56 | 2.97, 3.10 | 0.59, 0.46 | 30, 42 |
| 18 | -5.64 | 54 | 90.93 | 5.12 | 3.75 | 2.81, 2.84, 2.98 | 0.94, 0.91, 0.77 | 26, 42, 27 |
| 19 | 4.43 | 55 | 100.90 | 5.22 | 3.83 | 2.80, 2.84, 2.85 | 1.03, 0.99, 0.98 | 27, 42, 26 |
| 20 | 15.30 | 56 | 111.46 | 5.53 | 4.05 | 3.25 | 0.85 | 30 |
| 21 | -8.09 | 57 | 89.96 | 3.64 | 2.67 | 0.81, 1.18 | 1.86, 1.49 | 43, 26 |
| 22 | -6.67 | 58 | 80.59 | 14.43 | 10.58 | 5.80, 5.98, 6.04 | 4.78, 4.60, 4.54 | 30, 44, 26, 27 |
| 23 | 1.10 | 59 | 97.34 | 5.38 | 3.95 | 6.45 | -2.50 | 45 |
| 24 | -52.72 | 60 | 42.39 | 6.58 | 4.83 | 4.46 | 0.37 | 46 |
| 25 | -45.82 | 61 | 50.84 | 5.03 | 3.69 | 3.52 | 0.17 | 46 |
| 28 | -38.52 | 64 | 56.99 | 6.18 | 4.53 | 3.70, 3.75 | 0.83, 0.78 | 47, 48 |
| 29 | -47.46 | 65 | 49.08 | 5.15 | 3.78 | 3.18, 3.26 | 0.60, 0.52 | 30, 49 |
| 31 | -102.62 | 67 | -5.47 | 4.53 | 3.32 | 3.13, 3.75 | 0.19, -0.43 | 43, 50 |
| 32 | -199.01 | 31 | -102.62 | 5.30 | 3.89 | 4.77 | -0.88 | 51 |
| 33 | -96.21 | 68 | 1.06 | 4.42 | 3.24 | 3.09 | 0.15 | 26 |
| 34 | -103.22 | 69 | -6.80 | 5.27 | 3.86 | 3.35 | 0.51 | 42 |
| 35 | -54.01 | 70 | 42.10 | 5.58 | 4.09 | 3.40 | 0.69 | 51 |
| 36 | 29.22 | 71 | 125.18 | 5.74 | 4.21 | 1.30, 1.36, 1.45 | 2.91, 2.85, 2.76 | 27, 26, 52, 51 |
| H2O | -82.31 | H3O+ | 19.38 |
| Compound | ΔHf (Kcal/mol) | ΔS (cal/mol K) | ΔGf a (Kcal/mol) | Mol fractions of conformers or tautomersb | Weighted average ΔGf c (Kcal/mol) |
|---|---|---|---|---|---|
| 1 | 23.20 | 68.11 | 2.90 | ||
| 2 | 14.89 | 76.07 | -7.78 | ||
| 3 | 9.86 | 86.55 | -15.93 | ||
| 4 | 4.38 | 93.33 | -23.48 | ||
| 5 | -0.41 | 97.49 | -29.46 | ||
| 6s | -25.82 | 86.73 | -51.67 | N6s = 0.09 | -52.93 |
| 6t | -27.77 | 84.82 | -53.05 | N6t = 0.91 | |
| 7 | 16.47 | 112.82 | -17.15 | ||
| 8s | -1.02 | 115.97 | -35.58 | N8a = 0.57 | -35.51 |
| 8t | -0.97 | 115.61 | -35.42 | N8b = 0.43 | |
| 9s | -80.34 | 109.42 | -112.95 | N9a = 0.44 | -113.03 |
| 9t | -79.82 | 111.68 | -113.10 | N9b = 0.56 | |
| 10s | -40.59 | 121.95 | -76.93 | N10a = 0.00 | -82.08 |
| 10t | -45.00 | 124.42 | -82.08 | N10b = 1.00 | |
| 11 | -39.97 | 101.01 | -70.07 | ||
| 12 | 57.30 | 110.02 | 24.51 | ||
| 13a | -23.18 | 75.95 | -45.81 | N13a = 0.00 | -50.34 |
| 13b | -28.23 | 74.19 | -50.34 | N13b = 1.00 | |
| 14s | -14.94 | 83.20 | -39.74 | N14s = 0.28 | -40.14 |
| 14t | -15.09 | 84.59 | -40.3 | N14t = 0.72 | |
| 15a | 26.92 | 81.95 | 2.50 | N15a = 0.00 | -5.68 |
| 15b | 17.32 | 77.17 | -5.68 | N15b = 1.00 | |
| 16a | -126.62 | 92.81 | -154.28 | N16a = 1.00 | -154.28 |
| 16b | -112.87 | 93.42 | -140.71 | N16b = 0.00 | |
| 17 | -21.66 | 73.79 | -43.65 | ||
| 18 | 16.33 | 76.76 | -6.54 | ||
| 19 | 27.51 | 79.75 | 3.74 | ||
| 20 | 40.88 | 82.31 | 16.35 | ||
| 21 | 14.89 | 84.82 | -10.39 | ||
| 22a | 16.69 | 76.03 | -5.96 | N22a = 1.00 | -5.96 |
| 22b | 37.36 | 78.10 | 14.09 | N22b = 0.00 | |
| 23 | 27.40 | 91.44 | 0.15 | ||
| 24a | -32.65 | 93.58 | -60.54 | N24a = 0.41 | -60.32 |
| 24b | -31.30 | 94.64 | -59.50 | N24b = 0.08 | |
| 24c | -31.37 | 96.57 | -60.15 | N24c = 0.21 | |
| 24d | -32.49 | 93.49 | -60.35 | N24d = 0.30 | |
| 25a | -26.49 | 102.59 | -57.06 | N25a = 0.18 | -57.31 |
| 25b | -25.71 | 107.07 | -57.62 | N25b = 0.47 | |
| 25c | -25.70 | 104.98 | -56.98 | N25c = 0.17 | |
| 25d | -26.36 | 103.04 | -57.06 | N25d = 0.18 | |
| 26a | -2.11 | 113.23 | -35.85 | N26a = 0.60 | -35.62 |
| 26b | -0.69 | 111.98 | -34.06 | N26b = 0.03 | |
| 26c | -0.64 | 112.57 | -34.19 | N26c = 0.04 | |
| 26d | -1.97 | 112.55 | -35.51 | N26d = 0.33 | |
| 27a | 4.50 | 125.10 | -32.78 | N27a = 0.54 | -32.56 |
| 27b | 4.95 | 121.27 | -31.19 | N27b = 0.04 | |
| 27c | 5.02 | 121.98 | -31.33 | N27c = 0.05 | |
| 27d | 4.68 | 124.97 | -32.56 | N27d = 0.37 | |
| 28s | -12.90 | 80.90 | -37.01 | N28s = 0.50 | -37.01 |
| 28t | -12.81 | 81.17 | -37.00 | N28t = 0.50 | |
| 29s | -23.98 | 88.93 | -50.48 | N29s = 0.59 | -50.39 |
| 29t | -23.88 | 88.52 | -50.26 | N29t = 0.41 | |
| 30s | 6.57 | 105.44 | -24.85 | N30s = 0.47 | -24.89 |
| 30t | 6.46 | 105.33 | -24.93 | N30t = 0.53 | |
| 31a | -84.13 | 85.45 | -109.59 | N31a = 1.00 | -109.59 |
| 31bs | -72.64 | 86.22 | -98.33 | N31b = 0.00 | |
| 31bt | -71.99 | 86.04 | -97.62 | N31c = 0.00 | |
| 31cs | -72.63 | 85.32 | -98.06 | ||
| 31ct | -70.93 | 81.13 | -95.11 | ||
| 32 | -186.31 | 79.52 | -210.13 | ||
| 33ss | -65.43 | 94.48 | -93.59 | N33ss = 0.48 | -93.52 |
| 33st | -63.30 | 95.82 | -91.85 | N33st = 0.03 | |
| 33ts | -65.43 | 94.52 | -93.60 | N33ts = 0.48 | |
| 33tt | -63.16 | 95.20 | -91.53 | N33tt = 0.01 | |
| 34ss | -71.88 | 103.55 | -102.74 | N34ss = 0.65 | -102.49 |
| 34st | -70.05 | 103.73 | -100.96 | N34st = 0.03 | |
| 34ts | -71.86 | 102.01 | -102.26 | N34ts = 0.29 | |
| 34tt | -69.86 | 104.01 | -100.85 | N34tt = 0.03 | |
| 35s | -34.15 | 86.57 | -59.95 | N35s = 0.61 | -59.85 |
| 35t | -34.02 | 86.13 | -59.69 | N35t = 0.39 | |
| 36 | 52.32 | 78.49 | 28.93 | ||
| H2O | -59.44 | 44.99 | -72.85 |
| Compound | ΔHf (Kcal/mol) | ΔS (cal/mol K) | ΔGf a (Kcal/mol | Mol fractions of conformers or tautomersb | Weighted average ΔGf c (Kcal/mol) |
|---|---|---|---|---|---|
| 37 | 121.80 | 68.59 | 101.36 | ||
| 38 | 113.73 | 79.14 | 90.15 | ||
| 39 | 109.00 | 86.50 | 83.22 | ||
| 40 | 103.32 | 93.27 | 75.53 | ||
| 41 | 98.58 | 96.84 | 69.72 | ||
| 42s | 72.67 | 86.97 | 46.75 | N42s = 0.53 | 46.78 |
| 42t | 72.66 | 86.73 | 46.81 | N42t = 0.47 | |
| 43a | 115.66 | 113.65 | 81.79 | N43a = 0.00 | 1.00 |
| 43b | 109.85 | 112.55 | 76.31 | N43b = 1.00 | |
| 44s | 99.68 | 116.00 | 65.11 | N44s = 0.26 | 64.64 |
| 44t | 99.60 | 117.86 | 64.48 | N44t = 0.74 | |
| 45s | 20.63 | 113.10 | -13.07 | N45s = 0.71 | -12.92 |
| 45t | 20.69 | 111.56 | -12.55 | N45t = 0.29 | |
| 46s | 61.58 | 122.15 | 25.18 | N46s = 0.00 | |
| 46t | 56.29 | 122.48 | 19.79 | N46t = 1.00 | |
| 47 | 59.29 | 101.27 | 29.11 | ||
| 48 | 156.51 | 109.33 | 123.93 | ||
| 49 | 77.90 | 75.96 | 55.26 | ||
| 50s | 86.40 | 87.29 | 60.39 | N50s = 0.98 | 60.44 |
| 50t | 86.71 | 80.44 | 62.74 | N50t = 0.02 | |
| 51 | 127.96 | 81.08 | 103.80 | ||
| 52 | -6.43 | 94.86 | -34.70 | ||
| 53 | 81.79 | 74.22 | 59.67 | ||
| 54 | 118.24 | 77.23 | 95.23 | ||
| 55 | 129.46 | 80.21 | 105.56 | ||
| 56 | 141.60 | 82.75 | 116.95 | ||
| 57a | 122.34 | 85.33 | 96.91 | N57a = 1.00 | 96.91 |
| 57b | 152.00 | 85.62 | 126.49 | N57b = 0.00 | |
| 57c | 151.94 | 86.06 | 126.29 | N57c = 0.00 | |
| 58a | 115.72 | 76.66 | 92.88 | N58a = 0.00 | 85.14 |
| 58b | 108.61 | 78.75 | 85.14 | N58b = 1.00 | |
| 59a | 127.09 | 92.35 | 99.57 | N59a = 0.71 | 99.72 |
| 59b | 127.52 | 92.01 | 100.10 | N59b = 0.29 | |
| 60a | 69.61 | 96.97 | 40.71 | N60a = 0.58 | 40.79 |
| 60b | 71.11 | 94.92 | 42.82 | N60b = 0.00 | |
| 60c | 70.92 | 94.36 | 42.80 | N60c = 0.00 | |
| 60d | 69.46 | 95.86 | 40.89 | N60d = 0.42 | |
| 61a | 76.06 | 103.79 | 45.13 | N61a = 0.47 | 45.33 |
| 61b | 76.84 | 99.34 | 47.24 | N61b = 0.01 | |
| 61c | 76.75 | 104.25 | 45.68 | N61c = 0.19 | |
| 61d | 75.93 | 102.62 | 45.35 | N61d = 0.33 | |
| 62a | 100.67 | 115.08 | 66.37 | N62a = 0.71 | 66.59 |
| 62b | 102.48 | 112.86 | 68.85 | N62b = 0.01 | |
| 62c | 101.96 | 112.37 | 68.47 | N62c = 0.02 | |
| 62d | 100.51 | 112.60 | 66.97 | N62d = 0.26 | |
| 63a | 107.58 | 122.27 | 71.14 | N63a = 0.15 | 70.46 |
| 63b | 108.32 | 122.08 | 71.94 | N63b = 0.04 | |
| 63c | 107.81 | 121.03 | 71.74 | N63c = 0.05 | |
| 63d | 107.41 | 124.95 | 70.17 | N63d = 0.76 | |
| 64s | 90.19 | 81.96 | 65.76 | N64s = 0.46 | 65.71 |
| 64t | 90.14 | 82.15 | 65.66 | N64t = 0.54 | |
| 65s | 78.97 | 89.14 | 52.41 | N65s = 0.38 | 52.23 |
| 65t | 78.90 | 89.85 | 52.12 | N65t = 0.62 | |
| 66s | 110.11 | 109.01 | 77.63 | N66s = 0.64 | 77.75 |
| 66t | 109.97 | 107.36 | 77.97 | N66t = 0.36 | |
| 67ss | 31.76 | 86.71 | 5.92 | N67ss = 0.35 | 5.95 |
| 67st | 32.52 | 86.50 | 6.74 | N67st = 0.09 | |
| 67ts | 31.65 | 87.04 | 5.71 | N67ts = 0.50 | |
| 67tt | 32.66 | 86.12 | 7.00 | N67tt = 0.06 | |
| 68ss | 39.09 | 95.33 | 10.68 | N68ss = 0.40 | 10.77 |
| 68st | 41.15 | 97.48 | 12.10 | N68st = 0.04 | |
| 68ts | 39.01 | 95.71 | 10.49 | N68ts = 0.55 | |
| 68tt | 41.17 | 96.63 | 12.37 | N68tt = 0.02 | |
| 69ss | 31.32 | 105.80 | -0.21 | N69ss = 0.97 | -0.15 |
| 69st | 34.51 | 98.56 | 5.14 | N69st = 0.00 | |
| 69ts | 33.75 | 106.83 | 1.91 | N69ts = 0.03 | |
| 69tt | 34.56 | 103.65 | 3.67 | N69tt = 0.00 | |
| 70s | 68.87 | 87.07 | 42.92 | N70s = 0.53 | 42.95 |
| 70t | 68.85 | 86.82 | 42.98 | N70t = 0.47 | |
| 71 | 155.79 | 78.92 | 132.27 | 133.05 | |
| H3O+ | 46.81 | 45.91 | 33.13 |
| Conjugate base (B) | ΔGf kcal/mol | Conjugate acid (BH+) | ΔGf kcal/mol | δΔGf a kcal/mol | pKa(BH+)b | Exp. pKa(BH+)c | Absolute error between pKa(calc.) and pKa(exp.) | Referencesc |
|---|---|---|---|---|---|---|---|---|
| 1 | 2.90 | 37 | 101.36 | 7.52 | 5.51 | 5.27, 5.28 | 0.24, 0.23 | 23, 24, 25 |
| 2 | -7.78 | 38 | 90.15 | 8.05 | 5.90 | 5.67, 5.70, 5.75 | 0.23, 0.20, 0.15 | 26, 27, 28, 29 |
| 3 | -15.93 | 39 | 83.22 | 6.83 | 5.01 | 5.70 | -0.69 | 30 |
| 4 | -23.48 | 40 | 75.53 | 6.97 | 5.11 | 5.72 | -0.61 | 30 |
| 5 | -29.46 | 41 | 69.72 | 6.80 | 4.99 | 5.82 | -0.83 | 30 |
| 6 | -52.93 | 42 | 46.78 | 6.27 | 4.59 | 4.90, 4.95 | -0.31, -0.36 | 31, 32 |
| 7 | -17.15 | 43 | 76.31 | 12.52 | 9.18 | 8.55 | 0.63 | 33 |
| 8 | -35.51 | 44 | 64.64 | 5.83 | 4.28 | 4.87 | -0.59 | 34 |
| 9 | -113.03 | 45 | -12.92 | 5.87 | 4.30 | 4.67 | -0.37 | 35 |
| 10 | -82.08 | 46 | 19.79 | 4.11 | 3.01 | 3.67 | -0.66 | 36 |
| 11 | -70.07 | 47 | 29.11 | 6.80 | 4.98 | 5.47 | -0.49 | 31 |
| 12 | 24.51 | 48 | 123.93 | 6.56 | 4.81 | 4.75 | 0.06 | 37 |
| 13 | -50.34 | 49 | 55.26 | 0.38 | 0.28 | 4.80, 4.86 | -4.52, -4.58 | 27, 38, 39, 40 |
| 14 | -40.14 | 50 | 60.44 | 5.40 | 3.96 | 4.78, 4.88, 4.90 | -0.82, -0.92, -0.94 | 26, 40, 38, 27 |
| 15 | -5.68 | 51 | 103.80 | -3.50 | -2.56 | 2.28 | -4.84 | 19 |
| 16 | -154.28 | 52 | -34.70 | -13.60 | -9.97 | 3.22 | -13.19 | 41 |
| 17 | -43.65 | 53 | 59.67 | 2.66 | 1.95 | 2.97, 3.10 | -1.14 | 30, 42 |
| 18 | -6.54 | 54 | 95.23 | 4.21 | 3.08 | 2.81, 2.84, 2.98 | 0.27, 0.24, 0.10 | 26, 42, 27 |
| 19 | 3.74 | 55 | 105.56 | 4.16 | 3.05 | 2.80, 2.84, 2.85 | 0.15, 0.21, 0.20 | 27, 42, 26 |
| 20 | 16.35 | 56 | 116.95 | 5.38 | 3.94 | 3.25 | 0.69 | 30 |
| 21 | -10.39 | 57 | 96.91 | -1.32 | -0.97 | 0.81, 1.18 | -1.78, -2.15 | 43, 26 |
| 22 | -5.96 | 58 | 85.14 | 14.88 | 10.90 | 5.80, 5.98, 6.04 | 5.10, 4.92, 4.86 | 30, 44, 26, 27 |
| 23 | 0.15 | 59 | 99.72 | 6.41 | 4.70 | 6.45 | -1.75 | 45 |
| 24 | -60.32 | 60 | 40.79 | 4.87 | 3.57 | 4.46 | -0.89 | 46 |
| 25 | -57.31 | 61 | 45.33 | 3.34 | 2.45 | 3.52 | -1.07 | 46 |
| 26 | -35.62 | 62 | 66.59 | 3.77 | 2.76 | 3.80 | -1.04 | 46 |
| 27 | -32.56 | 63 | 70.46 | 2.96 | 2.17 | 3.66 | -1.49 | 46 |
| 28 | -37.01 | 64 | 65.71 | 3.26 | 2.39 | 3.70, 3.75 | -1.31, -1.36 | 47, 48 |
| 29 | -50.39 | 65 | 52.23 | 3.36 | 2.46 | 3.18, 3.26 | -0.72, -0.80 | 30, 49 |
| 30 | -24.89 | 66 | 77.75 | 3.34 | 2.45 | 3.18 | -0.73 | 26 |
| 31 | -109.59 | 67 | 5.95 | -9.56 | -7.00 | 3.13, 3.75 | -10.13, -10.75 | 43, 50 |
| 32 | -210.13 | 31 | -109.59 | 5.44 | 3.99 | 4.77 | -0.78 | 51 |
| 33 | -93.52 | 68 | 10.77 | 1.69 | 1.24 | 3.09 | -1.85 | 26 |
| 34 | -102.49 | 69 | -0.15 | 3.64 | 2.67 | 3.35 | -0.68 | 42 |
| 35 | -59.85 | 70 | 42.95 | 3.18 | 2.33 | 3.40 | -1.07 | 51 |
| 36 | 28.93 | 71 | 133.05 | 1.86 | 1.36 | 1.30, 1.36, 1.45 | 0.06, 0.00, -0.09 | 27, 26, 52, 51 |
| H2O | -72.85 | H3O+ | 33.13 |
Conclusion
Acknowledgements
References
- Güven, A.; Jones, R.A. J. Chem. Research. 1993, 362–363.
- Güven, A.; Jones, R.A. J. Chem. Research. 1993, 2411–2428.
- Güven, A.; Jones, R.A. Tetrahedron 1993, 49, 11145–11154.
- Güven, A.; Öğretir, C. J. Mol. Struct. (Theochem) 1998, 427, 65–77.
- Güven, A.; Öğretir, C. J. Mol. Struct. (Theochem) 1998, 430, 85–95.
- Güven, A.; Öğretir, C. J. Mol. Struct. (Theochem) 1998, 434, 7–28.
- Güven, A.; Kanışkan, N. J. Mol. Struct. (Theochem) 1999, 488, 125–134.
- Güven, A.; Yekeler, H.; Özkan, R. J. Mol. Struct. (Theochem) 2000, 499, 13–19.
- Hür, D.; Güven, A. J. Mol. Struct. (Theochem) 2002, 583, 1–18.
- Güven, A. J. Mol. Struct. (Theochem) 2004, 683, 221–229.
- Katritzky, A.R.; Lagowski, J.M. Advances in Heterocyclic Chemistry. 1963, 1–81, 311–437. [Google Scholar]
- Elguero, J.; Marzin, C.; Katritzky, A.R.; Linda, P. Advances in Heterocyclic Chemistry Supplement 1; Academic Press Inc., 1976. [Google Scholar]
- Dewar, M.J.S.; Zoebisch, E.G.; Healy, E.F.; Stewart, J.J.P. AM1. J. Am. Chem. Soc. 1985, 107, 3092. [Google Scholar]
- Stewart, J.J.P. MOPAC 2000. Fujitsu Limited: Tokyo, Japan.
- Stewart, J.J.P. PM5. J. Mol. Model. 2004, 10, 6. [Google Scholar]
- Stewart, J.J.P. MOPAC 2002. Fujitsu Limited: Tokyo, Japan.
- Klamt, A.; Schüümann, G. COSMO. J. Chem. Soc. Perkin Trans. 1993, 2, 799–805. [Google Scholar]
- ChemOffice CambridgeSoft Corporation 100 Cambridge Park Drive Cambridge, MA 021140 USA.
- Katritzky, A.R.; Lagowski, J.M. Advances in Heterocyclic Chemistry. 1963, 352, 311–437. [Google Scholar]
- Albert, A.A.; Barlin, G.B. J. Chem. Soc. 1959, 2384.
- Mason, S.F. J. Chem. Soc. 1959, 1281.
- Mason, S.F. J. Chem. Soc. 1958, 3619.
- Millero, F.J.; Ahluwalia, J.C.; Hepler, L.G. J. Phys. Chem. 1964, 68, 3435.
- Perkampus, H. H.; Prescher, G. Ber. Bunsenges. Che. 1968, 72, 429.
- Phan-Tan-Luu, R.; Surzur, J.M.; Metzger, J.; Aune, J.P.; Dupuy, C. Bull. Soc. Chim. Fr. 1968, 3274.
- Green, R.W. Aust. J. Chem. 1969, 22, 721.
- Fischer, A.; Galloway, W.J.; Vaughan, J. J. Chem. Soc., B 1964, 3591.
- http://tera.chem.ut.ee/~manna/pkadacat/html.
- Phan-Tan-Luu, R.; Surzur, J.M.; Metzger, J.; Aune, J.P.; Dupuy, C. Bull. Soc. Chim. Fr. 1968, 3274.
- Perkampus, H. H.; Prescher, G. Ber. Bunsenges. Che. 1968, 72, 429.
- Jencks, W.P. http://research.chem.psu.edu/brpgroup/pKa_compilation.pdf.
- Tissier, M.; Tissier, C. Bull. Soc. Chim. Fr. 1967, 3155.
- Guseva, E. A.; Porai-Koshits, B.A. Reakts Sposoboots. Org. Soedin (Tartu) 1965, 2, 29. [Google Scholar]
- Barlow, R.B.; Thompson, G.M. Brit. J. Pharmacol. 1969, 37, 555.
- Katritzky, A.R.; Kucharska, H.Z.; Rowe, J.D. J .Chem. Soc. 1965, 3093.
- Jones, R.A.; Katritzky, A.R. Aust. J. Chem. Soc. 1964, 17, 455.
- Golding, S.; Katritzky, A.R.; Kucharska, H.Z. J. Chem. Soc. 1965, 3090.
- Beggiato, G.; Favoro, G.; Mazzucato, U. J. Heterocyclic. Chem. 1970, 7, 583.
- Albert, A.; Philips, J. N. J. Chem. Soc. 1956, 1294.
- Mason, S.F. J. Chem. Soc. 1958, 674.
- Mason, S.F. J. Chem. Soc. 1959, 1253.
- Evans, R.F.; Brown, H.C. J. Org. Chem. 1962, 27, 3127.
- Clarke, K.; Rothwell, K. J. Chem. Soc. 1960, 1885.
- Bryson, A. J. Am. Chem. Soc. 1960, 82, 4558, 4862, 4871.
- Mason, S. F. J. Chem. Soc. 1960, 219.
- Cruege, F.; Girault, G.; Coustal, S.; Lascombe, J.; Rumpf, P. Bull. Soc. Chim. Fr. 1970, 3889.
- Jones, R.A.; Katritzky, A.R. J. Chem. Soc. 1959, 1317.
- Laviron, E. Bull. Soc. Chim. Fr. 1961, 2325.
- Tirouflet, J.; Laviron, E. Compt. Rend. 1958, 247, 217.
- Cabani, S.; Conti, G. Gazz. Chim. Ital. 1965, 95, 533.
- Joule, J.A.; Smith, G.F. Heterocyclic Chemistry, 2nd Ed. edVan Nostrand Reinhold (UK) Co. Ltd.: Berkshire, England, 1978; p. 68. [Google Scholar]
- Jaffe, H.H.; Doak, G.O. J. Am. Chem. Soc. 1955, 77, 4441.
- Mason, S.F. J. Chem. Soc. 1959, 1247.
© 2005 by MDPI (http://www.mdpi.org). Reproduction is permitted for non-commercial purposes.
Share and Cite
Güven, A. Acidity Study on 3-Substituted Pyridines. Int. J. Mol. Sci. 2005, 6, 257-275. https://doi.org/10.3390/i6110257
Güven A. Acidity Study on 3-Substituted Pyridines. International Journal of Molecular Sciences. 2005; 6(11):257-275. https://doi.org/10.3390/i6110257
Chicago/Turabian StyleGüven, Alaattin. 2005. "Acidity Study on 3-Substituted Pyridines" International Journal of Molecular Sciences 6, no. 11: 257-275. https://doi.org/10.3390/i6110257
APA StyleGüven, A. (2005). Acidity Study on 3-Substituted Pyridines. International Journal of Molecular Sciences, 6(11), 257-275. https://doi.org/10.3390/i6110257




