Molecular Mechanics Study of Nickel(II) Octaethylporphyrin Adsorbed on Graphite(0001)
Abstract
:1 Introduction
2 Stereochemistry
3 Computational Details
3.1 Intramolecular Potential
3.2 Modelling of Graphite Layer
3.3 Geometry Optimization
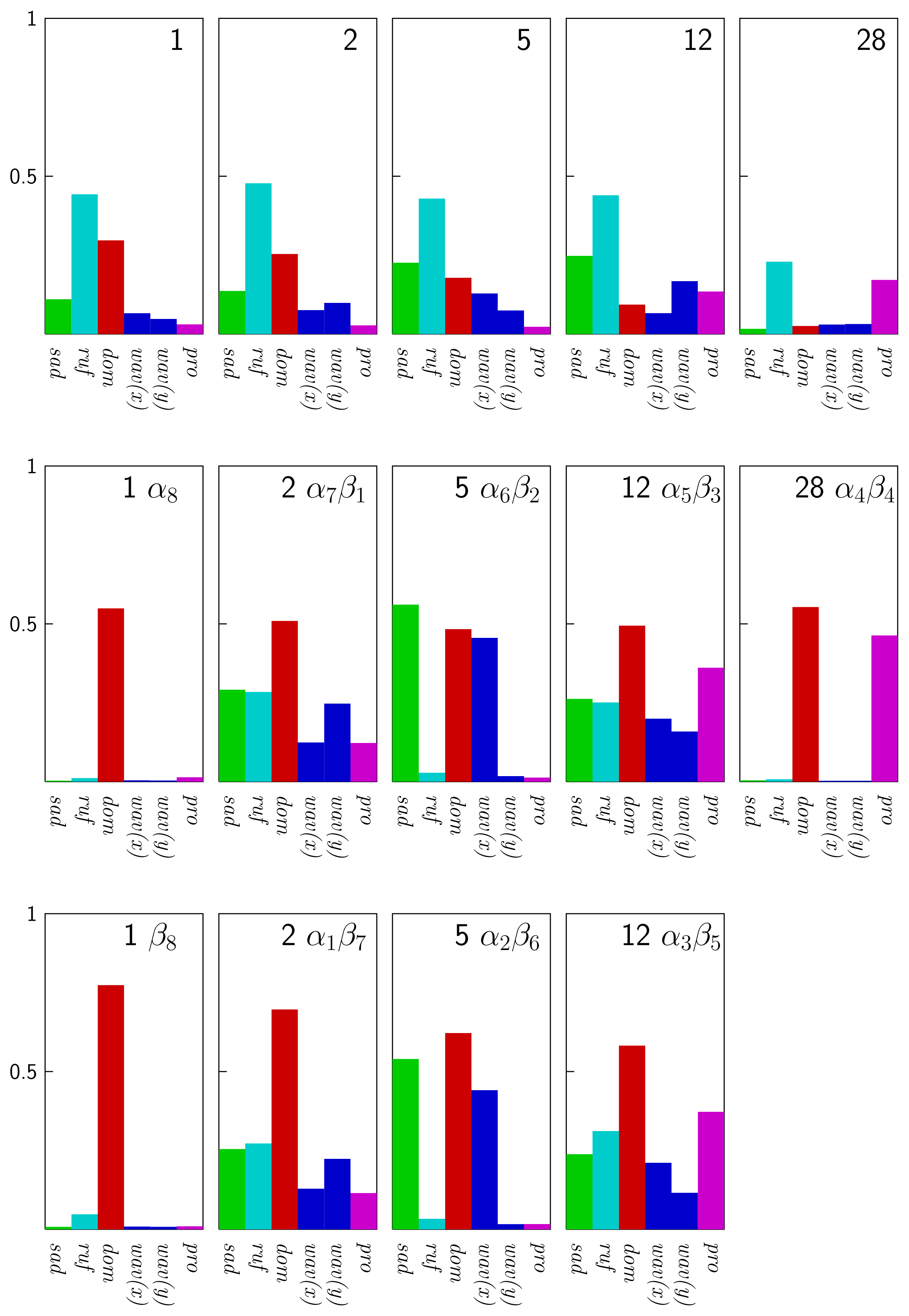
3.4 Normal-coordinate Structural Decomposition
4 Results and Discussion
4.1 Nickel(II)octaethylporphyrin, Ni(OEP) (isolated)
4.2 Nickel(II)octaethylporphyrin Adsorbed on Graphite
4.3 Movement of Ni(OEP) in the vicinity of graphite(0001) surface
5 Concluding remarks
Appendix
| Ni(OEP), 19 (Triclinic A) | Ni(OEP), 18 (Triclinic B) | Ni(OEP), 16 (Tetragonal) | Ni(OEP), 28 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MMa | X-rayb | DFTc | MMa | X-rayd | DFTc | MMa | X-raye | DFTc | MMa | DFTc | |
| Distances (Å) | |||||||||||
| Ni-N | 1.955 | 1.958(2) | 1.961 | 1.955 | 1.952(4) | 1.963 | 1.953 | 1.929(3) | 1.970 | 1.955 | 1.962 |
| N-Cα | 1.375 | 1.376(6) | 1.376 | 1.375 | 1.385(6) | 1.376 | 1.375 | 1.386(2) | 1.376 | 1.375 | 1.376 |
| Cα-Cβ | 1.341 | 1.443(3) | 1.450 | 1.341 | 1.444(7) | 1.450 | 1.341 | 1.449(5) | 1.450 | 1.341 | 1.450 |
| Cβ-Cβ | 1.338 | 1.346(2) | 1.369 | 1.338 | 1.331(8) | 1.369 | 1.338 | 1.362(5) | 1.368 | 1.337 | 1.368 |
| Cα-Cm | 1.369 | 1.371(4) | 1.383 | 1.369 | 1.363(8) | 1.383 | 1.369 | 1.372(2) | 1.382 | 1.369 | 1.383 |
| Angles (deg) | |||||||||||
| N-Ni-N | 90.0(6) | 90.15(9) | 90.02 | 89.9(3) | 89.9(2) | 90.0 | 90.03(6) | 90.0 | 90.0 | 90.0 | 90.0 |
| Ni-N-Cα | 126.7 | 128.0(2) | 127.6 | 126.9 | 128.0(3) | 127.6 | 127.1 | 127.4(2) | 127.7 | 127.1 | 127.6 |
| N-Cα-Cm | 126.8 | 124.4(3) | 124.8 | 126.8 | 124.4(5) | 124.8 | 126.7 | 124.0(2) | 124.9 | 126.9 | 124.8 |
| N-Cα-Cβ | 108.6 | 111.6(3) | 111.4 | 108.6 | 110.8(5) | 111.4 | 108.5 | 110.6(2) | 111.5 | 108.5 | 111.4 |
| Cα-N-Cα | 104.9 | 103.9(4) | 104.8 | 105.5 | 104.1(4) | 104.8 | 105.7 | 105.1(3) | 104.6 | 105.7 | 104.8 |
| Cα-Cm-Cα | 121.9 | 125.1(1) | 124.0 | 121.8 | 125.2(5) | 124.1 | 121.8 | 124.1(2) | 124.3 | 121.7 | 124.1 |
| Cα-Cβ-Cβ | 108.3 | 106.5(4) | 106.2 | 108.5 | 107.2(5) | 106.2 | 108.5 | 106.8(3) | 106.2 | 108.5 | 106.2 |
| Core Deformations | |||||||||||
| Dipf (Å) | 0.453 | 0.130 | n.r. | 0.450 | 0.149 | n.r. | 0.477 | 0.332 | n.r. | 0.446 | n.r |
| Doopf (Å) | 0.363 | 0.087 | n.r. | 0.414 | 0.138 | n.r. | 0.772 | 1.461 | n.r. | 0.291 | n.r |
| Doop | B2u | B1u | A2u | Eg(x) | Eg(y) | A1u | |
|---|---|---|---|---|---|---|---|
| 1 (free) | 0.5507 | 0.1100 | 0.4425 | 0.2965 | 0.0657 | 0.0477 | 0.0306 |
| 1α8 | 0.5493 | 0.0031 | 0.0113 | 0.5490 | 0.0043 | 0.0036 | 0.0137 |
| 1β8 | 0.7751 | 0.0079 | 0.0476 | 0.7735 | 0.0085 | 0.0078 | 0.0094 |
| 2 (free) | 0.5718 | 0.1364 | 0.4775 | 0.2533 | 0.0755 | 0.0985 | 0.0275 |
| 2α7β1 | 0.7186 | 0.2911 | 0.2842 | 0.5092 | 0.1242 | 0.2472 | 0.1225 |
| 2α1β7 | 0.8385 | 0.2541 | 0.2719 | 0.6964 | 0.1286 | 0.2232 | 0.1149 |
| 3 (free) | 0.6701 | 0.0233 | 0.6370 | 0.1790 | 0.0781 | 0.0678 | 0.0065 |
| 3α6β2 | 0.8174 | 0.0115 | 0.6145 | 0.4913 | 0.1472 | 0.1657 | 0.0035 |
| 3α2β6 | 0.8464 | 0.0047 | 0.5681 | 0.6029 | 0.1186 | 0.1265 | 0.0039 |
| 4 (free) | 0.3983 | 0.0960 | 0.2479 | 0.1409 | 0.0945 | 0.2203 | 0.1033 |
| 4α6β2 | 0.6594 | 0.0225 | 0.0042 | 0.4872 | 0.1319 | 0.3392 | 0.2539 |
| 4α2β6 | 0.7780 | 0.0476 | 0.0110 | 0.6327 | 0.1337 | 0.3448 | 0.2566 |
| 5 (free) | 0.5379 | 0.2259 | 0.4291 | 0.1782 | 0.1283 | 0.0745 | 0.0229 |
| 5α6β2 | 0.8698 | 0.5607 | 0.0283 | 0.4830 | 0.4556 | 0.0175 | 0.0129 |
| 5α2β6 | 0.9345 | 0.5395 | 0.0331 | 0.6217 | 0.4406 | 0.0163 | 0.0166 |
| 6 (free) | 0.4555 | 0.2188 | 0.3243 | 0.1684 | 0.0804 | 0.0953 | 0.1024 |
| 6α6β2 | 0.9499 | 0.5517 | 0.5439 | 0.4843 | 0.0141 | 0.0144 | 0.2593 |
| 6α2β6 | 1.0473 | 0.5416 | 0.5921 | 0.6194 | 0.0234 | 0.0194 | 0.2614 |
| 7 (free) | 0.5021 | 0.1358 | 0.3588 | 0.1200 | 0.1472 | 0.2616 | 0.0194 |
| 7α6β2 | 0.8552 | 0.0226 | 0.5348 | 0.4782 | 0.3358 | 0.3215 | 0.0118 |
| 7α2β6 | 0.9563 | 0.0261 | 0.5464 | 0.6164 | 0.3366 | 0.3489 | 0.0182 |
| 8 (free) | 0.5207 | 0.2299 | 0.3666 | 0.1276 | 0.0715 | 0.2493 | 0.0168 |
| 8α6β2 | 0.7980 | 0.5596 | 0.0152 | 0.5094 | 0.0104 | 0.2522 | 0.0116 |
| 8α2β6 | 0.8679 | 0.5453 | 0.0397 | 0.6222 | 0.0221 | 0.2576 | 0.0177 |
| 9 (free) | 0.6084 | 0.0774 | 0.5469 | 0.0586 | 0.1259 | 0.2075 | 0.0513 |
| 9α5β3 | 0.6939 | 0.2956 | 0.2976 | 0.5100 | 0.1095 | 0.1225 | 0.1361 |
| 9α3β5 | 0.7183 | 0.2783 | 0.2755 | 0.5597 | 0.1365 | 0.1105 | 0.1361 |
| 10 (free) | 0.3653 | 0.1828 | 0.2447 | 0.1065 | 0.0975 | 0.1324 | 0.0423 |
| 10α5β3 | 0.7981 | 0.2659 | 0.3455 | 0.4845 | 0.2612 | 0.3587 | 0.1237 |
| 10α3β5 | 0.7833 | 0.2709 | 0.2550 | 0.5544 | 0.2006 | 0.3390 | 0.1124 |
| 11 (free) | 0.7191 | 0.2007 | 0.6539 | 0.0983 | 0.0935 | 0.1677 | 0.0518 |
| 11α5β3 | 1.0417 | 0.2643 | 0.8444 | 0.4685 | 0.2447 | 0.0841 | 0.1258 |
| 11α3β5 | 1.0924 | 0.2315 | 0.8783 | 0.5236 | 0.2153 | 0.1651 | 0.1436 |
| 12 (free) | 0.5601 | 0.2476 | 0.4395 | 0.0931 | 0.0661 | 0.1674 | 0.1347 |
| 12α5β3 | 0.7557 | 0.2620 | 0.2509 | 0.4941 | 0.1994 | 0.1589 | 0.3610 |
| 12α3β5 | 0.8296 | 0.2379 | 0.3112 | 0.5819 | 0.2107 | 0.1156 | 0.3721 |
| 13 (free) | 0.6031 | 0.0565 | 0.5378 | 0.0775 | 0.2327 | 0.0896 | 0.0564 |
| 13α5β3 | 0.8505 | 0.2988 | 0.2560 | 0.4877 | 0.5336 | 0.1765 | 0.1218 |
| 13α3β5 | 0.9236 | 0.2630 | 0.3212 | 0.5520 | 0.5550 | 0.2271 | 0.1282 |
| 14 (free) | 0.4536 | 0.2760 | 0.1055 | 0.0569 | 0.2494 | 0.2243 | 0.0521 |
| 14α5β3 | 0.7829 | 0.2360 | 0.2563 | 0.5061 | 0.4428 | 0.1509 | 0.1293 |
| 14α3β5 | 0.8239 | 0.2419 | 0.2669 | 0.5683 | 0.4379 | 0.1313 | 0.1312 |
| 15 (free) | 0.5795 | 0.5318 | 0.1117 | 0.0929 | 0.1221 | 0.1241 | 0.0404 |
| 15α5β3 | 1.0230 | 0.8073 | 0.2653 | 0.4912 | 0.1317 | 0.2249 | 0.1233 |
| 15α3β5 | 1.0382 | 0.7668 | 0.2976 | 0.5668 | 0.1238 | 0.2232 | 0.1223 |
| 16 (free) | 0.7718 | 0.7205 | 0.2720 | 0.0168 | 0.0181 | 0.0440 | 0.0076 |
| 16α4β4 | 1.1796 | 1.0548 | 0.0260 | 0.5270 | 0.0100 | 0.0109 | 0.0076 |
| 17 (free) | 0.3728 | 0.0209 | 0.0998 | 0.0153 | 0.3468 | 0.0895 | 0.0090 |
| 17α4β4 | 0.8387 | 0.0387 | 0.0163 | 0.5230 | 0.6542 | 0.0102 | 0.0030 |
| 18 (free) | 0.4138 | 0.0874 | 0.3642 | 0.0565 | 0.0824 | 0.1444 | 0.0086 |
| 18α4β4 | 0.5988 | 0.0092 | 0.0587 | 0.5119 | 0.0406 | 0.3016 | 0.0216 |
| 19 (free) | 0.3628 | 0.0212 | 0.1015 | 0.0141 | 0.2200 | 0.2688 | 0.0064 |
| 19α4β4 | 0.6448 | 0.0181 | 0.0356 | 0.5383 | 0.2482 | 0.2507 | 0.0017 |
| 20 (free) | 0.7076 | 0.0770 | 0.6727 | 0.0557 | 0.0794 | 0.1599 | 0.0846 |
| 20α4β4 | 0.8511 | 0.0275 | 0.5806 | 0.5130 | 0.0494 | 0.2296 | 0.2609 |
| 21 (free) | 0.7512 | 0.3919 | 0.6051 | 0.0479 | 0.1882 | 0.0820 | 0.0115 |
| 21α4β4 | 0.9776 | 0.4995 | 0.5779 | 0.4966 | 0.3218 | 0.1473 | 0.0183 |
| 22 (free) | 0.4930 | 0.3414 | 0.1580 | 0.0166 | 0.2199 | 0.2131 | 0.0863 |
| 22α4β4 | 0.9016 | 0.5156 | 0.0146 | 0.5282 | 0.3376 | 0.3101 | 0.2401 |
| 23 (free) | 0.7243 | 0.3089 | 0.6155 | 0.0100 | 0.1118 | 0.1944 | 0.0032 |
| 23α4β4 | 1.0013 | 0.5019 | 0.5874 | 0.5104 | 0.1470 | 0.3514 | 0.0054 |
| 24 (free) | 0.7597 | 0.2458 | 0.6863 | 0.0523 | 0.1914 | 0.0780 | 0.0107 |
| 24α4β4 | 1.0416 | 0.5398 | 0.6240 | 0.4917 | 0.3653 | 0.1702 | 0.0125 |
| 25 (free) | 0.3738 | 0.0664 | 0.2168 | 0.0451 | 0.1856 | 0.2276 | 0.0071 |
| 25α4β4 | 0.8193 | 0.0361 | 0.1308 | 0.4841 | 0.4526 | 0.4619 | 0.0176 |
| 26 (free) | 0.8315 | 0.0173 | 0.8306 | 0.0133 | 0.0201 | 0.0241 | 0.0050 |
| 26α4β4 | 1.2080 | 0.0122 | 1.1109 | 0.4742 | 0.0017 | 0.0018 | 0.0025 |
| 27 (free) | 0.6144 | 0.0149 | 0.5860 | 0.0175 | 0.1589 | 0.0329 | 0.0845 |
| 27α4β4 | 0.8896 | 0.0175 | 0.5422 | 0.5116 | 0.4235 | 0.0597 | 0.2291 |
| 28 (free) | 0.2907 | 0.0165 | 0.2289 | 0.0253 | 0.0298 | 0.0317 | 0.1713 |
| 28α4β4 | 0.7215 | 0.0043 | 0.0075 | 0.5532 | 0.0027 | 0.0028 | 0.4631 |

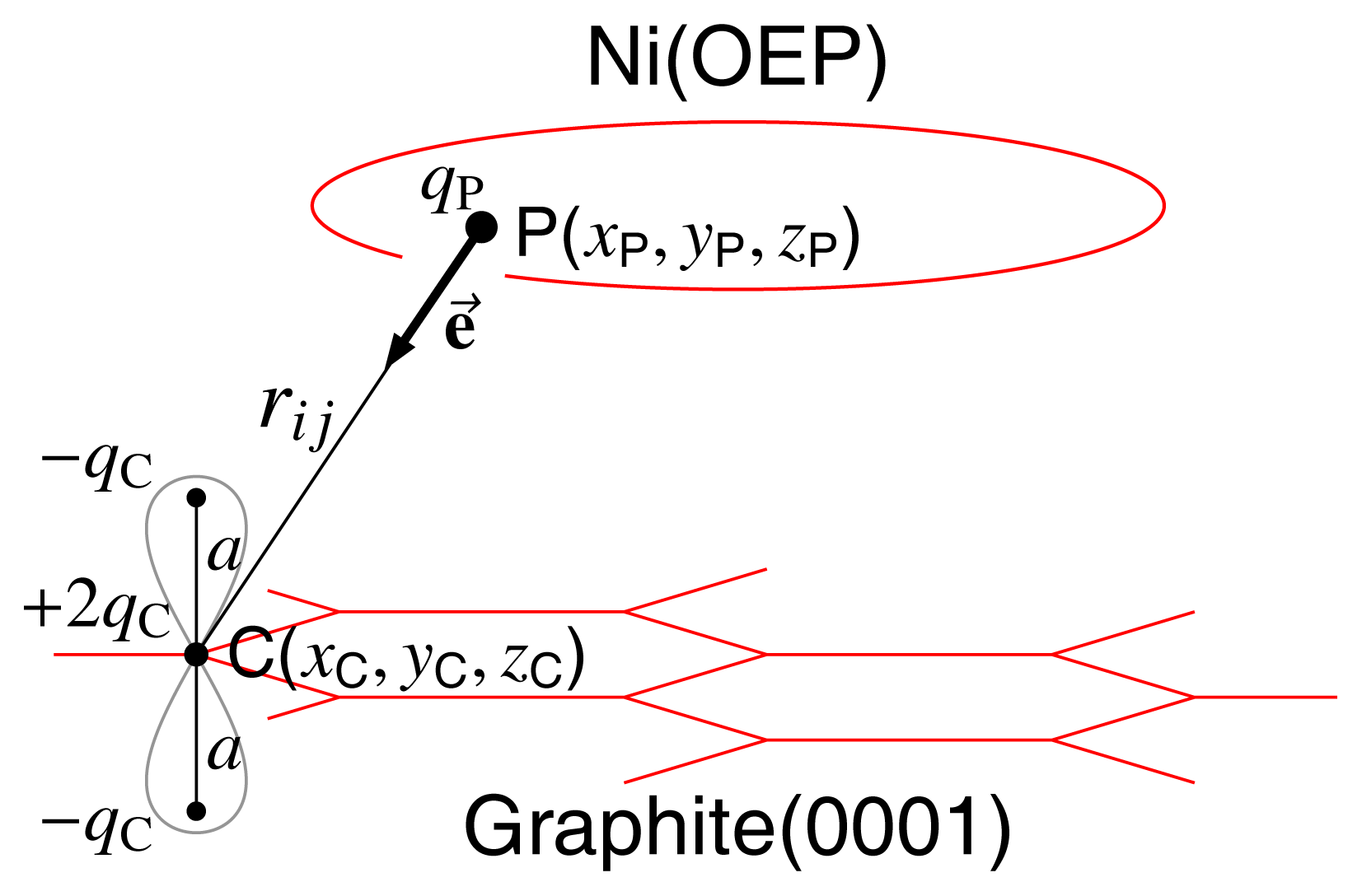


| Conf. | ΔE | Etotal | Eb | Eθ | Eφ | EvdW | Ec | P | Doop |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.71 | −17.40 | 0.67 | 15.15 | 1.24 | −9.13 | −25.33 | 0.83 | 0.551 |
| 2 | 1.25 | −17.86 | 0.67 | 15.05 | 1.12 | −9.19 | −25.52 | 1.81 | 0.572 |
| 3 | 0.86 | −18.25 | 0.70 | 14.89 | 1.19 | −9.36 | −25.66 | 3.50 | 0.670 |
| 4 | 1.07 | −18.04 | 0.65 | 14.90 | 1.04 | −9.08 | −25.56 | 2.46 | 0.398 |
| 5 | 1.18 | −17.93 | 0.67 | 14.91 | 1.06 | −9.07 | −25.49 | 2.04 | 0.538 |
| 6 | 1.19 | −17.92 | 0.66 | 14.91 | 1.02 | −9.07 | −25.43 | 2.01 | 0.456 |
| 7 | 1.09 | −18.02 | 0.67 | 14.89 | 1.19 | −9.20 | −25.56 | 2.38 | 0.502 |
| 8 | 1.88 | −17.23 | 0.69 | 15.20 | 1.15 | −9.01 | −25.27 | 0.62 | 0.521 |
| 9 | 1.41 | −17.70 | 0.70 | 14.96 | 1.34 | −9.18 | −25.52 | 1.38 | 0.608 |
| 10 | 0.66 | −18.45 | 0.64 | 14.77 | 0.85 | −9.10 | −25.62 | 4.91 | 0.365 |
| 11 | 0.48 | −18.63 | 0.70 | 14.75 | 1.20 | −9.46 | −25.83 | 6.66 | 0.719 |
| 12 | 0.70 | −18.41 | 0.67 | 14.75 | 1.08 | −9.18 | −25.74 | 4.59 | 0.560 |
| 13 | 0.76 | −18.35 | 0.68 | 14.74 | 1.18 | −9.23 | −25.72 | 4.15 | 0.603 |
| 14 | 1.53 | −17.58 | 0.67 | 14.50 | 1.22 | −9.02 | −25.44 | 1.13 | 0.454 |
| 15 | 1.54 | −17.57 | 0.68 | 15.15 | 0.91 | −8.97 | −25.34 | 1.11 | 0.580 |
| 16 | 2.00 | −17.11 | 0.72 | 15.34 | 0.97 | −8.94 | −25.20 | 0.51 | 0.772 |
| 17 | 1.13 | −17.98 | 0.66 | 14.94 | 1.02 | −9.04 | −25.56 | 2.22 | 0.373 |
| 18 | 1.13 | −17.98 | 0.66 | 14.81 | 1.05 | −9.04 | −25.47 | 2.22 | 0.414 |
| 19 | 1.81 | −17.30 | 0.67 | 15.12 | 1.22 | −8.96 | −25.35 | 0.70 | 0.363 |
| 20 | 1.05 | −18.06 | 0.73 | 14.85 | 1.34 | −9.32 | −25.66 | 2.54 | 0.708 |
| 21 | 1.03 | −18.08 | 0.72 | 14.89 | 1.30 | −9.32 | −25.66 | 2.63 | 0.751 |
| 22 | 1.11 | −18.00 | 0.67 | 14.95 | 1.01 | −9.06 | −25.56 | 2.30 | 0.493 |
| 23 | 0.96 | −18.15 | 0.72 | 14.90 | 1.24 | −9.32 | −25.69 | 2.96 | 0.724 |
| 24 | 1.02 | −18.09 | 0.74 | 14.92 | 1.32 | −9.40 | −25.67 | 2.67 | 0.760 |
| 25 | 0.32 | −18.79 | 0.64 | 14.67 | 0.85 | −9.21 | −25.74 | 8.73 | 0.374 |
| 26 | 0.00 | −19.11 | 0.75 | 14.67 | 1.19 | −9.72 | −26.00 | 14.98 | 0.832 |
| 27 | 0.22 | −18.89 | 0.68 | 14.66 | 0.97 | −9.36 | −25.86 | 10.33 | 0.614 |
| 28 | 0.40 | −18.71 | 0.63 | 14.67 | 0.71 | −9.00 | −25.72 | 7.62 | 0.291 |
| Intramolecular | Intermolecular | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ΔE | Etotal | Eb | Eθ | Eφ | EvdW | EC | EvdW | EQ | |
| 1α8 | 0.00 | −64.74 | 0.60 | 15.71 | 1.99 | −9.13 | −23.99 | −36.97 | −12.95 |
| 2α7β1 | 1.59 | −63.15 | 0.63 | 15.90 | 3.00 | −9.92 | −24.61 | −36.43 | −11.72 |
| 3α6β2 | 2.54 | −62.20 | 0.67 | 15.62 | 3.25 | −10.32 | −25.08 | −35.55 | −10.79 |
| 4α6β2 | 3.49 | −61.25 | 0.67 | 16.18 | 4.14 | −10.45 | −25.15 | −36.08 | −10.56 |
| 5α6β2 | 3.25 | −61.49 | 0.70 | 16.15 | 4.14 | −10.57 | −25.20 | −35.99 | −10.72 |
| 6α6β2 | 3.06 | −61.68 | 0.71 | 16.08 | 4.07 | −10.61 | −25.25 | −35.96 | −10.72 |
| 7α6β2 | 3.24 | −61.50 | 0.71 | 16.09 | 4.23 | −10.64 | −25.26 | −36.03 | −10.60 |
| 8α6β2 | 2.35 | −62.39 | 0.64 | 16.08 | 2.89 | −9.86 | −24.60 | −36.59 | −10.95 |
| 9α5β3 | 3.94 | −60.80 | 0.66 | 15.90 | 3.44 | −10.18 | −24.98 | −35.86 | −9.78 |
| 10α5β3 | 4.96 | −59.78 | 0.72 | 15.98 | 4.68 | −10.81 | −25.60 | −35.23 | −9.52 |
| 11α5β3 | 4.10 | −60.64 | 0.78 | 15.90 | 4.35 | −10.98 | −25.79 | −35.36 | −9.54 |
| 12α5β3 | 5.61 | −59.13 | 0.74 | 16.40 | 5.42 | −10.94 | −25.69 | −35.74 | −9.32 |
| 13α5β3 | 5.51 | −59.23 | 0.76 | 16.40 | 5.50 | −11.10 | −25.74 | −35.72 | −9.33 |
| 14α5β3 | 4.57 | −60.17 | 0.71 | 16.24 | 4.37 | −10.44 | −25.19 | −36.17 | −9.69 |
| 15α5β3 | 4.31 | −60.43 | 0.72 | 16.27 | 4.04 | −10.49 | −25.23 | −36.09 | −9.65 |
| 16α4β4 | 5.25 | −59.49 | 0.76 | 16.44 | 3.98 | −10.38 | −25.22 | −36.33 | −8.74 |
| 17α4β4 | 6.76 | −57.98 | 0.79 | 16.48 | 5.81 | −10.89 | −25.77 | −36.00 | −8.40 |
| 18α4β4 | 6.26 | −58.48 | 0.68 | 15.78 | 4.34 | −10.37 | −25.37 | −34.93 | −8.61 |
| 19α4β4 | 5.54 | −59.20 | 0.67 | 16.08 | 3.88 | −10.07 | −25.02 | −35.94 | −8.80 |
| 20α4β4 | 6.61 | −58.13 | 0.76 | 16.08 | 5.37 | −10.72 | −25.64 | −35.52 | −8.46 |
| 21α4β4 | 6.29 | −58.45 | 0.78 | 16.10 | 5.11 | −10.80 | −25.69 | −35.48 | −8.47 |
| 22α4β4 | 6.54 | −58.20 | 0.78 | 16.50 | 5.58 | −10.85 | −25.73 | −36.11 | −8.37 |
| 23α4β4 | 5.54 | −59.20 | 0.78 | 16.02 | 4.66 | −10.74 | −25.70 | −35.61 | −8.61 |
| 24α4β4 | 5.98 | −58.76 | 0.79 | 16.01 | 4.88 | −10.76 | −25.73 | −35.40 | −8.55 |
| 25α4β4 | 7.53 | −57.21 | 0.79 | 16.20 | 6.30 | −11.26 | −26.16 | −34.86 | −8.22 |
| 26α4β4 | 5.17 | −59.57 | 0.90 | 15.62 | 4.80 | −11.35 | −26.31 | −34.71 | −8.52 |
| 27α4β4 | 6.89 | −57.85 | 0.81 | 16.18 | 6.01 | −11.27 | −26.16 | −35.23 | −8.19 |
| 28α4β4 | 8.21 | −56.53 | 0.80 | 16.62 | 7.09 | −11.28 | −26.15 | −35.58 | −8.03 |
| 15α3β5 | 7.20 | −57.54 | 0.79 | 16.28 | 5.01 | −10.52 | −25.62 | −35.97 | −7.51 |
| 14α3β5 | 8.55 | −56.19 | 0.78 | 16.32 | 6.03 | −10.59 | −25.62 | −35.66 | −7.45 |
| 13α3β5 | 9.35 | −55.39 | 0.85 | 16.34 | 7.30 | −11.11 | −26.21 | −35.34 | −7.22 |
| 12α3β5 | 9.46 | −55.28 | 0.83 | 16.45 | 7.20 | −11.03 | −26.12 | −35.51 | −7.10 |
| 11α3β5 | 7.78 | −56.96 | 0.88 | 15.88 | 5.72 | −11.10 | −26.22 | −34.75 | −7.37 |
| 10α3β5 | 8.00 | −56.74 | 0.77 | 16.08 | 5.57 | −10.82 | −25.95 | −35.08 | −7.31 |
| 9α3β5 | 7.89 | −56.85 | 0.71 | 15.97 | 4.95 | −10.34 | −25.42 | −35.11 | −7.61 |
| 8α2β6 | 9.45 | −55.29 | 0.76 | 16.19 | 5.53 | −10.23 | −25.47 | −35.54 | −6.53 |
| 7α2β6 | 10.18 | −54.56 | 0.86 | 16.13 | 7.01 | −10.84 | −26.11 | −35.36 | −6.25 |
| 6α2β6 | 10.30 | −54.44 | 0.87 | 16.21 | 7.07 | −10.83 | −26.10 | −35.40 | −6.26 |
| 5α2β6 | 10.51 | −54.23 | 0.83 | 16.28 | 7.01 | −10.72 | −26.01 | −35.38 | −6.24 |
| 4α2β6 | 10.48 | −54.26 | 0.81 | 16.30 | 6.94 | −10.67 | −26.00 | −35.46 | −6.18 |
| 3α2β6 | 8.76 | −55.98 | 0.78 | 15.78 | 5.12 | −10.50 | −25.88 | −34.84 | −6.44 |
| 2α1β7 | 10.65 | −54.09 | 0.80 | 16.02 | 5.98 | −10.27 | −25.87 | −35.47 | −5.28 |
| 1β8 | 12.69 | −52.05 | 0.79 | 15.93 | 6.36 | −9.90 | −25.73 | −35.23 | −4.27 |
6 Acknowledgments
- 1The reason for neglecting other orientations of Ni(OEP) with respect to graphite(0001) layer will be explained below.
References
- Lei, S.B.; Wang, C.; Yin, S.X.; Wang, H.N.; Xi, F.; Liu, H.W.; Xu, B.; Wan, L.J.; Bai, C.L. Surface Stabilized Porphyrin and Phthalocyanine Two-Dimensional Network Connected by Hydrogen Bonds. J. Phys. Chem. B 2001, 105, 10838–10841. [Google Scholar]
- Yin, J.; Guo, Q.; Palmer, R.E.; Bampos, N.; Sanders, J.K.M. Supramolecular Monolayers of Zinc Porphyrin Trimers on Graphite. J. Phys. Chem. B 2003, 107, 209–216. [Google Scholar]
- Ikeda, T.; Asakawa, M.; Goto, M.; Miyake, K.; Ishida, T.; Shimizu, T. STM Observation of Alkyl-Chain-Assisted Self-Assembled Monolayers of Pyridine-Coordinated Porphyrin Rhodium Chlorides. Langmuir 2004, 20, 5454–5459. [Google Scholar]
- Zhou, Y.; Wang, B.; Zhu, M.; Hou, J.G. Observation of co-existence of face-on and edge-on stacking styles in a porphyrin monolayer. Chem. Phys. Lett 2005, 403, 140–145. [Google Scholar]
- Boyd, P.D.W.; Hodgson, M.C.; Rickard, C.E.F.; Oliver, A.G.; Chaker, L.; Brothers, P.J.; Bolskar, R.D.; Tham, F.S.; Reed, C.A. Selective Supramolecular Porphyrin/Fullerene Interactions. J. Am. Chem. Soc 1999, 121, 10487–10495. [Google Scholar]
- Olmstead, M.M.; Costa, D.A.; Maitra, K.; Noll, B.C.; Phillips, S.L.; Van Calcar, P.M.; Balch, A.L. Interaction of Curved and Flat Molecular Surfaces. The Structures of Crystalline Compounds Composed of Fullerene (C60, C60O, C70, and C120O) and Metal Octaethylporphyrin Units. J. Am. Chem. Soc 1999, 121, 7090–7097. [Google Scholar]
- Maree, C.H.; Roosendaal, S.J.; Savenije, T.J.; Schropp, R.E.I.; Schaafsma, T.J.; Habraken, F.H.P.M. Photovoltaic effects in porphyrin polymer films and heterojunctions. J. Appl. Phys 1996, 80, 3381–3389. [Google Scholar]
- Harima, Y.; Okazaki, H.; Kunugi, Y.; Yamashita, K.; Ishii, H.; Seki, K. Formation of Schottky barriers at interfaces between metals and molecular semiconductors of p- and n-type conductances. Appl. Phys. Letters 1996, 69, 1059–1061. [Google Scholar]
- Liu, C.Y.; Pan, H.I.; Fox, M.A.; Bard, A.J. High-density nanosecond charge trapping in thin films of the photoconductor ZnODEP. Science 1993, 261, 897–899. [Google Scholar]
- Reimers, J.R.; Lu, T.X.; Crossley, M.J.; Hush, N.S. Molecular electronic properties of fused rigid porphyrin-oligomer molecular wires. Nanotechnology 1996, 7, 424–429. [Google Scholar]
- Edelwirth, M.; Freund, J.; Sowerby, S.J.; Heckl, W.M. Molecular mechanics study of hydrogen bonded self-assembled adenine monolayers on graphite. Surf. Sci 1998, 417, 201–209. [Google Scholar]
- Yin, S.; Wang, C.; Xu, B.; Bai, C. Studies of CuPc adsorption on graphite surface and alkane adlayer. J. Phys. Chem. B 2002, 106, 9044–9047. [Google Scholar]
- Ortmann, F.; Schmidt, W.G.; Bechstedt, F. Attracted by Long-Range Electron Correlation: Adenine on Graphite. Phys. Rev. Lett 2005, 95, 186101–186104. [Google Scholar]
- Rosei, F.; Schunack, M.; Naitoh, Y.; Jiang, P.; Gourdon, A.; Laegsgaard, E.; Stensgaard, I.; Joachim, C.; Besenbacher, F. Properties of large organic molecules on metal surfaces. Progr. Surf. Sci 2003, 71, 95–146. [Google Scholar]
- Moresco, F.; Meyer, G.; Rieder, K.H.; Tang, H.; Gourdon, A.; Joachim, C. Conformational changes of single molecules induced by scanning tunneling microscopy manipulation: a route to molecular switching. Phys. Rev. Lett 2001, 86, 672–675. [Google Scholar]
- Shelnutt, J.A.; Song, X.-Z.; Ma, J.-G.; Jia, S.-L.; Jentzen, W.; Medforth, C.J. Nonplanar porphyrins and their significance in proteins. Chem. Soc. Rev 1998, 27, 31–42. [Google Scholar]
- Senge, M.O. The Porphyrin Handbook; Volume 1, Kadish, K.M., Smith, K.M., Guilard, R., Eds.; Academic Press: New York, 2000; p. 239. [Google Scholar]
- Song, X.; Jentzen, W.; Jaquinod, L.; Khoury, R.G.; Medforth, C.J.; Jia, C.J.; Ma, J.G.; Smith, K.M.; Shelnutt, J.A. Substituent-Induced Perturbation Symmetries and Distortions of meso-tert-Butylporphyrins. Inorg. Chem 1998, 37, 2117–2128. [Google Scholar]
- Song, X.Z.; Jaquinod, L.; Jentzen, W.; Nurco, D.J.; Jia, S.L.; Khoury, R.G.; Ma, J.G.; Medforth, C.J.; Smith, K.M.; Shelnutt, J.A. Metal Dependence of the Contributions of Low-Frequency Normal Coordinates to the Sterically Induced Distortions of Meso-Dialkyl-Substituted Porphyrins. Inorg. Chem 1998, 37, 2009–2019. [Google Scholar]
- Jentzen, W.; Simpson, M.C.; Hobbs, J.D.; Song, X.Z.; Ema, T.; Nelson, N.Y.; Medforth, C.J.; Smith, K.M.; Veyrat, M.; Mazzanti, M.; Ramasseul, R.; Marchon, J.C.; Takencki, T.; Goddard, W.A., III; Shelnutt, J.A. Ruffling in a Series of Nickel(II) meso-Tetrasubstituted Porphyrins as a Model for the Conserved Ruffling of the Heme of Cytochromes c. J. Am. Chem. Soc 1995, 117, 11085–11097. [Google Scholar]
- Huang, Q.; Medforth, C.J.; Schweitzer-Stenner, R. Nonplanar Heme Deformations and Excited State Displacements in Nickel Porphyrins Detected by Raman Spectroscopy at Soret Excitation. J. Phys. Chem. A 2005, 109, 10493–10502. [Google Scholar]
- Jentzen, W.; Song, X.Z.; Shelnutt, J.A. Structural characterization of synthetic and protein-bound porphyrins in terms of the lowest-frequency normal coordinates of the macrocycle. J. Phys. Chem. B 1997, 101, 1684–1699. [Google Scholar]
- Gruden, M.; Grubišić, S.; Coutsolelos, A.G.; Niketić, S.R. Conformational analysis of octa- and tetrahalogenated tetraphenylporphyrins and their metal derivatives. J. Mol. Struct 2001, 595, 209–224. [Google Scholar]
- Gruden-Pavlović, M.; Grubišić, S.; Niketić, S.R. Conformational analysis of octa- and tetrabromo tetraphenylporphyrins and their Ni(II) and Tb(III) complexes. J. Inorg. Biochem 2004, 98, 1293–1302. [Google Scholar]
- Meyer, E.F. Crystal and molecular structure of nickel(II) octaethylporphyrin. Acta Crystallogr. B 1972, 28, 2162–2167. [Google Scholar]
- Cullen, D.L.; Meyer, E.F. Crystal and molecular structure of the triclinic form of 1,2,3,4,5,6,7,7-octaethylporphinatonickel(II). Comparison with the tetragonal form. J. Am. Chem. Soc 1974, 96, 2095–2102. [Google Scholar]
- Brennan, T.D.; Scheidt, W.R.; Shelnutt, J.A. New crystalline phase of (octaethylporphinato) nickel(II): effects of π-π interactions on molecular structure and resonance Raman spectra. J. Am. Chem. Soc 1988, 110, 3919–3924. [Google Scholar]
- Niketić, S.R.; Rasmussen, Kj. The Consistent Force Field: A Documentation. In Lecture Notes in Chemistry; Volume 3, Springer: Berlin, 1977. [Google Scholar]
- Beveridge, G.S.G.; Schechter, R.S. Optimization: Theory and Practice; McGraw-Hill Kogakusha: Tokyo, 1970; p. 629. [Google Scholar]
- Vernov, A.; Steele, W.A. The electrostatic field at a graphite surface and its effect on molecule-solid interactions. Langmuir 1992, 8, 155–159. [Google Scholar]
- Nicholson, D.; Cracknell, R.F.; Parsonage, N.G. Evaluation of a Model Potential Function for Ar Graphite Interaction using Computer Simulation. Molecular Simulation 1990, 5, 307–314. [Google Scholar]
- Zhao, X.C.; Johnson, J.K. An effective potential for adsorption of polar molecules on graphite. Molecular Simulation 2005, 31, 1–10. [Google Scholar]
- Whitehouse, D.B.; Buckingham, A.D. Experimental determination of the atomic quadrupole moment of graphite. J. Chem. Soc., Faraday Trans 1993, 89, 1909–1913. [Google Scholar]
- Hansen, F.Y.; Bruch, L.W.; Roosevelt, S.E. Electrostatic forces and the frequency spectrum of a monolayer solid of linear molecules on graphite. Phys. Rev. B 1992, 45, 11238–11248. [Google Scholar]
- Lozman, O.R.; Bushby, R.J.; Vinter, J.G. Complementary polytopic interactions (CPI) as revealed by molecular modelling using the XED force field. J. Chem. Soc. Perkin Trans. 2 2001, 1446–1452. [Google Scholar]
- Hirschfelder, J.O.; Curtiss, C.F.; Bird, R.B. Molecular Theory of Gases and Liquids; John Wiley and Sons: New York, 1954; pp. 26–28. [Google Scholar]
- Stoll, L.K.; Zgierski, M.Z.; Kozlowski, P.M. Density Functional Theory Analysis of Nickel Octaethylporphyrin Ruffling. J. Phys. Chem. A 2002, 106, 170–175. [Google Scholar]
- Schweizer, W.B.; Dunitz, J.D. Quantum Mechanical Calculations for Benzene Dimer Energies: Present Problems and Future Challenges. J. Chem. Theory Comput 2006, 2, 288–291. [Google Scholar]
- Ogunrinde, A.; Hipps, K.W.; Scudiero, L. A Scanning Tunneling Microscopy Study of Self-Assembled Nickel(II) Octaethylporphyrin Deposited from Solutions on HOPG. Langmuir 2006, 22, 5697–5701. [Google Scholar]
© 2007 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Gruden-Pavlović, M.; Grubišić, S.; Zlatar, M.; Niketić, S.R. Molecular Mechanics Study of Nickel(II) Octaethylporphyrin Adsorbed on Graphite(0001). Int. J. Mol. Sci. 2007, 8, 810-829. https://doi.org/10.3390/i8080810
Gruden-Pavlović M, Grubišić S, Zlatar M, Niketić SR. Molecular Mechanics Study of Nickel(II) Octaethylporphyrin Adsorbed on Graphite(0001). International Journal of Molecular Sciences. 2007; 8(8):810-829. https://doi.org/10.3390/i8080810
Chicago/Turabian StyleGruden-Pavlović, Maja, Sonja Grubišić, Matija Zlatar, and Svetozar R. Niketić. 2007. "Molecular Mechanics Study of Nickel(II) Octaethylporphyrin Adsorbed on Graphite(0001)" International Journal of Molecular Sciences 8, no. 8: 810-829. https://doi.org/10.3390/i8080810
APA StyleGruden-Pavlović, M., Grubišić, S., Zlatar, M., & Niketić, S. R. (2007). Molecular Mechanics Study of Nickel(II) Octaethylporphyrin Adsorbed on Graphite(0001). International Journal of Molecular Sciences, 8(8), 810-829. https://doi.org/10.3390/i8080810




