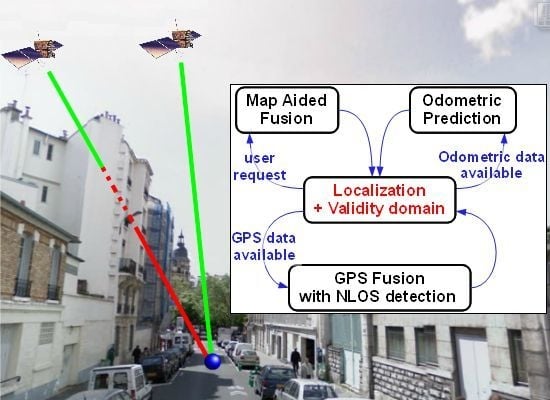
About Non-Line-Of-Sight Satellite Detection and Exclusion in a 3D Map-Aided Localization Algorithm
Abstract
:1. Introduction
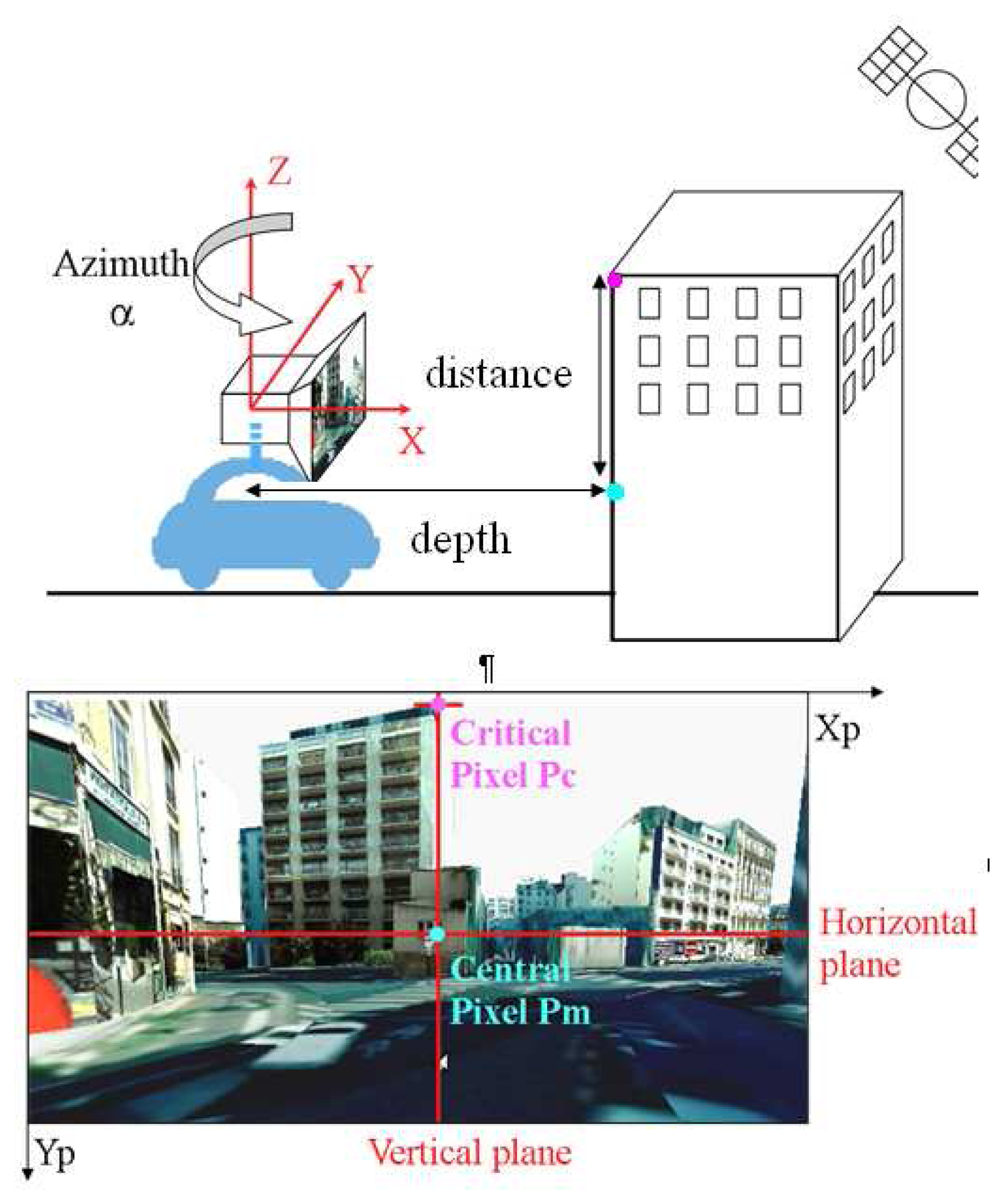
2. Presentation of the NLOS Detection Method
3. Presentation of the Positioning Method with Road Constraints
3.1. Definition of the Vehicle Configuration (Figure 3)
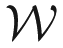 : (O, i⃗0, j⃗0, k⃗0) as this world reference frame and
: (O, i⃗0, j⃗0, k⃗0) as this world reference frame and
 : (M, i⃗3, j⃗3, k⃗3) as the vehicle reference frame (Figure 3). By definition, the vehicle configuration states the pose of the vehicle reference frame with respect to the world frame. In the 3D Euclidian world, it may be defined by:
: (M, i⃗3, j⃗3, k⃗3) as the vehicle reference frame (Figure 3). By definition, the vehicle configuration states the pose of the vehicle reference frame with respect to the world frame. In the 3D Euclidian world, it may be defined by:
 by 4 elementary operations: one translation (OM⃗) and 3 successive rotations (ψ, θ, φ). Note that one considers here a vehicle without suspension. The (ψ, θ, φ) orientation angles are thus only induced by the geometry of the road and the path followed by the vehicle.
by 4 elementary operations: one translation (OM⃗) and 3 successive rotations (ψ, θ, φ). Note that one considers here a vehicle without suspension. The (ψ, θ, φ) orientation angles are thus only induced by the geometry of the road and the path followed by the vehicle.3.2. Kinematic Model Processing
- ○
- E denotes the track, e.g., the distance between the centers of the left and right wheels,
- ○
- ωr (resp. ωl) is the measured rotation speed of the right (resp. left) wheel,
- ○
- Rr (resp. Rl) is the radius of the right (resp. left) wheel, assumed to be known.
 ) between the successive time samples tk and tk+1.
) between the successive time samples tk and tk+1.3.3. Localization Method
- GPS localization is obtained by a positioning algorithm at the update rate of the receiver (4 Hz). A complete localization may be scarce in environments with poor satellite visibility
- odometric data are generated by the wheel speed sensors of the ABS (Anti-Blocking System). When some data become available, the configuration is updated by using Equation (5),
- geographic data, 3D polylines modelling the road network, are given upon request but require a map-matching procedure prior to using them for localization.
Odometric and GPS Data Fusion
Map-Aided Fusion
- Map-matching, i.e., the selection of the road segment on which the vehicle is supposed to be. The segment should minimize a criterion calculated from (1) the 3D distance between the current estimation of the localization and the segment and (2) the angular error between the velocity vector of the state and direction of the segment.
- Exploitation of the geometric attributes of the road segment selected as constraints of the configuration (2). Constraints are defined from the 3D polylines by taking into account the width of the way and the uncertainty on the altitude. The ellipsoidal set-membership method computes the minimum volume ellipsoid resulting from the intersection of the current ellipsoidal domain and constraints. The final map-aided solution is obtained [22].
4. Improving the NLOS Detection Method and Experimental Results
4.1. Experimental Set-Up and Test Data
- a CAN (Controller Area Network) bus connection (for the odometry),
- a low-cost automotive GPS receiver LEA-6T from U-blox (for raw data and NMEA GGA [23], Global Positioning System Fix Data, and GSV, Satellites in view, sequences at 4 Hz) and its patch antenna,
- the MRT (Reference Trajectory Measurement) dedicated specific equipment, LANDINS of the IXSEA society, from which the reference trajectory of the present experiment is issued. Its accuracy is about 10 centimeters,
- a Marlin video camera (not used here).
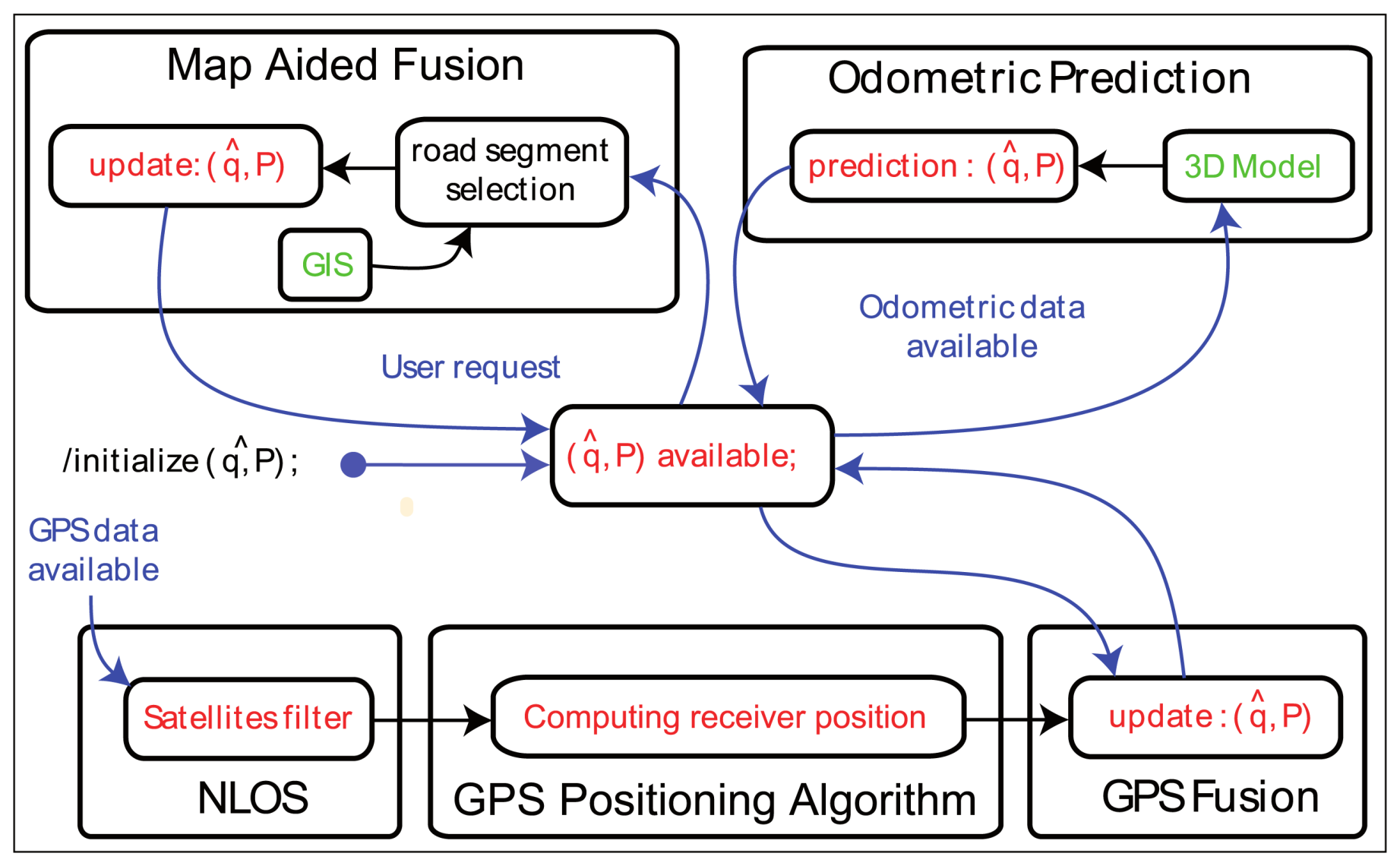
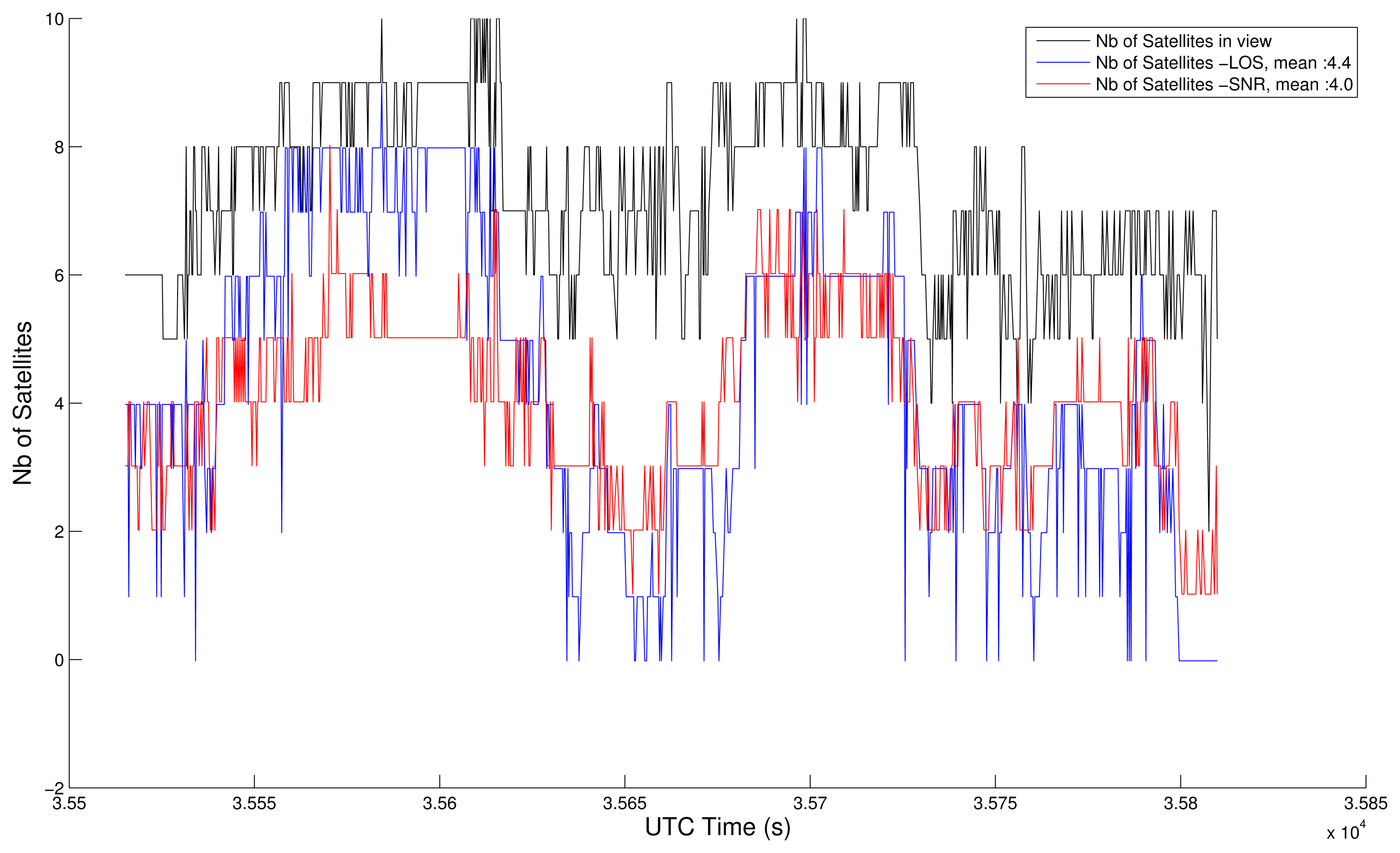
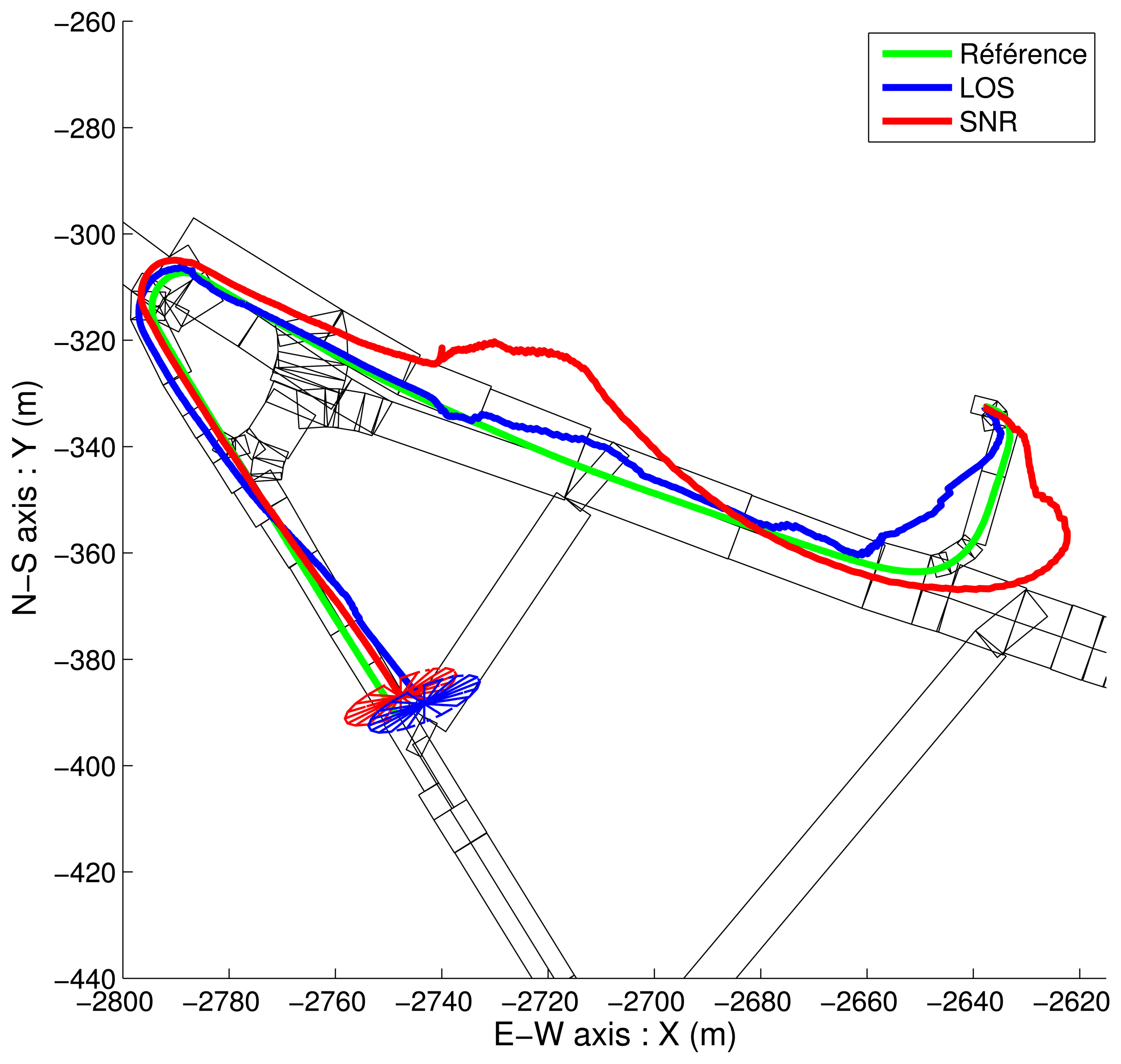
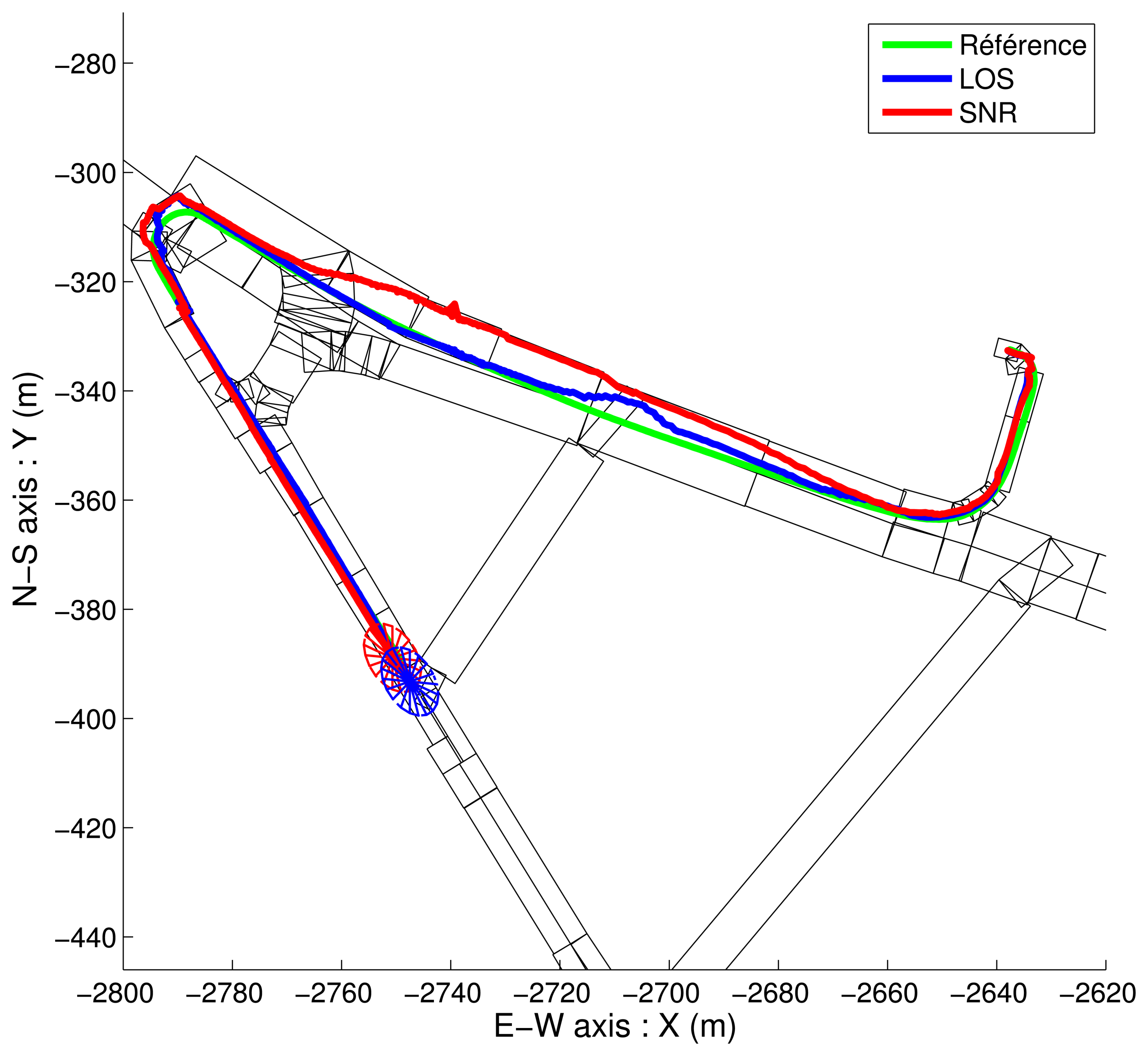
4.2. NLOS Detection Based on Map-Aided Solutions
- The LOS satellites are only fed to the GPS Positioning Algorithm and fused with the odometry. It yields non-map-aided or “free” solutions. In this case, we collect the updated position and covariance of the “GPS Fusion” task.
- The LOS satellites are only fed to the GPS Positioning Algorithm, fused with the odometry, and constrained again by the road map. It yields map-aided or constrained solutions and we collect the updated position and covariance of the “Map-Aided Fusion” task. This very last implementation can run in closed-loop, since its solution can be returned to the image extractor, which makes the duplication of the “Map-Aided Fusion” task not necessary.
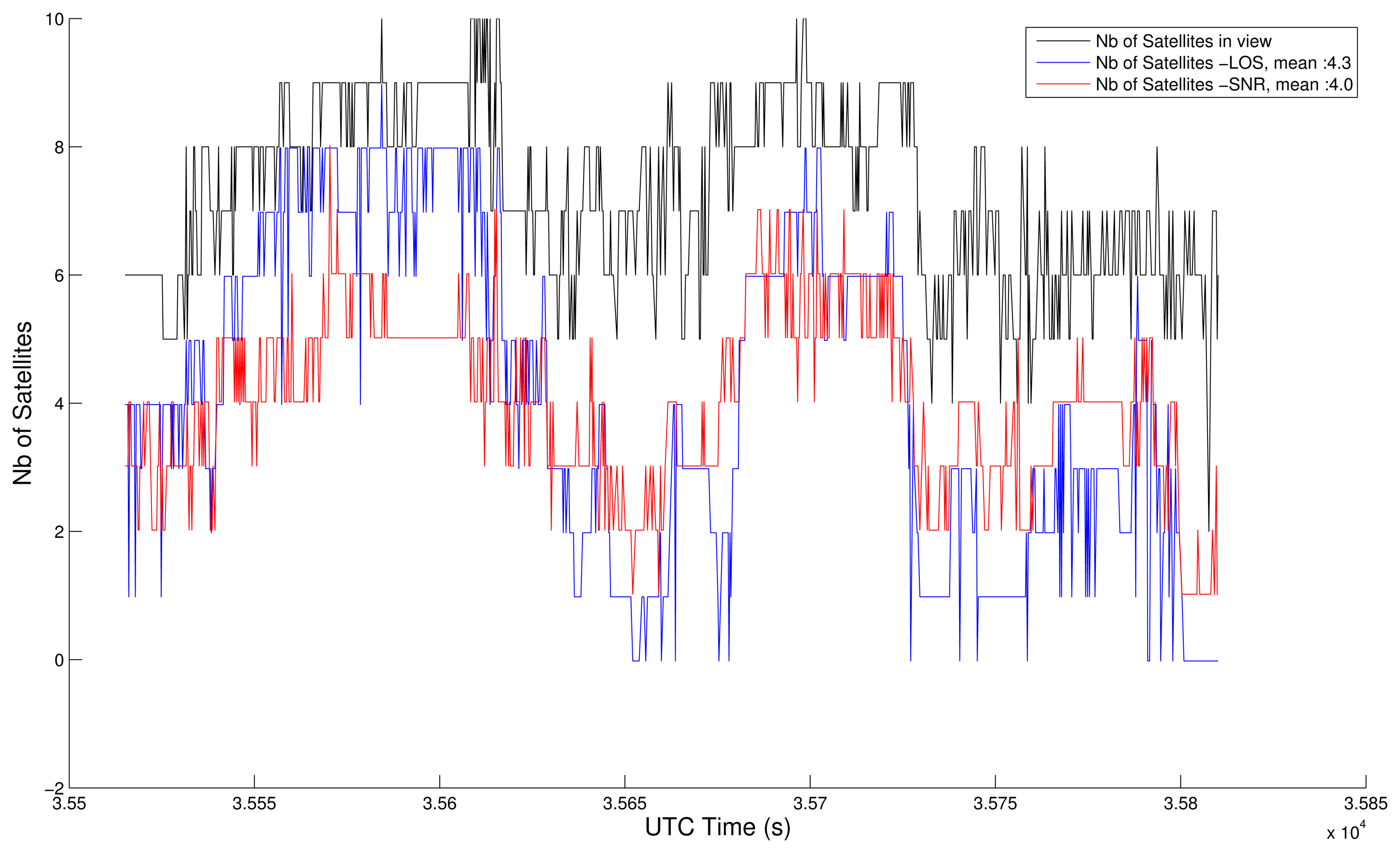
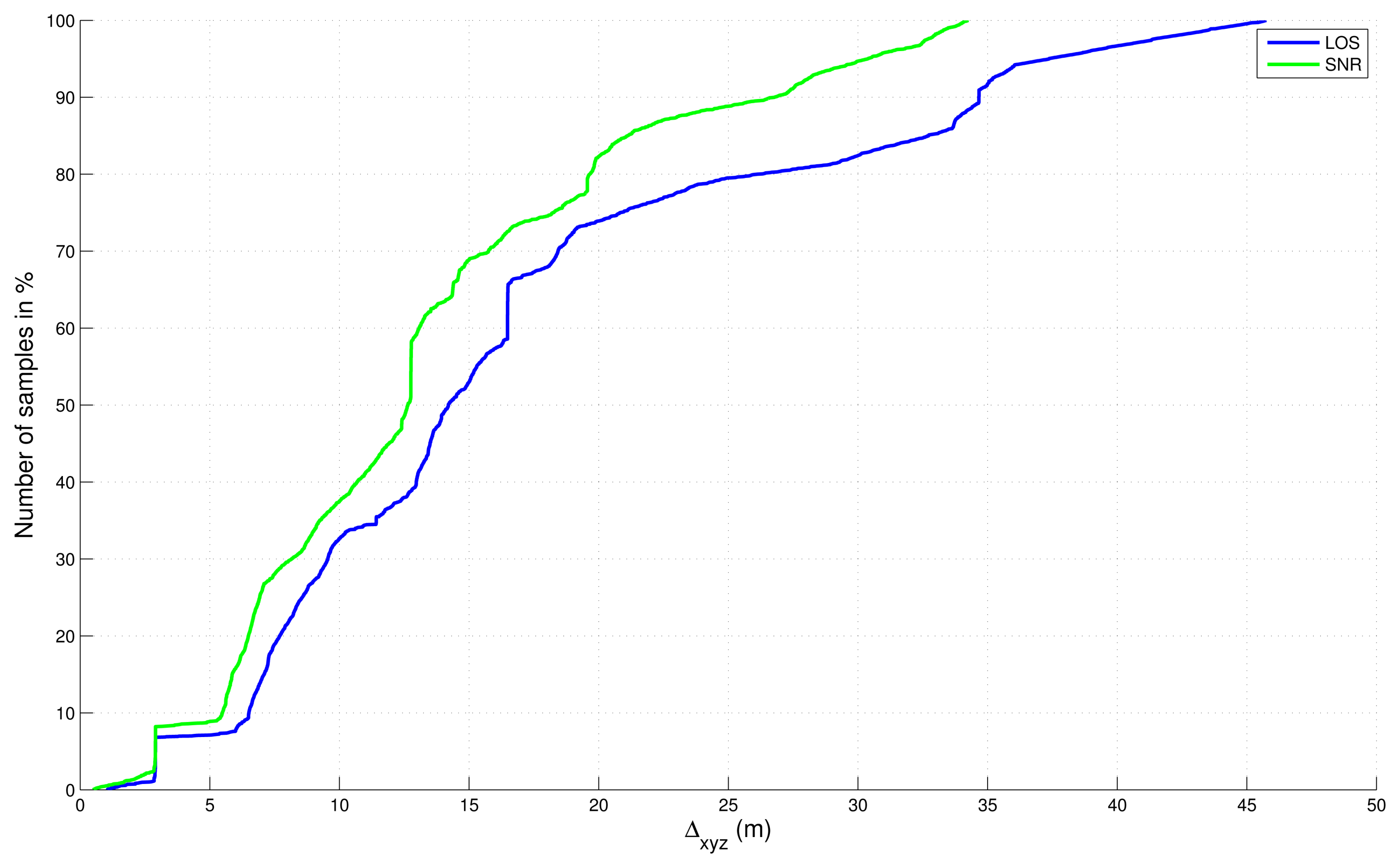
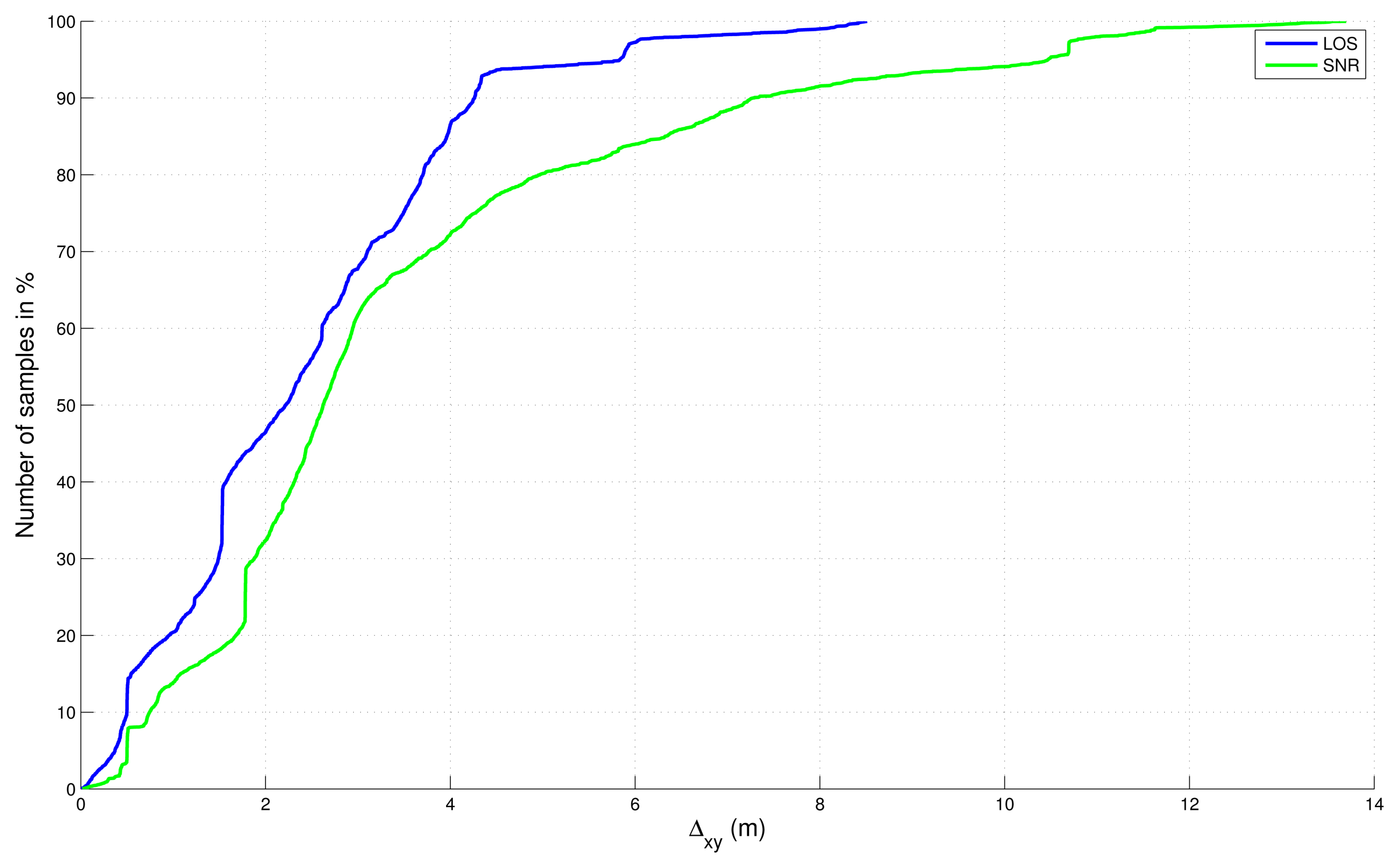
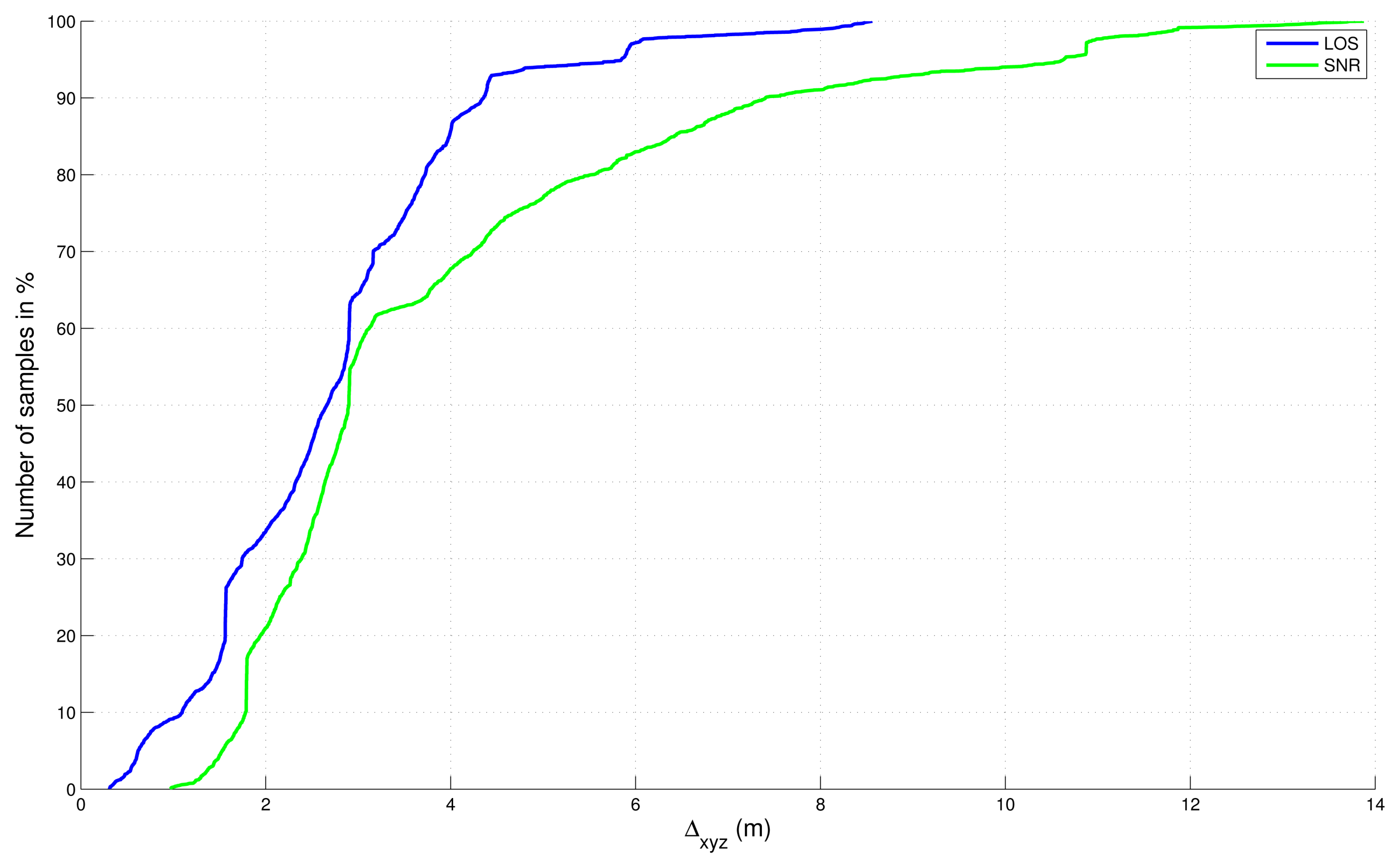
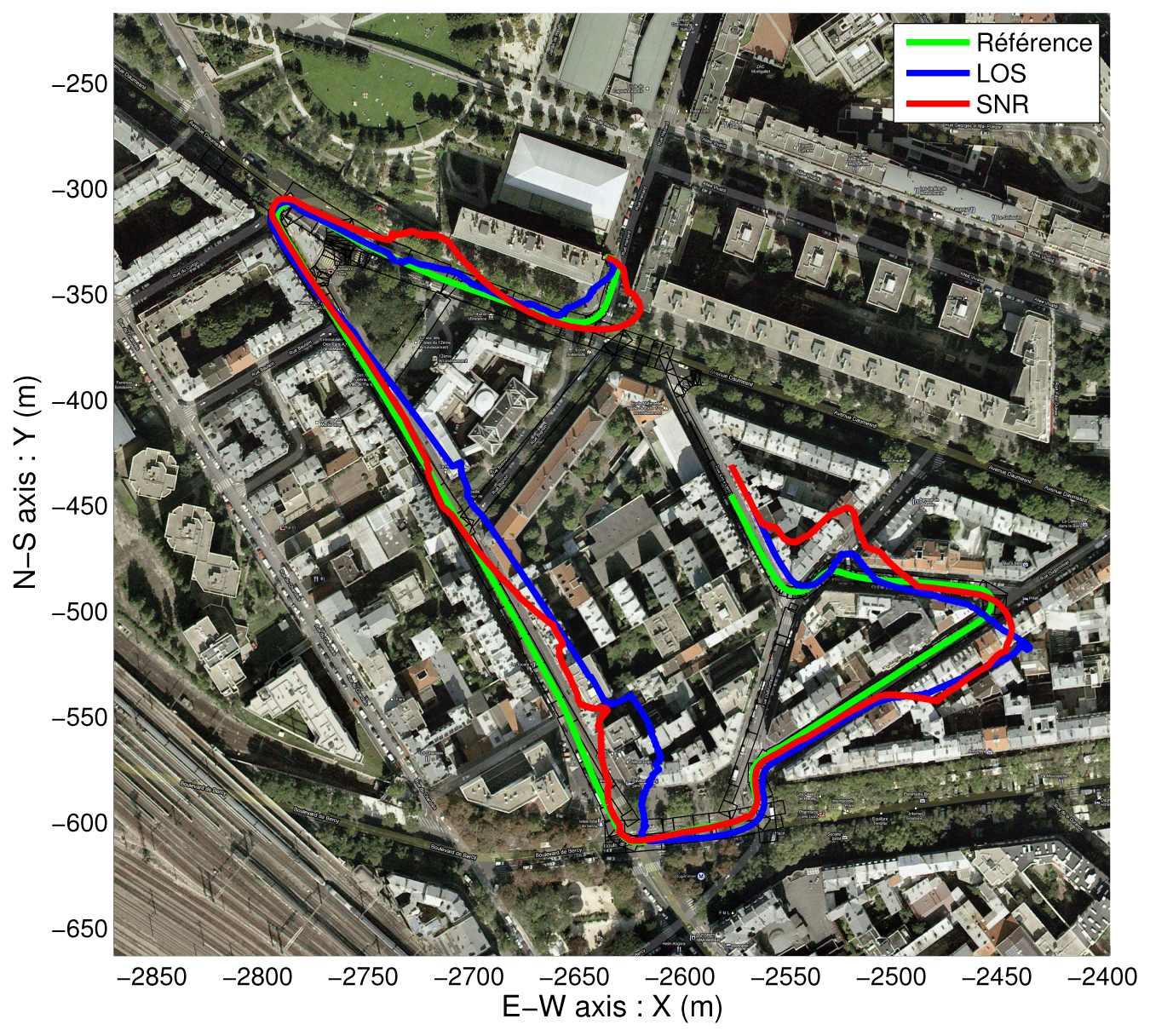
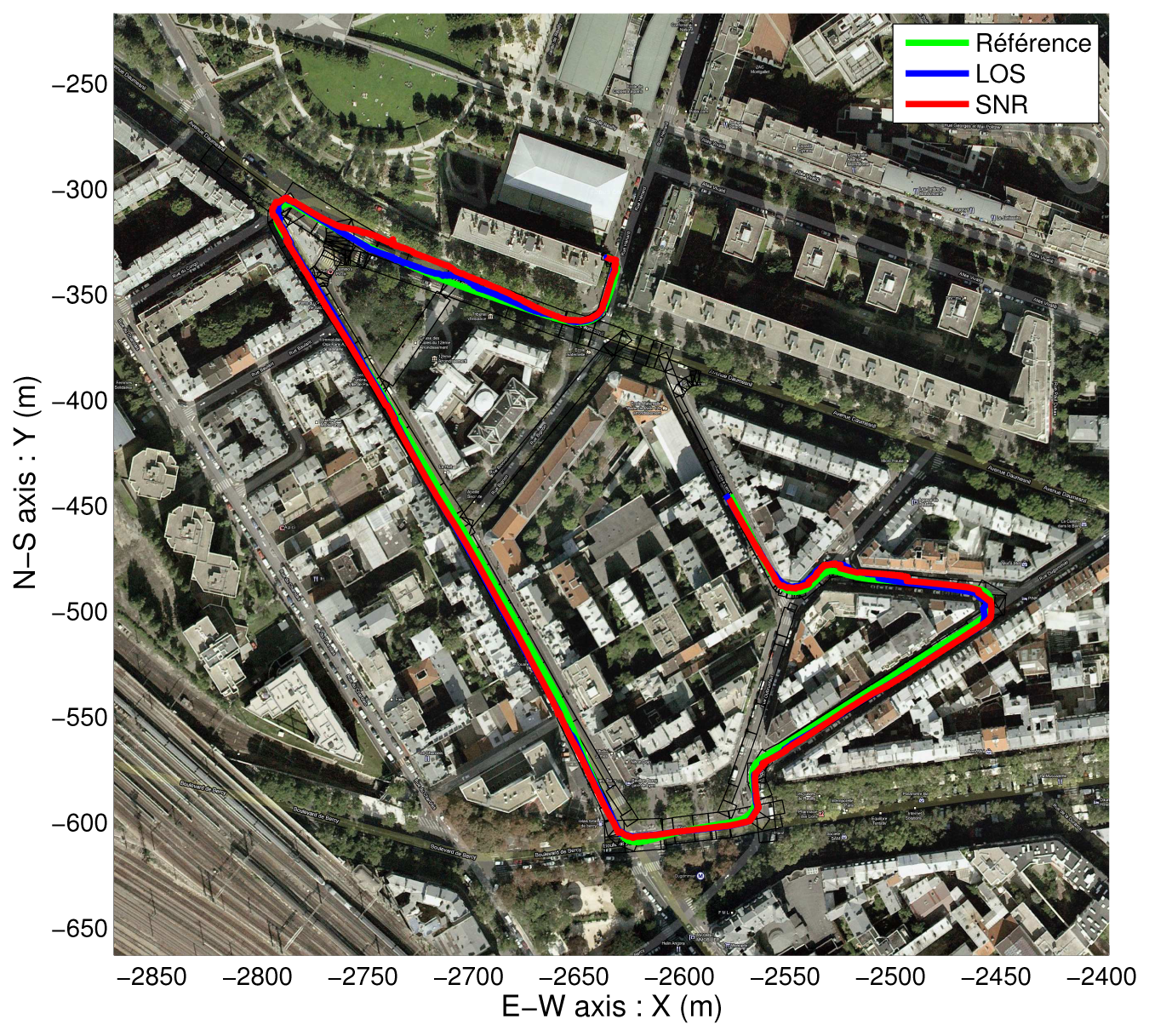
4.3. Comparison with the SNR-Based Selection
- ○
- 1 - SNR-based satellite selection, no final map-aiding,
- ○
- 2 - LOS-based satellite selection, no final map-aiding,
- ○
- 3 - SNR-based satellite selection, and final map-aiding,
- ○
- 4 - LOS-based satellite selection, and final map-aiding.
5. Conclusions and Future Works
5.1. Conclusions
5.2. Future Work
Acknowledgments
References and Notes
- Marais, J.; Berbineau, M.; Frimat, O.; Franckart, J.-P. A New Satellite-Based Fail-Safe Train Control and Command for Low Density Railway Lines; TILT Seminar (Technological Innovations for Land Transportation): Lille, France, December 2003. Available online: http://www.ertico.com/assets/download/locoprol/arttilt.pdf (accessed on 21 December 2012).
- Bradbury, J.; Ziebart, M.; Cross, P.; Boulton, P.; Read, A. Code Multipath Modelling in the Urban Environment Using Large Virtual Reality City Models: Determining the Local Environment. J. Navig. 2007, 60, 95–105. [Google Scholar]
- Suh, Y.; Shibasaki, R. Evaluation of Satellite-Based Navigation Services in Complex Urban Environments Using a Three-Dimensional GIS. IEDE Trans. Commun. 2007, E90-B, 1816–1825. [Google Scholar]
- CityVIP Website. Available online: http://www.lasmea.univ-bpclermont.fr/CityVip (accessed on 21 December 2012).
- Peyret, F.; Bétaille, D.; Mougel, F. Non-Line-Of-Sight GNSS signal detection using an on-board 3D model of buildings. Proceedings of IEEE ITST 2011: the 11th International Conference on ITS Telecommunications, Saint-Petersburg, Russia, 23– 25 August 2011.
- Pinana-Diaz, C.; Toledo-Moreo, R.; Bétaille, D.; Gomez-Skarmeta, A. GPS multipath detection and exclusion with elevation-enhanced maps. Proceedings of IEEE ITSC 2011: The 14th IEEE Conference on Intelligent Transportation Systems, Washington, DC, USA, 5– 7 October 2011.
- Obst, M.; Bauer, S.; Wanielik, G. Urban Multipath Detection and mitigation with Dynamic 3D Maps for Reliable Land Vehicle Localization. Proceedings of IEEE /ION Position Location and Navigation Symposium (PLANS) 2012, Myrtle Beach, SC, USA, 23– 26 April 2012.
- Bourdeau, A.; Sahmoudi, M.; Tourneret, J.Y. Tight Integration of GNSS and a 3D City Model for Robust Positioning in Urban Canyons. Proceedings of ION GNSS 2012, Nashville, TN, USA, 18–21 September 2012.
- Groves, P.D. Shadow matching: A new GNSS positioning technique for urban canyons. J. Navig. 2011, 64, 417–430. [Google Scholar]
- Wang, L.; Groves, P.D.; Ziebart, M. GNSS Shadow Matching: Improving Urban Positioning Accuracy Using a 3D City Model with Optimized Visibility Prediction Scoring. Proceedings of ION GNSS 2012, Nashville, TN, USA, 18–21 September 2012.
- Groves, P.D.; Jiang, Z.; Wang, L.; Ziebart, M. Intelligent Urban Positioning using Multi-Constellation GNSS with 3D Mapping and NLOS Signal Detection. Proceedings of ION GNSS 2012, Nashville, TN, USA, 18–21 September 2012.
- BeNomad Website. Available online: http://www.benomad.com (accessed on 21 December 2012).
- Paparoditis, N.; Papelard, J.-P.; Cannelle, B.; Devaux, A.; Soheilian, B.; David, N.; Houzay, E. Stereopolis II: A multi-purpose and multi-sensor 3D mobile mapping system for street visualisation and 3D metrology. Revue Franaise de Photogrammétrie et de Télédétection 2012, 200, 69–79. [Google Scholar]
- Tournaire, O.; Soheilian, B.; Paparoditis, N. Towards a sub-decimetric georeferencing of ground-based mobile mapping systems in urban areas: Matching ground-based and aerial-based imagery using roadmarks. Revue Franaise de Photogrammétrie et de Télédétection 2007, 185, 84–89. [Google Scholar]
- Details on the Reference Trajectory Measurement. Available online: http://www.gnss-test-portal.eu/tools/view/43 (accessed on 21 December 2012).
- Since we consider the kinematic configuration of a slow vehicle induced by the road and not its dynamic state, we prefer to use heading in place of yaw, slope in place of pitch and cross slope in place of roll.
- Peyraud, S.; Renault, S.; Meizel, D. 3D Localization and Map Matching of Urban Vehicles. Proceedings of 6th Europe/Japan Congress on Mecatronics, Yokohama, Japan, 22–24 November 2010.
- Kelly, A. A 3D State Space Formulation of a Navigation Kalman Filter for Autonomous Vehicles; Technical Report CMU-RI-TR-94-19; Carnegie Mellon University: Pittsburgh, PA, USA, 1994. [Google Scholar]
- Cheung, M.F. On optimal algorithms for parameter set estimation. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, December 1991. [Google Scholar]
- The positive definite matrix Pk may be linked with a validity domain of a Gaussian estimation (q̂k, ) with a p0 probability. is the covariance matrix of the estimation error. It comes then: .
- Bonnifait, P.; Bouron, P.; Crubillé, P.; Meizel, D. Data fusion of four ABS Sensors and GPS for an enhanced Localization of car-like vehicles. Proceedings of the IEEE Conference on Robotics & Automation (ICRA'01), Seoul, Korea, 21– 26 May 2001; pp. 1597–1602.
- Peyraud, S. Localisation 3D de mobile en milieu urbain par fusion dinformations satellitaires, proprioceptives et cartographiques. Ph.D. Thesis, Université de Limoges, Limoges, France, Octobre, 2012. [Google Scholar]
- NMEA GGA: Latitude, Longitude and Altitude computed by the receiver from raw data with its own algorithm.
- Details on the Aroccam multithread software architecture. Available online: http://www.lasmea.univ-bpclermont.fr/spip.php7rubriquel20 (accessed on 21 December 2012).

 and
and
 respectively.
respectively.
 and
and
 respectively.
respectively.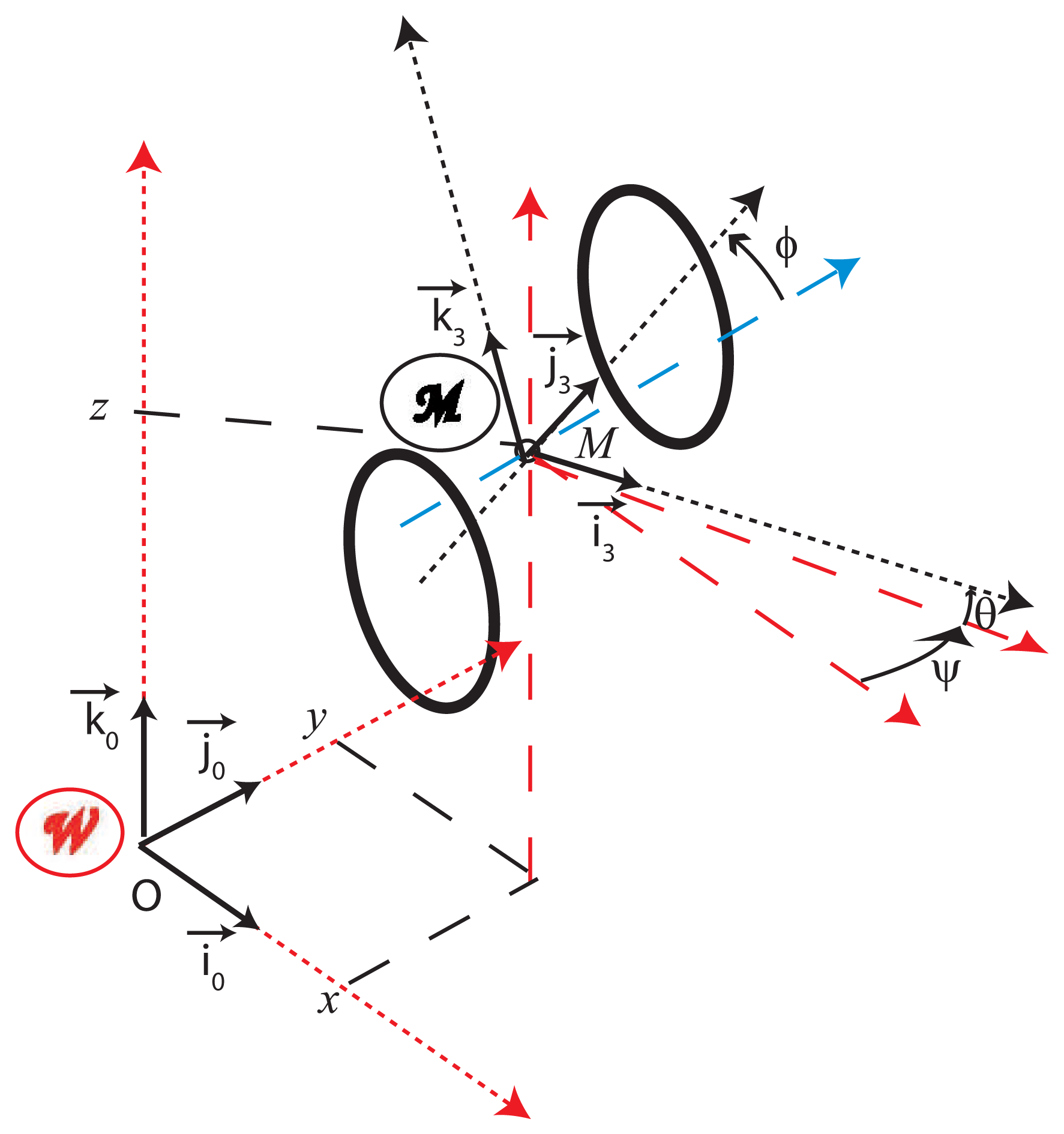


© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Peyraud, S.; Bétaille, D.; Renault, S.; Ortiz, M.; Mougel, F.; Meizel, D.; Peyret, F. About Non-Line-Of-Sight Satellite Detection and Exclusion in a 3D Map-Aided Localization Algorithm. Sensors 2013, 13, 829-847. https://doi.org/10.3390/s130100829
Peyraud S, Bétaille D, Renault S, Ortiz M, Mougel F, Meizel D, Peyret F. About Non-Line-Of-Sight Satellite Detection and Exclusion in a 3D Map-Aided Localization Algorithm. Sensors. 2013; 13(1):829-847. https://doi.org/10.3390/s130100829
Chicago/Turabian StylePeyraud, Sébastien, David Bétaille, Stéphane Renault, Miguel Ortiz, Florian Mougel, Dominique Meizel, and François Peyret. 2013. "About Non-Line-Of-Sight Satellite Detection and Exclusion in a 3D Map-Aided Localization Algorithm" Sensors 13, no. 1: 829-847. https://doi.org/10.3390/s130100829
APA StylePeyraud, S., Bétaille, D., Renault, S., Ortiz, M., Mougel, F., Meizel, D., & Peyret, F. (2013). About Non-Line-Of-Sight Satellite Detection and Exclusion in a 3D Map-Aided Localization Algorithm. Sensors, 13(1), 829-847. https://doi.org/10.3390/s130100829