Hysteresis Compensation of Piezoresistive Carbon Nanotube/Polydimethylsiloxane Composite-Based Force Sensors
Abstract
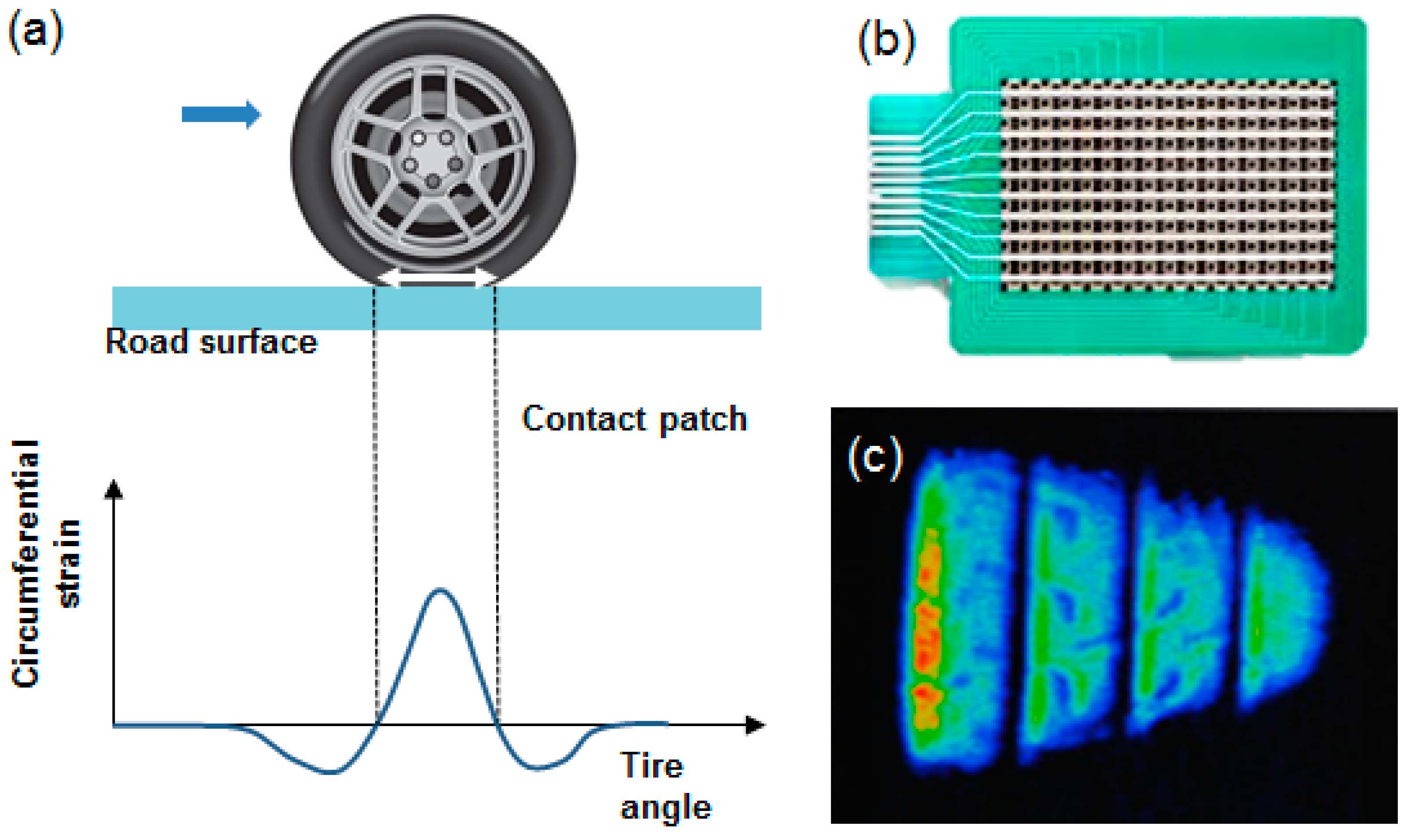
:1. Introduction
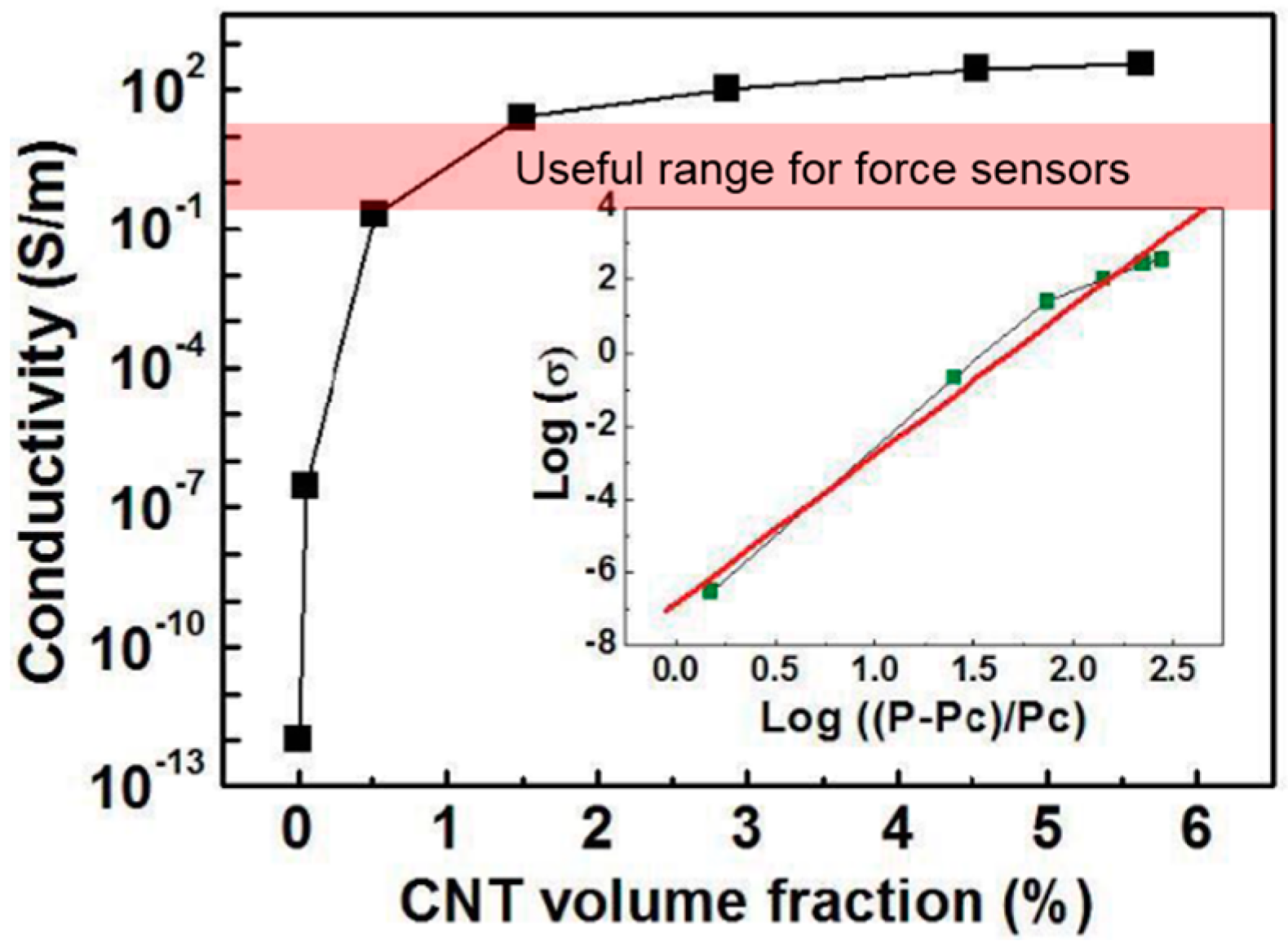
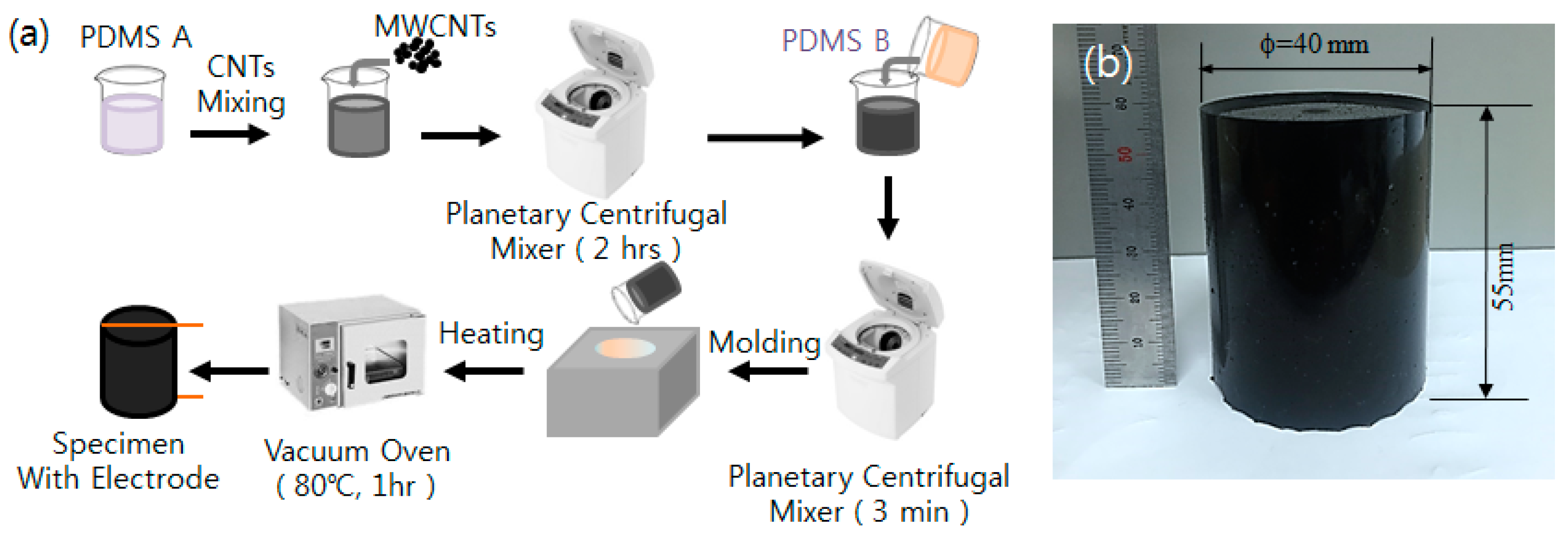
2. Fabrication of the CNT/PDMS Composite
3. Characterization: Piezoresistive Response
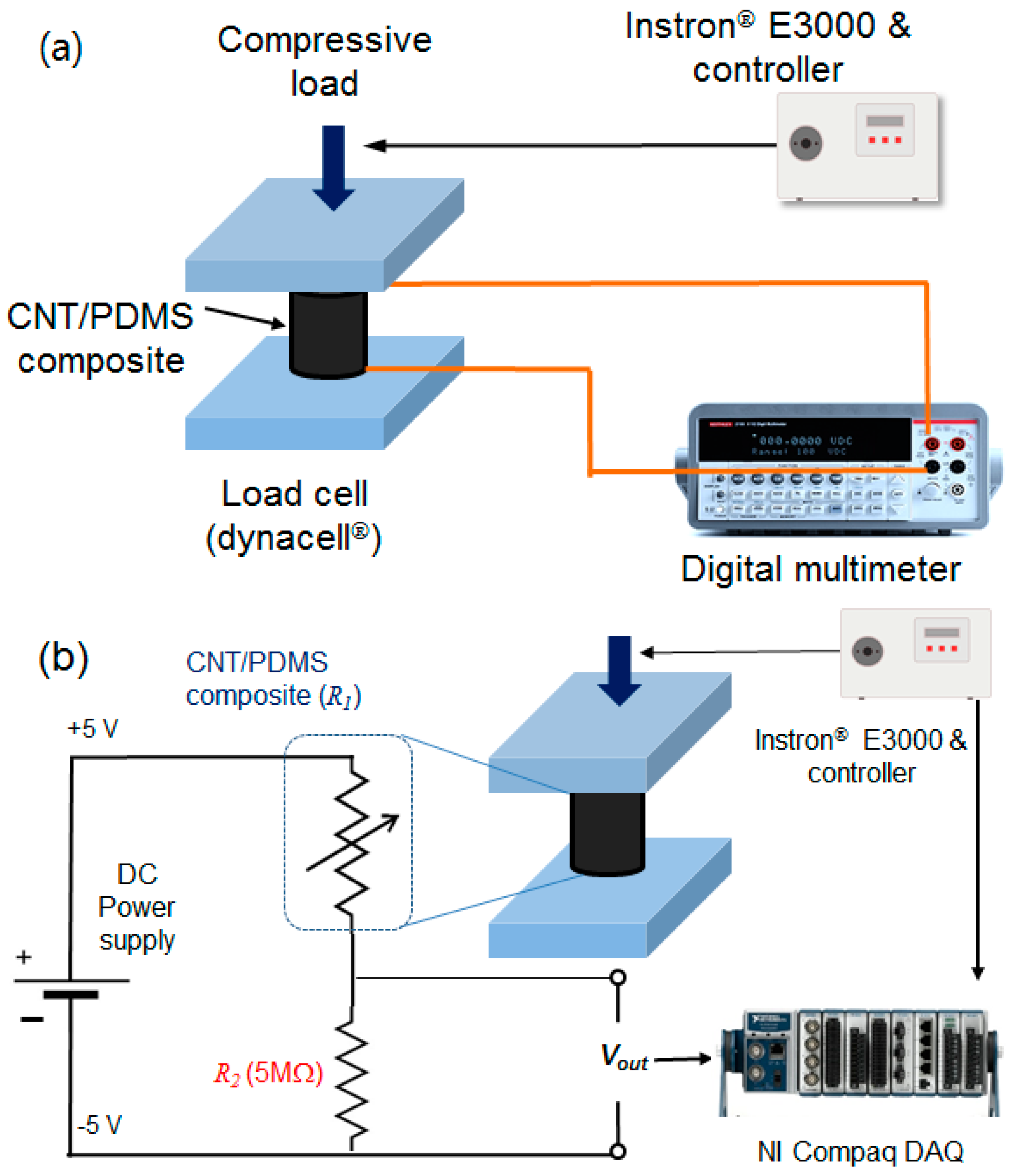
3.1. Experiment Set-Up
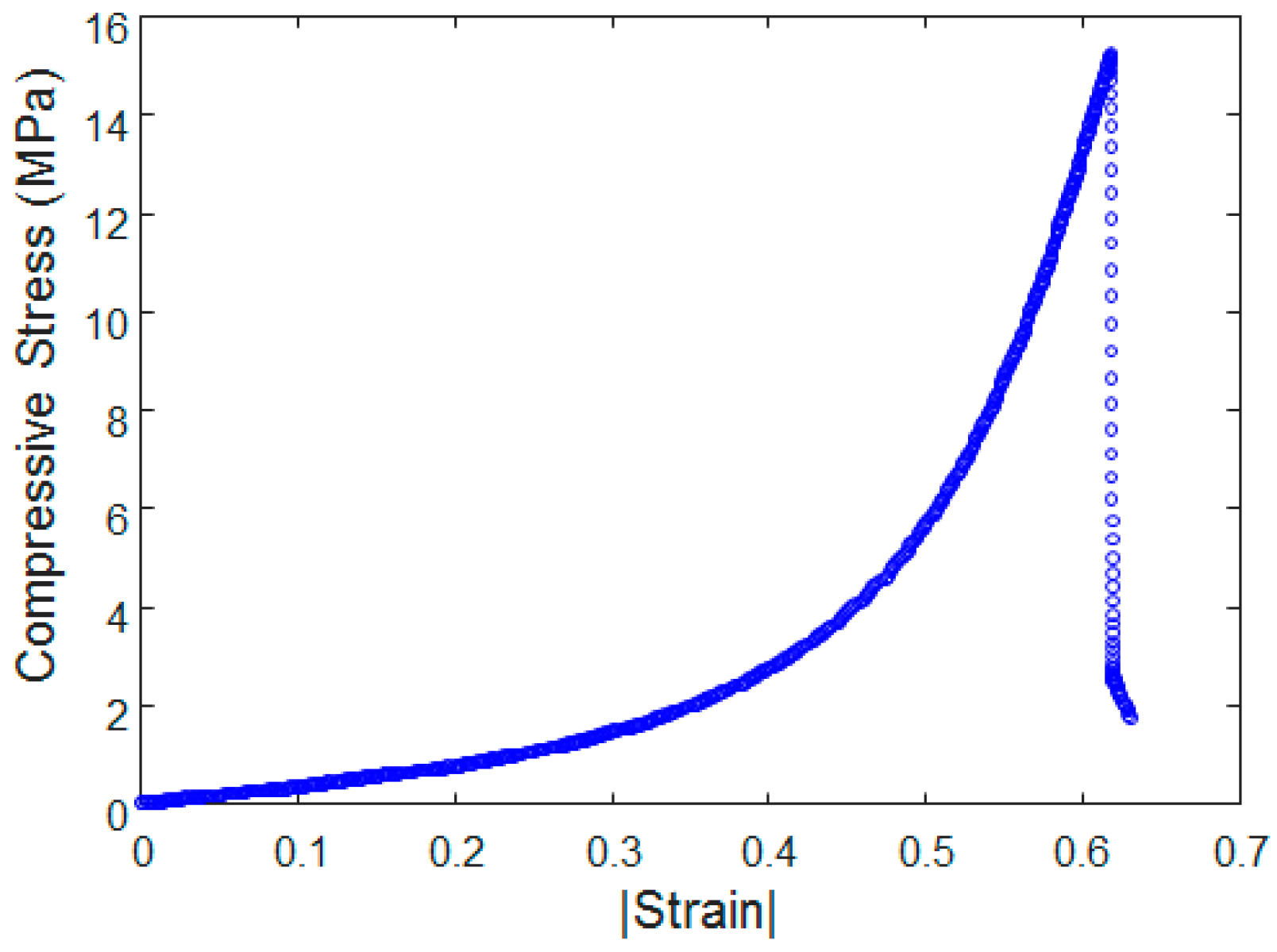
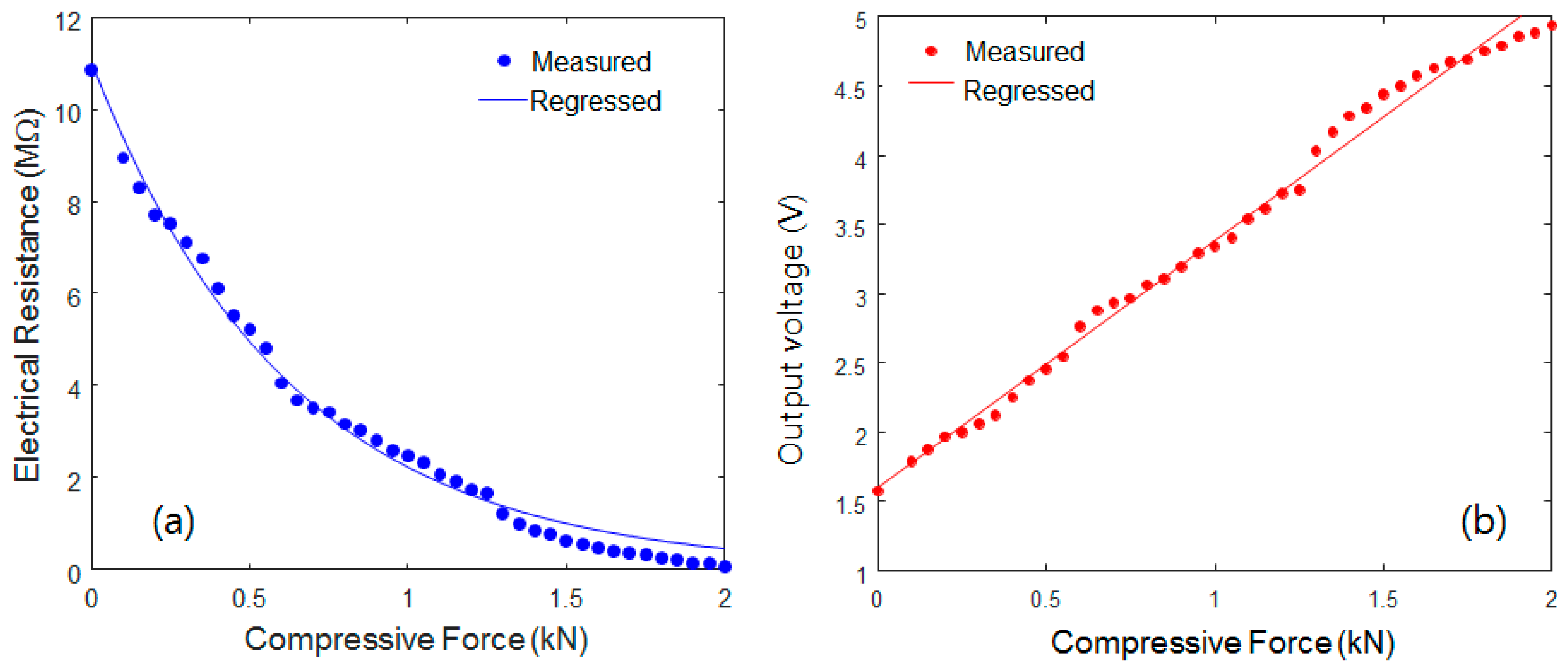
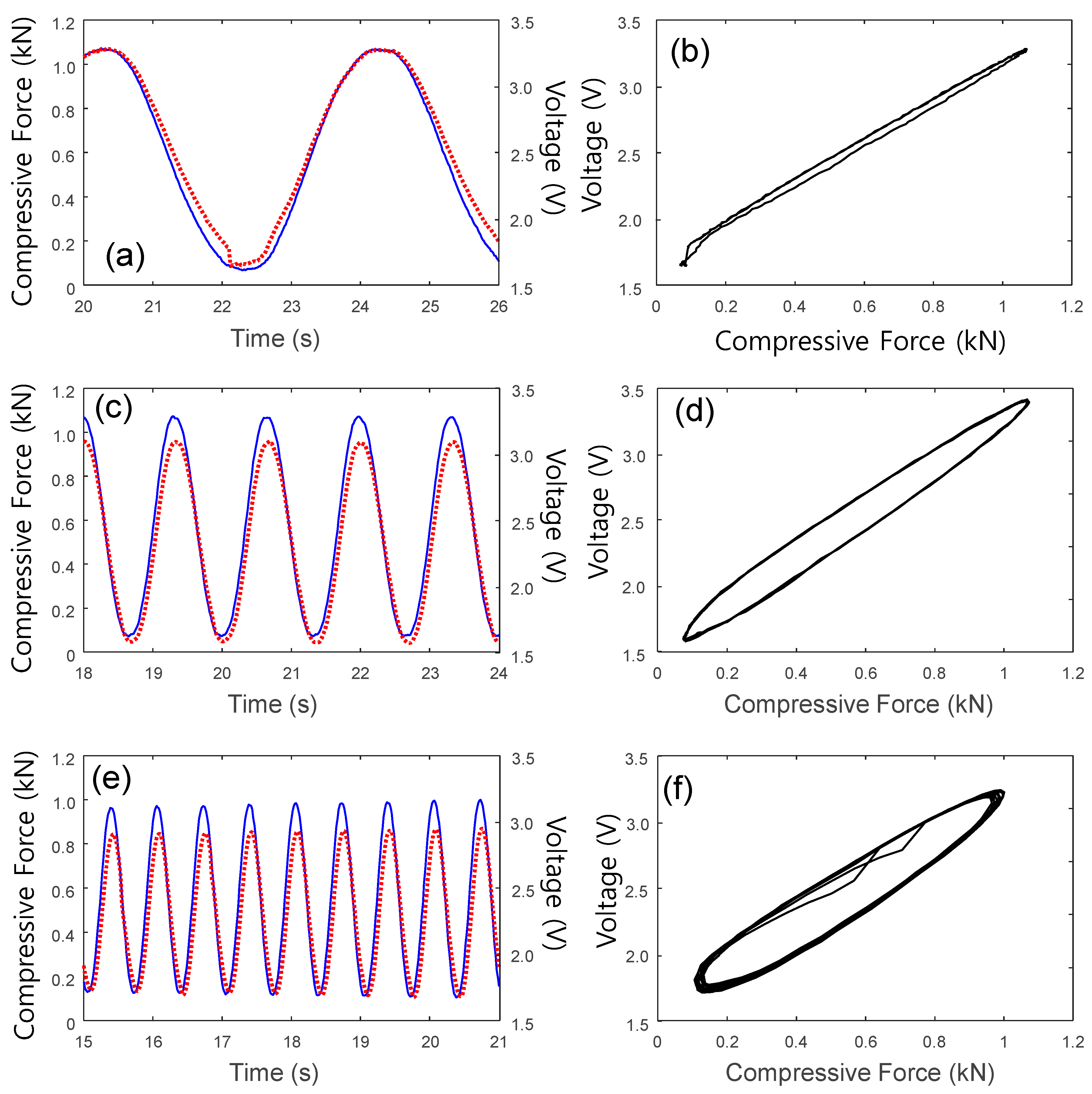
3.2. Results and Discussion
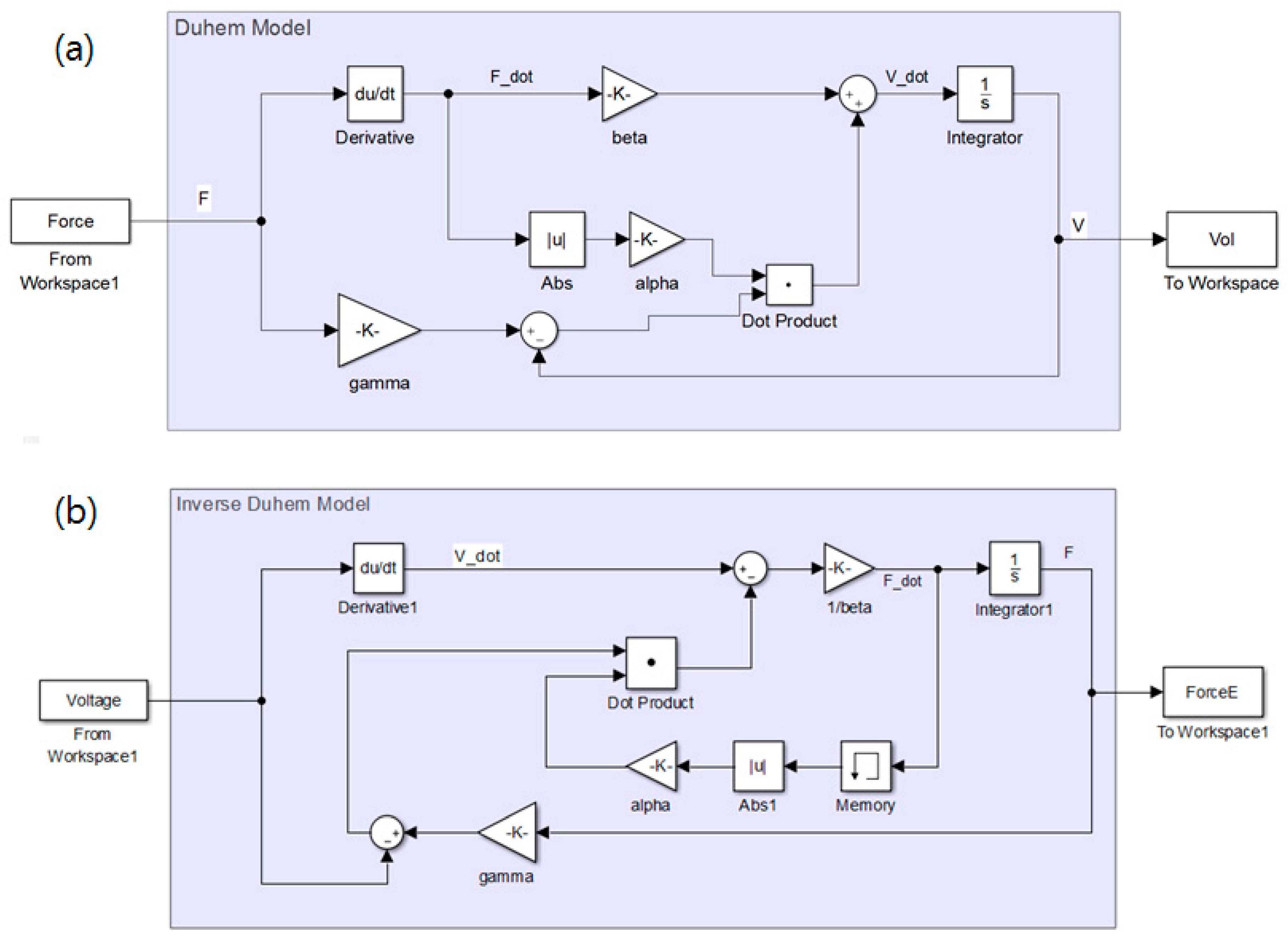
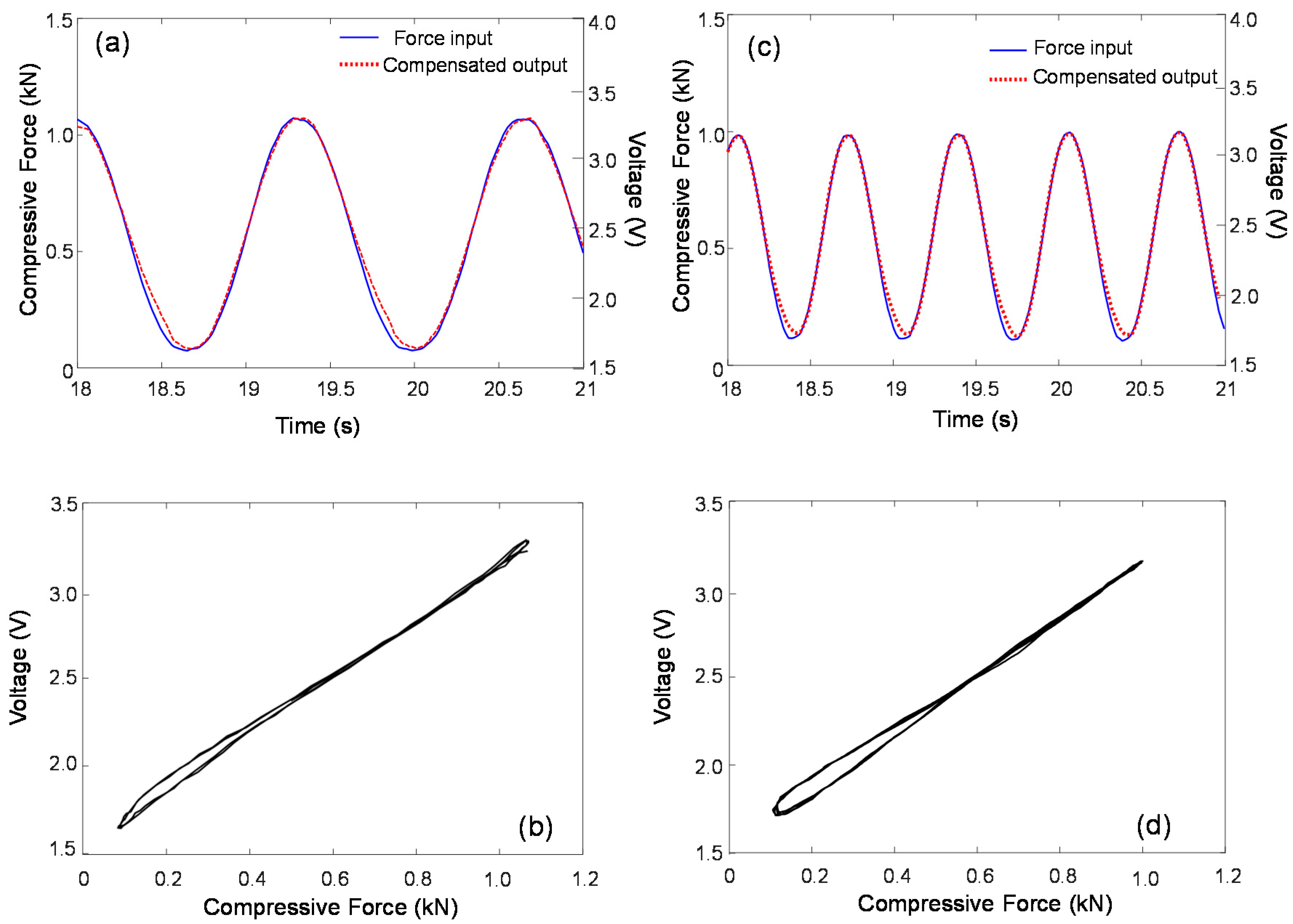
4. Frequency-Dependent Hysteresis Model and Compensation
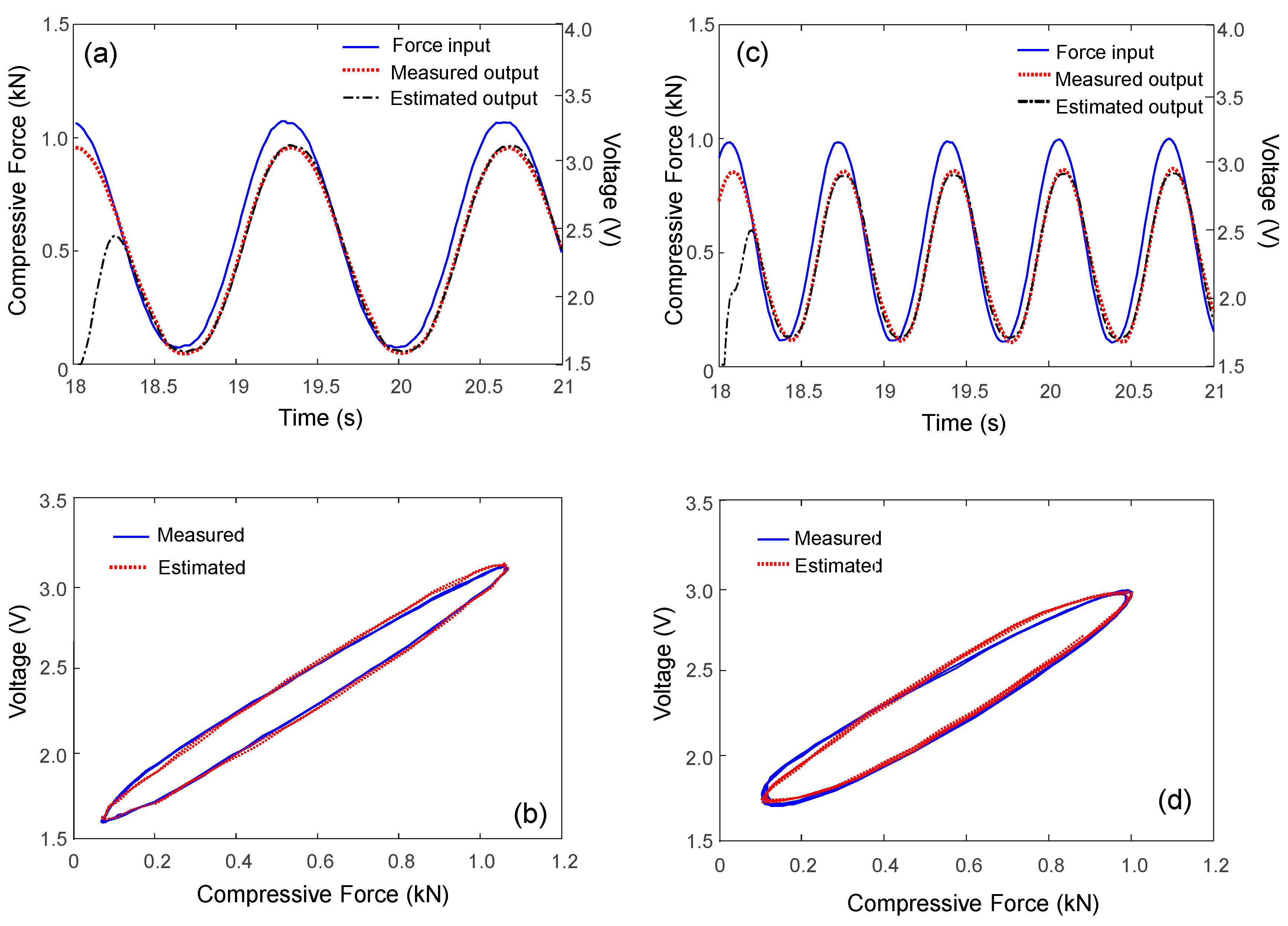
5. Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, C.; Thostenson, E.T.; Chou, T.-W. Sensors and actuators based on carbon nanotubes and their composites: A review. Compos. Sci. Technol. 2008, 68, 1227–1249. [Google Scholar] [CrossRef]
- Kim, Y.J.; Shin, T.S.; Choi, H.D.; Kwon, J.H.; Chung, Y.C.; Yoon, H.G. Electrical conductivity of chemically modified multiwalled carbon nanotube/epoxy composites. Carbon 2005, 43, 23–30. [Google Scholar] [CrossRef]
- Norkhairunnisa, M.; Azizan, A.; Mariatti, M.; Ismail, H.; Sim, L.C. Thermal stability and electrical behavior of polydimethylsiloxane nanocomposites with carbon nanotubes and carbon black fillers. J. Compos. Mater. 2011, 46, 903–910. [Google Scholar] [CrossRef]
- Yu, X.; Kwon, E. A carbon nanotube/cement composite with piezoresistive properties. Smart Mater. Struct. 2009, 18, 055010. [Google Scholar] [CrossRef]
- Cho, M.Y.; Kim, J.S.; Lee, H.G.; Choi, S.B.; Kim, G.W. Styrene-butadiene Rubber (SBR)/Carbon Nanotube-based Smart Force Sensor for Automotive Tire Deformation Monitoring. Proc. SPIE 2016, 9802. [Google Scholar] [CrossRef]
- Dang, Z.M.; Jiang, M.J.; Xie, D.; Yao, S.H.; Zhang, L.Q.; Bai, J. Supersensitive linear piezoresistive property in carbon nanotubes/silicone rubber nanocomposite. J. Appl. Phys. 2008, 104, 024114. [Google Scholar] [CrossRef]
- Yoon, H.; Jang, J. Conducting-polymer nanomaterials for high-performance sensor applications: Issues and challenges. Adv. Funct. Mater. 2009, 19, 1567–1576. [Google Scholar] [CrossRef]
- Sahoo, N.G.; Rana, S.; Cho, J.W.; Li, L.; Chan, S.H. Polymer nanocomposites based on functionalized carbon nanotubes. Prog. Polym. Sci. 2010, 35, 837–867. [Google Scholar] [CrossRef]
- Hu, N.; Fukunaga, H.; Atobe, S.; Liu, Y.; Li, J. Piezoresistive Strain Sensors Made from Carbon Nanotubes Based Polymer Nanocomposites. Sensors 2011, 11, 10691–10723. [Google Scholar]
- Lu, J.; Lu, M.; Bermak, A.; Lee, Y.-K. Study of Piezoresistance Effect of Carbon Nanotube-PDMS Composite Materials for Nanosensors. In Proceedings of the 7th IEEE International Conference on Nanotechnology, Hong Kong, China, 2–5 August 2007; pp. 1240–1243.
- Hu, C.H.; Liu, C.H.; Chen, L.Z.; Peng, Y.C.; Fan, S.S. Resistance-pressure sensitivity and a mechanism study of multiwall carbon nanotube networks/poly dimethylsiloxane composites. Appl. Phys. Lett. 2008, 93, 033108. [Google Scholar] [CrossRef]
- Liu, Y.; Sheng, Q.; Muftu, S.; Khademhosseini, A.; Wang, M.L.; Dokmeci, M.R. A stretchable and transparent SWNT strain sensor encapsulated in this PDMS films. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 1091–1094.
- Product Catalog. Available online: http://www.carbonnano.co.kr/ (accessed on 5 June 2016).
- Chu, K.; Kim, D.; Sohn, Y.; Lee, S.; Moon, C.; Park, S. Electrical and Thermal Properties of Carbon-Nanotube Composite for Flexible Electric Heating-Unit Applications. IEEE Electron Device Lett. 2013, 34, 668–670. [Google Scholar] [CrossRef]
- Stassi, S.; Cauda, V.; Canavese, G.; Pirri, C.F. Flexible Tactile Sensing Based on Piezoresistive Composites: A Review. Sensors 2014, 14, 5296–5332. [Google Scholar] [CrossRef] [PubMed]
- Cho, M.-Y.; Kim, J.-S.; Kim, G.-W. Piezoresistive Behavior of a Carbon Nanotube/Synthetic Rubber-based Nanocomposite. In Proceedings of the 10th Asian-Australasian Conference on Composite Materials, Busan, Korea, 16–19 October 2016. Poster No. 1-54.
- Hu, N.; Karube, Y.; Yan, C.; Masuda, Z.; Fukunaga, H. Tunneling effect in a polymer/carbon nanotube nanocomposite strain sensor. Acta Mater. 2008, 56, 2929–2936. [Google Scholar] [CrossRef] [Green Version]
- Yin, G.; Hu, N.; Karube, Y.; Liu, Y.; Li, Y.; Fukunaga, H. A carbon nanotube/polymer strain sensor with linear and anti-symmetric piezoresistivity. J. Compos. Mater. 2011, 45, 1315–1323. [Google Scholar]
- Adriaens, H.J.M.T.S.; De Koning, W.L.; Banning, R. Modeling Piezoelectric Actuators. IEEE/ASME Trans. Mechatron. 2000, 5, 331–341. [Google Scholar] [CrossRef]
- MATLAB/Signal Processing Toolbox™ V7.6 User’s Guide; The Mathworks: Natick, MA, USA, 2008.
- Xiong, Y.; Tuononen, A. A laser-based sensor system for tire tread deformation measurement. Meas. Sci. Technol. 2014, 25, 115103. [Google Scholar] [CrossRef]
- Kim, G.-W. Tire with Conductive Tread and In-Situ Measuring Method of Tire Tread Deformation. Korea Patent No. 10-2016-0037065, 2017. pending. [Google Scholar]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-S.; Kim, G.-W. Hysteresis Compensation of Piezoresistive Carbon Nanotube/Polydimethylsiloxane Composite-Based Force Sensors. Sensors 2017, 17, 229. https://doi.org/10.3390/s17020229
Kim J-S, Kim G-W. Hysteresis Compensation of Piezoresistive Carbon Nanotube/Polydimethylsiloxane Composite-Based Force Sensors. Sensors. 2017; 17(2):229. https://doi.org/10.3390/s17020229
Chicago/Turabian StyleKim, Ji-Sik, and Gi-Woo Kim. 2017. "Hysteresis Compensation of Piezoresistive Carbon Nanotube/Polydimethylsiloxane Composite-Based Force Sensors" Sensors 17, no. 2: 229. https://doi.org/10.3390/s17020229
APA StyleKim, J.-S., & Kim, G.-W. (2017). Hysteresis Compensation of Piezoresistive Carbon Nanotube/Polydimethylsiloxane Composite-Based Force Sensors. Sensors, 17(2), 229. https://doi.org/10.3390/s17020229




