Wind Tunnel Measurements for Flutter of a Long-Afterbody Bridge Deck
Abstract
:1. Introduction
2. Aerodynamic Force Model
3. Wind Tunnel Test
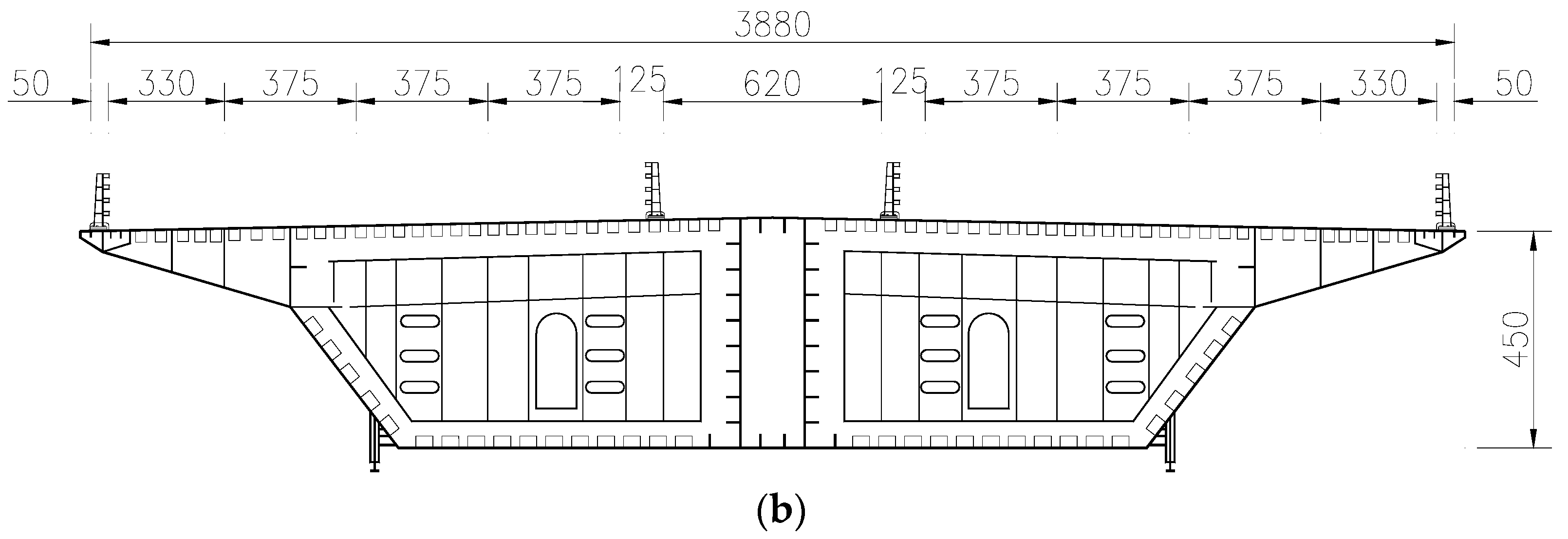
3.1. Bridge Overview
3.2. Static Force Measurement
3.3. Flutter Derivatives Test
3.4. Aeroelastic Test for Flutter Measurement
4. Result and Discussion
4.1. Aerodynamic Force
4.2. Flutter Derivatives
4.3. Critical Flutter Wind Speed
5. Concluding Remarks
- (1)
- The aerodynamic forces of the test models during the operation stage and the construction stage are different. This is ascribed to the effect of accessories installed in the operation stage. The maximum lift and moment force occurs at the wind attack angle of around .
- (2)
- The critical wind speeds determined from the observed flutter derivative measurements are acceptable. This suggests that the observed derivatives are reasonable and the calculating method for the critical flutter wind speeds (in Section 2) is applicable.
- (3)
- The critical wind speeds in the operation stage is smaller than those in the construction stage, which suggests that the flutter of the bridge deck in the operation stage is prone to occur. This could be ascribed to the effect of accessories in the operation stage.
- (4)
- The directly measured or identified wind speeds in the construction and the operation stages are much larger than the corresponding allowable values, which suggests that the flutter instability of the bridge is good.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jia, Z.; Ma, X.; Liu, W.; Lu, W.; Li, X.; Chen, L.; Wang, Z.; Cui, X. Pose measurement method and experiments for high-speed rolling targets in a wind tunnel. Sensors 2014, 14, 23933–23953. [Google Scholar] [CrossRef] [PubMed]
- López, A.; Molina-Aiz, F.D.; Valera, D.L.; Peña, A. Wind tunnel analysis of the airflow through insect-proof screens and comparison of their effect when installed in a mediterranean greenhouse. Sensors 2016, 16, 690. [Google Scholar] [CrossRef] [PubMed]
- Gu, M.; Zhang, R.; Xiang, H. Identification of flutter derivatives of bridge decks. J. Wind Eng. Ind. Aerodyn. 2000, 84, 151–162. [Google Scholar] [CrossRef]
- Ge, Y.; Xiang, H.; Tanaka, H. Application of a reliability analysis model to bridge flutter under extreme winds. J. Wind Eng. Ind. Aerodyn. 2000, 86, 155–167. [Google Scholar] [CrossRef]
- Gu, M.; Chang, C.; Wu, W.; Xiang, H. Increase of critical flutter wind speed of long-span bridges using tuned mass dampers. J. Wind Eng. Ind. Aerodyn. 1998, 73, 111–123. [Google Scholar] [CrossRef]
- Scanlan, R. The action of flexible bridges under wind, I: Flutter theory. J. Sound Vib. 1978, 60, 187–199. [Google Scholar] [CrossRef]
- Billah, K.Y.; Scanlan, R.H. Resonance, tacoma narrows bridge failure, and undergraduate physics textbooks. Am. J. Phys. 1991, 59, 118–124. [Google Scholar] [CrossRef]
- Scanlan, R.H. State-of-the-Art Methods for Calculating Flutter, Vortex-Induced, and Buffeting Response of Bridge Structures; Report FHWA/RD-80/050; U.S. Federal Highway Administration: Washington, DC, USA, 1981. [Google Scholar]
- Scanlan, R.H. On flutter and buffeting mechanisms in long-span bridges. Probab. Eng. Mech. 1988, 3, 22–27. [Google Scholar] [CrossRef]
- Chen, X.; Matsumoto, M.; Kareem, A. Aerodynamic coupling effects on flutter and buffeting of bridges. J. Eng. Mech. 2000, 126, 17–26. [Google Scholar] [CrossRef]
- Diana, G.; Falco, M.; Bruni, S.; Cigada, A.; Larose, G.; Darnsgaard, A.; Collina, A. Comparisons between wind tunnel tests on a full aeroelastic model of the proposed bridge over stretto di messina and numerical results. J. Wind Eng. Ind. Aerodyn. 1995, 54, 101–113. [Google Scholar] [CrossRef]
- Kwok, K.C.S.; Qin, X.; Fok, C.; Hitchcock, P.A. Wind-induced pressures around a sectional twin-deck bridge model: Effects of gap-width on the aerodynamic forces and vortex shedding mechanisms. J. Wind Eng. Ind. Aerodyn. 2012, 110, 50–61. [Google Scholar] [CrossRef]
- Scanlan, R.H.; Tomo, J. Air foil and bridge deck flutter derivatives. J. Soil Mech. Found. Div. 1971, 97, 1717–1737. [Google Scholar]
- BogunovićJakobsen, J.; Hjorth-Hansen, E. Determination of the aerodynamic derivatives by a system identification method. J. Wind Eng. Ind. Aerodyn. 1995, 57, 295–305. [Google Scholar] [CrossRef]
- Zasso, A.; Cigada, A.; Negri, S. Flutter derivatives identification through full bridge aeroelastic model transfer function analysis. J. Wind Eng. Ind. Aerodyn. 1996, 60, 17–33. [Google Scholar] [CrossRef]
- Chowdhury, A.G.; Sarkar, P.P. A new technique for identification of eighteen flutter derivatives using a three-degree-of-freedom section model. Eng. Struct. 2003, 25, 1763–1772. [Google Scholar] [CrossRef]
- Gu, M.; Qin, X.-R. Direct identification of flutter derivatives and aerodynamic admittances of bridge decks. Eng. Struct. 2004, 26, 2161–2172. [Google Scholar] [CrossRef]
- Xu, F.Y.; Chen, A.R.; Wang, D.L. Pursuit method for searching critical flutter wind velocity of flat plates. Eng. Mech. 2005, 22, 48–53. [Google Scholar]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter; NASA Technical Reports Server (NTRS): Washington, DC, USA, 1949. [Google Scholar]
- Chen, A.; He, X.; Xiang, H. Identification of 18 flutter derivatives of bridge decks. J. Wind Eng. Ind. Aerodyn. 2002, 90, 2007–2022. [Google Scholar] [CrossRef]
- Xu, F.Y.; Chen, A.R.; Zhang, Z.; Wang, D.L. Practical technique for determining critical flutter wind speed of bridge model. J. Vib. Shock 2008, 12, 024. [Google Scholar]
- Lo, K.H.; Kontis, K. Static and wind-on performance of polymer-based pressure-sensitive paints using platinum and ruthenium as the luminophore. Sensors 2016, 16, 595. [Google Scholar] [CrossRef] [PubMed]
- Schotzko, T.; Lang, W. Embedded strain gauges for condition monitoring of silicone gaskets. Sensors 2014, 14, 12387–12398. [Google Scholar] [CrossRef] [PubMed]
- Park, H.S.; Kim, J.Y.; Kim, J.G.; Choi, S.W.; Kim, Y. A new position measurement system using a motion-capture camera for wind tunnel tests. Sensors 2013, 13, 12329–12344. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kwok, K.; Melbourne, W.H. Wind-induced lock-in excitation of tall structures. J. Struct. Div. 1981, 107, 57–72. [Google Scholar]
- Kwok, K.; Melbourne, W. The effects of freestream turbulence on a galloping square tower. In Proceedings of the 6th Australasian Hydraulics and Fluid Mechanics Conference, Adelaide, South Australia, Australia, 5–9 December 1977.
- Poulsen, N.K.; Damsgaard, A.; Reinhold, T.A. Determination of flutter derivatives for the great belt bridge. J. Wind Eng. Ind. Aerodyn. 1992, 41, 153–164. [Google Scholar] [CrossRef]
- Xiang, H.; Bao, W.; Chen, A.; Lin, Z.; Liu, J. Wind-Resistant Design Specification for Highway Bridges; Ministry of Communications of the People’s Republic of China: Beijing, China, 2004. [Google Scholar]











| Parameters | Units | Scale Ratios | Prototype | Required Value | Test Value | Errors (%) | |
|---|---|---|---|---|---|---|---|
| Dimensions | Height | m | 1/50 | 4.5 | 0.09 | 0.09 | 0 |
| Width | m | 1/50 | 38.8 | 0.776 | 0.776 | 0 | |
| Mass per unit length | kg/m | 1/502 | 34,754 | 13.092 | 13.89 | 6.1 | |
| Mass moment of inertia per unit length | kg·m2/m | 1/504 | 3681,159 | 0.589 | 0.586 | 0.5 | |
| Radius of gyration | m | 1/50 | 10.29 | 0.2058 | 0.2054 | 0.07 | |
| Fundamental frequency | Bending | Hz | 5.464 | 0.5162 | 2.821 | 2.82 | 0.04 |
| Torsion | Hz | 5.476 | / | / | 0.32 | / | |
| Damping ratio | Bending | % | 1 | 1.0782 | 5.9 | 5.91 | 0.17 |
| Torsion | % | 1 | / | / | 0.32 | / | |
| Wind Attack Angles (°) | Construction Stage (m/s) | Operation Stage (m/s) | ||||
|---|---|---|---|---|---|---|
| Directly Measured | Identified | Allowable Value | Directly Measured | Identified | Allowable Value | |
| +5 | / | 275.4 | 66.2 | 102.04 | 92.6 | 79.8 |
| +3 | >140 | 289.3 | 135.45 | 145.7 | ||
| 0 | >170 | 398.3 | >162.54 | 213.4 | ||
| −3 | >170 | 411.3 | >171.57 | 298.2 | ||
| −5 | / | 417.9 | >171.57 | 356.6 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.-S.; Zhang, C.; Wang, X.; Ma, C.-M. Wind Tunnel Measurements for Flutter of a Long-Afterbody Bridge Deck. Sensors 2017, 17, 335. https://doi.org/10.3390/s17020335
Chen Z-S, Zhang C, Wang X, Ma C-M. Wind Tunnel Measurements for Flutter of a Long-Afterbody Bridge Deck. Sensors. 2017; 17(2):335. https://doi.org/10.3390/s17020335
Chicago/Turabian StyleChen, Zeng-Shun, Cheng Zhang, Xu Wang, and Cun-Ming Ma. 2017. "Wind Tunnel Measurements for Flutter of a Long-Afterbody Bridge Deck" Sensors 17, no. 2: 335. https://doi.org/10.3390/s17020335
APA StyleChen, Z.-S., Zhang, C., Wang, X., & Ma, C.-M. (2017). Wind Tunnel Measurements for Flutter of a Long-Afterbody Bridge Deck. Sensors, 17(2), 335. https://doi.org/10.3390/s17020335






